Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
Water SA
versión On-line ISSN 1816-7950
versión impresa ISSN 0378-4738
Water SA vol.47 no.2 Pretoria abr. 2021
http://dx.doi.org/10.17159/wsa/2021.v47.i2.10923
TECHNICAL NOTE
Parameters to characterize the internal recirculation of an oxidation ditch
Shao Po WangI, II, III; Jing Jie YuI, II, III; Hua Ji MaI, II, III
ITianjin Key Laboratory of Aquatic Science and Technology, Tianjin Chengjian University, Tianjin 300384, China
IISchool of Environmental & Municipal Engineering, Tianjin Chengjian University, Tianjin 300384, China
IIIMunicipal Experimental Teaching Demonstration Center of Environmental and Municipal Engineering, Tianjin Chengjian University, Tianjin 300384, China
ABSTRACT
Mixed liquor circulates ceaselessly in the closed-loop corridor in an oxidation ditch (OD), which is significantly different from other wastewater treatment processes. The internal recirculation ratio (IRR), i.e., the ratio between circulation flow rate (QCC) and influent flow rate (QJ, and the circulatory period (T), i.e. the time consumed for the mixed liquor to complete one lap in the circular corridor, was used to quantify the internal recirculation characteristics of the OD system. In order to elucidate the characteristics and applicability of IRR and T, this study obtained the numerical relationship between IRR and T by formula derivation. It also discusses the factors influencing IRR and analyses the applications of IRR and T. The results showed that IRR = QCC/QIn = HRT/T = HRT · IRF (HRT = hydraulic retention time of the mixed liquor in the circular corridor; IRF = internal recirculation frequency). Moreover, three kinds of parameters had an effect on IRR: QIn; reactor dimensions, i.e., length (Lmid), width (ß), and height (H) of the circular corridor; and horizontal velocity of the mixed liquor in the circular corridor (v). QInchanged IRR by altering HRT. However, B, H, Lmid, and v changed IRR by altering IRF and T. Furthermore, the same IRR corresponded to many different HRT and IRF. Therefore, when QIn and QCC varied in the OD system, using HRT and IRF to evaluate the variation of QIn and QCC, respectively, was better than using IRR to evaluate their synthetical variation. IRF and T were useful for directly and precisely characterizing the circulation speed and circulation flow rate in the circular corridor, while IRR was more useful for evaluating the dilution effect of reflux on influent.
Keywords: Oxidation Ditch; Hydraulic Retention Time; Internal Recirculation Ratio; Circulatory Period; Internal Recirculation Frequency
INTRODUCTION
The oxidation ditch (OD) is a kind of sewage treatment technology widely used worldwide in wastewater treatment plants (WWTPs) (Wang et al., 2019a). The mixed liquor circulates ceaselessly in closed-loop corridors of the OD (Izadi et al. 2020), which is significantly different from other wastewater treatment processes. However, as the initial OD is only used for organic matter removal (Izadi et al., 2020), without consideration for nitrogen and phosphorus removal, dissolved oxygen (DO) is always uniformly and sufficiently supplied, so internal recirculation characteristics are never mentioned or used at the beginning of an OD application.
As stricter environmental protection requirements emerge, simultaneous nitrogen, phosphorus, and organic matter removal is required. Therefore, the OD technology is being developed continuously. By setting an anaerobic zone upstream from the circular corridor, biological phosphorus removal can be accomplished (Insel et al., 2005). Adjusting aeration devices in the circular corridor, spatial interval distribution of the aerobic and the anoxic zone can be performed, organic matter oxidation and nitrification can be achieved in the aerobic zone, and denitrification can be fulfilled in the anoxic zone. Optimization of the aerator operation (Insel et al., 2005; Alaya et al., 2010; Wei et al., 2016) and aeration mode (Chen et al., 2012; Guo et al., 2013; Zhou et al., 2015; Ratanatamskul and Kongwong, 2017) have been widely studied to improve nutrient removal efficiencies in the OD system.
A few researchers also began to study the internal recirculation characteristics of the OD system. The internal recirculation ratio (IRR), namely the ratio of circulation flow rate to influent flow rate in the circular corridor (Insel et al., 2005; Tang and Huang, 2006; Guo et al., 2013; Cakirgöz et al., 2021), is usually mentioned or used to study the influence of internal recirculation characteristics on nutrient removal performance of OD systems. For instance, Insel et al. (2005) mentioned that IRR was adjusted to 100, characterizing a high internal flow rate in an OD system. Guo et al. (2013) considered that a large IRR caused lower substrate concentration and denitrification rates. Tang and Huang (2006) calculated the required IRR for the effluent COD concentration to reach the expected results. Abusam et al. (2002) mentioned that the variation of horizontal velocity in the range of 0.25 to 0.60 m/s led the IRR to change from 60 to 120. Abusam et al. (2002) also considered that a high IRR affected the DO profile along the circular corridor, which consequently affected nutrient removal performance. According to the influent ammonia concentration and the expected effluent nitrate concentration, Argaman (1984) obtained a simplified formula of IRR in OD based on the requirement of nitrified mixed liquor needed to return to the anoxic zone during a traditional denitrification process. The internal recirculation period (7), i.e., the time taken for the mixed liquor to complete one lap in the circular corridor (Wang et al., 2019b), is another parameter that can characterize the internal recirculation of an OD system, and was occasionally used. For instance, based on the oxygen supply and demand balance and the invariable number of aerators, Chen et al. (2012) studied the effectiveness of a dual DO control technology in OD systems when Τ varies with the recirculation speed.
However, the numerical relationship between IRR and T has not been studied, and the characteristics and applications of IRR and T have not been considered either.
Therefore, in order to elucidate the characteristics and applicability of IRR and T, the numerical relationship between IRR and T, and the physical meanings of those parameters, were obtained by formula derivation in this study. Moreover, the influencing factors which could change IRR and T are discussed. Finally, the unfitness of IRR use was illustrated by an example.
Numerical relationship between IRR and T
As shown in Fig. 1, the arc part, at both ends of the circular corridor, was assumed to be a semicircle with a radius of B. Therefore, Eq. 1 was obtained:

where V is the effective volume of the circular corridor (m3); B is the width of the circular corridor (m); H is the effective water depth of the circular corridor (m); is the midline perimeter of the circular corridor, namely the length of the broken line shown in Fig. 1 (m); Lmid_lineis the straight-line segments of the midline perimeter (m); and Lmid_circleis the round segments of the midline perimeter (m).
The original definition of IRR in an oxidation ditch is the ratio of circulation flow rate to influent flow rate (Insel et al., 2005; Tang and Huang, 2006; Guo et al., 2013; Cakirgöz et al., 2021), so IRR could be described as Eq. 2:
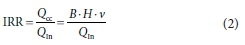
where Qcc is the circulation flow rate in the circular corridor (m3/d); is the inflow rate of the OD system (m3/d); and v is the horizontal velocity of the mixed liquor in the circular corridor (m/s).
Considering Eq. 3:

where HRT is the hydraulic retention time of the mixed liquor in the circular corridor (Tchobanoglous et al., 2003) (h); Eq. 3 could be rewritten as:

Placing Eq. 4 into Eq. 2:

Because:

where T is the circulation period, namely the time consumed for the mixed liquor to complete one lap in the circular corridor (h) (Wang et al., 2019b).
According to Wang et al. (2019b):
where IRF is the internal recirculation frequency, namely the laps performed by the mixed liquor in the circular corridor during 1 h (h-1) (Wang et al., 2019b).
Inserting Eq. 6 and Eq. 7 into Eq. 5:
Therefore, another physical meaning for IRR was obtained, namely the number of laps performed by the mixed liquor in the circular corridor during the hydraulic retention time.
V and Lmidwere always fixed, and and Qcc usually changed in the established full-scale OD system. So it can be known, from Eqs 6 and 7, that IRF and T directly and precisely characterized the circulation speed and circulation flow rate in the circular corridor. It can be concluded, from Eq. 2, that IRR didn't realize the role of IRF and T because of the simultaneous variation of QIn. Nevertheless, IRR was still more useful for evaluating the dilution effect of reflux on influent.
Analysis of influencing factors
According to the formulas deduced above, the physical aspects of IRR, IRF, and T, and their influencing factors, are summarized in Fig. 2.
It could be summarized from Fig. 2 that three kinds of parameters have an effect on IRR. One is the influent flow rate (QIn); the other is the dimensions of the circular corridor (B, H, and Lmid); and the third is the horizontal velocity of the mixed liquor in the circular corridor (v). The independent effects of the above influencing factors on HRT, IRF, T, and IRR under different conditions are listed in Table 1.
As shown in Table 1, for the established OD system, with variation of QIn, IRF and T do not change - only HRT and IRR change. Moreover, the numerical change of IRR was actually caused by the change of HRT, according to Eq. 8. Therefore, when varies, HRT is enough to evaluate the variation in nutrient removal performance of an OD system.
During the design of the OD system, the dimensions of the circular corridor (B, H, and Lmid) influenced the internal recirculation characteristics, which affected IRF, T and IRR. For the established OD system, the cross-sectional area (BH) and the horizontal velocity of the mixed liquor in the circular corridor (v) also affected the internal recirculation characteristics, which influenced IRF, T and IRR as well. Under these circumstances, the quantitative change in IRR was actually caused by the change in IRF and T, according to Eq. 8, so IRF or T were enough to evaluate the variation in internal recirculation characteristics and nutrient removal performance in the OD system.
Illustration of IRR's unfitness
In a full-scale WWTP with an OD system, QIn and QCCalways change. However, for the established OD system in which Β·Η and Lmld are fixed, the variation of QCC is only caused by the change of v. That is, even if QIn remains fixed, QCC still changes if v varies. When QIn varies, QCC remains constant if v remains fixed. Therefore, the following three situations were considered: QIn and QCC varied at the same time; only QIn changed; and only Qcc changed.
Simultaneous variation of QIn and QCC
The horizontal velocity in the OD system varies between 0.20 and 0.70 m/s, and the typical values are between 0.25 and 0.35 m/s (Liu et al., 2013). Therefore, it could be assumed that QIn fluctuated to 1.5QIn and 2QIn, at the same time that QCC changed to 1.5QCC and 2QCC. Therefore, IRR did not change because: IRR = QIn/QCC = 1.5QIn/1.5QCC = 2QIn/2QCC. Nevertheless, HRT varied to 0.67 HRT and 0.5 HRT, and IRF varied to 1.5 IRF and 2 IRF. Thus, under these circumstances, it could not be easily concluded that the nutrient removal performance of the OD did not change, similarly to the IRR.
Single variation of QIn
With a single change of QIn, both HRT and IRR varied. Therefore, HRT was enough to evaluate the variation of nutrient removal performance of the OD system.
Single variation of QCC
With a single change of QCC, both IRF and IRR varied. Therefore, IRF or T were enough to evaluate the variation of internal recirculation characteristics and nutrient removal performance of the OD system.
It can be concluded that the same IRR could correspond to many different HRT and IRF. So, when QIn and QCC varied at the same time, using HRT and IRF to evaluate the QInand QCCvariation, respectively, was better than using IRR to evaluate their synthetical variation. For the same reason, when QInor QCCvaried separately, using HRT or IRF to evaluate QInand QCCvariation, respectively, was better than using IRR.
CONCLUSION
The original definition of IRR in an oxidation ditch is the ratio of circulation flow rate to influent flow rate. By formulaic deduction, IRR = QCC/QIn = HRT/T = HRT-IRF. Based on this, a second physical meaning of IRR was obtained, which was the number of laps performed by the mixed liquor in the circular corridor during the hydraulic retention time.
Three kinds of parameters had an effect on IRR. The influent flow rate (QIn), the dimensions of the circular corridor (Β, Η and Lmid), and the horizontal velocity of the mixed liquor in the circular corridor (v). QIn changed IRR by altering HRT, but Β, H, Lmid, and v changed IRR by altering IRF and T. Moreover, the same IRR could correspond to many different HRT and IRF. Therefore, when QInand QCCvaried in the OD system, using HRT and IRF to evaluate the variation of QIn and QCC, respectively, was better than using IRR to evaluate their synthetical variation.
IRF and T were useful for directly and precisely characterizing the circulation speed and circulation flow rate in the circular corridor. However, IRR didn't realize the role of IRF and T. Nevertheless, IRR was more useful for evaluating the dilution effect of reflux on influent.
ACKNOWLEDGEMENTS
This research work was financially supported by the National Natural Science Foundation of China (No. 51108299 and No. 51678388).
REFERENCES
ABUSAM A, KEESMAN KJ, SPANJERS H, VAN STRATEN G and MEINEMA K (2002) Effect of oxidation ditch horizontal velocity on the nitrogen removal process. Eur. Water Manage. Online 2002 1-8. [ Links ]
ALAYA SB, HAOUECH L, CHERIF H and SHAYEB H (2010) Aeration management in an oxidation ditch. Desalination 252 (1-3) 172-178. https://doi.org/10.1016/j.desal.2009.11.001 [ Links ]
ARGAMAN Y (1984) Single sludge nitrogen removal in an oxidation ditch. Water Res. 18 (12) 1493-1500. https://doi.org/10.1016/0043-1354(84)90123-4 [ Links ]
CAKIRGÖZ M, BAYRAKDAR A and CALLI B (2021) How do the influent COD/Nitrogen and internal recirculation ratios affect the oxidation ditch type pre-anoxic landfill leachate treatment?. J. Environ. Manage. 278 (2) 111598. https://doi.org/10.1016/j.jenvman.2020.111598 [ Links ]
CHEN X, FUJIWARA T, NAKAMACHI K, KAWAGUCHI Y, NISHIMURA F and OHTOSHI K (2012) Evaluation of a novel oxidation ditch system with dual DO control technology for biological nutrient removal by mass balance analysis. Desalination 286 (1) 24-33. https://doi.org/10.1016/j.desal.2011.10.032 [ Links ]
GUO CZ, FU W, CHEN XM, PENG DC and JIN PK (2013) Nitrogen-removal performance and community structure of nitrifying bacteria under different aeration modes in an oxidation ditch. Water Res. 47 (4) 3845-3853. https://doi.org/10.1016/j.watres.2013.04.005 [ Links ]
INSEL G, ARTAN N and ORHON D (2005) Effect of aeration on nutrient removal performance of oxidation ditch system. Environ. Eng. Sci. 22 (6) 802-814. https://doi.org/10.1089/ees.2005.22.802 [ Links ]
IZADI P, IZADI P and ELDYASTI A (2020) Design, operation and technology configurations for enhanced biological phosphorus removal (EBPR) process: a review. Rev. Environ. Sci. Bio/Technol. 19 561-593. https://doi.org/10.1007/s11157-020-09538-w [ Links ]
LIU Y, SHI H, WANG Z, FAN L and SHI H (2013) Approach to enhancing nitrogen removal performance with fluctuation of influent in an oxidation ditch system. Chem. Eng. J. 219 520-526. https://doi.org/10.1016/jxej.2012.09.085 [ Links ]
RATANATAMSKUL C and KONGWONG J (2017) Impact of intermittent aeration mode on enhancement of biological nutrient removal by the novel prototype IT/OD-MBR (Inclined Tube/ Oxidation-Ditch Membrane Bioreactor) for high-rise building's wastewater recycling. Int. Biodeterioration Biodegrad. 124 36-44. https://doi.org/10.1016/j.ibiod.2017.06.005 [ Links ]
TANG LH and HUANG M (2006) Discussion of circulation ratio of oxidation ditch. Water Purif. Technol. 25 (4) 58-61. [ Links ]
TCHOBANOGLOUS G, BURTON FL and STENSEL HD (2003) Wastewater Engineering: Treatment and Reuse (4th edn). Metcalf and Eddy Inc. and McGraw Hill, New York. [ Links ]
WANG X, CHEN T, JIN P, ZHANG A, GAO C, QI X and ZHANG Y (2019a) Enhanced total nitrogen removal performance in a full scale Orbal oxidation ditch by a novel step aeration mode. Bioresour. Technol. 294 122228. https://doi.org/10.1016/j.biortech.2019.122228 [ Links ]
WANG SP, YU JJ, SU FK, GAO F and SUN LP (2019b) Particular internal recirculation frequency scope for enhancing denitrifying phosphorus removal in an oxidation ditch. Water Sci. Technol. 80 (1) 191-202. https://doi.org/10.2166/wst.2019.265 [ Links ]
WEI W, BAI Y and LIU Y (2016) Optimization of submerged depth of surface aerators for a carrousel oxidation ditch based on large eddy simulation with Smagorinsky model. Water Sci. Technol. 73 (7) 1608-1618. https://doi.org/10.2166/wst.2015.638 [ Links ]
ZHOU X, HAN Y and GUO X (2015) Identification and evaluation of SND in a full-scale multi-channel oxidation ditch system under different aeration modes. Chem. Eng. J. 259 (2015) 715-723. https://doi.org/10.1016/j.cej.2014.07.133 [ Links ]
 Correspondence:
Correspondence:
Jing Jie Yu
Email: Yjj.mary@yahoo.com; Yjj.mary@163.com
Received: 20 November 2019
Accepted: 15 April 2020














