Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Water SA
On-line version ISSN 1816-7950
Print version ISSN 0378-4738
Water SA vol.47 n.2 Pretoria Apr. 2021
http://dx.doi.org/10.17159/wsa/2021.v47.i2.10916
RESEARCH PAPER
Integration of ANFIS with PCA and DWT for daily suspended sediment concentration prediction
Nguyen Mai DangI; Duong Tran AnhII
IThuyloi University, 175 Tay Son Street, Dong Da district, Hanoi, Vietnam
IIHo Chi Minh City University of Technology (HUTECH), 475A Bien Bien Phu street, Binh Thanh District, Ho Chi Minh City, Vietnam
ABSTRACT
Quantifying sediment load is vital for aquatic and riverine biota and has been the subject of various environmental studies since sediment plays a key role in maintaining ecological integrity, river morphology and agricultural productivity. However, predicting sediment concentration in rivers is difficult because of the non-linear relationships of flow rates, geophysical characteristics and sediment loads. It is thus very important to propose suitable statistical methods which can provide fast, accurate and robust prediction of suspended sediment concentration (SSC) for management guidance. In this study, we developed coupled models of discrete wavelet transform (DWT) with adaptive neuro-fuzzy inference system (ANFIS), named DWT-ANFIS, and principal component analysis (PCA) with ANFIS, named PCA-ANFIS, for SSC time-series modeling. The coupled models and single ANFIS model were trained and tested using long-term daily SSC and river discharge which were measured on the Schuylkill and Iowa Rivers in the United States. The findings showed that the PCA-ANFIS performed better than the single ANFIS and the coupled DWT-ANFIS. Further applications of the PCA-ANFIS should be considered for simulation and prediction of other indicators relating to weather, water resources, and the environment.
Keywords: machine learning; Schuylkill River; Iowa River; suspended sediment
INTRODUCTION
Monitoring and predicting suspended sediment concentration (SSC) in river systems is important for ecological conservation, sustainable livelihood protection, and aquatic and agricultural production (Madsen et al., 2001; Naiman et al., 2010; Dang et al., 2018). River erosion and sediment pollution, among the topmost environmental problems related to sediment fluxes, are also of concern to water resource engineers and policy makers. Nevertheless, the sediment concentration varies largely with time and space and is driven by turbulent currents (Walling, 1983). The recent development of manmade structures like reservoirs strongly obstructs the natural pattern of sediment transport (Kondolf et al., 2018). Sediment modeling is thus pivotal for guiding management.
In the past, numerous studies of sediment processes have been conducted by using numerical modeling and statistical methods. Coupled hydrodynamic and sediment models have been used to assess the large-scale impact of water infrastructure development and sealevel rise on sedimentation (Paiva et al., 2011; Dang, 2018). Process-based hydrodynamic models could also simulate the diffusion of sediment concentration in three-dimensional space based on different physical equations, but to a much smaller extent (Wu et al., 2000). However, because there are many obscure parameters related to sediment transport, the governing equations of these process-based hydrodynamic models might not fully represent the complex processes. Besides process-based modeling, time-series models (e.g., auto-regressive integrated moving average and multi-linear regression) could also be predicted by using sediment concentration. Nevertheless, the mentioned models are linear models which require stationary data and which are unable to capture the non-linearity of processes.
Simple statistical methods were then replaced by more sophisticated machine-learning approaches because of their capability in capturing non-linear behaviour (e.g. Choi and Seo, 2018; Valero and Bung, 2018). Among these techniques, artificial neural networks (ANN) and ANFIS have successfully been employed in various fields, especially water resources (Rajaee, 2011). Zhu et al. (2007) applied the ANN model to simulate monthly suspended sediment fluxes in the Longchuanjiang River basin. The results exhibited that the ANN model could simulate the target variable with fairly good accuracy, considering all environmental factors and a dataset of the previous 3 months' sediment concentrations. To predict suspended sediment load (SSL), the butterfly optimization algorithm (BOA) and the genetic algorithm (GA) were incorporated with machine learning models by Fadaee et al. (2020). They concluded that the BOA is superior to the GA in improving the performance of the learning process. Kisi et al. (2009) stated that the adaptive neuro-fuzzy (ANF) has the best performance compared to other models in suspended sediment prediction. The performance of these AI-based methods could then be further enhanced with pre-processing methods to reduce noise in the input data.
Due to the stochastic nature of hydrodynamic processes, data pre-processing might allow machine-learning models to handle non-stationary data adequately. Recently, many scholars have paid attention to combined methods, such as the hybrid wavelet-ANN and hybrid wavelet-ANFIS models (Kaveh et al., 2017). These hybrid models have a good performance when employed individually in water resources and environmental management problems. For drought prediction, Kim and Valdés (2003) applied the wavelet-ANN model in Mexico, while this method was also proposed for a case study in Italy (Cannas et al., 2005). The coupled wavelet-autoregressive models were applied to predict annual rainfall by Tantanee et al. (2005). Improvement of the ANN model performance by using continuous and discrete wavelet transform were presented by Cannas et al. (2006). Zounemat-Kermani et al. (2018) used different data-driven methods (ANN, ANFIS), and wavelet neural network to evaluate the incipient motion velocity of bed sediments. The results show that the wavelet neural network model yields better results compared to other methods. These methods presented that the ANN model combined with pre-processing methods can improve significantly improve model performance. To predict suspended sediment concentration, the hybrid wavelet-neuro fuzzy (NF) model was applied to a case study in the USA by Rajaee (2010). The results indicated that the proposed model had a better performance than other models. The PCA method is one of the popular data-processing methods that was used to convert the possibly correlated data into linearly uncorrelated data (principal components). In so doing, this method helped to reduce data dimensions. To predict SSL and BL, Zounemat-Kermani et al. (2020) indicated that the integrative ML model has outstanding performance compared to standalone ANFIS and SVR.
In this paper, the hybrid models PCA, DWT and ANFIS were applied to predict SSC. The purpose of combining the PCA and ANFIS model is to enhance the accuracy of SSC prediction by removing redundant data. Statistical performance indeces were used to evaluate and compare the model performance of the PCA-ANFIS, DWT-ANFIS and traditional ANFIS. There are several published studies that have proposed and applied a hybrid of DWT-ANFIS or PCA-ANFIS in several fields like prediction of SSC (Bajirao et al., 2021; Alizadeh et al., 2017; Olyaie et al., 2015; Ehteram et al., 2019), groundwater level prediction (Seifi et al., 2020; Nourani et al., 2016), rainfall downscaling (Pham et al., 2019), and biochemical oxygen demand (Solgi et al., 2017). Therefore, the single application of DWT-ANFIS or PCA-ANFIS for SSC is not a new topic in the field of environment or hydrology. However, there is limited research that has been conducted to compare the performance of ANFIS model coupled with DWT and PCA for SSC prediction. This study intends to fill this gap and enrich the literature available to researchers considering to adopt such models for future studies.
Hydrometry stations and data analysis
The historical data were obtained from the gauging station in Schuylkill River (latitude: 40° 01' 41" N and longitude: 75° 13' 44" W and basin area: 4 739 km2, and the Iowa River (latitude: 41° 10' 48" N and longitude: 91° 10' 57" W and basin area: 32 372 km2) and presented in Fig. 1 (US Geological Survey (USGS)). The historical data were used for training (calibrate) and testing (validate) the proposed models.
Daily river discharge (Qt) and SSCt of gauging stations were obtained from the USGS website system (http://co.water.usgs.gov/sediment/seddatabase.cfm). For the Schuylkill River station, 83% of the data (1 January 1949 - 31 December 1952) and the remaining 17% of the data (1 January 1954 - 31 December 1955) were used for training and testing, respectively. For the Iowa River station, 5 years' data (January 1, 1979 - December 31, 1983) and 1 year's data (1 January 1984 - 31 December 1984) were used for the training and testing model, respectively. Figure 2 provides the historical daily discharge and SSC data.
The correlation between river discharge (Q) and SSC was computed to gain an appropriate input pattern for the proposed models. Table 1 shows that the correlation coefficients between SSCt and river discharge time-series at the Iowa River station were very low; however, they were high at the Schuylkill River station. This table also shows higher correlations between SSCt , SSCt-1, SSCt-2, and SSCt-3 in the Iowa River in comparison to the Schuylkill River. The input variables have different scales, units and ranges. To eliminate their dimensions and treat these equally for each variable, all input variables were pre-processed by scaling them by the following formula:

where xin: the rescaled value of variable i; xi: the original value; ximin : minimum of variable i; and ximax : the maximum of variable i.
METHODS
The single ANFIS model
The ANFIS model could be trained without the requirement for expert input due to the standard design of the ANFIS model (Jang, 1993). The introduction of a basic ANFIS is shown in Fig. 3. The network structure of the ANFIS model consists of nodes presented by a node function and links. Each node was presented by a node function with fixed or adjustable parameters.
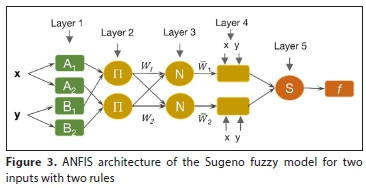
In a neural network, training phase processing aims to find the suitable value of parameters that fit the training data. The back-propagation method is well-known as one of the basic learning rules. This method tries to seek the minimum measure of error which presents as a sum of squared differences of outputs and desired outputs of the network (Kaya et al., 2002). Sugeno's system is one of three types of fuzzy inference systems. This system is the most commonly used, with a crisp output and is less time consuming (Takagi and Sugeno, 1993). There are two fuzzy IF/THEN rules in first-order Sugeno's system, which can be presented as (Sayed et al., 2003):
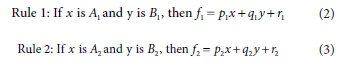
In Layer 1, each node produced membership grades of an input variable. The output of the ithnode could be calculated as the equation below by assuming that the membership function is a generalized bell function:
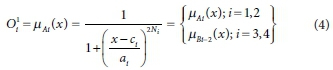
where x is input to node I; and {ai, cj, Ni} are adaptable variables.
Layer 2: Every node multiplied the incoming signals.
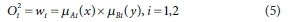
Layer 3: The ithnode was calculated by the normalized firing strengths as:
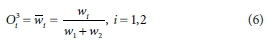
Layer 4: Node i calculated the contribution of the ithrule towards the model output and was computed by the following node function:
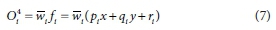
where, w is the output of Layer 3, and {pi, qi, ri} are parameters set which are referred to as consequent parameters.
Layer 5: The single node calculated the overall output of the ANFIS model (Jang and Sun, 1995).
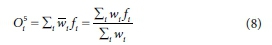
Discrete wavelet transform (DWT) analysis
The DWT approach is one ofthe time-dependent spectral analyses. Wavelet transform is a robust approach to capture the feature of a time-series and expose localized events in a non-stationary data series (Gupta and Gupta, 2007). When a time-series is considered as a linear combination of some base functions, WT was similar to the Fourier transform. The base functions were translations and dilation of one function called the mother wavelet.
In this study, the main concepts of the DWT approach are briefly presented, the readers can refer to Labat et al. (2000) for more detailed information on the theory and applications of WT. WT performed to decompose the target time-series data into a group of functions (Cohen and Kovacevic, 1996):
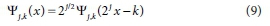
where, Ψ.(χ) is calculated from a mother wavelet Ψ(χ) which is dilated by j and translated by k, Ψ(χ) must satisfy the following condition:

The DW function of a signal f (x) can be calculated by the following equation:
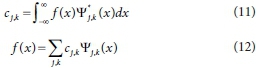
where, cj,kis the approximate coefficient of a signal. The Ψ(χ) is produced from the scaling function φ(χ) as:
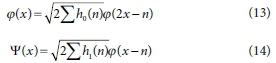
where, h1(n) = (-1)n h0(1 - n)
Principal component analysis (PCA)
PCA mathematically relies upon an eigenvector decomposition of the covariance matrix or correlation matrix of the process variables. The non-iterative partial least squares (NIPALS) algorithm was the first application for computing the principal components sequentially when there is a large number of variables. The number of major components offers an adequate explanation of the data and could be determined using several methods (Jackson, 1991). PCA could be used to decompose the data matrix X as the outer products and a residual matrix E:
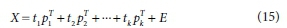
where k must be less than or equal to the smaller dimension of X, the t, vectors are identified as main component scores and include the relationship of the samples. The ptvectors are identified as loading and include information on the relationship of the variables. In the PCA decomposition, the p vectors are eigenvectors of the covariance matrix, i.e., for each pj:

where λ is the eigenvalue associated with the eigenvector pj. The tjform an orthogonal set (tTtj = 0 for i Φ j), while the pj are orthogonal (pTp. = 0 for j Φ j, pTpj = 1 for j = j). The xtand tt and P pair satisfy the equation below:

The score vector tt was defined by the linear combination of P and x. tjis the projection of X onto pj. li is represented by the pjand is a measure of the amount of variance.
Because the pjis in descending order of λi, the first pair captured the most information, and each subsequent pair captured the largest possible amount of variance at that step. The variance of each pair could be accumulated and compared with a given constant to identify the important components of all the pairs. The data could be sufficiently defined using fewer parameters than the original variables by using this PCA approach. This approach avoids loss of significant information and the issue of collinearity in the data. Once the number of important components is selected that adequately represents the original dataset, a regression can be performed to improve an inferential model. The selected important component scores were used in the PCA algorithm instead of using the original variables as inputs to the inferential model.
The DWT-ANFIS model
Q and SSC time-series are obtained to apply DWT-ANFIS. To develop the DWT-ANFIS model, first measured Q and SSC time-series were decomposed to multi-frequency time-series by DWT. The river discharge time-series were decomposed as Qd1(t), Qd2 (t), Qdjj(t); Q(ta) and SSC time-series were decomposed as SSCd1(t), SSCd2 (t), .„, SSCdj (t), SSC(ta). The dj is the decomposed time-series at jth level and a is the approximate time-series.
Then the decomposed Q and SSC time-series at different scales were inputted to the ANFIS method to predict the 1-day-ahead SSC. The mother wavelets were used to decompose the observed Q and SSC time-series at two decomposition levels (1 and 2). As an example, the Level 2 decomposition of the Q signal which yields 3 sub-signals (approximation at Level 2, and details 1, and 2) by coif1 wavelet are presented in Fig. 4 for the Schuylkill River Station.
The PCA-ANFIS model
In this study, the 1-day-ahead SSC was predicted by using the hybrid PCA-ANFIS approach, which is a combination of the PCA and the adaptive neuro-fuzzy inference system (ANFIS) model. The transparent modeling of fuzzy logic was promoted by incorporating the neuro-fuzzy model and the pattern recognition capabilities of neural networks. To emulate a complex (nonlinear) and multi-dimensional mapping function, a mean of training a family of membership functions was offered in the form of the neuro-fuzzy approach. The PCA algorithm was combined with the inferential model architecture to deal with the multi-collinearity problem within the process data.
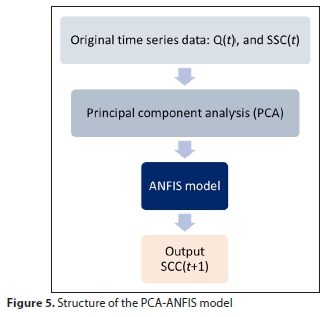
Due to a complex of interrelated variables, the central idea of PCA was applied to decrease the dimensionality of a dataset; however, this model could retain the diversity of variables in the original dataset (Jolliffe, 1986). This was gained by transforming to a new set of variables which were presented as principal components (PCs). The new set of variables were uncorrelated and ordered. The first few preserve almost all of the variation in the original variables. When using the PCA initialization model, the process data could be maintained sufficiently with fewer parameters than the original variables. To develop a correlation model, the regression could be performed once the number of principal components was selected to sufficiently represent the features of the original dataset. The selected principal components from the PCA algorithm were used instead of the original variables as input data for ANFIS. The PCA-ANFIS model used in this study is illustrated in Fig. 5.
Evaluation criteria and application of the proposed models
Evaluation criteria
For model evaluation, the correlation coefficient has been indicated to be an inappropriate index (Legates and McCabe, 1999). Coefficient of determination (R2), root mean square error (RMSE), and mean absolute error (MAE) are the evaluation criteria which have been frequently used by many scholars to evaluate their poposed models (Pham et al., 2021; Mohammadi et al., 2020; Costache et al., 2020; Abba et al., 2020; Pham et al., 2019). In this study, the performance of ANFIS models was evaluated by using R2, RMSE, and MAE. The models have a good performance when the value of R2is close to 1 and RMSE and MAE are close to 0. The performance evaluation criteria R2, RMSE, and MAE could be calculated with the following equations:
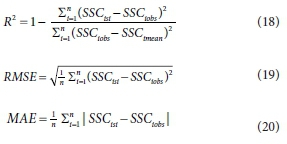
where SSC(obs) is measured SSC, SSC(si) is simulated SSC using the ANFIS models, and n is the length of the data series.
Application of the ANFIS model
The ANFIS model is considered as an effective tool to handle nonlinear and noisy data when the relationships among physical processes or relationships between predictors (e.g., discharge, antecedent suspended sediment) and target output (e.g., suspended sediment, sediment load) are not completely understood. Rajaee et al. (2009) indicated that the ANFIS model could be applied to model the complex systems. Different input values (i.e., Q and SSC) were considered in order to predict the 1-day-ahead SSC in this study. The statistical analysis is shown in Table 1. The variables at time t-3 were ignored due to its low correlation; the combinations which were used in this study are presented below:
Combination 1: Q at time t (Qt), SSC at t-1 (SSCt-1)
Combination 2: Q at time t, t-1 and t-2 (Qt, Qt-1 and Qt2), SSC at t-1 and t-2 (SSCt-1, SSCt-2)
Combination 3: Q at time t-1 (Qt-1), SSC at t-1 (SSCt-1)
Combination 4: Q at time t-1 and t-2 (Qt-1 and Qt-2), SSC at t-1 and t-2 (SSCt-1 and SSCt-2)
Combination 5: Q at time t and t-1(Qt, Qt-1), SSC at t-1 and t-2 (SSCt-1, SSCt-2)
Combination 6: Q at time t (Qt), SSC at t-1 and t-2 (SSCt-1, SSCt-2)
A fuzzy inference model of the Sugeno type was applied for the ANFIS models (Jang et al., 1997). By using optimization algorithms, the membership function (MF) parameters were adjusted to suit a given input-output set. Each rule comprises many parameters of MF and each variable might contain several values in the ANFIS model. For instance, if each variable contains 3 rules and each rule contains 2 parameters, there were 6n (i.e., n multiply 3 multiply 2) parameters for the determination in Layer 1 in Fig. 3. These MFs were trained by the ANFIS model using the training data. In Layer 2, these rules produce 2n neurons, and there are 2n χ (n + 1) undetermined parameters within the denazification process in Layer 4. Selecting the number of MFs for each input reflects the complication of choosing parameters of the ANFIS model. In this study, different ANFIS models were studied to predict the SSC values in the rivers. For each input, three Gaussian membership functions have the best performance in all these models.
Application of the DWT-ANFIS model
In this study, the DWT-ANFIS technique which employs DWT was used to improve the performance of a single ANFIS. To this end, the decomposed SSC and Q are used as the input to the ANFIS to predict the SSC 1 day ahead. Selection of a proper mother wavelet is a crucial part, the analysis is then performed using the shifted and dilated version of this wavelet. The second important part is to find the optimum number of decomposition levels. Rajaee (2011) indicated that high decomposition levels lead to a large number of input data with the complex nonlinear relationship in the ANN model, which may result in a decrease in the model performance of DWT-ANN. The non-linear relationship between input and target variables can be trained and fitted by the training data, but there are errors in predicting future values that could be created in each parameter. Subsequently, the performance of the model is decreased because of the net errors. So, Decomposition Level 2 should be considered as a suitable level while choosing more decomposition levels (more than 2 levels) may result in decreasing the performance of the prediction model (e.g., ANN). As a result, different types of mother wavelets with two different decomposition levels were chosen to find the most efficient model in this study. To this aim, the Q and SSC data are decomposed to one and two levels by different mother wavelets consisting of Daubechies-2 (db2) wavelet (Mallat, 1989), sym5, bior4.4, dmeyer, and coif1 wavelet.
Application of the PCA-ANFIS model
As mentioned previously, the main aim of this study was to propose and evaluate the ability of the PCA-ANFIS for SSC prediction 1 day ahead. To this aim, the original SSC and Q data were inputted to the PCA box and the outputs were considered as inputs for the ANFIS model. The components of lesser significance can be ignored. After some insignificant components were removed, the final input samples have fewer dimensions than the original data. For instance, a dataset has n dimensions, and so n eigenvectors and eigenvalues can be calculated, but only the first p eigenvectors are insignificant components and are chosen. Therefore, the final input has only p dimensions. Since the original time-series data were two dimensional (Qt, and SSCt), the PCA box produced two components in order of significance. In the current study, we also investigated the impact of removing the second component which had lesser significance. As an example, the principal component analysis of Q and SSC time-series for the Iowa River Station is plotted in Fig. 6.
RESULTS AND DISCUSSION
Suspended sediment simulation by the ANFIS model
The ANFIS models were used for SSC simulation using all the different input combinations. The results are listed in Table 2.
For the Iowa River, the ANFIS model had the best performance for Combination 5, where the highest value of R2 = 0.7275 and the lowest RMSE = 144.371 (mg/L) and MAE = 59.680 (mg/L) were observed, followed by Combinations 6, 4, 3, 2, 1. For the
Schuylkill River, the values of R2, RMSE, and MAE implied that the results are more complex compared to that of Iowa River, and showed that the best performances were for Combinations 5, 6, and 2, respectively. The ANFIS model, in this case, performed better than the ANN, NF, MLR and SRC models discussed in Rajaee et al. (2009) (R2ranging from 0.0002 to 0.697).
Suspended sediment simulation by the DWT-ANFIS model
In Table 3, the performance of the DWT-ANFIS model is shown. As can be seen from this table, for the Schuylkill River, the model using Bior 4.4 as mother wavelet provides the best performance at Decomposition Level 2. For this river, the DWT-ANFIS model improves the values of R2, RMSE, and MAE from 0.7186, 26.639 (mg/L), and 14.575 (mg/L) to 0.8443, 15.828 (mg/L), and 7.8211 (mg/L) in comparison to the best ANFIS models, respectively. At the Iowa River Station, the DWT-ANFIS configurations provided the best efficiency for Bior 4.4 mother wavelet at Decomposition Level 1, where it had the highest value of R2 = 0.6613 and the lowest RMSE = 161.054 (mg/L) and MAE = 68.882 (mg/L).
However, the results obtained for this river station indicated that the DWT-ANFIS model was not always able to improve the model performance. In this research, the results obtained by the PCA-ANFIS model were compared to those obtained by DWT-ANFIS and single ANFIS, for Schuylkill and Iowa Rivers, respectively.
Suspended sediment simulation by the PCA-ANFIS model
Table 4 presents the prediction results performed by PCA-ANFIS model for SSC prediction at the Schuylkill and Iowa River Stations.
According to Table 4, in both rivers, the PCA-ANFIS configuration provided the best efficiency when there was no reduction in dimension sizes. As expected, by ignoring the second component the accuracy of the model was reduced. However, the model performance was still better than the ANFIS and DWT-ANFIS models because the second component has less significance in comparison to the first component. As seen in
this table, at the Schuylkill River Station, the PCA-ANFIS model improved the best values of R2, RMSE, and MAE from 0.8443, 15.828 (mg/L), and 7.8211 (mg/L) to 0.9776, 5.7642 (mg/L), and 3.2592 (mg/L), respectively. For the Iowa River Station, it could be observed that the best values of R2, RMSE, and MAE were 0.7275, 144.371 (mg/L), and 59.680 (mg/L), respectively, while these were 0.9898, 27.4903 (mg/L), and 13.8879 (mg/L) for the PCA-ANFIS model. The temporal variations of the observed and predicted SSC using DWT-ANFIS and PCA-ANFIS methods for the Schuylkill River are shown in Fig. 7. In Fig. 8, the temporal variations of the observed and predicted SSC using single ANFIS and PCA-ANFIS models for the Iowa River are plotted.
Modeling comparison and discussion
As seen in Figs 7 and 8, for both river stations, the PCA-ANFIS model comes up with better results for SSC prediction than those estimated by the single ANFIS and DWT-ANFIS models. The ANFIS and DWT-ANFIS methods almost over-predict measured values in peaks. Meanwhile, the PCA-ANFIS model shows a good agreement with the observed time series, even for peaks. The magnitude of the low, medium and high SSC predictions by the PCA-ANFIS model is closer to the observed values in comparison with the other two models. Additionally, the results of the PCA-ANFIS model for both river stations are closer to the 45° straight lines in the scatter plots, compared to the other models. It can be said that the single ANFIS and DWT-ANFIS models are comparable in terms of prediction accuracy whereas the PCA-ANFIS model performed remarkably better than those. Since PCA reduces dimensional sizes of training data, the efficiency of PCA-ANFIS was also higher.
Figure 9a and Figure 9b illustrate measured and estimated (using wavelet ANFIS and PCA-ANFIS) cumulative suspended sediment load for the testing period at the Schuylkill and Iowa River Stations, respectively.
In Fig. 9a, both the PCA-ANFIS and DWT-ANFIS models over-predict the measured SSL values for Schuylkill River. However, the PCA-ANFIS model shows better performance. The measured cumulative SSL in the verification period is over 66 x 103 tons. The PCA-ANFIS and DWT-ANFIS models overestimate SSL by nearly 72 and 80 x 103 tons, respectively. It can be observed that at the Iowa River Station, the PCA-ANFIS model overestimates observed SSL while SSL is underestimated by the ANFIS method. In this river, the measured cumulative SSL is 3 051 x 103 tons. The PCA-ANFIS and ANFIS models predict an amount of 3 115 and 3 0 1 7 x 103 tons, respectively. At first glance, it can be said that ANFIS model predicts the cumulative SSL better than the PCA-ANFIS model.
In reservoir management and river engineering, the computation of cumulative SSL is a necessary step (Walling, 1983; Kondolf, 2018). Likewise, in designing and operating canals, dams, dikes, embankments and diversions, the accuracy of SSL calculation is crucial. The calculation of annual SSL is a priority because it is important for decision making. The cumulative SSL was predicted well by PCA-ANFIS in this study. When numerical studies have high computational cost, data-driven approaches, such as modeling frameworks, could be used to replace the physically based models. The applicability of using both PCA-ANFIS and DWT-ANFIS to obtain dynamic interaction and feedback associated with other flow variables, such as velocity or water depth, remains a prospective research question. Finally, the use of the statistical methods cannot replicate extrapolated input beyond the range of data used for training. This would limit the application of this model to study future changes, so traditional modelling methods are still necessary.
CONCLUSIONS
The single model (i.e., ANFIS) and the hybrid models (i.e., PCA-ANFIS and DWT-ANFIS) were examined for predicting SSC in the Schuylkill and Iowa rivers. The construction of empirically based hydrological models is time-consuming and laborious, while intelligent computing tools can develop fast and accurate models. Pre-processing approaches then help to provide better prediction by removing noise from hydrological time-series data. It can be concluded that the PCA-ANFIS model outperformed the single ANFIS and the DWT-ANFIS models in all the goodness-of-fit statistics used in this study (i.e., R2, RMSE and MAE). The DWT-ANFIS model took advantage of wavelet analysis to improve model performance, but the performance of PCA-ANFIS was even better than that of DWT-ANFIS. We suggest using this model for simulation of time series for weather, water resources, and other environmental factors.
REFERENCES
ABBA SI, PHAM QB, SAINI G, LINH NTT, AHMED AN, MOHAJANE M, KHALEDIAN M, ABDULKADIR RA, and BACH QV (2020) Implementation of data intelligence models coupled with ensemble machine learning for prediction of water quality index. Environ. Sci. Pollut. Res. 27 (33) 41524-41539. https://doi.org/10.1007/s11356-020-09689-x [ Links ]
ALIZADEH MJ, NODOUSHAN EJ, KALARESTAGHI N and CHAU KW (2017) Toward multi-day-ahead forecasting of suspended sediment concentration using ensemble models. Environ. Sci. Pollut. Res. 24 (36) 28017-28025. https://doi.org/10.1007/s11356-017-0405-4 [ Links ]
BAJIRAO TS, KUMAR, P, KUMAR M, ELBELTAGI A and KURIQI A (2021) Superiority of hybrid soft computing models in daily suspended sediment estimation in highly dynamic rivers. Sustain-ability 2021. 13 (2) 542. https://doi.org/10.3390/su13020542 [ Links ]
CANNAS B, FANNI A, SEE L and SIAS G (2006) Data preprocessing for river flow forecasting using neural networks: wavelet transforms and data partitioning. Phys. Chem. Earth, Parts A/B/C. 31 (18) 1164-1171. https://doi.org/10.1016/j.pce.2006.03.020 [ Links ]
CANNAS B, FANNI A, TROCI S and ZEDDA MK (2005) River flow forecasting using neural networks and wavelet analysis. EGU, European Geosciences Union, Vienna, Austria. 24-29. [ Links ]
CHOI SY and SEO IW (2018) Prediction of fecal coliform using logistic regression and tree-based classification models in the North Han River, South Korea. J.Hydro-Environ. Res. 21 96-108. https://doi.org/10.1016/j.jher.2018.09.002 [ Links ]
COHEN A and KOVACEVIC J (1996) Wavelets: The mathematical background. In Proc. IEEE. 84 (4) 514-522. https://doi.org/10.1109/5.488697 [ Links ]
COSTACHE R, TINCU R, ELKHRACHY I, PHAM QB, POPA MC, DIACONU DC, AVAND M, COSTACHE I, ARABAMERI A and BUI DT (2020) New neural fuzzy-based machine learning ensemble for enhancing the prediction accuracy of flood susceptibility mapping. Hydrol. Sci. J. 65 (16) 2816-2837. https://doi.org/10.1080/02626667.2020.1842412 [ Links ]
DANG TD, COCHRANE TA and ARIAS ME (2018) Quantifying suspended sediment dynamics in mega deltas using remote sensing data: A case study of the Mekong floodplains. Int. J. Appl. Earth Observ. Geoinf. 68 105-115. https://doi.org/10.1016/j.jag.2018.02.008 [ Links ]
DANG TD (2018) The effect of water infrastructure development on flow regimes and sedimentation in the Mekong floodplains. Department of Civil and Natural Resources Engineering, University of Canterbury. [ Links ]
EHTERAM M, GHOTBI S, KISI O, NAJAH AHMED A, HAYDER G, MING FAI C, KRISHNAN M ABDULMOHSIN AFAN H and EL-SHAFIE A (2019) Investigation on the potential to integrate different artificial intelligence models with metaheuristic algorithms for improving river suspended sediment predictions. Appl. Sci. 9 (19) 4149. https://doi.org/10.3390/app9194149 [ Links ]
FADAEE M, MAHDAVI-MEYMAND A and ZOUNEMAT-KERMANI M (2020) Suspended sediment prediction using integrative soft computing models: on the analogy between the butterfly optimization and genetic algorithms. Geocarto Int. https://doi.org/10.1080/10106049.2020.1753821 [ Links ]
GUPTA KK and GUPTA R (2007) Despeckle and geographical feature extraction in SAR images by wavelet transform. ISPRS J. Photogram. Remote Sens. 62 (6) 473-484. https://doi.org/10.1016/j.isprsjprs.2007.06.001 [ Links ]
JACKSON JE (1991) A User's Guide to Principal Components. Wiley, New York. [ Links ]
JANG JSR (1993) ANFIS: adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 23 (3) 665-685. https://doi.org/10.1109/21.256541 [ Links ]
JANG JSR and SUN CT (1995) Neuro-fuzzy modeling and control. Proc. IEEE. 83 (3) 378-406. https://doi.org/10.1109/5364486 [ Links ]
JANG JSR, SUN CT and MIZUTANI E (1997) Neuro-Fuzzy and Soft Computing: A Computational Approach to Learning and Machine Intelligence. Prentice Hall, Inc., Upper Saddle River, NJ. [ Links ]
JOLLIFFE IT (1986) Principal Component Analysis. Springer-Verlag, NY. [ Links ]
KAVEH K, BUI MD and RUTSCHMANN P (2017) A comparative study of three different learning algorithms applied to ANFIS for predicting daily suspended sediment concentration. Int. J. Sediment Res. 32 (2017) 340-350. https://doi.org/10.1016/j.ijsrc.2017.03.007 [ Links ]
KAYA MD, HA$ILOGLU A and HAKKI Y (2002) To estimate the design of functional sizes of chairs and desks on the basis of ISO 5970 using adaptive neuro-fuzzy inference system. FSSIMIE 2002, 5-7 May 2002. 2 29-31. [ Links ]
KONDOLF GM, SCHIMTT RJ, CARLING P, DARBY S, ARIAS M, BIZZI S, CASTELLETTI A, COCHRANE TA, GIBSON S, KUMMU M and OEURNG C (2018) Changing sediment budget of the Mekong: Cumulative threats and management strategies for a large river basin. Sci. Total Environ. 625 114-134. https://doi.org/10.1016/j.scitotenv.2017.11.361 [ Links ]
KIM TW and VALDÉS JB (2003) Nonlinear model for drought forecasting based on a conjunction of wavelet transforms and neural networks. J. Hydrol. Eng. 8 (6) 319-328. https://doi.org/10.1061/(ASCE)1084-0699(2003)8:6(319) [ Links ]
KISI O, HAKTANIR T, ARDICLIOGLU M, OZTURK O, YALCIN E and ULUDAG S (2009) Adaptive neuro-fuzzy computing technique for suspended sediment estimation. Adv. Eng. Softw. 40 (6) 438444. https://doi.org/10.1016/j.advengsoft.2008.06.004 [ Links ]
LABAT D, ABABOU R and MANGIN A (2000) Rainfall-runoff relations for karstic springs. Part II: continuous wavelet and discrete orthogonal multiresolution analyses. J. Hydrol. 238 (3) 149178. https://doi.org/10.1016/S0022-1694(00)00322-X [ Links ]
LEGATES DR and GREGORY JM (1999) Evaluating the use of "goodness-of-fit" measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 35 (1) 233-241. https://doi.org/10.1029/1998WR900018 [ Links ]
MADSEN JD, CHAMBERS PA, JAMES WF, KOCH EW and WESTLAKE DF (2001) The interaction between water movement, sediment dynamics and submersed macrophytes. Hydrobiologia. 444 (1-3) 71-84. https://doi.org/10.1023/A:1017520800568 [ Links ]
MALLAT SG (1989) A theory for multiresolution signal decomposition: the wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 11 (7) 674-693. https://doi.org/10.1109/34.192463 [ Links ]
MOHAMMADI B, LINH NTT, PHAM QB, AHMED AN, VOJTEKOVÁ J, GUAN Y, ABBA SI and El-SHAFIE A (2020) Adaptive neuro-fuzzy inference system coupled with shuffled frog leaping algorithm for predicting river streamflow time series. Hydrol. Sci. J. 65 (10) 1738-1751. https://doi.org/10.1080/02626667.2020.1758703 [ Links ]
NAIMAN RJ, DECAMPS H and MCLAIN ME (2010) Riparia: Ecology, Conservation, and Management of Streamside Communities. Academic Press, San Diego. [ Links ]
NOURANI V, ALAMI MT and VOUSOUGHI FD (2016) Hybrid of SOM-clustering method and wavelet-ANFIS approach to model and infill missing groundwater level data. J. Hydrol. Eng. 21 (9) 05016018. https://doi.org/10.1061/(ASCE)HE.1943-5584.0001398 [ Links ]
OLYAIE E, BANEJAD H, CHAU KW and MELESSE AM (2015) A comparison ofvarious artificial intelligence approaches performance for estimating suspended sediment load of river systems: a case study in United States. Environ. Monit. Assess. 187 (4) 1-22. https://doi.org/10.1007/s10661-015-4381-1 [ Links ]
PAIVA RC, COLLISCHONN W and TUCCI CE (2011) Large scale hydrologic and hydrodynamic modeling using limited data and a GIS based approach. J. Hydrol. 406 (3-4) 170-181. https://doi.org/10.1016/j.jhydrol.2011.06.007 [ Links ]
PHAM QB, YANG TC, KUO CM, TSENG HW and YU PS (2019) Combing random forest and least square support vector regression for improving extreme rainfall downscaling. Water. 11 (3) 451. https://doi.org/10.3390/w11030451 [ Links ]
PHAM QB, MOHAMMADPOUR R, LINH NTT, MOHAJANE M, POURJASEM A, SAMMEN SS and ANH DT (2021) Application of soft computing to predict water quality in wetland. Environ. Sci. Pollut. Res. 28 (1) 185-200. https://doi.org/10.1007/s11356-020-10344-8 [ Links ]
RAJAEE T, MIRBAGHERI SA, ZOUNEMAT-KERMANI M and NOURANI V (2009) Daily suspended sediment concentration simulation using ANN and neuro-fuzzy models. Sci. Total Environ. 407 (17) 4916-4927. https://doi.org/10.1016/j.scitotenv.2009.05.016 [ Links ]
RAJAEE T (2010) Wavelet and neuro-fuzzy conjunction approach for suspended sediment prediction. Clean Soil, Air, Water. 38 (3) 275286. https://doi.org/10.1002/clen.200900191 [ Links ]
RAJAEE T (2011) Wavelet and ANN combination model for prediction of daily suspended sediment load in rivers. Sci. Total Environ. 409 (15) 2917-2928. https://doi.org/10.1016/j.scitotenv.2010.11.028 [ Links ]
SAYED T, TAVAKOLIE A and RAZAVI A (2003) Comparison of adaptive network based fuzzy inference systems and B-spline neuro-fuzzy mode choice models. J. Comput. Civ. Eng. 17 (2) 123-130. https://doi.org/10.1061/(ASCE)0887-3801(2003)17:2(123) [ Links ]
SEIFI A, EHTERAM M, SINGH VP and MOSAVI A (2020) Modeling and uncertainty analysis of groundwater level using six evolutionary optimization algorithms hybridized with ANFIS, SVM, and ANN. Sustainability. 12 (10) 4023. https://doi.org/10.3390/su12104023 [ Links ]
SOLGI A, POURHAGHI A, BAHMANI R and ZAREI H (2017) Improving SVR and ANFIS performance using wavelet transform and PCA algorithm for modeling and predicting biochemical oxygen demand (BOD). Ecohydrol. Hydrobiol. 17 (2) 164-175. https://doi.org/10.1016/j.ecohyd.2017.02.002 [ Links ]
TAKAGI T and SUGENO M (1993) Fuzzy identification of systems and its applications to modeling and control. In: Dubois D, Prade H and Yager RR (eds) Readings in Fuzzy Sets for Intelligent Systems. Morgan Kaufmann.. 387-403. [ Links ]
TANTANEE S, PATAMATAMMAKUL S, OKI T, SRIBOONLUE V and PREMPREE T (2005) Coupled waveletautoregressive model for annual rainfall prediction. J. Environ. Hydrol. 13 124-146. [ Links ]
VALERO D and BUNG DB (2018) Artificial neural networks and pattern recognition for air-water flow velocity estimation using a single-tip optical fibre probe. J. Hydro-Environ. Res. 19 150-159. https://doi.org/10.1016/j.jher.2017.08.004 [ Links ]
WALLING DE (1983) The sediment delivery problem. J. Hydrol. 65 (1-3) 209-237. https://doi.org/10.1016/0022-1694(83)90217-2 [ Links ]
WU W, RODI W and WENKA T (2000) 3D numerical modeling of flow and sediment transport in open channels. J. Hydraul. Eng. 126 (1) 4-15. https://doi.org/10.1061/(ASCE)0733-9429(2000)126:1(4) [ Links ]
ZOUNEMAT-KERMANI M, MAHDAVI-MEYMAND A, ALIZAMIR M, ADARSH S and YASEEN ZM (2020) On the complexities of sediment load modeling using integrative machine learning: Application of the great river of Loíza in Puerto Rico. J. Hydrol. 585 (June 2020) 124759. https://doi.org/10.1016/j.jhydrol.2020.124759 [ Links ]
ZOUNEMAT-KERMANI M, MEYMAND AM and AHMADIPOUR M (2018) Estimating incipient motion velocity of bed sediments using different data-driven methods. Appl. Soft Comput. 69 (August 2018) 165-176. https://doi.org/10.1016/j.asoc.2018.04.041 [ Links ]
 Correspondence:
Correspondence:
Nguyen Mai Dang
Email: dang@tlu.edu.vn
Received: 21 March 2020
Accepted: 25 March 2021














