Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
Water SA
versión On-line ISSN 1816-7950
versión impresa ISSN 0378-4738
Water SA vol.46 no.3 Pretoria jul. 2020
http://dx.doi.org/10.17159/wsa/2020.v46.i3.8658
RESEARCH PAPERS
Sensitivity analysis on a three-phase plant-wide water and resource recovery facility model for identification of significant parameters
DS Ikumi
Future Water Institute, New Engineering Building (NEB), University of Cape Town, Rondebosch, 7701, Cape Town, South Africa
ABSTRACT
Water and resource recovery facility (WRRF) mathematical models have been advancing towards their widespread application for sizing and operation of treatment plants to minimize energy consumption and cost while maximizing nutrient recovery and effluent quality. Effective utilisation of these models requires that they are well calibrated. However, difficulties (with important parameters not identified and uncertainties in interpretation of model output results) can be experienced in model calibration, especially due to (i) the intricate relationships of model output variables with model input factors (where parameters are inter-related to various model outputs), resulting in non-linearity, and (ii) the limitations (due to expensive and/or time-consuming experimental methods) experienced in procuring and reconciling data required for determination of the model input factors. This paper presents the performance of a sensitivity analysis, reinforced with expert-based reasoning, on a three-phase (aqueous-gas-solid) plant-wide model (PWM_SA, Ikumi et al., 2015), for identification of significant parameters, and highlights the ones requiring experimental determination, specific to the system. The sensitivity analysis exercise was performed using two methods - i.e., Morris screening (screening method) and standardised regression coefficient (SRC; based on regression). This process was useful towards detection of the parameters, which are not normally measured at WRRFs, but may require attention for future application of mathematical models in decision-making processes for WRRFs. These included the influent fractions of unbiodegradable and readily biodegradable organics, the kinetic constants for hydrolysis of biodegradable particulates, the elemental composition of the organics and the specific growth rate of autotrophic nitrifying biomass.
Keywords: sensitivity analysis, activated sludge, anaerobic digestion, plant-wide modelling
INTRODUCTION
Continuous advancements are being made towards a more system-wide approach to modelling waste treatment systems, that incorporate the fate of the products being generated (e.g., mineral precipitates, stable organic sludge, biogas, etc.) in view of resource recovery. Because the functions of these water and resource recovery facilities (WRRFs) stretches beyond simply meeting effluent requirements (i.e., also includes optimisation of products to be generated), a high level of accuracy in predicting system response is required. However, with the increased size of these mathematical models, difficulties (with important model parameters not identified and uncertainties in intepretation of model output results) can be experienced in model calibration, especially due to the non-linearity brought about by (i) the intricate relationships of model output variables with model input factors (where parameters are inter-related to various model outputs) and (ii) the limitations experienced in procuring and reconciling data (due to expensive and/or time-consuming experimental methods) required for determination of the model input factors (this is especially when the model has significantly large numbers of unknown parameters and model components). Further, the inclusion of phosphorus (P) into system-wide models that could mimic the continuously evolving WRRFs has resulted in various complexities that necessitate a rigourous and systematic method of determining significant parameters and their values for confidence in the model predicted outputs. Phosphorus is removed from wastewater by transforming it from the dissolved liquid phase to the intracellular solid phase. Hence, for system-wide models, it was noted that the anaerobic digestion (AD) of P-rich sludge from biological excess P removal (EBPR) activated sludge (AS) systems, requires three-phase mixed weak acid/base chemistry because the release of biomass P or polyphosphate (PP) not only affects the system alkalinity but also can induce mineral (e.g., struvite) precipitation (Van Rensburg et al., 2003; Harding et al., 2010).
Various research groups have worked both collaboratively, and separately on related topics, towards development of WRRF mathematical models that integrate bioprocess stoichiometry and physicochemical transformations, for inclusion of processes such as nutrient release and multiple mineral precipitation (Batstone et al., 2012; Kazadi et al., 2015; Flores Alsina et al., 2016; Wang et al., 2016). Bioprocess stoichiometry and physicochemical transformations are also included in the presentation of a new 'three-phase' (aqueous-gas-solid) plant-wide model that includes P, (PWM_SA) (Brouckaert et al., 2010; Ikumi et al., 2015) which includes compatible activated sludge (AS; ASM2-3P) and anaerobic digestion (AD; UCTSDM3P) bioprocess model components and uses strict mass-balance principles to track P through the unit processes of a WRRF (with recognition of its impact on the mutual interaction between the connected unit operations). This paper presents the performance of a sensitivity analysis on a three-phase (aqueous-gas-solid) plant-wide model (PWM_SA, Ikumi et al., 2015), for identification of significant parameters and highlights the ones requiring experimental determination, specific to the system (i.e., where a generic value from literature cannot be used).
Sensitivity analysis has been applied in various studies as part of the standard processes of calibration of water and wastewater treatment system models (Vanrolleghem et al., 2003; Brun et al., 2001; Ikumi et al., 2014). Different methods have been applied based on the objectives of the study and the complexity of the model involved. Some applications in the field of anaerobic digestion (AD) modelling include: (i) the use of non-dimensional logarithmic sensitivity functions (i.e., partial derivatives of the state variables) by Noykova and Gyllenberg (2000) to compare the influence of different parameters and variables in a modified version of the Hill and Bath (1977) AD model; (ii) the application of decoupled direct method (DDM; i.e., decoupling the auxiliary equations from the model equations) applied by Silva and De Bortoli (2020) for an AD model of cellulose degradation for biogas production; (iii) calculation of the sensitivity index (Sobol, 1993) to define the most sensitive parameters for production of biogas (i.e., the methane yield), using the International Water Association (IWA) Anaerobic Digestion Model No. 1 (ADM1; Batstone et al., 2002) with optimized kinetic parameters in the anaerobic digestion of food waste (Zhao et al., 2019). As noted from the literature sources, various methods can be used in identification of influential model parameters. There have been some comparisons between various methods of sensitivity analysis (Neumann, 2012; Cosenza et al., 2013). Some of the methods that stood out in these comparisons included standard regression coefficient (SRC; is a linear correlation-based approach) method, Morris screening (Morris, 1991; determination of the elementary effects) and Extended-FAST (Fourier Amplitude Sensitivity Testing; an analysis of variance-based approach).
Sensitivity analysis objectives usually considered are factor prioritisation (identifying the model parameters with the greatest effect on model outputs) or factor fixing (identifying non-influential factors that could be 'fixed') (Neumann, 2012; Mannina et al., 2011). However, modellers may find it useful to identify both important (factor prioritization) and non-influential (factor fixing) input parameters. In the study conducted by Neumann (2012) it was shown that, although the SRC method was applied outside its' validity range, it still identified similar important parameters to Extended-FAST. In applying a sensitivity analysis of the UCTSDM3P model of Ikumi et al. (2015) used to simulate an upflow anaerobic sludge blanket (UASB) reactor, Ghoor (2020), noted the SRC method to be useful in factor prioritisation, although it assumes existence of a linear relationship between input parameters and output variables. Ghoor (2020) notes that, despite this linear relationship not being true for bioprocess models such as that for AD systems, the correlation coefficient of greater than 0.7 can allow for an assumption that the applied linear model in SRC explains the relationships reasonably well and accounts for 70% of the variance in the data. This made the SRC simpler to understand, when compared with the more complex methods such as Extended-FAST. For similar reasons to those stated by Ghoor (2020), the SRC method was selected to be used in factor prioritisation for this study. However, because it was deemed useful to assess both linear and/or non-linear effects of all the model parameters on the output variables (Mannina et al., 2011), Morris screening was selected as a second method of analysis because of its capabilities in factor fixing and identifying non-linear relations between parameters and variables (Gamerith et al., 2011).) Further, Morris screening was recommended by Herman et al. (2013) as an efficient method that can identify the most and least sensitive parameters, similar to a more complex variance-based Sobol sensitivity index method (Sobol, 1993), at a reasonable computational cost.
EXPERIMENTAL SYSTEM LAYOUT
The experimental layout of Ikumi (2011) is used in this study. It replicates at laboratory scale three WWTP schemes, comprising (i) a Modified Ludzack-Ettinger (MLE) nitrification-denitrification (ND) activated sludge (AS) system treating raw sewage (MLE 1) with anaerobic digestion (AD) of its waste activated sludge (WAS) in AD system number 1 (i.e., AD1), (ii) an identical MLE system (MLE 2) treating settled sewage with AD of its WAS in AD2, and (iii) a membrane (MBR) University of Cape Town (UCT) ND enhanced biological P removal (NDEBPR) system treating settled sewage with (i) AD of its WAS in AD3. All three AS systems (UCT, MLE 1 and MLE 2) were operated at steady state, at a 10-day system sludge age (SRT), and were fed the same 600 mgCOD/L settled wastewater, except that the UCT system influent included same additives (i.e., 200 mgCOD/L acetate and 40 mg/L P from di-potassium hydrogen phosphate (KH2PO4)). The MLE systems had no chemical additives but to one of them (MLE 2) a measured constant flux (gCOD/d) of macerated PS collected from the Athlone WWTP (Cape Town) was added to the same settled WW to make up raw sewage influent and increase its COD from the basic 600 mgCOD/L to 1 000 mgCOD/L. The added PS, the WAS from the three AS systems, and a blend of PS - MLE1 WAS were also anaerobically digested. Hence, the AD systems constituted 5 separate flow-through anaerobic digestion (AD) systems operated successively at different solid retention times (SRTs). To initiate the calibration process, the sensitivity analysis procedure was perfomed with simulation of the MBR UCT NDEBPR system and the AD system that digested its WAS (Fig. 1 shows the experimental set-up). Table 1 and Table 2 show the operating parameters for the UCT AS and AD systems, respectively. The prepared experimental set-up allowed for the tracking of COD, N and P through the aerobic and anaerobic unit processes of the WWTP. Table 3 presents a guide indicating all measurements performed on samples taken from the unit processes of the plant configuration.
MODEL DESCRIPTION AND VERIFICATION
The UCT three-phase plant-wide model (Ikumi et al., 2015) was developed for simulating the biological processes to track and predict the output of materials (COD, carbon (C), hydrogen (H), oxygen (O), nitrogen (N), phosphorus (P), magnesium (Mg), potassium (K) and calcium (Ca)) along the unit processes of a WWTP. It comprises three sub-models, integrated for simulation of the entire WWTP under various configurations (e.g., NDBEPR AS system linked to an AD or an anoxic-aerobic digestion (AAD) for WAS stabilisation). These sub-models include:
1.The ionic speciation model (Brouckaert et al., 2010). This model includes pairing of ionic components (the set of model ionic species is given in Table 4) and inter-phase transfers of component species. Table 5 gives an example of a set of equilibrium and mass-balance equations used in the ionic speciation subroutine.
2.The ASM2-3P model: This is the Activated Sludge Model No. 2 (ASM2, Henze et al., 1995), modified to include the ionic speciation model (Brouckaert et al., 2010), the Inorganic Settleable Solids (ISS) model of Ekama and Wentzel (2004) and including multiple mineral precipitation according to Musvoto et al. (2000a,b).
3.The UCTSDM3P Model: This is the University of Cape Town Anaerobic Digestion Model (UCTADM; Sötemann et al., 2005), modified to include the hydrolysis of multiple organic sludge types (PS, ND WAS, NDBEPR WAS and PS-WAS blends), the Ekama and Wentzel (2004) ISS model, multiple mineral precipitation processes according to Musvoto et al. (2000a, b) and the Brouckaert et al. (2010) aqueous speciation model which facilitates ionic speciation (Ikumi et al., 2015).
For their compatibility, the ASM2-3P and UCTSDM3P models have the same comprehensive set of model components (supermodel approach, Volcke et al., 2006; model components given in Table 6 and applied stoichiometric processes in Table 7), including parameterized stoichiometry for the bioprocesses and sharing the same ionic speciation subroutine model. All the model components and parameters were defined and named according to the standard notational framework proposed by Corominas et al. (2010).
Model verification: To initiate the evaluation of the PWM_SA model, the systematic method proposed by Hauduc et al. (2010) was applied to verify that material (COD, C, H, O N, P, Mg K and Ca) balances were achieved in the determination of all stoichiometric processes.
Parameter values: The initial (prior) values for suitable kinetic and stoichiometric parameters as obtained experimentally or from literature were entered, and given the typical value range (θi_min to θi_max), determined according to the methods proposed by Brun et al. (2002) considering 3 classes:
•Accurately known - these have a relative uncertainty of 5% (Class 1)
•Moderately inaccurately known parameters with a relative uncertainty of 20% (Class 2)
•Very poorly known parameters with a relative uncertainty of 50% (Class 3)
Tables 8 and 9 show the model parameters for ASM2-3P and UCTSDM3P, respectively.
SENSITIVITY ANALYSIS
The importance of sensitivity analysis in model calibration is prompted by the notable limitation in the applicability of various WWTP dynamic models, based on the complexities brought about by wide ranges of parameters and the intricate dependence of output variables on these parameters and other state variables. For simpler steady-state models (i.e., those of Wentzel et al. (1990) for BEPR AS systems and and Sötemann et al. (2005); Ekama (2009); Ikumi (2011) for AD systems) the identification of major stoichiometric parameters could be identified intuitively, since these models contain explicit equations linking parameters to output variables. However, the more complex dynamic models are based on differential equations, for prediction of output variables due to changing material loads and flows. The performance of a complete sensitivity analysis on the dynamic model allowed for assement of both linear and/or non-linear effects of all the model parameters on the output variables.
Two sensitivity analysis methods were applied in this study - i.e., Morris screening (screening method) and standardised regression coefficients (based on regression). The application of multiple sensitivity analysis methods with multiple objectives was done as recommended by Neumann (2012), as this is expected to lead to more robust conclusions. The results obtained using these methods were used to identify (i) important parameters that would cause a significant change in model outputs, and hence need to be known well, (ii) non-influential parameters (those that can be set to any value within their range without much change in outputs) and (iii) interacting parameters (Neumann, 2012).
To initiate the sensitivity analysis process, uncertainty propagation was conducted by a Monte Carlo (MC) simulation of the model by random sampling of parameter values. The parameter value ranges (i.e., lower (θi_min) and upper (θi_max) prior bounds for the MC simulation) were chosen according to the method proposed by Brun et al. (2002). These parameters were assumed to be uniformly distributed within their ranges. A 1 000 simulations were performed using the WEST software (Vanhooren et al., 2003), with 1 000 sets of random parameter values generated in this way, to provide 1 000 sets of values for the selected output variables, which could then be visualised as histograms or density distributions or characterised in terms of descriptive statistics.
Standard regression coefficient method
The standard regression coefficients (SRCij) due to each parameter quantify the effect on variable j when parameter i is changed (hence allows prioritisation of important parameters). The SRC method involves the fitting of a multivariate linear model to the output of the MC simulation (Martin et al., 2010; Neumann et al., 2012). The SRC´s multivariate linear regressions relate each output variable (yj) to all uncertainty parameters (θj), to get an equation of the form:
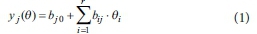
The standard regression coefficient is defined as
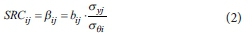
where bi is the slope obtained from linear regression; σθij is the standard deviation of the 1 000 parameter values generated for parameter I, and σyj is the resulting standard deviation of output variable yj. Finally, the coefficient of determination (R2), that indicates how well the multilinear regression model fits the variable's responses, was also calculated using the R program (R Development Core Team, 2011). This indicates how much confidence can be placed in using the calculated values in predicting future results. For variables with R2 > 0.7, the SRCs (βi) are a valid measure of sensitivity (Saltelli et al., 2004).
Morris screening method
Morris's screening method (Morris, 1992) is a method used to determine elementary effects for each parameter, to identify which parameters affect the model output variables significantly, and to eliminate non-influential parameters. The computation of these elementary effects requires the variation of one parameter at a time (OAT) across a select number of k levels (in this case 10), requiring k∙r simulations (where r is the number of parameters). In this design, each model parameter is varied within a selected uncertainty range of p, which is also determined using the method proposed by Brun et al. (2002). While a particular parameter was varied, all others were assigned their mid-range values. The elementary effect of parameter θi on variable yj is calculated as:
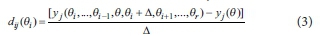
where y(θ) is the output variable obtained when all parameters are set to their prior values, i.e., y(θ1,θ2...θr).
The mean (μij) and standard deviation (σij) of the calculated k elementary effects are determined for each parameter as measures of the parameter importance. μij is used to detect parameters with an important overall influence on the output, while σij is used to detect parameters involved in interaction with other parameters or whose effect is non-linear (Neumann, 2012; Campolongo et al., 2007).
RESULTS
Neumann (2012) proposes interpretation of sensitivity analysis results through considering the parameters that are most important (which would cause significant changes in model outputs, hence are a priority to be known), and non-influential (hence can be placed anywhere within their uncertainty range without incurring much of a change). In the following sensitivity analysis, the parameters are grouped into those that are kinetic (hence affect the process rates) and those that are non-kinetic (mainly used in determination of the input component characteristics (e.g., the X, Y, Z, A and B values of biomass elemental composition CXHYOZNAPB) or yield for OHO biomass growth, YH)).
Table 10 shows the standardised regression coefficients (SRC, βij) and resulting coefficient of determination for the most important parameters (having the greatest SRC magnitudes) of selected output variables, from the ASM2-3P and UCTSDM3P models. The SRCs are taken to be a valid measure of sensitivity as long as the resulting coefficient of determination, R2, is greater than 0.7 (Saltelli et al., 2004). However, lower degrees of linearity indicate that the SRC is being used outside the application range, which could cause the underestimation of important parameters, hence cannot offer a useful contribution towards the estimates of parameter prioritisation (Neumann, 2012). Additional to SRC data, the results from the Morris screening method are also presented - by plotting the expectancy (μ*) of the absolute values of the elementary effects against the standard deviation σ of the elementary effects for each parameter.
Activated sludge (AS) systems
In this section the results from the sensitivity analysis of the PWM_SA model parameters, when used to simulate the NDBEPR UCT system (see Fig. 1), are presented.
Biological P removal involves (i) the anaerobic utilisation of volatile fatty acids to form PHB, which occurs with polyphosphate release to OP, and (ii) the aerobic breakdown of PHB for PAO growth and PP synthesis and uptake. The various parameters identified to be of importance using the SRC and Morris screening sensitivity analysis techniques for the relevant bio P removal model predicted outputs are discussed below. These include (i) biomass growth and oxygen utilisation due to organic removal, (ii) ammonia utilisation and nitrate generation by autotrophic nitrifying organisms (ANOs), and (iii) bio-P removal through PP accumulation.
Breakdown of organics for biomass growth and oxygen utilisation
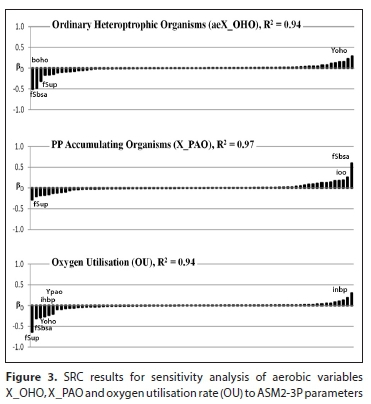
The UCT plant-wide model (PWM_SA) defines the character-istics of sewage biodegradable organics by parameterising the molar fraction elements from its given generic stoichiometric formula (i.e. X, Y, Z, A, B in CXHYOZNAPB). During simulations the mass-balanced stoichiometric processes are then used to track the energy, materials (C, H, O, N and P) and charge towards prediction of the unit process outputs. The energy (COD) and the nutrients (N and P) bound in biodegradable organics are biologically utilised in the reactors, while those in the unbiodegradable organics remain conserved (without participating in the biochemical reactions) and accumulate in the system with the solid (for particulate unbiodegradables, UPO) and liquid retention times (for particulate unbiodegradables, UPO, and soluble unbiodegradables, USO, respectively). The volatile fatty acids (VFAs, sourced from the influent or generated through anaerobic fermentation) play a significant role in bio-P removal, as they are taken up by PAOs as their source of substrate. It can be noticed from Figs 2 and 3 that the fractionation of influent waste and determination of the fraction of influent COD that is unbiodegradable particulate (fS'up) and VFA (fSbsa) are very important parameters that influence the growth of biomass (hence sludge generation) and oxygen utilisation in the AS system.
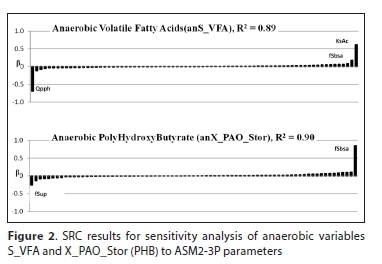
For the reactor VFA concentration, the SRC method exhibits that KsAC (i.e., the saturation/inhibition coefficient for acetate utilisation) and Qpph (i.e., the rate constant for storage of polyβ-hydroxybutyrate (PHB)) are also significant parameters (Fig. 2). The PAOs rely mostly on anaerobic uptake of readily biodegradable material for growth (i.e., fermentable biodegradable soluble organics (FBSO) and VFAs). These readily biodegradable organics are converted to an energy storage compound (poly3-hydroxy-butyrate, PHB) that is later used aerobically for growth and polyphosphate storage (Wentzel et al., 1990). By dictating the rate of PHB uptake, Qpph significantly influences the quantity of substrate allocated for growth of PAOs, with the remainder of the biodegradable organics mainly apportioned to the OHOs. This substrate allocation, of course, depends on the availability of VFAs (that are present in the influent or are generated through anaerobic fermentation FBSOs), for conversion to PHB. Intuitively, it is also expected that the Ypao (yield coefficient for utilisation of PHB in PAO biomass growth) would have a significant positive influence on the predicted reactor PAO population, since it dictates the substrate allocation for anabolic utilisation of PHB in the aerobic zone of the AS system. This is not clearly reflected by the SRC results (Fig. 3) but can be noted by the Morris screening results (Fig. 4), which show Ypao with the greatest influence and mupao (the maximum specific growth rate of PAOs) with the highest degree of non-linearity.
The OHO biomass has various parameters of importance, as indicated by Fig. 3. This includes the kinetic parameter boho (i.e., the rate constant for lysis and decay of OHO biomass) and stoichiometric parameter Yoho (i.e., the yield coefficient for OHO biomass growth). The Morris screening method also indicates Yoho to be the significant parameter, with mupao (the maximum specific growth rate of OHOs) having the highest degree of non-linearity (Fig. 4). The parameters that contribute to biomass elemental formulation (i.e., inoiho, ioo and ino - the H, O and N molar content in biomass elemental formula, respectively) are also expected to be significant because their values will determine the electron-donating capacity of the biomass, hence their electron requirements to carry out their metabolic processes. The fraction of energy allocated from breakdown of biodegradable organics to build up biomass cells depends on the biomass yield (i.e., Yoho), hence the notable positive impact of this parameter. The boho is shown to have a significant (though negative) influence on reactor OHO concentration because it determines rate of OHO biomass death and degradation (hence a high boho value would result in low biomass population, for a given system sludge age). The Qpph is also expected to have a negative influence here because the biodegradable organics in the influent that are taken up by PAOs are deducted from the organics utilisable by OHOs (the configuration of NDBEPR systems allows for the influent to be exposed to the anaerobic zone prior to aerobic, ensuring that the readily biodegradables are first available for sequestering by PAOs before the OHOs can utilise them aerobically - this allows the PAOs the competitive advantage required for them to co-exist with OHOs as mixed cultures in the NDEBPR AS system). The capability of the model to replicate this system behaviour was evaluated by Ikumi et al. (2015) by applying the PWM_SA model to a Modified Ludzack Ettinger (MLE) system, whereby in this case no PAO growth (hence no PP storage) occurred. However, the same MLE system with little or no nitrification (the unaerated zone now anaerobic) exhibits growth of PAOs. Likewise, sufficiently high quantities of nitrate being recycled to the anaerobic reactor of an N and P removal system would supress EBPR, as observed during winter in 3 and 5-stage Bardenpho systems, when denitrification is lower (Ikumi, 2011).
Both the SRC and Morris screening methods indicate that the biomass yield (Yoho and Ypao) parameters have a significant influence on oxygen utilisation. The SRC results also show that the elemental composition of the biodegradable organics (i.e., inbpihbp, iobp - the H, O and N molar content in biodegradable organics elemental formulae, respectively) to be significant. This is expected because the biomass yield values dictate the proportion of substrate (biodegradable organics) electrons that are allocated to biomass, with the remainder apportioned to oxygen for generation of energy (hence the negative influence with SRC).
Utilisation of ammonia
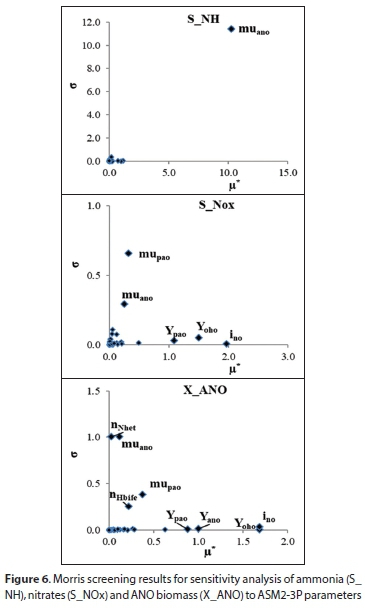
According to the SRC method, the most significant parameters for prediction of effluent ammonia (NH4) concentration include KsNhan (i.e., the saturation coefficient of autotrophs for ammonium), muano (i.e., maximum growth rate of autotrophic nitrifying organisms) and ino (See Fig. 5). This is expected because the ino dictates the nitrogen requirement, to be sourced from the pool of ammonia in the reactor, for biomass growth. In the activated sludge (AS) models, the ammonia use gives priority to its use as a nutrient during anabolism of faster growing biomass (OHO and PAO) before the 'excess' ammonia is used for nitrification (the nitrifying organisms that use the ammonia as e-donor are slower growing microorganisms). This is possibly also the reason for ino being a significant parameter for effluent nitrate (NO3-) concentrations. Despite this, the ammonia used for nitrification is usually higher than that for biomass growth; hence the parameters that drive the kinetics of this process (muano and KsNhan) have a significant influence. Similar to ammonia and nitrates, the ANO biomass is influenced by ino and bano (Fig. 5). Moreover, the fraction of influent COD as VFA (fSbsa), together with the elemental composition of the biodegradable particulate organics (notable by the significance of inbp, ihbp, iobp parameters), are influential towards ANO growth and reactor nitrate concentration.

The Morris screening results indicate similar parameters as being of significance to SRC (muano, has a high µ* value and also a relatively significant degree of non-linearity for ammonia concentration. For the ANO growth and reactor nitrate concentration, muano appears to have more of a non-linear influence, but still a relatively low µ* value. However, also similar to SRC, the results show that ino is the most important parameter for these variables. Further notable parameters influencing ANO growth and reactor nitrate concentration are Yoho and Ypao (Fig. 6). This is possible because the increased growth of OHO and PAO biomass would result in a greater N requirement as nutrient source, especially if the ino value is high.
Biological phosphorus removal
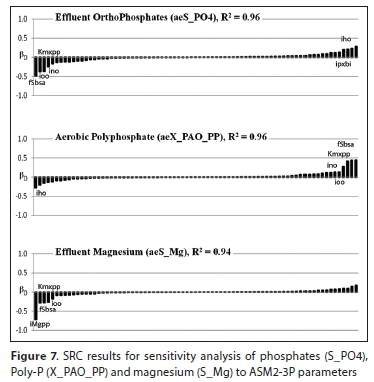
Figures 7 and 8 indicate the parameters of significance for P removal via aerobic PP uptake and prediction of effluent OP concentration. According to the SRC method of sensitivity analysis, the most important parameters for OP are kmxpp (i.e., the maximum polyphosphate (PP) content of PAO biomass), fSbsa, ipbp (the P molar content in biodegradable organics elemental formula) and elemental composition of biomass (dictated by notable iho, ino and ioo parameters). From the ASM2-3P model (Ikumi et al., 2015), PHB is aerobically utilised for PAO growth and for storage of PP. The kmxpp parameter dictates the quantity of reactor OP to be utilised for PP formation, for each new PAO biomass formed (with sufficient PHB available aerobically, higher kmxpp results in lower effluent OP). The ipbp informs the quantity of P that could be released as OP from biodegradable particulates; hence - apart from the influent OP - act as a significant source of reactor OP that could be used in this process. Since most of the OP used aerobically is utilised for the generation of PP (the OP taken up for biomass growth and released in biomass endogenous death is usually much lower), it can also be observed that the same parameters that are significant to OP also impact PP, but in the opposite way (PP increase results in OP decrease so the parameters that would have a negative effect on the formation of PP would have a positive effect on concentration of OP; see Fig. 7). Moreover, because Mg is also a crucial component to be utilised in generation of PP, similar parameters influencing OP concentration (fSbsa, Kmxpp and ioo) are noted to be important for prediction of effluent Mg concentration. The only difference with Mg is that imgpp (i.e., the Mg molar content in polyphosphate) is an added significant parameter for aerobic concentration of Mg. An increase in imgpp indicates that more Mg is required for PP formation, which would result in decreased concentration of effluent Mg. This is observed in both the SRC and Morris screening method (see Figs 7 and 8) where imgpp has the highest μ* value (i.e., is the most important). Also, similar to SRC, the results from the Morris screening method also indicate Kmxpp, iho, ino and ioo to be significant parameters for aerobic PP and OP concentrations. However, other parameters of importance are the biomass yield values (i.e., Yoho and Ypao with high μ* values) and mupao (with the highest degree of non-linearity, σ).
Anaerobic digestion unit process
In simulating the AD of sludge generated (from PS and NDBEPR WAS) with the UCTSDM3P model, the selected output variables to be applied during the sensitivity analysis were those considered to be indicative of system performance and resource recovery. These variables included residual biodegradable organics (BPO), methane (CH4), ammonia (NH4+), ortho-phosphates (HPO42- and H2PO4-), metals (Mg, K and Ca), precipitates (mainly struvite), alkalinity (for carbonate, H2CO3*Alk. and phosphate, H3PO4 Alk., weak acid/base systems) and the system pH. The BPO removal and methane generation is associated with energy recovery potential; the prediction of low system pH indicates a warning for system failure and the aqueous phase products (e.g., NH4+, OP, Mg, K and Ca) are later generated in the dewatering liquor that would either be recycled upstream or transferred to side-stream treatment processes.
BPO removal
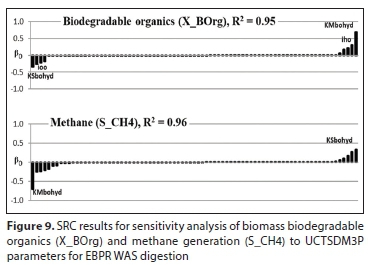
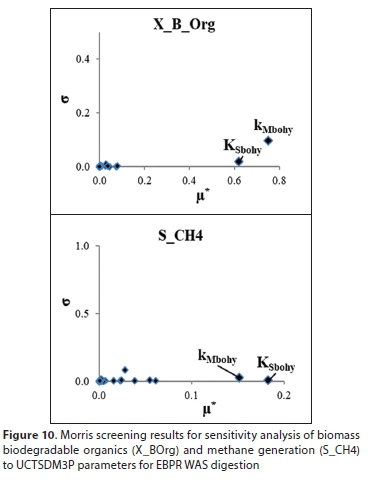
The kinetics of hydrolysis of biomass BPO is usually the slowest process in AD and ends up determining the residual BPO and the nutrients released in the process, contributing towards final AD products. From Fig. 9, it can be noticed that for the WAS biomass BPO, the most important parameters are Ksbohyd and kMbohyd (i.e., the half saturation coefficient for hydrolysis of biomass BPO and the maximum specific hydrolysis rate constant for WAS biomass BPO, respectively). These are the hydrolysis rate kinetic constants that drive the breakdown of biomass BPO. The Morris screening results agree with the SRC, by showing the same hydrolysis kinetic constants to be most influential (see Fig. 10). For the AD of PS, the Ksbihyd and kMbihyd are also important for PS BPO removal (Fig. 11). However, the unbiodegradable fraction of PS COD (fSup) is also significant (especially notable in the case of CH4 evolution), since it significantly impacts the quantity of substrate available for conversion to biogas (where, since soluble influent organics are acceptably of low concentrations, the BPO COD available for conversion to CH4 COD is mainly (1−fSup) of PS COD).
Ammonia release and associated alkalinity change
From Fig. 12, it can be noticed that for modelling ammonia (NH4) releases in WAS AD, the most significant parameter is ino, and equivalently inbp, for hydrolysis of PS. These parameters are depicted to have a positive influence on ammonia generation (Figs 12 and 13, its higher values would result in increased ammonia concentration). The results are intuitively adequate, because the A value from CXHYOZNAPB of BPO (parameterised in the UCTSDM3P model as ino for biomass BPO and inbp for PS) dictates the ammonia to be released into the AD from the N bound in hydrolysed BPO. The PS additionally has fSup, ihbp and iobp as influential parameters.
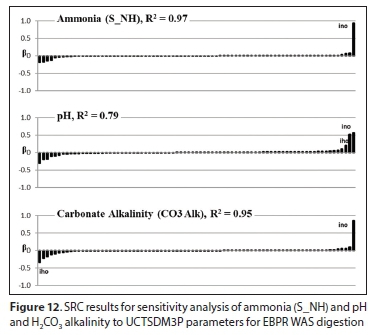
The results from the Morris screening method (Fig. 14) also agree with the SRC data (which can be accepted due to the high R2 value of 0.97) on the importance of ino in NH4 release prediction. According to the SRC method of analysis, the same parameter that had a strong influence on NH4 release (i.e., ino) has a significant impact on the sensitivity of the system pH and carbonate alkalinity. For mixed weak acid/base systems controlled by the inorganic carbon system, bicarbonate (HCO3-) production is the main generator of H2CO3* alkalinity (i.e., H2CO3* alkalinity ≈ [HCO3-]; Ikumi et al., 2015) and the establishment of system pH. According to the weak acid/base equilibrium formulations (Loewenthal et al., 1994), the [CO32-] is a relatively very small species of the carbonate system in the steady-state methanogenic AD pH ranges (around 6.5 to 8). Hence, the AD is modelled such that the stoichiometric products that assist in uptake of H+ from dissolved CO2 (H2CO3*) are the main factors that promote increase in H2CO3* Alk, hence also increasing the pH (− log [H+]). The organically bound N is modelled to be released as NH3 (non-ionic form of ammonia, that is a non-reference species for the ammonia weak acid/base system), which picks up this H+ from H2CO3* of the inorganic carbon (IC) system forming HCO3-. This results in the ammonia releases from organic N causing an increase in alkalinity generation and hence increased system pH. However, for the pH and H2CO3* Alk variables, the Morris screening method does not reflect the same results as SRC but instead indicates the Yppac (the yield value for acetate uptake during anaerobic PP release) as the most significant parameter. However, these results are also possible because in AD-fed P-rich sludge, the PP release process has a significant impact on the system pH (see section below). For P-rich systems with PP, the aqueous H2CO3* alkalinity increase also depends on PP and cell-bound P release because PP is released as H2PO4 and biomass P is released as H3PO4, which interact with the other weak acid/base systems and influence pH.
Orthophosphate release and struvite precipitation potential
The four main forms of P in AD include organically bound P, PP, OP and precipitate P. The release of OP from breakdown of NDBEPR WAS in AD has been noted to impact the system alkalinity and mineral precipitation potential (Ikumi et al., 2015). Figure 15 shows the most important parameter for orthophosphate concentration in the AD effluent is ino followed by ipo. The influence of ino on AD effluent OP is possible because: (i) increase in ammonia release with BPO (WAS biomass) breakdown causes increase in alkalinity and pH (as discussed the section above), and (ii) ammonia is a component part of struvite (MgNH4PO4), hence influences struvite precipitation potential (this precipitation requires OP uptake).
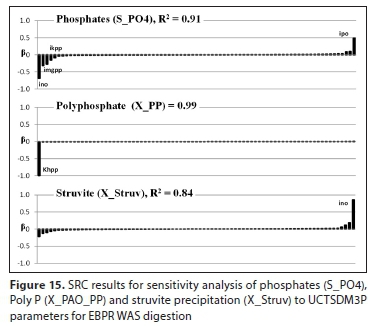
It is expected that most of the OP generated in the AD aqueous phase is due to the occurrence of PP breakdown. This PP breakdown process is modelled in a similar way in AD to that in the anaerobic reactor of the parent AS system - i.e., most of the PP is released immediately to generate energy for synthesis of PHA from acetate (Harding et al., 2010; Ikumi, 2011). This is because the environmental requirements for this process (i.e., sufficient quantities of acetate, from fermentation of biodegradable organics and the lack of an external terminal electron acceptor) are also present in AD reactors. However, after all PP is rapidly broken down in the AD (PP - i.e., MgcKdCaePO3, breakdown results in release of its constituent Mg, K, Ca and OP), there is ample supply of OP and some Mg in the aqueous phase of the AD reactor. This, together with the release of NH4+, which occurs with BPO hydrolysis, increases the precipitation potential of struvite (MgNH4PO4) - when the concentration of the ions contributing to formation of the struvite mineral (i.e., Mg, NH4+ and PO43-) are significantly high. Because struvite precipitation is encouraged by higher pH, the increased alkalinity associated with higher N releases from BPO (mainly due to the high ino values) further encourages struvite precipitation. The struvite precipitation in turn uses OP, resulting in reduction in OP present in the aqueous phase of AD mixed liquor, hence the negative impact of ino on OP (i.e., OP decreases with increase in ino). Conversely, the ipo represents the amount of P bound to the biodegradable organic material entering the AD, hence dictates the amount of OP to eventually be released with complete utilisation of these biodegradable organics. The P bound to biodegradable organics is much smaller than that in PP and gets released at a much slower rate (with the degradation of biodegradable organic material). Hence, relative to PP the organically bound P is not expected to have a major impact on OP released, although it does contribute to the total OP present in the AD system and add to the precipitation potential of struvite.
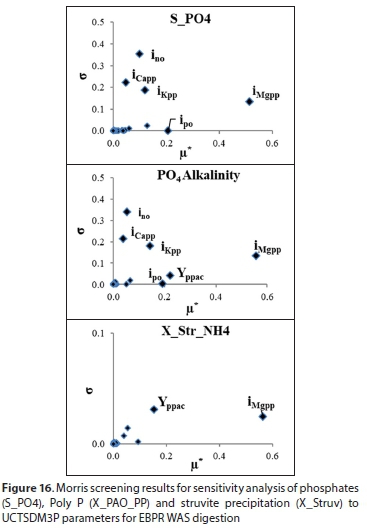
The Morris screening analysis results (Fig. 16) show that imgpp is the important parameter influencing OP concentration in AD. At longer sludge ages, where almost all the ammonia is released, the Mg (most made available from PP release and hydrolysis) is usually the component (out of Mg, OP and NH4, which form struvite) with the lowest concentration. Hence, it usually plays a role as the limiting factor for struvite precipitation (i.e., struvite precipitation comes to a stop after Mg gets depleted).
For AD systems that treat WAS from BEPR plants, containing PAOs and PP, significant alkalinity gets generated from OP (through MePO3 + H2O → Me+ + H2PO4-). The H2PO4- is a non-reference species for the OP weak acid system that results from the breakdown of PP in the AD. It is noted further that since the phosphate weak acid/base sub-system (for H2PO4-/HPO42- speciation) has a pKp2 value at 7.13, some of the H2PO4- consumes H2CO3* Alk.
This substantiates the observations in Fig. 14, where the pH is also sensitive to changes in Yppac. It was noted that the imgpp parameter controls the Mg content of PP and hence the amount of Mg eventually available (after PP hydrolysis) to promote P precipitation. Therefore, increasing this Mg content in PP would increase the P precipitation as struvite causing a decreased OP concentration in the aqueous phase. Moreover, the utilisation of OP with P precipitation brings about further adjustments in establishment of the system's alkalinity and pH.
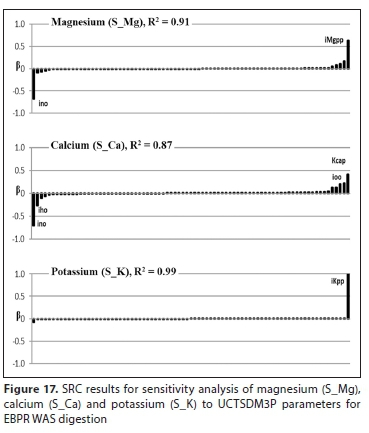
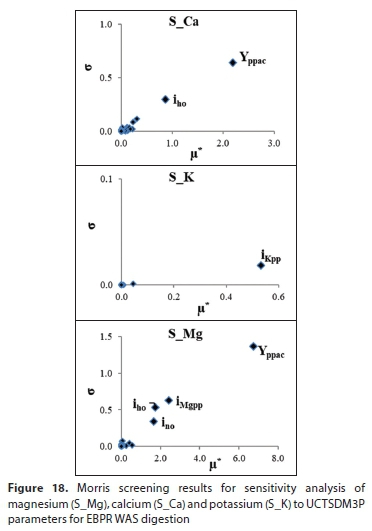
Metals (Mg, K and Ca)
The three main metallic ions released with PP breakdown in AD are Mg, K and Ca. The Mg and K are most influenced by changes in their respective molar contents in PP (i.e., imgpp for Mg and ikpp for K) (see Fig. 17). The molar fraction of Ca in PP is usually significantly smaller than that for Mg and K - hence icapp doesn't seem to have a significant impact on Ca concentration in the aqueous phase. Instead, the parameters likely to influence system pH, hence Ca precipitation potential (to calcium phosphate or calcium carbonate), are indicated to have an impact. These parameters include ino, iho, ioo and KCap (the rate constant for ACP precipitation). The Morris screening results also show that ikpp and imgpp are significant parameters for K and Mg, respectfully (see Fig. 18). However, Yppac is included as the most significant of parameters for Ca and Mg. It is expected then that Yppac would also be important for K, but this is not reflected in the results. The probable reason for this is due to K being the only metal that was released and usually least likely to participate in mineral precipitation (K - struvite, MgKPO4, has a high solubility product relative to the ionic product of Mg, K and PO43- in the aqueous phase). This may amplify the influence of ikpp relative to other parameters.
CONCLUSION
A sensitivity analysis was performed on ASM2-3P and UCTSDM3P (which together form PWM_SA) models using the standardized regression coefficient (SRC) and the Morris screening methods. The sensitivity analysis was useful towards detection of the significant parameters (prioritisation, using the SRC method) and non-influential parameters (with low µ and low σ, hence can be 'fixed', using the Morris screening method). For these sampled parameter sets, simulations have been conducted and predicted model outputs were compared with observed experimental outputs (Ikumi et al., 2015).
From this investigation it can be noted that various parameters, which are not normally measured at WRRFs, may require attention for future application of mathematical models in decision-making processes for WRRFs. These parameters include: for the AS system, fSup, fSbsa, muano and biodegradable organics elemental composition; and for the AD system fed WAS, the parameters driving kinetics of hydrolysis (i.e, Ksbohyd and kMbohyd) and substrate elemental composition (ino, ioo, iho, ipo, imgpp, ikpp and icapp). The development of sophisticated augmented batch tests that work together with mathematical model parameter estimation techniques (i.e., as proposed by Botha and Ekama, 2015) could be used towards this process.
However, although some of the significant parameters could be applied generically for different systems (e.g., the yield values and endogenous death rates), other paramaters may require measurements specific to the system being designed or operated in order to obtain accurate predictions of system response.
ACKNOWLEDGEMENTS
This research was supported by the Water Research Commission, the National Research Foundation and the University of Cape Town and is published with their permission.
REFERENCES
BATSTONE DJ, KELLER J, ANGELIDAKI I, KALYUZNHYI SV, PAVLOSTATHIS SG, ROZZI A, SANDERS WTM, SIEGRIST H and VAVILIN VA (2002) Anaerobic digestion model No. 1 (ADM1). Scientific and Technical Report No 9. International Water Association (IWA), London. [ Links ]
BATSTONE DJ, AMERLINCK Y, EKAMA G, GOEL R, GRAU P, JOHNSON B, KAYA I, STEYER J-P, TAIT S, TAKÁCS I, VANROLLEGHEM PA, BROUCKAERT CJ and VOLCKE E (2012) Towards a generalized physicochemical framework. Water Sci. Technol. 66 (6) 1147-1161. https://doi.org/10.2166/wst.2012.300 [ Links ]
BROUCKAERT CJ, IKUMI DS and EKAMA GA (2010) A 3-phase anaerobic digestion model. Proc. 12th IWA Anaerobic Digestion Conference (AD12), 1-4 November 2010, Guadalajara, Mexico. [ Links ]
BRUN R, KÜHNI M, SIEGRIST H, GUJER W and REICHERT P (2002) Practical identifiability of ASM2d parameters-systematic selection and tuning of parameter subsets. Water Res. 36 4113-4127. https://doi.org/10.1016/S0043-1354(02)00104-5 [ Links ]
CAMPOLONGO F, CARIBONI J and SALTELLI A (2007) An effective screening design for sensitivity analysis of large models. Environ. Model. Softw. 22 1509-1518. https://doi.org/10.1016/j.envsoft.2006.10.004 [ Links ]
COROMINAS LL, RIEGER L, TAKÁCS I, EKAMA GA, HAUDUC H, VANROLLEGHEM PA, OEHMEN A, GERNAEY KV, VAN LOOSDRECHT MC and COMEAU Y (2010) New framework for standardized notation in wastewater treatment modelling Water Sci. Technol. 61 (4) 841-857. https://doi.org/10.2166/wst.2010.912 [ Links ]
COSENZA A, MANNINA G, VANROLLEGHEM PA and NEUMANN MB (2013) Global sensitivity analysis in wastewater applications: A comprehensive comparison of different methods. Environ. Model. Softw. 49 40-52. https://doi.org/10.1016/j.envsoft.2013.07.009 [ Links ]
EKAMA GA and WENTZEL MC (2004) A predictive model for the reactor inorganic suspended solids concentration in activated sludge systems. Water Res. 38 (19) 4093-4106. https://doi.org/10.1016/j.watres.2004.08.005 [ Links ]
EKAMA GA, WENTZEL MC and SÖTEMANN SW (2006) Mass balanced-based plant-wide wastewater treatment plant models - Part 2: Tracking the influent inorganic suspended solids. Water SA. 32 (3) 277-285. https://doi.org/10.4314/wsa.v32i3.5272 [ Links ]
EKAMA GA (2009) Using bio-process stoichiometry to build a steady state plant-wide wastewater treatment plant model. Water Res. 43 (8) 2101-2120. https://doi.org/10.1016/j.watres.2009.01.036 [ Links ]
FLORES-ALSINA X, SOLON K, KAZADI MBAMBA C, TAIT S, JEPPSSON U, GERNAEY KV and BATSTONE DJ (2016) Modelling phosphorus, sulphur and iron interactions during the dynamic simulation of anaerobic digestion processes. Water Res. 95 370-382. https://doi.org/10.1016/j.watres.2016.03.012 [ Links ]
GAMERITH V, NEUMANN MB and MUSCHALLA D (2011) Applied global sensitivity analysis in sewer flow and water quality modelling. Proc. 12th International Conference of Urban Drainage, 10-15 September 2011, Porto Alegre, Brazil. [ Links ]
GHOOR T (2020) Developments in anaerobic digestion modelling. Department of Civil Engineering, University of Cape Town, Rondebosch, 7701, Western Cape, South Africa [ Links ]
HARDING TH, IKUMI DS and EKAMA GA (2010) A steady state stoichiometric model describing the anaerobic digestion of biological excess phosphorus removal waste activated sludge. Research Report W132 (MSc thesis), Department of Civil Engineering, University of Cape Town, South Africa. [ Links ]
HAUDUC H, RIEGER L, TAKÁCS I, HÉDUIT A, VANROLLEGHEM PA and GILLOT S (2010) A systematic approach for model verification: Application on seven published activated sludge models. Water Sci. Technol. 61 (4) 825-839. https://doi.org/10.2166/wst.2010.898 [ Links ]
HENZE M, GUJER W, MINO T, MATSUO T, WENTZEL MC and MARAIS GVR (1995) Activated sludge model No.2 (ASM2). IWA Scientific and Technical Report No. 3. IWA Publishing, London. [ Links ]
HENZE M, VAN LOOSDRECHT MCM, EKAMA GA and BRDJANOVIC D (2008) Biological Wastewater Treatment: Principles, Design and Modelling. IWA Publishing, London. 620 pp. [ Links ]
HERMAN JD, KOLLAT JB, REED PM and WAGENER T (2013) Technical Note: Method of Morris effectively reduces the computational demands of global sensitivity analysis for distributed watershed models. Hydrol. Earth Syst. Sci. 10 (4) 4275-4299. https://doi.org/10.5194/hessd-10-4275-2013 [ Links ]
HILL DT and BARTH CL (1977) A dynamic model for simulation of animal waste digestion. J. Water Pollut. Control Fed. 49 (10) 2129-2143. [ Links ]
IKUMI DS (2011) The development of a three-phase plant-wide mathematical model for sewage treatment. PhD thesis, Water Research Group (WRG), Department of Civil Engineering. University of Cape Town. [ Links ]
IKUMI D, VANROLLEGHEM PA, BOUCKAERT V, NEUMANN M and EKAMA G (2014) Towards calibration of phosphorus (P) removal plant-wide models. Proc. 4thIWA/WEF Wastewater Treatment Modelling Seminar (WWTmod2014), 30 March-2 April 2014, Spa, Belgium. 197-206. [ Links ]
IKUMI DS, HARDING TH, VOGTS M, LAKAY MT, MAFUNGWA HZ, BROUCKAERT CJ and EKAMA GA (2015) Mass balances modelling over wastewater treatment plants III. WRC Report No. 1822/1/14. Water Research Commission, Pretoria. [ Links ]
IKUMI DS, HARDING TH and EKAMA GA (2014) Plant-wide wastewater treatment modelling (1) - Biodegradability of wastewater and activated sludge organics in anaerobic digestion. Water Res. 56 (1) 267-279. https://doi.org/10.1016/j.watres.2014.02.008 [ Links ]
IKUMI DS, HARDING TH, VOGTS M, LAKAY MT, MAFUNGWA HZ, BROUCKAERT CJ and EKAMA GA (2015) Mass balances modelling over wastewater treatment plants III. WRC Report No. 1822/1/14. Water Research Commission, Pretoria. [ Links ]
KAZADI MBAMABA C, FLORES-ALSINA X, BATSTONE DJ and TAIT S (2015) A systematic study of multiple minerals precipitation modelling in wastewater treatment. Water Res. 85 359-370. https://doi.org/10.1016/j.watres.2015.08.041 [ Links ]
LIZARRALDE I, FERNÁNDEZ-ARÉVALOA T, BROUCKAERT CJ, VANROLLEGHEM PA, IKUMI DS, EKAMA GA, AYESA E and GRAU P (2015) A new general methodology for incorporating physicochemical transformations into multi-phase wastewater treatment process models. Water Res. 74 (5) 239 -256. https://doi.org/10.1016/j.watres.2015.01.031 [ Links ]
LOEWENTHAL RE, KORNMULLER URC and VAN HEERDEN EP (1994) Modelling struvite precipitation in anaerobic treatment systems. Water Sci. Technol. 30 (12) 107-116. https://doi.org/10.2166/wst.1994.0592 [ Links ]
MANNINA G, COSENZA A, VANROLLEGHEM PA and VIVIANI G (2011) A practical protocol for calibration of nutrient removal wastewater treatment models. J. Hydroinf. 13 (4) 575-595. https://doi.org/10.2166/hydro.2011.041 [ Links ]
McCARTY PL (1975) Stoichiometry of biological reactions. Prog. Water Technol. 7 (1) 157-172. [ Links ]
MOOSBRUGGER RE, WENTZEL MC, EKAMA GA and MARAIS GVR (1993b) A five-pH point titration method for determining the carbonate and SCFA weak acid/bases in anaerobic systems. Water Sci. Technol. 28 (2) 237-246. https://doi.org/10.2166/wst.1993.0112 [ Links ]
MORRIS MD (1991) Factorial sampling plans for preliminary computational experiments. Technometrics. 33 (2) 161-174. https://doi.org/10.1177/001872086700900503 [ Links ]
MUSVOTO EV, WENTZEL MC and EKAMA GA (2000) Integrated chemical-physical processes modelling I. Development of a kinetic based model for weak acid/base systems. Water Res. 34 (6) 1857-1867. https://doi.org/10.1016/S0043-1354(99)00334-6 [ Links ]
NEUMANN MB (2012) Comparison of sensitivity analysis methods for pollutant degradation modelling: A case study from drinking water treatment. Sci. Total Environ. 433 530-537. https://doi.org/10.1016/j.scitotenv.2012.06.026 [ Links ]
NOYKOVA NA and GYLLENBERG M (2000) Sensitivity analysis and parameter estimation in a model of anaerobic wastewater treatment processes with substrate inhibition. Bioprocess Biosyst. Eng. 23 (4) 343-349. DOI: https://doi.org/10.1007/s004499900169 [ Links ]
SALTELLI A, TARANTOLA S and CHAN KP (1999) A quantitative model-independent method for global sensitivity analysis of model output. Technometrics. 41 (1) 39-56. https://doi.org/10.1080/00401706.1999.10485594 [ Links ]
SALTELLI A, TARANTOLA S, CAMPOLONGO F and RATTO M (2004) Sensitivity Analysis in Practice, a Guide to Assessing Scientific Models. Wiley, New York. [ Links ]
SILVA MI and DE BORTOLI AL (2020) Sensitivity analysis for verification of an anaerobic digestion model. Int. J. Appl. Comput. Math. 6 (38). DOI: https://doi.org/10.1007/s40819-020-0791-z [ Links ]
SOBOL' I (1993) Sensitivity analysis for non-linear mathematical models. Math. Model. Comput. Exp. (Engl. Transl.). 1 407-414. [ Links ]
SOLON K, FLORES-ALSINA X, KAZADI MBAMBA C, IKUMI D, VOLCKE EIP, VANEECKHAUTE C, EKAMA GA, VANROLLEGHEM PA, BATSTONE DJ, GERNAEY KV and JEPPSSON U (2017) Plant-wide modelling of phosphorus transformations in wastewater treatment systems: Impacts of control and operational strategies. Water Res. 113 97-110. https://doi.org/10.1016/j.watres.2017.02.007 [ Links ]
SÖTEMANN SW, RISTOW NE, WENTZEL MC and EKAMA GA (2005) A steady-state model for anaerobic digestion of sewage sludges. Water SA. 31 (4) 511-527. https://doi.org/10.4314/wsa.v31i4.5143 [ Links ]
SÖTEMANN SW, VAN RENSBURG P, RISTOW NE, WENTZEL MC, LOEWENTHAL RE and EKAMA GA (2005b) Integrated chemical, physical and biological processes modelling Part 2 - Anaerobic digestion of sewage sludges Water SA. 31 545-568. https://doi.org/10.4314/wsa.v31i4.5145 [ Links ]
TAIT S, SOLON K, VOLCKE EIP and BATSTONE DJ (2012) A unified approach to modelling wastewater chemistry: model corrections. Proc. 3rd Wastewater Treatment Modelling Seminar (WWTmod2012), 26-28 February 2012, Mont-Sainte-Anne, Quebec, Canada. [ Links ]
VANHOOREN H, MEIRLAEN J, AMERLINCK Y, CLAEYS F, VANGHELUWE H and VANROLLEGHEM PA (2003) WEST: modelling biological wastewater treatment. J. Hydroinf. 5 27-50. https://doi.org/10.2166/hydro.2003.0003 [ Links ]
VAN RENSBURG P, MUSVOTO EV, WENTZEL MC and EKAMA GA (2003) Modelling multiple mineral precipitation in anaerobic digester liquor. Water Res. 37 (13) 3087-3097. https://doi.org/10.1016/S0043-1354(03)00173-8 [ Links ]
VANROLLEGHEM PA, INSEL G, PETERSEN B, SIN G, DE PAUW D, NOPENS I, WEIJERS S and GERNAEY K (2003) A comprehensive model calibration procedure for activated sludge models. Proc. WEF 26thAnnual Technical Exhibition and Conference (WEFTEC, 2003), 11-15 October 2003, Los Angeles. https://doi.org/10.2175/193864703784639615 [ Links ]
VOLCKE EIP, VAN LOOSDRECHT MCM and VANROLLEGHEM PA (2006) Continuity-based model interfacing for plant-wide simulation: A general approach. Water Res. 40 2817-2828. https://doi.org/10.1016/j.watres.2006.05.011 [ Links ]
WANG R, YONGMEI L, CHEN W, ZOU J and CHEN Y (2016) Phosphate release involving PAOs activity during anaerobic fermentation of EBPR sludge and the extension of ADM1. Chem. Eng. J. 297 (1) 436-447. https://doi.org/10.1016/j.cej.2015.10.110 [ Links ]
WENTZEL MC (1988) Biological excess phosphorus removal in activated sludge systems. PhD thesis, Water Research Group, Department of Civil Engineering, University of Cape Town. [ Links ]
WENTZEL MC, EKAMA GA, DOLD PL and MARAIS GVR (1990) Biological excess phosphorous removal - steady state process design Water SA. 16 (1) 29-48. [ Links ]
ZHAO X, LI L, WU D, XIAO T, MA Y and PENG X (2019) Modified Anaerobic Digestion Model No. 1 for modelling methane production from food waste in batch and semi-continuous anaerobic digestions. Bioresour. Technol. 271 109-117. https://doi.org/10.1016/j.biortech.2018.09.091 [ Links ]
 Correspondence:
Correspondence:
DS Ikumi
Email: david.ikumi@uct.ac.za
Received: 16 July 2019
Accepted: 23 June 2020














