Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Water SA
On-line version ISSN 1816-7950
Print version ISSN 0378-4738
Water SA vol.46 n.3 Pretoria Jul. 2020
http://dx.doi.org/10.17159/wsa/2020.v46.i3.8652
RESEARCH PAPERS
Application of logistic model to estimate eggplant yield and dry matter under different levels of salinity and water deficit in greenhouse and outdoor conditions
Mohammad Rafie Rafiee; Mehdi Mahbod
Department of Water Sciences & Engineering, College of Agriculture, Jahrom University, Jahrom, 74137-66171, I.R. Iran
ABSTRACT
Eggplant is an important product in greenhouse cultivation in the world. However, much of its production is done on the farm. Few studies have been conducted on modelling of its growth and yield. Considering the simplicity of the logistic models, only the temperature and dry matter data during the growing season are needed to calibrate them. Hence, we evaluated the performance of the logistic model in growth and yield prediction of eggplant in greenhouse and farm conditions. Eggplants were planted in 2012 and 2013 under different treatments of irrigation and salinity with a complete randomized block statistical design. Irrigation frequency treatments consisted of: daily (I1), weekly, (I2) and every 2 weeks of irrigation (I3). Each pot was irrigated to field capacity level. Four levels of salinity treatments are as follows: electrical conductivities (EC) of 0.8 (J1); 2.5 (J2); 5.0 (J3) and 7.0 (J4) dS∙m-1. The amount of plant dry matter was measured during the growing season (DM) and the amount of product (Y) at the end of the growing season. The logistic model was calibrated with the first-year data and validated with the second-year data. Logistic equation coefficients and harvest index were estimated as a function of the depth and electrical conductivity of irrigation water. The results showed that the accuracy of the logistic model for estimating DM during the growing season was good and predicted the product at the end of the growing season with acceptable accuracy. Also, the model's agreement with the measured DM and Y was good.
Keywords: crop modelling, greenhouse, logistic model, salinity
INTRODUCTION
Crop modelling has been gaining momentum over the past decade; partly due to the necessity of sustainable agriculture under environmental degradation along with population growth (Overman and Martin, 2001; Overman et al., 2003; Sepaskhah et al. 2011; Du et al., 2014; Camargo et al., 2015; Ramírez-Pérez et al., 2018). Such models help to assess the most appropriate planning in agro-environmental systems, through optimization of water and fertilizer application and finally maximizing returns to farmers. However, crops are highly dynamic systems emerging from an interface between cultivar factors, environmental conditions and management practices. The interaction of these determinants induces various stress patterns, resulting in different yield and growth patterns (Casadebaig et al., 2016). Deficiency in irrigation water quantity and quality leads to a reduction of water uptake and therewith significant evapotranspiration and yield limitation. Crop yield prediction according to water requirement or evapotranspiration is important in irrigation system design and evaluation (Ünlükara et al., 2010).
However, prearranged reduction of water application at certain stages of the growing season, called deficit irrigation, has been extensively studied and considered as a suitable irrigation strategy in dry regions (Rodrigues and Pereira, 2009; Geerts and Raes, 2009; Ghaemi and Rafiee, 2016). To obtain a precise description of crop growth features, a large number of variables have to be simultaneously taken into consideration, of which many are usually not available. Accordingly, crop models are divided into two general categories: dynamic and empirical (simple) models. Dynamic models simulate plant growth and development processes in relation to environmental factors and the movement of water in the soil. Consequently, these models require a large number of inputs, as model calibration is needed in various segments of such models. Measurement of some environmental factors and the calibration process are financially expensive and time-consuming (Kasampalis et al., 2018). A number of models, namely, WOFOST (Van Diepen et al., 1989), STICS (Brisson et al., 2003), APSIM (Keating et al., 2003), DSSAT (Jones et al., 2003), have been employed by researchers since they were first presented (Jin et al., 2018). In contrast, in empirical models, a detailed look at the mechanism of the environmental factors affecting plant growth is not considered. Instead, these models require fewer inputs. Further, they can be easily calibrated for a given location. Some examples of well-validated models in the country of the present study are presented by Ziaei and Sepaskhah (2003), Pirmoradan and Sepaskhah (2006), and Shabani et al. (2015). Simple models are still quite attractive to researchers (Basso and Ritchie. 2015), as they require fewer parameters and allow researchers to use literature or limited crop data to provide reasonable estimates of crop components (Dzotsi et al., 2015). Simple crop growth simulation models can be outlined as non-linear functions of a dependent variable (plant height, biomass accumulation or fruit growth dynamics) and an independent variable (time or growing degree days) (Lopez et al., 2000; Ruiz et al., 2012). One commonly used model is the logistic model, based on a sigmoid function of cumulative heat units (Shabani et al., 2015, 2018a, 2018b).
Sepaskhah et al. (2011) developed a logistic model based on cumulative heat units, considering the effect of seasonal water and nitrogen application on maize dry matter and grain yield. The harvest index (HI) was also related to the applied water and nitrogen as another empirical model. Wardhani and Kusumastuti (2013) showed the superiority of logistic models in describing maize growth height in comparison with the Gompertz model. They suggested two different models for the two distinct stages of plant growth, i.e., vegetative and generative stage. Mahbod et al. (2015) estimated yield and dry matter of winter wheat with the logistic model under different irrigation water regimes and nitrogen application rates. The total irrigation water, rainfall and nitrogen, plus residual soil mineral nitrogen, applied in the logistic model coefficients and the harvest index, predicted above-ground dry matter and grain yield with good accuracy.
Eggplant is an important vegetable crop, produced as 35.3 million tons from 1.9 million ha worldwide. Eggplant is ranked third within the greenhouse products, after tomato, pepper and cucumber. Around 94% of eggplant is produced in Asia (FAOSTAT, http://www.fao.org/faostat/). Despite extensive investigations on cereal crop growth modelling, few researchers have investigated vegetable crops such as eggplant (Keating et al., 2014; Zurayk et al., 1993). However, it is important that the use of low-quality water and its effect on crop growth dynamics should be taken into consideration, given ever-increasing water supply limitations throughout the world. For example, Assaha et al. (2013) assessed the salinity tolerance of eggplant under two levels of salinity stress. Abd El-Azeem et al. (2012) elucidated the effects of inoculation with plant growth-promoting rhizobacteria on eggplant growth, yield, and mineral content under salt stress. Therefore, this study aims to use the logistic model to simulate the effect of salinity and drought stresses on eggplant yield and above-ground dry matter in greenhouse and outdoor cultivation environments.
MATERIALS AND METHODS
Experimental procedure
On 5 May 2012 and 18 May 2013, uniform seedlings of eggplant (Anamur RZ cultivar) were transplanted to both the field and plastic pots in the adjacent greenhouse located in Badjgah (29°36'N, 52°32'E), College of Agriculture, Shiraz University, Shiraz, Iran. Each pot (with 35 cm diameter and 60 cm height), filled with the same field soil from the same depth, functioned as a microlysimeter. Some physical and chemical properties of the soil are presented in Table 1. Before transplanting, 1 g mono-ammonium phosphate was added to each soil pot, and 1 g, 0.5 g and 0.5 g potassium nitrate was applied to each pot, respectively, in the three different stages of the growth period (i.e. transplant, beginning of flowering and start of harvest). Weather parameters including net radiation (Rn), air temperature (Ta) and relative humidity (RH) were collected simultaneously from two automatic stations installed inside and outside the greenhouse. Changes of such parameters during the experimental periods are shown in Fig. 1.
Irrigation and salinity treatments were initiated after the establishment of plants (14 days after transplanting). The experiment was laid out according to a complete randomized design with 3 replicates per treatment. Irrigation frequency treatments consisted of: daily (I1), weekly (I2) and every 2 weeks of irrigation (I3). Each pot was irrigated to the soil field capacity level. Four levels of salinity treatments were as follows: electrical conductivities (EC) of 0.8 (J1); 2.5 (J2); 5.0 (J3) and 7.0 (J4) dS∙m-1. Pots were weighed prior to each irrigation, and the weight of irrigation water amount (WI) was computed as:

where W and WFC are each pot weight (g) just before irrigation and at field capacity, respectively. WFC is calculated as the weight summation of plastic pots (Wplastic pots), dry soil (Wdry soil), water at field capacity (WθFC) and plant (Wplant).

Wplastic pots, Wdry soil and WθFC (ρb × θFC × soil volume) were defined at the beginning of the experiment and Wplant was assessed using pot weight (Wtotal) and soil moisture (θi−1) a day before irrigation as:
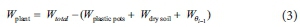
where Wθi1 is mass of soil water 1 day before irrigation, calculated as ρb × θi−1 × soil volume.
Leaching fraction (LF) of 0.15 was considered for efficient irrigation as proposed by Ayers and Westcot (1985). Leachate was gathered and weighed after irrigation using empty pans placed underneath each pot. Table 2 shows the number of irrigations and total water applied in the outdoor and greenhouse treatments.
Crop dry matter (DM) was determined during 7 stages at 2-week intervals including harvest time. Seven extra pots were reserved for each treatment, the plants from which were used to measure dry matter at 6 stages during the growing season. Fruits per plant were gathered and weighed during August and September. Shoot and root dry weights were determined next. It should be noted that in eggplant cultivation there is the possibility of periodic and continuous harvests after the first crop. Therefore, harvest index values were calculated as the ratio of fruit weight at the first harvest to weight of above-ground dry matter.
Model theory
Logistic models using 'calendar days after planting' as the independent variable, may provide unsatisfactory estimates in regions with different climatic conditions (Mahbod et al., 2015). On the other hand, temperature is one of the most important factors governing plant growth (Sadek et al., 2013). Growing degree-days is considered as an important factor for all biological development due to its simple estimations of the accumulated heat energy available over the growing season or life cycle of an organism. The rate of growth and phenological development of individual plants has been found to increase almost linearly from a base to a limiting temperature threshold (Cesaraccio et al., 2001; Fealy, 2008). Therefore, to designate variable environmental conditions during growing season and planting dates, cumulative heat unit (GDD) was calculated as follows:
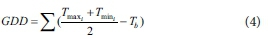
where Tmin and Tmax are the daily minimum and maximum air temperature at Day i (°C), Tb is the base temperature of 11°C according to Rouphael et al. (2010). No degree days were considered for days with average temperatures equal or below Tb.
Distinct plant features such as crop height, canopy, population and biomass growth can be modelled by 'S-shaped' logistic functions of GDD as below (Shabani et al., 2018a):
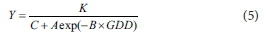
In this study, Y is considered as eggplant DM, and K, A, B and C are coefficients of the equation. In the calibration phase, K, A, B and C were determined using DM values measured in the first year of the experiment by Solver tool in MS Excel. These coefficients were then fitted to quadratic functions of seasonal applied water (I) and water salinity (EC) via stepwise multiple regression analysis. The calibrated experimental logistic model was then used to estimate eggplant DM for the second year. Finally, the predicted DM values were compared with the measured values in order to validate the model in the greenhouse and outdoor environments.
Statistical evaluation
Statistical parameters used to describe the model accuracy were coefficient of determination (R2) (interpreted as the proportion of the variance in the dependent variable that is predictable from the independent variable, indicating the extent to which the dependent variable is predictable), normalized root mean square error (NRMSE), index of agreement (d) and F-test (Willmott et al., 1985):
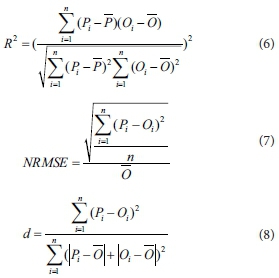
where Pi and Oi are the predicted and observed values, respectively, n is the data number, Ō and P are the observed and predicted mean values, respectively. The simulation is considered excellent with a NRMSE less than 0.1, good if the NRMSE is greater than 0.1 and less than 0.2, fair if the NRMSE is greater than 0.2 and less than 0.3, and poor if the NRMSE is greater than 0.3 (Jamieson et al., 1991; Mahbod et al., 2015). According to the d-index, the closer the index value is to 1, the better the agreement between the two variables that are being compared and vice versa.
RESULTS AND DISCUSSION
Table 3 indicates some eggplant growth traits, including final fruit yield per plant (Y), fruit size and shoot dry matter weights (shoot DM). As designated in Table 3, both irrigation and salinity significantly affected eggplant fruit yield. Nevertheless, the yield values were not significantly different in I1 and I2 treatments in either environment, except for outdoor cultivation in the second year (Table 4). Moreover, the deleterious effects of salt stress were reinforced by the prolongation of irrigation intervals, as has been reported by Rameshwaran (2015). Table 3 also shows ECe values for each irrigation and water salinity treatment. Such values ranged from 2.7 (I1J1) to 18.8 (I3J4) and 1.6 to 16.4 dSm-1 for outdoor and greenhouse pots, respectively. As the salinity of irrigation water (ECw) increased, ECe tended to increase significantly for all watering frequency treatments in both outdoor and greenhouse environments. The higher ECe value observed in the outdoor treatments in comparison to the greenhouse pots was due to the higher evaporation occurring from the surface, as reported by Aragüés et al. (2005). As shown in Table 3, longer irrigation intervals from I1 to I3, escalate ECe values in both outdoor and greenhouse environments. Both water deficit and salinity significantly affected ECe values according to ANOVA analysis.
Considering the environment as a cause of variations, a compound analysis of variance was exercised to compare the results of I and J treatments on greenhouse yields with the outdoor ones. As shown in Table 5, no significant effect of environment was met on Y and ECe values, while it significantly affected ETC at 5%.
Given that the obtained results showed no significant difference in salinity of the saturated extract in the greenhouse and the outdoor conditions, ECe could not be considered as the effective factor for obtaining quadratic equations for estimation of B, C, and K, whereas irrigation water salinity was considered as an effective factor for its simplicity. On the other hand, due to the difference in the mean DM in the greenhouse and outdoor conditions, independent and separate logistic functions were fitted for the mentioned conditions.
Crop growth modelling
Model calibration
First-year values of total plant dry matter accumulation (DM) and GDD were used to obtain the coefficients of Eq. 4 that are presented in Table 6 for greenhouse and outdoor conditions. As reported by Sepaskhah et al. (2011), the calibration coefficients are affected by agronomic management parameters. A similar trend was observed for this study, so that, K and B values increased with increasing levels of water and salinity. Furthermore, B values increased with higher water application levels and decreased at higher salinity levels. Thus, the calibrated K, B and C coefficients were fitted to quadratic functions based on seasonal applied water (I) and water salinity (EC) using stepwise multiple regression analysis. Such functions are given as follows:
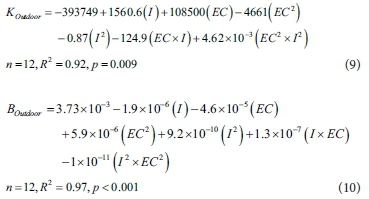

where n is the number of observations and p is the probability level. Values of A were not noticeably different at different levels of salinity and applied water, which agreed with the results of Mahbod et al. (2015), in which the values of A were assumed constant at different irrigation levels and nitrogen rates. Therefore, A was considered as a constant value of 100 000 according to the average of calculated A in each treatment.
Figure 2 demonstrates sample results of measured and predicted DM changes with GDD for I1 irrigation water level under different salinity levels. According to the results, the developed logistic equations properly predicted DM values in both environments. Shabani et al. (2014) reached the same results estimating yield and dry matter of rapeseed. According to their study, statistical parameters indicated that logistic equation was fitted very accurately for all irrigation and water salinity treatments. To investigate the model accuracy over all treatments, measured DM values during the growing season (DMm) are compared with the estimated ones (DMP) with the 1:1 line in Fig. 3. The satisfying values of d (0.96, 0.97); NRSME (0.13, 0.11) and R2 (0.91, 0.89) in outdoor and greenhouse conditions, respectively, along with regression line slopes close to 1 (1.02, 0.89), statistically confirm that the calibrated empirical models accurately estimated eggplant dry matter.
Harvest index and yield
Using multiple regression analysis, harvest index (HI) as a function of seasonal irrigation water and water salinity, is determined as follows:
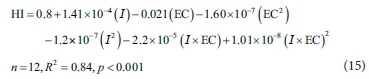
Eggplant dry fruit yield (YP) was estimated from HI equation (Eq. 15) multiplied by predicted DM values at harvest time in 2012. The relationship between predicted (YP) and measured (YM) dry fruit yields in the first year are shown in Fig. 4. Low scatter of data, shown by high values of R2 along with statistical factors d and NRSME close to 1 and 0, respectively, indicates high accuracy of the calibrated model in prediction of fruit yield.
Model validation
Total dry matter
Measured values of irrigation water in the second year of experiment (2013), along with water salinity, were applied to estimate K, B and C coefficients using Eqs 9-14 for 2013. The obtained values are presented in Table 7. Total dry matter (DMP) values for the second year were then obtained using the developed logistic model and GDD data. Such values were compared with the measured DM during the second growing season (DMm) in order to validate the model.
Figure 5 indicates the comparison between DMP and DMm during the growing season for I2 treatments in outdoor and greenhouse conditions. Satisfying agreement between the measured and predicted values of DM was also obtained for other treatments with good accuracy. The linear relationship between measured and estimated values of DM was compared with the 1:1 line to evaluate the model in Fig. 6. The slopes were close to 1.0 in both environmental conditions and the values of NRMSE (0.12, 0.15) and d (0.97, 0.93) and R2 (0.91 and 0.84 for outdoor and greenhouse, respectively) indicated accurate estimations in either environment. Xiangxiang et al. (2014) predicted DM values of winter wheat under different irrigation treatments in China's Loess Plateau using logistic function and obtained relative errors from 2-15%. Mahbod et al. (2015) and Shabani et al. (2015) found similar results for wheat and winter sorghum under different water and nitrate fertilization treatments, with NRMSE values of 0.11 and 0.02, respectively. Results of the present study alongside previous investigations indicate that logistic functions can properly predict DM values during the growing season.
Fruit yield (Y)
Fruit yield was predicted using the estimated DM values (Eqs 5 and 9−14) and HI values obtained from Eq. 15 in the second year of experiment. The relationship between predicted and measured values of final DM, HI and DY are shown in Fig. 7, for outdoor (a), greenhouse (b) and total (c) treatments. NRMSE values in Fig. 7 show proper estimations of dry matter at the end of cropping season, inside and outside of the greenhouse. The outdoor value of the d index was close to 1 (0.9) indicating model accordance with measured values; however, the value obtained in the greenhouse was smaller (0.69). Despite the high value of R2 in outdoor conditions, a considerably lower value was obtained for greenhouse conditions, implying that the fitted function in greenhouse conditions could not predict the variation of changes in total DM. On the other hand, accuracy in HI estimations was uppermost, obtaining NRMSE values of 0.04 in both conditions. Shabani et al. (2015) also found 0.02 for NRMSE in HI estimations and, according to Mahbod et al. (2015), HI values were predicted with proper precision. Errors of Y estimation in outdoor and greenhouse estimations increased up to 0.22 and 0.27, respectively, due to integration of total HI and DM estimation errors. Similar results were found by Mahbod et al. (2015) in which NRMSE values of crop estimation were 0.11 higher than those of DM. Generally, the logistic model precision was acceptable for eggplant crop yield estimation in both greenhouse and outdoor conditions.
CONCLUSIONS
The effect of irrigation regimes and water salinity on eggplant evapotranspiration, dry matter, and yield was studied in greenhouse and outdoor conditions, during two 110-day experiments conducted in two successive years (2012 and 2013). Final dry matter and fruit yield of eggplant were simulated with an empirical logistic growth model based on GDD under different levels of water deficit and salinity. Such models can only be applied for the same weather conditions under which models were developed. Therefore, the model was first calibrated using the measured DM values during the first year of experiment. Logistic function coefficients and the harvest index were related to total irrigation water application and water salinity. Finding acceptable accuracy in the calibrated model, the model was validated according to the DM and fruit yield data collected during the second year. Statistical analysis indicated that the accuracy of the model in DM, HI and Y estimations was fair, excellent and fair, respectively. d index values showed good accordance of the model with measured data. Hence, the logistic model can be used to predict eggplant DM and fruit yield.
REFERENCES
ABD EL-AZEEM SAM, ELWAN MWM, SUNG JK and OK YS (2012) Alleviation of salt stress in eggplant (Solanum melongena L.) by plant-growth-promoting rhizobacteria. Commun. Soil Sci. Plant Anal. 43 (9) 1303-1315. https://doi.org/10.1080/00103624.2012.666305 [ Links ]
ARAGÜÉS R, PUY J, ROYO A and ESPADA JL (2005) Three-year field response of young olive trees (Olea europaea L., cv. Arbequina) to soil salinity: Trunk growth and leaf ion accumulation. Plant Soil. 271 (1-2) 265-273. https://doi.org/10.1007/s11104-004-2695-9 [ Links ]
ASSAHA DVM, UEDA A and SANEOKA H (2013) Comparison of growth and mineral accumulation of two solanaceous species, Solanum scabrum Mill. (huckleberry) and S. melongena L. (eggplant), under salinity stress. Soil Sci. Plant Nutr. 59 (6) 912-920. https://doi.org/10.1080/00380768.2013.858300 [ Links ]
AYERS RS and WESTCOT DW (1985) Water quality for agriculture. FAO Irrigation and Drainage 29, Rev. 1. FAO, Rome. [ Links ]
BASSO B and RITCHIE JT (2015) Simulating crop growth and biogeochemical fluxes in response to land management using the SALUS model. In: Hamilton SK, Doll JE and Robertson GP (eds) The Ecology of Agricultural Landscapes: Long-Term Research on the Path to Sustainability. Oxford University Press, New York. 252-274. [ Links ]
BRISSON N, GARY C, JUSTES E, ROCHE R, MARY B, RIPOCHE D, ZIMMER D, SIERRA J, BERTUZZI P, BURGER P and co-authors (2003) An overview of the crop model STICS. Eur. J. Agron. https://doi.org/10.1016/S1161-0301(02)00110-7 [ Links ]
CAMARGO DC, MONTOYA F, CÓRCOLES JI and ORTEGA JF (2015) Modeling the impacts of irrigation treatments on potato growth and development. Agric. Water Manage. 150 119-128. https://doi.org/10.1016/j.agwat.2014.11.017 [ Links ]
CASADEBAIG P, ZHENG B, CHAPMAN S, HUTH N, FAIVRE R and CHENU K (2016) Assessment of the potential impacts of wheat plant traits across environments by combining crop modeling and global sensitivity analysis. PLoS ONE. 11 (1). https://doi.org/10.1371/journal.pone.0146385 [ Links ]
CESARACCIO C, SPANO D, DUCE P and SNYDER RL (2001) An improved model for determining degree-day values from daily temperature data. Int. J. Biometeorol. 45 (4) 161-169. https://doi.org/10.1007/s004840100104 [ Links ]
CROSS HZ and ZUBER MS (1972) Prediction of flowering dates in maize based on different methods of estimating thermal units 1. Agron. J. 64 (3) 351-355. https://doi.org/10.2134/agronj1972.00021962006400030029x [ Links ]
DU T, KANG S, ZHANG X and ZHANG J (2014) China's food security is threatened by the unsustainable use of water resources in north and northwest China. Food Energ. Secur. (1) 7-18. https://doi.org/10.1002/fes3.40 [ Links ]
DZOTSI KA, BASSO B and JONES JW (2015) Parameter and uncertainty estimation for maize, peanut and cotton using the SALUS crop model. Agric. Syst. 135 31-47. https://doi.org/10.1016/j.agsy.2014.12.003 [ Links ]
FEALY R and FEALY RM (2008) The spatial variation in degree days derived from locational attributes for the 1961 to 1990 period. Irish J. Agric. Food Res. 47 1-11. [ Links ]
GEERTS S and RAES D (2009) Deficit irrigation as an on-farm strategy to maximize crop water productivity in dry areas. Agric. Water Manage. 96 (9) 1275-1284. https://doi.org/10.1016/j.agwat.2009.04.009 [ Links ]
GHAEMI AA and RAFIEE MR (2016) Evapotranspiration and yield of eggplant under salinity and water deficit: a comparison between greenhouse and outdoor cultivation. Mod. Appl. Sci. 10 (11) 8. https://doi.org/10.5539/mas.v10n11p8 [ Links ]
JAMIESON PD, PORTER JR and WILSON DR (1991) A test of the computer simulation model ARCWHEAT1 on wheat crops grown in New Zealand. Field Crops Res. 27 (4) 337-350. https://doi.org/10.1016/0378-4290(91)90040-3 [ Links ]
JIN X, KUMAR L, LI Z, FENG H, XU X, YANG G and WANG J (2018) A review of data assimilation of remote sensing and crop models. Eur. J. Agron. 92 141-152. https://doi.org/10.1016/j.eja.2017.11.002 [ Links ]
JONES JW, HOOGENBOOM G, PORTER CH, BOOTE KJ, BATCHELOR WD, HUNT LA, WILKENS PW, SINGH U, GIJSMAN AJ and RITCHIE JT (2003) The DSSAT cropping system model. Eur. J. Agron. https://doi.org/10.1016/S1161-0301(02)00107-7 [ Links ]
KASAMPALIS D, ALEXANDRIDIS T, DEVA C, CHALLINOR A, MOSHOU D and ZALIDIS G (2018) Contribution of remote sensing on crop models: a review. J. Imaging 4 (4) 52. https://doi.org/10.3390/jimaging4040052 [ Links ]
KEATING BA, CARBERRY PS, HAMMER GL, PROBERT ME, ROBERTSON MJ, HOLZWORTH D, HUTH NI, HARGREAVES JNG, MEINKE H, HOCHMAN Z and co-authors (2003) An overview of APSIM, a model designed for farming systems simulation. Eur. J. Agron. https://doi.org/10.1016/S1161-0301(02)00108-9 [ Links ]
KEATINGE JDH, LIN LJ, EBERT AW, CHEN WY, HUGHES JDA, LUTHER GC, WANG JF and RAVISHANKAR M (2014) Overcoming biotic and abiotic stresses in the Solanaceae through grafting: Current status and future perspectives. Biol. Agric. Hortic. 30 (4). https://doi.org/10.1080/01448765.2014.964317 [ Links ]
LÓPEZ S, FRANCE J, GERRITS WJ, DHANOA MS, HUMPHRIES DJ and DIJKSTRA J (2000) A generalized Michaelis-Menten equation for the analysis of growth. J. Anim. Sci. 78 (7) 1816. https://doi.org/10.2527/2000.7871816x [ Links ]
MAHBOD M, SEPASKHAH AR and ZAND-PARSA S (2014) Estimation of yield and dry matter of winter wheat using logistic model under different irrigation water regimes and nitrogen application rates. Arch. Agron. Soil Sci. 60 (12) 1661-1676. https://doi.org/10.1080/03650340.2014.917169 [ Links ]
OVERMAN AR and MARTIN FG (2001) Fisher information and crop model parameters. Commun. Soil Sci. Plant Anal. 32 (17-18) 2809-2818. https://doi.org/10.1081/CSS-120000963 [ Links ]
OVERMAN AR, SCHOLTZ RV and MARTIN FG (2003) In defense of the extended logistic model of crop production. Commun. Soil Sci. Plant Anal. 34 (5-6) 851-864. https://doi.org/10.1081/CSS-120018979 [ Links ]
PIRMORADIAN N and SEPASKHAH (2006) A very simple model for yield prediction of rice under different water and nitrogen applications. Biosyst. Eng. 93 (25-34). https://doi.org/10.1016/j.biosystemseng.2005.09.004 [ Links ]
RAMESHWARAN P, TEPE A, YAZAR A and RAGAB R (2015) The effect of saline irrigation water on the yield of pepper: experimental and modelling study. Irrig. Drain. 64 (1) 41-49. https://doi.org/10.1002/ird.1867 [ Links ]
RAMÍREZ-PÉREZ LJ, MORALES-DÍAZ AB, BENAVIDES-MENDOZA A, DE-ALBA-ROMENUS K, GONZÁLEZ-MORALES S and JUÁREZ-MALDONADO A (2018) Dynamic modeling of cucumber crop growth and uptake of N, P and K under greenhouse conditions. Sci. Hort. 234 250-260. https://doi.org/10.1016/j.scienta.2018.02.068 [ Links ]
RODRIGUES GC and PEREIRA LS (2009) Assessing economic impacts of deficit irrigation as related to water productivity and water costs. Biosyst. Eng. 103 (4) 536-551. https://doi.org/10.1016/j.biosystemseng.2009.05.002 [ Links ]
ROUPHAEL Y, CARDARELLI M, AJOUZ N, MARUCCI A and COLLA G (2010) Estimation of eggplant leaf number using thermal time model. J. Food Agric. Environ. 8 (2) 847-850. [ Links ]
RUIZ TE, TORRES V, FEBLES G, DIAZ H and GONZLLEZ J (2012). Empleo de la modelación para estudiar el crecimiento del material vegetal 23 de Tithonia diversifolia. Rev. Cubana Cien. Agríc. 46 (1) 23-29. [ Links ]
SADEK B, SHEHAB S, WIECEK M, SUBRAMANIAN D, SHAFIULLAH M, KIEĆ-KONONOWICZ K and ADEM A (2013) Anticonvulsant properties of histamine H3 receptor ligands belonging to N-substituted carbamates of imidazopropanol. Bioorganic Med. Chem. Lett. 23 (17) 4886-4891. https://doi.org/10.1016/j.bmcl.2013.06.075 [ Links ]
SEPASKHAH AR, FAHANDEZH-SAADI S and ZAND-PARSA S (2011) Logistic model application for prediction of maize yield under water and nitrogen management. Agric. Water Manage. 99 (1) 51-57. https://doi.org/10.1016/j.agwat.2011.07.019 [ Links ]
SHABANI A, SEPASKHAH AR and KAMGAR-HAGHIGHI AA (2014) Estimation of yield and dry matter of rapeseed using logistic model under water salinity and deficit irrigation. Arch. Agron. Soil Sci. 60 (7) 951-969. https://doi.org/10.1080/03650340.2013.858807 [ Links ]
SHABANI Ali, SEPASKHAH AR and KAMGAR-HAGHIGHI AA (2015) A model to predict the dry matter and yield of rapeseed under salinity and deficit irrigation. Arch. Agron. Soil Sci. 61 (4) 525-542. https://doi.org/10.1080/03650340.2014.938645 [ Links ]
SHABANI A, SEPASKHAH AR and KAMGAR-HAGHIGHI AA (2018b) Selecting best double sigmoid function to describe growth and growth rate of rapeseed under water stress. Int. J. Plant Prod. 12 (4) 225-241. https://doi.org/10.1007/s42106-018-0019-x [ Links ]
SHABANI A, SEPASKHAH AR, KAMGAR-HAGHIGHI AA and HONAR T (2018a) Using double logistic equation to describe the growth of winter rapeseed. J. Agric. Sci. 156 (1) 37-45. https://doi.org/10.1017/S0021859617000934 [ Links ]
ÜNLÜKARA A, KURUNÇ A, KESMEZ GD, YURTSEVEN E and SUAREZ DL (2010) Effects of salinity on eggplant (Solanum melongena L.) growth and evapotranspiration. Irrig. Drain. 59 (2) 203-214. https://doi.org/10.1002/ird.453 [ Links ]
VAN DIEPEN CA, WOLF J, VAN KEULEN H and RAPPOLDT C (1989) WOFOST: a simulation model of crop production. Soil Use Manage. 5 (1) 16-24. https://doi.org/10.1111/j.1475-2743.1989.tb00755.x [ Links ]
WARDHANI WS and KUSUMASTUTI P (2014) Describing the height growth of corn using logistic and Gompertz model. AGRIVITA, J. Agric. Sci. 35 (3) 237-241. [ Links ]
WILLMOTT CJ, ROWE CM and MINTZ Y (1985) Climatology of the terrestrial seasonal water cycle. J. Climatol. 5 (6) 589-606. https://doi.org/10.1002/joc.3370050602 [ Links ]
XIANGXIANG W, QUANJIU W, JUN F, LIJUN S and XINLEI S (2014) Logistic model analysis of winter wheat growth on China's Loess Plateau. Can. J. Plant Sci. 94 (8) 1471-1479. https://doi.org/10.4141/cjps2013-293 [ Links ]
ZIAEI AN and SEPASKHAH AR (2003) Model for simulation of winter wheat yield under dryland and irrigated conditions. Agric. Water Manage. 58 (1) 1-17. https://doi.org/10.1016/S0378-3774(02)00080-X [ Links ]
ZURAYK R, NIMAH M and HAMZÉ M (1993) The salt tolerance potential of local cultivars of eggplant (Solanum melongena L.). Biol. Agric. Hort. 9 (4) 317-324. https://doi.org/10.1080/01448765.1993.11978502 [ Links ]
 Correspondence:
Correspondence:
Mohammad Rafie Rafiee
Email:mrrafiee73@gmail.com
Received: 21 April 2019
Accepted: 2 June 2020














