Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Water SA
On-line version ISSN 1816-7950
Print version ISSN 0378-4738
Water SA vol.46 n.3 Pretoria Jul. 2020
http://dx.doi.org/10.17159/wsa/2020.v46.i3.8650
RESEARCH PAPERS
Estimation of surface depression storage capacity from random roughness and slope
Mohamed AM Abd ElbasitI, II; Majed M Abu-ZreigIII, IV; Chandra SP OjhaV; Hiroshi YasudaVI; Liu GangVII
IAgricultural Research Council - Soil Climate and Water, Pretoria 0001, South Africa
IISchool of Geography, Archaeology, and Environmental Studies, University of the Witwatersrand, Johannesburg 2000, South Africa
IIICivil Engineering Department, Jordan University of Science and Technology, Irbid, Jordan
IVInternational Platform for Dryland Research and Education, Tottori University, Tottori, Japan
VDepartment of Civil Engineering, Indian Institute of Technology, Roorkee, India
VIOrganization for Educational Support and International Affairs, Tottori University, Koyama Minami 4-101, Tottori 680-8550, Japan
VIIState Key Laboratory of Soil Erosion and Dryland Farming on the Loess Plateau, Institute of Soil and Water Conservation, Northwest A&F University, Yangling 712100, People's Republic of China
ABSTRACT
Depression storage capacity (DSC) models found in the literature were developed using statistical regression for relatively large soil surface roughness and slope values resulting in several fitting parameters. In this research, we developed and tested a conceptual model to estimate surface depression storage having small roughness values usually encountered in rainwater harvesting micro-catchments and bare soil in arid regions with only one fitting parameter. Laboratory impermeable surfaces of 30 x 30 cm2 were constructed with 4 sizes of gravel and mortar resulting in random roughness values ranging from 0.9 to 6.3 mm. A series of laboratory experiments were conducted under 9 slope values using simulated rain. Depression storage for each combination of relative roughness and slope was estimated by the mass balance approach. Analysis of experimental results indicated that the developed linear model between DSC and the square root of the ratio of random roughness (RR) to slope was significant at p < 0.001 and coefficient of determination R2 = 0.90. The developed model predicted depression storage of small relief at higher accuracy compared to other models found in the literature. However, the model is based on small-scale laboratory plots and further testing in the field will provide more insight for practical applications.
Keywords: modelling, depression storage, surface roughness, arid regions, runoff
INTRODUCTION
Surface depressions and micro-relief play a significant role in surface runoff, sediment yield and dissolved compounds of agricultural fields (Dunne et al., 1991; Hairsine et al., 1992; Huang and Bradford, 1992; Govers et al., 2000; Takken et al., 2001; Darboux et al., 2002; Chu et al., 2013; Rossi and Ares, 2017). However, quantifying this storage at the watershed and field scale is one of the most challenging tasks for scientists. Therefore, estimating the depression storage capacity (DSC) of a land surface has continued to receive wide attention from researchers worldwide.
The surface storage can be classified into depression storage and surface detention (Stammers and Ayers, 1957). The difference between the depression and detention storages is that the depression storage does not contribute in the recession area in the hydrograph. On the other hand, the detention storage has two possibilities: to infiltrate and/or to appear as the recession part of the hydrograph (Fig. 1). Mathematically, this concept can be explained by the water mass balance. Geometrically, a soil depression is a subsidence/puddle point on the soil surface compared to adjacent/surrounding points. The depression storage is a depth of water in soil pits (Antoine et al., 2012). Soil depression storage capacity (DSC) is the maximum depth of water that can be stored in soil depression areas.
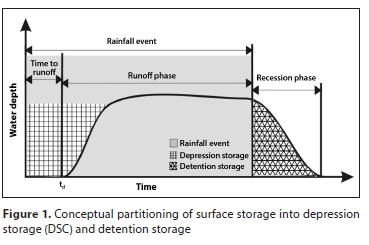
Depression storage capacity is affected by a wide range of parameters related to soil, topography, agricultural practices and environmental conditions. To simplify such a complex set of factors, researchers have tried to develop soil roughness indices that best describe or quantify DSC for land surfaces. Soil roughness is a measure of the variations in surface elevation. The research has intensified by the development of digital and laser scanning techniques that enable researchers to obtain digital elevation maps, thus estimating soil surface roughness parameters with proper computer algorithms with relative precision and in a short time. Therefore, calculating DSC based on well-estimated soil roughness parameters became possible (Mitchell and Jones, 1976, 1978; Moore and Larson, 1979, Ullah and Dickinson, 1979; Kamphorst and Duval, 2001; Abedini, 1998; Abd Elbasit et al., 2009).
Several soil roughness parameters have been developed by researchers to predict DSC accurately for a given soil condition (Onstad, 1984; Linden et al., 1986; Zobeck and Onstad, 1987; Sneddon and Chapman, 1989; Huang and Bradford, 1990; Mwendera and Feyen, 1992; Hansen et al., 1999; Kamphrost et al., 2000; Borselli and Torri, 2010). Those parameters include: random roughness (RR), tortuosity, limiting elevation difference and slope, and the mean upslope depression. The relative roughness (RR) soil surface seems to be one of the most popular single soil surface parameters that has been related to DSC. The relative roughness index is the population standard deviation of micro- and macro-relief elevations for a soil plot and was first introduced by Allmaras et al. (1966). Monteith (1974) presented the first linear model that relates DSC to RR. However, many other researchers have shown that the relationship between DSC and RR is a second-degree polynomial.
Hansen et al. (1999) developed a model based on a physically measured roughness index named mean upslope depression (MUD), and used it to estimate the depression storage capacity (DSC) for 32 Danish tilled soil surfaces. But they observed that MUD seemed to overestimate small DSC and underestimate large DSC values. In a field study scanning more than 200 tilled soil surfaces in Europe, Kamphorst et al. (2000) compared several roughness indices including random roughness (RR), tortusity, limiting elevation difference and slope and mean upslope depression (MUD), with their ability to predict maximum depression storage (DSC) calculated from the digital elevation model. They concluded that RR was the best index, describing the DSC linearly with coefficient of determination R2 = 0.8, but there is a need for a different prediction model for low DSC values (Onstad, 1984; Linden et al., 1988; Hansen et al., 1999). In recent studies, Chu et al. (2012) pointed out the importance of RR data processing on DSC prediction and that the MUD index is more suitable than RR for tillage surfaces and steeper slopes.
Borselli and Torri (2010) were the first to present a conceptual model where the rate of change of depression storage is related to the stored volume itself and the rate of change of some soil parameter, i.e., RR or P100 of Abbot-Firestone curve. They showed by integration that the relationship between DSC and RR is exponential. They then postulated that the effect of slope on DSC will also follow an exponential decay function and that there will always be a minimum storage volume that should be included in the equation. The final relationship of their model is shown in Table 1, along with models developed by other researchers.

Most of the models presented in the literature are empirical and based on the statistical relationship between DSC and relative roughness and slope, resulting in several fitting parameters. The validity of those models beyond the experimental values from which the model was developed is in doubt. In addition, these models have been developed and tested on surfaces with large values for soil roughness, i.e., tilled soil. However, the models' performance is questionable on soil surfaces having small roughness indices, similar to arid land soil surfaces or those usually encountered in the macro-catchments used for rainwater harvesting in arid and semi-arid lands. Rossi and Ares (2017; 2016) reported that the average soil roughness in the arid lands of Patagonia varied from 6.6 mm for vegetated surface to only 0.76 mm for bare soil surfaces. Farmers use micro-catchments to enhance runoff in the catchment area and channel it to cropping area to enhance crop growth. The roughness of these micro-catchments is initially small and expected to decrease exponentially with time due to rainfall (Zobeck and Onstad, 1987; Potter, 1990; Bertuzzi et al., 1990). Therefore, the objective of this study was to develop and test a model that integrates roughness coefficients and land slope, and its ability to describe DSC under relatively small roughness values and a wide range of surface slopes.
EXPERIMENTAL METHODS
Fabrication and elevation measurement of experimental plots
Impermeable surfaces with different roughness values were constructed using cement, gypsum and 4 gravel sizes: 5, 10, 20, and 30 mm, named P1, P2, P3 and P4, respectively. Impermeable surfaces were used to separate the influence of depression storage on runoff from infiltration (Kamphorst et al., 2000). Four wooden trays with dimension 300 x 300 x 30 mm (depth) were used and filled with a layer of cement to 15 mm depth; the gravel was fixed on the cement mortar and left for 24 h at room temperature for drying. After drying, a layer of gypsum and wax was sprayed on the cement gravel surface to create a rough and impermeable surface, as shown in Fig. 2 (for further details, see Abd Elbasit et al., 2009).
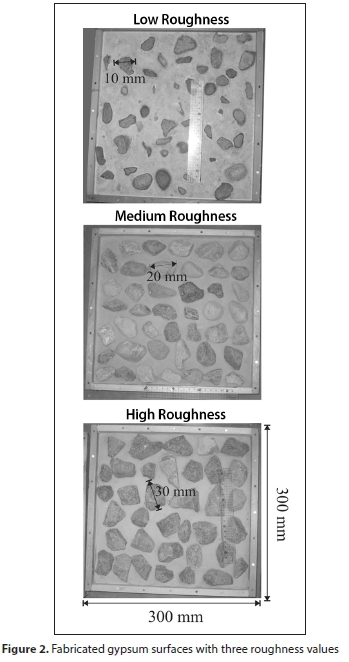
A 30 steel pin micro-relief device was used to measure the relative elevation for 900 points in each plot with cell size equal to 10 x 10 mm as described by Abd Elbasit et al. (2009). The variation in surface elevation was marked as the variation of the pins' red mark on a graph paper. Abd Elbasit et al. (2009) present a detailed description for the surface construction and pin-micro-relief device. The random roughness index (RR) for each plot was calculated from the 900 elevation data points as follows (Allmaras et al., 1966):
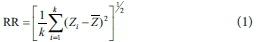
where RR is random roughness; Zi is elevation at i point, Z is average elevation; k is number of points, in this case equal to 900. The resulting RR values for R1, R2, R3 and R4 were 0.88, 1.83, 3.91, and 6.33 mm, respectively (Fig. 2)
Measurement of depression storage capacity (DSC)
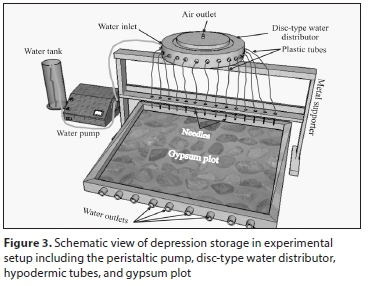
The DSC was determined under 4 roughness levels and 9 slopes using water mass balance between inflow and outflow water volumes (Antoni et al., 2010). In each experiment an inflow water with known rate was applied at the upstream end of the plots using a disc-shaped distributer device with a peristaltic water pump, as shown in Fig. 3. The disc distributor dispenses inflow water to the plots evenly through 30 outlets consisting of plastic tubes and needles. At the downstream end of the plots the outflow water was monitored using a graduated cylinder. The difference between steady-state inflow and outflow rates represents the depression the detention storage (Antoni et al., 2010). At the end of each experiment the mass of the water remaining on the plot was measured and recorded as the depression storage capacity (DSC) for that surface. The experiments were carried out using 9 slopes, 1°, 2°, 3°, 4°, 5°, 8°, 10°, 15°, and 20°, replicated 3 times. The mean and standard deviation of DSC were calculated for each surface-slope combination.
Conceptual model
Depression storage capacity models found in the literature were developed using statistical regression between DSC values and some surface parameters, mostly RR and slope. In this research, we attempted to hypothesize the shape of the relationship between DSC and RR and slope, based on simple concepts, rather than developing the equation based on stepwise regression. This approach was taken not to develop a physically based model, but rather to reduce the fitting parameters of the equation to 2 or 1 fitting parameter/s.
The overland flow can be described using Manning's equation for wide channel as:
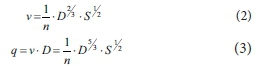
where v = flow velocity, m/s; q is the unit width discharge m2/s; D = water depth or storage, m; S = channel slope (bed slope) and n is the Manning's roughness coefficient, s/m(1/3). The overland flow can also be related to surface roughness η and water depth or storage D to the power m (Stammers and Ayers, 1957), where m varied between ½ and ⁵/₃.

Equating Eqs 3 and 4 will reveal the following proportional equation:

We postulated that the left-hand side represents water storage with dimension L, and n∙η represents relative roughness RR to the power equal to that of the slope. We may envisage the shape of the equation by selecting m = 2/3, equal to the power of the hydraulic radius in Manning's equation and using only 2 fitting parameters, namely, a constant λ, as a slope factor and a constant β representing the minimum storage capacity, as suggested by Borselli and Torri (2010). The final form of the DSC equation with 2 fitting parameters will be as follows:

Equation 6 will be validated with the experimental data and therefore the λ and β values will be determined.
RESULTS AND DISCUSSION
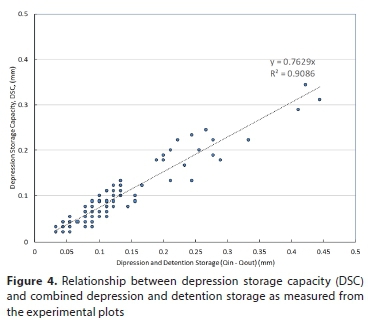
The combined depression storage (DSC) and detention storage (DS) were calculated from the difference between the inflow and outflow, and compared to the residual DSC as measured at the end of each experiment. Figure 4 shows a linear relationship between DSC and combined DSC plus DS, R2 = 0.9 and p < 0.05, confirming the concept presented by Antoni et al. (2010). DSC values seemed to be 24% lower than that of depression and detention. The DSC values were used in the analysis that follows.
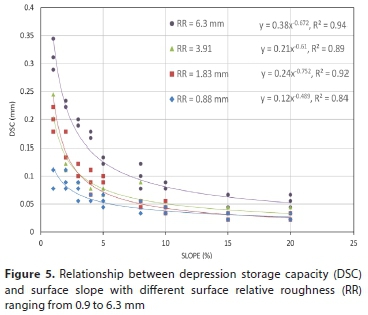
The interrelationships between DSC, RR and slope are explored in Figs 4, 5 and 6. First, the relationship of DSC with slope for each RR value is shown in Fig. 5. As expected, the DSC increased with RR and follows a decay power function in relation to the slope with coefficient of determination R2 varyinf from 0.84 to 0.94 (p < 0.001). The power constant ranges from −0.49 for RR = 0.88 mm to 0.67 for RR of 6.3 mm. This in agreement with the investigations carried out by Burselli and Torri (2010), who showed a decaying power relationship between DSC and plot slope using experimental data and the inclined cup model. Other researchers have reported an inverse relationship between DSC and slope, but these relationships were linear (Onstad, 1984; Mwendera and Feyen, 1992), squared (Hansen et al., 1999) or trigonometric (Chu et al., 2012).
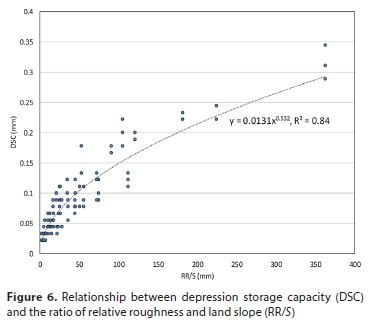
Data analysis showed that DSC is inversely proportional to slope and directly proportional to RR. In fact, most of the studies reported in the literature have also confirmed this type of relationship at plot- and field-scale (Huang and Bradfrod, 1990; Onstad, 1984; Kamphorst et al., 2000; Hansen, 1999; Borselli and Torri, 2012), although some of these relationships and models were not properly developed, resulting in negative DSC values in some cases for small RR values (Onstad, 1984; Mwendera and Feyen, 1992). Therefore, we proposed a simple correlation between DSC and the ratio of RR and slope (RR/S, mm) and presented the data in Fig. 6. As shown in Fig. 6, there is a strong and significant relationship (p < 0.001 and R2 = 0.84) between DSC and RR/S, represented by the following power function:
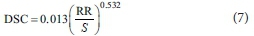
The previous model is not linear and has a low coefficient of determination that would be expected when DSC is related to either RR or S separately. Therefore, we attempted to simplify and linearize the model by using a rationally developed relationship that relates the DSC to the square root of RR/S presented in Eq. 6. The proposed relationship fits the data significantly with R2 = 0.89 and p < 0.001 as shown in Fig. 7:
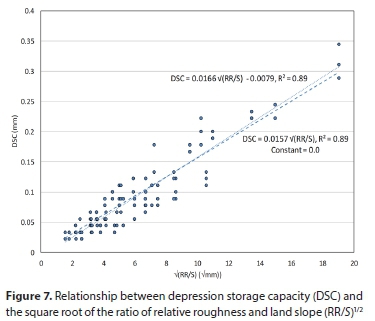
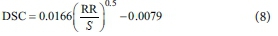
A regression test revealed that the constant −0.0079 is not significantly different than zero (p < 0.01), and therefore is assumed to be zero. Physically, this constant represents the amount of detention storage of the surface that has been excluded from the DSC measured data and therefore should be equal to zero. Therefore, we performed a second regression equation assuming the constant β equal to zero, resulting in the following equation with R2 = 0.899, p < 0.001. (Fig. 7):
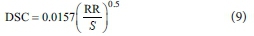
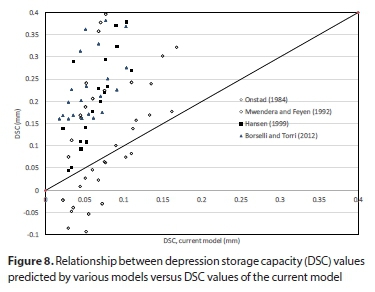
The current model presented in Eqs 8 and 9 was quite similar and gave lower DSC values compared to other models. Equation 9 is the simplest equation found in the literature, and gave similar results to that of Eq. 8, as shown in Fig. 7, and could predict the DSC of the micro-catchment with low roughness values with reasonable accuracy. Other DSC models found in the literature mostly dealt with tilled surfaces with relatively large roughness values. To test the validity of some of the popular models found in the literature, the DSC values predicted by these models were plotted against the DSC predicted by the current model and the results are shown in Fig. 8. Models tended to largely overpredict DSC compared to the current model, especially at lower DSC values (Hansen, 1999; Borselli and Torri, 2012). Two of the models fail completely to predict low DSC values and gave negative values, as shown in Fig. 8 (Onstad, 1984; Mwendera and Feyen, 1992). We postulated that these large differences between the current model and the previous models are attributed mostly to large surface roughness and the land slope. Therefore, the predicted DSC values using various models were plotted against the land slope as shown in Fig. 9 for a specific value of RR = 0.7 mm. Hansan's (1999) model seemed to slightly under-predict DSC values for RR = 7 mm but failed for smaller RR values and gave negative DSC values.
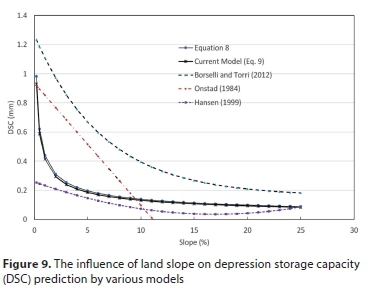
We analysed the effect of slope on the DSC prediction for the current model as compared to others. The effect of slope in the current model is large when the slope varied from 1 to 5% but the slope effect for large slope values was insignificant. These results are in disagreement with the model presented by Hansan (1999) that shows a large linear decrease in the DSC value with slope, and with the model of Borsello and Tori (2012) that shows a gradual decrease of DSC values for a wide range of slope values. The current work agreed with Chu et al. (2013), who pointed out the nonlinear nature of the relationship between DSC and land slope. DSC values for low surface roughness seem to have a strong dependence on small slope values, compared to large slopes at which DSC variation is minimal.
CONCLUSION
A conceptual and simple model with 1 fitting parameter was developed to predict the surface depression storage from the square root of relative roughness and land slope. The model is particularly applicable on surfaces with low relative roughness, similar to that of fallow agricultural land and that usually encountered in rainwater harvesting micro-catchments. The model has been successfully tested using impervious plots with a wide range of relative roughness values, installed at various slopes with coefficient of determination = 0.9 and at a probability level of 99%. The model improves our understanding of factors affecting runoff from natural surfaces and can be used as a subcomponent in future rainfall-runoff models in small areas. It should be noted that the current study is based on small-scale laboratory plots and further studies in the field will provide more insight for practical applications.
AUTHOR CONTRIBUTIONS
Abd Elbasit designed the experiments and carried them out with the assistant of Ojha, Yasuda and others. Abu-Zreig developed the model concept and prepared the figures and tables. Abu-Zreig and Abd Elbasit prepared the manuscript with contributions from all co-authors. In-depth and continuous discussion has been carried out among all authors during the preparation of the paper and the development of the conceptual model.
COMPETING INTERESTS
The authors declare that they have no conflict of interest.
DATA AVAILABILITY STATEMENT
Some or all data and models used during the study are available from the corresponding author on request.
ACKNOWLEDGEMENT
This research was financially supported by the Japan Society for Promotion of Science and the Global Center of Excellence for Dry Land Studies. Also we thank Mr Shunichi Yamamoto for his help in laboratory experiments.
REFERENCES
ABD ELBASIT MAM, ANYOJI H, YASUDA H and YAMAMOTO S (2009) Potential of low cost close-range photogrammetry system in soil microtopography quantification. Hydrol. Process. 23 1408-1417. https://doi.org/10.1002/hyp.7263 [ Links ]
ABEDINI MJ (1998) On depression storage, its modeling and scale. PhD thesis, University of Guelph, Guelph, Canada. https://www.collectionscanada.gc.ca/obj/s4/f2/dsk2/tape15/PQDD_0028/NQ33293.pdf [ Links ]
BERTUZZI P, RAUWS G and COURAULT D (1990) Testing roughness indices to estimate soil surface roughness changes due to simulated rainfall. Soil Tillage Res. 17 87-99. https://doi.org/10.1016/0167-1987(90)90008-2 [ Links ]
ALLMARAS RR, BURWELL RE, LARSON WE and HOLT RF (1966) Total porosity and random roughness on the interrow zone as influenced by tillage. USDA, Conservation Research Report no. 7. US Government Print Office, Washington, DC. https://www.ars.usda.gov/ARSUserFiles/50701000/cswq-t1914-allmaras.pdf [ Links ]
ANTOINE M, CHALON C, DARBOUX F, JAVAUX M and BIELDERS C (2012) Estimating changes in effective values of surface detention, depression storage and friction factor at the interrill scale, using a cheap and fast method to mold the soil surface micro-topography. Catena 91 10-20. https://doi.org/10.1016/j.catena.2010.11.003 [ Links ]
BORSELLI L and TORRI D (2010) Soil roughness, slope and surface storage relationship for impervious area. J. Hydrol. 393 389-400. https://doi.org/10.1016/j.jhydrol.2010.09.002 [ Links ]
CHU X, NELIS J and REDISKE R (2013) Preliminary study on the effects of surface microtopography on tracer transport in a coupled overland and unsaturated flow system. J. Hydrol. Eng. 18 1241-1249. https://doi.org/10.1061/(ASCE)HE.1943-5584.0000729 [ Links ]
CHU X, YANG J and CHI Y (2012) Quantification of soil random roughness and surface depression storage: Methods, applicability, and limitations. Trans. ASABE 55 1699-1710. https://doi.org/10.13031/2013.42361 [ Links ]
DARBOUX F, DAVY P, GASCUEL-ODOUX C and HUANG C (2002) Evolution of soil surface roughness and flowpath connectivity in overland flow experiments. Catena 46 125-139. https://doi.org/10.1016/S0341-8162(01)00162-X [ Links ]
DUNNE T, ZHANG W and AUBREY D (1991) Effects of rainfall, vegetation and microtopography on infiltration and runoff. Water Resour. Res. 27 2271-2285. https://doi.org/10.1029/91WR01585 [ Links ]
GOVER, G, TAKKEN I and HELMING K (2000) Soil roughness and overland flow. Agronomie 20 131-146. https://doi.org/10.1051/agro:2000114 [ Links ]
HAIRSINE PB, MORAN CJ and ROSE CW (1992) Recent developments regarding the influence of soil surface characteristics on overland flow and erosion. Aust. J. Soil Res. 30 (3) 249-264. http://www.publish.csiro.au/sr/SR9920249 [ Links ]
HANSEN B, SCHJØNNING P and SIBBESEN E (1973) Roughness indices for estimation of depression storage capacity of tilled soil surfaces. Soil Till. Res. 52 103-111. https://doi.org/10.1016/S0167-1987(99)00061-6 [ Links ]
HUANG C and BRADFORD JM (1990) Depressional storage for Markov-Gaussian surfaces. Water Resour. Res. 26 2235-2242. https://doi.org/10.1029/WR026i009p02235 [ Links ]
KAMPHORST EC, JETTEN V, GUERIF J, PITKANEN J, IVERSEN BV, DOUGLAS J and PAZ A (2000) Predicting depressional storage from soil surface roughness. Soil Sci. Soc. Am. J. 64 1749-1758. http://doi.org/10.2136/sssaj2000.6451749x [ Links ]
LINDEN DR and VAN DOREN DM JR (1986) Parameters for characterizing tillage-induced soil surface roughness. Soil Sci. Soc. Am. J. 50 1560-1565. http://doi.org/10.2136/sssaj1986.03615995005000060035x [ Links ]
LINDEN DR, VAN DOREN DM and ALLMARAS RR (1988) A model of the effects of tillage-induced soil surface roughness on erosion. In: 11th Int. Conf. Proc., vol. I, ISTRO, July 1988, Edinburgh, Scotland. 373-378. [ Links ]
MITCHELL JK and JONES BA Jr (1976) Micro-relief surface depression storage: Analysis of models to describe the depth storage function. Water Resour. Bull. 12 (6) 1205-1222. https://doi.org/10.1111/j.1752-1688.1976.tb00256.x [ Links ]
MITCHELL JK and JONES BA Jr (1978) Micro-relief surface depression storage: changes during rainfall events and their application to rainfall-runoff models. Water Resour. Bull. 14 (4) 777-802. [ Links ]
MONTEITH NH (1974) The role of surface roughness in runoff. Soil Conserv. J. 30 42-45. [ Links ]
MOORE ID and LARSON CL (1979) Estimating micro-relief surface storage from point data. Trans. ASAE 22 1073-1077. https://doi.org/10.13031/2013.35158 [ Links ]
MWENDERRA EJ and FEYEN J (1992) Estimation of depression storage and Manning's resistance coefficient from random roughness measurement. Geoderma 52 235-250. https://doi.org/10.1016/0016-7061(92)90039-A [ Links ]
ONSTAD CA (1984) Depression storage on tilled soil surface. Trans. ASAE 27 729-732. http://doi.org/10.13031/2013.32861 [ Links ]
POTTER KN (1990) Soil properties effect on random roughness decay by rainfall. Trans. ASAE 33 1889-1892. https://doi.org/10.13031/2013.31554 [ Links ]
ROSSI MJ and ARES JO (2016) Overland flow from plant patches: Coupled effects of preferential infiltration, surface roughness and depression storage at the semiarid Patagonian Monte. J. Hydrol. 533 603-614. https://doi.org/10.1016/j.jhydrol.2015.12.028 [ Links ]
ROSSI MJ and ARES JO (2017) Water fluxes between inter-patches and vegetated mounds in flat semiarid landscapes. J. Hydrol. 546 219-229. https://doi.org/10.1016/j.jhydrol.2017.01.016 [ Links ]
SNEDDON J and CHAPMAN TG (1989) Measurement and analysis of depression storage on a hillslope. Hydrol. Process. 3 1-13. https://doi.org/10.1002/hyp.3360030102 [ Links ]
STAMMERS WN and AYERS HD (1957) The effect of slope and microtopography on depression storage and surface detention. General Assembly of Toronto, 3-14 September 1957, Volume III. 89-93. [ Links ]
TAKKEN I and GOVERS G (2000) Hydraulics of interrill overland flow on rough, bare soil surfaces, Earth Surf. Proc. Land. 25 1387-1402. https://doi.org/10.1002/1096-9837(200012)25:13%3C1387::AID-ESP135%3E3.0.CO;2-D [ Links ]
ULLAH W and DICKINSON WT (1979) Quantitative description of depression storage using a digital surface model: I. Determination of depression storage. J. Hydrol. 42 63-75. https://doi.org/10.1016/0022-1694(79)90006-4 [ Links ]
ZOBECK TM and ONSTAD CA (1987) Tillage and rainfall effects on random roughness: a review, Soil Tillage Res. 9 1-20. http://doi.org/10.1016/0167-1987(87)90047-X [ Links ]
 Correspondence:
Correspondence:
Majed M Abu-Zreig
Email:majed@just.edu.jo; drmajedo@gmail.com
Received: 6 August 2019
Accepted: 15 June 2020














