Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Water SA
On-line version ISSN 1816-7950
Print version ISSN 0378-4738
Water SA vol.46 n.2 Pretoria Apr. 2020
http://dx.doi.org/10.17159/wsa.2020.v46i2.8246
RESEARCH PAPER
Evaluation of bio-coagulants for colour removal from dye synthetic wastewater: characterization, adsorption kinetics, and modelling approach
IA Obiora-OkafoI; OD OnukwuliI; NC Eli-ChukwuII
IDepartment of Chemical Engineering, Nnamdi Azikiwe University, Awka, Nigeria
IIDepartment of Electrical Engineering, Alex Ekwueme-Federal University, Ndufu-Alike, Ikwo, Nigeria
ABSTRACT
Dye usage for industrial applications has been on the increase and these activities generate large amounts of dye-constituted wastewater that should be treated before environmental discharge or reuse. Various studies have shown the application of natural organic polymer (NOP) coagulants in dye removal from industrial wastewater. In this research, the coagulation performances of Vigna unguiculata (VU) and Telfairia occidentalis (TO) for colour removal from crystal Ponceau 6R dye synthetic wastewater was studied. The proximate compositions, structure, and surface morphologies of the coagulants were investigated using standard methods, i.e. Fourier-Transform infrared (FTIR) spectroscopy, and scanning electron microscopy (SEM). Colour removal was evaluated through the time-dependent decrease in particle concentration and thus growth of flocs. Effects of the process parameters, including pH, coagulant dosage, dye concentration (DC), settling time, and temperature were preliminarily tested and the best range experimentally determined. The optimal operating conditions established were pH 2, 800 mg-L-1 coagulant dosage, 100 mg-L-1 dye concentration, 300 min, and 303 K. The order of greatest removal was VUC > TOC with optimum efficiency of 93.5% and 90.7%, respectively. The values of K and a obtained for VUC and TOC were 8.09 x 10-4 L-mg-1-min-1, 1.7 and 9.89 x 104 L-mg-1-min-1, 1.6, respectively. Coagulation time, Tag, calculated and deduced from the particle distribution plot, showed a rapid coagulation process. Coagulation-adsorption kinetics indicated agreement with the pseudo-second-order model deducing that chemisorption is the rate-controlling step. It further indicates that particle adsorption on the polymer surfaces occurred mostly as a mono-molecular layer and according to the chemisorption mechanism. Cross-validation showed good prediction of the experimental data. The selected coagulants have the potential for application as efficient coagulants while also showing significant adsorption characteristics. The application of kinetics and modelling in separation processes involving particle transfer is especially required in wastewater treatment.
Keywords: coagulation-flocculation, coagulation kinetics, mass transfer modelling, polymer adsorption kinetics, spectrometry colour removal
INTRODUCTION
The textile industry is now one of the sectors posing a pollution threat to the world considering the wastewater content and high volume of discharge into the environment. Presently, about 10,000 commercial dyes and pigments are being used and over 7.11 x 107 kg-yr-1 is produced worldwide (Moghazy, 2019; Zonoozi et al., 2008). Dye usage in the world has been traced back to the origin of man and its application, importance, and menace are globally known.
Dye-containing wastewater, when discharged to the aquatic environment, can be toxic to aquatic life, slows down self-purification of streams by reducing light penetration, retards photosynthetic activity, and inhibits the growth of aquatic biota (Moghaddam et al., 2010). In addition, they might be mutagenic, carcinogenic and could cause severe damage to human organs when inhaled or consumed (Miranda-Mandujano et al., 2018). At very low concentrations (less than 1 mg-L-1), dyes in wastewater could be considered undesirable and require removal before the wastewater is considered acceptable for environmental discharge (Moghaddam et al., 2010). Thus dye-containing wastewater generated from industrial processes has to be treated properly in accordance with discharge standards.
Coagulation-flocculation is classified as one of the most efficient methods widely used for colour removal from wastewater because it is efficient, cost-effective, and simple to operate (Gao et al., 2007). Coagulation is the process of destabilization of aqueous particles initially present in a suspension by the addition of a coagulant (natural or synthetic), so that the charged particles are neutralized to enable them to be attracted to each other to form settleable flocs. Aqueous particles generally have a net negative charge, thereby repelling one another. In addition, aqueous particles (1 nm - 1 um) generally do not settle at all or without assistance in a reasonable time. Therefore, the surface charge of particles can be reduced or destabilized by adding a coagulant carrying an opposite charge (Long et al., 2016; Obiora-Okafo and Onukwuli, 2015). Commonly used coagulants are inorganic salts such as Al(SO4)3 or FeCl3, as well as synthetic organic polymers. Although these chemicals are effective in removing dyes and other contaminants from wastewater, several disadvantages have recently been discovered, such as their impact on human life, with diseases such as Alzheimer's disease being associated with certain inorganic salts, and neurotoxins being associated with acrylic amid (Papic et al., 2004).
Due to the need for sustainable development, research on wastewater treatment has been re-focused on the use of natural coagulants (either plant-based or animal-based) because of their abundant source, cost-effectiveness, eco-friendliness, multifunctionality, biodegradability in water purification processes, low sludge volume production, and because they do not alter the pH of the treated wastewater (Obiora-Okafo and Onukwuli, 2016). A good choice of natural polymer coagulant enhances the aggregation of particles for formation of large flocs, which are capable of rapid settling through particle adsorption, charge neutralization, enmeshment in a precipitate, and inter-particle bridging mechanisms. The existence of adsorptive capacity in water is common when natural organic polymers (NOPs) of high molecular weight are used as coagulants. Particles' interaction by adsorption occurs when there is some affinity between polymer segments and particle surfaces. Adsorption interactions are possible by electrostatic force, hydrogen bonding and ionic bonding (Bolto and Gregory, 2007). NOPs may be anionic, cationic or non-ionic in nature (Beltran-Heredia et al., 2011).
Cowpea (Vigna unguiculata) is a legume of West African origin whose seeds are rich in protein and are widely consumed by poor populations throughout the tropics. Cowpea seed is a source of nutrition for humans as well as livestock. It is a good source of dietary protein. Protein extracts from cowpea seed have a molecular weight of 6-16 kDa and are cysteine-rich cationionic polypeptides (Mariângela et al., 2003). Fluted pumpkin (Telfairia occidentalis) is a perennial plant with great economic importance in Nigeria. Its seed has high nutritive values, being rich in essential nutrients and with a high protein content of about 28.09%. High protein content in organic polymers such as Vigna unguiculata and Telfairia occidentalis, is one of the indicators of their potential usage as coagulants for water and wastewater treatment (Kuku et al., 2014).
Any coagulation-flocculation study of contaminant removal is incomplete without an adequate knowledge of process kinetics. The study of kinetics is often neglected in mass transfer processes. Coagulation kinetics is of primary interest in investigating the hydrodynamic interactions involving particle-particle transfer (John et al., 1992). Different methods have been employed in monitoring the reduction in particle concentrations and kinetics during coagulation experiments: bulk techniques, and single particle techniques (Coulter counter, flow cytometer, single particle light scattering). Bulk technique is a widely used procedure for coagulation-flocculation kinetics because it monitors particle concentration with time (Stechemesser and Sonntag, 2005).
Coagulation rate dynamics addresses how rapidly or slowly suspended particles will coagulate. Coagulation rate has immense practical implications and plays an important role in the mathematical modelling, design and control of water treatment plants. Von Smoluchowski (1917) was the first to study the rate of coagulation of particles due to Brownian motion with the diffusion coefficient of particles taken as constant. Mathematical modelling describes the time-dependent behaviour of a process. It is a set of equations (including necessary input observations to solve the equations) that predict the behaviour of a process. It is suitable for simulating the dynamic behaviour, studying control strategies and in designing a coagulation-flocculation process. Process modelling of coagulation-flocculation improves and optimizes the design of equipment and develops better insight into process operation. In the theoretical study ofthe coagulation-flocculation process, the prediction of particle reduction in response to a set of coagulation conditions is an area of interest. Brownian collisions on a spherical target are analysed in more detail because this captures the essential kinetics of many mass transfer processes, including coagulation-flocculation of colloidal particles, diffusion growth, and diffusion-controlled chemical reactions (Stechemesser and Sonntag, 2005).
Coagulation kinetics is a complex phenomenon that requires adequate models to predict the mass transfer behaviour of particles. The model of Jimoda et al. (2013) adequately predicts the particle transfer rate during the coagulation-flocculation process.
This paper investigates the performance of active protein agents from bio-coagulants in colour removal from synthetic dye wastewater. Detailed physicochemical characterizations of the precursors were conducted. The novel approach of extracting active coagulant agent was adopted in the coagulation-flocculation process. Coagulant and dye types were selected for high-performance jar testing, based on their ionic composition. Spectrophotometry was used to observe the dynamic behaviour of particle concentrations at optimal conditions. The study also explores the kinetics of particle transfer, and uses modelling to predict the real-time particle transfer rate during the coagulation-flocculation process.
MATERIALS AND METHODS
Coagulant preparation
Dried seeds of Vigna unguiculata and Telfaria occidentalis were purchased from local market of Enugu city. Mature seeds showing no signs of discolouration were used. The dry seeds of the sample were ground to a fine powder (63-600 |im) using a food processor (Model BL 1012, Khind), to achieve solubilisation of active ingredients.
Extraction of active component
The active proteins from the coagulants were extracted by adding 2 g of powdered sample to 100 mL distilled water to make a suspension. The suspension was stirred vigorously at 120 r-min-1 using a magnetic stirrer (Model 78HW-1, U-Clear England) for 20 min at room temperature to accomplish extraction and to enhance and activate the cationic agent present in the precursors. A sieve cloth was used to filter the suspension, to enable nano, micro, and macro-particles to be present in the filtrate for enhanced coagulation-flocculation. The resultant filtrate solution was used as coagulant at required dosages. Fresh solutions were prepared daily and kept refrigerated to prevent any ageing effects (such as change in pH, microbial activity, viscosity, and coagulation activity). Before each experiment, solutions were shaken vigorously and used immediately for each sequence of the experiment.
Characterization of coagulants
Yield, bulk density, moisture content, ash content, protein content, fat content, carbohydrate content, and fibre content of the seed powders were determined by the standard methods of analysis of the AOAC (1990). Fourier transform infra-red (FTIR) spectrophotometer supplied by IR Affinity-1, Shimadzu Kyoto, Japan, was used to study the chemical structure and functional groups present in the samples. The spectra were measured in the range of 4 000-400 cm-1. Surface structures and morphologies of the seed powders were studied using a scanning electron microscope (SEM) supplied by Phenom Prox., world Eindhoven, Netherlands.
Decolourization procedure
Dye preparation and spectrophotometric colour removal procedure
Acid Red 44 (AR 44) (chemical name: Crystal Ponceau, a water-soluble dye provided by May & Baker, England, with molecular structure as shown in Fig. 1a, was used. Dye physicochemical characteristics are summarized in Table 1. Dye with commercial purity was used without further purification. The absorption spectrum of the dye was obtained by dissolving 1 000 mg-L-1 of AR 44 in distilled water. A sample of the solution was scanned against the blank in the range of 200-850 nm using a UV-Vis spectrophotometer (Shimadzu, Model UV-1800). The maximum wavelength (λmax) of 511 nm was obtained as shown in Fig. 1b. A stock solution of 1 000 mg-L-1 of dye was prepared by dissolving AR 44 in separate doses of 1 L distilled water. The desirable experimental concentrations of 10-100 mg-L-1 were prepared by diluting the stock solution with distilled water. The wavelength of maximum absorbance (λmax) and calibration curve at λmax were determined. The colour concentrations (mg-L-1) were determined through calibration analysis (Jeffrey et al., 2001).

Coagulation studies
A conventional jar test apparatus supplied by Phipps and Bird, VA, USA, equipped with 6 beakers of 1 L capacity and 6 paddle stirrers was used to perform the coagulation-flocculation experiment. The jar test was conducted to evaluate the coagulation performance of the active agent, extracted based on the method adopted by Obiora-Okafo and Onukwuli (2016), and also to establish the best operating conditions for the process. The procedure involved 4 min of rapid mixing at 100 r-min-1. The mixing speed was reduced to 40 r-min-1 for another 25 min. All suspensions were left for settling for 30-480 min. Supernatant samples were withdrawn (after settling) for absorbance analysis using UV-Vis spectrophotometer (Shimadzu, model 1800) at set maximum wavelength of 511 nm. The study was conducted by varying a few experimental parameters, including pH, coagulant dosage, dye concentration, and settling time. Colour concentration (mg-L-1) measurement was determined by comparing absorbance to concentration on a calibration curve. The pH was adjusted to the desired value using 0.1 M HCl and 0.1 M NaOH. The colour removal efficiency was obtained according to Eq. 1 as:
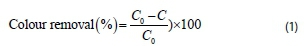
where C0 and C are the initial and final colour concentration (mg-L-1) in dye solutions before and after coagulation-flocculation treatment, respectively.
Theoretical principles of coagulation-flocculation kinetics
The study of coagulation kinetics is very important in understanding coagulation-flocculation of particles. It can be used to investigate the colloidal and hydrodynamic interactions involved in particle-particle transfer. When two particles of comparable size collide with each other, the collision may lead to doublet formation; the process involved is termed coagulation-flocculation (Masliyah and Bhattachayer, 2006). In this study, coagulation kinetics of spherical particle interaction was studied following a Brownian controlled diffusion mechanism (peri-kinetic coagulation). The equations in Von Smoluchowski's model have formed the core of almost all later research in coagulation-flocculation modelling (Von Smoluchowski, 1917; Schick and Hubbard, 2005).
Coagulation of two particles to form a single new aggregate might not be described fully as a second-order rate process as recorded by some authors without obtaining the order of reaction (Ani et al., 2012). In this study, the Von Smoluchowski theory and equation for the kinetics of Brownian coagulation of mono-disperse particles at early stage were used to determine the coagulation rate constant and order of coagulation-flocculation reaction using Polymath software. The equation describing the kinetics of aggregation is given in Eq. 2:

where C is the primary particle concentration at time t, a is the order of coagulation-flocculation reaction, K is the ath order rate constant or absolute coagulation rate constant. Putting Eq. (2) in a linear form gives:
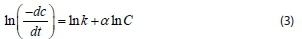
Hence, a plot of ln () against ln C yields a straight line, from which K (rate constant) and a (order of reaction), can be determined from the intercept and slope, respectively.
The rate constant (first derived by Smoluchowski) has remarkable features, in that for mono-disperse particles it is independent of particle size and for the total formation. The rate constant can be calculated from Brownian hydrodynamics (Jonas and Clive, 2005) as:

where kBis the Boltzmann's constant (J/K), T is absolute temperature (K) and u is viscosity of the medium.
The equation describing the timed-based evolution of the cluster of kind K is as follows:
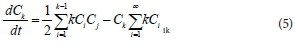
where, 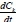 is the rate of change of concentration of particle size k, kijdt.. is the coagulation constant which depends on details of the collision process between i-mers and j-mers = (k- i) mer. This kernel embodies the dependence on i and j of the meeting of i-mer and j-mer, including the mutual diffusion coefficient (Dij) and collision radius of the sphere (R.j). By this means, the coagulation constant, k.. = k. assuming a constant kernel, is:
is the rate of change of concentration of particle size k, kijdt.. is the coagulation constant which depends on details of the collision process between i-mers and j-mers = (k- i) mer. This kernel embodies the dependence on i and j of the meeting of i-mer and j-mer, including the mutual diffusion coefficient (Dij) and collision radius of the sphere (R.j). By this means, the coagulation constant, k.. = k. assuming a constant kernel, is:

where K1is the Von Smoluchowski rate constant for rapid coagulation, R is the particle radius and D is the Brownian diffusion coefficient of the particles.
Von Smoluchowski rate constant for rapid coagulation is related to Stokes-Einstein (SE) diffusion coefficient for translational sphere diffusion (Philipse, 2011), with the following expression:

Equations 4 and 7 relate the second-order rate constant and Von Smoluchowski constant as:

Particle collisions lead to flocculation and hence a reduction in the total number of particles and an increase in the particle average size. The rate of floc growth was determined by the frequency of these collisions. Based on the work of Von Smoluchowski (1917), it is shown that the frequency f.. of binary collision between particles of type i and j is given as:

where Ciand C.are the respective number of concentrations of two particle types. ß(vi, vj) is the collision frequency factor. The rate of particles of size k forming per unit volume by collision of particles of size i and j is given by:

The factor in Eq. 10 is present because each collision is counted twice in the summation. Equation 10 is due to the generation of the kthspecies. In turn, particle k collides with other particles leading to particle volumes larger than vk. The disappearance term is given by:

The total balance equation for kthspecies is given by:
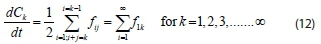
Using Eq. 9, the above equation becomes:
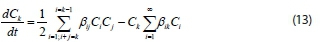
where ß.. = ß(vi, vj)
After inclusion of an efficiency factor, Eq. 9 is replaced by:

where Eij.. is the efficiency factor for collision between i and j-particles or flocs, fijis the rate of collision between particles of size i and j.
Taking note of the collision efficiency, the collision frequency function for Brownian motion (peri-kinetic aggregation) is given as (Von Smoluchowski, 1917; Schick and Hubbard, 2005):

and

K is a constant independent on particle size. Relating Eqs. 4, 15 and 16 yields another relationship between collision frequency factor and Von Smoluchowski rate constant:

The population balance, Eq. 13, when compared with Eq. 16 becomes:

Thus, the total concentration of particles per unit volume in a closed system at time, t, is:

Summing Eq. 20, overall particles K = 1, 2, 3, ..., °° obtains:
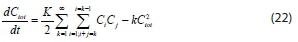
The first term on the right-hand side of the above equation is given by (- tot , leading to:

The above Eq. 23 for Brownian coagulation is analogous to second-order reaction kinetics. The condition is given by Ctot= Coat t = 0. Integrating Eq. 23 leads to:

Equation 24 shows the decay in the total number of particles with time. Using Eq. 24 shows that:
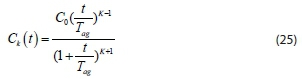
where

The characteristic time, T , is known as the coagulation-flocculation time and is the time taken for the concentration to halve (Probstein, 2003). Flocculation in a later stage involves the formation of triplet, quadruplet, quintuplet, etc., number of k-mers, which can be solved by means of Eq. 25.
Therefore:

The model governing equation
In this study, a model equation was investigated and used to describe the time-dependent behaviour of particle transfer towards the adsorbing particles during the coagulation-flocculation process triggered by coagulation mechanisms (Jimoda et al., 2013). The following assumptions were considered: model was governed and derived from Fick's law, that angular symmetry exists for the particles, a homogeneous system exists, single-dimensional particle transfer occurs, the process is isothermal, and external resistance to particle transport is negligible.
The coefficient of diffusion, D, is an important transport property of a colloidal particle and represents the role of Brownian motion on particle movement. The diffusion coefficient is generally associated with Fick's law (Coulson and Richardson, 2008):

where I is the particle diffusive flux, C is its concentration and is the concentration gradient of the number of particles. Diffusion is associated with particle transport from a high concentration region to a low concentration region due to Brownian motion. Figure 2 demonstrates a spherical particle transfer considering a microscopic system.
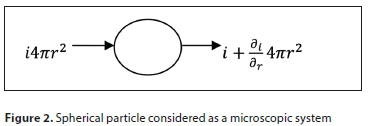
The basic differential equation for mass transfer in a particle is obtained by taking a material balance (continuity equation) over a spherical shell as derived in Eq. 32 below:

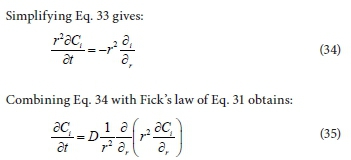
where C is the concentration of the spherical particle i and r is the radial coordinate of the sphere.
Equation 35 becomes a partial differential equation that describes the rate of mass transfer of particles during the coagulation-flocculation process studied in this research. Equation 35 is similar to that for mass transfer to a sphere in a homogeneous fluid by Coulson and Richardson (2008). Substituting Cr2 for C, Eq. 35 becomes:

Where Ceois the concentration of spherical particles in the system and is in equilibrium with the surface concentrations at both boundaries, and Ciois the initial particle concentration.
Proceeding to non-dimensional and normal dependent variables and boundary conditions, and then using the following dimensionless parameters:
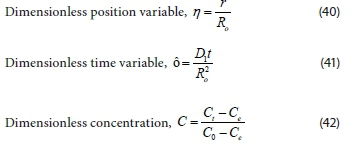
Changes in the initial and boundary conditions due to dimensionless function, gives:

Substituting dimensionless variables into Eq. 36 gives:

Equation 46 is a dimensionless equation predicting rate of particle mass transfer at different operating process conditions. A similar result was found by Jimoda et al. (2013).
Numerical solution technique (separation of variables)
The dimensionless partial differential Eq. 46 was solved using the separation of variables technique, which entails seeking a solution in which the time variable (t) is separated from the space variable (j) (Stroud and Dexter, 2003; Perry and Green, 2007). To solve this equation, we first assume that the solution is the product of two functions, one of time and one of space:

where X is a function of t only, T is a function of n only.
Assuming we simplify the symbols to C = XT and denoting derivatives with respect to their own independent variables by primes, we have:
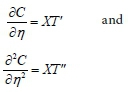
The dimensionless Eq. 46 can then be written as:

Separating the variables, we obtained:

Putting Eq. 49 back into derivative form, we have:

Then let both sides of Eq. 50 be equal to a separation constant (-P2); solving it independently, gives:
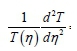
Therefore:

Also,
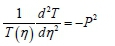
Therefore:

The partial differential Eq. 46 is reduced to ordinary differential Eqs 51 and 52. The integrated form of Eq. 51 gives:

Also, the general solution for Eq. 52 is:
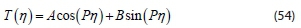
Where A and B are constants to be determined.
Combining Eqs 53 and 54 gives:
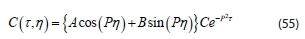
Applying necessary boundary conditions of Eqs 44 and 45 as: C = 0 when N = 0 for all values of t. But P = A, then:
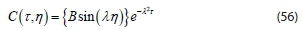
C = 0 when N = 1 for all values of t.

Since B ‡ 0 or C(t, j) would be identically zero,, sin (λ) = 0. Then, the discrete values are assumed, Eigenvalue is λ = nn, for n = 1, 2, 3... and Eigen function is sin (nnn)
Substituting the Eigenvalue into Eq. 56 gives characteristic function:
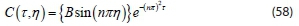
The solution equation in form of a series for an infinite number from Eq. 58 with different values of n is obtained in the form:
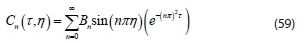
Finally, applying the remaining initial condition of Eq. 43 to Eq. 59 gives:
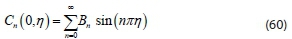
Applying orthogonal properties and integrating the functions across the domain to determine Bn(Stroud and Dexter, 2003; Brown and Churchill, 2001):
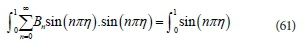
The sum of the left-hand side (LHS) of Eq. 61 results in many terms; however, they are zero except when n = m. This leads to:

Integrating the right-hand side of Eq. 62 and applying boundary conditions gives

Then

Substituting all dimensionless variables into Eq. 64 gives:
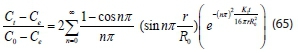
Thus, expressing Eq. 65 as, Ctin order to determine the concentration of organic particles in the system at any process time t:
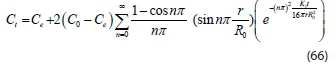
Therefore, Eq. 66 is a mathematical model equation used in predicting colour particle transfer in dye-containing wastewater at any process time.
where Ct= concentration of particles during process at time, t Co= concentration of particles during process at time t = 0 Ce= concentration of particles at equilibrium time.
The resultant Eq. 66 from the numerical analysis was implemented and verified in MATLAB 9.3 by developing codes to obtain different concentrations of the contaminants during the coagulation-flocculation process at different operating times. MATLAB is a powerful code-based mathematical and engineering program (Carnell, 2003: Mahon, 2007). The criterion used to check the accuracy of each model was the mean relative percentage deviation modulus (%M)which explains the mean divergence of the predicted data from measured data (Greenspan, 1977). It is calculated by the expression below:
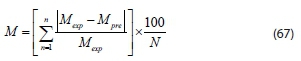
where Mexp= experimental value and Mpre= predicted value Values of %M less than 5 show an extremely good fit; %M value between 5 and 10 represents a reasonably good fit, and %M value greater than 10 shows poor fit (Mundada et al., 2010). Furthermore, the relationship between the experimental data and predicted data was subjected to statistical tools such as: coefficient of determination (R2), Chi-square (x2) F-test, and t-test using Microsoft Excel spreadsheet.
Polymer adsorption studies
Due to the polymeric nature of the coagulants, the adsorption mechanism plays an important role in the colour removal process. Determination of adsorption capacity, adsorption equilibrium, and adsorption kinetics studies were needed to discover the adsorptive nature of the polymers. The parameter extensively used in adsorption studies is adsorption capacity (q). Our study found that contaminant removal by coagulation-flocculation occurs through various mechanisms. The first mechanism is charge neutralization; there is destabilization of colloids which might be governed by chemical interactions between molecules of the coagulant (cationic, positively charged) and the contaminant (anionic, negatively charged). Then, once the coagulant-contaminant complex is formed, flocs begin to grow by adsorption mechanisms. A previous study found the coagulation capacity (q) to be a suitable evaluation parameter (Beltran-Heredia et al., 2011). Polymer adsorption capacity (q) at any contaminant concentration is determined according to the following equation:
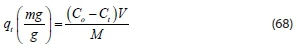
where Cois the initial contaminant concentration (mg-L-1) Ct is the contaminant concentration at time t in the bulk solution (mg-L-1), V is the volume of solution (L), and M is the coagulant mass (mg-L-1)
Polymer adsorption kinetics theory
To gain more insight into the rate of particle transfer, adsorption kinetics was studied. Adsorption kinetics provides knowledge of the controlling mechanism of adsorption processes which in turn governs mass transfer and residence time (Zhang et al., 2011). The kinetic data were analysed using pseudo-first-order, pseudo-second-order and Elovich models.
Lagergren proposed the pseudo first-order kinetic equation (Lagergren and Svenska., 1898) in the form of:
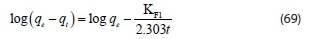
where qtis the amount of adsorbate adsorbed at time t (mg-g-1), qe the adsorption capacity at equilibrium (mg-g-1), KFIthe pseudofirst-order rate constant (min-1), and t is the time (min). The value of the adsorption rate constant, KFI, was determined from the plot of log qe-qtagainst t.
Pseudo-second-order equation (Ho and Mc Kay, 1999) predicts the behaviour over the whole range of adsorption with chemisorption being the rate-controlling step, represented by:

Where k2is the pse u do-second- order rate constant (g-mg-1-min-1). The linear plot of 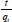 versus t will give
versus t will give 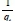 as the slope and
as the slope and 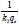 as the intercept. The initial adsorption rate (h-mg-1-min-1) at t = 0 is defined as follows:
as the intercept. The initial adsorption rate (h-mg-1-min-1) at t = 0 is defined as follows:

qeis obtained from the slope of 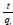 versus t and k2from the intercept, h is obtained from Eq. 71.
versus t and k2from the intercept, h is obtained from Eq. 71.
Elovich kinetic model equation, one of the most useful methods describing chemisorption processes (Aharoni and Tompkins, 1970), is defined as:

Where a (mg-g-1-min-1) is the initial sorption rate and ß (g-mg-1) is related to the extent of surface coverage and activation energy for chemisorption. The value of 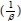 is indicative of the available number of sites for adsorption while
is indicative of the available number of sites for adsorption while 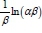 is the adsorption quantity when ln t = 0.
is the adsorption quantity when ln t = 0.
The suitability of the kinetic model to describe the adsorption process was validated by the normalized standard deviation, Δq (%) given by:
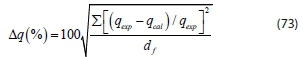
where dfis the degrees of freedom of the fitting equation. The number of degrees of freedom is as follows: N-np, where N is the number of data points and npis the number of parameters. Qexp (mg-g-1) and qcal(mg-g-1) are the experimental and calculated adsorption capacities, respectively.
RESULTS AND DISCUSSION
Characterization results
Proximate analysis
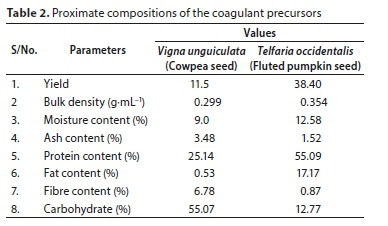
The proximate analyses of coagulant precursors were summarized in Table 2. Moisture content values show the water absorption ability of the coagulants. High crude protein values of 25.14% and 55.09% for Vigna unguiculata and Telfaria occidentalis, respectively, recorded in the precursors, indicate the presence of protein (Mariângela et al., 2003; Kuku et al., 2014). The presence of fibre proved that the precursors are organic polymers with repeating small molecules that could extend as tails and loops when dispersed in water (Bolto and Gregory, 2007). These characteristics led to a new discovery of an adsorption mechanism as relevant in the coagulation-flocculation process. The presence of crude protein, moisture contents, carbohydrate, and fibre contents, justifies the choice of plant seed powders as a potential coagulant in this study.
FTIR analysis of the coagulants
Figures 3 and 4 represent the FTIR peaks of the coagulants. The ranges representing the FTIR peaks of the coagulants before and after the coagulation experiment are shown in Tables 3 and 4. Figure 3 represents the FTIR peaks of Vigna unguiculata coagulant (VUC). The figure shows an absorption peak of 3 656.92 cm-1 which was attributed to the stretching vibration of -OH groups and vibration of water absorbed, or complexes in the coagulant (Zouboulis et al., 2008). The free hydroxyl groups confirm presence of carboxylic acids, alcohols, and phenols in the coagulant. These bands also correspond to the -OH stretching vibrations of cellulose, pectin, and lignin. The results from proximate analysis shown in Table 2 agree with the -OH signalling of the presence of moisture (water), oil, and carbohydrate (glycerides). The FTIR spectral studies revealed that the characteristic absorption peak for amines was clear in 3 656.92 cm-1 for aliphatic primary amine (N-H stretch). The presence of N-H stretching signals in the peaks also shows the presence of amino compounds which confirms the protein contents present in the coagulant as shown in Table 2. A major band present in the broad region of 2 083.06-1 867.04 cm-1 usually indicates presence of a C=O group (carbonyl compound). The FTIR values in Table 3 shows that some peaks shifted or disappeared as seen in 3 286.60 cm-1 and 2 700.26 cm-1, and new peaks were also detected. These changes were observed in the functional groups -C=C-H, C=CH, C-H stretching and -CH2-, and are an indication of the possible involvement of those functional groups in the coagulation-flocculation and surface adsorption of the particles onto polymer surfaces. The diminished peaks showed that all the functional groups are completely involved in the process. In addition, there was a strong adsorption peak at 721.59 and 694.36 cm-1 for both, which is the characteristic frequency for C-H out-of-plane deformation groups. The C-H out-of plane bending is typically the most informative regarding the location and spatial geometry of the double bond (Coates, 2000).
Figure 4 represents the FTIR spectrum of Telfaria occidentalis coagulant. The figure shows an absorption peak in the broad range of 3 780.36-3 224.85 cm-1, attributed to the stretching vibration of -OH groups and vibration of water absorbed, or complexes in the coagulant (Zouboulis et al., 2008). The free hydroxyl groups present in the spectrum confirms the presence of the free hydroxyl groups of carboxylic acids, alcohols, and phenols in the coagulant. This band also corresponds to the -OH stretching vibrations of cellulose, pectin, and lignin. The medium peaks in the range of 2 545.96-2 588.40 cm-1 (2 545.96 cm-1 before coagulation and 2 588.40 cm-1 after coagulation), were attributed to the bending vibration of -OH groups in the water molecule, namely, the H-O-H angle distortion frequency, indicating that the coagulant before and after experiment may contain structural and adsorbed water.
The IR spectral studies revealed that the characteristic absorption peak for amines was evident in the range of 3 656.92-3 780.36 cm-1 for heterocyclic amine (N-H stretch) and 2 545.96-2 588.40 cm-1 for primary amine. Existence of N-H stretching signals in the peaks also confirms that amino compounds are present.
In conclusion, the FTIR spectrum of the two coagulants showed similar peaks and interpretations. The spectral and the proximate analysis results presented in Table 2 suggest the existence of moisture, proteins and esters, which justified using the coagulants for the study.
Scanning electron microscopy (SEM) analysis
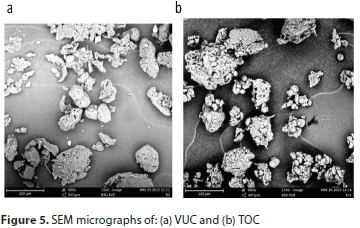
SEM was used to study the surface morphologies of the coagulants as shown in Figs 5a and 5b for VUC and TOC, respectively, at 600x magnification. The images revealed pores of different shapes and sizes. The pore sizes (micro-pores, macropores, and meso-pores) are properties that are unique to organic polymers. Rough surfaces as observed show that the coagulants are coarse fibrous substances largely composed of cellulose and lignin, which confirms their polymeric characteristics. Particles could be attached to these polymer chains through adsorption, inter-particle bridging or electrostatic contacts. The morphology also showed a compact-net structure which is more favourable to particle coagulation-flocculation due to adsorption and bridge formation among flocs, as compared to a branched structure (Zheng and Park, 2009).
Effect of settling time on colour removal efficiency
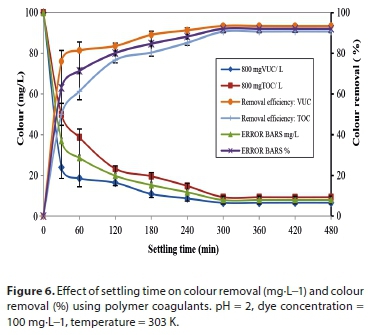
Growth of flocs involves both interactions of coagulant hydroxide precipitate following hydrolysis reaction and contact with particles. Coagulation-flocculation performance is usually evaluated by thetime-dependent decrease in particle concentration, and consequently coincides with the growth of aggregates. The effect of coagulation-flocculation performance is analysed at various settling times at optimal experimental pH, dosages, dye concentration, (DC) and temperature.
Figure 6 shows the kinetic effect of colour concentration and its removal efficiency. The highest reduction in concentration is observed at 800 mgVUC/L, resulting in a removal efficiency of 93.5%. The sudden reduction observed within 30 min indicates a rapid coagulation process which reveals the possible coagulation time (Tag). This rapid decrease in concentration observed between 0 and 30 min could be as a result of either charge neutralization or a combination of charge neutralization/sweep flocculation mechanism. The slow decrease in colour concentration with time after 30 min indicates that, as the reaction proceeds, the amount of particle available for coagulation decreases. This is probably because of complex coagulation-flocculation mechanisms that may involve a formation of a net-like structure, which does not require a very long time. The process was fast at onset, resulting in over 80% removal within 120 min, and slowed down afterwards. The longer flocculation time could be due to the presence of an adsorption mechanism which requires a longer process time to be completed. The reduction in concentration did not vary significantly after 300 min showing that equilibrium was reached. Aggregate destabilization could set in after this time due to saturation of the active sites, which does not allow for further particle adsorption, and so prolongs settling time.
Coagulation-flocculation kinetics
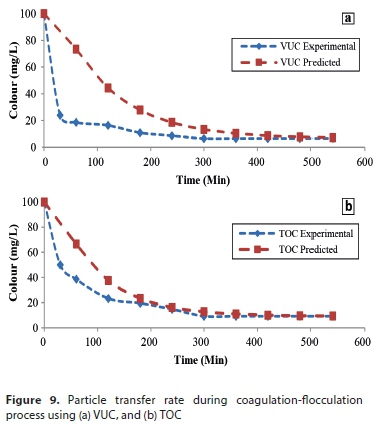
To obtain the order ofthe coagulation-flocculation reaction, analysis was done at the 95% confidence level. Coagulation parameters obtained from the linear regression analysis are presented in Table 5. Coagulation rate, K and order of reaction, a, were obtained from the intercept and slope, respectively, of the equation describing the kinetics of aggregation (Eq. 3). The values of a obtained from the plot for VUC and TOC are 1.7 and 1.6, respectively. The result shows that the order of reaction did not shift significantly from the conventional theory (Menkiti et al., 2009), confirming the reasons the linear regression method was adopted. The order of reaction confirms the best reaction order for the process, showing an approximately second-order reaction, which affects K inversely. The distribution coefficient (R2) values show high agreement and significance of the fit of the kinetic data studied. The value of Tag is inversely related to the contaminant initial concentration. This implies that the greater the contaminant concentration, the lower the coagulation-flocculation time required for removal. The value of the collision efficiency (E) obtained confirms the attainability assumption that the collision between particles and coagulants throughout the dispersion is 100% efficient before aggregation occurs. There is a probability that all particles will stick together after collision and there is an even particle or coagulation complex distribution during the process (Probstein, 2003).
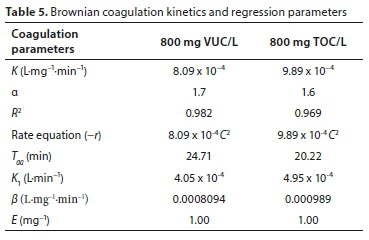
Particle distribution behaviour as a function of time
The variations in CT, C1, C2, C3and C4with time for initially mono-dispersed particles are shown in Fig. 7. Colour concentration, Ct, and concentration of the species, Ci,both decrease monotonically with increasing time. From the plots, the concentrations of C2(t), C3(t) and C4(t) pass through a maximum. This is because they are not present at t = 0 and C0= 0 (Von Smoluchowski, 1917). The number of singlets can be seen to decrease more rapidly than the total number of particles, because of the increasing rate of single particle flocculation as time increases. Thus, the total number of particles decreases according to a bi-molecular reaction. From the plots, we also observe that the lower the value of K, the higher the coagulation time Tagwith respect to Co. At low values of K, the rate is very slow, giving rise to a greater time for the coagulation-flocculation process. The rapid coagulation time agrees with the computed time obtained.
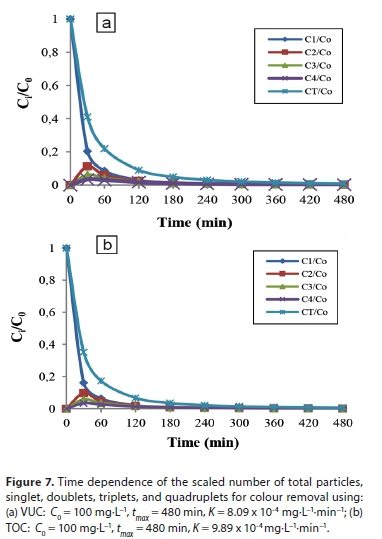
Coagulation-adsorption kinetics
Kinetic models are adopted to study the kinetic make-up of particle transfer, as shown in Fig. 8. The kinetic parameters obtained are summarized in Table 6. The correlation coefficients for the models were relatively low except for the pseudo-second-order model. The experimental data show good agreement with the pseudo-second-order kinetic model data, with the lowest normalized standard deviation, Aq (%) values of 1.12% and 3.15% for VUC and TOC, respectively. The fitting of the pseudo-second-order kinetic model with a high coefficient of determination of R2 > 0.999 further confirms coagulation-flocculation process as a second-order process. Slight agreement with the Elovich model gives further insight to the adsorption-chemisorption process, implying specific adsorption without site competition which is also common for organic ions, and thus leading to the importance of the Langmuir model in the coagulation/ adsorption process. This suggests that the overall rate of the adsorption process was controlled more by chemisorption which involved valence forces through electron sharing between the polymer and contaminant.
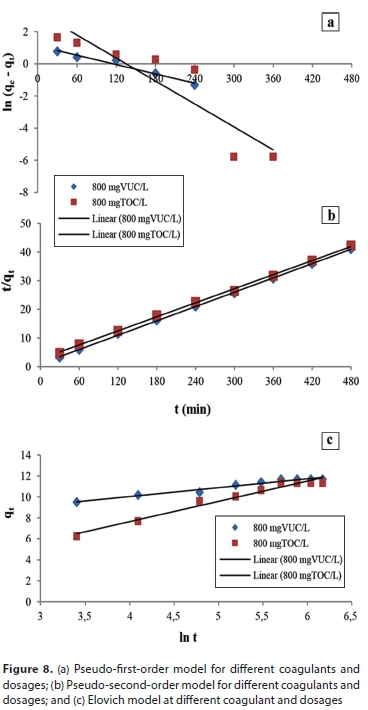
Prediction of spherical particle transfer rate
Verification of particle transfer rate was based on the colour concentration measurement from concentration-time graphs as indicated in Fig. 9. The experimental and predicted particle transfer rates during the process for different coagulants are shown in the plots. The predicted results showed that concentration reduction and, consequently, the rate of mass transfer was rapid at the beginning of the process. A close relationship between the experimental and predicted concentration reductions was observed.
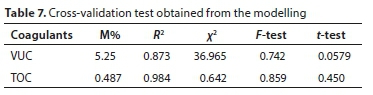
The comparative statistical analysis between experimental and predicted data was done using mean relative deviation modulus (M%), correlation coefficient (R2), Chi-square (x2), F-test, and t-test, as shown in Table 7. The value of M% is less than 10% which indicates a good prediction of experimental data. The R2results gave high values ranging from 0.816-1.000. The correlation coefficients are all near unity indicating strong positive correlation. The F-test and t-test values were found to be significant at the 5% level. The trend found of predicted particle reduction during the coagulation-flocculation process is also similar to that reported by Jimoda et al. (2013) for modelling of mass transfer rate during bio coagulation-flocculation of coal-rich wastewater, as well as Bina et al. (2009) for the effectiveness of Moringa oleifera coagulant protein as natural coagulant aid in the removal of turbidity and bacteria from turbid water.
CONCLUSION
The present study showed the effectiveness of the two bio-coagulants in clarifying AR 44 dye wastewater. The efficacy of the coagulants was due to their coagulation and adsorption characteristics. Proximate analysis showed that VUC and TOC have the features of being potential coagulants. FTIR analysis indicated that some chemical bonds such as -OH, N-H, C=H were present in the coagulant precursor. SEM image revealed rough surfaces, different pores sizes, and compact-net structure. The characterization result showed the coagulants ability: to destabilize contaminant particles, to enhance floc formation due to their polymer characteristics; and to adsorb particles on its surfaces due to their different pores and rough surfaces. Operational parameters studied (pH, coagulant dosage, dye concentration, settling time, and temperature) strongly influenced the colour removal process. The coagulation-flocculation study showed a time-dependent process and was incomplete without an adequate knowledge of the kinetics. The values of K and a were in agreement with the conventional theory of coagulation being a second-order process. Coagulation kinetics results showed a high agreement with pseudo-second-order kinetics with a positive R2. The adsorption process occurred more as a second-order rate process, showing that the rate depends on the square of the particle concentration. Thus, at high particle concentrations, flocculation rate was very high. These results further confirmed that the overall coagulation and adsorption processes were second-order and also controlled by the chemisorption mechanism. Modelling showed a close agreement between the experimental and predicted particle reduction rate. It demonstrated a satisfactory prediction with M% values of less than 10%. High values of R2 were obtained, at 0.873 and 0.984 for VUC and TOC, respectively. The model studied could be used to monitor and predict the colour particle transfer rate as implied by the operating conditions, without using an experimental approach. It could also be adopted to extrapolate space and time not specified by the experimental result. This research has demonstrated the need for application of kinetics studies in wastewater treatment and other masstransfer processes.
REFERENCES
AOAC (1990) Official Methods of Analysis (15th edn). Association of Official Analytical Chemists, Washington DC. [ Links ]
APHA-AWWA-WEF (1999) Standard Methods for the Examination of Water and Wastewater (21st edn). American Public Health Association, American Water Works Association, and Water Environment Federation, Washington, DC. 362-372. [ Links ]
AHARONI C and TOMPKINS FC (1970) Kinetics of adsorption and desorption and the Elovich equation. Adv. Catal. 21 1-40. https://doi.org/10.1016/S0360-0564(08)60563-5 [ Links ]
ANI JU, NNAJI NJ, ONUKWULI OD, and OKOYE CO (2012) Nephelometric and functional parameters response of coagulation for the purification of industrial wastewater using Detarium microcarpum. J. Hazardous Mater. 243 59-66. https://doi.org/10.1016/j.jhazmat.2012.09.069 [ Links ]
BELTRAN-HEREDIA J, SANCHEZ-MARTIN J, and DAVILA-ACEDO MA (2011) Optimization of the synthesis of a new coagulant from a tannin extract. J. Hazardous Mater. 186 1704-1712. https://doi.org/10.1016/j.jhazmat.2010.12.075 [ Links ]
BINA B, YARAHAMADI M and HOSSIENI M (2009) Application of Moringa oleifera seed extract and Polyaluminium chloride in water treatment. World Appl. Sci. J. 7 (8) 962-967. [ Links ]
BOLTO B and GREGORY J (2007) Organic polyelectrolytes in water treatment. Water Res. 41 2301-2324. https://doi.org/10.1016/j.watres.2007.03.012 [ Links ]
BROWN JW and CHURCHILL RV (2001) Fourier Series and Boundary Value Problems (6th edn). McGraw-Hill, New York. 13 pp. [ Links ]
CARNELL AC (2003) MATLAB applications in chemical engineering. North Carolina State University. [ Links ]
COATES J (2000) Interpretation of Infrared Spectra, a Practical Approach in Encyclopedia of Analytical Chemistry. John Wiley & Sons Ltd, Chichester. 10815-10837. [ Links ]
COULSON JM and RICHARDSON JF (2008) Fluid Flow, Heat Transfer and Mass Transfer (6th edn). Elsevier Butter Worth Heinemann, Oxford. 617-630. [ Links ]
GAO BY, WANG Y, YUE QY, WEI JC and LI Q (2007) Color removal from simulated dye water and actual textile wastewater using a composite coagulant prepared by polyferric chloride and polydimethyl diallylammonium chloride. Sep. Purif. Technol. 54 157-163. https://doi.org/10.1016/j.seppur.2006.08.026 [ Links ]
GREENSPAN L (1977) Humidity fixed points of binary saturated aqueous solutions. J. Res. Natl Bureau Standards A Phys. Chem. 81A 89-96. https://doi.org/10.6028/jres.081A.011 [ Links ]
HO YS and MC KAY G (1999) Pseudo-second-order model for sorption processes. Process Biochem. 34 451-465. https://doi.org/10.1016/S0032-9592(98)00112-5 [ Links ]
JEFFREY GH, BASSAT J, MENDHAM J and DENNEY RC (2001) Textbook of Quantitative Chemical Analysis (5th edn). Longman Scientific & Technical, Harlow. 649-720. [ Links ]
JIMODA LA, OKE EO and SALAM KK (2013) Modelling of mass transfer rate during bio coagulation-flocculation of coal-rich wastewater. J. Sci. Res. Rep. 2 (1) 376-390. https://doi.org/10.9734/JSRR/2013/3492 [ Links ]
JOHN H, VAN Z and MENACHEM E (1992) Determination of absolute coagulation rate constants by multi-angle light scattering. J. Colloid. Interf. Sci. 154 101-110. https://doi.org/10.1016/0021-9797(92)90072-T [ Links ]
JONAS AP (2005) Coagulation and flocculation; structure formation in dispersed systems. Taylor and Francis Group, LLC. Surfactant Science Series 126. 162 pp. [ Links ]
KUKU A, ETTI UJ and IBIRONKE IS (2014) Processing of fluted pumpkin seed, Telfairia occidentalis (Hook F) as it affects growth performance and nutrient metabolism in rats. Plant Physiol. Biochem. 11 137-146. [ Links ]
LAGERGREN S and SVENSKA BK (1898) About the theory of so-called adsorption of soluble substances, Kungliga Svenska Vetenskapsakademiens Handlingar 24 1-39. [ Links ]
LONG L, JIAKUN T, YAOLI P, WENCHENG X and GUANGYUAN X (2016) The role of polyaluminum chloride in kaolinite aggregation in the sequent coagulation and flocculation process. J. Colloid. Interf. Sci. 468 57-61. https://doi.org/10.1016/j.jcis.2016.01.039 [ Links ]
MARIÂNGELA SSD, ANDRÉ OC and VALDIRENE MG (2003) Purification and molecular mass determination of a lipid transfer protein exuded from Vigna unguiculata seeds.Braz. J. Plant Physiol. 15 417-421. https://doi.org/10.1590/S1677-04202003000300007 [ Links ]
MASLIYAH JH and BHATTACHAYER SB (2006) Electrokinetic and Colloid Transport Phenomena. John Wiley and Sons, Inc., New Jersey. 433 pp. https://doi.org/10.1002/0471799742 [ Links ]
MCMAHON D (2007) Matlab Demystified. McGraw Hill Companies, New Jersey. [ Links ]
MENKITI MC, NNAJI PC and ONUKWULI OD (2009) Coag-flocculation kinetics and functional parameters response of periwinkle shell coagulant (PSC) to pH variation in organic rich coal effluent medium. Nat. Sci. 7 (6) 1-18. [ Links ]
MIRANDA-MANDUJANO E, MOELLER-CHÁVEZ G, VILLEGAS-ROSAS O, GERMAN BUITRÓN and GARZÓN-ZÜNIGA MA (2018) Decolourization of Direct Blue 2 by peroxidases obtained from an industrial soybean waste. Water SA 44 204-210. https://doi.org/10.4314/wsa.v44i2.06 [ Links ]
MOGHADDAM SS, ALAVIMOGHADDAM MR and ARAMI M (2010) Coagulation/flocculation process for dye removal using sludge from water treatment plant: optimization through response surface methodology. J. Hazardous Mater. 175 651-657. https://doi.org/10.1016/j.jhazmat.2009.10.058 [ Links ]
MOGHAZY RM (2019) Activated biomass of the green microalga Chlamydomonas variabilis as an efficient biosorbent to remove methylene blue dye from aqueous solutions Water SA 45 20-28. https://doi.org/10.4314/wsa.v45i1.03 [ Links ]
MUNDADA M, HATHAN BS and MASKE S (2010) Convective dehydration kinetics of osmotically pretreated promegranate arils. Biosyst. Eng. 107 (4) 307-316. https://doi.org/10.1016/j.biosystemseng.2010.09.002 [ Links ]
OBIORA-OKAFO IA and ONUKWULI OD (2016) Optimization of coagulation-flocculation process for particle removal from dye using natural polymers: Response surface methodological approach. Der Pharm. Chem. 8 (20) 1-12. [ Links ]
OBIORA-OKAFO IA and ONUKWULI OD (2015) Optimization of a coagulation-flocculation process for colour removal from synthetic dye wastewater using natural organic polymers: Response surface methodology applied. Int. J. Sci. Eng. Res. 6 693-704. [ Links ]
PAPIC S, KOPRIVANAC N, BOZIC AL and METES A (2004) Removal of some reactive dyes from synthetic wastewater by combined Al (III) coagulation/carbon adsorption process. Dyes Pigm. 62 29-298. https://doi.org/10.1016/S0143-7208(03)00148-7 [ Links ]
PERRY RH and GREEN DW (2007) Perry's Chemical Engineers' Handbook (8th edn). McGraw-Hill, New York. [ Links ]
PHILIPSE AP (2011) Notes on Brownian diffusion: Brownian encounters. Utrecht University, Debye Institute. Van't Hoff Laboratory. Phys. Colloid Chem. (2011) 7-63. [ Links ]
PROBSTEIN RF (2003) Physicochemical Hydrodynamics, An Introduction (2nd edn). Wiley Inter-science, New York. [ Links ]
SCHICK MJ and HUBBARD AT (2005) Coagulation and flocculation: Experimental and modelling studies, structure formation in dispersed systems. Taylor & Francis Group, LLC. Surfactant Science Series 126 162-813. [ Links ]
STECHEMESSER H and SONNTAG H (2005) Coagulation and flocculation; coagulation kinetics. Taylor and Francis group, LLC. Surfactant Science Series 126 89-92. https://doi.org/10.1201/9781420027686 [ Links ]
STROUD KA and DEXTER JB (1996) Advanced Engineering Mathematics: Partial Differential Equations. (4th edn). Palgrave Macmillan, Tottenham. 415-434. [ Links ]
VON SMOLUCHOWSKI M (1917) Versucheiner mathemtischentheorie der koagulations kinetic kolloider lousungen. Z. Phys. Chem. 92 129-168. [ Links ]
ZHANG T, LI QR, LIU Y, DUAN YL and ZHANG WY (2011) Equilibrium and kinetics studies of fluoride ions adsorption on FeO2/Al2O3 composites pre-treated with non-thermal plasma. Chem. Eng. J. 168 665-671. https://doi.org/10.1016/jxej.2011.01.054 [ Links ]
ZHENG Y and PARK J (2009) Characterization and coagulation performance of a novel inorganic polymer coagulant: Poly-zinc-silicate-sulphate. Colloids Surf. A: Physicochem. Eng. Aspects 334 147-154. https://doi.org/10.1016/jxolsurfa.2008.10.009 [ Links ]
ZONOOZI MH, MOGHADDAM RM and ARAMI AG (2008) Removal of Acid Red 398 dye from aqueous solutions by coagulation/ flocculation process. Environ. Eng. Manage. J. 7 695-699. https://doi.org/10.30638/eemj.2008.092 [ Links ]
ZOUBOULIS AI, MOUSSAS PA and VASILAKOU F (2008) Polyferric sulphate: preparation, characterization and application in coagulation experiments. J. Hazardous Mater. 155 459-468. https://doi.org/10.1016/j.jhazmat.2007.11.108 [ Links ]
 Correspondence:
Correspondence:
IA Obiora-Okafo
Email: ifyobioraokafo@yahoo.com
Received: 09 October 2018
Accepted: 10 December 2019














