Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Water SA
On-line version ISSN 1816-7950
Print version ISSN 0378-4738
Water SA vol.46 n.1 Pretoria Jan. 2020
http://dx.doi.org/10.17159/wsa/2020.v46.i1.7885
RESEARCH PAPERS
Numerical investigation of leakage behaviour in long radius elbows
Moustafa S DarweeshI, II; Osama S HussienI, III
ICivil Engineering Department, Northern Border University, Arar, Saudi Arabia
IICivil Engineering Department, Assiut University, Assiut, Egypt
IIICivil Engineering Department, Al-Azhar University, Cairo, Egypt
ABSTRACT
This paper focuses on the relationship between leakage opening areas and pressure heads for 90° long radius elbows under elastic limits using finite element analysis (SAP 2000). The results indicate that leakage opening areas grow linearly as the system pressure increases and the relation is described by the pressure-area slope (M). A sensitivity study was performed to show the effect of various parameters on M, as well as the leakage exponent (N). It was found that elbow internal diameter has the largest influence on the pressure-area slope, followed by the modulus of elasticity and finally elbow wall thickness. The longitudinal stress and Poisson's ratio have a negligible effect on M. Furthermore, leak quantity is related to the pressure raised to a power ranging from 0.495 to 0.592. Regression analysis was used to derive an empirical equation to predict the pressure-area slope of round holes within elbows with different properties.
Keywords: finite element analysis, leakage, leakage exponent, long radius elbows, pressure
INTRODUCTION
A hydraulic transient can generate excessively high pressures, causing severe damage to pump components, pipes, bends, elbows and other fittings (Bentley Systems et al., 2007). Leakage is a focal problem, because it not only reduces the reliability and efficiency of water distribution systems (WDSs), but causes intrusion of contaminants as well as damage to the infrastructure. Farley and Trow (2003) reported that the leakage rate through WDSs represents 50% of the total water produced and might reach 80% for some networks. Mora et al. (2014) pointed out that leak discharge is dependent on soil type, water quality, specifications and construction quality, materials, infrastructure age, operational practices and maintenance. In addition, leaks can occur as a consequence of a cross-section crack, crushing and longitudinal cracks. Flow through pipe leaks can reasonably be modelled by the classical Torricelli's equation, which describes the conversion of all the potential energy, in the form of pressure, to kinetic energy:

where QL is leakage rate, Cd is discharge coefficient, AL is orifice (leak) area, g is acceleration due to gravity and h is pressure head differential over the orifice. Shao et al. (2019) demonstrated experimentally that intrusion and leakage rates through cracks in pipelines do not follow the standard orifice expression, because this ignores the main pipe flow velocity effectiveness.
However, Eq. 1 considers leakage opening area as being constant relative to fluid pressure, whereas actually the hole area changes with pressure variation (De Marchis and Milici, 2019; Van Zyl and Malde, 2017; Van Zyl et al., 2017). A leak can be described by the following general equation (Adedeji et al., 2018; Raei et al., 2019):

where C is leakage coefficient and N is leakage exponent. Several studies have shown that the leakage exponent can differ significantly from the theoretical orifice value of 0.5 and generally covers a range of 0.36-2.95 (Schwaller and Van Zyl, 2015). Van Zyl and Clayton (2007) demonstrated factors that account for the high variation of N values: pipe material properties, leakage hydraulics, soil hydraulics and finally water demand.
According to Cassa and Van Zyl (2013, 2014) and Latchoomun et al. (2015), the following relationship can describe all leakage types, under elastic status:

where Ao is orifice initial area and M is pressure-area slope. By substituting Eq. 3 into Eq. 1, one can get the fixed and variable area discharge (FAVAD) equation (May, 1994), or Cassa and Van Zyl (2010) expression:

Equation 4 indicates that leakage flow rate is proportional to the pressure head in the pipe raised to a power varying from 0.5 to 1.5.
A new dimensionless parameter, leakage number LN, can be introduced for any system by dividing the variable and fixed parts of a leak as follows (Schwaller et al., 2015):

Cassa and Van Zyl (2014) suggested a formula that can convert leakage exponent to leakage number:

In this research, the relationship between the leak area and pressure and the effects of bent pipe features (modulus of elasticity, Poisson's ratio, pipe wall thickness, longitudinal stress and internal diameter) and hole size on the slope of the pressure-area curve for long radius elbows were investigated. The finite element model was established using the SAP 2000 program, and only the elastic deformation was considered.
METHODOLOGY
Finite element procedure
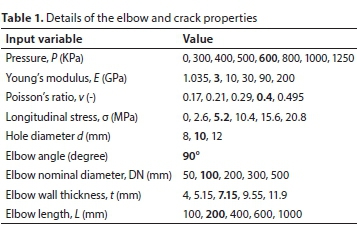
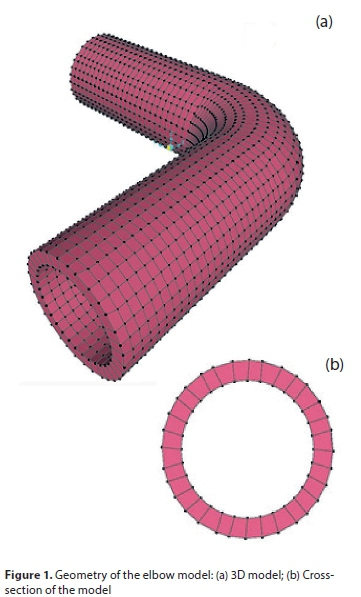
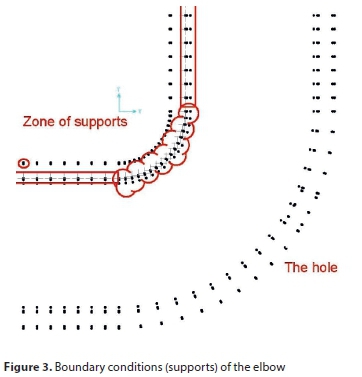
The finite element method (FEM) is a numerical technique that can represent an object, such as an elbow, as a group of elements or mesh. Each element is solved separately and is then recombined to give a final solution. The solution of this method is reached by assuming the displacement function to describe the displacements within the element instead of the infinite series for the whole elbow. This study included finite elements to analyse the behaviour of circular cracks in bent pipes under pressure by the 3D model, as shown in Fig. 1(a); the cross-section of the model is presented in Fig. 1(b). The SAP finite element software was used in this investigation as well as a software program designed by the authors to determine the area of the deflected shape. The dimensions and attributes of the test elbow are given in Table 1. Eight-node solid elements (Fig. 2) were proposed throughout the elbows; the elements range in size and are smaller around the hole to improve the accuracy of the model. The boundary conditions of the quarter bend are hinged support as shown in Fig. 3.

The elbow was loaded with a uniform internal load as a pressure (toward the outside), and external stresses at the elbow ends to simulate the longitudinal pipe stresses. The bowed pipe was assumed to be level horizontally. In the biaxial load state, the longitudinal stress was calculated using Eq. 7 (Gere and Goodno, 2009):

where σ is the longitudinal stress, D is the inner diameter of the elbow, P is the internal pressure, and t is the wall thickness of the elbow.
Finite element model (used leakage model)
To illustrate the role of the different parameters in hole behaviour under various pressures in long radius elbows, a base model of a 90° elbow with 100 mm nominal diameter and a wall thickness of 7.15 mm was applied as a base model (Standard: ASME B16.9-2001; ASME, 2001). In order to assess the impact of each parameter on the pressure-area slope of the elbow, a sensitivity analysis was considered by varying one parameter at a time, while the rest of the parameters remained constant. Table 1 shows the values for the elbow pipe and the crack characteristics that were used in the analysis; the base model's values are in bold. The selected magnitudes cover a wide range of values that are commonly used in WDSs.
RESULTS AND DISCUSSION
Effect of different parameters on pressure-area slope (M)
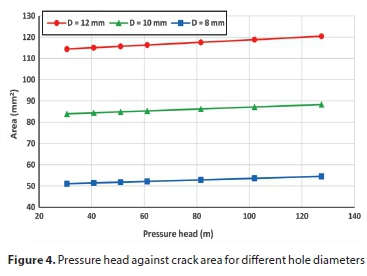
Figure 4 displays the relationship between the internal pressure and crack area for different hole sizes in long radius elbows. From Fig. 4, it is seen that opening size expands as the pressure increases. A linear trend line fits the FEM data almost completely, as confirmed theoretically by Cassa and Van Zyl (2013) and experimentally by Nsanzubuhoro (2016).
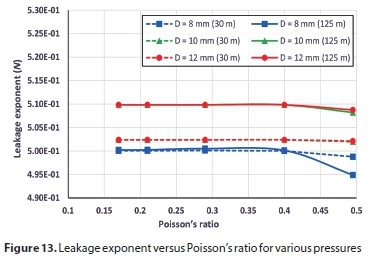
To examine the role of each variable in determining the slope of the pressure-area curve, all parameters were fixed except the studied variable. Figures 5 to 9 show the variation of pressure-area slope against the studied parameter. Figure 5 shows that M is inversely proportional to the modulus of elasticity (E) for the three hole sizes. In Fig. 6, the pressure-area curve slope is directly proportional to the elbow internal diameter raised to the power of 1.27, 1.38 and 2.30 for hole sizes 12 mm, 10 mm and 8 mm, respectively. From Figs 7 and 8 one can see that the Poisson's ratio (υ) and longitudinal stress (σ) have a negligible influence on pressure curve slope. Also, Fig. 7 reveals that M becomes negative at high Poisson's ratios (0.495), which indicates that the deformed area is less than the original one, thereby resulting in a leakage exponent of less than 0.5. This occurs due to local deformations around the hole which lead to increases in local stresses, generating a smaller opening area (Nsanzubuhoro, 2016). It is evident from Fig. 9 that the three holes display the same behaviour; as the elbow wall thickness increases the pressure-area slope decreases. The relationship between the slope M and wall thickness can be expressed as a power function: −1.11, −1.06 and −1.04 for holes of 12 mm, 10 mm and 8 mm, respectively. Figures 5 to 9 show that the behaviour of the small hole (8 mm) does not conform to the trend when the holes are larger (10 mm and 12 mm); this could be due to the rigidity of the elbow material and the lower stress concentration as compared with larger hole sizes.
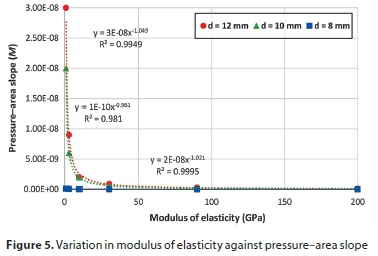
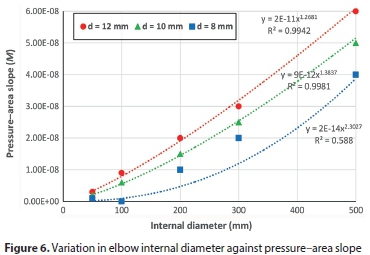
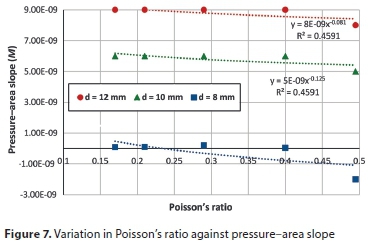
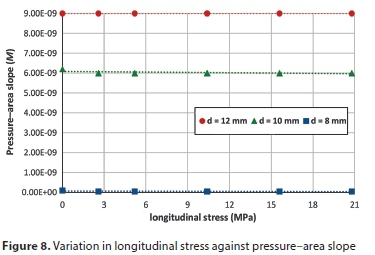
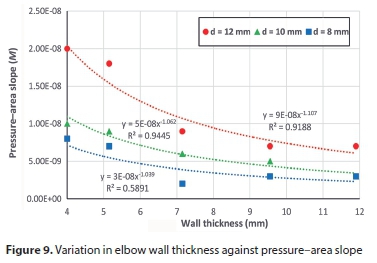
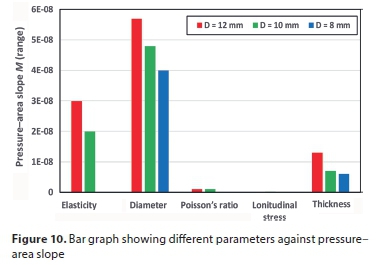
In order to determine which of the parameters has the largest effect on the pressure-area slope, the FEM output data for the pressure-area slope was plotted against all the studied variables, as depicted in the bar graph (Fig. 10). From the figure, it can be seen that the elbow internal diameter has the dominant influence on the head slope for all holes, followed by the modulus of elasticity and then elbow wall thickness. Poisson's ratio and the longitudinal stress have an insignificant impact on slope M. These results agree with the experimental findings of Nsanzubuhoro (2016) for leaks through circular holes in straight water tubes.
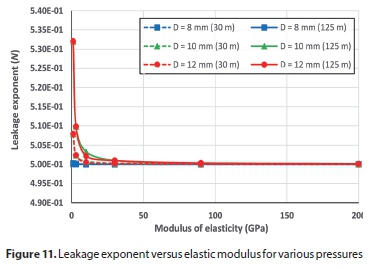
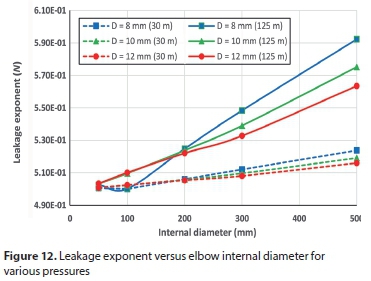
Effect of different parameters on leakage exponent (N)
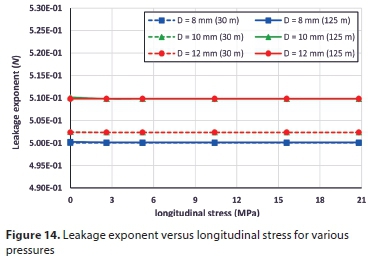
It is common for practitioners to use leakage exponent N in practice. Firstly, leakage number was calculated by Eq. 5 at two pressure values; one high (125 m H2O) and the other low (30 m H2O); thereafter N can be determined by Eq. 6. Figures 11 to 15 present the variation of leak exponent against the various parameters at the two pressure heads for several opening sizes. From the figures, it can be deduced that leakage exponent N for pressurized long radius elbows varies between 0.495 and 0.592, which differs substantially from the prevalent number of 0.5, which Torricelli's equation states. In addition, the leak exponent is inversely proportional to both elastic modulus and wall thickness, while it is directly proportional to the elbow internal diameter. For example, for 500 mm internal diameter with 8 mm hole and at 125 m H2O, N will be 0.592, while it drops to 0.575 and 0.563 for 10 mm and 12 mm holes, respectively. The leakage exponent, N, varies slightly with Poisson's ratio or the longitudinal stress.

Mathematical relationship for predicting the pressure-area slope (M)
Regression analysis is a statistical method used to find relationships between variables. In this work, multiplicative regression modelling (Chatterjee and Hadi, 2012) was performed to obtain a relationship that describes pressure-area slope as a function of the elbow characteristics (material and geometry) and hole dimensions. The empirical formulas (SI units) obtained for circular openings in long radius elbows are:
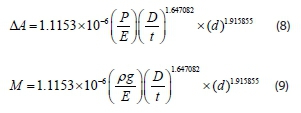
As discussed previously, the Poisson's ratio and the longitudinal stress have a negligible effect on the pressure-area slope, and thus were dropped from the equations. By substituting M into Eq. 4, the leakage discharge through an orifice becomes:
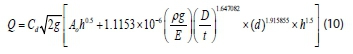
From this empirical equation, which reasonably fits the FEM data with a correlation (R2) of 97.87%, the pressure-area slope can be predicted for 90° long radius elbows using its properties and the hole diameter.
It should be noted that supplemental research is needed to investigate the behaviour of single and multiple holes with different shapes and sizes in elbows with many angles, and subjected to elastic and plastic conditions.
CONCLUSIONS
This article concentrates on the behaviour of round holes in 90° long radius elbows under elastic deformations only, using the finite element method. It was found that the opening area enlarges linearly as the pressure increases. A sensitivity analysis was done to show the influence of different parameters on the pressure-area slope M, as well as leakage exponent N. It was observed that elbow internal diameter has the greatest effect on pressure-area slope, then Young's modulus and finally the elbow wall thickness. The longitudinal stress and Poisson's ratio have a negligible effect on slope M, and for small hole diameters the sensitivity analysis shows varying results as compared with larger hole diameters. Also, it was noted that leakage outflow is related to the fluid pressure raised to a power ranging from 0.495 to 0.592. A regression model was used to develop an empirical formula that may be utilized to obtain the pressure-area slope for various elbows and hole opening properties and dimensions.
RECOMMENDATIONS
It is recommended that further research be conducted based on actual experiments on the existing elbows to verify the obtained numerical results.
ACKNOWLEDGMENTS
First and foremost, we would like to express our gratitude to ALLAH for giving us the will to fulfil this work. The authors gratefully acknowledge the approval and the support of this research study by the grant no. ENG-2018-3-9-F-7607 from the Deanship of Science Research at Northern Border University, Arar, K.S.A.
REFERENCES
ADEDEJI KB, HAMAM Y, ABE BT and ABU-MAHFOUZ AM (2018) Pressure management strategies for water loss reduction in large-scale water piping networks: A review. In: Gourbesville P, Cunge J and Caignaert G (eds): Advances in Hydroinformatics: SimHydro 2017 - Choosing the Right Model in Applied Hydraulics. Springer Water series, Springer Singapore publisher. 465-480. URL: http://93.174.95.29/_ads/C0B3C493C5700CFD207D6FB235567771. [ Links ]
ASME (American Society of Mechanical Engineers) Standard: ASME B16.9-2001 (2001) Factory-made wrought buttwelding fittings. ASME, New York. 46 pp. [ Links ]
BENTLEY SYSTEMS, WALSKI TM, CHASE DV, SAVIC DA, GRAYMAN W, BECKWITH W and KOELLE E (2007) Advanced Water Distribution Modeling and Management (1st edn). Haestad Methods Press, Exton, Pennsylvania. URL: http://93.174.95.29/_ads/C30B096034A608869AA80DBFA5D362FA. [ Links ]
CASSA AM, VAN ZYL JE and LAUBSCHER RF (2010) A numerical investigation into the effect of pressure on holes and cracks in water supply pipes. Urban Water J. 7 (2) 109-120. https://doi.org/10.1080/15730620903447613. [ Links ]
CASSA AM and VAN ZYL JE (2013) Predicting the head-leakage slope of cracks in pipes subject to elastic deformations. J. Water Supply Res. Technol. AQUA 62 (4) 214-223. https://doi.org/10.2166/aqua.2013.094. [ Links ]
CASSA AM and VAN ZYL JE (2014) Predicting the leakage exponents of elastically deforming cracks in pipes. Procedia Eng. 70 302-310. https://doi.org/10.1016/j.proeng.2014.02.034. [ Links ]
CHATTERJEE S, and HADI AS (2012) Regression Analysis by Example (5th edn). John Wiley & Sons, Inc., New York. 1-421. URL: http://93.174.95.29/_ads/A30F8ED6699DECBAC569C06927BFBB7E. [ Links ]
DE MARCHIS M and MILICI B (2019) Leakage estimation in water distribution network: effect of the shape and size cracks. J. Water Resour. Manage. 33 (3) 1167-1183. https://doi.org/10.1007/s11269-018-2173-4. [ Links ]
FARLEY M and TROW S (2003) Losses in Water Distribution Networks: A Practitioner's Guide to Assessment, Monitoring and Control. IWA Publishing, London. 1-296. URL: https://doi.org/10.2166/9781780402642. [ Links ]
GERE JM and GOODNO BJ (2009) Mechanics of Materials (7th edn). Cengage Learning. URL: http://93.174.95.29/_ads/E49A3A1A695B4CB87EF61FB1079F2932. [ Links ]
LATCHOOMUN L, AH KING RTF, BUSAWON K, MAWOOA D and KAULLY RG (2015) Laboratory investigation of the leakage characteristics of unburied HDPE pipes. Procedia Eng. 119 91-100. https://doi.org/10.1016/j.proeng.2015.08.858. [ Links ]
MAY JH (1994) Pressure dependent leakage. World Water and Environmental Engineering, October 1994. Technical Report. Water Environment Federation, Washington, DC. [ Links ]
MORA-RODRIGUEZ J, DELGADO X, RAMOS H and LÓPEZ-JIMÉNEZ PA (2014) An overview of leaks and intrusion for different pipe materials and failures. Urban Water J. 11 (1) 1-10. https://doi.org/10.1080/1573062X.2012.739630. [ Links ]
NSANZUBUHORO R (2016) Predicting variations in the areas of circular leaks in water pipes due to changes in pressure. MSc thesis, Civil Engineering Department, University of Cape Town, South Africa. [ Links ]
RAEI E, SHAFIEE ME, NIKOO MR and BERGLUND E (2019) Placing an ensemble of pressure sensors for leak detection in water distribution networks under measurement uncertainty. J. Hydroinf. 21 (2) 223-239. https://doi.org/10.2166/hydro.2018.032https://doi.org/10.2166/hydro.2018.032. [ Links ]
SCHWALLER J and VAN ZYL JE (2015) Modeling the pressure-leakage response of water distribution systems based on individual leak behavior. J. Hydraul. Eng. 141 (5) 04014089-1-04014089-8. https://doi.org/10.1061/(ASCE)HY.1943-7900.0000984. [ Links ]
SCHWALLER J, VAN ZYL JE and KABAASHA AM (2015) Characterising the pressure-leakage response of pipe networks using the FAVAD equation. Water Sci. Technol. Water Suppl. 15 (6) 1373-1382. https://doi.org/10.2166/ws.2015.101. [ Links ]
SHAO Y, YAO T, GONG J, LIU J, ZHANG T and YU T (2019) Impact of main pipe flow velocity on leakage and intrusion flow: an experimental study. Water J. 11(1) 118-129. https://doi.org/10.3390/w11010118. [ Links ]
VAN ZYL JE and CLAYTON CRI (2007) The effect of pressure on leakage in water distribution systems. Water Manage. J. 160 (2) 109-114. https://doi.org/10.1680/wama.2007.160.2.109. [ Links ]
VAN ZYL JE, LAMBERT AO and COLLINS R (2017) Realistic modeling of leakage and intrusion flows through leak openings in pipes. J. Hydraul. Eng. 143 (9) 04017030-1-04017030-7. https://doi.org/10.1061/(ASCE)HY.1943-7900.0001346. [ Links ]
VAN ZYL JE and MALDE R (2017) Evaluating the pressure-leakage behaviour of leaks in water pipes. J. Water Supply Res. Technol. 66 (5) 287-299. https://doi.org/10.2166/aqua.2017.136. [ Links ]
 Correspondence:
Correspondence:
Moustafa S Darweesh
eng_taftaf82@yahoo.com
Received: 23 April 2019
Accepted: 11 November 2019














