Serviços Personalizados
Artigo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em Google
Similares em Google
Compartilhar
Water SA
versão On-line ISSN 1816-7950
versão impressa ISSN 0378-4738
Water SA vol.45 no.4 Pretoria Out. 2019
http://dx.doi.org/10.17159/wsa/2019.v45.i4.7550
RESEARCH PAPERS
Assessment of straight and meandering furrow irrigation strategies under different inflow rates
S Sayari; M Rahimpour*; M Zounemat-Kermani
Water Engineering Department, Shahid Bahonar University of Kerman, Kerman, 76169-133, Iran
ABSTRACT
This paper reports the effect of straight furrow (SF) and meandering furrow (MF) irrigation strategies, as well as inflow rate, on infiltration and hydraulic parameters including advance time, recession time, and runoff hydrograph. The performance of SF and MF irrigation in terms of runoff ratio, deep percolation, and application efficiency was evaluated in 6 furrow fields at Shahid Bahonar University of Kerman, Iran. The required data were collected from the farm, consisting of free drainage furrows with length 70 m, top width 0.8 m, depth 0.25 m, and slope 0.2%. The advance and recession times were significantly longer in MF than SF irrigation. The infiltration was estimated by Lewis-Kostiakov equation. The infiltration coefficients were calculated: The values of k were higher and of a were lower in MF furrows than in SF furrows. The average runoff ratio and application efficiency for the SF irrigation events were 50.53% and 49.07%, respectively, while those of the MF irrigation events were 7.04% and 52.94%, respectively. Based on the results, the velocity of water advance in MF irrigation is decreased and, thus, the runoff, erosion losses, mass of fertilizer lost and surface water contamination were reduced. Using a lower inflow rate and appropriate irrigation time leads to better management outcomes in irrigation systems.
Keywords: meandering furrow irrigation, straight furrow irrigation, advance and recession time, runoff ratio, irrigation performance
INTRODUCTION
Furrow irrigation is the most common method of surface irrigation because of its low cost and energy. However, these systems are usually associated with low application efficiency and high labour requirements for land levelling and setting up the system (Spaskhah and Shaabani, 2007). In Iran, agricultural water uses over 90% of the water supply (Mergen, 2014). The application efficiency of surface irrigation is low and a large volume of water is lost. Improving application efficiency can reduce water application without affecting productivity. Several researchers have made recommendations to improve irrigation performance (Moravejalahkami, 2012; Reddy et al., 2013) or for the use of alternate furrow irrigation to increase productivity (Barios-Masias and Jackson, 2016; Mintesinot et al., 2004; Siyal et al., 2016; Xiao et al., 2015). One of the solutions to this problem is using innovative and high-tech irrigation methods (drip, sprinkler, etc.). However, farmers in Iran or other developing countries often refuse to use these methods because of the high cost of set-up, performance, and maintenance.
In many countries, farmers cover the furrows and canals with straw to minimize water velocity and soil erosion in the first irrigation (Roldán-Cañas et al., 2015). Some farmers in Iran use meandering furrow (MF) irrigation. In MF irrigation, compared to straight furrow (SF) irrigation, water flows in a furrow that has a meandering path and, therefore, the velocity of water advance decreases, leading to a higher irrigation efficiency. In addition, decreasing the flow velocity will increase infiltration volume and decrease runoff and erosion losses (Mostafazadeh-Fard et al., 2010; Soroush et al., 2012). Distribution uniformity and application efficiency are affected by the furrow inflow rate, especially as the inflow is reduced (Alazba, 1999; Gharbi et al., 1993; Gillies et al., 2007). Prediction of the values of infiltration parameters is required to design surface irrigation (Spaskhah and Afshar-Chamanabad, 2002; Zerhun et al., 1996). The very small changes in the inflow rate could have a considerable impact on infiltration parameters (McClymont and Smith, 1996).
Mostafazadeh-Fard and Moravejalahkami (2006) studied the performance of snake-shaped furrow irrigation. For this purpose, they used three experimental farms with different soil textures and field slopes. The results showed that by increasing the slope and keeping the other parameters the same, the application efficiency of the snake-shaped furrow irrigation increases, but the application efficiency of the straight furrow irrigation decreases. Sepaskhah and Shaabani (2007) studied infiltration parameters, flow hydraulics, and geometric parameters in an anguiform furrow, and compared these parameters with those of straight furrow irrigation. Compared to the straight furrow irrigation, the recession time and infiltration rate were higher in the anguiform furrow. According to Mostafazadeh-Fard et al. (2010), erosion and runoff are lower in MF than SF irrigation. Soroush et al. (2012) investigated the influence of the meandering and standard furrow on distribution uniformity and fertilizer losses. The results showed that the mass of nitrogen losses is notably less for meandering than standard furrow irrigation because of the lower runoff from MF irrigation. Roldán-Cañas et al. (2015) studied MF irrigation in an experimental field in Bolivia. Ten irrigation events were evaluated by measuring advance and recession times, inflow, and runoff rate. The results revealed that the furrow irrigation system was poorly managed and performed poorly.
In surface irrigation, run-off losses lead to soil erosion which can be damaging because it results in the loss of productive soil on the farm (Lehrsch et al., 2014), especially when the soil is bare or plant growth is in its early stages, or in fields that slope steeply. In deep percolation losses, soil erosion decreases, and part of the applied irrigation water is unreachable. Deep percolation results in the transport of dissolved salts from the root zone. Therefore, it is useful for saline soils (Letey et al., 2011). Water for irrigation is a major limitation to agricultural production in many countries. In Iran, 90% of water use is for agriculture. Therefore, the management of water consumption is important. When the soil is saline, leaching by irrigation water is vital. The type of soil and slope of the field can be important for choosing the type of furrow irrigation (SF or MF).
The primary objective of this study was to describe, characterize and evaluate meandering furrow irrigation by conducting irrigation field experiments at different inflow rates, and to compare the results with that of standard furrow irrigation. To this end, the operating and performance variables were measured by field monitoring of irrigation events.
MATERIALS AND METHODS
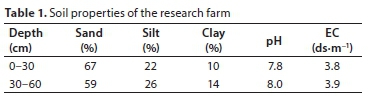
The furrows (straight and meandering) were constructed in the agricultural farm of Shahid Bahonar University of Kerman (SBUK), Iran. The research farm is located in Southeast Kerman (57°10´E, 30°20´N) on sandy loam soil, at 1 750 m amsl. The field had been prepared for planting tomatoes, but the experiments were performed on bare soil. Soil properties of the research farm are presented in Table 1. The experiment was laid out using a complete randomized design with 3 replications. During the field experiments, advance times, recession times and runoff were measured. The experiments were conducted on furrows of 70 m length and 0.75 m width. Inflow and outflow discharge values were measured by a V-notch weir and 1-inch Parshall flume, respectively. For the MF irrigation method, the width of each bend was 4 m. The longitudinal slope of both furrows was 0.2% and the lateral slope in MF was zero. Twenty-four stations were marked along the length of the furrows, and the advance and recession times were measured at each station by recording when the water reached a station and when it disappeared from it. Figure 1 presents an overview of the experimental furrows.
Data were collected from the first irrigation in each furrow. Inflow rates were determined by control valves connected to a concrete pipe at the upstream end of the field. Furrow cross-section parameters are based on the furrow geometry equation:
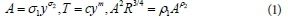
where A is the cross-sectional area, T is the top width, y is the furrow depth, and R is the hydraulic radius, presented in Table 2 as measured before the first irrigation.

Infiltration parameters can be estimated by the observed advance data (Elliott et al., 1983; McClymont and Smith, 1996) or by a combination of advance and runoff data (Gillies and Smith, 2005; Scaloppi et al., 1995). The two-point method computes infiltration parameters with the measured advanced data (Gillies and Smith, 2005; Gillies et al., 2007; Guardo et al., 2000). Infiltration in the furrow was computed by the Lewis-Kostiakov equation Z = kτa + f0τ, where Z is the water infiltrated volume per unit length of the furrow, τ is the intake opportunity time, f0 is the final infiltration rate, and k and a are empirical parameters. The advance equation can be used to calculate infiltration parameters a and k in furrow irrigation as follows (Walker, 1989):

where x is the advance distance, tadv is the advance time, and p and r are advance parameters. Walker and Skogerboe (1987) combined Lewis-Kostiakov, advance, and water balance equations and obtained the following equation:
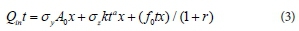
where Qin is the inflow rate; A0 is the water cross-sectional area upstream of the furrow calculated from A0 = (Qinn/(ρ1S1/2))1/ρ2 (Walker, 1989), n is the Manning coefficient, ρ1 and ρ2 are the furrow geometrical parameters, σy is the surface storage water profile shape factor assumed to be 0.75, and σz is the infiltrated water profile shape factor computed by the following equation (Walker, 1989):
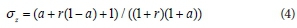
where a is the exponent of the Lewis-Kostiakov equation and r is the advance curve parameter. Instead of using the two-point method, all the data from the stations have to be used to estimate k and a for each irrigation, since the slope and inflow rate are different throughout the furrow length. Therefore, Eq. 2 can be rewritten as follows (Sepaskhah and Shaabani, 2007):
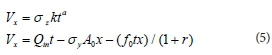
The infiltration of the Lewis-Kostiakov equation can be calculated from Eq. 5. The values of Vx1 (the Vx parameter at 1 min interval) and a are estimated by regression analysis for Vx and t. Then, the k parameter is computed from K = Vx1/σz.
The infiltration parameters and properties of the experi-mental furrow for each irrigation event are shown in Table 3.
The application efficiency (Ea) for each experiment was computed by Eq. 6:
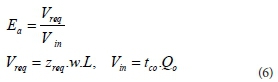
where Vin is the total volume of water applied at each irrigation; Vreq is the water volume required in the soil profile; zreq is the soil moisture extracted by the crop between irrigations; L is furrow length; w is furrow spacing; tco is cut-off time; and Qo is inflow rate. The amount of water required in the root zone was assumed to be 50 mm for all experiments.
Runoff ratio was calculated from the following equation:
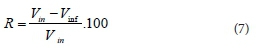
where Vinf is the infiltrated volume. Deep percolation (Dp) is the percentage of the infiltrated water that is unreachable for the plants and penetrates to the lower depths. Dp was obtained from Eq. 8.
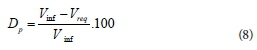
RESULTS AND DISCUSSION
The advance and recession curves for both irrigation methods are presented in Figs 2 to 4. The advance times in the irrigation events S1, S2, S3, M1, M2, and M3 were 40.25, 23.16, 19.38, 63.36, 35.28, and 15.83 min, respectively. It can be observed that the advance time was significantly greater in MF than SF. In irrigation events M1 and M2, the advance time was, respectively, 57% and 52% larger than its counterpart in irrigation events S1 and S2. These results indicate that the flow velocity was lower in MF than in SF.
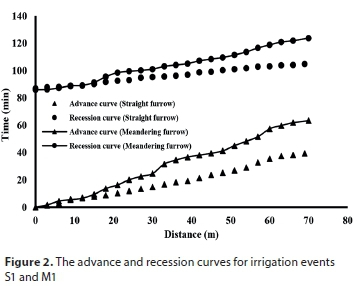
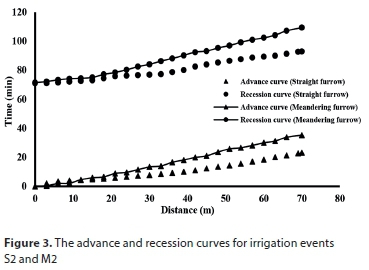
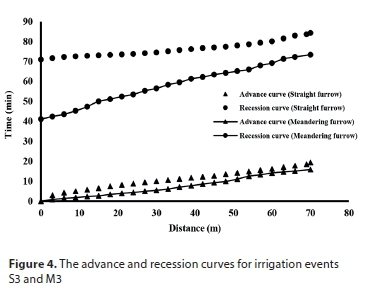
While the flow rate increased from 0.6 to 1.2 L∙s−1, the advance time was reduced 42% and 44% for SF and MF irrigations, respectively. By varying the flow rate from 0.6 to 2.4 L∙s−1 for SF irrigation and from 1.2 to 3.6 L∙s−1 for MF irrigation, the advance time decreased 51% and 55%, respectively. The impact of changing the flow rate is almost the same for both irrigation methods, although the reduction of advance time is slightly greater in MF irrigation than SF irrigation.
The recession time was greater for MF than SF because of the higher water storage at the stations. During irrigation events M1 and M2, the recession time was 17% longer than its counterpart in irrigation events S1 and S2. The disappearance of water in the recession phase of MF irrigation is mostly because of the infiltration and not because of the outflow downstream of the furrow. The advance and recession curves were almost parallel for both furrow irrigation methods, which shows uniform infiltration throughout the furrows. As can be seen from Figs 2 and 3, advance times decrease when inflow rate increases and the difference in advance times between the two irrigation methods also decreases.
The values of inflow during irrigation events were 0.6, 1.2, 2.4, and 3.6 L∙s−1. The runoff hydrographs of each irrigation event are presented in Figs 5-7. Runoff was notably less in MF than SF irrigation. As water flows in the MF, the direction of flow changes along the furrow, leading to an increase in the wetted perimeter and the infiltration depth. Furthermore, because of the lower velocity in MF irrigation, soil erosion is less compared to SF irrigation. The volumes of inflow and outflow during each irrigation event are shown in Table 3.
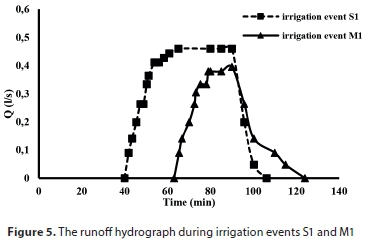
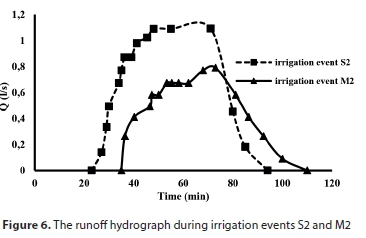
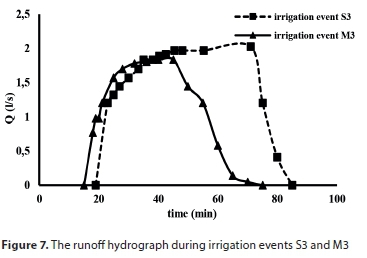
The flow rate and depth of water are affected by the basic infiltration rate (Sepaskhah and Afshar-Chamanabad, 2002), as confirmed by the findings of the present study (Table 3). According to Table 3, the basic infiltration rate for the same inflow is greater in MF than SF irrigation due to a higher wetted perimeter and flow depth. The parameters of the Kostiakov-Lewis equation for each experiment are presented in Table 3. In MF irrigation, the value of k is higher and the value of a is lower than in SF irrigation.
The values of k in MF irrigation with inflow rates of 0.6 and 1.2 L∙s−1 are 18% and 67% higher than that for SF irrigation. By increasing the flow rate, the value of k is also increased in MF irrigation. The values of a decreased 18% and 46% for inflow rates of 0.6 and 1.2 L∙s−1, respectively, in MF compared to SF irrigation. The runoff percentage, deep percolation, and application efficiency for each irrigation event are given in Table 4.
For MF irrigation (irrigation events M1 and M2), the runoff losses are 11.55-21.86 times lower than they are in SF irrigation (irrigation events S1 and S2). When the inflow rate was increased, the runoff also increased in SF irrigation. The deep percolation losses are significantly greater in MF than SF irrigation. MF irrigation can be recommended for plants with a deep root zone, heavy textured soil, and sloping fields.
The water application efficiency ranged from 25.66% (irrigation event S3) to 82.15% (irrigation event M1). In both methods, the lowest application efficiency values occurred with high inflow rates (irrigation events S3 and M3). In contrast, the highest application efficiency values occurred with low inflow rates. The application efficiency of MF irrigation is slightly greater than that of SF irrigation. According to Table 4, the difference in advance time between the two methods is not significant at the 5% level in S3 and M3 irrigation events. Despite the inflow rate in the M3 irrigation event being higher than in S3, the advance times are 95% similar. The table also shows that there is no difference in outflow volume between S1 and M3 irrigation events. The inflow rate in the M3 irrigation event is 6 times higher than for the S1 irrigation event and the outflow volumes are the same due to the fact that meandering furrow irrigation reduces the velocity of flow throughout the furrow and increases infiltrated water volume.
Batista et al. (2012) and Roldán-Cañas et al. (2013) reported that lower runoff losses and high application efficiency could be achieved by using low inflow rates. The values of the exponents and coefficients of the advance equations are presented in Table 5. These parameters are varied for straight and meandering furrows since the hydraulic condition is different in these furrows. These results also indicate that the flow velocity is lower in MF than SF.
Irrigation events must be carefully implemented to achieve high efficiency. The MF system often requires a much greater labour input for construction and deep percolation in sandy soil is very high. Therefore, the type of soil and available labour are important factors in choosing the MF system. Harvesting requires a labour-intensive method in the MF system and harvest machines are not able to move easily in MF furrows. Therefore, further research is recommended into conducting, managing and harvesting with meandering furrow irrigation.
CONCLUSION
Field irrigation events were undertaken to evaluate the impact of MF and SF irrigation on performance and hydraulic and infiltration parameters. Advance and recession times were considerably greater in MF irrigation than SF irrigation. The average infiltrated water was lower in SF irrigation than MF irrigation. The recession times in MF irrigation were higher because of greater water storage in upstream stations. The parameters of the advance equation were estimated for MF and SF furrow irrigation and the results showed that the velocity of water advance was reduced in MF irrigation; therefore, runoff and erosion losses were also reduced. The disappearance of water in the recession phase would mostly be due to infiltration in MF irrigation and runoff in SF irrigation. The basic infiltration rate in the meandering furrow is higher than in the ordinary furrow. The coefficient of the infiltration equation, k, was higher and the exponent a was lower in the MF irrigation than in the SF irrigation. The application efficiency was better in the MF irrigation event with the inflow rate of 0.6 L∙s−1 compared with other irrigation events. Therefore, selecting MF irrigation, reducing the inflow rate, and choosing an appropriate cut-off time can lead to improved irrigation efficiency. MF irrigation can be a viable alternative to expensive irrigation systems such as sprinkler or trickle irrigation.
REFERENCES
ALAZBA AA (1999) Simulating furrow irrigation with different inflow patterns. J. Irrig. Drain. Eng. 125 (1) 12-18. http://dx.doi.org/10.1061/(ASCE)0733-9437(1999)125:1(12) [ Links ]
BARRIOS-MASIAS FH and JACKSON LE (2016) Increasing the effective use of water in processing tomatoes through alternate furrow irrigation without a yield decrease. Agric. Water Manage. 177 107-117. http://dx.doi.org/10.1016/j.agwat.2016.07.006 [ Links ]
BAUTISTA E, SCHLEGER JL and STRELKOFF TS (2012) WinSRFR 4.1, software and user manual. Arid Land Agricultural Research Center, Maricopa, AZ. [ Links ]
ELLIOTT RL, WALKER WR and SKOGERBOE GV (1983) Infiltration parameters from furrow irrigation advance data. Trans. ASAE 26 (6) 1726-1731. http://dx.doi.org/10.13031/2013.33833 [ Links ]
GHARBI A, DAGHARI H and CHERIF K (1993) Effect of flow fluctuations on free draining, sloping furrow and border irrigation systems. Agric. Water Manage. 24 (4) 299-319. http://dx.doi.org/10.1016/0378-3774(93)90009-Y [ Links ]
GILLIES MH, SMITH RJ and RAINE SR (2007) Accounting for temporal inflow variation in the inverse solution for infiltration in surface irrigation. Irrig. Sci. 25 (1) 87-97. http://dx.doi.org/10.1007/s00271-006-0037-9 [ Links ]
GILLIES MH and SMITH RJ (2005) Infiltration parameters from surface irrigation advance and run-off data. Irrig. Sci. 24 (1) 25-35. http://dx.doi.org/10.1007/s00271-005-0004-x [ Links ]
GUARDO M, OAD R and PODMORE TH (2000) Comparison of zero-inertia and volume balance advance-infiltration models. J. Hydraul. Eng. 126 (6) 457-465. http://dx.doi.org/10.1061/(ASCE)0733-9429(2000)126:6(457) [ Links ]
LEHRSCH GA, LENTZ RD, BJORNEBERG DL and SOJKA RE (2014) Erosion: Irrigation-induced. Reference module in Earth Systems and Environmental Sciences (Online database) 1-11. http://dx.doi.org/10.1016/B978-0-12-409548-9.09019-9 [ Links ]
LETEY J, HOFFMANB GJ, HOPMANSC JW, GRATTANC SR, SUAREZD D, CORWIND DL, OSTERA JD, WUA L and AMRHEINA C (2011) Evaluation of soil salinity leaching requirement guidelines. Agric. Water Manage. 98 502-506. http://dx.doi.org/10.1016/j.agwat.2010.08.009 [ Links ]
MCCLYMONT DJ and SMITH RJ (1996) Infiltration parameters from optimization on furrow irrigation advance data. Irrig. Sci. 17 (1) 15-22. http://dx.doi.org/10.1007/s002710050017 [ Links ]
MERGEN L (2014) The last station's water crisis. Energy New Comes Magazine 51 86-88 (in Persian). [ Links ]
MINTESINOT B, VERPLANCKE H, VAN RANST E and MITIKU H (2004) Examining traditional irrigation methods, irrigation scheduling and alternate furrows irrigation on vertisols in northern Ethiopia. Agric. Water Manage. 64 (1) 17-27. http://dx.doi.org/10.1016/S0378-3774(03)00194-X [ Links ]
MOSTAFAZADEH-FARD B, KAVEI-DEYLAMI R, SAGHAIAN-NEJAD SH and JALALIAN A (2010) The comparison of erosion of meandering and standard furrow irrigation under different field slopes. Aust. J. Agric. Eng. 1 (2) 29-37. http://dx.doi.org/10.1007/s10795-010-9093-7 [ Links ]
MOSTAFAZADEH-FARD B and MORAVEJALAHKAMI B (2006) The performance of Gholam-gardeshi furrow irrigation. Int. J. Agric. Biol. 8 (5) 698-702. [ Links ]
REDDY JM, JUMABOEV K, MATYAKUBOY B and ESHMURATOV D (2013) Evaluation of furrow irrigation practices in Fergana valley of Uzbekistan. Agric. Water Manage. 117 133-144. http://dx.doi.org/10.1016/j.agwat.2012.11.004 [ Links ]
ROLDÁN-CAÑAS J, CHIPANA R, MORENO-PÉREZ M F and CHIPANA G (2015). Description and evaluation of zigzag furrow irrigation in the Inter-Andean Valleys of Bolivia. J. Irrig. Drain. Eng. 141 (11) 04015019(10). http://dx.doi.org/10.1061/(ASCE)IR.1943-4774.0000902 [ Links ]
ROLDÁN-CAÑAS J, MORENO-PÉREZ MF, GARCÍA MORENO FJ and CHIPANA R (2013) Application of WinSRFR4 program to zigzag corrugated furrow irrigation in Bolivia. Proc. 2013 European Geosciences Union (EGU) General Assembly. European Geosciences Union (EGU), Munich, Germany. [ Links ]
SCALOPPI EJ, MERKLEY GP and WILLARDSON LS (1995). Intake parameters from advance and wetting phases of surface irrigation. J. Irrig Drain. Eng. 121 (1) 57-70. http://dx.doi.org/10.1061/(ASCE)0733-9437(1995)121:1(57) [ Links ]
SEPASKHAH AR and AFSHAR-CHAMANABAD H (2002) Determin-ation of infiltration rate for every other furrow irrigation. Biosyst. Eng. 82 (4) 479-484. http://dx.doi.org/10.1006/bioe.2002.0088 [ Links ]
SEPASKHAH AR and SHAABANI MK (2007) Infiltration and hydraulic behavior of an anguiform furrow in heavy texture soils of Iran. Biosyst. Eng. 98 (2) 248-256. http://dx.doi.org/10.1016/j.biosystemseng.2007.03.024 [ Links ]
SIYAL AA, MASHORI AS, BRISTOW KL and VAN GENUCHTEN MTh (2016) Alternate furrow irrigation can improve water productivity of okra. Agric. Water Manage. 173 55-60. http://dx.doi.org/10.1016/j.agwat.2016.04.026 [ Links ]
SOROUSH F, MOSTAFAZADEH-FARD B, MOUSAVI SF and ABBASI F (2012) Solute distribution uniformity and fertilizer losses under meandering and standard furrow irrigation methods. Aust. J. Agric. Eng. 6 (5) 884-890. [ Links ]
WALKER WR and SKOGERBOE GV (1987) Surface Irrigation: Theory and Practice. Prentice- Hall, Inc., Englewood Cliffs, New Jersey. 399 pp. [ Links ]
WALKER WR (1989) Guidelines for designing and evaluating surface irrigation systems. FAO Irrigation and Drainage Paper No. 45. FAO, Rome. [ Links ]
XIAO Y, ZHANG J, JIA TT, PANG XP and GUO ZHG (2015) Effects of alternate furrow irrigation on the biomass and quality of alfalfa. Agric. Water Manage. 161 147-154. http://dx.doi.org/10.1016/j.agwat.2015.07.018 [ Links ]
ZERHUN D, FEYEN J and REDDY JM (1996) Sensitivity analysis of furrow irrigation performance parameters. J. Irrig. Drain. Eng. 122 49-57. http://dx.doi.org/10.1061/(ASCE)0733-9437(1996)122:1(49) [ Links ]
Received 8 June 2018
Accepted in revised form 23 September 2019
* Corresponding author, email: Rahimpour@uk.ac.ir














