RESEARCH PAPERS

 

Developing a fuzzy logic model for predicting soil infiltration rate based on soil texture properties

 

 

Ahmed Z Dewidar^{I, *}; Hussein Al-Ghobari^I; Abed Alataway^II

^IAgricultural Engineering Department, King Saud University, Riyadh 11451, Kingdom of Saudi Arabia
^IIPSIPW Chair, Prince Sultan Institute for Environmental, Water and Desert Research, King Saud University, Kingdom of Saudi Arabia

 

 

---

ABSTRACT

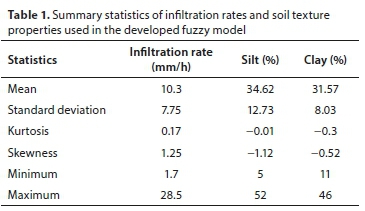
The prediction of the soil infiltration rate is advantageous in hydrological design, watershed management, irrigation, and other agricultural studies. Various techniques have been widely used for this with the aim of developing more accurate models; however, the improvement of the prediction accuracy is still an acute problem faced by decision makers in many areas. In this paper, an intelligent model based on a fuzzy logic system (FLS) was developed to obtain a more accurate predictive model for the soil infiltration rate than that generated by conventional methods. The input variables that were considered in the fuzzy model included the silt and clay contents. The developed fuzzy model was tested against both the observed data and multiple linear regression (MLR). The comparison of the developed fuzzy model and MLR model indicated that the fuzzy model can simulate the infiltration process quite well. The coefficient of determination, root mean square error, mean absolute error, model efficiency, and overall index of the fuzzy model were 0.953, 1.53, 1.28, 0.953, and 0.954, respectively. The corresponding MLR model values were 0.913, 2.37, 1.92, 0.913, and 0.914, respectively. The sensitivity results indicated that the clay content is the most influential factor when the FLS-based modelling approach is used for predicting the soil infiltration rate.

Keywords: FLS, infiltration rate, MLR, modelling, sensitivity analysis

---

 

 

INTRODUCTION

Soil and water are the main natural resources that can be used in a crop production system. The process of the percolation of rainwater or irrigation water into the soil is commonly known as infiltration. Increased infiltration control would aid in solving such wide-ranging problems as upland flooding, declining water tables, surface and groundwater pollution, inefficient irrigation of agricultural lands, and wastage of useful water (Hajiaghaei et al., 2014; Singh et al., 2018). Soil infiltration measurement is an important indicator of irrigation and drainage efficiency and is used for optimizing water availability for plant growth and metabolism, improving crop yield, and reducing erosion (Patle et al., 2018).

Infiltration rate (IR) is defined as the rate at which filtration occurs through the soil (Vand et al., 2018). Soil IR is the main factor that affects surface irrigation uniformity and efficiency owing to its mechanism of distributing water from the surface to the soil profile (Hajiaghaei et al., 2014). The IR is affected by a number of parameters, such as rainfall, vegetation cover, initial soil moisture, and fertilization and physical characteristics of the soil (Suryoputro et al., 2018). The physical characteristics of soil are influenced by the soil textures, which comprise mineral particles including sand, silt, and clay (Haghnazari et al., 2015). Clay particles are important because of their small size which allows them to fill the voids between the larger particles, and their charge orientation which makes them play a crucial role in binding the soil matrix into larger structures (Haghnazari et al., 2015). Several studies have focused on investigation of the physical characteristics of soil and their relationship with infiltration. Some of these have been focused on porosity (Bouma, 1982; Smettem, 1987), whereas others have concentrated on aggregation and structure (Helming et al., 1998), soil texture (Doerr et al., 2000; Ramos et al., 2003), and organic matter (Lado et al., 2004).

Field measurements of soil infiltration require considerable time and are costly. In contrast, infiltration models could significantly reduce the required time and cost (Mudiare and Adewumi, 2000). Many researchers have developed various conventional models to estimate the IR (Kostiakov, 1932; Philip, 1957; Sihag et al., 2017). Alternatively, the IR can be modelled using soft computing techniques such as the artificial neural network, adaptive neuro-fuzzy inference system, and fuzzy logic system (FLS) approaches (Singh et al., 2018; Singh et al., 2019). The conventional models are site specific and require model parameters, whereas the soft computing-based models are used generally for the study area. FLS is one of the methods that has been used as a dominant tool in solving and overcoming water resource problems (Azamathulla et al., 2016; Kisi et al., 2017; Kumar et al., 2018). The main advantage of fuzzy logic is its ability to deal with uncertain data in the form of reasonably continuous categories (Metternicht, 2001) and to accomplish more flexible knowledge-based modelling (Tran et al., 2002).

The fuzzy logic model (Zadeh, 1965) is a logical mathematical procedure based on the 'IF-THEN' rule system, which allows the human thought process to be reproduced in a mathematical form. According to Zadeh (1975), four basic units are required for the effective application of any fuzzy modelling strategy: the fuzzification unit (process that converts traditional inputs into fuzzy inputs), fuzzy rules unit (IF-THEN logical system that links the input to output variables), fuzzy inference unit (process that explains and combines rule outputs), and defuzzification unit (process that converts the fuzzy output to a traditional output). The methodologies proposed by Mamdani (1974) and Takagi and Sugeno (1985) are the most widespread in the development of fuzzy rule systems. The fuzzy model presented by Mamdani (1974) can represent a general class of systems that may include static or dynamic nonlinear systems.

Fuzzy logic applications have been used in estimating the daily reference evapotranspiration (Odhiambo et al., 2001), predicting multiple soil properties (Lee et al., 2003), assessing the water quality in rivers (Ocampo-Duque et al., 2006), determining irrigation efficiency (Kangrang and Chaleeraktrakoon, 2007), developing rainfall-runoff models to describe the nonlinear relationship between the rainfall and runoff in a real system (Jacquin and Shamseldin, 2006), and predicting the suspended sediment content of a river (Demirci and Baltaci, 2013). Abdel and Adeeb (2014) showed that the design, management, operation, and hydraulic evaluation associated with on-farm water applications depends heavily on the infiltration attributes of the soil. This is because the infiltration behaviour of the soil directly determines essential parameters such as inflow rate, run time, application time, and percolation depth in irrigation systems. Therefore, prediction of the soil IR is an important issue in agricultural engineering, water resource management, and soil desalination. The aims of this study were to: (i) develop a predictive model for soil IR using FLS, (ii) assess the performance of the developed fuzzy model using a statistical comparison between the results of the soil infiltration obtained from the developed fuzzy model and experimental findings, and (iii) compare the developed fuzzy model with the MLR in terms of their appropriateness for predicting the soil IR. Moreover, a sensitivity analysis (SA) was also performed and discussed to evaluate the effects of the input parameters on the infiltration modelling process.

 

MATERIALS AND METHODS

Data and site description

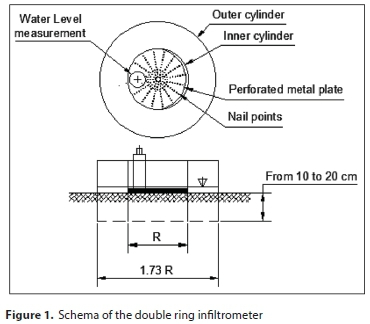
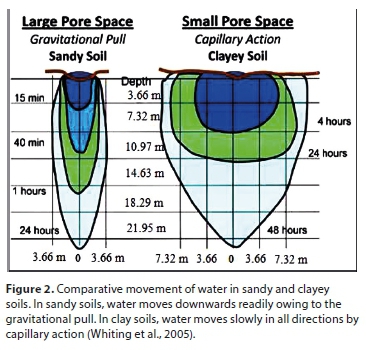
Data used in building the fuzzy model were obtained from an experiment published by Hajiaghaei et al. (2014). The published experiment was conducted at the agricultural fields of Karaj, Alborz Province, Iran (35° 59′ N, 51° 6′ E and altitude of 1 300 m amsl). The climate in the centre of Iran is classified as semi-arid (345 mm rainfall annually). The infiltration rates were estimated with the help of a cylindrical infiltrometer for all the selected treatments (Fig. 1). As shown in Fig. 1, the cylindrical infiltrometer has two concentric rings. The initial reading of the water level was taken once the two rings were filled with water. The level of water in the inner ring of the infiltrometer was recorded at a regular interval of 2.5, 5, 10, 15, 20, 25 and 30 munities until the rate of infiltration became constant. The IR was then calculated from the observed cumulative infiltration data. The summary statistics of infiltration rates and soil texture properties which greatly affect the infiltration process (Fig. 2) are listed in Table 1.

 

 

 

 

 

 

Fuzzy logic system

The FLS is a theory in formal mathematics that enables a definitive solution to be obtained for problems that are complex, uncertain, and unstructured (Bojórquez-Tapia et al., 2002). A general fuzzy system (Zadeh, 1975) is composed of four primary elements: fuzzification, fuzzy rules, a fuzzy inference engine, and defuzzification (Fig. 3).

Fuzzification

Fuzzification is a process that transforms a numerical value into a fuzzy value. Fuzzification is usually created with fuzzy sets that are defined by a membership function. Fuzzy sets commonly assign a domain of interest to the interval [0, 1]. The fuzzy set A X is given by:

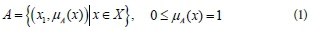
where x₁ are the elements of the universe of discourse (X), and μ_A (x) is the membership function of x in A.

Trapezoidal and triangular shapes are the most commonly used membership functions (Kosko and Toms, 1993).

Fuzzy rule base

The fuzzy rule base comprises fuzzy rules that represent all possible fuzzy relations between the input and output variables. These rules are expressed in IF-THEN statements (Eq. 2) (Ross, 2005). The number of rules is determined by the number of input parameters along with the membership functions.

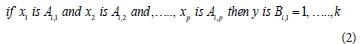
where y is the variable to be inferred, and x₁, x₂, …, x_p are the input variables. A_i,j are the terms that linguistic variables can assume (fuzzy sets), and i is the index of the rule k. B_i is the term assumed by the output linguistic variable.

Fuzzy inference engine

The fuzzy inference engine is the strategic unit that takes into consideration all the possible fuzzy rules in the fuzzy rule base and learns how to transform a set of inputs into corresponding outputs. The fuzzy inference engine uses IF-THEN rules along with the connectors 'OR' or 'AND' for drawing essential decision rules (Zadeh, 1975). The methodologies introduced by Mamdani (1974) and Takagi and Sugeno (1985) are the most commonly used for the fuzzy inference system. Figure 4 shows the Mamdani strategy represented in Eq. 2 for two simple rules.

Defuzzification

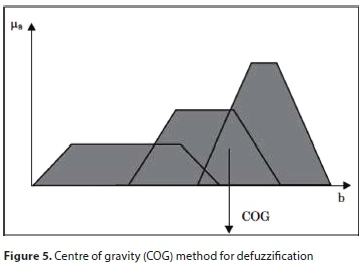
The defuzzification is the process by which the fuzzy results of the inference are transformed into a numerical output (Van-Leekwijck and Kerre, 1999). The methods frequently utilised in the defuzzification procedure are the mean of the maximums, smallest of the maximums, centre of gravity (COG) and the centroid of area. More detailed descriptions of fuzzy logic and fuzzy inference system models can be found in Ross (2005). An example of deffuzification using COG is presented in Fig. 5.

 

 

Building the fuzzy model

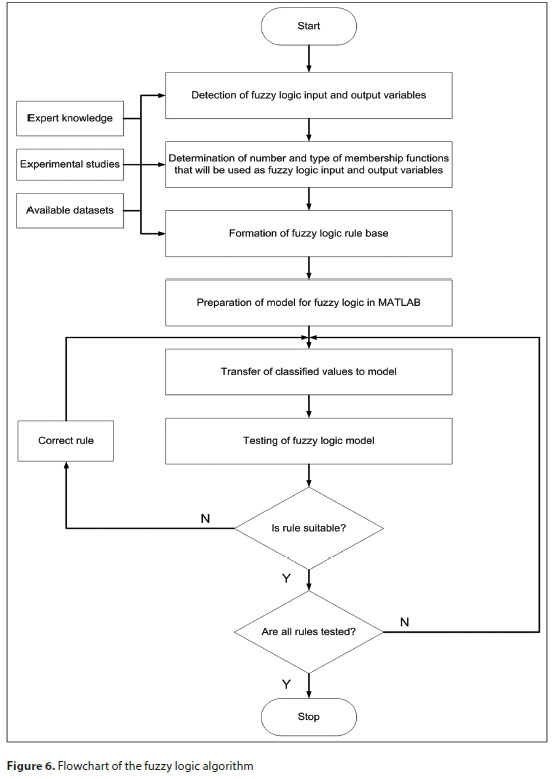
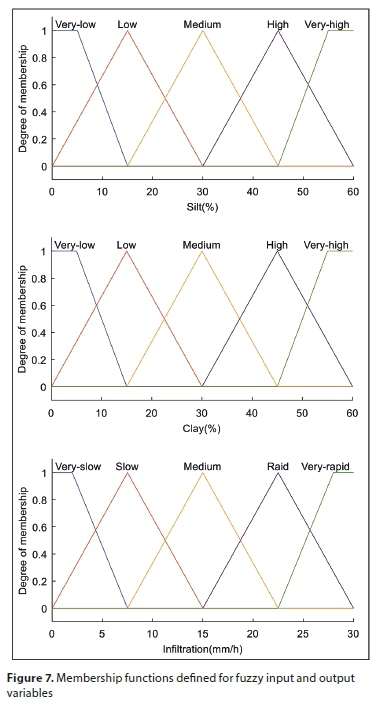
The fuzzy model was developed in the fuzzy logic toolbox of MATLAB software (Mathworks, 2016) using the Mamdani minimum-maximum inference engine. Flowchart of the FLS for modelling the soil IR is represented schematically in Fig. 6. The input and output variables that were considered in the fuzzy model were silt content (%), clay content (%), and IR (mm/h). The numerical inputs and output were transformed into fuzzy variables. The input variables were then described using 5 linguistic terms: 'very low' (VL), 'low' (L), 'medium' (M), 'high' (H), and 'very high' (VH) which are used to describe all the possible fuzzy inputs. The output variable was also categorised into 5 classes: 'very slow' (VS), 'slow' (S), 'medium' (M), 'rapid' (R), and 'very rapid' (VR) to characterise all the possible fuzzy outputs. The fuzzy model was trained using the triangular membership functions for both the input and output parameters (Fig. 7). The choice of the number of membership functions and their initial values was based on knowledge of the system and experimental conditions (Eqs 3-5). The developed fuzzy model relied on 25 rules generated by the rule editor to describe all relationships between the input and output variables (Table 2). Finally, COG was used, which is the most popular defuzzification method for obtaining a real-value (numerical) output.

 

 

 

 

 

 

 

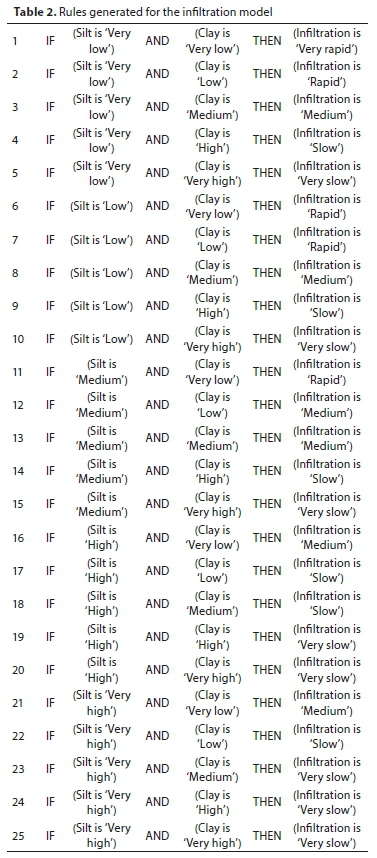
Multiple linear regression

MLR is a method that is used to model the linear relationship between a dependent variable (response) and one or more independent variables (predictors). The corresponding general equation is as follows:

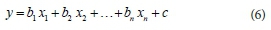
where y is the dependent variable; b₁, b₂, …, b_n are the coefficients of regression; and x₁, x₂,…,x_n are the explanatory variables (predictors).

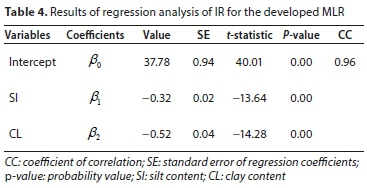
In this study, the MLR was built using the data used in the fuzzy model to create a mathematical relationship for predicting the IR as a function of the silt and clay contents (Eq. 7). The standard error (SE), coefficient of correlation (CC), t statistic and probability value (p-value) of independent parameters were employed to evaluate the accuracy of the predictive MLR:

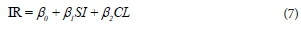
where IR is infiltration rate (mm/h); SI is silt content (%); and CL is clay content (%).

Criteria for evaluation

The performance of both the fuzzy and MLR models was evaluated by the coefficient of determination (R²), mean absolute error (MAE), root mean square error (RMSE), overall index (OI), and model efficiency (ME). The R², MAE, RMSE, OI, and ME were calculated using Eqs 8-12, as presented in Table 3 (Rahman and Bala, 2010; Alazba et al., 2011; Zangeneh et al., 2012). The higher values of R² represent a greater similarity between the observed and predicted values. On the other hand, the lower values of MAE and RMSE show a high accuracy between the observed and predicted values. An ME and OI value of 1 implies that the observed and predicted results agree well (Alazba et al., 2011). In other words, the MAE and RMSE values have to be closer to zero, whereas the values of R², OI, and ME should approach 1 as much as possible.

 

 

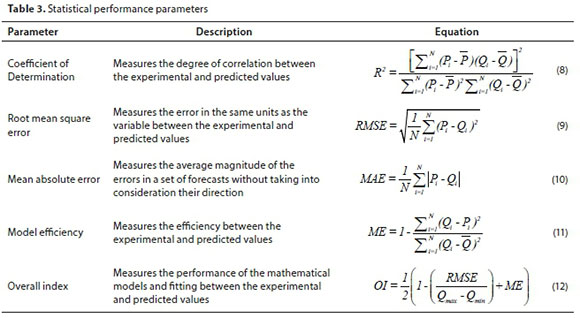
P_i and P- represent the predicted and average predicted values, respectively; Q_i and Q- represent the observed and average of the observed values, respectively; Q_max is the maximum observed value; Q_min is the minimum observed value; and N is the number of data points.

Sensitivity analysis

A sensitivity analysis (SA) is a useful tool for determining the contribution and relative importance of parameters in the modelling process. The SA assesses and describes how the model output values are affected by changes in the input values. The cosine amplitude method (CAM) was used in this study to distinguish the most sensitive factors affecting the soil IR. This is an effective method of performing an SA (Ross, 2005). The degree of sensitivity of each input factor (silt and clay contents) was assigned by establishing the strength of the relationship (R_ij) between the IR and the input factors under consideration. A higher CAM value indicates a greater impact on the IR.

Let us assume that n data samples are gathered from a common data array X; then the datasets employed to construct a data array X are defined as follows:

Each of the elements x_i in the data array X is a vector of length m, that is

Thus, each of the data pairs can be thought of as a point in an m-dimensional space, wherein each point requires m coordinates for a complete description. The strength of the relationship between the data pairs x_i and x_j is estimated and demonstrated using the following equation:

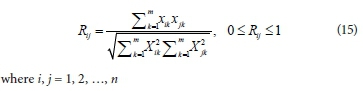
RESULTS AND DISCUSSION

Fuzzy logic model

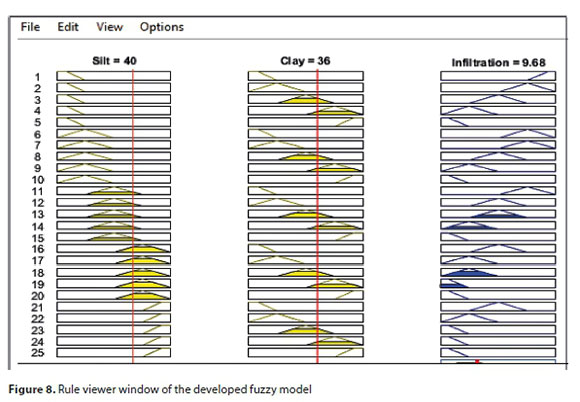
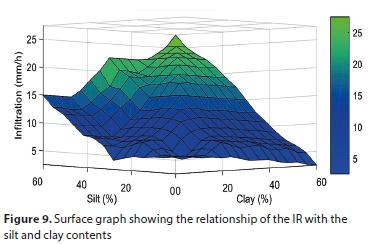
Figure 8 shows the graphical depiction of the 25 rules produced to map the inputs (silt and clay contents) into the output (IR). In this figure, we observe that each rule is represented in a row individually, whereas the variables are represented in individual columns. The first two columns of the plot describe the membership functions for the input factors, which is indicated through the antecedent (IF-part) of each rule. The third column shows the membership functions represented via the consequent (THEN-part) of each rule. The vertical red lines inside the first and second columns show the current data of the inputs. A yellow patch under the actual curve of the membership function is used to represent the value of the fuzzy membership. Thus, the properties of each variable in relation to the input index line are presented. The lowest plot inside the right column is the combination of each consequent. The value of the defuzzified output is indicated by a bold vertical line crossing the aggregate fuzzy set. For example, for the system inputs of 40% silt and 36% clay, the defuzzified IR is found to be 9.68 mm/h. Furthermore, the surface viewer model provides a three-dimensional curve that maps the silt and clay contents to the IR (Fig. 9). In Fig. 9, the IR values decrease with the increasing clay content of the soil. Similarly, the same trend was observed in the case of the silt content. However, the relative change was smaller.

 

 

 

 

Simulating the fuzzy model

The fuzzy model was simulated in the Simulink environment of the MATLAB software which is a graphical programming environment for modelling, simulating, and analysing multi-domain dynamic systems (Fig. 10). As shown in Fig. 10, two inputs of silt content (40%) and clay content (36%) are multiplexed and sent into the fuzzy logic controller, while the output of the IR (9.60 mm/h) is captured on a display box. It is apparent that there is a close agreement between the observed (9.60 mm/h) and predicted (9.68 mm/h) values of the IR. This high level of agreement between the observed and predicted values demonstrates the effectiveness of the developed fuzzy model for predicting the soil IR.

MLR model

The effect of the independent variables (SI and CL) and their interactions on the dependent variable (IR) were statistically analysed. The SE, t-statistic and p-value are presented in Table 4. On examining the p-value, a significant effect was observed between the independent variables and the IR at an alpha level of 0.05. Both the SI and CL were found to be influential variables within the calculation of the IR, wherein the SE of those variables were ±0.02 and ±0.04, respectively. Moreover, Fig. 11 shows the observed and predicted values of the IR using the MLR. From this figure, it can be observed that the values predicted by the MLR are in conformity with those obtained from the field. Also the SI and CL variables are inversely proportional to the IR. These results agree with the results of Hajiaghaei et al. (2014).

 

 

Comparing the fuzzy model with MLR

Figure 12 compares the experimental and predicted values of the soil IR using the fuzzy and MLR models. The dotted line represents the condition in which the outputs and targets are equal, whereas the circles represent data points. The solid line represents the best fit between the outputs and targets. It is apparent that the data points (circles) are clustered along the dotted line, which emphasizes that the IR values correlated by the developed fuzzy model and MLR provide a good match between the experimental and predicted results. However, results generated by the fuzzy model are more accurate than those calculated using the MLR. The higher level of agreement is also reflected in the values of the statistical parameters, such as correlation coefficient (R), which was 0.97654 and 0.95554 for the fuzzy model and MLR, respectively. Generally, a close agreement between the observed and predicted results demonstrates the consistency of the developed fuzzy model for predicting the soil IR.

Validating the developed fuzzy model

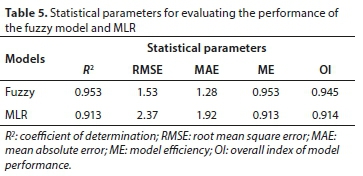
Table 5 shows the results of R², MAE, RMSE, OI, and ME, which are used to evaluate the agreement between the measured and predicted results. The developed fuzzy model had R², OI, and ME values that were approximately 4.3%, 94.5%, and 95.3%, respectively, more accurate than those from MLR, which demonstrates a close agreement between the observed and predicted results by the FLS. Also, it should be noted (Table 5) the MLR had RMSE and MAE values that were approximately 1.5 times as high as those obtained using the developed fuzzy model. Furthermore, a graph of the relative errors for the fuzzy model and MLR using the soil IR dataset is shown in Fig. 13. The fuzzy model was found to have the ability to predict the soil IR with errors (93% of the values) fluctuating mostly from −0.5 to +0.5. In contrast, the values of relative error obtained from the MLR which fall within ±0.5% were less than 85% of the entire error values. In conclusion, the comparison between the developed fuzzy model and MLR demonstrated that the fuzzy model can predict the soil IR more effectively than MLR.

 

 

Sensitivity analysis

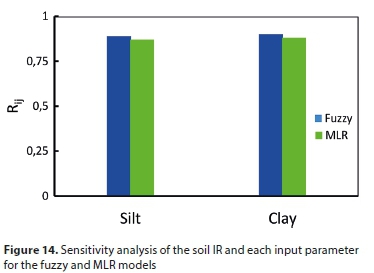
Using Eq. 14, a series of SAs was conducted on the input and output parameters. The values of R_ij between the IR values predicted by the fuzzy and MLR models and related input factors using the CAM method are shown in Fig. 14. As shown, the obtained R_ij values for all the inputs were not significantly different but close to 1, which indicates that all inputs strongly contributed to the developed fuzzy and MLR models. Furthermore, this indicates that all the inputs were important in predicting the soil IR and none should be neglected. The obtained results agree with the findings of Hajiaghaei et al. (2014).

 

 

CONCLUSIONS

Knowledge of infiltration processes is imperative in irrigation management and other agricultural studies. In this study, an intelligent model based on the fuzzy logic system was developed as an alternative algorithm to estimate the infiltration rate of the soil. For this study, a dataset containing 100 observations in the field, obtained by double ring infiltrometer, was analysed. Based on the obtained results, the fuzzy model has a suitable capability to predict the infiltration rate of the soil. The fuzzy model also provides better performance than the MLR model that was used for evaluation purposes. Sensitivity analysis suggests that the clay content is the most effective parameter for the estimation of soil infiltration rate.

 

ACKNOWLEDGEMENTS

This project was supported by the Vice Deanship of Research Chairs at King Saud University.

 

REFERENCES

ABDEL DAM and ADEEB WAM (2014) Comparison between hydro-flume and open field head ditch irrigation systems at Kenana Sugar Scheme, Sudan. Agric. Sci. 5 (07) 588-603. https://dx.doi.org/10.4236/as.2014.57062        [ Links ]

ALAZBA AA, MATTAR MA, ELNESR MN and AMIN MT (2011) Field assessment of friction head loss and friction correction factor equations. J. Irrig. Drain. Eng. 138 (2) 166-176. https://doi.org/10.1061/(ASCE)IR.1943-4774.0000387        [ Links ]

AZAMATHULLA HM, HAGHIABI AH and PARSAIE A (2016) Prediction of side weir discharge coefficient by support vector machine technique. Water Sci. Technol. Water Suppl. 16 (4) 1002-1016. https://doi.org/10.2166/ws.2016.014        [ Links ]

BOJÓRQUEZ-TAPIA LA, JUÁREZ L and CRUZ-BELLO G (2002) Integrating fuzzy logic, optimization, and GIS for ecological impact assessments. Environ. Manage. 30 (3) 418-433. https://doi.org/10.1007/s00267-002-2655-1        [ Links ]

BOUMA J (1982) Measuring the hydraulic conductivity of soil horizons with continuous macropores 1. Soil Sci. Soc. Am. J. 46 (2) 438-441. https://doi.org/10.2136/sssaj1982.03615995004600020047x        [ Links ]

DEMIRCI M and BALTACI A (2013) Prediction of suspended sediment in river using fuzzy logic and multilinear regression approaches. Neural Comput. Appl. 23 (1) 145-151. https://doi.org/10.1007/s00521-012-1280-z        [ Links ]

DOERR SH, SHAKESBY RA and WALSH R (2000) Soil water repellency: Its causes, characteristics and hydro-geomorphological significance. Earth-Sci. Rev. 51 (1-4) 33-65. https://doi.org/10.1016/S0012-8252(00)00011-8        [ Links ]

HAGHNAZARI F, SHAHGHOLI H and FEIZI M (2015) Factors affecting the infiltration of agricultural soils. Int. J. Agron. Agric. Res. 6 (5) 21-35.         [ Links ]

HAJIAGHAEI A, RASHIDI M, SADEGHI MA, GHOLAMI M and JABERINASA B (2014) Prediction of soil infiltration rate based on silt and clay content of soil. Am.-Euras. J. Agric. Environ. Sci. 14 (8) 702-706.         [ Links ]

HELMING K, RÖMKENS MJM and PRASAD S (1998) Surface roughness related processes of runoff and soil loss: A flume study. Soil Sci. Soc. Am. J. 62 (1) 243-250. https://doi.org/10.2136/sssaj1998.03615995006200010031x        [ Links ]

JACQUIN AP and SHAMSELDIN AY (2006) Development of rainfall-runoff models using Takagi-Sugeno fuzzy inference systems. J. Hydrol. 329 (1-2) 154-173. https://doi.org/10.1016/j.jhydrol.2006.02.009        [ Links ]

KANGRANG A and CHALEERAKTRAKOON C (2007) A fuzzy-GAs model for determining varied irrigation efficiency. Am. J. Appl. Sci. 4 (6) 339-345. https://doi.org/10.3844/ajassp.2007.339.345        [ Links ]

KISI O, KESHAVARZI A, SHIRI J, ZOUNEMAT-KERMANI M and OMRAN ESE (2017) Groundwater quality modeling using neuro-particle swarm optimization and neuro-differential evolution techniques. Hydrol. Res. 48 (6) 1508-1519. https://doi.org/10.2166/nh.2017.206        [ Links ]

KOSKO B and TOMS M (1993) Fuzzy Thinking: The New Science of Fuzzy Logic. Hyperion, New York. 350 pp.         [ Links ]

KOSTIAKOV AN (1932) On the dynamics of the coefficient of water percolation in soils and the necessity of studying it from the dynamic point of view for the purposes of amelioration. Trans. Sixth Commission of the International Society of Soil Science 1 7-21.         [ Links ]

KUMAR M, RANJAN S, TIWARI NK and GUPTA R (2018) Plunging hollow jet aerators-oxygen transfer and modelling. ISH J. Hydraul. Eng. 24 (1) 61-67. https://doi.org/10.1080/09715010.2017.1348264        [ Links ]

LADO M, PAZ A and BEN-HUR M (2004) Organic matter and aggregate size interactions in infiltration, seal formation, and soil loss. Soil Sci. Soc. Am. J. 68 (3) 935-942. https://doi.org/10.2136/sssaj2004.9350        [ Links ]

LEE K, ZHANG N and DAS S (2003) Comparing adaptive neuro-fuzzy inference system (ANFIS) to partial least-squares (PLS) method for simultaneous prediction of multiple soil properties. Paper number 033144, 2003 ASAE Annual Meeting American Society of Agricultural and Biological Engineers. https://doi.org/10.13031/2013.15017        [ Links ]

MAMDANI EH (1974) Application of fuzzy algorithms for control of simple dynamic plant. In: Proc. Inst. Elec. Eng. 121 (12) 1585-1588. http://dx.doi.org/10.1049/piee.1974.0328        [ Links ]

MATHWORKS (2016) MATLAB and Fuzzy Logic Toolbox. MathWorks, Inc., Natick, Massachusetts, United States.         [ Links ]

METTERNICHT G (2001) Assessing temporal and spatial changes of salinity using fuzzy logic, remote sensing and GIS. Foundations of an expert system. Ecol. Model. 144 (2) 163-179. https://doi.org/10.1016/S0304-3800(01)00371-4        [ Links ]

MUDIARE OJ and ADEWUMI JK (2000) Estimation of infiltration from field-measured sorptivity values. Nigerian J. Soil Res. 1 1-3.         [ Links ]

OCAMPO-DUQUE W, FERRE-HUGUET N, DOMINGO JL and SCHUHMACHER M (2006) Assessing water quality in rivers with fuzzy inference systems: A case study. Environ. Int. 32 (6) 733-742. https://doi.org/10.1016/j.envint.2006.03.009        [ Links ]

ODHIAMBO LO, YODER RE and YODER DC (2001) Estimation of reference crop evapotranspiration using fuzzy state models. Trans. ASAE 44 (3) 543-550.         [ Links ]

PATLE GT, SIKAR TT, RAWAT KS and SINGH SK (2018) Estimation of infiltration rate from soil properties using regression model for cultivated land. Geol. Ecol. Landscapes 3 (1) 1-13. https://doi.org/10.1080/24749508.2018.1481633        [ Links ]

PHILIP JR (1957) The theory of infiltration: 1. The infiltration equation and its solution. Soil Sci. 83 (5) 345-358.         [ Links ]

RAHMAN MM and BALA BK (2010) Modelling of jute production using artificial neural networks. Biosyst. Eng. 105 (3) 350-356. https://doi.org/10.1016/j.biosystemseng.2009.12.005        [ Links ]

RAMOS MC, NACCI S and PLA I (2003) Effect of raindrop impact and its relationship with aggregate stability to different disaggregation forces. Catena 53 (4) 365-376. https://doi.org/10.1016/S0341-8162(03)00086-9        [ Links ]

ROSS TJ (2005) Fuzzy Logic with Engineering Applications (2^nd edn). Wiley, Hoboken.         [ Links ]

SIHAG P, TIWARI NK and RANJAN S (2017) Estimation and inter-comparison of infiltration models. Water Sci. 31 (1) 34-43. https://doi.org/10.1016/j.wsj.2017.03.001        [ Links ]

SINGH B, SIHAG P and DESWAL S (2019) Modelling of the impact of water quality on the infiltration rate of the soil. Appl. Water Sci. 9 (1) 15-23. https://doi.org/10.1007/s13201-019-0892-1        [ Links ]

SINGH B, SIHAG P and SINGH K (2018) Comparison of infiltration models in NIT Kurukshetra campus. Appl. Water Sci. 8 (2) 63-70. https://doi.org/10.1007/s13201-018-0708-8        [ Links ]

SMETTEM KRJ (1987) Characterization of water entry into a soil with a contrasting textural class: spatial variability of infiltration parameters and influence of macroporosity. Soil Sci. 144 (3) 167-174.         [ Links ]

SURYOPUTRO N, SOETOPO W, SUHARTANTO ES and LIMANTARA LM (2018) Evaluation of infiltration models for mineral soils with different land uses in the tropics. J. Water Land Dev. 37 (1) 153-160. https://doi.org/10.2478/jwld-2018-0034        [ Links ]

TAKAGI T and SUGENO M (1985) Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst. Man Cybernetics SMC-15 (1) 116-132. http://dx.doi.org/10.1109/TSMC.1985.6313399        [ Links ]

TRAN LT, RIDGLEY MA, DUCKSTEIN L and SUTHERLAND R (2002) Application of fuzzy logic-based modeling to improve the performance of the revised universal soil loss equation. Catena 47 (3) 203-226. https://doi.org/10.1016/S0341-8162(01)00183-7        [ Links ]

VAND AS, SIHAG P, SINGH B and ZAND M (2018) Comparative evaluation of infiltration models. KSCE J. Civ. Eng. 22 (10) 4173-4184. https://doi.org/10.1007/s12205-018-1347-1        [ Links ]

VAN-LEEKWIJCK W and KERRE EE (1999) Defuzzification: criteria and classification. Fuzzy Sets Syst. 108 (2) 159-178. https://doi.org/10.1016/S0165-0114(97)00337-0        [ Links ]

WHITING D, WILSON C and CARD A (2005) Managing soil tilth: Texture, structure and pore space. Gardening Series. Colorado Master Gardener; no. 7.723. https://hdl.handle.net/10217/183047        [ Links ]

ZADEH LA (1965) Fuzzy sets. Inf. Control 8 (3) 338-353. https://doi.org/10.1016/S0019-9958(65)90241-X        [ Links ]

ZADEH LA (1975) The concept of a linguistic variable and its application to approximate reasoning-I. Inf. Sci. 8 (3) 199-249. https://doi.org/10.1016/0020-0255(75)90036-5        [ Links ]

ZANGENEH M, OMID M and AKRAM A (2012) A comparative study between parametric and artificial neural networks approaches for economical assessment of potato production in Iran. Span. J. Agric. Res. 9 (3) 661-671. https://doi.org/10.5424/sjar/20110903-371-10        [ Links ]

 

 

Received 25 August 2017
Accepted in revised form 7 June 2019

 

 

* Corresponding author, email: dewidar@ksu.edu.sa