Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Water SA
On-line version ISSN 1816-7950
Print version ISSN 0378-4738
Water SA vol.45 n.2 Pretoria Apr. 2019
http://dx.doi.org/10.4314/wsa.v45i2.10
Neuro-fuzzy systems to estimate reference evapotranspiration
Mousaab ZakhroufI; Hamid BouchelkiaI; Madani StamboulII
IURMER Laboratory, Faculty of Technology, Department of Hydraulic, University of Tlemcen, Tlemcen, Algeria
IIFaculty of Engineering Science, Department of Civil Engineering, Laghouat University, Laghouat, Algeria
ABSTRACT
Routine and rapid estimation of evapotranspiration (ET) at regional scale is of great significance for agricultural, hydrological and climatic studies. A large number of empirical or semi-empirical equations have been developed for assessing ET from meteorological data. The FAO-56 PM is one of the most important methods used to estimate evapotranspiration. The advantage of FAO-56 PM is a physically based method that requires a large number of climatic parameter data. In this paper, the potential of two types of neuro-fuzzy system, including ANFIS based on subtractive clustering (S_ANFIS), ANFIS based on the fuzzy C-means clustering method (F_ANFIS), and multiple linear regression (MLR), were used in modelling daily evapotranspiration (ET0). For this purpose various daily climate data - air temperature (T), relative humidity (RH), wind speed (U) and insolation duration (ID) - from Dar El Beidain Algiers, Algeria, were used as inputs for the ANFIS and MLR models to estimate the ET0 obtained by FAO-56 based on the Penman-Monteith equation. The obtained results show that the performances of S_ANFIS model yield superior to those of F_ANFIS and MLR models. It can be judged from results of the Nash-Sutcliffe efficiency coefficient (EC) where S_ANFIS (EC = 94.01%) model can improve the performances of F_ANFIS (EC = 93.00%) and MLR (EC = 92.12%) during the test period, respectively.
Keywords: modelling, FAO-56 PM evapotranspiration, S-ANFIS, F-ANFIS, MLR, semi-arid regions, Algeria
INTRODUCTION
Evapotranspiration is an important component of the hydrological cycle and influenced by many meteorological parameters. It is a combination of water loss from the soil surface by evaporation and from crops by transpiration (ET0) (Aytek, 2008). Models for predicting ET0 range from deterministically based combined energy balance-vapour transfer approach to empirical relationships based on climatological variables, or to evaporation from a standard evaporation pan. A large number of empirical or semi-empirical equations have been developed for assessing ET0 from meteorological data. The Penman-Monteith (PM) equation for estimating reference evaporation was used in this study. The PM is a physically based method; comparatives studies strongly suggest that the PM formula is preferred to other empirical models (Jensen et al., 1990). But the use of PM requires a large number of climatic parameters, such as daily maximum temperature and minimum temperature, solar radiation, relative humidity and wind speed. However, records for such weather variables are often incomplete or not always available for many locations, which is a weakness of the PM model (Allen et al., 1998). Neuro-fuzzy provides an efficient way of handling the uncertainty for complex systems without sufficient data or with only vague information (Ross, 1995; Cox, 1999), and clustering processes can be a very effective technique to identify natural groupings in data from a large dataset, thereby allowing concise representation of relationships embedded in the data. Therefore, two neuro-fuzzy systems, (i) fuzzy c-means clustering (FCM) based fuzzy inference system, named F-ANFIS, and (ii) subtractive clustering based fuzzy inference system, named S-ANFIS, are used in mapping the nonlinear relationship between the daily reference evapotranspiration and meteorological data and also for investigating the effectiveness of the parameters. These NF use daily climatic data (air temperature, relative humidity, wind speed and the insolation duration) as inputs, and ET0 values estimated by the Penman-Monteith formula as outputs.
FAO-56: Penman Monteith method
The Penman-Monteith (PM) model was recommended as the sole standard method of calculating ET0 by the United Nations Food and Agriculture Organization (FAO) and the World Meteorological Organization (WMO), whenever the sufficient necessary data are available. The PM equation for estimating reference evaporation used in this study is based on most recent FAO-56 PM model described in the FAO's Irrigation and Drainage Paper No. 56 (Allen et al., 1998).

where ET0 = reference evapotranspiration (mm∙day−1); Δ = slope of the saturation vapour pressure function (kPa∙°C−1); Rn = net radiation (MJ∙m−2∙day−1); G = soil heat flux density (MJ m−2∙day−1); γ = psychometric constant (kPa∙°C−1); T = mean air temperature (°C); U2 = average 24 h wind speed at 2 m height (m∙s−1), ea is the saturation vapour pressure (kPa), ed is the actual vapour pressure (kPa). Trajkovic and Kolakovic (2009) examined the potential of the FAO-56 PM equation in estimating the ET0 under humid conditions from limited weather data. They concluded that the minimum and maximum of air temperature and local default wind speed value were the minimum data requirements in order to use the FAO-56 PM equation successfully under humid conditions.
Adaptive network-based fuzzy inference system (ANFIS)
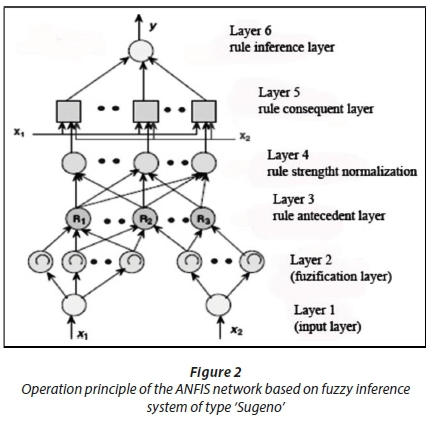
Neuro-fuzzy systems are fuzzy systems formed by a learning algorithm inspired by the theory of neural networks. The learning technique operates according to local information and a unique production of local changes in the original fuzzy system. So the interest is to establish a predictive system based on the integration of neural networks and fuzzy inference systems (FIS). Fuzzy inference systems is based on the linguistic rules of the type (IF-THEN) to translate knowledge on the dynamic system (Dastorani et al., 2010) (Fig. 1). ANFIS is a fuzzy inference (FIS) 'Sugeno' type supervised learning 'Takagi', implemented in the framework of adaptive neural networks; the first introduction of this system was by Jang (Jang, 1993; Takagi and Sugeno, 1985).
In the literature a wide variety of rule generation techniques can be found. Clustering is one of the most important methods used to generate fuzzy rules. The purpose of these algorithms is to organize data in homogeneous groups, to account for the membership of an element in several classes.
A wide variety of rule generation techniques are found in the literature by the fuzzy clustering method, and among the most used are subtractive clustering, and fuzzy C-means clustering.
Subtractive clustering
The idea is to find regions in the feature space with high densities of data points. The point with the highest number of neighbours is selected as centre of the cluster. The data points within a prespecified fuzzy radius are then removed, and the algorithm looks for a new point with the highest number of neighbours (Cobaner, 2011). Consider a collection of n data points in an m-dimensional space. Without loss of generality, the data points are assumed to have been normalized within a hypercube. Since each data point is a candidate for cluster centres, a density measure at data point xi is defined as:

where cluster radius ra is a positive constant. Thus, a data point that has many neighbouring data points will have a high potential of being a cluster centre. The radius ra defines a neighbourhood. Data points outside this radius have little effect on the density measure.
After the density measure of each data point has been calculated, the first cluster centre is chosen to be the data point with the highest density measure. Suppose xc1 is the point selected and Dc1 is its density measure. Then, the density measure for each data point xi is revised by the formula:
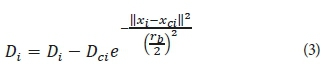
where rb is a positive constant. Note that the data points near the first cluster centre xc1 will have significantly reduced density measures, so that they are unlikely to be selected as the next cluster centre.
The constant rb defines a neighbourhood to be reduced in density measure. It is normally larger than ra to prevent closely spaced cluster centres; typically, rb= 1.5·ra. After the density measure for each point is revised, the next cluster centre xc2 is selected and all the density measures are revised again. The process is repeated until a sufficient number of cluster centres are generated.
Fuzzy C-means clustering
Bezdek (1981) introduced the fuzzy C-means clustering method in 1981, with the development of the fuzzy theory. This algorithm is used for analysis based on distance between various input data points. The clusters are formed according to the distance between data points and the cluster centres are formed for each cluster. In fact, FCM is a data-clustering technique (Chen and Zhang, 1998; Hui, 2008) in which a dataset is grouped into n clusters with every data point in the dataset related to every cluster; it will have a high degree of belonging (connection) to that cluster and another data point that lies far away from the centre of a cluster will have a low degree of belonging to that cluster. It is based on minimization of the following objective function:

where m is any real number greater than 1; it was set to 2 by Bezdek (Bezdek, 1981), uij is the degree of membership of xi,in the cluster j; xi is the ith of d-dimensional measured data; cj is the d dimension centre of the cluster and ||*|| is any norm expressing the similarity between any measured data and the centre. Fuzzy partitioning is carried out through an iterative optimization of the objective function shown above, with the update of membership uij and the cj cluster centres by:
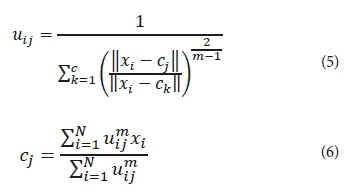
The operation principle of adaptive neuro-fuzzy inference system (ANFIS) is presented in (Fig. 2). It has 6 functional blocks (input layer, based on rules database, a unit of decision-interface fuzzification and defuzzification interface) which are generated using 6 layers of neurons:
•Layer 1: input layer.
•Layer 2: consists of a number of nodes whose activation functions are membership functions (MFs)
•Layer 3: the output layer provides the minimal value of its inputs
•Layer 4: Layer 4, normalized with respect to the other input, where the output node i is equal to the input i divided by the sum of the inputs
•Layer 5: the output of the node i, is a linear function of the output and the signal input of the controller
•Layer 6: is the summation of the signal input
Performance criteria
The statistical parameters used in this work are: mean absolute relative error (MARE), mean square error (MSE), mean error (ME) and the Nash-Sutcliffe efficiency coefficient (EC) (Abrahart, 2004). These parameters are given by the following relationships:

where Et0i is the measured evapotranspiration rate value,  0i is the evapotranspiration rate calculated by the model,
0i is the evapotranspiration rate calculated by the model,  0 is the average evapotranspiration measured, 0 is the average evapotranspiration simulated, and N is the number of data.
0 is the average evapotranspiration measured, 0 is the average evapotranspiration simulated, and N is the number of data.
CASE STUDY
In the present study, the aforementioned fuzzy inference systems are applied to the daily climatic data of Dar El Beida automated weather station (36°43′ N; 03°15′ E) in the north-centre of (Algiers) Algerian County (Fig. 3). Dar El Beida weather station is located 24 m amsl. The climate in Algiers is classified as a Mediterranean Sea climate.
In this part of the study, different input combinations, including various daily climatic data, that is, (air temperature, relative humidity, wind speed and the insolation duration) were used in NF models to estimate reference evapotranspiration. The available dataset consisting of 1 673 days was separated into 3 parts, the training set containing 1 095 days, validation set containing the third set of 365 days of the dataset and the testing set containing 213 days of the dataset. The daily statistical parameters of climatic data and FAO-56 PM ET0 values are shown in (Table 1).
Reference evapotranspiration estimation using adaptive NF techniques
To realize the approximation of evapotranspiration using a neuro-fuzzy network, two types of neuro-fuzzy system including ANFIS based on subtractive clustering (S_ANFIS) and ANFIS based on the duzzy C-means clustering method (F_ANFIS) were used.
In order to investigate the effect of daily climatic data on ET0, the final architecture of the ANFIS models was determined via an extensive trial-and-error process. The number of clusters of the F-ANFIS model was found based on this approach. In order to generate fuzzy rules using S-ANFIS, it is critical to determine the proper cluster radius (radii).
The cluster radius indicates the range of influence of a cluster when you assume the data space to be a unit hypercube (range [0, 1]). Generally, specifying a small cluster radius will result in many small clusters in the data (with many rules), and specifying a large cluster radius will result in a few large clusters in the data, (with fewer rules). Good values for radii are usually between 0.2 and 0.5 (Samhouri, 2009). In this paper, the optimum number of cluster and radii values were determined according to the MARE criterion in the testing phase.
RESULTS AND DISCUSSION
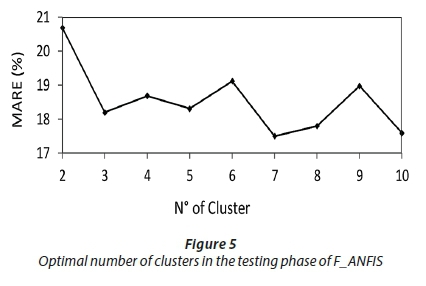
The effect of the value of radii changing on the quality of results of S_ANFIS is shown in Fig. 4. From Fig. 4 it can be deduced that the optimal radius value of 0.45 gives us the best results. The effect of number of cluster changes on the quality of the results from F_ANFIS is shown in Fig. 5; from Fig. 5 it was observed that the F_ANFIS model having 7 clusters estimated the minimum value of MARE.

Results obtained for the S_ANFIS, F_ANFIS and MLR approaches proposed in this paper are presented in Table 2.
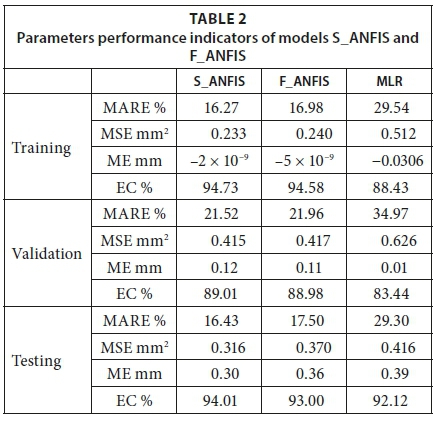
The three models are evaluated based on the indices described. The NASH criterion (EC) provides an overall assessment of the quality of estimation. Models with NASH values close to 0.9 are generally of good quality, while models with NASH values close to 1 are deemed to produce near-perfect estimation. The NASH values for the S_ANFIS and F_ANFIS models are all over 90%, which indicates that both types of models achieved a good quality result. The overall quality of estimation of the S_ANFIS model is better than the F_ANFIS and multiple linear regression (MLR) models, which indicates that the NASH values of the S-ANFIS model are higher than those of the F_ANFIS and MLR models.
The magnitude of systematic overestimation or underestimation of a model is evaluated using the ME and MARE indices. The results indicate that the three models generally underestimate evapotranspiration quantiles. Based on the MSE index, the S_ANFIS and F_ANFIS models are the least biased models, while the MLR is the most biased model. The MARE index provides the measure of bias in the absolute relative scale. Based on the MARE index, the S_ ANFIS model has slightly higher biases than the F_ANFIS and MLR models.
Figure 6 shows the scatter plot between the observed and modelled flows by S_ANFIS, F_ANFIS and MLR models. It was observed that the flow forecast by the ANFIS model was close to the 45° line. From Rindex, it is worth mentioning that the performance of S_ANFIS was better than that of F_ANFIS and MLR models.
The distribution of relative error, computed by S_ANFIS, F_ANFIS, and MLR models during the testing phase is presented in Figs 7(b), 7(c), and 7(d), in which it can be observed that the estimation of ET0 was better using S_ANFIS than the F_ANFIS and MLR models.
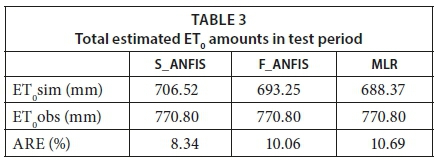
The estimation of total FAO-56 PM ET0 obtained from the estimated ET0 values was also considered for comparison due to its importance in irrigation systems (in determining the irrigation channel and/or tube, and total required irrigation water demand and its storage capacity, etc.). The total estimated ET0 amounts in the test period are given in Table 3. The S-ANFIS, F-ANFIS and MLR models whose input parameters are T, RH, U and ID, estimate the total FAO-56 PM ET0 value of 770.80 mm as 706.52 mm and 693.25 mm, with an underestimation of 8.34%, 10.06% and 10.69%, respectively.
CONCLUSION
The estimation of evapotranspiration using climatic variables was predicted by the adaptive NF techniques based on subtractive clustering and fuzzy c-means clustering-based fuzzy inference systems. The developed models were validated using the FAO-56 PM ET0 values of Dar El Beida, in Algiers, Algeria. The validations of the developed models with 4 input parameters, including daily climatic data, namely, temperature, relative humidity, wind speed and the insolation duration.
The results obtained in this study showed the effectiveness of subtractive clustering algorithm based fuzzy inference systems to estimate the FAO-56 PM ET0. The use of this hybrid method is an alternative fully justified for good water management. These encouraging results introduce a number of perspectives; it would be interesting to try hybrid models by coupling wavelet transform with neuro-fuzzy systems, and simultaneously optimizing by genetic algorithm: membership functions, scaling factors, and conclusions of fuzzy rules.
REFERENCES
ABRAHART RJ, KNEALE PE and SEE LM (2004) Neural Networks for Hydrological Modelling. Taylor & Francis, Hoboken, NJ. 304 pp. [ Links ]
ALLEN RG, PEREIRA LS, RAES D and SMITH M (1998) Crop evapotranspiration guidelines for computing crop water requirements. Paper No. 56. FAO Irrigation and Drainage, Food and Agriculture Organization of the United Nations, Rome. [ Links ]
AYTEK A, GUVEN A, ISHAK YUCE M and AKSOY H (2008) An explicit neural network formulation for evapotranspiration. Hydrol. Sci. J. 53 893-904. https://doi.org/10.1623/hysj.53.4.893 [ Links ]
BEZDEK JC (1981) Pattern Recognition with Fuzzy Objective Function Algorithms. Plenum Press, New York. https://doi.org/10.1007/978−1-4757-0450−1 [ Links ]
CHEN S and ZHANG D (1998) Robust image segmentation using FCM with spatial constraints based on new kernel-induced distance measure. IEEE Trans. Syst. Man Cybern. 34 1907-1916. https://doi.org/10.1109/TSMCB.2004.831165 [ Links ]
COBANER M (2011) Evapotranspiration estimation by two different neuro-fuzzy inference systems. J. Hyd. 398 (2011) 292-302. https://doi.org/10.1016/j.jhydrol.2010.12.030 [ Links ]
COX E (1999) The Fuzzy Systems Handbook (2nd edn). Academic Press, California. [ Links ]
DASTORANI M, MOGHADAMNIA A, PIRI J and RICO-RAMIREZ M (2010) Application of ANN and ANFIS models for reconstructing missing flow data. Environ. Monit. Assess. 166 421-434. https://doi.org/10.1007/s10661-009−1012-8 [ Links ]
JANG JS (1993) ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 23 (1993) 665-685. https://doi.org/10.1109/21.256541 [ Links ]
JENSEN ME, BURMAN RD and ALLEN RG (1990) Evapotranspiration and irrigation water requirements. ASCE Manuals and Reports on Engineering Practices no. 70. ASCE, New York. [ Links ]
HUI L (2008) Method of image segmentation on high-resolution image and classification for land covers. Fourth International Conference on Natural Computation, vol. 5. 563-566. [ Links ]
ROSS TJ (1995) Fuzzy Logic with Engineering Applications. McGraw Hill Co, New York. [ Links ]
SAMHOURI M, ABU-GHOUSH M, YASEEN E and HERALD T (2009) Fuzzy clustering-based modeling of surface interactions and emulsions of selected whey protein concentrate combined to ı-carrageenan and gum arabic solutions. J. Food Eng. 91 10-17. https://doi.org/10.1016/j.jfoodeng.2008.07.029 [ Links ]
TAKAGI T and SUGENO M (1985) Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst. Man Cybern. 15 116-132. https://doi.org/10.1109/TSMC.1985.6313399 [ Links ]
Received 16 December 2017
Accepted in revised form 8 March 2019.
* To whom all correspondence should be addressed.e-mail: bouchelkiahamid@gmail.com