REVIEW

 

Design norms for soil and water conservation structures in the sugar industry of South Africa

 

 

Daniel Otim^{I, II, *}; Jeff Smithers^{I, III}; Aidan Senzanje^I; Rianto van Antwerpen^{IV, V}

^IAgricultural Engineering, School of Engineering, College of Agriculture, Engineering and Science, University of KwaZulu-Natal, Pietermaritzburg, South Africa
^IIDepartment of Agricultural Mechanisation and Irrigation Engineering, Busitema University, PO Box 236, Tororo, Uganda
^IIINational Centre for Engineering in Agriculture, University of Southern Queensland, Toowoomba, Australia
^IVSouth African Sugarcane Research Institute, Mount Edgecombe, South Africa
^VDepartment of Soil, Crops and Climate Sciences, University of the Free State, PO Box 339, Bloemfontein 9300, South Africa

 

 

---

ABSTRACT

This paper contains a critical review of the norms employed in the design of soil and water conservation structures in the South African sugar industry and highlights research needs in order to update them. Sugarcane in South Africa is grown on wide-ranging soils, sometimes in non-ideal climates and on steep topographies where soils are vulnerable to erosion. A consequence of unsustainable soil loss is reduction in field production capacity. Sugarcane fields are protected against erosion through, inter alia, the use of engineered waterways, contour banks and spill-over roads. The South African Sugarcane Research Institute (SASRI), previously known as the South African Sugar Experiment Station (SASEX), developed a nomograph to easily compute the maximum width of field panels based on soil type, tillage method, replant method, surface structures to control runoff, surface cover and slope. This was followed by guidelines and norms for the design of soil and water conservation structures. However, the nomograph was developed based on an acceptable soil loss of 20 t·ha⁻¹·yr⁻¹, yet soil formation rates in South Africa range between 0.25 and 0.38 t·ha⁻¹·yr⁻¹. Comparisons between design norms in the National Soil Conservation Manual and norms used in the sugar industry clearly show discrepancies that need to be investigated. The design of soil conservation structures includes the design of both contour bank spacing and hydraulic capacity. The sustainable soil loss method is recommended in the design of contour spacing and it determines contour spacing based on evaluation of site-specific sheet and rill erosion potential of the planned contour spacing while the hydraulic design employs Manning's equation. Considering that increases in both design rainfall and design floods are anticipated in South Africa, it is necessary to incorporate these projections in the design of soil and water conservation structures. Many soil loss models exist, of which empirical models are the most robust and provide stable performances. The majority of empirical models are lumped models which estimate average annual soil loss. The Modified Universal Soil Loss Equation (MUSLE) estimates event-based erosion and, given that the majority of soil erosion occurs during a few extreme events annually, the design norms should be updated using the MUSLE.

Keywords: contour banks, hydraulic, hydrologic, soil erosion, USLE, waterways

---

 

 

INTRODUCTION

Soil conservation is defined as the prevention and reduction of the amount of soil lost through erosion (Sustainet, 2010). The purpose of soil conservation is to ensure that the rate of soil formation is not exceeded by the rate of soil loss (Morgan, 2005), and it ensures increases in the amount of water seeping into the soil, thereby slowing down and reducing the amount of water running off (Sustainet, 2010). Soil is the most important resource on which agriculture is based. Thus, the proper management of soil is vital to ensuring long-term sustainability of agricultural productivity. According to Morgan (2005), soil erosion control is dependent on the selection of appropriate strategies for soil conservation, which in turn requires a thorough understanding of the processes and mechanics of erosion. Many soil conservation practices exist and they include mechanical structures (e.g. contour bunds, terraces, check dams), soil management practices and agronomic measures (e.g. cover crops, tillage, mulching, vegetation strips, re- vegetation, and agroforestry) (Krois and Schulte, 2014). It is recommended that all approaches to soil conservation, i.e., agronomic, soil management and mechanical means, be used to manage runoff from cultivated lands (Reinders et al., 2016).

Erosion is the process by which soil particles are detached and transported by erosive agents (Ellison, 1944). When the erosive agent is rainfall and/or runoff, the process is referred to as soil erosion by water (Ferro, 2010). Erosion of soil is a serious problem that emanates from a combination of agricultural intensification, soil degradation and intense rainstorms (Amore et al., 2004). Soil is functionally a non-renewable resource and while topsoil develops over centuries, the world's growing human population has actively depleted the resource over decades (Cohen et al., 2006). According to Cogo et al. (1984), soil erosion from cultivated cropland continues to be a major concern with significant associated problems, which range from the losses of a non-renewable resource and nutrients at its source to the contamination that occurs in the downstream areas (Guo et al., 2015). Shabani et al. (2014) reported that soil erosion is one of the most important factors degrading fertile agricultural soils around the world. According to Lewis (1981) and Nyakatawa et al. (2001), erosion may lead to the development of a rough and thin soil layer having little or no capacity to store water. This reduces soil fertility, thereby resulting in land degradation and environmental problems (Sutherst and Bourne, 2009). The average predicted soil erosion rate in South Africa based on the general pattern of relative differences is 12.3 t·ha⁻¹·yr⁻¹ (Le Roux et al., 2008), while the rate of soil formation within favourable conditions based on a 40-year period is in the range 0.25 to 0.38 t·ha⁻¹·yr⁻¹ (Matthee and Van Schalkwyk, 1984). Similarly, Australia has an average soil erosion rate of 4.1 t·ha⁻¹·yr⁻¹ (Le Roux et al., 2008) and soil formation rates below 0.5 t·ha⁻¹·yr⁻¹ in the eastern regions and effectively zero in the other areas (Edwards, 1988). The USA has an average soil erosion rate of 15.1 t·ha⁻¹·yr⁻¹ and soil formation rates over 5 t·ha⁻¹·yr⁻¹ (Magleby et al., 1995). However, the concept of an average erosion rate on a continental scale is illogical because of temporal and spatial variability in erosion rates (Boardman, 1998). Unsustainable soil loss from a field results in a reduction in the capacity of the field to sustain crop yield (Russell, 1998b).

Research on soil erosion only started in 1915 in the USA, which has continued to lead the world in this field (Matthee and Van Schalkwyk, 1984). According to Haylett (1961), research to determine the effects of soil cover on runoff and erosion was started in 1929 in South Africa. Many studies have since then tried to estimate the historical and current soil and subsequent soil water-holding capacity losses in the country due to soil erosion (Matthee and Van Schalkwyk, 1984). For example, Platford (1979) conducted research focusing on soil and water losses from sugarcane fields in South Africa to produce recommendations for protective practices. Various studies in the area of soil and water losses in South Africa are also documented in literature (e.g. Schulze and Arnold, 1979; McPhee et al., 1983; Platford and Thomas, 1985; Platford, 1987; Haywood and Schulze, 1990; Haywood, 1991; Russell, 1994; Russell and Gibbs, 1996; Smithers et al., 1996).

According to Platford (1987), sugarcane in South Africa is regularly grown in adverse climatic and topographic conditions and on a range of soils. Soils in sugarcane growing areas are predominantly granular, leached and are characterised by high rates of erosion after the removal of the natural vegetation. Protection of cropped land in areas experiencing high rainfall has traditionally been provided by water-carrying terrace banks built across the hillside at gentle slopes, but sugarcane is not always grown on the relatively gentle slopes for which this control system was designed (Platford, 1987). Therefore, strip planting, rotational crops, reduced tillage and other management practices which provide sufficient protection should be used in place of, or in addition to, terrace banks.

SASA (2002) developed guidelines and norms for the design of land-use plans in the sugar industry, which includes soil conservation structures (e.g. waterways, contour banks and spill-over roads), surface water management and cane extraction road networks. The nomograph included for the design of soil and water conservation structures as shown in Fig. 1, was developed by Platford (1987), who used observations from runoff plots, small catchments and the long-term average annual soil loss simulated using the Universal Soil Loss Equation (USLE) (Wischmeier and Smith, 1965, Wischmeier and Smith, 1978). The USLE is a model widely used in the estimation of soil erosion and supporting soil conservation measures (Song et al., 2005), and is the standard technique for soil conservation workers (Morgan, 2005).

The sugar industry design norms for spacing of contour banks advocate that specific designs should be used to design soil conservation structures for slopes less than 3% or greater than 30% (Russell, 1994), although the sugar industry design nomograph includes slopes of up to 40% (Platford, 1987; SASA, 2002). There are also differences between the design norms contained in the National Soil Conservation Manual (Van Staden and Smithen, 1989; DAWS, 1990) and design norms used in the sugar industry (Platford, 1987; SASA, 2002) (e.g. maximum slope and cover factors for sugarcane). The sugar industry design nomograph does not (Smithers, 2014):

•Include any regional variations of climate and the impact on soil erosion and runoff

•Account for large runoff events and how frequently these occur

•Account for unplanned events (e.g. runaway fires) which do occur

•Include vulnerability during break cropping where the cover may be reduced

•Include the potential impact of climate change on runoff and soil loss

In addition to the above, Platford (1987) used an acceptable soil loss of 20 t·ha⁻¹·yr⁻¹ in the development of the nomograph, which is not sustainable. It is not clear as to why an unsustainable soil loss was used by Platford (1987), but it is suspected that it was considered more economic to implement wider spaced structures which result from design rules with the higher acceptable loss. For the above reasons, there is a need to update the design methodologies/norms currently used in the sugar industry.

The main aim of this article is to review the design norms for soil and water conservation structures in the South African sugar industry, compare and contrast the norms with national norms and international practices and to identify research gaps required to update the current design norms.

 

AGRONOMIC PRACTICES IN THE SUGARCANE PRODUCTION SYSTEM

Sugarcane production systems in South Africa involve activities ranging from land preparation to the transportation of the harvested crop to the mill (SASRI, 2011). A typical production cycle lasts for about 10 years which is the time frame that allows a farmer to maintain the economic viability of sugarcane (Platford, 1987; SASA, 2002; SASRI, 2015). The agronomic practices which constitute production systems in the sugar industry include land preparation, planting, weed, pest and disease control, and harvesting of sugarcane (SASA, 2002). Sugarcane production systems are briefly discussed to illustrate the relevance and/or the impact of management practices on design considerations for soil conservation.

Land preparation

According to Meyer (2005), the goal of land preparation is to produce a tilth which results in good bud germination and subsequent root development of the new crop. Land preparation includes conventional tillage and minimum tillage practices. SASRI (1998) and SASA (2002) advocate for minimum tillage practices on slopes greater than 11% for erodible soils, slopes greater than 13% for moderately erodible soils and slopes greater than 16% for resistant soils. On the other hand, conventional tillage is acceptable on slopes with smaller gradients as long as ploughing is conducted across the slope and not up and down the slope (SASA, 2002).

Planting

Planting of sugarcane can be done either by hand (manually) or mechanically (Meyer, 2005). SASEX (1974) advocated for sugarcane strip planting and harvesting across all steep slopes other than short run slopes which are in, and adjacent to, valley bottoms. Strip planting involves growing various plant species in adjacent panels (Głowacka, 2014). Planting of sugarcane in strips is practiced so as to minimise soil loss and it is recommended on all slopes exceeding 2%, except on certain layouts used for irrigation (SASRI, 2015). However, where strip planting is not practiced, dimensions and location of conservation structures have been adjusted in conformity with the SASA (2002) nomograph. According to SASA (2002) and SASRI (2015), the strip widths at right angles to the contour should not exceed thrice the maximum distance between contour banks as long as the alternate strips have a difference in age which is not less than 6 months. SASA (2002) and SASRI (2015) further stress the need for alternate strip planting to be practiced on all slopes greater than 12%.

Weed, pest and disease control

Weed control is achieved either by mechanical means or via spraying of chemicals while pest and disease control is achieved through manual and mechanical application of chemicals. Both conventional tillage and conservation tillage practices are vital in the control of weeds but it is conservation tillage which ensures soil and water conservation through maintaining as much crop residue as possible on the soil surface (Russell, 1998a). The crop residues reduce the impact of raindrop splash on the soil surface, reduce the velocity of surface runoff and protect the soils from erosion. Crop rotation is a practice which is required for the control of pests and diseases (Sustainet, 2010). According to SASRI (2015), land should be used in accordance with a crop rotation system so as to promote addition of organic matter to soils, soil fertility, reduction of pests and diseases, and erosion control. Crop rotation is achieved through growing secondary crops that enhance soil health. Generally, after 5 to 6 harvests, sugarcane yield might have been decreased significantly thus calling for rejuvenation of the field (Zuurbier and Van de Vooren, 2008). Rejuvenation of a sugarcane field is usually performed by planting an annual leguminous food crop. The legumes improve soil quality, prevent soil erosion and contribute to food production (Zuurbier and Van de Vooren, 2008).

Harvesting

Harvesting of sugarcane should be planned so as to minimise negative environmental impacts, and equipment having the least impact on the environment should be used (SASA, 2002). Burning and mulching are alternative sugarcane harvesting procedures practiced in South Africa (SASRI, 2015). The burning of sugarcane prior to harvesting is a widespread practice in South Africa and the main reason is to eliminate excess residue so as to improve harvesting, handling and milling of the cane (SASRI, 2010). Approximately 90% of sugarcane in South Africa is burnt at harvest with the rest harvested green (SASRI, 2013). According to SASRI (2014), accidental and runaway fires are common occurrences and often spread over entire hillsides, thereby exposing the land to potential erosion. Serious erosion can be experienced if heavy rains follow soon after burning, thus making it necessary to leave the tops and residues scattered over the soil surface so as to protect the soil and reduce the velocity of runoff (SASRI, 2014). It is a requirement for all burning to comply with the Conservation of Agricultural Resources Act (CARA, 1983) and the National Veld and Forest Fire Act (NVFFA, 1998). In addition, codes of practice on burning which provide acceptable ways of complying with legislation and minimising negative impacts on the environment while aiding crop production are in place (SASRI, 2013). Burning of sugarcane at harvest is associated with a number of disadvantages compared to green cane harvesting and it should be avoided wherever possible (SASRI, 2010; SASRI, 2013). Soil and water conservation and yield improvement are some of the benefits associated with green cane harvesting, among others (SASRI, 2010). SASA (2002) and SASRI (2015) advocate for mulching wherever possible for maximum conservation of soil and water, particularly on steep slopes and erodible soils.

In summary, the agronomic practices in the sugarcane production systems discussed above play a role in soil and water conservation and they should be considered when updating design norms for soil and water conservation structures in the sugar industry.

 

DESIGN FOR SOIL AND WATER CONSERVATION STRUCTURES

Design norms are guidelines applied in the design of structures. The commonly used structures in soil and water conservation are waterways and contour banks and their designs entail both hydrologic and hydraulic designs.

Hydrologic design

Hydrologic design entails estimation of design floods which is important in the sizing of hydraulic structures and thus to quantify and limit the risk of failure of the structures (Reinders et al., 2016). The risk of failure is related to the return period and it is quantified as a probability of exceedance, as shown in Eq. 1.

where:

P_e = risk of failure

T = return period (years)

ASABE (2012) recommended a 10-yr return period, 24-h storm for the design of contour banks but stresses the need for the selection of larger design storms appropriate to the level of risk of failure. A 10-yr return period is also recommended for the design of soil conservation structures in Australia and in situations where failure would threaten public safety or lead to severe damage, larger return periods are recommended (Carey et al., 2015).

Matthee and Van Schalkwyk (1984) recommended that soil conservation structures should be designed so as to cope with 10-25 year return period floods while SASA (2002) specifies a 10-yr return period for the design of soil and water conservation structures in the South African sugar industry.

According to Russell (1994), the Soil Conservation Service (SCS) method (SCS, 1972) of runoff estimation should be used for the design of structures on cultivated land while the Rational Method (Kuichling, 1889) is to be used for storage dam and gulley stabilization design in natural catchments. The SCS method (Eq. 2) is widely used and it is not as sensitive to user inputs as the Rational Method (Eq. 4) (Smithers, 2012). Schmidt et al. (1987) utilised the developments and verifications by Schulze and Arnold (1979), Schulze (1982), Schmidt and Schulze (1984) and Dunsmore et al. (1986) to adapt the SCS method for application in South Africa (SCS-SA) which included additional soil classes, temporal distribution of rainfall and the impact of antecedent moisture conditions on runoff generation in South Africa.

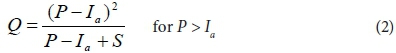
where:

Q = stormflow depth (mm)

P = daily rainfall depth (mm)

I_a = initial abstraction prior to stormflow commencement (0.1S for South Africa) (mm)

S = potential maximum soil water retention (mm)

The peak discharge) estimated using the SCS-SA approach depends on storm flow depth, catchment area, catchment lag time, and the effective storm duration shown in Eq. 3 (Schulze, 1995a).

where:

q_p = peak discharge (m3·s⁻¹)

A = catchment area (km²)

Q = stormflow depth (mm)

D_e = effective storm duration (h)

L = catchment lag time (h)

The Rational Method is extensively used worldwide for both small rural and urban catchments (Alexander, 2001). Parak and Pegram (2006) reported that the Rational Method is the most widely used method for estimating design peak discharges from rainfall events and is easy to understand and simple to use. The method, which only computes flood peaks, is sensitive to the input design rainfall intensity and the runoff coefficient, whose selection is based on the experience of the user (Smithers, 2012). The algorithm for the Rational Method is shown in Eq. 4.

where:

q_p = peak discharge (m³·s⁻¹)

C = runoff coefficient

I = rainfall intensity over catchment (mm·h⁻¹)

A = area of catchment (km²)

Hydraulic design

The hydraulic design of soil and water conservation structures entails selecting the placement, size, shape and slope of physical protection works, namely contour banks and waterways.

Contour bank design

According to SASA (2002), contour banks are defined as structures designed hydraulically and placed in the field to protect the land situated immediately below. Design of contour banks involves the selection of vertical and horizontal spacing between contour banks, and the sizing of the contour to safely convey the design discharge (Reinders et al., 2016).

Spacing of contour banks / conservation terraces

Two methods, namely, vertical interval method and sustainable soil loss method, are employed in the determination of contour bank spacing (ASABE, 2012).

The vertical interval method is an empirical method developed by the SCS in the 1950s and is not soil, cropping system, or rainfall specific (ASABE, 2012). The existing land slope is the slope used in the equation and thus the method does not account for the effect of terrace shape on the constructed land slope. Frequently the maximum terrace spacing computed by use of the vertical interval method is more conservative than that obtained using the sustainable soil loss method (ASABE, 2012). The vertical interval equation is shown in Eq. 5.

where:

VI = vertical interval (m)

X = variable ranging from 0.4 to 0.8 for graded terraces and 0.8 for terraces that are level (ASABE, 2012)

= variable with limits ranging from 0.10 to 0.60 for South Africa (Matthee and Van Schalkwyk, 1984)

Y = variable ranging from 0.304 to 1.22 depending on erosivity of soil, cropping systems and practices of crop management (ASABE, 2012)

= variable within limits ranging from 0.30 to 2.30 recommended for South Africa depending on soil erodibility, crop nature and cropping system (Matthee and Van Schalkwyk, 1984)

S = land slope (%)

With the VI known, the horizontal interval (HI in m) is obtained using Eq. 6.

where:

HI = horizontal interval (m)

VI = vertical interval (m)

S = land slope (%)

Equation 5 was developed in USA with factors X and Y based on runoff and soil loss experiments (Reinders et al., 2016). Van Staden and Smithen (1989) recommended Eq. 7 for use in South Africa.

where:

VI = vertical interval (m)

S = land slope (%)

The sustainable soil loss method is the preferred method for determining contour bank spacing and it determines contour spacing based on evaluation of site-specific sheet (inter-rill) and rill erosion potential of the planned contour spacing by employing a sheet and rill erosion prediction tool such as the Revised Universal Soil Loss Equation − Version 2 (RUSLE2) (ASABE, 2012). The RUSLE2 (USDA-ARS, 2001) is the model used by the Natural Resources Conservation Service (NRCS) in the computation of site-specific sheet and rill erosion based on local climate, soil types, planned cropping system, and slope (USDA-NRCS, 2011). The maximum allowable spacing for contour systems is based on the NRCS planning criteria for the maximum allowed sheet and rill erosion rate for the site and the value is termed tolerable soil loss (USDA-NRCS, 2011). Various tolerable soil loss values within South Africa are documented in literature as shown in Table 1.

 

 

Platford (1987) employed the USLE in the development of a nomograph to determine contour bank spacing in the South African sugar industry. The algorithm for the USLE is shown in Eq. 8 and the nomograph for determining contour bank spacing in the South African sugar industry is shown in Figure 1.

where:

A_y = average annual soil loss (t·ha⁻¹·yr⁻¹)

R = rainfall-runoff erosivity factor (MJ·ha⁻¹·mm·h⁻¹)

K = soil erodibility factor ( t·MJ⁻¹·h·mm⁻¹)

L = slope length factor

S = slope gradient factor

C = crop factor

P = conservation practice factor

If A_y is the acceptable soil loss for a specific field, then R, K and S can be fixed and the USLE equation solved for either L with a known C or C solved with a defined L (Platford, 1987). Values for acceptable soil loss within the South African sugar industry generally range from 4 t·ha⁻¹·yr⁻¹ to 12 t·ha⁻¹·yr⁻¹ (Platford, 1987) but 20 t·ha⁻¹·yr⁻¹ was used by Platford (1987) as the acceptable soil loss in the development of the nomograph to determine contour bank spacing in the South African sugar industry. Maintaining soil losses within sustainable limits is paramount in sustaining crop yields from cultivated lands (Russell, 1998b), as illustrated in Fig. 2. The USLE was employed by Platford (1987) to make predictions of soil loss for all possible combinations of factors and thereafter the results were used to prepare the nomograph.

 

 

Similarly, Van Staden and Smithen (1989) developed a nomograph used for the estimation of contour bank spacing for various crops by employing the USLE, as shown in Fig. 3.

The nomographs developed by Van Staden and Smithen (1989) and by Platford (1987) are different. Differences also exist between these norms and norms employed elsewhere (e.g. USA and Australia) as shown in Table 2.

Designing the cross-sectional area and slope of contour banks

According to ASABE (2012), contour banks installed on agricultural land should have the capacity to convey the peak rate of runoff anticipated from a 10-yr return period, 24-h storm without overtopping, as a minimum. The 10-yr-24-h storm caters for effects of moderately intense and moderately infrequent storms which are most likely to cause severe ponding (USDA-ARS, 2008). Design of earth bank contours is relatively simple and involves determination of the correct width, depth, shape and slope to safely discharge the required design discharge (Reinders et al., 2016). Manning's equation for open channel flow is used in the hydraulic design of contour banks and its algorithm is shown in Eq. 9:

where:

v = flow velocity (m·s⁻¹),

R = hydraulic radius (m)

n = Manning's roughness coefficient, and

S_o = channel slope (m·m⁻¹).

Design and sizing of waterways

Waterways are hydraulic structures suitably protected by vegetation or paving and are designed to safely convey the discharge from contour banks to a natural stream or river (SASA, 2002). Vegetated channels are designed for both stability and capacity conditions (Reinders et al., 2016). Stability design is for conditions when vegetation has been recently established or cut short while capacity design is for conditions when the vegetation is fully established in the waterway. The basis for design of waterways is the Manning's equation as shown in Eq. 9.

 

MODELS FOR SOIL EROSION ESTIMATION

In recent decades, soil erosion by water has become a relevant worldwide issue due to climate change, and as soils are more exposed to erosion for various reasons, including inappropriate agricultural practices and forest fires (Terranova et al., 2009). Consideration should be given to individual rainfall events as they trigger key hydrological responses such as stormflow and sediment yield (Schulze et al., 2011). Erosion models are necessary for soil and water conservation and non-point-source pollution assessments. According to Amore et al. (2004), a number of planning and management theories and formulae have been developed in order to reduce soil loss from catchments. Various models for prediction of erosion are widely documented in literature (e.g. Zingg, 1940; Smith, 1941; Wischmeier and Smith, 1978; Renard et al., 1997; Angima et al., 2003; Morgan, 2005; Cohen et al., 2006; Prasannakumar et al., 2012).

Categories of erosion models

Over time, soil erosion models have been developed to increase knowledge, mitigation and degree of resilience regarding erosion processes (Merritt et al., 2003). Erosion and sediment transport models are sub-divided into three main categories, depending on the physical processes simulated, the model algorithms describing these processes and the data dependence of the model. The three erosion model categories are empirical, conceptual and physics-based (Terranova et al., 2009).

Many different soil erosion prediction models are available, ranging across the three model categories described above. The models differ in complexity, the modelled processes, the scale of application, and the assumptions on which they are based (Merritt et al., 2003). Complex deterministic models (i.e. conceptual and physics-based models) which represent erosion processes and sediment transport are desirable for the accurate estimation of soil loss. However, use of complex models is limited and not practical due to the requirements of input parameters which are generally only available from research catchments, and the reliance of the complex models on calibration (Lorentz and Schulze, 1995). Simpler models (i.e. empirical models) are more robust, thereby providing more stable performances than more complex models (Merritt et al., 2003). Due to these reasons, simple empirical models have proved to be more effective in the provision of sufficient estimates of soil loss for initial planning and design purposes (Lorentz and Schulze, 1995). An overview of these empirical models is presented below.

Empirical models

The USLE (Eq. 8) was initially developed by Wischmeier and Smith (1965) and further refined by Wischmeier and Smith (1978). The USLE was the first and is the most important empirical model which calculates the long-term average annual soil loss from a field resulting from rill and interrill erosion (Terranova et al., 2009). It has received the most recognition worldwide with the most application and it is the foundation for many other empirical equations (Lorentz and Schulze, 1995). The USLE and its successors, the Revised Universal Soil Loss Equation (RUSLE) (Renard et al., 1991) and the RUSLE2 (USDA-ARS, 2001), are the most used models for prediction of soil erosion (Auerswald et al., 2014).

The RUSLE (Renard et al., 1991) is the revised version of the USLE (Wischmeier and Smith, 1965; Wischmeier and Smith, 1978) and it has been used at numerous spatial scales through sub-division of areas of application into sub-areas with homogeneous factors and combined with GIS applications (Renard et al., 1991). The RUSLE is a set of mathematical equations which estimate average annual soil loss and sediment yields emanating from rill and inter-rill erosion (Ranzi et al., 2012). The RUSLE is applied to estimate soil erosion over extended areas and in different contexts (Renard et al., 1997). Similar to the USLE, the RUSLE does not allow any estimate for deposit and size of sediment for the spatial and temporal distribution of erosion, but it is able to assess mean annual soil loss (Terranova et al., 2009). The algorithm for the RUSLE is similar to the USLE algorithm shown in Eq. 8.

The RUSLE2 (USDA-ARS, 2001) model is largely used for official purposes by the United States Department of Agriculture (USDA) - Natural Resources Conservation Services (NRCS) field offices in estimating field erosion (Foster et al., 2001). The RUSLE2 model is founded on the RUSLE that is used in the estimation of average annual sediment yield per unit area based on soil properties, land use, and daily precipitation and temperature data (Sommerlot et al., 2013). According to Foster et al. (2003), the RUSLE2 structure is based on the USLE (Wischmeier and Smith, 1965; Wischmeier and Smith, 1978) and RUSLE (Renard et al., 1991) models but the method used to solve governing equations in the RUSLE2 is what differentiates the RUSLE2 from the USLE and the RUSLE. The RUSLE2 encompasses both empirical and process-based science in the prediction of rill and interrill soil erosion by rainfall and runoff (Lloyd et al., 2013). The RUSLE2 algorithm is shown in Eq. 10 (USDA-ARS, 2008).

where:

a_i = long-term average soil loss for the ith day (t·ha⁻¹·yr⁻¹)

r_i = erosivity factor (MJ·ha⁻¹·mm·h⁻¹)

k_i = soil erodibility factor (t·MJ⁻¹·h·mm⁻¹)

l_i = soil length factor

S = slope steepness factor

c_i = cover management factor

p_i = supporting practices factor

The RUSLE2 model has a database which is a large collection of input data values (climate, soil, topography and land use) for the USA (USDA-NRCS, 2013). The user of the RUSLE2 model selects entries from the database to describe site-specific field conditions.

Williams (1975) modified the USLE by replacing the rainfall erosivity factor with a stormflow factor and the modification is termed the Modified Universal Soil Loss Equation (MUSLE) (Lorentz and Schulze, 1995). The MUSLE (Williams, 1975) allows for direct prediction of sediment yield, hence eliminating sediment delivery ratios, and is applicable for individual storm events (Williams and Berndt, 1977, Hui-Ming and Yang, 2009). Erosive and transport energies are accounted for by the MUSLE through the inclusion of stormflow volume and peak discharge, respectively, both of which are projected to change in the intermediate and distant future (Williams and Berndt, 1977). The algorithm for the MUSLE is shown in Eq. 11 (Hui-Ming and Yang, 2009).

where:

Y_sd = event sediment yield (t)

α_sy = location specific MUSLE coefficient

Q_v = stormflow volume for the event (m³)

q_p = event peak discharge, (m³·s⁻¹)

β_sy = location specific MUSLE coefficient

K = soil erodibility factor (t·h·N⁻¹·ha⁻¹)

L = slope length factor

S = slope steepness factor

C = cover management factor

P = supporting practices factor

The MUSLE is embedded in the Agricultural Catchments Research Unit (ACRU) (Schulze, 1975) modelling system and it has been verified locally and internationally (Schulze et al., 1995). Additionally, various options are offered for the estimation of the K, L, S, C, and P factors (Schulze, 1995b).

The Soil Loss Estimator for Southern Africa (SLEMSA) model (Eq. 12), developed by Elwell (1978), was developed mainly with data from the Zimbabwe Highveld, for the purpose of evaluating erosion emanating from various farming systems, and was used to develop recommendations for appropriate conservation measures (Morgan, 2005). The factors employed by SLEMSA were specifically derived for the Zimbabwean Highveld and sub-models have been employed to give best estimates of inter-rill erosion within Zimbabwe and in other areas in southern Africa (Smith, 1999). The SLEMSA is a modelling framework with no mechanistic system description and therefore cannot be universally applied (Smith, 1999).

where:

Z = average annual soil loss (t·ha⁻¹)

K = average annual soil loss from a standard field plot (t·ha⁻¹)

X = slope length and steepness factor

C = dimensionless crop management factor

The input parameters for the MUSLE (Williams, 1975) and the RUSLE (Renard et al., 1991) have been extensively researched for southern African conditions (Lorentz and Schulze, 1995; Le Roux et al., 2007). Hence, the MUSLE and RUSLE would be most suitable for application in southern Africa. Generally, climate has the greatest influence on erosion controlling factors, followed by the soil parent material, while the influence of slope factors are masked by climatic and parent material effects (Manyevere et al., 2016). However, crop cover is the most sensitive parameter and it masks the effects of soil erodibility and slope factors on erosion (Gwapedza et al., 2018; Otim, 2018).

 

CLIMATE CHANGE IMPACTS ON DESIGN FLOODS

The frequency of climatic fluctuations, including extreme weather events, is expected to increase as a result of changes in climate (Heltberg et al., 2009). Hallegatte (2009) lists land-use planning as one of the sectors in which decisions should take into account climate change since it involves long-term planning, long-term investments and some irreversibility in choices, and it is subjected to changes in climate conditions. There is a likelihood that the frequency of heavy rainfall events has increased over most areas, and the average precipitation may reduce in some regions (Bates et al., 2008). From a global perspective, some areas are expected to experience an increase in runoff while other areas shall have less runoff, and trends in runoff do not necessarily follow the trend in precipitation (Bates et al., 2008). Climate change impacts on hydrological processes have been projected and they vary between regions and seasons (Kundzewicz et al., 2008). Knoesen (2012) projected an increase in both design rainfall and design floods in South Africa as a result of climate change with projections of design floods being larger than those for design rainfall.

According to Smithers (2012), the estimation of design floods will be impacted by the changes and distribution of rainfall and runoff. For instance, climate change impacts on design rainfall must be quantified in order to assess the impact on the estimated design flood. There is thus a need for new and updated methods of design flood estimation so as to account for the impacts of climate change on design flood estimation (Smithers, 2012).

There is a possibility that climate change resulting from increases in temperature, and the subsequent impact on rainfall regimes, will lead to increases in the intensity and frequency of extreme rainfall events of both short duration (< 24 h and down to 5 min) and long duration (1 day to 7 days) and the associated flooding (Schulze, 2011). This would have serious repercussions on the design of hydraulic structures as the failure of such structures is associated with potential economic, environmental and societal repercussions. Based on studies on climate circulation models, rainfall in the Western Cape and South Africa at large is expected to become more intense and extreme (Du Plessis and Burger, 2015). Generally across South Africa, an increase of up to 10% in short-duration design rainfalls may be expected in the intermediate future (2046-2065) (Schulze, 2011). This stresses the need for adjustments to future hydrological designs that are based on short-duration extreme rainfalls. Schulze (2011) projected increases in design rainfalls of long duration over much of South Africa and the implication is that such increments should be considered in future designs of hydraulic structures. Similar trends have been observed in KwaZulu-Natal by Schulze (2013) and the Western Cape by De Waal et al. (2017) and Du Plessis and Schloms (2017).

 

DISCUSSION AND CONCLUSIONS

Soil erosion is a serious problem emanating from a combination of agricultural intensification, soil degradation and intense rainstorms. It is estimated that South Africa has an average soil erosion rate of 12.3 t·ha⁻¹·yr⁻¹ while the estimated rate of soil formation ranges between 0.25 and 0.38 t·ha⁻¹·yr⁻¹. Moreover, when the rate of soil loss is unsustainable, it leads to a reduction in crop yield and hence the need to limit soil losses to sustainable levels. The mechanical means of soil conservation in the South African sugar industry is by use of contour banks/terrace roads and waterways, and standards and guidelines for the design of soil conservation structures have been published by SASA (2002). Strip planting, rotational crops, reduced tillage and other management practices which provide a degree of soil protection should be used in addition to these mechanical means of soil conservation. A nomograph for determining the spacing of soil and water conservation structures in the sugar industry of South Africa was developed by Platford (1987) who used observations from runoff plots and the long-term average annual soil loss simulated using the USLE. The USLE estimates annual soil loss, but erosion occurs on an event basis. Likewise, the RUSLE and SLEMSA predict and aggregate the annual soil loss while the RUSLE2 predicts the long-term average soil loss on a given day. The MUSLE, on the other hand, is an event-based model. Thus, it is necessary to develop updated design norms using an event-based erosion prediction model since erosion occurs on an event basis, and it is expected that most of the soil erosion occurs from only a few extreme events per year. Hence, the design approach should focus on limiting the erosion during these extreme events. The MUSLE is well suited for this application and various options for estimation of the MUSLE parameters are available.

Hydrologic design is an important aspect that feeds into the hydraulic design of soil and water conservation structures. Two methods, namely the SCS and Rational Method, are used in estimation of design floods and are suited to cultivated lands and natural catchments, respectively. The SCS- SA was specifically adapted for South Africa and is widely used for estimation of design floods from small catchments. The current design norms for the sugar industry specify that soil and water conservation structures be designed for a 10-yr return period but are silent on the duration of the rainfall events that are used in their designs, yet a 10-yr return period, 24-h storm is the minimum recommended. Considering that increases in both design rainfall and design floods are anticipated in South Africa as a result of climate change, the 10-yr return period currently recommended may not be adequate due to the projected levels of risk and the fact that a few large events are likely to be responsible for the majority of the erosion. In addition, short-duration storms with high intensities are more likely to cause erosion than long-duration storms with low intensities. Therefore, it would be necessary to incorporate short-duration storms (i.e. < 24 h and down to 5 min) in the design of soil and water conservation structures. Hence, the impact of rainfall duration, intensity and frequency as well as potential climate change needs to be accommodated in the design of conservation structures. Increasing the return period and decreasing the storm duration would ensure that the projected extreme events likely to cause erosion are adequately accommodated in the updated design norms, thereby maintaining soil losses to sustainable levels.

Climate has the greatest influence on erosion-controlling factors, followed by the soil parent material, while the influence of slope factors is masked by climatic and parent material effects. The nomograph for the design of soil and water conservation structures in the sugar industry does not include any regional variations of climate and the impact on soil erosion and runoff. Therefore, it is imperative to incorporate regional variations in climate in the updated design norms for the design of soil and water conservation structures.

The design of conservation terraces involves two aspects, i.e., spacing and hydraulic design. Contour bank spacing can be achieved by applying one of two methods, namely, the sustainable soil loss method and the vertical interval method, of which the former is the preferred method. The sustainable soil loss method employs a sheet and rill erosion prediction tool to determine contour spacing. The simulation conducted by Platford (1987) generated various values used in the construction of the nomograph for the design of soil conservation structures in the South African sugar industry. However, most of the soil loss values used in the construction of the nomograph exceed the 20 t·ha⁻¹·yr⁻¹ fixed by Platford (1987), which in itself exceeds the acceptable soil loss value of 9 t·ha⁻¹·yr⁻¹ proposed by Van Staden and Smithen (1989). The soil loss of 20 t·ha⁻¹·yr⁻¹ is not sustainable, thus giving unsustainable contour bank spacing for soil losses in excess of 9 t·ha⁻¹·yr⁻¹. In addition, the acceptable soil loss value of 9 t·ha⁻¹·yr⁻¹ is not sustainable considering that it is in excess of the soil formation rates in South Africa, which range between 0.25 and 0.38 t·ha⁻¹·yr⁻¹. The nomograph employed in the South African sugar industry also deviates from the nomograph contained in the National Soil Conservation Manual (e.g. maximum slope, cover factors for sugarcane and maximum contour spacing) and norms employed in the USA and Australia. The design norms for soil and water conservation structures in the sugar industry also advocate for specific designs whenever slopes are less than 3% or greater than 30% although the design nomograph used in the sugar industry caters for slopes up to 40%. Some slopes in the sugar production industry exceed 40% and yet the nomograph has a maximum slope of 40% and cannot be used to design structures on land where slopes are greater than 40% or less than 3%. The 40% slope is also greater than the 20% maximum slope contained in the National Soil Conservation Manual (Van Staden and Smithen, 1989). Hence, these anomalies need to be revised and harmonised in the updated design norms for the design of soil and water conservation structures.

The nomograph used in the local sugar industry further assumes strip planting, which is generally no longer practiced in South Africa. Failure to practice strip cropping exposes the soils to erosion and hence recommendations for practices like mulching would limit the amount of soil loss.

Accidental and runaway fires are common occurrences in sugarcane harvesting in South Africa and often spread over entire hillsides, thereby exposing the land under sugarcane production to potential erosion (SASRI, 2014). Such an unforeseen occurrence is not accounted for in the design norms for soil and water conservation structures in the sugar industry and should be considered in future design norms.

Crop rotation is important in sugar production, ensuring soil fertility and reduction of pests and diseases, yet this important practice is not included in the design norms for soil and water conservation structures in the sugar industry. During the rotation period, the cover factor of the rotation crops is different to the sugarcane cover factors. Hence, some practices allowed during sugar production, like spraying pests and diseases and burning at harvest, may not be performed as a result of crop rotation. The design nomograph used in the sugar industry does not include vulnerability during break cropping where the cover may be reduced as a result of field rejuvenation and replanting of sugarcane. The sugarcane cover factors in the National Soil Conservation Manual range between 0.15 and 0.20 (DAWS, 1990), while the factors in the sugar industry design norms range between 0.09 and 0.15 (Platford, 1987).

In conclusion, there is a need to accommodate climate change variations, significant events of soil erosion, production and management practices, unforeseen occurrences which may occur, and regional differences in climate, soils and slopes in future design norms for soil and water conservation structures in the sugar industry of South Africa.

 

REFERENCES

ALEXANDER WJR (2001) Flood risk reduction measures: Incorporating flood hydrology for Southern Africa. Department of Civil and Biosystems Engineering, University of Pretoria, Pretoria, RSA. 459 pp.         [ Links ]

AMORE E, MODICA C, NEARING MA and SANTORO VC (2004) Scale effect in USLE and WEPP application for soil erosion computation from three Sicilian basins. J. Hydrol. 293 (1-4) 100-114. https://doi.org/10.1016/j.jhydrol.2004.01.018        [ Links ]

ANGIMA SD, STOTT DE, O'NEILL MK, ONG CK and WEESIES GA (2003) Soil erosion prediction using RUSLE for central Kenyan highland conditions. Agric. Ecosyst. Environ. 97 (1-3) 295-308. https://doi.org/10.1016/S0167-8809(03)00011-2        [ Links ]

ASABE Standard (2012) S268.5. Design layout construction and maintenance of terrace systems. ASABE, St. Joseph, USA.         [ Links ]

AUERSWALD K, FIENER P, MARTIN W and ELHAUS D (2014) Use and misuse of the K factor equation in soil erosion modeling: An alternative equation for determining USLE nomograph soil erodibility values. Catena 118 220-225. https://doi.org/10.1016/j.catena.2014.01.008        [ Links ]

BATES B, KUNDZEWICZ ZW, WU S and PALUTIKOF J (2008) Climate change and water: Technical paper. IPCC Secretariat, Geneva, Switzerland. 200 pp.         [ Links ]

BOARDMAN J (1998) An average soil erosion rate for Europe: myth or reality? J. Soil Water Conserv. 53 (1) 46-50.         [ Links ]

CARA (Conservation of Agricultural Resources Act) (1983) RSA Government Gazette No. 43 of 1983: 25 May 1984, No. R.1048. Cape Town, RSA.         [ Links ]

CAREY BW, STONE B, NORMAN PL and SHILTON P (2015) Contour banks. In: Butcher S, Campbell C, Green D, Hamilton F, Skopp L and Willson M (eds) Soil Conservation Guidelines for Queensland. Department of Science, Information Technology and Innovation, Brisbane, Australia.         [ Links ]

COGO NP, MOLDENHAUER WC and FOSTER GR (1984) Soil loss reductions from conservation tillage practices. Soil Sci. Soc. Am. J. 48 (2) 368-373. https://doi.org/10.2136/sssaj1984.03615995004800020029x        [ Links ]

COHEN MJ, BROWN MT and SHEPHERD KD (2006) Estimating the environmental costs of soil erosion at multiple scales in Kenya using energy synthesis. Agric. Ecosyst. Environ. 114 (2-4) 249-269. https://doi.org/10.1016/j.agee.2005.10.021        [ Links ]

DAWS (1990) Predicting raifall erosion losses. In: Mathee JFlG (ed.) National Soil Conservation Manual. Directorate: Agricultural Engineering and Water Supply, Pretoria.         [ Links ]

DE WAAL JH, CHAPMAN A and KEMP J (2017) Extreme 1-day rainfall distributions: Analysing change in the Western Cape. S. Afr. J. Sci. 113 (7/8) 43-50. https://doi.org/10.17159/sajs.2017/20160301        [ Links ]

DU PLESSIS J and BURGER G (2015) Investigation into increasing short-duration rainfall intensities in South Africa. Water SA 41 (3) 416-424. https://doi.org/10.4314/wsa.v41i3.14        [ Links ]

DU PLESSIS J and SCHLOMS B (2017) An investigation into the evidence of seasonal rainfall pattern shifts in the Western Cape, South Africa. J. S. Afr. Inst. Civ. Eng. 59 (4) 47-55. https://doi.org/10.17159/2309-8775/2017/v59n4a5        [ Links ]

DUNSMORE SJ, SCHULZE RE and SCHMIDT EJ (1986) Antecedent soil moisture in design runoff volume estimation. WRC Report No. 155/1/86. Water Research Commission, Pretoria. 110 pp.         [ Links ]

EDWARDS K (1988) How much soil loss is acceptable. Search 19 (3) 136-140.         [ Links ]

ELLISON WD (1944) Studies of raindrop erosion. Agric. Eng. 25 (4) 131-136.         [ Links ]

ELWELL HA (1978) Modelling soil losses in southern Africa. J. Agric. Eng. Res. 23 (2) 117-127. https://doi.org/10.1016/0021-8634(78)90043-4        [ Links ]

FERRO V (2010) Deducing the USLE mathematical structure by dimensional analysis and self-similarity theory. Biosyst. Eng. 106 (2) 216-220. https://doi.org/10.1016/j.biosystemseng.2010.03.006        [ Links ]

FOSTER GR, YODER DC, WEESIES GA, MCCOOL DK, MCGREGOR KC and BINGNER RL (2003) User's Guide-Revised Universal Soil Loss Equation Version 2 (RUSLE 2). USDA-ARS, Washington, D.C.d. 77 pp.         [ Links ]

FOSTER GR, YODER DC, WEESIES GA and TOY TJ (2001) The design philosophy behind RUSLE2: Evolution of an empirical model. In: Ascough II JC and Flanagan DC (eds) Soil Erosion. ASABE, Honolulu, USA.         [ Links ]

GŁOWACKA A (2014) The influence of strip cropping and adjacent plant species on the content and uptake of N, P, K, Mg and Ca by maize (Zea mays L.). Romanian Agric. Res. 31 219-227.         [ Links ]

GUO Q-K, LIU B-Y, XIE Y, LIU Y-N and YIN S-Q (2015) Estimation of USLE crop and management factor values for crop rotation systems in China. J. Integrative Agric. 14 (9) 1877-1888. https://doi.org/10.1016/S2095-3119(15)61097-8        [ Links ]

GWAPEDZA D, SLAUGHTER A, HUGHES D and MANTEL S (2018) Regionalising MUSLE factors for application to a data-scarce catchment. Proc. International Association of Hydrological Sciences 377 19-24. https://doi.org/10.5194/piahs-377−19-2018        [ Links ]

HALLEGATTE S (2009) Strategies to adapt to an uncertain climate change. Glob. Environ. Change 19 (2) 240-247. https://doi.org/10.1016/j.gloenvcha.2008.12.003        [ Links ]

HAYLETT DG (1961) Runoff and soil erosion studies at Pretoria. S. Afr. J. Agric. Sci. 3 (3) 379-395.         [ Links ]

HAYWOOD RW (1991) Model evaluation for simulating runoff from sugarcane fields. MScEng, University of Natal.         [ Links ]

HAYWOOD RW and SCHULZE RE (1990) Modelling runoff from sugarcane fields. In: Proceedings of South Africa Sugar Technologists' Association, June 1990, Durban, RSA.         [ Links ]

HELTBERG R, SIEGEL PB and JORGENSEN SL (2009) Addressing human vulnerability to climate change: Toward a 'no-regrets' approach. Glob. Environ. Change 19 (1) 89-99. https://doi.org/10.1016/j.gloenvcha.2008.11.003        [ Links ]

HUDSON NW (1981) Soil Conservation. BT Batsford Ltd, London, UK. 391 pp.         [ Links ]

HUFFMAN RL, DELMAR DF, WILLIAM JE and STEPHEN RW (2013) Terraces and vegetated water ways. In: (ed.) Soil and Water Conservation Engineering. ASABE, St. Joseph, Michigan.         [ Links ]

HUI-MING S and YANG CT (2009) Estimating overland flow erosion capacity using unit stream power. Int. J. Sediment Res. 24 (1) 46-62. https://doi.org/10.1016/S1001-6279(09)60015-9        [ Links ]

KNOESEN DM (2012) Integrating hydro-climatic hazards and climate changes as a tool for adaptive water resources management in the Orange river catchment. PhDEng Thesis, University of KwaZulu-Natal, Pietermaritzburg.         [ Links ]

KROIS J and SCHULTE A (2014) GIS-based multi-criteria evaluation to identify potential sites for soil and water conservation techniques in the Ronquillo watershed, northern Peru. Appl. Geogr. 51 131-142. https://doi.org/10.1016/j.apgeog.2014.04.006        [ Links ]

KUICHLING E (1889) The relation between the rainfall and the discharge of sewers in populous districts. Trans. Am. Soc. Civ. Eng. 20 (1) 1-56.         [ Links ]

KUNDZEWICZ ZW, MATA LJ, ARNELL NW, DÖLL P, JIMENEZ B, MILLER K, OKI T, ŞEN Z and SHIKLOMANOV I (2008) The implications of projected climate change for freshwater resources and their management. Hydrol. Sci. J. 53 (1) 3-10. https://doi.org/10.1623/hysj.53.1.3        [ Links ]

LE ROUX J, MORGENTHAL T, MALHERBE J, PRETORIUS D and SUMNER P (2008) Water erosion prediction at a national scale for South Africa. Water SA 34 (3) 305-314.         [ Links ]

LE ROUX JJ, NEWBY T and SUMNER P (2007) Monitoring soil erosion in South Africa at a regional scale: Review and recommendations. S. Afr. J. Sci. 103 (7-8) 329-335.         [ Links ]

LEWIS LA (1981) The movement of soil materials during a rainy season in western Nigeria. Geoderma 25 (1-2) 13-25. https://doi.org/10.1016/0016-7061(81)90003-3        [ Links ]

LLOYD W, PALLICKARA S, DAVID O, LYON J, ARABI M and ROJAS K (2013) Performance implications of multi-tier application deployments on infrastructure-as-a-service clouds: Towards performance modeling. Future Generation Comput. Syst. 29 (5) 1254-1264. https://doi.org/10.1016/j.future.2012.12.007        [ Links ]

LORENTZ SA and SCHULZE RE (1995) Sediment yield. In: Schulze RE (ed.) Hydrology and Agrohydrology: A Text to Accompany the ACRU 3.00 Agrohydrological Modelling System. Department of Agricultural Engineering, University of Natal, Pietermaritzburg, RSA.         [ Links ]

MAGLEBY R, SANDRETTO C, CROSSWHITE W and OSBORN C (1995) Soil Erosion and Conservation in the United States. Agricultural Economic Report No. 718. Natural Resources and Environment Division, Economic Research Service, United States Department of Agriculture, Washington, DC, USA.         [ Links ]

MANYEVERE A, MUCHAONYERWA P, MNKENI PNS and LAKER MC (2016) Examination of soil and slope factors as erosion controlling variables under varying climatic conditions. Catena 147 245-257. https://doi.org/10.1016/j.catena.2016.06.035        [ Links ]

MATTHEE JFlG and VAN SCHALKWYK CJ (1984) A primer on soil conservation. Department of Agriculture, Pretoria. 126 pp.         [ Links ]

MCPHEE PJ, SMITHEN AA, VENTER CJ, HARTMANN MO and CROSBY CT (1983) The South African rainfall simulator programme for assessing soil loss and run-off. In: South African National Hydrological Symposium - Proceedings, 8-9 September 1983, Pretoria, RSA.         [ Links ]

MERRITT WS, LETCHER RA and JAKEMAN AJ (2003) A review of erosion and sediment transport models. Environ. Model. Softw. 18 (8) 761-799. https://doi.org/10.1016/S1364-8152(03)00078−1        [ Links ]

MEYER E (2005) Machinery systems for sugarcane production in South Africa. MScEng Seminar Paper, South African Sugarcane Research Institute, Mount Edgecombe, RSA.         [ Links ]

MORGAN RPC (2005) Soil Erosion and Conservation. Blackwell Publishing, Malden, USA. 304 pp.         [ Links ]

National Veld and Forest Fire Act (1998) RSA Government Gazette No. 101 of 1998: 27 November 1998, No. 1536.27. Cape Town, RSA.         [ Links ]

NYAKATAWA EZ, REDDY KC and BROWN GF (2001) Residual effect of poultry litter applied to cotton in conservation tillage systems on succeeding rye and corn. Field Crops Res. 71 (3) 159-171. https://doi.org/10.1016/S0378-4290(01)00155−1        [ Links ]

OTIM D (2018) Development of updated design norms for soil and water conservation structures in the sugar industry of South Africa. PhDEng Draft Thesis, School of Engineering, University of KwaZulu-Natal.         [ Links ]

PARAK M and PEGRAM GG (2006) The rational formula from the runhydrograph. Water SA 32 (2) 163-180.         [ Links ]

PLATFORD GG (1979) Research into soil and water losses from sugarcane fields. In: Proc. South African Sugar Technologists' Association, June 1979, Durban, RSA.         [ Links ]

PLATFORD GG (1987) A new approach to designing the widths of panels in sugarcane fields. In: Proc. South Africa Sugar Technologists' Association, Mount Edgecombe, RSA.         [ Links ]

PLATFORD GG and THOMAS CS (1985) The small catchment project at La Mercy. In: Proc. South Africa Sugar Technologists' Association, June 1985, Durban, RSA.         [ Links ]

PRASANNAKUMAR V, VIJITH H, ABINOD S and GEETHA N (2012) Estimation of soil erosion risk within a small mountainous sub-watershed in Kerala, India, using Revised Universal Soil Loss Equation (RUSLE) and geo-information technology. Geosci. Front. 3 (2) 209-215. https://doi.org/10.1016/j.gsf.2011.11.003        [ Links ]

RANZI R, LE TH and RULLI MC (2012) A RUSLE approach to model suspended sediment load in the Lo river (Vietnam): Effects of reservoirs and land use changes. J. Hydrol. 422-423 17-29. https://doi.org/10.1016/j.jhydrol.2011.12.009        [ Links ]

REINDERS FB, OOSTHUIZEN H, SENZANJE A, SMITHERS JC, VAN DER MERWE RJ, VAN DER STOEP I and VAN RENSBURG L (2016) Development of technical and financial norms and standards for drainage of irrigated lands. WRC Report No. TT 655/15. Water Research Commission, Pretoria.         [ Links ]

RENARD KG, FOSTER GR, WEESIES GA, MCCOOL DK and YODER DC (1997) Predicting Soil Erosion by Water: A Guide to Conservation Planning with the Revised Universal Soil Loss Equation (RUSLE). US Government Printing Office, Washington, D.C.         [ Links ]

RENARD KG, FOSTER GR, WEESIES GA and PORTER JP (1991) RUSLE: Revised Universal Soil Loss equation. J. Soil Water Conserv. 46 (1) 30-33.         [ Links ]

RUSSELL WB (1994) CEDARA Report: Standards and norms for soil and water conservation planning in KwaZulu-Natal. Report No. N/A/93/32. KwaZulu-Natal Department of Agriculture, Pietermaritzburg, RSA. pp.         [ Links ]

RUSSELL WB (1998a) Conservation tillage practices. In: Abbott MA (ed.) Conservation of Farmland in KwaZulu-Natal. KwaZulu-Natal Department of Agriculture, Pietermaritzburg.         [ Links ]

RUSSELL WB (1998b) The cost of farmland degradation. In: Abbott MA (ed.) Conservation of Farmland in KwaZulu-Natal. KwaZulu-Natal Department of Agriculture, Pietermaritzburg.         [ Links ]

RUSSELL WB and GIBBS MD (1996) CEDARA report: Ten years of soil and water loss monitoring on the CEDARA runoff plots. Cedara Report No. N/A/96/4. KwaZulu-Natal Department of Agriculture, Pietermaritzburg, RSA.         [ Links ]

SASA (South African Sugar Association) (2002) Standards and guidelines for conservation and environmental management in the South African sugar industry. South African Sugar Association, Mount Edgecombe. 57 pp.         [ Links ]

SASEX (South African Sugar Association Experiment Station) (1974) Soil conservation: a guide to farming practices in the sugarcane industry. South African Sugar Association Experiment Station, Mount Edgecombe. 27 pp.         [ Links ]

SASRI (South African Sugarcane Research Institute) (1998) Information Sheet 4.10: Minimum tillage. South African Sugarcane Research Institute, Mount Edgecombe, RSA.         [ Links ]

SASRI (South African Sugarcane Research Institute) (2010) Information Sheet 4.7: The pros and cons of trashing or burning at harvest. South African Sugarcane Research Institute, Mount Edgecombe, RSA.         [ Links ]

SASRI (South African Sugarcane Research Institute) (2011) South African sugar industry visitors' guide. SASRI, Mount Edgecombe, RSA. 16 pp.         [ Links ]

SASRI (South African Sugarcane Research Institute) (2013) Information Sheet 4.8: Industrial guidelines for burning sugarcane. South African Sugarcane Research Institute, Mount Edgecombe.         [ Links ]

SASRI (South African Sugarcane Research Institute) (2014) Information Sheet 4.1: Management of fire cane. South African Sugarcane Research Institute, Mount Edgecombe.         [ Links ]

SASRI (South African Sugarcane Research Institute) (2015) Sustainable sugarcane farm management system. South African Sugarcane Research Institute, Mount Edgecombe. 137 pp.         [ Links ]

SCHMIDT EJ and SCHULZE RE (1984) Improved Estimates of Peak Flow Rates Using Modified SCS Lag Equations. WRC Report No. TT 31/87. Water Research Commission, Pretoria. 145 pp.         [ Links ]

SCHMIDT EJ, SCHULZE RE and DENT MC (1987) Flood Volume and Peak Discharge from Small Catchments in Southern Africa Based on the SCS Technique. WRC Report No. TT 31/87. Water Research Commission, Pretoria, RSA. 164 pp.         [ Links ]

SCHULZE RE (1975) Catchment evapotranspiration in the Natal Drakensberg. Unpublished PhD Thesis, University of Natal.         [ Links ]

SCHULZE RE (1982) Adapting the SCS stormflow equation for application to specific events by soil moisture budgeting. ACRU Report No. 15. Department of Agricultural Engineering, University of Natal, Pietermaritzburg, RSA.         [ Links ]

SCHULZE RE (1995a) Peak discharge. In: Schulze RE and Schmidt EJ (eds) Hydrology and Agrohydrology: A Text to Accompany the ACRU 3.00 Agrohydrological Modelling System. Department of Agricultural Engineering, University of Natal, Pietermaritzburg.         [ Links ]

SCHULZE RE (1995b) Sediment yield. In: Lorentz SA and Schulze RE (eds) Hydrology and Agrohydrology: A Text to Accompany the ACRU 3.00 Agrohydrological Modelling System. Department of Agricultural Engineering, University of Natal, Pietermaritzburg, RSA.         [ Links ]

SCHULZE RE (2011) A 2011 Perspective on climate change and the South African water sector. WRC Report No. 1843/2/11. Water Research Commission, Pretoria. 366 pp.         [ Links ]

SCHULZE RE (2013) Modelling impacts of land use on hydrological responses in South Africa with the ACRU Model by sub-delineation of quinary catchments into land use dependent hydrological response units. Internal report. Centre for Water Resources Research, University of KwaZulu-Natal, Pietermaritzburg. 41 pp.         [ Links ]

SCHULZE RE, ANGUS GR, LYNCH SD and SMITHERS JC (1995) ACRU: Concepts and structure. In: Lorentz SA and Schulze RE (eds) Hydrology and Agrohydrology: A Text to Accompany the ACRU 3.00 Agrohydrological Modelling System. Department of Agricultural Engineering, University of Natal, Pietermaritzburg, RSA.         [ Links ]

SCHULZE RE and ARNOLD H (1979) Estimation of volume and rate of runoff in small catchments in South Africa. ACRU Report No. 8. Department of Agricultural Engineering, University of Natal, Pietermaritzburg, RSA. 79 pp.         [ Links ]

SCHULZE RE, HEWITSON BC, BARICHIEVY KR, TADROSS MA, KUNZ RP, HORAN MJC and LUMSDEN TG (2011) Methodological approaches to assessing eco-hydrological responses to climate change in South Africa. WRC Report No. 1562/1/10. Water Research Commission, Pretoria. 197 pp.         [ Links ]

SCS (1972) Design hydrographs. In: Mockus V (ed.) National Engineering Handbook. USDA, Washington D.C.         [ Links ]

SHABANI F, KUMAR L and ESMAEILI A (2014) Improvement to the prediction of the USLE K factor. Geomorphology 204 229-234. https://doi.org/10.1016/j.geomorph.2013.08.008        [ Links ]

SMITH DD (1941) Interpretation of soil conservation data for field use. Agric. Eng. 22 (5) 173-175.         [ Links ]

SMITH HJ (1999) Application of empirical soil loss models in southern Africa: a review. S. Afr. J. Plant Soil 16 (3) 158-163. https://doi.org/10.1080/02571862.1999.10635003        [ Links ]

SMITHERS JC (2012) Methods for design flood estimation in South Africa. Water SA 38 (4) 633-646. https://doi.org/10.4314/wsa.v38i4.19        [ Links ]

SMITHERS JC (2014) Effective Surface Water Management. South African Sugar Association, Mount Edgecombe, RSA.         [ Links ]

SMITHERS JC, MATHEWS P and SCHULZE RE (1996) The simulation of runoff and sediment yield from catchments under sugarcane production at La Mercy. ACRUcons Report No. 13. Department of Agricultural Engineering, University of Natal, Pietermaritzburg. 104 pp.         [ Links ]

SOMMERLOT AR, NEJADHASHEMI AP, WOZNICKI SA, GIRI S and PROHASKA MD (2013) Evaluating the capabilities of watershed-scale models in estimating sediment yield at field-scale. J. Environ. Manage. 127 228-236. https://doi.org/10.1016/j.jenvman.2013.05.018        [ Links ]

SONG Y, LIU L, YAN P and CAO T (2005) A review of soil erodibility in water and wind erosion research. J. Geogr. Sci. 15 (2) 167-176. https://doi.org/10.1007/BF02872682        [ Links ]

SUSTAINET EA (2010) Technical manual for farmers and field extension service providers: conservation agriculture. Sustainable Agriculture Information Initiative, Nairobi. 6 pp.         [ Links ]

SUTHERST RW and BOURNE AS (2009) Modelling non-equilibrium distributions of invasive species: A tale of two modelling paradigms. Biol. Invasions 11 (6) 1231-1237. https://doi.org/10.1007/s10530-008-9335-x        [ Links ]

TERRANOVA O, ANTRONICO L, COSCARELLI R and IAQUINTA P (2009) Soil erosion risk scenarios in the Mediterranean environment using RUSLE and GIS: An application model for Calabria (southern Italy). Geomorphology 112 (3-4) 228-245. https://doi.org/10.1016/j.geomorph.2009.06.009        [ Links ]

USDA-ARS (2001) Revised Universal Soil Loss Equation Version 2 Handbook. USDA-ARS, Washington, D.C. 78 pp.         [ Links ]

USDA-ARS (2008) Draft User's Reference Guide: RUSLE2. USDA-ARS, Washington D.C. 431 pp.         [ Links ]

USDA-NRCS (2011) Terraces. In: Engineering Field Handbook. Part 650. USDA-NRCS, Washington D.C.         [ Links ]

USDA-NRCS (2013) RUSLE2 Website. http://www.rusle2.org/: (Accessed 26 August 2016).         [ Links ]

VAN STADEN H and SMITHEN AA (1989) Protection of cultivated lands. In: Mathee JFlG (ed.) National Soil Conservation Manual. Directorate of Agricultural Engineering and Water Supply, Pretoria, RSA.         [ Links ]

WILLIAMS J and BERNDT H (1977) Sediment yield prediction based on watershed hydrology. Trans. ASAE 20 (6) 1100-1104. https://doi.org/10.13031/2013.35710        [ Links ]

WILLIAMS JR (1975) Sediment-yield prediction with universal equation using runoff energy factor. In: Present and Prospective Technology for Predicting Sediment Yields and Sources. 244-252.         [ Links ]

WISCHMEIER WH and SMITH DD (1965) Rainfall erosion losses from cropland east of the rocky mountains. In: Guide for Selection of Practices for Soil and Water Conservation. Agricultural Handbook No. 282, USDA, Washington D.C., USA.         [ Links ]

WISCHMEIER WH and SMITH DD (1978) Predicting Rainfall Erosion Losses - A guide to Conservation Planning. USDA, Washington D.C. 63 pp.         [ Links ]

ZINGG AW (1940) Degree and length of land slope as it affects soil loss in run-off. Agric. Eng. 21 59-64.         [ Links ]

ZUURBIER P and VAN DE VOOREN J (2008) Introduction to sugarcane ethanol contributions to climate change mitigation and the environment. In: Zuurbier P and Van de Vooren J (eds) Sugarcane Ethanol. Wageningen Academic Publishers, Wageningen, The Netherlands.         [ Links ]

 

 

Received 12 March 2018
Accepted in revised form 4 December 2018.

 

 

* To whom all correspondence should be addressed.e-mail: danotim@gmail.com