Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Water SA
On-line version ISSN 1816-7950
Print version ISSN 0378-4738
Water SA vol.45 n.1 Pretoria Jan. 2019
http://dx.doi.org/10.4314/wsa.v45i1.14
ORIGINAL ARTICLES
Modelling the unsaturated hydraulic conductivity of a sandy loam soil using Gaussian process regression
Naji Mordi N Al-DosaryI, *; Mohammed A Al-SulaimanII; Abdulwahed M AboukarimaI, III
IDepartment of Agricultural Engineering, College of Food and Agriculture Sciences, King Saud University, PO Box 2460, Riyadh 11451, Saudi Arabia
IIShaqra University, PO Box 300, Huraimla 11962, Saudi Arabia
IIIAgricultural Engineering Research Institute (AEnRI), Agricultural Research Centre, PO Box 256, Giza, Egypt
ABSTRACT
Unsaturated soil hydraulic conductivity is a main parameter in agricultural and environmental studies, necessary for predicting and managing water and solute transport in soils. This parameter is difficult to measure in agricultural fields; thus, a simple and practical estimation method would be preferable, and quantitative methods (analytical and numerical) to predict the field parameters should be developed. Field experiments were conducted to collect water quality data to model the unsaturated hydraulic conductivity of a sandy loam soil. A mini disk infiltrometer (MDI) was used to measure soil infiltration rate. Input variables included electrical conductivity and the sodium adsorption ratio of irrigation water. Suction rate (pressure head), soil bulk density, and soil moisture content acted as inputs, with unsaturated soil hydraulic conductivity as output. The performance of Gaussian process regression (GPR) was analysed, with multiple linear regression (LR) and multi-layer perceptron (MLP) models used for comparison. Three performance criteria were compared: correlation coefficient (r), root mean square error (RMSE), and mean absolute error (MAE). The simulations employed the Waikato environment for knowledge analysis (WEKA) open source tool. The results indicate that the GPR with Pearson VII function-based universal kernel (PUK kernel), cache size 250007, Omega 1.0 and Sigma 1.0 performs better than other kernels when evaluating test split data, with a correlation coefficient of 0.9646. The RMSEs for GPR (PUK kernel), MLP, and LR were 1.16 × 10−04, 1.87 × 10−04, and 2.22 × 10−04 cm·s−1, respectively. Predictive data mining algorithms (DMA) enable an estimate of unknown values based on patterns in a database. Therefore, the present methodology can be put to use in predictive tools to manage water and solute transport in soils, as the GPR model provides much greater accuracy than the LR and MLP models in predicting the unsaturated hydraulic conductivity of a sandy loam soil.
Keywords: multiple linear regression, multi-layer perceptron, data mining, infiltration rate, water management
INTRODUCTION
Water management is vital to improve the efficiency and sustainability of agricultural systems, as water is scarce in semi-arid regions such as Saudi Arabia. Soil hydraulic conductivity is a main parameter in agricultural and environmental studies (Gonçalves, et al., 2007). Unsaturated soil hydraulic conductivity controls water movement (Fatehnia et al., 2014), and measuring it is a challenging task, requiring costly, time-consuming, and skilled experimentation (Wosten and Van Genuchten, 1988; Malaya and Sreedeep, 2013). Various techniques have been developed to measure unsaturated hydraulic conductivity in the laboratory and in the field (Klute and Dirksen, 1989). Unfortunately, laboratory studies using repacked soil may have limited use in predicting the effects of water characteristics on soil hydraulic properties (Menneer et al., 2001). Additionally, the number of measurements of unsaturated hydraulic conductivity required to adequately characterize an area can be prohibitive. Thus, it is better to have means to estimate, in a simple and practical manner, the unsaturated hydraulic conductivity (Mbonimpa et al., 2004). The unsaturated hydraulic conductivity of soil could be estimated based on soil texture, the hydraulic conductivity of the soil, soil water properties, the amounts of gypsum and lime present, and the actual and apparent distributions of particle size (Zhuang et al., 2001). Moosavi and Sepaskhah (2012a) developed pedotransfer functions for prediction of unsaturated hydraulic conductivity. The most influential physical soil characteristics in prediction of soil hydraulic conductivity using pedotransfer functions were the soil particle fractions, bulk density, total soil porosity, and initial and near-saturated volumetric soil water content. Mainly, the unsaturated hydraulic conductivity measurements were achieved at diverse tensions of soil moisture (0.2, 0.15, 0.1, 0.06, 0.03, and 0 m). The study results indicated that the pedotransfer function predictions of unsaturated soil hydraulic conductivities at all of the soil tensions were accurate enough for most applications, except for the measured unsaturated soil hydraulic at a tension of 0.1 m and to some extent at a tension of 0.03 m, which were less accurate than the other unsaturated soil hydraulic predictions.
Neshat and Farhad (2012) carried out an experiment, using calculations to estimate the unsaturated hydraulic conductivity of a soil, to derive a relationship between the soil's unsaturated hydraulic conductivity and its physical properties. Amer et al. (2009) proposed an equation to predict unsaturated hydraulic conductivity based on water viscosity, acceleration due to gravity, water density, ratio of total volume of pores, and the radius of equivalent cylindrical pore size. To predict the unsaturated hydraulic conductivity of soil, Moosavi and Sepaskhah (2012b) used an artificial neural network model with input parameters of sand, silt, clay, bulk density, soil organic matter, and initial and saturated volumetric water content. The study results showed that an artificial neural network model could accurately estimate the unsaturated hydraulic conductivity, and silt, clay, sand, bulk density, and soil organic matter were the most influential input variables.
Water quality has substantial effects on soil hydraulic conductivity and infiltration (Crescimanno et al., 1995; Springer et al., 1999). Xiao et al. (1992) studied the effect of irrigation water quality on the unsaturated hydraulic conductivity of undisturbed soil in the field. Results showed that, within the operating soil suction range of disc permeameters (0-1.6 KPa), the higher the electrical conductivity of irrigation water, the higher the soil unsaturated hydraulic conductivity. Unsaturated hydraulic conductivity doubled when the electrical conductivity of irrigation water increased from 0.1 to 6.0 dS·m−1. Also, a high irrigation water sodium adsorption ratio (SARw) has an inverse effect on soil unsaturated hydraulic conductivity. Soil unsaturated hydraulic conductivity decreased with increasing SARw, especially when higher soil suction is present. Moosavi and Sepaskhah (2012c) reported that irrigating with low-quality water may change soil hydraulic properties due to excessive electrical conductivity and water sodium-adsorption ratio. Field experiments were performed with applied soil water tensions of 0-0.2 m to study water quality effects on hydraulic properties of a sandy clay loam soil. The mean unsaturated hydraulic conductivity varied as quadratic or power equations with changes in water electrical conductivity and water SARw, and application of water with a higher electrical conductivity and increased sodium absorption ratio led to lower hydraulic conductivity volumes as the applied tension was increased. The findings indicated that in these types of soils the use of saline waters with an electrical conductivity < 10 dS·m−1 can improve soil hydraulic properties.
With in-situ infiltration measurements via a mini disk infiltrometer, Schacht and Marschner (2015) studied the impact of treated wastewater versus fresh water on hydraulic conductivity of agricultural irrigation. The study reported that the mean hydraulic conductivity values decreased at all treated wastewater sites by 42.9-50.8%, compared with fresh water irrigation sites. Singh et al. (2017) also indicated that the water quality has an effect on the soil infiltration rate, which can be predicted based on cumulative time, the type of impurities in the water, the concentration of impurities in the water, and soil moisture content, by random forest regression.
Soil moisture content and soil bulk density have significant effects on soil unsaturated hydraulic conductivity. Bhatnagar et al. (1979) determined unsaturated hydraulic conductivity in the laboratory for some red and black soils, following water movement into a horizontal column of homogenous soil with uniform packing. A highly significant positive relationship was found between moisture content and hydraulic conductivity values in all soils studied. It was also concluded that the unsaturated hydraulic conductivity decreases rapidly with a decrease in moisture content; this decrease depends on the soil constituents and properties, and differences between soil types were clear. However, the effect of compaction on unsaturated hydraulic conductivity was not consistent. At the same water content value, unsaturated hydraulic conductivity was sometimes higher or lower in the compacted soil samples, compared with uncompacted soil (Andrade, 1971). In another study, the unsaturated hydraulic conductivity decreased with increasing bulk density (Dec et al., 2008).
Unsaturated flow should be estimated precisely, as its evaluation has important implications for transient infiltration processes due to the high nonlinearity of soil water characteristics. However, the methods available to obtain soil hydraulic parameters can be difficult and time-consuming to implement in practice (Angulo-Jaramillo et al., 2000). Thus, researchers have been developing analytical and numerical methods to calculate parameters that are difficult to measure in the field (Mollerup et al., 2008). Predictive data mining algorithms enable the estimation of unknown values based on patterns discovered from a database (MahaLakshmi, 2012). The main aim of the data mining process is to retrieve the data from a dataset and transform it into a more meaningful form with the help of algorithms (Jamil, 2016). Elbisy (2006) applied artificial neural network models (feed-forward back propagation, and radial basis function, RBF) to predict the field-saturated soil hydraulic conductivity of sandy soil based on basic saline and alkaline soil data. The results indicated that the back propagation neural network is more accurate than the RBF neural network. Moreover, the support vector machine methodology was successfully applied to develop pedo-transfer functions (PTFs) that used different input predictors to estimate soil hydraulic parameters (Twarakavi et al., 2009). Elbisy (2015) explored the use of data mining algorithms (support vector machine) to predict the field saturated soil hydraulic conductivity of sandy soil, based on basic soil properties of saline and alkaline soil datasets. Data inputs were hydraulic conductivity, clay/silt ratio, liquid limit, hydrocarbonate anions, chloride ions, and calcium carbonate content. The influence of three kernel functions (linear, radial basis, and sigmoid) on the performance of the support vector machine model (SVM) was investigated using field data. The radial basis model performed satisfactorily, with a modelling efficiency of 0.972 and a correlation coefficient of 0.976. The excellent performance of the support vector machine (SVM) with the radial basis model (RBF) demonstrated its potential as a useful tool for the indirect estimation, with maximum obtainable prediction accuracy, of soil hydraulic conductivity of sandy soil.
Sihag et al. (2017) predicted the unsaturated hydraulic conductivity of soil using adaptive neuro fuzzy inference system (ANFIS), multi-linear regression (LR), and artificial neural network (ANN). Laboratory experiments were carried out on 46 samples of sand, rice husk ash and fly ash mixture. The results suggest improved performance by Gaussian membership function than triangular and generalized bell-shaped membership-based ANFIS. LR is better than ANN and Gaussian membership function-based ANFIS for unsaturated hydraulic conductivity. Sihag (2018) developed fuzzy logic and ANN-based models for estimating the unsaturated hydraulic conductivity of soil. A mini disk infiltrometer is useful for determining infiltration characteristics. The mini disk infiltrometer (Decagon Devices, Inc.) at a suction rate (pressure head) varying from 1 to 6 cm was used to determine the unsaturated hydraulic conductivity of soil of sandy soil. All the measurements were done on predetermined initial condition of different proportions of rice husk ash and fly ash mixed with sand. For modelling, randomly selected (70%) data was applied for training and residual (30%) for the test. The prediction with ANN approach works well, with a correlation coefficient value of 0.8662 (RMSE, 4.5607 cm·h−1).
The increasing availability of large quantities of management data in agricultural activities enables data-driven approaches, which are gaining attention. There are various ways data-driven techniques can be applied, and each incorporates different assumptions about the nature of the underlying processes. Gaussian process regression (GPR) is a probabilistic and non-parametric model (Azman and Kocijan, 2007) and hence can model complex systems whilst handling uncertainty in a principled manner (Richardson et al., 2017). GPR has good nonlinear mapping ability. It can reflect the inherent nonlinearity, avoid the deficiency of traditional methods in nonlinearity, and can improve the accuracy and reliability of predictive results, thus making it an effective method to improve predictive accuracy (Dingwen, 2012). Gaussian process regression (GPR) has been successfully adopted for solving different problems. It was employed for predicting soil electrical resistivity based on soil thermal resistivity, percentage sum of the gravel and sand size fractions, and degree of saturation. The developed GPR was compared with an artificial neural network. The results showed that GPR is an efficient tool for predicting soil electrical resistivity (Samui, 2014). Moreover, GPR has been used for predicting stream water temperature. The proposed approach was compared with traditional modelling schemes on measurements obtained from the Drava River, Croatia. The presented methodology can be used as a basis for predictive tools for water resource managers (Grbić et al., 2013). In addition, in the study of Holman et al. (2014), GPR was employed for estimating reference crop evapotranspiration from alternative meteorological data sources and results showed that GPR models provide much greater accuracy than baseline least-square regression models. Sihag et al. (2018) applied the artificial neural network (ANN) approach to estimate the infiltration rate of the soil. The performance of ANN was employed with other types of artificial intelligence approaches (GPR, gene expression programming (GEP)), and generalized neural network (GRNN)). The GPR, GRNN, and GEP models provided good estimation performance, but the ANN model performed better than these types of artificial intelligence approaches (correlation coefficient of up to 0.9816). Vand et al. (2018) applied diverse infiltration models using support vector machine, GPR, and multiple linear approaches to predict the infiltration rates of some Iranian fields. The study concluded that the Pearson VII kernel function performed well in comparison to radial basis kernel function, in both support vector machine as well as GPR, in predicting the infiltration rate of soil.
Hence, in this study, field experiments using different water qualities were conducted to collect data that represent the unsaturated hydraulic conductivity of sandy loam soil. This field data was used for modelling the unsaturated hydraulic conductivity of the soil based on water and soil properties (i.e., electrical conductivity and the sodium-adsorption ratio of the irrigation water, soil moisture content, soil bulk density, and suction rate). In particular, this study aimed to analyse the performance of Gaussian process regression (GPR) in predicting unsaturated hydraulic conductivity. A multiple linear regression (LR) and a multi-layer perceptron (MLP) model were also used as baseline for comparison with the Gaussian process regression (GPR) model.
MATERIALS AND METHODS
Soil and water sample characteristics
Experiments were conducted in a field located in Huraimla Governorate, Riyadh, Saudi Arabia (coordinates: ٢٥.١١° N, ٤٦.١٢°E, captured using a Garmin GPS 60 with positional accuracy < 15 m). Three soil samples were taken from the top 20 cm of the soil. Soil samples were analysed in the laboratory of the Soil Department, College of Food and Agriculture Sciences, King Saud University, Riyadh, Saudi Arabia. The experimental field was classified as sandy loam soil, with sand content of 67%, silt content of 28% and clay content of 5%, organic matter of 1.95%, soil electrical conductivity of 2.65 dS·m−1, and soil pH of 8.9. The soil water content (%, dry basis (db)) during field experiments was measured using an electric oven for 24 h at 105°C. Soil bulk density was calculated based on dried soil mass and volume of the core sample.
Eight water samples were analysed by the Inspection, Diagnosis, and Analysis Lab Company (IDAC), Medical Biology Analytical Laboratories, Riyadh, Saudi Arabia to get the characteristics of water samples, such as Ca, Mg, Na, HCO3, Cl, SO4, pH and water electric conductivity (ECw). Sodium-adsorption ratio (SARw) in (meq·L−1)1/2 (Mohamed, 2017), a measure of the sodicity of water, is determined as follows (Suarez et al., 2008):

where Na+, Ca++, and Mg++ represent concentrations of sodium, calcium, and magnesium, respectively, expressed in milliequivalents per litre (meq·L−1).
Table 1 shows the chemical characteristics of water samples, electrical conductivity (ECw), sodium adsorption ratio (SARw), and pH of irrigation water used in the field experiments to study the interaction effect of irrigation water and sandy loam soil.
Measurement of unsaturated soil hydraulic conductivity
The unsaturated hydraulic conductivity was measured using a mini disk infiltrometer (MDI, Decagon Devices Inc., Pullman, Washington, USA). It consists of two chambers (water reservoir and bubble chamber), connected via a Mariette tube to provide a constant water pressure head of −0.5 to −7 cm (equivalent to −0.05 to −0.7 kPa). The bottom of the MDI contains a porous sintered steel disk. The water-filled tube is placed on the soil surface, resulting in water infiltrating into the soil, with the volume of water and speed of infiltration dependent on the sorptivity and hydraulic conductivity of the soil. Pressure heads (suction rates) of −1, −2, −3, −4, −5, and −6 cm were chosen for this study. At all test sites, the infiltration tests were conducted without any modification of the soil surface nor addition of water; similar soil water content and soil bulk density were observed in all undisturbed spots, and no rainfall occurred during the test period. The mini disk infiltrometer (MDI) measurements (Fig. 1) were taken 7 times for each water quality, and the average value used.

The respective measuring spots were typically several metres apart. During the measurement, the volume of the water in the reservoir chamber was documented at regular intervals. Infiltration was computed using Eq. 2, from the cumulative infiltration records versus time following Zhang (1997), Carsel and Parrish (1988), and Decagon Devices Inc. (2012) recommendations.

where I is the cumulative infiltration (cm), t is the time (s), and C1 (cm·s−1) and C2 (cm·(s−1)−0.5) are parameters. C1 is related to hydraulic conductivity and C2 is related to soil sorptivity. The hydraulic conductivity (Ki) of the soil is then computed from Eq. 3.

where C1 is the slope of the curve of the cumulative infiltration versus the square root of time and (A) is a value relating the Van Genuchten parameters for a given soil type to the suction rate and radius of the infiltrometer disk. The values of A can be calculated by Eq. 4 and Eq. 5 (Carsel and Parrish, 1988).

where n and α are the Van Genuchten parameters for the soil, r0 is the disk radius and ho is the suction at the disk surface. The Van Genuchten parameters for the 12 texture classes were obtained from Carsel and Parrish (1988). Sporadically occurring negative values for hydraulic conductivity indicate unsteadiness of the particular measurement and were ignored in the further calculation (Schacht and Marschner, 2015).
Datasets
The collected dataset contains a total of 48 field measurement instances having 4 attributes. The data were randomized, and the Waikato environment for knowledge analysis (WEKA) tool was used to obtain a percentage of the data for building the model (85%, 41 points), and the rest (15%, 7 points) were used for testing. The input variables in this study are SARw, ECw, soil moisture content, soil bulk density, and suction rate. Descriptive statistics for input and output variables are shown in Table 2 for the entire dataset.
Predictive data mining techniques examined in this research
The predictive data mining techniques examined in this research were Gaussian process regression, linear regression, and the multi-layer perceptron neural networks, and simulations were done using the WEKA open-source tool (Garner, 1995). The WEKA machine learning workbench provides an environment for automatic classification, regression, clustering, and common data mining problems in bioinformatics research. It has a user-friendly graphical interface to compare the various algorithm results (Frank et al., 2004). In the training phase, a model is constructed from the training instances selected by WEKA and in the testing phase, the model is used to assign a label to an unlabelled test instance.
Linear regression (LR) model
Linear regression analyses the relationship between several input variables, and a straight line is fitted to the input variables in the best manner possible. With a good fit, a linear regression model can be used to predict future values of the output variable. WEKA performs standard least-squares linear regression and implements ridge regression (Witten and Frank, 2005). Ridge regression is used to solve problems that are not well-posted, meaning that problems will have weak stability of algorithms to be solved (Wormstrand, 2011). In WEKA, a fixed small ridge parameter of 1.00 × 10−08 was used, and no attribute selection criterion was designated to perform linear regression.
Multi-layer perceptron (MLP) model
The MLP is an optimum feed-forward artificial neural network (ANN), trained with the back-propagation algorithm, that consists of neurons with substantially weighted interconnections where signals always travel in the direction of the output layer. These neurons are mapped as sets of input data onto a set of proper outputs with hidden layers (Turkan et al., 2016). The input signals are sent by the input layer to the hidden layer without executing any operations. Then, the hidden and output layers multiply the input signals by a set of weights, and either linearly or non-linearly transform the results into output values. The connection between units in following layers has an associated weight (Turkan et al., 2016), and these weights are optimized to compute reasonable prediction accuracy (Elish, 2014; Lek and Park, 2008). A typical MLP with one hidden layer can be described mathematically as follows (Turkan et al., 2016):

Equation 6 defines summing products of the inputs (Xi) and weight vectors (aij) and a bias term of hidden layer (a0j). Also, in Eq. 7, the outputs of hidden layer (Z j) are obtained by transforming this sum, defined in Eq. 6, by using the activation function g.

The most widely used activation function is the sigmoid function (Karlik and Olgac, 2011), defined in Eq. 8 for the input x. The hidden and output layers are based on this sigmoid function.

Eq. 9 defines summing the products of the hidden layer's outputs (Zj) and weight vectors (bjk) and the bias term of the output layer (bk0).
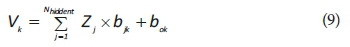
In Eq. 10, the outputs of the output layer (Yk) are obtained by transforming the sum calculated in Eq. 9, and using the sigmoid function g, defined in Eq. 8.

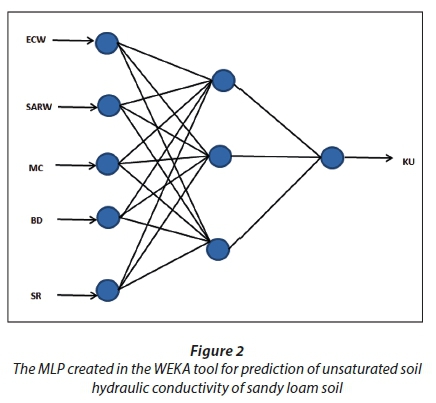
Figure 2 shows the MLP created in the WEKA tool and applied as an artificial neural network (ANN) based on the multilayer perceptron (MLP) algorithm in this study. The same dataset was used as in the linear regression (LR) run. A neural net with 3 nodes in the hidden layer was created by WEKA, as shown in Fig. 2. The neural net was trained for 500 epochs; with a learning rate of 0.3 and a momentum of 0.2 (the WEKA defaults). The number of epochs gives how long the neural net will run, while the learning rate and momentum indicate how the weights are adjusted (Wormstrand, 2011). The error per epoch was 8.2743 × 10−03 cm·s−1
Gaussian process
A Gaussian process is a collection of random variables, where any Gaussian process finite number has a joint Gaussian distribution (Rasmussen, 2003). A Gaussian process is completely specified by its mean function, and covariance and variance functions (Rasmussen and Williams, 2006). The details of GPR were obtained from Rasmussen (2003). Based on Samui and Jagan (2013) and Saini and Chandramouli (2013), the following noise dataset can be considered by Eq. 11.

where x is input, y is output and N is the number of data points. In this study, ECw, SARw, SR, MC and BD are used as input variables for the GPR. The output of GPR is χ. So, x value can be calculated by Eq. 12.

It is assumed that the above data are generated from Eq. 13:

where ε is the Gaussian noise term, ξ is Gaussian distribution (zero mean, variance σ2).
The joint distribution of Y is given by Eq. 14:

where K(x, x) is the kernel function and I is the identity matrix.
For a test input x*, GPR defines a Gaussian predictive distribution over the output y* with mean determined by Eq. 15 and variance by Eq. 16.

where T is the transpose.
To develop the GPR model, a suitable covariance function is required. In this study, the 4 kernel functions available in WEKA are used: the normalized polynomial kernel, the polynomial kernel, the RBF kernel, and the Pearson VII kernel.
Criteria for evaluating the accuracy of the selected predictive models
Experimentally, this study evaluated and compared the prediction accuracy of the selected predictive models based on three performance measurements frequently used in previous studies: correlation coefficient (r), root mean square error (RMSE), and mean absolute error (MAE). These performance measurements are formulated as shown in Table 3, with optimal values. Yi is the observed unsaturated soil hydraulic conductivity, the predicted unsaturated soil hydraulic conductivity is Ŷi, Yu is the mean of the observed unsaturated soil hydraulic conductivity, Yo is the mean of the predicted unsaturated soil hydraulic conductivity, and Nt is the number of data points in the testing dataset.

RESULTS
Water data analysis
The data were visualized using the WEKA tool. Table 1 shows high variations (CV) in water quality parameters for Ca, Mg, Na, HCO3, Cl, and SO4, of 44, 51, 49, 45, 34, and 69%, respectively. The investigated water bicarbonate (HCO3) content ranged from 2.09 to 8.00 meq·L−1, chloride content (Cl) ranged from 5.89 to 19.48 meq·L−1, and sulfate contents (SO4) ranged from 4.09 to 27.04 meq·L−1. The pH of the investigated water ranged from 6.83 to 8.20, with a mean value of 7.55 (Table 1). As shown in Table 2, SARw values in this study ranged from 2.46-5.92 (meq·L−1)1/2, with a mean of 4.21 (meq·L−1)1/2, water electrical conductivity ranged from 1.32-4.72 dS·m−1, with a mean of 2.66 dS·m−1, soil moisture content (MC) values ranged from 8.34-14.16% db, with a mean of 11.25% db, soil bulk density (BD) values ranged from 1.42-1.67 g·cm−3, with a mean of 1.58 g·cm−3, and observed unsaturated soil hydraulic conductivity values ranged from 1.15 × 10−08 to 2.34 × 10−03 cm·s−1, with a mean of 6.87 × 10−04 cm·s−1 (Table 2).
The WEKA linear regression model result for unsaturated soil hydraulic conductivity is calculated by Eq. 17.

where KU is unsaturated hydraulic conductivity of a sandy loam soil (cm·s−1), ECw is electrical conductivity of irrigation water (dS·m−1), SARw ((meq·L−1)1/2) is sodium adsorption ratio of irrigation water calculated based on the concentrations of Na, Ca, and Mg expressed in milli-equivalents per litre (meq·L−1), MC is soil moisture content (% db), BD is soil bulk density (g·cm−3) and SR is suction rate (pressure head, cm).
It can be seen from Eq. 17 that unsaturated hydraulic conductivity increases with increasing ECw and decreases with increasing SARw; these findings are in agreement with those obtained by Moosavi and Sepaskhah (2012c) , who indicated that use of saline waters with an ECw of < 10 dS·m−1 can improve soil hydraulic properties in sandy clay loam soils and that irrigation waters with SARw < 20 (meq·L−1)1/2 may not adversely affect hydraulic attributes when the water is first applied; although higher SARw may negatively affect them. Andrade (1971) reported a very large decrease in soil hydraulic conductivity as water content decreased, and that the effect of compaction on unsaturated hydraulic conductivity (KU) was not consistent and at the same value of water content; unsaturated hydraulic conductivity was sometimes higher in the compacted samples. However, the positive correlation between KU and BD in this study can be attributed to the KU measurements, taken on undistributed soil with different soil moisture content. Also, in this study, the unsaturated soil hydraulic conductivity decreased with increased suction rate (SR), and this finding was in agreement with those obtained by Moosavi and Sepaskhah (2012c), Simunek et al. (1999) and Matula et al. (2015).
DISCUSSION
According to the water quality analysis, HCO3 may not cause irrigation problems, as its concentration was within the range of recommended guidelines for irrigation water quality, of 0-10 meq·L−1 (Ayers and Westcot, 1994; Shahinasi and Kashuta, 2008). Also, chloride content was within tolerance for irrigation water, under the recommended limit of 30 meq·L−1. Although the sulfate concentrations in the study area vary considerably, only 6 water samples fell within the acceptable limits of 0-20 meq·L−1 for irrigation water. W7 and W8 exceed sulfate concentration limits, with values of 22 meq·L−1 and 27.04 meq·L−1, respectively, (Table 1). The pH values were within the permissible limit for irrigated agriculture water, 6.5-8.4 (Ayers and Westcot, 1994). Hence, the investigated water presented no restrictions for irrigation use.
The two most common water quality factors which influence the movement of water into soil (infiltration) are salinity and the sodium content relative to the Ca and Mg content. High salinity water will increase infiltration. Low salinity water, or water with high Na to Ca and Mg ratio, will decrease infiltration. Both factors can operate concurrently. The infiltration rate generally increases with increasing salinity and decreases with either decreasing salinity or increasing Na content relative to Ca and Mg. Therefore, the two factors, salinity and SAR, provide information on the ultimate effect of the water quality on the water infiltration rate (Nata et al., 2009). On almost all soils, the range of water SAR that can be used for irrigation, with a low risk of the emergence of harmful levels of exchangeable Na, is 0-10 (Ayers and Westcot, 1994).
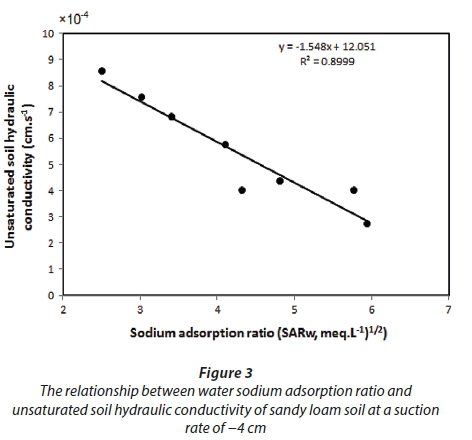
To study the impact of SARw on unsaturated soil hydraulic conductivity of a sandy loam soil, a pressure head of −4 cm was employed as a mean value. Figure 3 shows the relationship between SARw and unsaturated soil hydraulic conductivity of sandy loam soil at a suction rate of −4 cm. It is clear that unsaturated soil hydraulic conductivity decreased linearly, with high correlation (R2 = 0.8999) with an increase of SARw, and this finding agrees with data presented by Xiao et al. (1992). Figure 4 illustrates the relationship between suction rate and unsaturated soil hydraulic conductivity of sandy loam soil at SARw of 2.46 (meq·L−1)1/2 (ECw was 4.72 dS∙m−1, average MC and BD were 12.12% db and 1.63 g·cm−3, respectively). A polynomial relationship was found, with R2 of 0.9698; the unsaturated soil hydraulic conductivity decreased with increase of suction rate (Fig. 4) and this finding agrees with data presented by Moosavi and Sepaskhah (2012c), Simunek et al. (1999) and Matula et al. (2015).

Prediction model performance
The objective of a learning algorithm is to develop a model with good generalization, so there can be a suitable practical model (Munir and Winarko, 2015). Table 4 shows the WEKA information and kernel used in the GPR model. Also, Fig. 5 shows the time spent building each of the selected predictive models. The GPR-Pearson VII kernel function model with a cache size of 250007, Omega of 1.0, and Sigma of 1.0 took the least time to build compared with other kernels.

The measured performance of the prediction models in terms of r, RMSE, and MAE, for all testing data, is presented in Table 5, which shows that all the listed models had good prediction performance. The RMSE statistics indicate only the model's ability to predict away from the mean. The MAE is the most natural and unambiguous measure of the average error magnitude. It appears that all the dimensioned evaluations and inter-comparisons of average model performance error should be based on the MAE (Elbisy, 2015). Considering both the MAE and RMSE criteria in the testing phase, the GPR model that was based on the GPR-Pearson VII kernel function obtained the highest prediction accuracy for unsaturated hydraulic conductivity of sandy loam soil. Furthermore, this function model achieved the best prediction accuracy based on all three performance measures. Depending on what settings were applied to the developed MLP, the results varied. The developed MLP is not optimally tuned, meaning that further runs with the MLP settings could improve the performance by finding better-suited local minima. Table 5 also shows the correlation coefficients related to the kernel function of the GPR model. It is clear that the Pearson VII kernel function (PUK) yielded higher correlation coefficient (0.9646) than other kernels.
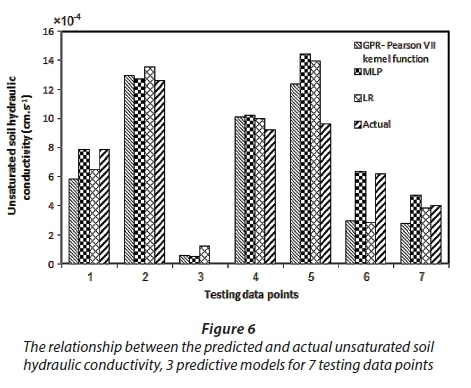
Figure 6 illustrates the relationship between the predicted and actual unsaturated soil hydraulic conductivity for all predictive models for 7 testing data points. The figure shows fair relationships between predicted and actual values. Apparently, the GPR-Pearson VII kernel function gives the best representation of actual experimental data, with the highest R2 at 0.9646 (Table 5). This approach provides great prediction capacity and does not require knowledge of the input parameters, but its prediction capability is limited by the information content of the data.
CONCLUSIONS
This research was mainly conducted to evaluate the potential for using data mining techniques for predicting the unsaturated hydraulic conductivity of a sandy loam soil based on water and soil properties. In particular, data mining algorithms of Gaussian processes, artificial neural network based on multilayer perceptron (MLP), and linear regression were generated and individually tested. The analytical results suggest that all of the tested models can provide good prediction accuracy, with correlation coefficients (r) ranging from 0.9162 to 0.9646. The Gaussian processes regression model with Pearson VII kernel function showed the best prediction accuracy as an individual data mining model. With the demonstrated potential of using data mining models to predict the unsaturated hydraulic conductivity of a sandy loam soil, future research can adopt this approach to study other variables in the field of managing water and solute transport in soils that cannot be more easily measured.
ACKNOWLEDGEMENTS
With sincere respect and gratitude, all would like to express deep thanks to Deanship of Scientific Research and Researchers Support Services Unit at the King Saud University for their technical support.
REFERENCES
AMER AM, LOGSDN SD, and DAVIS D (2009) Prediction of hydraulic conductivity in unsaturated soils. Soil Sci. 174 (9) 508-515. https://doi.org/10.1097/SS.0b013e3181b76c29 [ Links ]
ANDRDE RB (1971) The influence of bulk density on the hydraulic conductivity and water content-matric suction relation of two soils. Master's thesis, Utah State University, Logan, Utah. URL: https://digitalcommons.usu.edu/etd/2971 (Accessed 10 November 2017). [ Links ]
ANGULO-JARAMILL R, VANDERVAERE JP, ROULIER S, THONY JL, GAUDET JP and VAUCLIN M (2000) Field measurement of soil surface hydraulic properties by disc and ring infiltrometers. A review and recent developments. Soil Tillage Res. 55 (1-2) 1-29. https://doi.org/10.1016/S0167-1987(00)00098-2 [ Links ]
AYERS RS and WESTCOT DW (1994) Water quality for agriculture. FAO Irrigation and Drainage Paper 29 Rev. 1. FAO, Rome. [ Links ]
AZMAN K and KOCIJAN J (2007) Application of Gaussian processes for black-box modelling of biosystems. ISA Trans. 46 (4) 443-57. https://doi.org/10.1016/j.isatra.2007.04.001 [ Links ]
BHATNAGAR D, NAGARAJARAO Y and GUPT RP (1979) Influence of water content and soil properties on unsaturated hydraulic conductivity of some red and black soils. J. Plant Nutr. Soil Sci. 142 99-108. [ Links ]
CARSEL RF and PARRISH RS (1988) Developing joint probability distribution of soil water retention characteristics. Water Resour. Res. 24 755-769. https://doi.org/10.1029/WR024i005p00755 [ Links ]
CRESCIMANNO G, IOVINO M and PROVENZANO G (1995) Influence of salinity and sodicity on soil structural and hydraulic characteristics. Soil Sci. Soc. Am. J. 59 1701-1708. https://doi.org/10.2136/sssaj1995.03615995005900060028x [ Links ]
DEC D, DÖRNER J, BECKER-FAZEKAS O and HORN R (2008) Effect of bulk density on hydraulic properties of homogenized and structured soils. J. Soil Sci. Plant Nutr. 8 (1) 1-13. [ Links ]
DECAGON DEVICES (2012) Minidisk Infiltrometer. User's manual. URL: www.decagon.com. 26 pp. [ Links ]
DINGWEN D (2012) Mine gas emission prediction based on Gaussian process model. Procedia Eng. 45 334-338. https://doi.org/10.1016/j.proeng.2012.08.167 [ Links ]
ELBISY MS (2006) Prediction of saturated hydraulic conductivity of sandy soil using neural network. Ain Shams Eng. J. Ain Shams Univ. 41 (1) 480-493. [ Links ]
ELBISY MS (2015) Support Vector Machine and regression analysis to predict the field hydraulic conductivity of sandy soil. KSCE J. Civ. Eng. 19 (7) 2307-2316. https://doi.org/10.1007/s12205−015−0210-x [ Links ]
ELISH MO (2014) A Comparative Study of Fault Density Prediction in Aspect-oriented Systems using MLP, RBF, KNN, RT, DENFIS and SVR Models. Artif. Intell. Rev. 42 (4) 695-703. https://doi.org/10.1007/s10462−012-9348-9 [ Links ]
FATEHNIA M, TAWFIG K and ABICHOU T (2014) Comparison of the methods of hydraulic conductivity estimation from mini disk infiltrometer. Electron. J. Geotech. Eng. 19 (E) 1047-1063. [ Links ]
FRANK E, HALL M, TRIGG L, HOLMES G and WITTEN IH (2004) Data mining in bioinformatics using Weka. Bioinform. Appl. Note 20 (15) 2479-2481. https://doi.org/10.1093/bioinformatics/bth261 [ Links ]
GARNER SR (1995) WEKA: The Waikato Environment for Knowledge Analysis. In: Proc. New Zealand Computer Science Research Students Conference 1995. 57-64. [ Links ]
GONÇALVES RAB, FOLEGATTI MV, GLOAGUEN TV, LIBARDI PL, MONTES CR, LUCAS Y, DIAS CTS and MELFI AJ (2007) Hydraulic conductivity of a soil irrigated with treated sewage effluent. Geoderma 139 241-248. https://doi.org/10.1016/j.geoderma.2007.01.021 [ Links ]
GRBIĆ R, KURTAGIĆ D and SLIŠKOVIĆ D (2013) Stream water temperature prediction based on Gaussian process regression. Expert Syst. Appl. 40 7407-7414. https://doi.org/10.1016/j.eswa.2013.06.077 [ Links ]
HOLMAN D, SRIDHARAN M, GOWDA P, PORTER D, MAREK T, HOWELL T and MOORHEAD J (2014) Gaussian process models for reference ET estimation from alternative meteorological data sources. J. Hydrol. 517 28-35. https://doi.org/10.1016/j.jhydrol.2014.05.001 [ Links ]
JAMIL LS (2016) Data analysis based on data mining algorithms using WEKA workbench. Int. J. Eng. Sci. Res. Technol. 5 (8) 262-267. [ Links ]
KARLIK B and OLGAC AV (2011) Performance analysis of various activation functions in generalized MLP architectures of neural networks. Int. J. Artif. Intell. Expert Syst. 1 (4) 111-122. [ Links ]
KLUTE A and DIRKSEN HE (1989) Hydraulic conductivity and diffusivity: laboratory methods. In: Klute A (ed.) Method of Soil Analysis. Part 1. American Society of Agronomy, Madison, Wisconsin. pp. 687-734. [ Links ]
LEK S and PARK YS (2008) Multilayer perceptron. In: Jorgensen SE and Fath B (eds) Encyclopedia of Ecology. Academic Press, Oxford. 2455-2462. https://doi.org/10.1016/B978−008045405-4.00162-2 [ Links ]
MAHALAKSHIMI R (2012) A Comparative analysis on persuasive meta classification strategy for web spam detection. Int. J. Comput. Sci. Inf. Technol. Secur. (IJCSITS) 2 (4) 778-782. [ Links ]
MALAYA C and SREEDEEP S (2013) Correlation between grain size distribution curve and unsaturated hydraulic conductivity curve of soils. In: Proc. Indian Geotechnical Conf., 22-24 December 2013, Roorkee. [ Links ]
MATULA S, MIHÁLIKOVÁ M, LUFINKOVÁ J and BÁŤKOVÁ K (2015) The role of the initial soil water content in the determination of unsaturated soil hydraulic conductivity using a tension infiltrometer. Plant Soil Environ. 61 515-521. https://doi.org/10.17221/527/2015-PSE [ Links ]
MBONIMPA M, BÉDARD C, AUBERTIN M and BUSSIÈRE B (2004) A model to predict the unsaturated hydraulic conductivity from basic soil properties. In: Proceedings, 5th Joint CGS/IAH-CNC Conference, 57th Canadian Geotechnical Conference, 2004, Montreal, Quebec, Canada. pp. 16-23 [ Links ]
MENNEER JC, MCLAY CDA and LEE R (2001) Effects of sodium-contaminated waste water on soil permeability of two New Zealand soils. Aus. J. Soil Res. 39 (4) 877-891. https://doi.org/10.1071/SR99082 [ Links ]
MOHAMED AI (2017) Irrigation water resources and suitability for crops in Egypt. Merit Res. J. Agric. Sci. Soil Sci. 5 54-53. [ Links ]
MOLLERUP M, HANSEN S, PETERSEN C and KJAERSGAARD JH (2008) A MATLAB program for estimation of unsaturated hydraulic soil parameters using an infiltrometer technique. Comput. Geosci. 34 (8) 861-875. https://doi.org/10.1016/j.cageo.2007.12.002 [ Links ]
MOOSAVI AA and SEPASKHAH AR (2012a) Pedotransfer functions for prediction of near saturated hydraulic conductivity at different applied tensions in medium texture soils of a semi-arid region. Plant Knowl. J. 1 1-9. https://doi.org/10.1080/03650340.2010.512289 [ Links ]
MOOSAVI AA and SEPASKHAH AR (2012b) Artificial neural networks for predicting unsaturated soil hydraulic characteristics at different applied tensions. Arch. Agron. Soil Sci. 58 (2) 125-153. https://doi.org/10.1080/03650340.2010.512289 [ Links ]
MOOSAVI AA and SEPASKHAH AR (2012c) Determination of unsaturated soil hydraulic properties at different applied tensions and water qualities. Arch. Agron. Soil Sci. 58 (1) 11-38. https://doi.org/10.1080/03650340.2010.503956 [ Links ]
MUNIR AQ and WINARKO E (2015) Classification model disease risk areas endemicity dengue fever outbreak based prediction of patients, death, IR and CFR using forecasting techniques. Int. J. Comput. Appl. 114 (2) 21-25. [ Links ]
NATA T, BHEEMALINGESWARA K and BERHANE A (2009) Groundwater suitability for irrigation: a case study from Debre Kidane Watershed, Eastern Tigray, Ethiopia. Momona Ethiopian J. Sci. 1 (1) 36-58. [ Links ]
NESHAT A and FARHAD M (2012) A presentation of an experimental model for unsaturated hydraulic conductivity under affection of physical properties of Soil: A case-by-case study of Baghin Plain in Kerman, Iran. Acad. J. Plant Sci. 5 (3) 70-75. [ Links ]
RASMUSSEN CE (2003) Gaussian processes in machine learning. In: Bousquet O, Von Luxburg U, Rätsch G (eds) Advanced Lectures on Machine Learning. ML Summer Schools 2003, Canberra, Australia, February 2-14 2003, Tübingen, Germany, August ٤-16, 2003, Revised Lectures. 63-71 [ Links ]
RASMUSSEN CE and WILLIAMS CKI (2006) Gaussian Processes for Machine Learning. MIT Press, Cambridge, MA. 272 pp. [ Links ]
RICHARDSON RR, OSBORNE MA and HOWEY DA (2017) Gaussian process regression for forecasting battery state of health. J. Power Sources 357 209-219. https://doi.org/10.1016/j.jpowsour.2017.05.004 [ Links ]
SAINI I and CHANDRAMOULI P (2013) Prediction of elastic modulus of high strength concrete by Gaussian Process Regression. Int. J. Sci. Eng. Res. 4 (5) 197-198. [ Links ]
SAMUI P (2014) Utilization of Gaussian process regression for determination of soil electrical resistivity. Geotech. Geol. Eng. 32 (1) 191-195. https://doi.org/10.1007/s10706−013-9705-8 [ Links ]
SAMUI P and JAGAN J (2013) Determination of effective stress parameter of unsaturated soils: A Gaussian process regression approach. Front. Struct. Civ. Eng. 7 (2) 133-136. https://doi.org/10.1007/s11709−013−0202−1 [ Links ]
SCHACHT K and MARSCHNER B (2015) Treated wastewater irrigation effects on soil hydraulic conductivity and aggregate stability of loamy soils in Israel. J. Hydrol. Hydromech. 63 47-54. https://doi.org/10.1515/johh-2015−0010 [ Links ]
SHAHINASI E and KASHUTA V (2008) Irrigation water quality and its effects upon soil. Tirana Agricultural University, Tirana, Albania BALWOIS 2008, Ohrid, Republic of Macedonia, 27, 31 May 2008. [ Links ]
SIHAG P (2018) Prediction of unsaturated hydraulic conductivity using fuzzy logic and artificial neural network. Model. Earth Syst. Environ. 4 (1) 189-198. https://doi.org/10.1007/s40808−018−0434−0 [ Links ]
SIHAG P, TIWARI NK and RANJAN S (2017) Prediction of unsaturated hydraulic conductivity using adaptive neuro-fuzzy inference system (ANFIS). ISH J. Hydraul. Eng. 2017 1-11. [ Links ]
SIHAG P, SINGH B, SEPAH VAND A and MEHDIPOUR V (2018) Modeling the infiltration process with soft computing techniques. ISH J. Hydraul. Eng. 2018 1-15. https://doi.org/10.1080/09715010.2018.1464408 [ Links ]
SIMUNEK J, WENDROTH O and VAN GENUCHTEN MT (1999) Estimating unsaturated soil hydraulic properties from laboratory tension disc infiltrometer experiments. Water Resour. Res. 35 2965-2979. https://doi.org/10.1029/1999WR900179 [ Links ]
SINGH P, SIHAG P and SINGH K (2017) Modelling of impact of water quality on infiltration rate of soil by random forest regression. Model. Earth Syst. Environ. 3 (3) 999-1004. https://doi.org/10.1007/s40808−017−0347−3 [ Links ]
SPRINGER G, WIENHOLD BJ, RICHARDSON JL and DISRUB LA (1999) Salinity and sodicity induced changes in dispersible clay and hydraulic conductivity in sulfatic soils. Comm. Soil Sci. Plant Anal. 30 2211-2220. https://doi.org/10.1080/00103629909370366 [ Links ]
SUAREZ DL, WOOD JD and LESCH SM (2008) Infiltration into cropped soils: Effect of rain and sodium adsorption ratio-impacted irrigation water. J. Environ. Qual. 37 (5) Supplement 169-179. [ Links ]
TURKAN YS, AYDOGMUS HY and ERDAL H (2016) The prediction of the wind speed at different heights by machine learning methods. Int. J. Optim. Control: Theor. Appl. 6 179-187. https://doi.org/10.11121/ijocta.01.2016.00315 [ Links ]
TWARAKAVI NKC, SIMUNEK J and SCHAAP MG (2009) Development of pedotransfer functions for estimation of soil hydraulic parameters using support vector machines. Soil Sci. Soc. Am. J. 73 1443-1452. https://doi.org/10.2136/sssaj2008.0021 [ Links ]
VAND AS, SIHAG P, SINGH B and ZAND M (2018) Comparative evaluation of infiltration models. KSCE J. Civ. Eng. 22 (10) 4173-4184. https://doi.org/10.1007/s12205−018−1347−1 [ Links ]
WITTEN IH and FRANK E (2005) Data Mining: Practical Machine Learning Tools and Techniques. Morgan Kaufmann Pub. Elsevier, San Francisco. [ Links ]
WORMSTRAND O (2011) Electricity price prediction A comparison of machine learning algorithms. Master's Thesis, Ostfold University Collage, Halden, Norway. [ Links ]
WOSTEN JHM and Van GENUCHTEN MTH (1988) Using texture and other soil properties to predict the unsaturated soil hydraulic functions. Soil Sci. Soc. Am. J. 52 1762-1770. https://doi.org/10.2136/sssaj1988.03615995005200060045x [ Links ]
XIAO ZH, PRENDERGAST B and RENGASAMY P (1992) Effect of irrigation water quality on soil hydraulic conductivity. Pedosphere 2 (3) 237-244. [ Links ]
ZHANG R (1997) Determination of soil sorptivity and hydraulic conductivity from the disk infiltrometer. Soil Sci. Soc. Am. J. 61 1024-1030. https://doi.org/10.2136/sssaj1997.03615995006100040005x [ Links ]
ZHUANG J, NAKAYAMA K YU GR and MIYAZAKI T (2001) Predicting unsaturated hydraulic conductivity of soil based on some basic soil properties. Soil & Tillage Res. 59 143-154. [ Links ]
Received 13 November 2017
Accepted in revised form 28 November 2018
* To whom all correspondence should be addressed. e-mail: nalsawiyan@ksu.edu.sa














