Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
Water SA
versión On-line ISSN 1816-7950
versión impresa ISSN 0378-4738
Water SA vol.44 no.4 Pretoria oct. 2018
http://dx.doi.org/10.4314/wsa.v44i4.13
ORIGINAL ARTICLES
Theoretical solution for analysis and design of hydraulic jump on corrugated bed
Jahanshir Mohammadzadeh-Habili*; Tooraj Honar
Department of Water Engineering, College of Agriculture, Shiraz University, 7194685115 Shiraz, Iran
ABSTRACT
A hydraulic jump mainly serves as an energy dissipator downstream of hydraulic structures. For analysis and design of a hydraulic jump on a corrugated bed, the specific energy curve was used: the maximum possible amount of energy dissipation of the hydraulic jump, the minimum possible value of sequent depth for the hydraulic jump, and efficiency of energy dissipation of a smooth hydraulic jump are theoretically related to the inflow Froude number. A wide range of existing experimental data from hydraulic jumps on smooth and corrugated beds was also used. Results of this study indicate that the energy dissipation of a hydraulic jump on a corrugated bed is mainly influenced by horizontal distance from the sluice gate section to the start point of the corrugated bed. To reach the maximum value of energy dissipation (i.e., minimum value of subcritical sequent depth) and the minimum value of jump length, the corrugated bed should start from the gate opening.
Keywords: hydraulic jump, corrugated bed, energy dissipation, specific energy curve, sluice gate
A hydraulic jump is a phenomenon caused by a change in flow regime from supercritical to subcritical, with a considerable amount of energy dissipation and a rise in flow depth. It mainly serves as an energy dissipator to dissipate the excess energy of supercritical flow downstream of spillways, sluice gates, drops, etc. A hydraulic jump formed in a smooth bed rectangular horizontal channel is usually named a classical hydraulic jump (Peterka, 1958; Rajaratnam, 1967; Hager, 1992). Subcritical sequent depth ratio of classical jump y2* /y1 can be related to the inflow Froude number F1 by the Bélanger equation (Hager and Bremen, 1989):
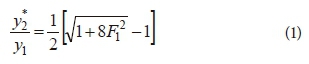
Hydraulic jumps have been extensively studied because of their frequent occurrence in nature and their use as an energy dissipator in outlet works of hydraulic structures (Carollo et al., 2007). A hydraulic jump can cause damage to the downstream bed and bank of the channel by a process of continuous erosion and degradation. In order to reduce the destruction caused by a hydraulic jump, larger energy dissipation along the hydraulic jump is required (Chern and Syamsuri, 2013). However, based on Chanson (2004), to avoid instabilities induced by near-critical flow condition, the Froude number of flow downstream of the hydraulic jump should not exceed 0.7. One method to increase dissipation of energy is to use a rough bed such as a corrugated bed. A hydraulic jump on a rough bed was first investigated by Rajaratnam (1968), who found that the jumps on rough beds were significantly shorter than the classical jumps.
For a hydraulic jump on a corrugated bed (Fig. 1), the corrugations act as depressions in the bed, to create a system of turbulent eddies which might increase the bed shear stresses (Ead and Rajaratnam, 2002). The toe of the jump usually adjusts at the start point of the corrugated bed. Influences of corrugation shape (triangular, trapezoidal, rectangular and sinusoidal), relative wave steepness t/s and roughness height t/y1 on hydraulic parameters of created jumps on corrugated beds have been studied by Ead and Rajaratnam (2002), Tokyay (2005), Yadav et al. (2007), Abbaspour et al. (2009a), Elsebaie and Shabayek (2010) and Samadi-Boroujeni et al. (2013), while influence of xc on jump properties has not yet been studied.
It can be concluded from these studies of hydraulic jumps on corrugated beds that if jumps were located on corrugated beds, there would be significant reductions in the required tailwater depth and jump length. The reason for the small required tailwater depth when creating a hydraulic jump on a corrugated bed is the increase in bed shear stresses, which can be attributed to the friction and exchange of momentum flux between the main flow and eddies trapped in the corrugations (Yadav et al., 2007). To avoid cavitation danger on corrugated beds, the crests of the corrugations should be at the level of the upstream bed that carries the supercritical flow and they should not protrude into the flow (Ead and Rajaratnam, 2002). The bottom shear stress in the sinusoidal corrugated beds is larger than that in triangular, trapezoidal and rectangular corrugated beds. This is the main reason for decreasing the length of jump for the sinusoidal corrugated bed (Chern and Syamsuri, 2013). Additionally, based on Mohammadzadeh-Habili et al. (2016), rounding the crest surface can reduce or eliminate the length of separation zone and reduce the cavitation danger. As a result, a corrugated bed with rounded corrugations, such as a sinusoidal corrugated bed, is preferred to the other shapes of corrugated beds. Results of Abbaspour et al. (2009a) indicate that t/s and t/y1 do not have a significant effect on different parameters of the hydraulic jump, including the sequent depth ratio, relative jump length and relative energy dissipation. This is due to the fact that the corrugations acted more like cavities and the influence of their dimensions is not important (Yadav et al., 2007).
To evaluate and design hydraulic jumps on a corrugated bed, the maximum possible amount of energy dissipation by hydraulic jump ΔEmax and therefore minimum possible value of sequent depth for hydraulic jump y2min for a given y1 are required. Despite the numerous studies of hydraulic jumps on corrugated beds, analytical expressions of ΔEmax and y2min have not yet been identified.
To study the effects of xc on properties of hydraulic jumps on a corrugated bed, to determine the maximum possible amount of energy dissipation, to determine the minimum possible value of required tailwater depth achievable by using corrugated bed, and to determine the optimum value for sequent depth of hydraulic jump on corrugated bed, this study uses a wide range of existing experimental data from hydraulic jumps on smooth and corrugated beds. Experimental data are then analysed by using the specific energy curve.
MATERIAL AND METHODS
Theoretical considerations
To evaluate the performance of a hydraulic jump on a corrugated bed and to design the geometry of the corrugated bed, maximum possible amount of energy dissipation and minimum possible value for sequent depth are required. Based on the specific energy curve (Fig. 2), when the sequent depth of the hydraulic jump is equal to critical depth yc, the maximum possible amount of energy dissipation and therefore the minimum possible value of sequent depth will be achieved. Using Fig. 2, the general equation for the relative maximum possible amount of energy dissipation of a hydraulic jump can be expressed as:
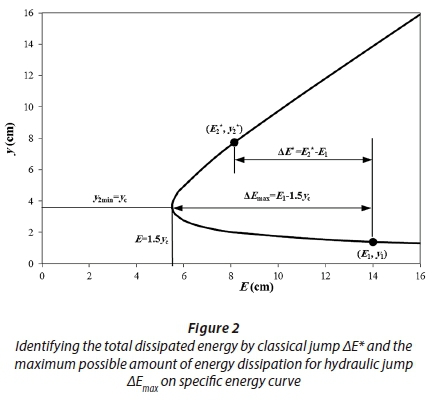

where E1 is the upstream specific energy of the hydraulic jump. Relative energy dissipation of the hydraulic jump is usually expressed based on inflow Froude number F1. To relate ΔEmax/E1 to F1, the definition of inflow Froude number F1=V1/(gy1)1/2 is used and y1 is expressed as:
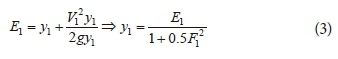
As yc3 = q2/g, flow depth y can also be related to yc and Froude number F as:
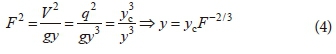
where V is the mean velocity of flow; q is the discharge intensity; and g is the acceleration due to gravity. Eq. 4 is applicable for relating y1 to F1 and also for relating y2 to F2. Substituting y1 from Eq. 4 into Eq. 3 and simplifying, yc/E1 is related to F1 as:

Substituting yc/E1 from Eq. 5 into Eq. 2, the general equation for the relative maximum possible amount of energy dissipation of the hydraulic jump is derived as:

The relative energy dissipation of a classical (smooth) hydraulic jump can also be related to F1 as (Kim et al., 2015):
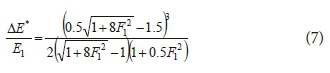
Defining the ratio of ΔE/ΔEmax as the efficiency of energy dissipation of hydraulic jump, efficiency of energy dissipation of smooth hydraulic jump η*(%) can be obtained by dividing both sides of Eq. 7 by Eq. 6 as:
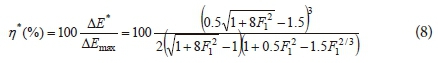
To obtain an equation for the minimum possible value of sequent depth, both sides of Eq. 3 are divided by yc and then inversed as:
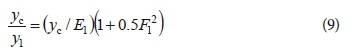
Replacing yc/E1 from Eq. 5 into Eq. 9 and taking into account that y2min = yc, the general equation for the minimum possible value of sequent depth for hydraulic jump is:

Based on specific energy curve, increase in energy dissipation leads to reduction in subcritical sequent depth of hydraulic jump. Due to the large energy dissipation, occurrence of near-critical flow downstream of a hydraulic jump on a corrugated bed is possible. Near-critical flows are characterized by a specific energy only slightly greater than the minimum specific energy and by a Froude number close to unity (i.e., 0.7 < F < 1.5 typically) (Chanson, 2004). Such flows are unstable and they should be avoided downstream of hydraulic structures, because any small change in bed elevation and roughness induces a large variation of flow depth. Given these explanations, reaching the maximum possible amount of energy dissipation is not suitable. To avoid near-critical flow downstream of the hydraulic jump, the Froude number of downstream flow should be less than 0.7. As a result, the flow depth at F = 0.7 can be taken as an optimum value for sequent depth of hydraulic jump. Setting y = y2opt and F = 0.7, y2opt is obtained from Eq. 4 as:

Dividing both sides of Eq. 11 by Eq. 4 and setting y = y1 and F = F1, y2opt is related to F1 and y1 as:

Details of experimental data
In this study, existing experimental data for hydraulic jumps on smooth and sinusoidal corrugated beds are used. Experiments for these studies were conducted on horizontal rectangular channels and hydraulic jumps were created downstream of the vertical sluice gates. Experimental data for hydraulic jumps on a smooth bed are taken from Hager and Bremen (1989), Wu and Rajaratnam (1996), Abbaspour et al. (2009a) and Wang and Chanson (2015). Experimental data for hydraulic jumps on sinusoidal corrugated beds are also taken from Ead and Rajaratnam (2002), Tokyay (2005), Yadav et al. (2007), Abbaspour et al. (2009a) and Elsebaie and Shabayek (2010). The flow channel section of the experiments in these studies is illustrated in Fig. 1. Corrugation geometry and flow conditions of the experimental data for hydraulic jumps on sinusoidal corrugated beds are also presented in Table 1.
RESULTS AND DISCUSSION
In Fig. 3, the energy dissipation of hydraulic jumps on a sinusoidal corrugated bed is compared with that of corresponding jumps on a smooth bed (the curve of Eq. 7 and experimental data from Hager and Bremen, 1989; Wu and Rajaratnam, 1996; Abbaspour et al. (2009a); Wang and Chanson, 2015) and the curve of maximum possible limit of energy dissipation (the curve of Eq. 6).
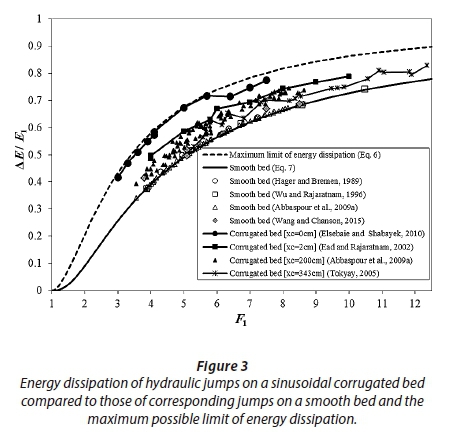
As can be seen from Fig. 3, a very good agreement is observed between the energy dissipation data for a smooth hydraulic jump with the curve of Eq. 7. For similar inflow Froude numbers, energy dissipation of a jump on a sinusoidal corrugated bed is greater than that on a smooth bed. Due to the large friction between the main flow with the channel bed and the transfer of momentum flux between the main flow and eddies trapped in the corrugations, energy dissipation of a jump on a corrugated bed is larger than that on a smooth bed. For similar values of F1, relative energy dissipation for a hydraulic jump on a sinusoidal corrugated bed is mainly influenced by xc. With reducing xc, ΔE/E1 increases and the approximately maximum possible amount of energy dissipation is achieved when xc = 0 cm (data from Elsebaie and Shabayek, 2010). As presented in Table 1, wave steepness value of corrugated bed t/s, relative roughness height t/y1 and inflow Froude number F1 of experimental data from hydraulic jumps on a sinusoidal corrugated bed are approximately in the same ranges. The main difference between the experimental data is the horizontal distance from the sluice gate section to the start point of corrugated bed xc. In the experimental method of Elsebaie and Shabayek (2010), the corrugated bed started from the gate section. Based on Resch et al. (1976), the maximum velocity on the bed surface of supercritical flow downstream of gates occurs at the gate section. With increasing xc from zero, velocity at the bed surface becomes equal to zero and in the vicinity of the bed surface velocity reduces (refer to Fig. 1). For xc = 0, the larger velocity at the bed surface leads to larger momentum exchange between the main flow and eddies trapped in corrugations. Therefore, starting the corrugated bed from the gate section leads to maximum energy dissipation.
In Fig. 4, the sequent flow depth ratio for hydraulic jumps on a sinusoidal corrugated bed is compared with those of corresponding jumps on a smooth bed (the curve of Eq. 1 and experimental data from Hager and Bremen, 1989; Wu and Rajaratnam, 1996; Wang and Chanson, 2015), the curve of minimum limit of sequent flow depth ratio (the curve of Eq. 10) and the curve of optimum value for sequent depth ratio (the curve of Eq. 12).
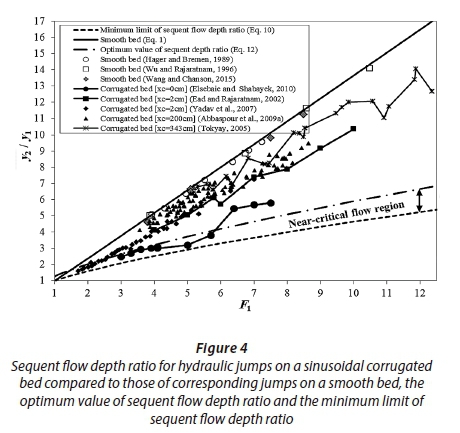
It follows from Fig. 4 that for similar inflow Froude numbers, the sequent depth ratio for hydraulic jumps on a sinusoidal corrugated bed is smaller than that on a smooth bed. Based on the specific energy curve (Fig. 2), increase in energy dissipation leads to a reduction in sequent flow depth of hydraulic jump. For similar values of F1, sequent flow depth ratio y2/y1 for a hydraulic jump on a sinusoidal corrugated bed is mainly influenced by xc. As a result of xc having the same value, the sequent depth ratio data from Ead and Rajaratnam (2002) and Yadav et al. (2007) can accurately be fitted by a single curve. With reducing xc, y2/y1 reduces. For xc = 0 (data from Elsebaie and Shabayek, 2010), sequent flow depth ratio data are approximately fitted along the curve of Eq. 12. Due to the large energy dissipation, some data points are placed in the near-critical flow region. To avoid near-critical flows, normal depth of flow downstream of the corrugated bed should be equal to or slightly larger than y2otp.
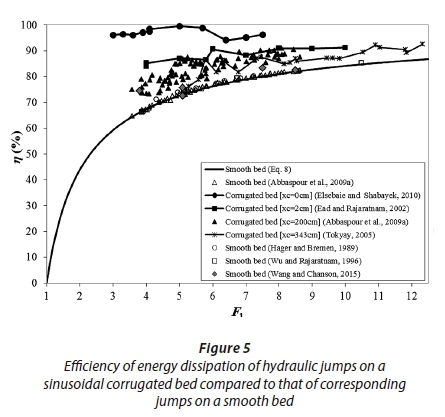
Figure 5 shows the efficiency of energy dissipation η(%) of hydraulic jumps on smooth and sinusoidal corrugated beds against inflow Froude number F1. Efficiency of energy dissipation from largest to smallest is observed as follows: (i) approximately 100% efficiency of energy dissipation on a sinusoidal corrugated bed when xc = 0 cm; (ii) a sinusoidal corrugated bed when xc = 2 cm; (iii) a sinusoidal corrugated bed when xc = 200 and 343cm; and (iv) a smooth bed.
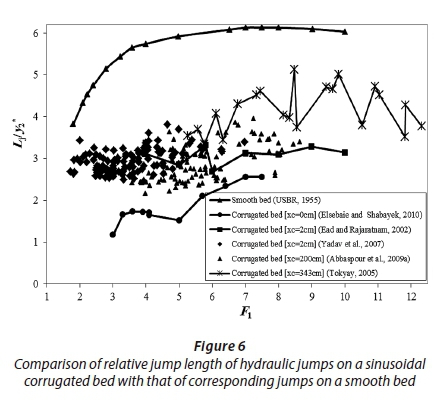
In Fig. 6, the relative jump length Lj/y2* of hydraulic jumps on a sinusoidal corrugated bed is compared with that of corresponding jumps on a smooth bed. For similar inflow Froude numbers, the length of a created jump on a sinusoidal corrugated bed is significantly smaller than that on a smooth bed. Minimum length of jump occurs on a sinusoidal corrugated bed when xc = 0 cm (data from Elsebaie and Shabayek, 2010). In this case, the jump length is smaller than 2.55y2*.
In the experimental setup of Ead and Rajaratnam (2002) and Elsebaie and Shabayek (2010), variation of flow depth along the length of supercritical flow is eliminated by rounding the gate edge (see Fig. 1). Experimental data of Wang and Chanson (2015) validates that this measure leads to uniform flow depth before the jump. When supercritical flow exits under a sluice gate with a sharp edge, a contraction section will occur just below the gate and after that supercritical flow depth will gradually increase. The maximum value of F1 will occur at the contraction section. When xc is large, as in the work of Tokyay (2005) and Abbaspour et al. (2009), the depth of the supercritical stream at the start of the jump will be larger than that just below the gate. As a result, for hydraulic jumps adownstream of sharp-edged gates, F1 is dependent on xc. Due to negligible energy loss, the specific energy along supercritical flow before the jump E1 and therefore relative critical depth yc/E1 are approximate constant values. Therefore, unlike F1, yc/E1 is not significantly influenced by xc. For analysis of energy dissipation on labyrinth weirs, yc/E1 is also used by Mohammadzadeh-Habili et al. (2018). Using the available experimental data in the literature, the relative energy dissipation of hydraulic jumps on smooth and sinusoidal corrugated beds is shown against the relative critical depth (Fig. 7). For comparison, maximum limit of energy dissipation (Eq. 2) is also plotted in Fig. 7. The curve of relative energy dissipation of a hydraulic jump on a smooth bed is also plotted by combining Eq. 5 with Eq. 7.
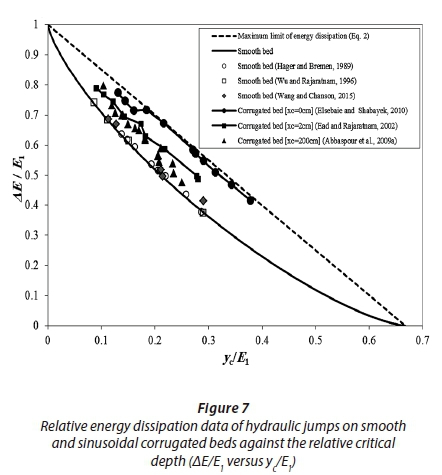
It follows from Fig. 7 that starting the corrugated bed from the gate section (xc = 0) leads to the maximum value of energy dissipation. For similar values of F1, relative energy dissipation of hydraulic jump on a sinusoidal corrugated bed is larger than that of corresponding jumps on a smooth bed. Additionally, for hydraulic jumps on sinusoidal corrugated bed, ΔE/E1 increases with decrease in xc. These results validate the results of Figs 3 through 5.
CONCLUSIONS
Using the specific energy curve, the relative maximum possible amount of energy dissipation of a hydraulic jump and the minimum possible value of sequent flow depth ratio for a hydraulic jump are theoretically related to the inflow Froude number. Using the obtained equations and existing experimental data in the literature, the performance of hydraulic jumps on sinusoidal corrugated bed has been evaluated. Results indicated that energy dissipation, sequent flow depth and jump length of hydraulic jumps on corrugated beds are mainly influenced by the horizontal distance from the head gate opening to the start point of the corrugation bed xc. For large values of xc, the influence of a corrugated bed on increasing the energy dissipation and therefore reducing the sequent flow depth of a hydraulic jump is not very great, while for xc = 0, the maximum value of energy dissipation and therefore the minimum value of sequent flow depth can be achieved. Additionally, starting the corrugated bed from the head gate section stabilizes the situation of the initial depth of the hydraulic jump at the gate opening. To avoid near-critical flows, normal depth of flow downstream of the corrugated bed should be equal to or slightly greater than 1.27yc. The results obtained from the present study are useful for the design of corrugated bed geometry.
REFERENCES
ABBASPOUR A, DALIR A, FARSADIZADEH D and SADRADDINI A (2009a) Effect of sinusoidal corrugated bed on hydraulic jump characteristics. J. Hydro-Environ. Res. 3 109-117. https://doi.org/10.1016/j.jher.2009.05.003 [ Links ]
ABBASPOUR A, DALIR A, FARSADIZADEH D and SADRADDINI A (2009b) Effect of sinusoidal corrugated bed on hydraulic jump characteristics. J. Water Soil Sci. 19 (1) 13-26 (in Persian). [ Links ]
CAROLLO F, FERRO V and PAMPALONE V (2007) Hydraulic jumps on rough beds. J. Hydraul. Eng. 133 (9) 989-999. https://doi.org/10.1061/(ASCE)0733-9429(2007)133:9(989) [ Links ]
CHANSON H (2004) The Hydraulics of Open Channel Flows: An Introduction. Butterworth-Heinemann, Oxford, UK. [ Links ]
CHERN M and SYAMSURI S (2013) Effect of corrugated bed on hydraulic jump characteristic using SPH method. J. Hydraul. Eng. 139 (2) 221-232. https://doi.org/10.1061/(ASCE)HY.1943-7900.0000618 [ Links ]
EAD S and RAJARATNAM N (2002) Hydraulic jumps on corrugated beds. J. Hydraul. Eng. 128 (7) 656-663. https://doi.org/10.1061/(ASCE)0733-9429(2002)128:7(656) [ Links ]
ELSEBAIE I and SHABAYEK S (2010) Formation of hydraulic jumps on corrugated beds. Int. J. Civ. Environ. Eng. 10 (1) 40-54. [ Links ]
HAGER W (1992) Energy Dissipators and Hydraulic Jump. Kluwer Academic, Dordrecht. https://doi.org/10.1007/978-94-015-8048-9 [ Links ]
HAGER W and BREMEN R (1989) Classical hydraulic jump: sequent depths. J. Hydrol. Res. 27 (5) 565-585. https://doi.org/10.1080/00221688909499111 [ Links ]
KIM Y, CHOI G, PARK H and BYEON S (2015) Hydraulic jump and energy dissipation with sluice gate. Water 7 (9) 5115-5133. https://doi.org/10.3390/w7095115 [ Links ]
MOHAMMADZADEH-HABILI J, HEIDARPOUR M and HAGHIABI A (2016) Comparison the hydraulic characteristics of finite crest length weir with quarter-circular crested weir. Flow Measur. Instrum. 52 77-82. https://doi.org/10.1016/j.flowmeasinst.2016.09.009 [ Links ]
MOHAMMADZADEH-HABILI J, HEIDARPOUR M and SAMIEE S (2018) Study of energy dissipation and downstream flow regime of labyrinth weirs. Iran. J. Sci. Technol. Trans. Civ. Eng. 42 111-119. https://doi.org/10.1007/s40996-017-0088-6 [ Links ]
PETERKA A (1958) Hydraulic design of stilling basins and energy dissipators. Engineering Monograph No. 25, U.S. Bureau of Reclamation, Denver. [ Links ]
RAJARATNAM N (1967) Hydraulic jumps. Adv. Hydrosci. 4 197-280. https://doi.org/10.1016/B978-1-4831-9935-1.50011-2 [ Links ]
RAJARATNAM N (1968) Hydraulic jumps on rough beds. Trans. Eng. Inst. Can. 11 (A-2) 1-8. [ Links ]
SAMADI-BOROUJENI H, GHAZALI M, GORBANI B and FATTAHI R (2013) Effect of triangular corrugated beds on the hydraulic jump characteristics. Can. J. Civ. Eng. 40 (9) 841-847. https://doi.org/10.1139/cjce-2012-0019 [ Links ]
RESCH F, LEUTHEUSSER H and COANTIC M (1976) Study of the kinematic and dynamic structure of the hydraulic jump. J. Hydraul. Res. 140 (4) 293-319. https://doi.org/10.1080/00221687609499663T [ Links ]
OKYAY N (2005) Effect of channel bed corrugations on hydraulic jumps. Impacts of global climate change conference. Proc., World Water and Environmental Resources Congress, 15-19 May 2005, Alaska. [ Links ]
USBR (United States Bureau of Reclamation) (1955) Research studies on stilling basins, energy dissipators and associated appurtenances. US Bureau of Reclamation, Hydraulic Laboratory Report No. Hyd-399. USBR, Denver. [ Links ]
WU S and RAJARATNAM N (1996) Transition from hydraulic jump to open channel flow. J. Hydraul. Eng. 122 (9) 526-528. https://doi.org/10.1061/(ASCE)0733-9429(1996)122:9(526) [ Links ]
YADAV P, AHMAD Z and ASAWA G (2007) Parameters of hydraulic jump on corrugated beds. ISH J. Hydraul. Eng. 13 (1) 93-105. https://doi.org/10.1080/09715010.2007.10514860 [ Links ]
WANG H and CHANSON H (2015) Experimental study of turbulent fluctuations in hydraulic jumps. J. Hydraul. Eng. 04015010. https://doi.org/10.1061/(ASCE)HY.1943-7900.0001010 [ Links ]
Received 18 November 2017
Accepted 25 September 2018
* To whom all correspondence should be addressed. e-mail: jahan_mohamadzadeh@yahoo.com














