ORIGINAL ARTICLES

 

Development of a deterministic design model for a high-rate algal pond

 

 

ISW van der Merwe*; IC Brink

Faculty of Engineering, University of Stellenbosch, Cnr Banhoek Road and Joubert Street, Stellenbosch, 7600, South Africa

 

 

---

ABSTRACT

Inadequate wastewater treatment is a major problem in South Africa. Existing wastewater treatment facilities often lack sufficient skilled labour, resulting in partially treated effluent. Increasing eutrophication in surface water bodies indicates that this problem needs rectification. The characteristics of the high-rate algal pond (HRAP) technology makes it an attractive option for effluent polishing in South Africa. It has the potential of simultaneous nutrient removal and nutrient recovery from partially treated effluent. A deterministic design model based on the mutualistic relationship between bacteria and algae in an HRAP was developed. The model includes kinetics of algae, ordinary heterotrophic organisms (OHOs), as well as ammonia-oxidising organisms (ANOs) and their interaction with organic compounds, nitrogen and phosphorus. After preliminary verifications, it was found that the deterministic model accurately represented the kinetics involved with the ammonia and nitrate/nitrite concentrations. However, it was also established that the major limitations of the deterministic model are its exclusion of phosphate precipitation and its failure to incorporate the production of particulate and soluble organics due to the respiration, excretion and mortality processes.

Keywords: high rate algal pond, HRAP, deterministic model, modelling, algae, nutrient removal, eutrophication prevention, effluent polishing

---

 

 

INTRODUCTION

The discharge of untreated or poorly treated wastewater is a major problem in developing countries (Mara, 2004; Henze et al., 2008). It can cause high levels of pollution in receiving water bodies, which, in turn, can cause serious harm to the environment (Mara, 2004). It is believed that the discharge of untreated or partially treated wastewater is a major contributor to eutrophication in South Africa. A recent study showed that only 26% of South Africa's wastewater is sufficiently treated. The rest is discharged into the receiving water bodies as untreated or partially treated wastewater (Turton, 2015).

Developing countries generally do not have the financial capacity and expertise to implement advanced wastewater treatment systems such as the activated sludge system (Mara, 2004). Besides the capital investment and expertise required for the design and construction of these wastewater treatment systems, developing countries struggle to educate and employ skilled labourers to maintain and operate these plants properly (Henze et al., 2008). Waste stabilisation ponds are used as a cost-effective and simple alternative for wastewater treatment in developing countries (Mara, 2004).

The high-rate algal pond (HRAP) is a type of waste stabilisation pond designed for enhanced nutrient removal from wastewaters through nutrient assimilation into algal biomass (Craggs, 2005b). The HRAP technology also has the advantage of nutrient recovery through harvesting of the algal biomass (Craggs, 2005b). An HRAP may consequently be an appropriate solution when nutrient removal and nutrient recovery are required.

In South Africa, waste stabilisation ponds, and HRAPs in particular, may serve as simple and cost-effective options for effluent polishing from underperforming wastewater treatment works (WWTWs). The nutrient removal and nutrient recovery capabilities of HRAPs make them particularly promising for effluent polishing. These ponds can potentially serve as a buffer between the underperforming plant and the receiving water body, and thus reduce eutrophication. HRAPs are especially suited to developing countries and cities where land is available and affordable for the relatively large surface area requirements of these systems.

The successful design and implementation of HRAPs for the purpose of effluent polishing can be greatly aided by a representative deterministic design model. Such a model may be applied for investigations of the effectiveness of HRAPs in different climates, determination of main design parameters and the creation of strategies for efficient operation.

 

BACKGROUND

The different biological processes that exist within an HRAP were investigated. These processes, together with fundamental reactor kinetics, served as the basis for the development of the deterministic HRAP model.

Defining the high-rate algal pond

The high-rate algal pond (HRAP) is a shallow pond where wastewater is driven along a circuit or raceway by a paddlewheel. This type of pond was developed with the purpose of simultaneously treating wastewater as well as recovering nutrients in algal biomass (Craggs, 2005b). The algal biomass can then be harvested for multiple uses such as fertilisation, animal feed, biofuels as well as vitamin and pigment extraction (Shilton, 2005; Park et al., 2011).

Biological processes within an HRAP

Algae-based water treatment is defined by a mutualistic symbiosis between heterotrophic bacteria and algae called 'photosynthetic oxygenation' (Craggs, 2005b).

Mara (2004) explains this relationship by referring to facultative and maturation ponds. He described these ponds as 'photosynthetic ponds', i.e., the oxygen required for organic degradation is supplied by algae through photosynthesis, and in return the carbon dioxide required by the algae for photosynthesis is produced during the organic degradation process. The use of algae therefore eliminates the need for aeration, which is a significant expense in conventional activated sludge plants. This relationship is illustrated in Fig. 1 and is applicable to many types of algae-based wastewater treatment systems, including HRAPs.

 

 

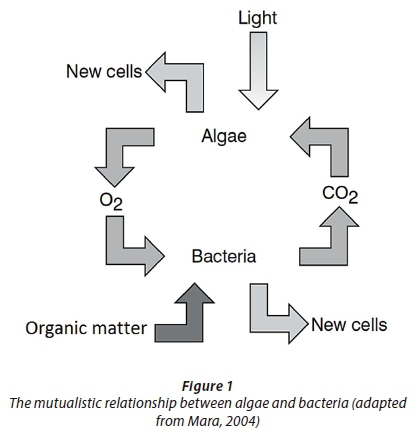
Algal and bacterial synthesis

Figure 1 suggests that the biological processes of concern in an HRAP include algae and bacteria. The types of bacteria that are generally of concern in an aerobic wastewater treatment environment are ordinary heterotrophic organisms (OHOs) for the degradation of organics and ammonia oxidising organisms (ANOs) for the nitrification of ammonia (Ekama and Wentzel, 2008a; Ekama and Wentzel, 2008b).

Green et al., (1996) stated that a typical formula for the cell composition of microalgae is C₁₀₆H₁₈₁O₄₅N₁₆P. The empirical formula for the active bacterial biomass that is found in wastewater treatment processes was approximated as C₆₀H₈₇O₂₃N₁₂P (Comeau, 2008). This formula was simplified to C₅H₇O₂N for processes where phosphorus is not considered (Comeau, 2008). The deterministic model developed in this research included the assimilation of phosphorus into the cells of the active bacteria during the growth process.

Craggs (2005a) approximated an equation, Eq. 1, for the synthesis of algae by assuming that ammonium is the source of nitrogen, phosphate is the source of phosphorus and water the source of oxygen and hydrogen. Shown in Eq. 2, is the approximation for growth of OHOs on a carbon source (glucose in this case) (Comeau, 2008).

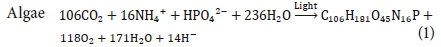
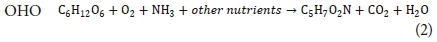
Nitrification was also considered in the model due to the aerobic nature of HRAPs. Nitrification is the aerobic process where nitrifying bacteria oxidise ammoniacal-N to nitrite and later nitrate. Ammonia-oxidising organisms (ANOs) oxidise ammonia into nitrite according to the equation below (Ekama and Wentzel, 2008b).

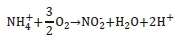
Nitrite-oxidising organisms (NNOs) oxidise the nitrite further to form nitrate as shown below (Ekama and Wentzel, 2008b).

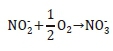
The total oxidation reaction for ammonia can then be written as shown below.

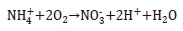
In most nitrification systems operated below 28°C, the ammonia-oxidising bacteria are rate limiting in the complete nitrification of ammonia to nitrate (Tchobanoglous et al., 2003). Consequently, nitrite is almost immediately oxidised into nitrate in most wastewater treatment systems (Ekama and Wentzel, 2008b). The only case where the NNOs might limit the rate of nitrification, is at very low dissolved oxygen concentrations (below 0.5 mg·L^-1) (Tchobanoglous et al., 2003). It is therefore generally safe to ignore NNOs from a nitrifying system provided that the system operates at dissolved oxygen concentrations above 0.5 mg·L^-1. Consequently, in the design of activated sludge systems, the assumption was made that the rate of complete nitrification only depends on the kinetics of the ANOs (Ekama and Wentzel, 2008b; Tchobanoglous et al., 2003).

Nitrification is restricted by solar-UV light and the slower nitrifying bacteria dominate when exposed to sunlight (Craggs, 2005a). Nitrification is consequently limited in an HRAP due to the high UV exposure (Craggs, 2005a). However, nitrification was observed in the laboratory experiment and was therefore still included in the deterministic model.

Nutrient removal mechanisms

Assimilation

A relatively large component of algal and bacterial cells consists of nutrients such as nitrogen and phosphorus. Nutrients are consequently removed from wastewater by assimilation through algal and bacterial growth. The effectiveness of this process depends on the density of the algal or bacterial cells, their composition and the growth rate. Other factors such as the organic material loading, nutrient concentration, hydraulic retention time, pH, hardness and temperature also affect the assimilation of nutrients (Craggs, 2005a).

Logic depicts that algae are more effective at nutrient assimilation than the bacteria. Bacteria require a significant number of organics as a carbon source for growth. Organics are normally depleted rapidly and the bacterial growth is thereby limited before a significant number of nutrients can be assimilated. Algae, however, use carbon dioxide as a carbon source. Since carbon dioxide is abundant in the atmosphere, algae can grow until a nutrient (commonly nitrogen or phosphorus) is depleted.

Precipitation of phosphate

Phosphates (PO₄^3-, HPO₄^2- and H₂PO₄^-) can bind with cations (Ca²⁺, Mg²⁺, Al³⁺, and Fe³⁺) to form insoluble compounds. These compounds are removed from the wastewater through precipitation and subsequent sedimentation. The efficiency of this process depends on pH, temperature and the cation concentration (Craggs, 2005a). Phosphate precipitation is most effective at a high pH and elevated cation concentrations (Craggs, 2005a). Elevated pH is common in HRAPs and it has been suggested that phosphate precipitation plays an important role in phosphate removal from these ponds (Craggs, 2005a).

Ammonia volatilisation

Nitrogen can be removed from wastewater through ammonia gas that escapes through the pond water surface. This process is called volatilisation. The rate at which volatilisation occurs depends on the pH, temperature, mixing conditions and the free ammonia concentration. Ammonia volatilisation can be the dominant process for nitrogen removal at the optimum pH and temperature. Ammonia volatilisation typically requires a pH between 7 and 9 and temperatures between 22 and 28°C. This process has been shown to account for 75% to 98% of nitrogen removal in WSPs (Craggs, 2005a).

Nitrification

Nitrification is a mechanism of ammonia removal in HRAPs. Nitrification is enhanced by a dissolved oxygen concentration greater than 1 g·m^-3, a temperature greater than 8°C and a pH between 6 and 9 (Craggs, 2005a).

Reactor kinetics

The deterministic model was developed from fundamental reactor kinetics. The defining principle of reactor kinetics is described by the general mass balance equation that is given below as Eq. 3 (Howe et al., 2012). This mass balance equation consequently also served as the basis for the development of a deterministic model for an HRAP.

The mass balance equations for the different components of the deterministic model were developed for a continuously mixed flow reactor (CMFR). CMFRs are ideal reactors that have an inflow and an outflow. It is assumed that the inflow into a CMFR is instantaneously and completely mixed within the reactor. The description of the CMFR approximation coincides with the conditions in an HRAP. It was assumed that the paddle wheel mixing and the turbulence in the pond would ensure sufficient mixing for a uniform concentration in the vertical and horizontal directions. It was therefore deemed that an HRAP could be accurately approximated as a CMFR.

 

MODEL DEVELOPMENT

The development of the deterministic HRAP model was based on the mutualistic relationship between bacteria and algae. Bacteria have been extensively used in wastewater treatment and the activated sludge model is widely used for heterotrophic and ammonia-oxidising bacteria modelling (Ekama and Wentzel, 2008a; Tchobanoglous et al., 2003). Algal modelling has been widely applied in surface water quality models. Bowie et al. (1985) developed a surface water quality model that included algae. This model and variations thereof are also widely used in water quality modelling (Chapra, 2008; Cole and Wells, 2013). The HRAP model was accordingly developed by combining the activated sludge model and the algal water quality model in a CMFR environment.

Model definition

In an HRAP system, there are several state variables that influence the system. A perfect model would include all the state variables that could be associated with the relevant process. However, a large amount of variables can make a model unnecessarily complex and incorporate uncertainty.

The state variables shown in Table 1 were selected for the development of the HRAP model.

 

 

Figure 2 depicts the biological interactions between the different state variables. Various other parameters such as carbon dioxide and dissolved oxygen are also part of the biological processes shown in Fig. 2 but were excluded from the model to maintain simplicity. The assumption was therefore made that carbon dioxide and dissolved oxygen are abundantly available and do not have any limiting influences on the processes shown in Fig. 2.

 

 

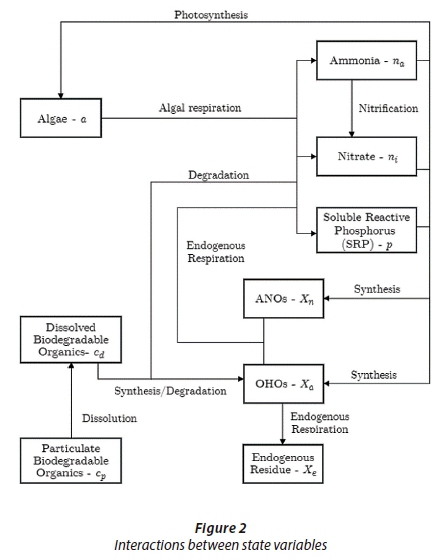
Modelling equations

A mass balance equation that incorporates the processes shown in Fig. 2 in a CMFR system was developed for each of the state variables.

Ordinary heterotrophic organisms

Equation 4 is the mass balance equation that was used to represent the OHOs in the HRAP model. It was developed from the kinetics used to represent the growth and endogenous respiration of OHOs in an activated sludge system (Marais and Ekama, 1976; Ekama and Marais, 1977; Ekama and Wentzel, 2008a; Tchobanoglous et al., 2003).

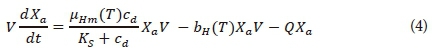
where

Q = flow rate (L·day^-1)

V = pond volume (L)

μ_Hm(T) = maximum specific growth rate as a function of temperature (day^-1)

K_S = half-saturation constant (mgCOD·L^-1)

b_H(T) = endogenous mass loss (death) rate as a function of temperature (day^-1)

Equation 4 shows that the endogenous respiration approach was selected to model the mass loss processes due to the OHOs' internal energy requirements for cell maintenance (Ekama and Marais, 1977). In the endogenous respiration model, a 'black box' approach is followed. Only the net reduction in the active mass is taken into account. All the different processes that cause this net reduction are consequently ignored. The causes for this net reduction in active mass are then attributed to the energy requirements of the endogenous respiration process and the unbiodegradable residue that forms during endogenous respiration (Ekama and Marais, 1977).

The maximum specific growth rate (μ_Hm(T)) and the endogenous respiration rate (b_H(T)) are temperature dependent and conform to the Arrhenius relationship (Tchobanoglous et al., 2003; Ekama and Wentzel, 2008a). This relationship adjusts the base growth rate at 20°C for temperature effects. Temperatures higher than 20°C will result in an increased growth rate and temperatures lower than 20°C will result in a decreased growth rate. Equation 5 is an example of the application of the Arrhenius relationship to the maximum specific growth rate (μ_Hm(T)) (Tchobanoglous et al., 2003).

where

μ_(Hm,20) = maximum specific growth rate at 20°C (day^-1)

θ_gXa = temperature factor for the maximum specific growth rate of OHOs

T = temperature (°C)

Ammonia oxidising organisms

The mass balance equation that represents the ANOs in the HRAP system is given in Eq. 6. It contains the kinetics for the growth of ANOs and the organisms' endogenous respiration as modelled in an activated sludge system (Ekama and Wentzel, 2008b).

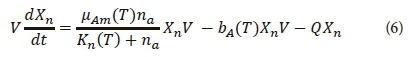
where

μ_Am(T) = maximum specific growth rate of ANOs as a function of temperature (day^-1)

K_n(T) = half-saturation coefficient for the growth of ANOs on ammonia (mgN·L^-1)

b_A(T) = endogenous respiration rate as a function of temperature (day^-1)

The temperature dependency of the maximum specific growth rate (μ_Am(T)), the half-saturation coefficient (K_n(T)) and the endogenous respiration rate (b_A(T)) in Eq. 6 also follows the Arrhenius relationship shown in Eq. 5.

Algae

The mass balance equation developed for the algae in an HRAP system is given in Eq. 7. It was developed from a surface water quality model that incorporates algae (Bowie et al., 1985; Chapra, 2008; Cole and Wells, 2013). All the algae-related processes that were deemed applicable to a HRAP system, were included.

where k_ga(T,N,I) = algal growth rate as a function of temperature, nutrients and solar radiation (day^-1)

k_rea(T) = rate of losses due to respiration and excretion (day^-1)

As mentioned above, the algae growth rate (k_ga(T,N,I)) depends on the temperature and the availability of light and nutrients. Equation 8 is used to calculate the applicable algal growth rate (Chapra, 2008). It uses a multiplier to adjust a measured algal growth rate at 20°C for temperature, nutrient and light limitation.

where

k_(ga,20) = algal growth rate at 20°C with no light or nutrient limitation (day^-1)

λ_T = multiplier for growth limiting/increase due to temperature

λ_I = multiplier for growth limiting due to light

λ_N = multiplier for growth limiting due to nutrients

Nutrient multiplier:

Algae require nutrients in order to grow. The major nutrients required for the growth of most microalgae are carbon, nitrogen, and phosphorus. Various other micronutrients and trace elements are also required for algal growth. However, normally one does not model the entire group of nutrients that algae require to grow. The assumption is generally made that all the trace elements and micronutrients as well as some macronutrients, are present in such high concentrations that they do not inhibit the growth of algae. Usually, and in the case of this model, it is assumed that the only limiting nutrients are nitrogen and phosphorus (Chapra, 2008).

The nutrient limiting factors can be computed using the Monod relationship (Cole and Wells, 2013). As mentioned above, algal growth depends on a number of nutrients. More than one nutrient can therefore be responsible for growth limitation. A minimum approach is most commonly used to incorporate more than one type of nutrient (Chapra, 2008; Cole and Wells, 2013; Bowie et al., 1985). This approach calculates a nutrient limiting multiplier for each nutrient (nitrogen and phosphorus) and then chooses the minimum value to be used as the multiplier for nutrient limitation in Eq. 8. Equation 9 shows the calculation of the multiplier for nutrient limitiation for this model where nitrogen and phosphorus are considered as the limiting nutrients (Chapra, 2008). Equation 9 can easily be expanded to include other nutrients that might be limiting.

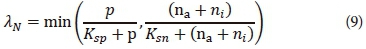
where

K_sp = half-saturation coefficient for phosphorus (mgP·L^-1)

K_sn = half-saturation coefficient for nitrogen (mgN·L^-1)

Light multiplier:

Chapra (2008) and Bowie et al. (1985) provided Eq. 10 for the calculation of growth rate limitation due to light. Equation 10 is the result of an integration over time and depth in order to obtain the mean value for light limitation (Chapra, 2008; Bowie et al., 1985).

where

f_ld = photoperiod (fraction of day with light/sunshine)

k_e = ight extinction coefficient (m^-1)

d = depth (m)

The light multiplier given in Eq. 10 does not only depend on the light intensity but also on the duration of the sunlight on each day, the turbidity of the water and the depth of the water. Light extinction differs over the depth of the pond and the light multiplier in Eq. 10 is consequently calculated as an average over the depth of the pond.

The variables α₁ and α₀ of Eq. 10 are used to simplify the equation and can be calculated with Eqs 11 and 12.

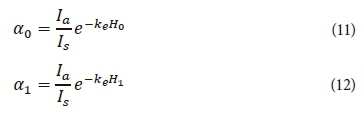
where

I_a = average light intensity (W·m^-2)

I_s = optimal light intensity (W·m^-2)

H₀ = depth at top of layer under consideration (0 if the top is the water surface) (m)

H₁ = depth at bottom of layer under consideration (m)

The average light intensity (I_a) is calculated by adjusting the maximum light intensity according to a half-sinusoid approximation that represents the light variation of the sun. The calculation for this adjustment is shown in Eq. 13.

where

I_m = the maximum light intensity measured at the surface (W·m^-2)

The light extinction coefficient (k_e) incorporates the loss of light intensity with water depth due to light absorbance of particles in the water as well as reflection from the water surface. The light extinction coefficient is determined with Eq. 14 (Riley et al., 1956).

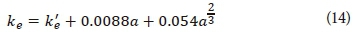
where

a = algal concentration (µgChla·L^-1)

k'_e = light extinction due to other factors than phytoplankton/algae (m^-1)

In pure and particle-free water, the light extinction is 0.04 m^-1 (Riley et al., 1956). However, algae rarely occur alone and are normally accompanied by other non-algal volatile solids and non-volatile suspended solids. The light extinction due to other factors than algae (k'_e) can either be directly measured or Eq. 15 can be used to calculate it from the concentrations of other non-algal suspended solids (Di Toro, 1978; Chapra, 2008).

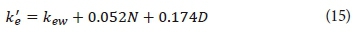
where

k_ew = light extinction in pure and particle free water (0.04 m^-1)

N = concentration of non-volatile suspended solids (mg·L^-1)

D = concentration of non-algal volatile suspended solids (or detritus) (mg·L^-1)

The calculation of the light extinction due to nonalgal suspended solids (k′_e) shown in Eq. 15 was adjusted to represent the nonalgal suspended solids that where included in the model. Eq. 16 shows the calculation for light extinction coefficient due to non-algal suspended solids in the model. In the development of Eq. 16, the assumption was made that, apart from algae, only the OHOs, ANOs, endogenous residue and the particulate biodegradable organics contribute to the light absorption. It was also assumed that the non-volatile suspended solids concentration is negligible and would not contribute to the light extinction.

Temperature multiplier:

The Arrhenius relationship is used to calculate the temperature multiplier as indicated in Eq. 17 (Chapra, 2008; Bowie et al., 1985). Equation 7 indicates that the algal respiration and excretion rate (k_rea(T)) are also temperature dependent. This temperature dependency is also modelled with the Arrhenius relationship as shown for OHOs in Eq. 5 (Chapra, 2008; Bowie et al., 1985).

where

θ_ga = temperature factor for algal growth rate

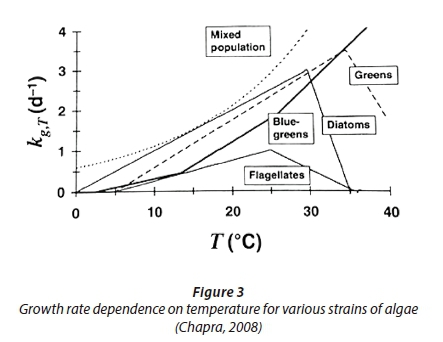
Algae growth is not only inhibited by low temperatures, but also by temperatures higher than the optimal growth temperature (Chapra, 2008). The temperature dependence of various strains of algae can be seen in Fig. 3. A limitation of the Arrhenius relationship is that it does not allow for growth limitation at temperatures above the optimum. However, when a mixed population of algae is considered, there will always be a certain strain of algae that will grow at any reasonable temperature. Therefore, the Arrhenius relationship can be accurately applied to model a mixed population (Chapra, 2008).

 

 

Endogenous residue

In the endogenous respiration method, a 'black box' approach is followed. Only the net reduction in the active mass is taken into account. All the different processes that cause this net reduction are consequently ignored. The causes for this net reduction in active mass are then attributed to the energy requirements of the endogenous respiration process and the unbiodegradable residue that forms during endogenous respiration (Ekama and Marais, 1977).

The mass balance equation for the endogenous residue that forms due to endogenous respiration in the HRAP system is given in Eq. 18 (Ekama and Marais, 1977; Ekama and Wentzel, 2008a).

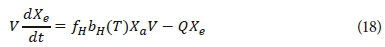
where

f_H = endogenous residue fraction of endogenous mass loss

Equation 18 shows that the model only accounts for endogenous residue produced by the OHOs. The literature did not clearly state the quantities of endogenous residue produced by algae and ANOs. The algal models that were researched also did not incorporate endogenous residue (Chapra, 2008; Bowie et al., 1985). It was therefore decided to only include the endogenous residue production from the OHOs which was well researched in the activated sludge models (Marais and Ekama, 1976; Ekama and Marais, 1977; Tchobanoglous et al., 2003).

Dissolved biodegradable organics

Equation 19 is the mass balance equation developed for the soluble biodegradable organics in the HRAP system (Chapra, 2008; Ekama and Marais, 1977; Marais and Ekama, 1976).

where

k_p = rate of particulate organic carbon dilution (day^-1)

c_d,in = influent dissolved biodegradable organics concentration (mgCOD·L^-1)

Equation 19 includes terms for the dissolution of particulate biodegradable organics, the degradation of the soluble biodegradable organics by OHOs and the flow of mass in the influent and effluent.

In the development of Eq. 19, the endogenous respiration model was applied for OHO, ANO, and algal respiration. In the endogenous respiration model, these organisms do not contribute to the soluble biodegradable organics concentration. It was assumed that all the organic carbon released during respiration is utilised by the organism for energy. Endogenous respiration has been accurately applied for OHOs and ANOs in the literature (Ekama and Wentzel, 2008a; Ekama and Wentzel, 2008b). However, there is no evidence of the accuracy of the endogenous respiration model for algal respiration. The algal water quality model does not give a relationship between algal respiration and soluble biodegradable organics (Bowie et al., 1985). It was consequently assumed that the endogenous respiration model could be accurately applied for algal respiration.

Particulate biodegradable organics

The mass balance equation for particulate biodegradable organics in a HRAP system is given in Eq. 20. The kinetics of this parameter were kept very simple. The mass balance equation, Eq. 20, only includes mass increase due to the influent and the mass decrease due to outflow and dissolution. The dissolution process is approximated with a first-order dissolution constant.

where

c_p,in = influent particulate biodegradable organics concentration (mgCOD·L^-1)

As for soluble biodegradable organics, the application of the endogenous respiration model for algal, OHO and ANO respiration assumes that the respiration of these organisms does not contribute to the particulate biodegradable organics concentration.

Ammonia

Equation 20 is the general mass balance equation developed for ammonia in an HRAP environment. Equation 20 was developed from the ammonia kinetics given in the algal surface water quality model by Chapra (2008) and the activated sludge model (Ekama and Wentzel, 2008b). Additional terms were also added for the ammonia uptake and release, due to the cell growth and respiration of OHOs and ANOs, as well as a term for ammonia release through the degradation of organics.

where n_a,in = ammonia concentration in the influent (mgN·L^-1)

a_na = ratio of nitrogen to chlorophyll a in algal biomass (mgN·mgChla^-1)

a_nv = the ratio of nitrogen to VSS in OHOs and ANOs (mgN·mgVSS^-1)

f_onc = the ratio of organically bound nitrogen to COD in the influent biodegradable organics (mgN·mgCOD^-1)

F_am = ammonium preference factor

The ammonium preference factor (F_am) represents the preference that the algae have for ammonium over nitrate/nitrite. This factor can by calculated with Eq. 22 (Cole and Wells, 2013) and is also included for nitrogen accumulation in OHO and ANO cell growth. It is assumed that the ammonia preference over nitrogen follows the same kinetics in OHO and ANO growth as in algal growth. The half-saturation concentration for ammonia preference is normally very low (Thomann and Fitzpatrick, 1982; Cole and Wells, 2013). This means that ammonia will almost exclusively be used for the nitrogen requirement until the ammonia concentration is almost zero. Thereafter nitrate will be used as the nitrogen source.

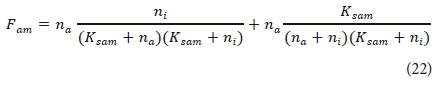
where

K_sam = half-saturation constant for ammonium preference (mgN·L^-1)

The following paragraphs explain the purpose of and the reasoning behind the different terms of Eq. 21.

The 1^st and 2^nd terms of Eq. 21 account for the ammonia release and uptake for algal respiration and growth (Chapra, 2008).

The 3^rd and 5^th terms were added for ammonia release due to the endogenous respiration process of OHOs and ANOs (Ekama and Wentzel, 2008a; Ekama and Wentzel, 2008b). During endogenous respiration, these organisms oxidise their own mass to produce energy. For the ammonia mass balance to hold, ammonia should be released during this process in the same ratio that it was taken up in the growth process.

The 4^th term in Eq. 21 accounts for the accumulation of ammoniacal-N into the cell mass of the OHOs during the growth process. Between 9% and 12% of the dry mass of OHOs consists of nitrogen (Ekama and Wentzel, 2008b). Nitrogen should therefore be accumulated with the growth of OHOs. The fourth term represents the utilisation of ammonia due to the nitrogen requirements of OHO growth.

The 6^th term of Eq. 21 accounts for the ammoniacal-N accumulation during the growth of ANOs. ANOs are normally present in low concentrations due to the slow growth rate. The literature therefore does not clearly state the cell composition of these organisms and they are normally classified with the OHOs. Due to the lack of knowledge about the cell composition of ANOs, the assumption was made that ANOs follow the same principles for ammoniacal-N accumulation as explained for OHOs in the previous paragraph.

The degradation of biodegradable organics by OHOs releases organically bound nitrogen in the form of ammonia. The 7^th term of Eq. 21 represents the release of ammonia due to the degradation of organically bound nitrogen.

The 8^th term of Eq. 21 represents the decrease of ammonia due to nitrification by ANOs. The last term accounts for the inflow and outflow of ammonia according to the assumptions of the CMFR.

Nitrate

Equation 23 is the mass balance equation developed for nitrate in an HRAP system. Equation 23 was also developed through a combination of the algal surface water quality model by Chapra (2008) and the activated sludge model (Ekama and Wentzel, 2008b). Equation 23 was developed on the assumption that nitrite is immediately nitrified to nitrate and consequently present in negligible concentrations.

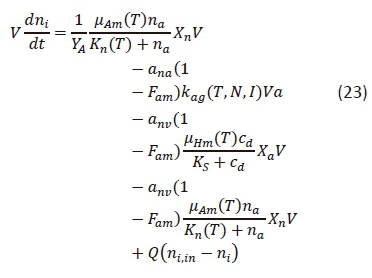
where

n_i,in = influent nitrate concentration (mgN·L^-1)

The following paragraphs explain the purpose of and the reasoning behind the different terms of Eq. 23.

The 1^st term of Eq. 23 accounts for the increase in the nitrate concentration due to nitrification as defined in the activated sludge model (Ekama and Wentzel, 2008b).

The 2^nd to 4^th terms represent the nitrate utilisation for algae, OHO and ANOs growth respectively (Chapra, 2008). The nitrite fraction of the total nitrogen utilisation is determined by the ammonia preference factor (Cole and Wells, 2013).

The last term accounts for the inflow and outflow of nitrate according to the assumptions of the CMFR.

SRP

The mass balance equation developed for SRP in an HRAP environment is given in Eq. 24. Equation 24 was developed by combining and modifying the surface water quality model given by Chapra (2008) and the activated sludge model (Ekama and Marais, 1977; Ekama and Wentzel, 2008a; Ekama and Wentzel, 2008b; Tchobanoglous et al., 2003; Marais and Ekama, 1976).

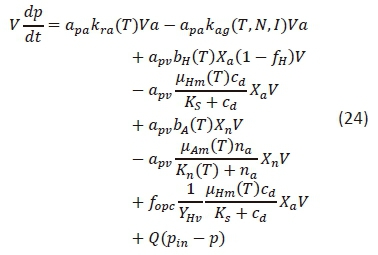
where

p_in = influent SRP concentration (mgP·L^-1)

a_pa = ratio of phosphorus to algae (mgP·mgChla^-1)

a_pv = phosphorus to VSS ratio in OHOs and ANOs (mgP·mgVSS^-1)

f_opc = organically bound phosphorus to COD ratio for the influent biodegradable organics (mgP·mgCOD^-1)

Equation 24 is very similar to the mass balance equation for ammonia in Eq. 21. Equation 24 also includes in its first 6 terms the SRP losses and gains due to the growth and respiration of algae, OHOs, and ANOs. These terms follow the same principles and assumptions as discussed for ammonia with the sole difference being the ratio in front of the terms that represents the ratios of phosphorus to chlorophyll a and VSS instead of nitrogen. Also seen in the ammonia mass balance equation, is the 2^nd to last term that represents the SRP release due to the degradation of organically bound phosphorus, and the last term that accounts for the SRP flux in the influent and effluent.

Volatile suspended solids

The volatile suspended solids (VSS) in the HRAP system can be estimated with Eq. 25. The VSS concentration does not explicitly form part of the model described in Fig. 2, but it is used to quantify the organisms included in the model into a measurable concentration.

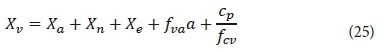
where

f_va = ratio of VSS to algal biomass (mgVSS·mgChla^-1)

The assumption was made that only the OHO, ANO, endogenous residue, algae, and particulate biodegradable organics concentrations would contribute to the VSS. In practice, there might be other components contributing to the VSS. However, in a HRAP system that receives secondary to tertiary settled wastewater, the bulk of the VSS will most likely consist of the parameters given above.

Model assumptions

Various assumptions were made during the model development described in the previous paragraphs. The following list is a summary of all the assumptions that were made during the development of the HRAP model:

1.Completely mixed conditions exist within the pond. The paddle wheel mixing and the turbulent flow conditions in an HRAP should ensure effective mixing of soluble compounds and suspended particulates. This assumption should also be further substantiated if the HRAP receives wastewater of effluent quality that generally has a low settleable and suspended solids content.

2.The dissolved carbon dioxide concentration does not limit the algal growth. Some sources suggest that carbon dioxide may become limiting in very dense algal cultures (Park et al., 2011) where this assumption may become concerning.

3.The dissolved oxygen concentration does not limit the growth of ordinary heterotrophic organisms (OHOs) and ammonia oxidising organisms (ANOs). This should generally be correct for most HRAPs. Due to the intense algal photosynthesis in these ponds, oxygen levels are generally above the saturation level (20 to 30 mg·L^-1 during the day) (Rose et al., 2002; Mara, 2004; Craggs, 2005b).

4.Ammonia volatilisation and phosphate precipitation are negligible. The elevated pH in HRAPs may result in significant ammonia volatilisation and phosphate precipitation (Craggs, 2005a). Preliminary verifications of the model showed clear signs of SRP precipitation. This assumption is consequently a major shortcoming of the HRAP model and the model should ideally be expanded to include these processes.

5.The endogenous respiration model can be applied for algal and ANO respiration. Preliminary model verifications indicated that the model underestimates the organic matter concentration. It is believed that this is due to the incorrect application of the endogenous respiration model. This is discussed in further detail in the 'Model verification' section.

6.Zooplankton are not present in the system. The high pH of HRAPs generally prevents the growth of zooplankton (Park et al., 2011). Preliminary testing also showed that the turbulent surface conditions of the HRAP are also sufficient in preventing the invasion of the algae-eating larvae of flying insects.

7.Evaporation losses are negligible. It was decided not to include evaporation losses in the preliminary design phase of this model. Evaporation losses were controlled during the laboratory experiment through the addition of water.

8.Only OHOs produce endogenous residue. Preliminary model verifications indicated that the model underestimated the VSS concentration. Endogenous residue contributes to the VSS concentration. The exclusion of algae and ANO endogenous residue may be a reason for the VSS underestimation.

9.Ammonia preference is the same for algae, OHOs, and ANOs. Preliminary model verifications suggested that this assumption was valid. However, due to a lack of experimental results, this assumption could not be officially supported or negated.

10.There is always enough nitrogen and phosphorus available for OHO and ANO cell accumulation. This assumption was necessary since the growth equations of OHOs and ANOs do not include nutrient limitations.

11.OHOs and ANOs have the same cell compositions. This assumption could not be supported or negated. However, due to the relatively low biomass production of ANOs, this assumption should not have a significant influence on the results obtained from the simulations.

12.Ammonia-oxidising organisms (ANOs), rather than nitrite-oxidising organisms (NNOs), are limiting in nitrification. This assumption is required by the activated sludge model (Ekama and Wentzel, 2008b).

13.Only algae, OHOs, ANOs, endogenous residue and the particulate biodegradable organics contribute to the light absorption. An actual HRAP should have additional suspended solids that contribute to light absorption besides those mentioned in the assumption. However, it is believed that the algae, OHOs, ANOs, endogenous residue and particulate biodegradable organics would contribute to the bulk of the suspended solids especially if the HRAP receives effluent quality wastewater.

 

TYPICAL RATES AND CONSTANTS

The HRAP model is dependent on multiple stoichiometric constants and kinetic rates. Table 2 contains all the rates and constants that are applicable to the HRAP model as well as the estimated typical ranges of these rates and constants as found in various literature.

 

MODEL DISCUSSION

The HRAP model was verified though a laboratory experiment. The experiment entailed a scale model HRAP with synthetic wastewater. The concentrations measured for the various state variables during the experiment were used to calibrate and evaluate the deterministic HRAP model. For the laboratory experiment, a batch system was used with zero inflow and outflow.

The deterministic HRAP model gave an accurate prediction of the ammonia and nitrate/nitrite concentrations. The model's prediction of the chlorophyll a was also satisfactory. The calibrated HRAP model was inaccurate in predicting the SRP, COD and VSS concentrations. This section considers possible sources that contributed to the calibrated model's inaccuracy in predicting these concentrations. Figure 4 shows the correlation between the simulated and measured nutrient concentrations from the laboratory experiment. Note that the low nutrient removal measured in the laboratory experiment was because the algal growth was limited by light due to the lower intensity of the artificial lights when compared to sunlight.

The inaccuracy of the deterministic model in predicting the SRP concentration indicates that there was an additional mechanism of SRP removal in the scale model HRAP that the model did not take into account. It is believed that this mechanism was SRP precipitation. The calibrated model only gave an estimation of the SRP assimilated by algae. SRP assimilation is often accompanied by SRP precipitation (Craggs, 2005a) and should be included in the HRAP model.

The HRAP model was also unsatisfactory in predicting the dissolved biodegradable COD concentration. The algal respiration, excretion, and mortality processes might have been a source of soluble organic carbon. The results obtained from experiments indicate that a significant amount of non-living organic carbon was present in the system. The deterministic model assumed that all the carbon released during the respiration processes are used for energy generation. The high COD indicates that the endogenous respiration model may have been incorrectly applied for algal respiration. The surface water quality model of Chapra (2008) that was used to develop the deterministic HRAP model ignores the algal mortality process and combines algal excretion and respiration. Figure 5, developed by Cole and Wells (2013), suggests that the algal mortality and excretion processes increase the soluble and particulate organic matter. The deterministic HRAP model therefore does not account for the possible contribution of algal respiration, excretion, and mortality towards the COD concentration.

 

 

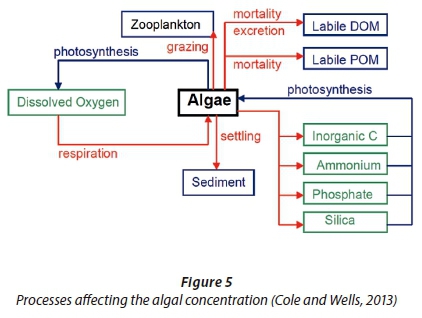
The reason for the poor VSS prediction by the HRAP model is the same as the reason for the poor COD correlation. The deterministic model failed to include all the processes involved with regard to the non-living soluble and particulate biodegradable organics. The actual soluble and particulate biodegradable organic concentrations were much higher than in the model simulations. Since soluble and particulate organics are a substrate for OHOs, the actual OHO (and endogenous residue) concentrations were also likely higher than the deterministic model suggested. The difference between the measured VSS concentrations and the simulated VSS concentrations is therefore likely due to non-living particulate biodegradable organics, OHOs, and endogenous residue that the model failed to consider.

It is also possible that the algal and ANO respiration processes produced a particulate unbiodegradable residue that was not included in the deterministic model. This particulate residue possibly contributed towards the inaccurate prediction of the VSS concentration.

 

LIMITATIONS AND RECOMMENDATIONS

The deterministic HRAP model is mostly limited by the kinetics of only two deterministic models. The HRAP model needs to be developed further to incorporate processes such as phosphate precipitation and the relation between the algal respiration, excretion and mortality processes to the soluble and particulate biodegradable non-living organics.

The deterministic model does not include the carbon dioxide concentration as a possible limitation to the algal growth. Although the dissolved carbon dioxide concentrations were not limiting during the preliminary verifications, Craggs (2005b) suggested that carbon dioxide might become limiting at high pH. More research is required on the dynamics of carbon dioxide in an HRAP and its limitation of algal growth.

Evaporation losses can potentially have a significant effect on an HRAP in warm and/or windy climates. It is recommended that the deterministic model is expanded to include the effect of evaporation losses.

The effects of pH, hardness and other environmental conditions, such as wind speed, humidity and soil temperatures that were not considered in this model, can form part of future research endeavours towards improving the model.

 

CONCLUSION

The preliminary verifications showed that the deterministic model can accurately predict the ammonia and nitrate/nitrite concentrations but is unsatisfactory in predicting the soluble reactive phosphorus (SRP) concentration, since it did not account for phosphorus precipitation. The model only accounted for the SRP assimilated by algae. The COD and VSS estimations were also inaccurate, presumably due to the model's deficiency in accounting for the increase in soluble and particulate organics, caused by the algal respiration, excretion and mortality processes.

The deterministic HRAP model developed herein has its shortcomings and further development is required before it can be implemented in the HRAP design and operation phases. However, the potential improvement that a fully developed deterministic HRAP model can bring to the design and operation phases is evident. It can potentially enable an accurate prediction of the nutrient and organics removal, as well as the potential biomass production. A fully developed deterministic model would also allow for a thorough investigation of the feasibility of HRAPs in different climates.

 

REFERENCES

BOWIE GL, MILLS WB, PORCELLA DB, CAMPBELL CL, PAGENKOPF JR, RUPP GL, JOHNSON KM, CHAN PWH and GHERINI SA (1985) Rates, Constants, and Kinetics Formulations in Surface Water Quality Modeling. United States Environmental Protection Agency, Athens, Georgia.         [ Links ]

CHAPRA SC (2008) Surface Water-Quality Modeling. Waveland Press, Inc., Long Grove.         [ Links ]

CLESCERI LS, GREENDBERG AE and EATON AD (1998) Standard Methods for the Examination of Water and Wastewater (20^th edn). American Public Health Association, Washington, DC.         [ Links ]

COLE TM and WELLS SA (2013) CE-QUAL-W2: A Two-Dimensional, Laterally Averaged, Hydrodynamic and Water Quality Model, Version 3.71. Portland State University, Portland.         [ Links ]

COMEAU Y (2008) Microbial Metabolism. In: Henze M, Van Loosdrecht MCM, Ekama GA and Brdjanovic D (eds) Biological Wastewater Treatment: Principles, Modelling and Design. IWA Publishing, London. 9-32.         [ Links ]

CRAGGS R (2005a) Nutrients. In: Shilton A (ed.) Pond Treatment Technology. IWA Publishing, Cornwall. 77-95.         [ Links ]

CRAGGS R (2005b) Advanced integrated wastewater ponds. In: Shilton A (ed.) Pond Treatment Technology. IWA Publishing, Cornwall. 282-310.         [ Links ]

DI TORO DM (1978) Optics of turbid estuarine waters: approximations and applications. Water Research 12 (12) 1059-1068. https://doi.org/10.1016/0043-1354(78)90051-9        [ Links ]

EKAMA GA and WENTZEL MC (2008a) Organic matter removal. In: Henze M, Van Loosdrecht MCM, Ekama GA and Brdjanovic D (eds) Biological Wastewater Treatment: Principles, Modelling and Design. IWA Publishing, London. 53-86.         [ Links ]

EKAMA GA AND WENTZEL MC (2008b) Nitrogen removal. In: Henze M, Van Loosdrecht MCM, Ekama GA and Brdjanovic D (eds) Biological Wastewater Treatment: Principles, Modelling and Design. IWA Publishing, London. 87-138.         [ Links ]

EKAMA GA and MARAIS G (1977) The activated sludge process. Part II-dynamic behaviour. Water SA 3 (1) 18-50.         [ Links ]

EPPERLEY RW (1972) Temperature and Phytoplankton growth in the sea. Fishery Bulletin 70 (4) 1063-1085.         [ Links ]

GREEN FB, BERNSTONE TJ, LUNDQUIST TJ and OSWALD WJ (1996) Advanced integrated wastewater pond systems for nitrogen removal. Water Science and Technology 33 (7) 207-217. https://doi.org/10.2166/wst.1996.0140        [ Links ]

HENZE M, VAN LOOSDRECHT MCM, EKAMA GA AND BRDJANOVIC D (2008) Wastewater Treatment Development. In: Henze M, Van Loosdrecht MCM, Ekama GA and Brdjanovic D (eds) Biological Wastewater Treatment: Principles, Modelling and Design. IWA Publishing, London. 1-8.         [ Links ]

HOWE KJ, HAND DW, CRITTENDEN JC, TRUSSELL RR and TCHOBANOGLOUS G (2012) Principles of Water Treatment. John Wiley and Sons, Inc., New Jersey.         [ Links ]

MARA DD (2004) Domestic Wastewater Treatment in Developing Countries. Earthscan, London.         [ Links ]

MARAIS G and EKAMA GA (1976) The activated sludge process part I-steady state behaviour. Water SA 2 (4) 164-200.         [ Links ]

PARK JBK, CRAGGS RJ and SHILTON AN (2011) Wastewater treatment high rate algal ponds for biofuel production. Bioresource Technology 102 (1) 35-42. https://doi.org/10.1016/j.biortech.2010.06.158        [ Links ]

RILEY GA, CONOVER SAM, DEEVEY GB, CONOVER RJ, WHEATLAND SB, HARRIS E and SANDERS HL (1956) Oceanography of Long Island Sound. Bulletin of The Bingham Oseanographic Collection 15 15-46.         [ Links ]

ROSE PD, HART OO, SHIPIN O and ELLIS PJ (2002) Integrated algal ponding systems and the treatment of domestic and industrial wastewaters Part 1: The AIWPS Model. WRC Report No. TT 190/02. Water Research Commission, Pretoria.         [ Links ]

SHILTON A (2005) Pond Treatment Technology. IWA Publishing, London.         [ Links ]

TCHOBANOGLOUS G, BURTON FL, STENSEL HD and EDDY M (2003) Wastewater Engineering: Treatment and Reuse (4th edn). McGraw-Hill, New York.         [ Links ]

THOMANN RV and FITZPATRICK JJ (1982) Calibration and Verification of a Mathematical Model of the Eutriphication of the Potomac Estuary. HydroQual, Inc., Washington D.C.         [ Links ]

TURTON A (2015) Sitting on the horns of a dilemma: water as a strategic resource in South Africa. @Liberty 6 (22) 1-28.         [ Links ]

 

 

Received 7 February 2017
Accepted in 25 September 2018

 

 

* To whom all correspondence should be addressed. +27 84 249 9177; e-mail: e-mail: iswvdm@gmail.com