Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Water SA
On-line version ISSN 1816-7950
Print version ISSN 0378-4738
Water SA vol.44 n.3 Pretoria Jul. 2018
http://dx.doi.org/10.4314/wsa.v44i3.09
ORIGINAL ARTICLES
Impact of variable speed pumps on water quality in distribution systems
Moustafa S Darweesh*
Civil Eng. Dept., Assuit University, Assuit, Egypt
ABSTRACT
Water quality has become a prominent issue in the study of water distribution networks. Variable speed pumps (VSPs) can control and improve the performance of water distribution systems. However, they may have effects on the water quality. The objective of this study was to investigate the impact of VSPs on water quality. The EPANET water quality simulator was applied for modelling water age and chlorine residual in a distribution network. In addition, intrusion of an active contaminant and analysis of leakage effects on residual chlorine concentration were performed through extended period simulations. Results indicate that VSPs may have negative impacts on water quality, including increased water age during low consumption times, and reduced disinfectant residuals at peak hours. In addition, the average rate of chlorine decay for fixed speed pumps (57%) is higher than that for VSPs (54%) when a conservative contaminant (sewage water) is considered.
Keywords: Water distribution systems, pumps, variable frequency drives, water quality, extended period simulation
INTRODUCTION
All public water systems are required to provide an adequate quantity and quality of water in a reliable manner at all times consistent with the requirements (WSDOH, 2009). Using fixed speed pumps (FSPs) for operating water distribution systems (WDSs) produces a situation where pressure may be significantly higher than required and could exceed specifications. The use of variable speed pumps (VPSs), pumps equipped with variable frequency drives (VFDs), provides the potential for significant improvements in the operating efficiency of water distribution systems, accompanied by energy and cost savings (Darweesh, 2018; Wood and Lingireddy, 1995). However, VSPs may have negative effects on water quality.
Kale et al. (2017) provided a basic understanding of variable frequency drive terms and its operation. VFDs, sometimes called adjustable-frequency drives, adjustable-speed drives or variable speed drives (VSDs), vary the rotational speed by changing supply frequency. VFD produces a variable voltage which is directly proportional to the frequency, and produces a constant magnetic flux in the motor. The motor speed will vary according to the applied frequency generated by the VFD and, as a result, its components, such as fans, pumps, and compressors, behave differently as their speed changes (Blair, 2017). By using VSP, Babaei et al. (2015) investigated the effects of time-dependent chlorine injection and pump speed, as well as different combinations of objective functions, for minimizing energy costs and maximizing hydraulic and quality reliability using multi-objective ant colony optimization algorithm. The results showed that the application of VSP and time-dependent chlorine injection results in improvements such as reduction in energy and disinfection costs.
Improved operations using variable-speed pumps may result in maintaining less overhead storage and a lower safety factor for fire protection. However, with ever-increasing water-quality concerns within distribution systems, maintaining large overhead storage results in longer retention times and may be undesirable (Lingireddy and Wood, 1998).
According to the aforementioned studies, little attention has been paid to VSPs' influence on water distribution network performance, especially for water quality. The present study was performed to investigate the difference between utilizing constant and variable speed pumps in terms of water quality through the supply systems. In this research, water quality simulations were performed using EPANET toolkit for a 72-h simulation. All further discussion will reference VFDs or VSDs as 'variable speed pumps'.
THEORETICAL APPROACHES
Hydraulic models are important for the analysis and design of water pipe networks. They are used for various important tasks by engineers, such as the design of new and analysis of existing distribution networks, and long-term master and operational planning (Harding and Walski, 2000). Computer-based mathematical models are useful tools for evaluating the water quality changes in drinking-water distribution systems.
Pump operation at variable speeds
The relations that govern pump operation at different rotational speeds are usually derived together with those that govern pump operation with different impeller diameters by the use of similitude theory, and are called affinity laws (Georgescu et al., 2014) as shown in Eqs 1 and 2:

where: Q represents the pump flow rate, Hp is the pump head, N is the impeller rotational speed and D is the impeller external diameter.
An analytical relationship (Sârbu and Borza, 1998) between two different speeds (N1 and N2) and the corresponding efficiencies (η1 and η2) is shown in Eq. 3:
Hydraulic model
Numerous computer models (software) have been developed to solve the network simulation equations. One of the more widely used models is EPANET, which can perform steady state and extended period simulation (EPS) of hydraulic performance and water quality in distribution networks (Rossman, 2000). EPANET was developed by the United States Environmental Protection Agency. This model is an explicit time-driven water-quality modelling algorithm for tracking transient concentrations of substances in pipe networks.
To conduct a water quality simulation in a given WDS, one must have a hydraulic model in which the quality model can be applied. Assume we have a pipe network with N junction nodes and NF fixed grade nodes (tanks and reservoirs). The flow-head loss relation in a pipe between nodes a and b is given by Eq. 4:
where: H is the nodal head, h is the head loss, n is the resistance coefficient, Q is the flow rate, f is the flow exponent, and m is the minor loss coefficient. The second set of equations that must be satisfied is the flow continuity around all nodes, N, shown in Eq. 5:
where: Da is the flow demand at node a and, by convection, flow into a node is positive. The method used in EPANET to simultaneously solve the head loss and flow continuity equations, Eq. 4 and Eq. 5, that characterize the hydraulic state of the pipe network at a given point in time, is called the 'Gradient Method' (Salgado et al., 1988). For extended period simulation, EPANET tracks the flow of water in each pipe, the pressure at each node for a fixed set of reservoir levels, tank levels, and the concentration of a chemical species throughout the network during a simulation period comprised of multiple time steps. In addition to chemical species, water age and source tracing can also be simulated. From one time-step to the next, reservoir levels and junction demands are updated according to their prescribed time patterns while tank levels are updated using the current flow solutions.
Water quality model
EPANET's water quality simulator uses a Lagrangian time-based approach to track the fate of discrete parcels of water as they move along pipes and mix together at junctions between fixed-length time steps. For each water quality time step, the contents of each segment are subjected to reactions, a cumulative account is kept of the total mass and flow volume entering each node, and the positions of the segments are updated.
A dissolved substance will travel down the length of a pipe with the same average velocity as the carrier fluid while at the same time reacting (either growing or decaying) at some given rate. Longitudinal dispersion is usually not an important transport mechanism under most operating conditions. This means there is no intermixing of mass between adjacent parcels of water traveling down a pipe. Transport of a chemical constituent within a pipe is represented by the classical advection equation, Eq. 6 (Rossman and Boulos, 1996):

where: Ci is the concentration (mass·volume-1) in pipe i as a function of distance x and time t, ui is the flow velocity (length·time-1) in pipe i, and r is the rate of reaction (mass·volume-1·time-1) as a function of concentration.
The concentration of a substance, such as chlorine, leaving the junction is simply the flow-weighted sum of the concentrations from inflowing pipes and external sources. For a specific node k the concentration is given by Eq. 7.
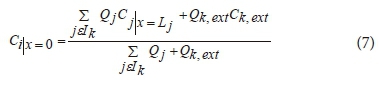
where: i is link with flow leaving node k, Ik is set of links with flow into k, Lj is length on link j, Qj is flow rate in link j, Qk,ext is external source flow entering the network at node k, and Ck,ext is concentration of the external flow entering at node k. The notation Ci|x=0 represents the concentration at the start of link i, while Ci|x=Li is the concentration at the end of the link. The concentration throughout a storage tank, under completely mixed conditions, is a blend of the current contents and that of any entering water. At the same time, the internal concentration could be changed due to reactions, r(Cs). Mass balance at the storage tanks is given by Eq. 8.
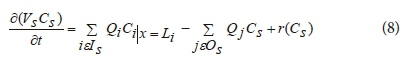
where: Vs is the storage volume at time t, Cs is the concentration within the storage facility, Is is the set of links providing flow into the facility, and Os is the set of links withdrawing flow from the facility. If the EPANET water quality model is applied to the entire network, Eqs 6, 7 and 8 are solved for Ci in each pipe i and Cs in each storage facility s. The solution is subjected to the initial conditions that specify Ci for all x in each pipe i and Cs in each storage facility s at time 0. Also, the solution is subjected to boundary conditions that specify values for Ck,ext, and Qk,ext for all time t at each node k, which has external mass inputs. The hydraulic simulation model provides the volume Vs in each storage facility s and the flow rate Qi in each link i at all time t. From one step to the next the water quality in each segment, link, node, and tank are updated.
METHODOLOGY
The goal of this study was to predict water quality within a drinking water distribution system operating over an extended period of time, for the variable and constant speed pumps. The EPANET water quality model was applied to simulate chlorine residual and changes in the age of water throughout a distribution system.
Effect of VSPs on water age in a distribution network
Water age is the time spent by a parcel of water in the network. New water entering the network from reservoirs or source nodes enters with age of zero. Water age provides a simple, non-specific measure of the overall quality of delivered drinking water. Internally, EPANET treats age as a reactive constituent whose growth follows zero-order kinetics with a rate constant equal to 1.0 (i.e., each second the water becomes a second older). The pump speed values (Table 1) are input to the EPANET quality modeller to show the difference between FSP and VSP effects on water quality.
Effect of VSPs on contaminant concentrations in distribution network
The aim of this section is to study the transport and behaviour of contaminants in a pipe network, for VSPs and FSPs. The following scenarios are performed using the EPANET quality solver:
Introduction of a conservative (non-reactive) contaminant (fluorides) at the water sources
Substances in water may be conservative or non-conservative, according to their behaviour during transport. 'Conservative' substances are those that do not degrade or chemically change during transport, while 'non-conservative' substances are those that undergo changes during the process. In these simulations constant flow of a contaminant, fluorides or organic material of concentration equal to 1.0 mg·L-1 is allowed to flow into the water distribution system through the two water sources (A and C) (Fig. 1); each is simulated separately.
Introduction of a non-conservative (reactive) substance (chlorine) at the two water sources
The aim here is to study the movement of chlorine to various points within a distribution network once injected at the chlorinating sources, for the two types of pumps. The main purpose of disinfection by chlorine is to protect the water supply by reducing many undesirable tastes and odours, destroying pathogens in the water, and to maintain the minimum required chlorine residual in the drinking water networks to provide some additional protection against subsequent contamination. According to the World Health Organization (WHO, 2011) and Egyptian code, the concentration of chlorine in a distribution network should not be less than 0.2 mg·L-1. Thus, sets of simulations are run for the studied network using FSPs, to find out the lowest initial chlorine dose necessary to maintain the minimum required chlorine concentration throughout the whole distribution system, which is found to be 0.35 mg·L-1. A constant feeding rate of chlorine equal to 0.35 mg·L-1 is supplied at the two water sources (Fig. 1). The pump speed values (Table 1) are entered to the EPANET quality modeller to show VSPs' effects on water quality.
Introduction of a non-conservative substance (sewage) at the water sources with an intrusion of organic material into the network
In this case the purpose is to simulate microbial intrusion (sewage, industrial wastewater, etc.) that reacts with chlorine present in the network and causes chlorine decay, for fixed and variable speed pumps. A scenario is modelled, by the EPANET software, involving the intrusion of sewage water with a 5% dilution into a distribution system containing a fixed residual chlorine dose of 0.35 mg·L-1. First-order reaction kinetic (Kb = 0.894 hr-1) for a 5% dilution of sewage into the system is used for the bulk water and the reaction at the pipe wall is neglected (AwwaRF, 2005). The intrusion is done using the setpoint booster source which sets the water leaving the node to have a certain concentration of contaminant which in this case is 50 mg·L-1. The contaminant is introduced into the network at Node 15 (Fig. 1); which has the lowest pressure in the network, and at the risk of having a rupture.
Introduction of a non-conservative substance at the water sources (chlorine) with a leakage through the network
In these simulations a leakage is created in Node 1 (Fig. 1), which has the highest pressure and lowest elevation in the network. The purpose is to see whether a leak will cause changes in the chlorine concentrations into the network for the two types of pumps or not. A leak can be simulated in the EPANET program by introducing an emitter in a node (Covelli et al., 2016). Emitters are devices that can be used to model flow through an orifice that discharges water to the atmosphere. The flow rate through an emitter can be calculated using Eq. 9 (Franchini and Lanza, 2014; Van Zyl and Malde, 2017):
Q = khn (9)
where: Q is leakage flow rate, k is the emitter coefficient, h is the pressure head differential over the emitter and n is the emitter exponent and it is dimensionless and equals to 0.5 for an orifice. It is assumed that a leakage is performed in EPANET with an emitter coefficient = 1.57 L·s-1·m-0.5.
CASE STUDY
Water supply system description
The configuration of the water supply system considered in this paper is that presented by Lingireddy and Wood (1998); the original data for this network can be found in Wood and Lingireddy (2006). The network consists of 7 loops, 28 pipes, 16 junctions, and 3 pumps, and is fed by 2 fixed head reservoirs (Fig. 1). The ID labels for the various components of the network are shown in Fig. 1. This represents a skeletal version of a medium-sized municipal water distribution system with an average daily demand of 0.68 m3·s-1 (24 ft3·s-1) which is distributed throughout the network. The pipes range in diameter from 150 to 500 mm (6 to 20 inches) with lengths of up to 1 680 m (5 500 ft). The three pumps have similar (but not identical) operating characteristics. In order to meet the operating objectives (demands and pressure requirements) using fixed-speed pumps, pumps denoted P1, P2 and P3 are operated continuously. In order to achieve reasonable precision, water quality analysis is performed with a 1.0 min time step.
Diurnal curve of demands
The demand and pressure requirements are satisfied by the pumps. A diurnal curve that makes water demands vary in a periodic way over the course of the day has been used to make the simulation more realistic for analysing an extended period of operation. The demand time pattern (Lingireddy and Wood, 1998) varies from 0.55 to 1.58 of the average daily demand, as shown in Table 2.
Residual chlorine reaction coefficients
Chlorine decay simulation conducted with the EPANET water quality model takes into consideration the phenomena of chlorine reaction with chemical species in bulk fluid (Kb) and pipe walls (Kw). Both Kb and Kw can depend on water characteristics and temperature and, moreover, the latter can be correlated to the pipe age, diameter and material. First-order bulk and wall reaction coefficients of −0.36·day-1 and -2.0 ft·day-1, as average values for those reported in the literature (Georgescu and Georgescu, 2012; Tamminen et al., 2008), were used.
RESULTS AND DISCUSSION
Variable and constant speed pumps have been assessed by simulating water age and chlorine residual concentration within a water distribution network using the EPANET 2 model. An extended period simulation was run continuously for all water quality simulations for a total duration of 72 h, while only the last 24 h (almost independent of the initial conditions) are considered for discussion.
Effect of VSPs on water age in distribution network
The obtained water ages are presented in the contour plots (Figs 2 and 3) for FSPs and VSPs at peak and low consumption hours, respectively. The average water ages at the low and peak consumption hours for FSPs are 0.45 h and 0.87 h, whereas using VSPs the average water ages are 0.43 h and 0.98 h, respectively. Variations in water ages during peak hours are due to the fact that VFDs have relative speed factors equal to 1.08, 1.02 and 0.94, for pumps P1, P2 and P3, respectively, which are greater than that for FSPs (relative speed factors for all pumps = 1.0). This leads to an increase in the fluid velocity and water is transported more rapidly through the network resulting in lower water duration. By contrast, during the off-peak hours, the relative speed factors of the VFDs are 0.77, 0.80 and 0.73, which are lower than for FSPs. Thus, the velocity of the fluid within the network is lower, resulting in higher water retention time. Also, it is seen from the previous numbers and Figs 2 and 3 that the change in water age values between FSPs and VSPs at maximum consumption are small compared to that at minimum-consumption hours. This might follow from the fact that during high-consumption hours the differences in pump speed for FSPs and VSPs are small (max. increase = 8%) compared to low-consumption hours (max. decrease = 27%). Longer residence time may contribute to DBP formation, decreased corrosion control effectiveness, nitrification and microbial growth (USEPA, 2002).
Scenario 1: Transport of non-reactive contaminant introduced at one water source
The propagation of the contaminant concentration in the network is presented in the contour plots (Figs 4 and 5) for both fixed and variable speed pumps. It is noted that whether the contaminant intrudes the network through Reservoir A or Reservoir C, the contaminant doesn't spread in a broad area in the network and only the area (points and pipes) beside the contaminant nodes is affected. Also, VSPs don't cause significant changes to the contaminant concentrations in the network, except for Node 8, where VSP increases the concentration at Node 8 from 0.0 to 0.3 mg·L-1 when the contaminant is introduced at Reservoir A, and decreases the concentration at Node 8 from 1.0 to 0.7 mg·L-1 when the contaminant is introduced at Reservoir C. We may discover the reason by performing trace analysis. A trace analysis determines the percentage of water at all nodes and links in the system from a specific source node (tanks or reservoirs). EPANET is also capable of tracking the source effect. When using FSPs, Node 8 receives 14.4 and 85.6% of its discharge from Tanks A and C, respectively, at the critical hour, while for VSPs these percentages change to 19.9 and 80.1% (figures not shown here). Thus, VSPs increase contaminant concentration at Node 8 during intrusion of contaminant through Reservoir A; in contrast, they decrease the concentration at Node 8 when the contaminant enters the network within Reservoir C.
Scenario 2: Transport of a reactive substance (chlorine) introduced at the two water sources
From the chlorine concentration contour plots (Figs 6 and 7), it is evident that VSP has lower chlorine concentrations than FSP during the high-consumption hours, while it has higher concentration than FSP at low consumption times. This behaviour is probably due to the fact that, during maximum demand, the variable speed pumps have relative speed factors (1.08, 1.02 and 0.94 for pumps P1, P2 and P3, respectively) which are greater than that for FSPs (= 1.0). In addition, a positive relationship between flow velocity and wall decay (water velocity increases wall decay rates) has been found (Hallam et al., 2002; Menaia et al., 2003). Thus, in the high consumption times the velocity of fluid in the network is higher and chlorine is transported more efficiently to the pipe wall increasing the chlorine decay and resulting in lower chorine concentrations. These low concentrations may decrease below minimum recommended concentrations, causing secondary development of microorganisms. On the other hand, during low demand periods, VSPs have a lower relative speed than FSPs (0.77, 0.80 and 0.73 to 1.0 for FSPs), which leads to the low flow velocity and thus smaller wall decay and results in higher chorine concentrations than FSPs.
Scenario 3: Effect of sewage intrusion on chlorine distribution
The resulting chlorine concentrations are shown in Figs 8 and 9. By comparing the plots of chlorine concentrations in the network without sewage intrusion (Figs 6 and 7) and the network with sewage intrusion (Figs 8 and 9), during low- and high-consumption hours for FSPs and VSPs, it can be seen that a small percentage (5%) of the contaminant can cause significant decay in chlorine concentrations, where it leads to faster reaction rates, and thus lower chlorine concentrations in the network. The average rate of chlorine decay for FSPs is 57%, while it decreases to 54% for VSPs during critical hours.
Scenario 4: Effect of leakage on chlorine distribution
By comparing the graphs of the chlorine concentrations in the network before and after the occurrence of leakage (Figs. 6, 7 and Figs. 10, 11) it can be seen that the differences in the chlorine concentrations are not significant (0.04%), which is probably due to the slight changes in velocity or the fairly low consumption in the leak node, thus leading to small leak flows. Figures 10 and 11 also illustrate that, as mentioned previously, VSP has lower chlorine concentrations than FSP at times of higher consumption, whereas it has higher chlorine concentrations than FSP at times of lower consumption.It is worth noting that the difference between variable and fixed speed pumps' effects on water quality may be greater for bigger network zones and if the number of pumps and their arrangements differ from that presented here.
CONCLUSIONS
In this research, the effects of variable speed pumps on water quality are simulated. The EPANET model is used for simulation of water age and chlorine decay in a distribution system. Intrusion of a contaminant and leakage effects on residual chlorine concentration are also studied. It is found that VSP increases residence time and free residual chlorine concentration in the network during the low-consumption hours (lower relative speed than FSP), due to lower flow velocity, and vice versa − during the peak consumption hours. Introduction of a leakage into the network does not cause significant changes in velocities or chlorine concentrations for the two used pumps. There are no large differences between FSPs and VSPs when a conservative contaminant is introduced at the water sources. Also, the average rate of chlorine decay for FSPs (57%) is higher than that for VSPs (54%) when a reactive contaminant (sewage water) is considered. Overall, these results indicate that hydraulic benefits and water quality parameters must be considered together for evaluating the use of variable speed pumps in water distribution systems.
REFERENCES
AwwaRF (AWWA Research Foundation) (2005) Impact of Distribution System Water Quality on Disinfection Efficacy. AWWA, Denver. 80235-3098. 282 pp. [ Links ]
BABAEI N, TABESH M and NAZIF S (2015) Optimum reliable operation of water distribution networks by minimizing energy cost and chlorine dosage. Water SA 41 (1) 149-156. https://doi.org/10.4314/wsa.v41i1.18 [ Links ]
BLAIR TH (2017) Variable frequency drive systems. In: Samad T (ed.) Energy Production Systems Engineering (1st edn). John Wiley & Sons, Inc., Hoboken, New Jersey. 441-466. [ Links ]
COVELLI C, COZZOLINO L, CIMORELLI L, DELLA MORTE R and PIANESE D (2016) Optimal location and setting of PRVs in WDS for leakage minimization. Water Resour. Manage. 30 (5) 1803-1817. https://doi.org/10.1007/s11269-016-1252-7 [ Links ]
DARWEESH MS (2018) Assessment of variable speed pumps in water distribution systems considering water leakage and transient operations. J. Water Suppl.: Res. Technol. AQUA 67 (1) 99-108. https://doi.org/10.2166/aqua.2017.086 [ Links ]
FRANCHINI M and LANZA L (2014) Leakages in pipes: generalizing Torricelli's equation to deal with different elastic materials, diameters and orifice shape and dimensions. Urban Water J. 11 (8) 678-695. https://doi.org/10.1080/1573062X.2013.868496 [ Links ]
GEORGESCU AM, COSOIU CI, PERJU S, GEORGESCU SC, HASEGAN L and ANTON A (2014) Estimation of the efficiency for variable speed pumps in EPANET compared with experimental data. Procedia Eng. 89 1404-1411. https://doi.org/10.1016/j.proeng.2014.11.466 [ Links ]
GEORGESCU AM and GEORGESCU SC (2012) Chlorine concentration decay in the water distribution system of a town with 50000 inhabitants. UPB Sci. Bull. Series D 74 (1) 103-114. URL: [ Links ]
HALLAM NB, WEST JR, FORSTER CF, POWELL JC and SPENCER I (2002) The decay of chlorine associated with the pipe wall in water distribution systems. Water Res. 36 (14) 3479-3488. https://doi.org/10.1016/S0043-1354(02)00056-8. [ Links ]
HARDING BL and WALSKI TM (2000) Long time-series simulation of water quality in distribution system. Water Resour. Plann. Manage. 126 (4) 199-209. https://doi.org/10.1061/(ASCE)0733-9496(2000)126:4(199) [ Links ]
KALE A, KAMDI NR, KALE P and YEOTIKAR AA (2017) A review paper on variable frequency drive. Int. Res. J. Eng. Technol. 4 (1) 1281-1284. URL: https://www.irjet.net/archives/V4/i1/IRJET-V4I1229.pdf. [ Links ]
LINGIREDDY S and WOOD DJ (1998) Improved operation of water distribution systems using variable-speed pumps. J. Energy Eng. 124 (3) 90-103. https://doi.org/10.1061/(ASCE)0733-9402(1998)124:3(90). [ Links ]
MENAIA J, COELHO ST, LOPES A, FONTE E and PALMA J (2003) Dependency of bulk chlorine decay rates on flow velocity in water distribution networks. Water Sci. Technol.: Water Supply 3 (1-2) 209-214. https://doi.org/10.2166/ws.2003.0105 [ Links ]
ROSSMAN LA (2000) EPANET 2 User's Manual. EPA/600/R-00/057. United States Environmental Protection Agency, Cincinnati. 200 pp. URL: https://nepis.epa.gov/Adobe/PDF/P1007WWU.pdf. [ Links ]
ROSSMAN LA and BOULOS PF (1996) Numerical methods for modelling water quality in distribution systems: A comparison. Water Resour. Plann. Manage. 122 (2) 137-146. http://dx.doi.org/10.1061/(ASCE)0733-9496(1996)122:2(137). [ Links ]
SALGADO R, TONIDI E and O'CONNELL PE (1988) Extending the gradient method to include pressure regulating valves in pipe networks. In: Proceedings of the International Symposium on Computer Modelling of Water Distribution Systems, 12-13 May 1988, University of Kentucky. [ Links ]
SÂRBU I and BORZA I (1998) Energetic optimization of water pumping in distribution systems. Periodica Polytechnica Mech. Eng. 42 (2) 141-152. URL: https://pp.bme.hu/me/article/viewFile/5462/4567. [ Links ]
TAMMINEN S, RAMOS H and COVAS D (2008) Water supply system performance for different pipe materials Part I: water quality analysis. Water Resour. Manage. 22 (11) 1579-1607. https://doi.org/10.1007/s11269-008-9244-x. [ Links ]
USEPA (United States Environmental Protection Agency) (2002) Effect of water age on distribution system water quality. Office of Ground Water and Drinking Water, US Environmental Protection Agency. 19 pp. URL: https://www.epa.gov/sites/production/files/2015-09/documents/2007_05_18_disinfection_tcr_whitepaper_tcr_waterdistribution.pdf. [ Links ]
VAN ZYL JE and MALDE R (2017) Evaluating the pressure-leakage behaviour of leaks in water pipes. J. Water Suppl.: Res. Technol. AQUA 66 (5) 287-299. https://doi.org/10.2166/aqua.2017.136. [ Links ]
WHO (World Health Organization) (2011) Guidelines for Drinking-Water Quality (4th edn) WHO, Geneva, Switzerland. 564 pp. URL: http://apps.who.int/iris/bitstream/10665/44584/1/9789241548151_eng.pdf. [ Links ]
WOOD DJ and LINGIREDDY S (1995) Using variable speed pumps to reduce leakage and improve performance. In: Cabrera E and Vela AF (eds) Improving Efficiency and Reliability in Water Distribution Systems. Water Science and Technology Library Series, Volume 14. Kluwer Academic Publishers, London. 135-163. https://doi.org/10.1007/978-94-017-1841-7_6 [ Links ]
WOOD DJ and LINGIREDDY S (2006) KYPIPE 2006 User's Manual. KYPipe, LLC, Civil Engineering Software Center, University of Kentucky, Lexington, Kentucky. URL: http://www.kypipe.com/. [ Links ]
WSDOH (Washington State Department of Health) (2009) Water system design manual. (DOH 331-123). Washington State Department of Health, Olympia, WA 98504-7828, December. 324 pp. URL: http://www.doh.wa.gov/Portals/1/Documents/Pubs/331-123.pdf. [ Links ]
Received 28 May 2017
Accepted in revised form 11 June 2018
* To whom all correspondence should be addressed. Current affiliation: College of Engineering, Northern Border University, Arar, Saudi Arabia. 00966544360831. e-mail: eng_taftaf82@yahoo.com














