Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
Water SA
versión On-line ISSN 1816-7950
versión impresa ISSN 0378-4738
Water SA vol.44 no.2 Pretoria abr. 2018
http://dx.doi.org/10.4314/wsa.v44i2.14
ORIGINAL ARTICLES
Variation of runoff source areas under different soil wetness conditions in a semi-arid mountain region, Iran
Hassan Rezaei-SadrI, *; Golfam SharifiII
IWater Resources Department, Nahrab Parseh Consulting Engineers Company, 61647-46111, Ahvaz, Iran
IIIranian Research Institute for Cultural Heritage & Tourism, Iran
ABSTRACT
Runoff source areas can serve as focus areas for water quality monitoring and catchment management. In this study, a conceptual form of the Soil Conservation Service Curve Number method (SCS-CN) is used to define variable-source runoff areas in a meso-scale catchment in the Zagros mountain region, southwest of Iran. The analysis indicates that for the average and dry antecedent soil wetness (the dominant soil moisture conditions), the original SCS-CN criterion that assumes the initial abstraction of rainfall to be equal to 20% of the maximum potential soil water retention fails to predict runoff source areas correctly, suggesting the ineffectiveness of the original form of the method for the study region. However, the determination of the initial abstraction based on hydrograph-hyetograph matching technique provides reasonable results, outperforms the original form of the SCS-CN based method and, more importantly, highlights the significance of having localized rainfall and runoff data. Under wet soil conditions, both techniques provide similar results; the robustness of the SCS-CN based method is thus supported only for wet soil conditions.
Keywords: rainfall-runoff, runoff generation mechanism, the SCS-CN method, variable-source runoff areas
INTRODUCTION
Water resource protection requires strategies and plans to avoid the release of pollutants into water bodies that are sources of freshwater (O'Connor, 2002; Krewski et al., 2004). In this regard, a sound knowledge of underlying hydrological processes and their impacts on water availability would be useful in the prediction of runoff production, in order to assess water yield and pollutant loads (Martinez-Mena et al., 1998). Information about areas that contribute to runoff is essential to modelling and managing catchments (Richards and Brenner, 2004). Therefore, it is important to define which areas deliver water to a river in order to identify the portion of the catchment that should be considered for management practices.
The basic assumption of variable source hydrology is based on the concepts of Hewlett and Hibbert (1967), Dunne and Black (1970a, b) and Dunne et al. (1975). Over the past two decades the theory has been further developed and applied by some researchers (Boughton, 1990; Srinivasan et al., 2000; Lyon et al., 2004; Richards and Brenner, 2004; Schneiderman et al., 2007; Leh et al., 2008). Variable source areas are those parts of the catchment in which saturation-excess runoff generation occurs (Steenhuis et al., 1995), due to local conditions such as concave slopes, soil infiltration characteristics and shallow ground waters. These parts are usually located at the boundaries of rivers where these conditions combine to produce saturation-excess runoff (Anderson and Burt, 1978; O'Brien, 1982). The location and extent of these areas can change for each storm due to catchment antecedent wetness, spatio-temporal variations of rainfall and soil heterogeneities (Beston and Marius, 1969; Richards and Brenner, 2004).
The Soil Conservation Service Curve Number (SCS-CN) method (now renamed as Natural Resource Conservation Service Curve Number method, NRCS-CN) was originally developed for conditions prevailing in the United States (SCS, 1964). Since then, it has been adapted for other parts of the world. Although some research centres have developed additional criteria, the basic concept is still widely used all over the world, probably due to its simplicity. It incorporates four main factors affecting runoff generation - soil type, land use and treatment, surface conditions and antecedent moisture conditions - in a single Curve Number (CN) parameter (Soulis et al., 2009; Rezaei-Sadr, 2017). This is a very important characteristic of this method which improves its applicability for regions with poor spatial distribution of runoff gauging stations.
Although curve numbers have been estimated for agricultural catchments very successfully, estimations for semi-arid rangelands and also forested catchments were not as successful (Hawkins, 1993). The same is true for mountain regions because there is often a complex interaction between rainfall-runoff processes and landscape factors (Rezaei-Sadr, 2015). While some of these factors (e.g., land use and cover, topography, soil characteristics, and hydrologic condition) have been defined for urban and agricultural catchments, runoff from mountainous catchments, especially in arid and semiarid climates, is poorly understood (Sprenger, 1978; Tedela, 2008; Rezaei-Sadr, 2015). Moreover, the relationship between the CN and the rainfall depth in such catchments reflects the inevitable effect of soil-cover complex spatial variability on the hydrological response (Soulis and Valiantzas, 2012). In this regard, Soulis and Valiantzas (2013) proposed a method to identify the spatial distribution of CN along the catchment by exploring the correlation between CN and rainfall depth.
Most Iranian basins, especially in mountain regions, are not equipped with enough runoff gauging stations, which limits available data records. The objective of this study was to explore the extent of the applicability of the SCS-CN method to delineate runoff source areas in a semi-arid mountain region, where water contamination negatively impacts on a growing population and on agricultural production. To this end, delineating runoff source areas resulting fro m two different methods, namely the original SCS-CN method and observed rainfall-runoff analysis, will be compared for a catchment dominated by highly permeable soils and located in the Zagros mountain region, in the south-west of Iran.
METHODS
Application of the SCS-CN method to variable-source area theory
The SCS-CN method estimates runoff depth for a storm by the SCS runoff equation (SCS 1972):

where Q is the direct runoff depth (mm), P is the depth of rainfall (mm), P is the depth of effective rainfall (mm) after runoff begins, S is the maximum potential soil water retention (mm) and I is the initial abstraction. Substituting Eq. 2 into Eq.1, the storm runoff depth is calculated from the expression:
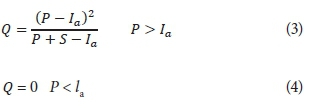
The value of S is deriveU from curve number (CN) as
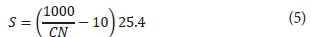
In order to estimate S from rea 1 ram fall-runoff data, Eq. 3 can be solved intermsof P and Q (Hawkins, 1979):
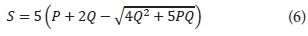
When specific values of P and Q are available, solving for S and substituting into Eq. 5 gives the observed CN for the evenl When SSorm variability is considered, a CN for application to ; specific l oc ulity can beobtained(Simanton et al., 1996).
Steenhuis etal.(1995) showed that Eq. 1 could be interpreted in terms of a saturation-excess runoff generation process. Once raindrops precipitate on the soil surface and if the rainfall ineensityislessthanthe infiltration rate, a moisture front spreada out and downward, increasing the soi moisture content until the soil becomes saturated, after whicl additional rainfall becomes runoff (Dingman, 1994). At this time, th e s aluratior^exc Ur run off generation mechanism starts to occur. During any short time period, the rate of runoff generation will be proportional to the fraction of the catchment (A) that is effectively saturated, which can be expressed as:

where ΔQ is the depth of excess rainfall generated during a time period over the whole catchment area and ΔP is the depth of rainfall during the same period (Schneiderman et al., 2007). According to Eq. 1, the contributing area is the derivative of Q with respect to P. By writing Eq. 1 in differential form and differentiating w ith respect to P, the fractional contributing area can be written as (Schneiderman et al., 2007):

Equation 8 has to satisfy the limits when Pe= 0 and when P approaches infinity. When P e= 0, the contributing area is zero and when Pe= ∞, the contributing area equals 1. Moreover, it indicates that when Peequals S, %75 of the catchment is contributing (Steenhuis et al., 1995).
By simply assuming that the dominant runoff generation mechanism is of the saturation-excess type, the conceptual method proposed by Steenhuis et al. (1995) provides a simple way to predict runoff source area in a catchment. In this method, based on the original SCS-CN method, it is assumed that the initial abstraction of rainfall (Γ) is 20% of the maximum potential soil water retention (S). Although this assumption is still used widely by engineers and practitioners for ungauged catchments, some researchers reported that this criterion did not result in accurate runoff prediction (Hawkins, 1979; Steenhuis et al., 1995; Jiang, 2001; Hawkins et al., 2002; Mishra and Singh, 2004; Baltas et al., 2007; Xiao et al., 2011). For this reason, as an alternative, the hydrograph-hyetograph matching technique is applied to determine the initial abstraction and the results are compared with the original criterion. In the rainfall-runoff analysis, each rainfall hyetograph matches with its corresponding runoff hydrograph and the rainfall depth before the recorded hydrograph starts to rise was considered as the initial abstraction. Then, the graphs depicting runoff contributing area as a function of effective rainfall are generated for different AMC classes using Eq. 8.
Site description
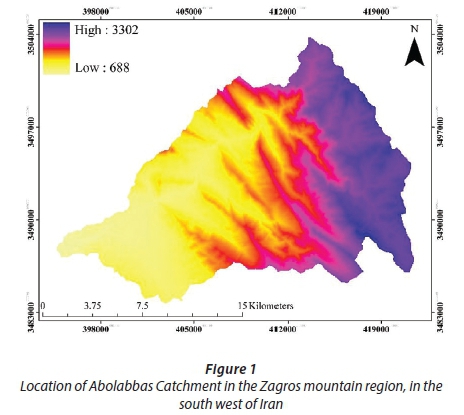
The study was conducted in Abolabbas catchment (279 km2) (49° 54' to 50° 05' E and 31° 42' to 31° 44' N) in the Zagros mountain region, in the south-west of Iran (Fig. 1). The catchment is characterized by irregular topography, high spatial variation of land use and cover, heterogeneous rainfall patterns and a semi-arid climate (Rezaei-Sadr, 2015). Average annual precipitation is about 680 mm which mostly occurs in the autumn-winter period (Rezaei-Sadr et al., 2012). The altitude ranges between 688 and 3 300 m and average elevation is 1 899 m. The average slope of the catchment is as high as 10% (Rezaei-Sadr, 2015). There is one rain gauging station with a weekly chart and one water level gauge recorder with a vertical scale at the outlet of the catchment. Twenty-four recorded rainstorms with 15-min time intervals from January 1981 to December 2007, which were monitored by Khuzestan Water and Power Authority, Ahvaz, Iran, along with their corresponding direct runoff values, were used (Table 1). To separate each rainfall from the subsequent event, the end of a rainfall event was defined when a 6-h period without rainfall occurred.
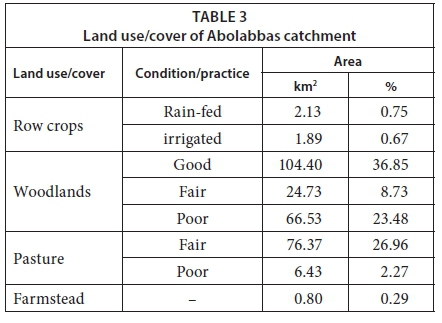
Soils are generally highly permeable, well-drained, calcareous, gravelly loams with large percentages of rock and gravel at the surface. The main geological formation series are Gachsaran (MIgs), Bakhtiari (Pibk), Asemari (Omas), Pabdeh(PeEpd)-Gurpi(Kgu), Fahlian-Darian (JKkgp) and Bangestan (Kbgp) as well as Alluvial deposits (Qft2) (Zarei, 2012; Rezaei-Sadr, 2015). The main characteristics of these formations are presented in Table 2. According to this table, approximately 85% of the catchment is covered by highly permeable soils caused by a large crack and fissure system on the surface. The remaining portions, comprising 15% of the catchment area, are covered by soils of low permeability (Zarei, 2012). The surface conditions of the catchment areas which were provided by remote-sensing images as well as field observations (Zarei, 2012) are presented in Table 3. Woodlands and pasture are the dominant land use (cover) which comprises about 98% of the catchment area.
RESULTS AND DISCUSSION
Dry wetness condition
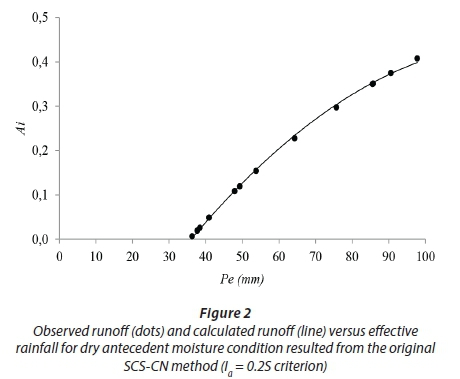
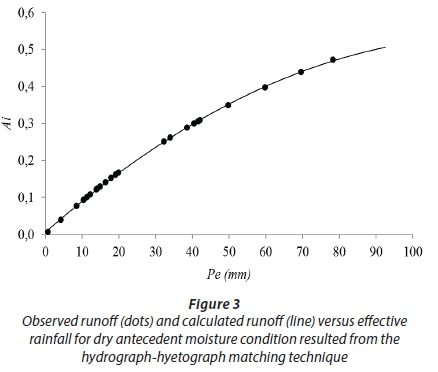
The relationships between effective rainfall (P) and the fraction of the catchment that is effectively saturated (A) resulting from both the original SCS-CN criterion and hydrograph-hyetograph matching are shown in Figs 2 and 3. In comparison with the original SCS-CN criterion, a different pattern results for the dry wetness condition when using hydrograph-hyetograph matching (Fig. 3). By applying the Ia= 0.2S criterion, a threshold of 36 mm effective rainfall depth is achieved, below which no area contributes to runoff (Fig. 2). However, this is not consistent with the recorded rainfall and runoff data.
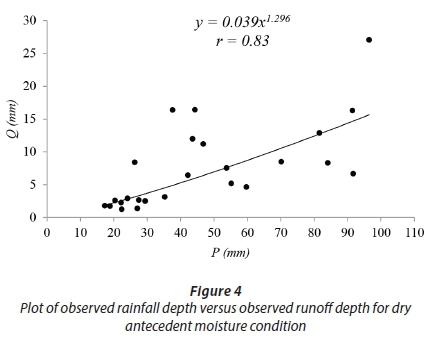
In Fig. 4, the plot of observed rainfall depths versus the corresponding runoff depths is shown for dry wetness condition and a power relationship is fitted to the data with a correlation coefficient of r = 0.83. It is clear that for the effective rainfall depth of 36 mm, approximately 5 mm runoff depth is expected, revealing that a portion of the catchment contributes to runoff. This result can be attributed to the geological and morphological aspects of the study region, which differ considerably from the prevailing conditions of the regions where the SCS-CN method was developed.
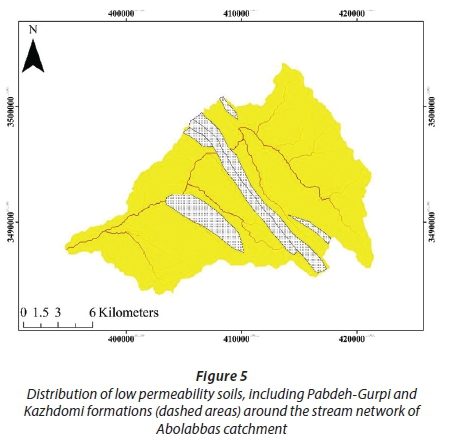
Based on the classification of the geological formations (Zarei, 2012), about 15% of the catchment is covered by soils of low permeability (Table 2). This causes the infiltration-excess runoff generation mechanism to occur shortly after the onset of rainfall, since the rainfall intensity exceeds the infiltration rate. These parts are located in the middle of the catchment on both sides of the main stream (Fig. 5), and the runoff originating from these areas is directly discharged into the Abolabbas River, causing the hydrologic response of these parts to be rapid. Moreover, the catchment area consists of steep slopes, with an average gradient of 10% (Rezaei-Sadr, 2012). The high velocity of water caused by these steep slopes, forces the surface runoff to move rapidly and the water transport process is dominated by the existing channel network rather than hillslopes. Therefore, at the beginning of the rainstorm a significant volume of runoff contributes to the surface flow and rapidly joins the main stream due to areas of low permeability as well as steep slopes. This is consistent with the left P-A. relationship in Figs 2 and 3, which was obtained from the hydrograph-hyetograph matching technique.
Average wetness condition
In Figs 6 and 7, P-A graphs obtained from both original SCS-CN criterion (I = 0.2S) and hydrograph-hyetograph comparison are shown. Similar to the dry wetness condition, for the original SCS-CN criterion, a threshold of 12 mm effective rainfall depth is detected, below which no area contributes to runoff. However, the hydrograph-hyetograph matching technique shows that after receiving 12 mm effective rainfall, nearly 20% of the catchment contributes to runoff showing a considerable difference between the two techniques.
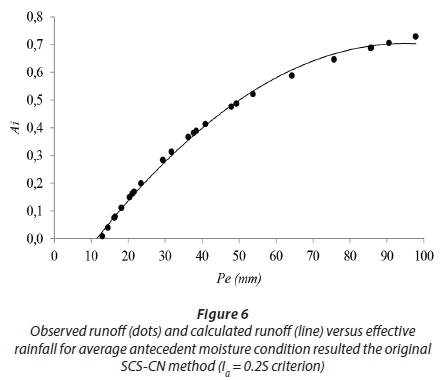
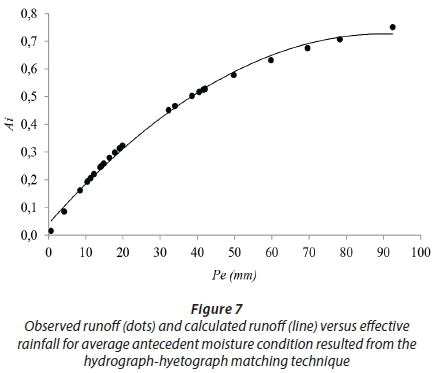
Hence, the proposed method by Steenhuis et al. (1995), in its original form which uses the criterion I = 0.2S, does not provide reliable results for dry and average wetness conditions, since the runoff generation mechanism is highly influenced by other factors such as rainfall intensity and soil permeability, leading to provocation of the infiltration-excess runoff generation mechanism. Moreover, the steep slopes diminish the rate of infiltration, leading the channel network to be the dominant mechanism of water transport throughout the catchment. On the other hand, the hydrograph-hyetograph matching technique provides more accurate results, probably because it incorporates the effects of all meteorological, geological and morphological aspects of the catchment. Since the overwhelming majority of rainfall events occur under dry and average moisture conditions throughout the region (Table 1), there is not enough evidence to support the reliability of the original SCS-CN method for delineating runoff source areas. In this regard, applying measured rainfall and runoff data to determine the initial abstraction of rainfall is strongly recommended.
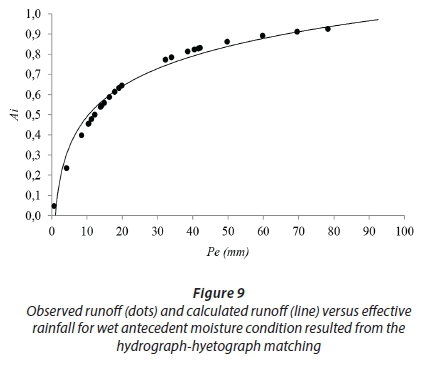
Wet condition
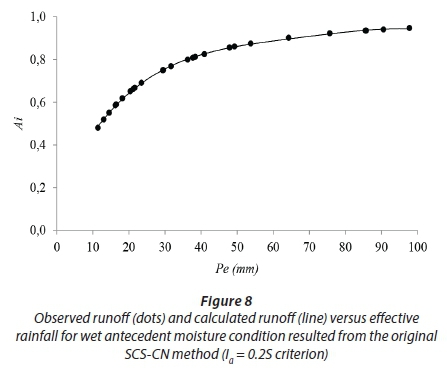
The P -A. graphs for wet conditions are shown in Figs 8 and 9. It is clear that both techniques yield very similar results under wet conditions. For example, both graphs show that after receiving 12 mm effective rainfall on the ground, approximately 48% of the catchment area contributes to runoff. In both graphs, at the beginning of rainfall, runoff contributing area increases sharply with the increase in effective rainfall. However, after about 30 mm of rainfall, which is nearly equal to the estimated maximum potential soil water retention (S) under wet conditions, the pattern is changed. The contributing area now increases slightly with increasing effective rainfall and asymptotically approaches a constant slope. According to these graphs, it is obvious that the two techniques predict the contributing area correctly in the limit of Eq. 8 when Pe= ∞. Moreover, both P-A relationships follow Eq. 8 that indicates that when Peequals S, 75% of the catchment is contributing to runoff. The fact that similar results were achieved via both methods confirms that the original form of the SCS-CN based method is reliable for wet soil conditions. This is because, at the time of rainfall, the antecedent wetness of soil is enough to provoke the saturation-excess runoff generation mechanism throughout the catchment. Under these circumstances, the fraction of rainfall which infiltrates into the soil is low, and therefore increased runoff contributes to surface flow which rapidly joins the channel network.
CONCLUSION
In order to define runoff generation mechanisms and variable-source runoff areas within a spatially highly heterogeneous catchment in the Zagros mountain region, southwest of Iran, a modified conceptual method based on the SCS-CN method (Steenhuis et al. (1995) is proposed. By simply assuming that the dominant runoff generation mechanism is saturation-excess type, the method provides a simple way to predict the fraction of catchment area producing saturation-excess runoff. Two techniques for determining initial abstraction, comprising the original SCS-CN criterion that assumes the initial abstraction equal to 0.2S and hydrograph-hyetograph matching, were applied.
It was proven that the method in its original form cannot provide accurate results for dry and average antecedent moisture conditions. However, using the hydrograph-hyetograph matching technique, which incorporates the effect of geological and morphological aspects such as soils of low permeability and steep slopes, can more accurately represent the actual runoff throughout the catchment. On the other hand, under wet soil conditions, similar results are obtained from both techniques. This demonstrates that the SCS-CN based method is reliable for wet moisture conditions because, at the time of rainfall, the antecedent wetness of soil is enough to provoke the saturation-excess runoff generation mechanism throughout the catchment.
ACKNOWLEDGMENTS
The authors would like to extend their appreciation to Khuzestan Water & Power Authority, Ahvaz, IRAN for providing rainfall-runoff data. The authors would also like to thank H. Zarei from Shahid Chamran University of Ahvaz for supplying the geological information of the study region.
REFERENCES
ANDERSON MG and BURT TP (1978) Toward more detailed field monitoring of variable source areas. Water Resour. Res. 14 1123-1131. https://doi.org/10.1029/WR014i006p01123 [ Links ]
BALTAS EA, DERVOS NA and MIMIKOU MA (2007) Determination of the SCS initial abstraction ratio in an experimental catchment in Greece. Hydrol. Earth Syst. Sci. 11 1825-1829. https://doi.org/10.5194/hess-11-1825-2007 [ Links ]
BESTON RP and MARIUS JB (1969) Source areas of storm runoff. Water Resour. Res. 5 574-582. https://doi.org/10.1029/WR005i003p00574 [ Links ]
BOUGHTON WC (1990) Systematic procedure for evaluating partial areas of catchment runoff. J. Irrig. Drain. Eng. ASCE 116 83-98. https://doi.org/10.1061/(ASCE)0733-9437(1990)116:1(83) [ Links ]
DINGMAN SL (1994) Physical Hydrology. McMillian, New York. 575 pp. [ Links ]
DUNNE T and BLACK RD (1970a) An experimental investigation of runoff production in permeable soils. Water Resour. Res. 6 (2) 478-499. https://doi.org/10.1029/WR006i002p00478 [ Links ]
DUNNE T and BLACK RD (1970b) Partial area contributions to storm runoff in a small New England catchment. Water Resour. Res. 6 1296-1311. https://doi.org/10.1029/WR006i005p01296 [ Links ]
DUNNE T, MOORE TR and TAYLOR CH (1975) Recognition and prediction of runoff-producing zones in humid regions. Hydrol. Sci. Bull. 20 305-327. [ Links ]
HAWKINS RH (1979) Runoff curve numbers for partial area catchments. J. Irrig. Drain. Eng. 105 (4) 375-389. https://doi.org/10.1061/(ASCE)0733-9437(1993)119:2(334) [ Links ]
HAWKINS RH (1993) Asymptotic determination of runoff curve numbers from data. J. Irrig. Drain. Eng. 99 (4) 519-523. [ Links ]
HAWKINS RH, JIANG R, WOODWARD DE, HJELMFELT AT, VAN MÜLLEM JA and QUAN QD (2002) Runoff curve number method: Examination of the initial abstraction ratio. In: Proceedings of the Second Federal Interagency Hydrologie Modeling Conference, ASCE Publications, 28 July-1 August 2002, Las Vegas, Nevada. [ Links ]
HEWLETT JD and HIBBERT AR (1967) Factors affecting the response of small catchments to precipitation in humid regions. In: Sopper WE and Lull HW (eds) Forest Hydrology. Pergamon Press, Oxford. [ Links ]
JIANG R (2001) Investigation of runoff curve number initial abstraction ratio. MSc thesis, University of Arizona. [ Links ]
KREWSKI D, BALBUS J, BUTLER-JONES D, HAAS C, ISAAC- RENTON J, ROBERTS KJ and SINCLAIR M (2004) Managing the microbiological risks of drinking water. J. Toxicol. Environ. Health 67 1591-1617. https://doi.org/10.1080/15287390490491909 [ Links ]
LEH MD, CHAUBEY I, MURDOCH J, BRAHANA JV and HAGGARD BE (2008) Delineating runoff processes and critical runoff source areas in a pasture hillslope of the Ozark Highlands. Hydrol. Process. 22 (21) 4190-4204. https://doi.org/10.1002/hyp.7021 [ Links ]
LYON SW, WALTER MT, GERARD-MARCHANT P and STEENHUIS TS (2004) Using a topographic index to distribute variable source area runoff predicted with the SCS curve number equation. Hydrol. Process. 18 2757-2771. https://doi.org/10.1002/hyp.1494 [ Links ]
MARTINEZ-MENA M, ALBALADEJO J and COSTILLO VM (1998) Factors influencing surface runoff generation in a Mediterranean semi-arid environment: Chicamo catchment, SE Spain. Hydrol. Process. 12 741-754. https://doi.org/10.1002/(SICI)1099-1085(19980430)12:5<741::AID-HYP622>3.0.CO;2-F [ Links ]
O'BRIEN AL (1982) Rapid water table rise. Water Resour. Bull. 18 713-715. https://doi.org/10.1111/j.1752-1688.1982.tb00056.x [ Links ]
O'CONNOR DR (2002) A strategy for safe drinking water. Report of the Walkerton Inquiry 2. Ministry of the Attorney General, Toronto. [ Links ]
REZAEI-SADR H (2012) Determination of spatio-temporal variations of rainfall and its relation with linear-nonlinear response of rainfall-runoff process in mountainous catchments. PhD thesis, Shahid Chamran University of Ahvaz. [ Links ]
REZAEI-SADR H, AKHOND-ALI AM, RADMANESH F and PARHAM GA (2012) Nonlinearity in storage-discharge relationship and its influence on flood hydrograph prediction in mountainous catchments. Int. J. Water Resour. Environ. Eng. 4 (6) 208-217. [ Links ]
REZAEI-SADR H (2015) Impact of rainfall temporal heterogeneity on relationship between curve number and rainfall depth in Zagros mountain region, Iran. J. Mt. Sci. 12(3) 689-698. https://doi.org/10.1007/s11629-014-3008-2 [ Links ]
REZAEI-SADR H (2017) Influence of coarse soils with high hydraulic conductivity on the applicability of the SCS-CN method. Hydrol.Sci. J. 62 (5) 843-848. [ Links ]
RICHARDS PL and BRENNER AJ (2004) Delineating source areas for runoff in depressional landscapes: Implications for hydrologic modeling. J. Great Lakes Res. 30 (1) 9-21. https://doi.org/10.1016/S0380-1330(04)70325-1 [ Links ]
SCHNEIDERMAN EM, STEENHUIS TS, THONGS DJ, EASTON ZM, ZION MS, NEAL AL, MENDOZA GF, and WALTER MT (2007) Incorporating variable source area hydrology into a curve-number-based catchment model. Hydrol. Process. 21 3420-3430. https://doi.10.1002/hyp.6556 [ Links ]
SCS (Soil Conservation Service) (1964) National Engineering Handbook, Section 4-Hydrology. Soil Conservation Service, USDA, Washington DC. [ Links ]
SCS (Soil Conservation Service) (1972) National Engineering Handbook, Part 630 Hydrology, Section 4. Chapter 10. Soil Conservation Service, USDA, Washington DC. [ Links ]
SIMANTON JR, HAWKINS RH, MOHSENI-SARAVI M and RENARD KG (1996) Runoff curve number variation with drainage area, Walnut Gulch, Arizona. Trans. ASAE 39 (4) 1391-1394. https://doi.org/10.13031/2013.27630 [ Links ]
SOULIS KX, VALIANTZAS JD, DERCAS N and LONDRA PA (2009) Investigation of the direct runoff generation mechanism for the analysis of the SCS-CN method applicability to a partial area experimental catchment. Hydrol. Earth Syst. Sci. 13 605-615. https://doi.org/10.5194/hess-13-605-2009 [ Links ]
SPRENGER FD (1978) Determination of direct runoff with the curve number method in the coastal area of Tanzania/East Africa. Wasser Boden I 13-16. [ Links ]
SRINIVASAN MS, WITTMAN MA, HAMLETT JM and GBUREK WJ (2000) Surface and subsurface sensors to record variable runoff generation areas. Trans. ASAE 43 651-660. https://doi.org/10.13031/2013.2746 [ Links ]
STEENHUIS TS, WINCHELL M, ROSSING J, ZOLLWEG JA and WALTER MF (1995) SCS runoff equation revisited for variable-source runoff areas. J. Irrig. Drain. Eng. 121 234-238. https://doi.org/10.1061/(ASCE)0733-9437(1995)121:3(234) [ Links ]
TEDELA N, McCUTCHEON S, RASMUSSEN T and TOLLNER W (2008) evaluation and improvements of the curve number method of hydrological analysis on selected forested catchments of Georgia. Report as of FY2007 for 2007GA143B, Georgia Water Resources Institute Report, Georgia. [ Links ]
XIAO B, WANG QH, FAN J, HAN FP and DAI QH (2011) Application of the SCS-CN model to runoff estimation in a small catchment with high spatial heterogeneity. Pedosphere 21 (6) 738-749. https://doi.org/10.1016/S1002-0160(11)60177-X [ Links ]
ZAREI H (2012) Baseflow separation using isotopic techniques and hydrochemical tracers, karstic basin in semiarid regions. PhD thesis, Shahid Chamran University of Ahvaz. [ Links ]
Received 20 April 2017
Accepted in revised form 3 April 2018
* To whom all correspondence should be addressed. ffi 0088-916-3011293 ; fax: 0088-611-3434012; e-mail: hrezaeisadr@yahoo.com














