http://dx.doi.org/10.4314/wsa.v44i1.14

 

Distribution of primary and secondary currents in sine-generated bends

 

 

Li He^*

Key Laboratory of Water Cycle and Related Land Surface Processes, Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing 100101, China

 

 

---

ABSTRACT

The secondary circulation in a meandering channel redistributes the velocity over the bend. However, the shift of primary flow by secondary currents is not quantitatively understood, due to the difficulty in isolating the role of curvature-driven secondary flow from that of topography-driven secondary flow in bed-deformed meanders. The influences of curvature-driven and topography-driven secondary currents on the redistribution of primary flow in sine-generated meandering channels were examined by CCHE2D. The model is calibrated using data measured in two sets of laboratory experiments including flat-bed flow and mobile-bed flow. Analysis indicated that topography-induced current mainly contributes to the redistribution of primary flow from inner to outer bank in the curved channels, rather than the secondary flow driven by curvature.

Keywords: primary flow, secondary flow, meander, numerical analysis

---

 

 

INTRODUCTION

Secondary (transverse) flows in meanders, including curvature-driven and topography-driven secondary currents, have been considered to be primarily responsible for redistributing or shifting the primary (longitudinal) flow (Chen and Tang, 2012). A curvature-driven secondary flow is caused by the difference in centrifugal forces between the upper and lower layers of a curved flow. However, the bed topography plays an important role in the shifting of shallow, open channel flow (Smith and Mclean, 1984; Nelson and Smith, 1989; Dietrich and Whiting, 1989; Abad and Garcia, 2009a, 2009b). Chen (2005) summarized previous experiments conducted in sine-generated channels and concluded that the core of maximum velocity remains at the inner bank, until reaching a crossover section in low-sinuosity channels with flat beds. Chen and Duan (2006) theoretically confirmed the above conclusion with an analytical flow solution in a sine-generated channel. Qualitatively, the core of maximum primary flow will gradually run across the channel centreline and shift towards the outer bank of bends as the channel develops into a large-sinuosity one with a deformed bed. Both curvature-driven and topography-driven secondary flows contribute to the shifting process. However, the shift of primary flow by secondary currents is not quantitatively understood. One of the major obstacles results from the difficulty in isolating the role of curvature-driven secondary flow from that of helical flow in bed-deformed meanders. Chen and Tang (2012) have evaluated the role of the two secondary currents in the evolution of sine-generated meanders by coupling Johannesson and Parker's (1989) one-dimensional flow model with the bank erosion and retreat model (BERM). However, the above flow model adopts the first-order analytical solution of Navier-Stokes equations, which is assumed to be valid only for mildly-curved channels.

This study aims at analysing the redistribution of primary flow in sine-generated channels by numerical simulation of CCHE2D. Firstly, the CCHE2D is calibrated using data measured in two laboratory experiments, including flat-bed (Da Silva, 1995) and deformed-bed (Termini, 2009). Then, two bends with different sinuosity and bed topography are analysed, with deflection angles of 30° and 110° representing 'small' and 'large' sinuosity respectively.

 

METHODS

Numerical model

CCHE2D is an integrated package for two-dimensional depth-integrated free surface hydrodynamics modelling (Jia et al., 2001). CCHE2D solves dynamic processes, e.g., river flows, non-uniform sediment transport, and morphologic processes, with the depth-integrated Reynolds equations, transport equations, sediment sorting equation, bedload and bed deformation equations. More importantly, two dispersion terms were included in the governing equations, which lead to a better simulation of particle movement in curved channels with large sinuosity (Jia et al., 1999, 2002). This model is based on the efficient element method, a collocation approach of the weighted residual method. Dry and wet capability enables one to simulate fluctuating flows with complex topography with ease. Equations by Wu and Wang (1999) and Wu (2001) have been used to calculate the bed roughness and bedload transport, respectively. Verification and validation using physical model data shows that it is capable of reproducing realistic physical mechanisms and giving a realistic estimation of the turbulence intensity of the flow. There have been many applications to natural channels with complex flow conditions, topography and hydraulic structures (Duan et al. 2001; Jia and Wang 1999; Jia et al., 2002; Da Silva et al., 2006; Termini, 2015; Nassar, 2011; Misiura and Czechowski, 2015; Rostami and Habibi, 2014; Tena et al., 2013; Zhuang et al., 2009; Kantoush et al., 2008; Huang and NG, 2007; Huang et al., 2013). Thus, it is adopted to simulate the flow, sediment transport, and bed deformation in these two sine-generated meandering channels. CCHE2D Mesh Generator is adopted to create a structured mesh.

Experimental setup

Experiments by Da Silva (1995) and Termini (2009) were chosen to represent immobile and mobile bed cases, respectively. The cross-sections of these two experiments are rectangular, and each has a length that is equal to two meander lengths. The simple schematic graphs of these flumes are shown in Fig. 1. For a flume with deflection angle of 110°, the width of the flume in Termini (2009) is different from that of the flume in Da Silva (1995), and no size information is shown in Fig. 1.

 

 

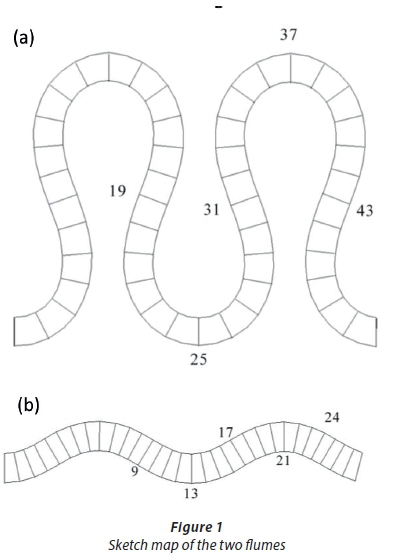
In the experiments by Da Silva (1995), the total length of the meandering channel is 5.4 m in the small sinuosity channel and 18.6 m in the large sinuosity channel. The bed of the flume is of quartz sand with D₅₀ = 2.2 mm. The upstream and the downstream end are connected to a straight (transitional) approach channel. The lengths for these two transitional channels are 0.8 m and 0.6 m, respectively.

In the experiments by Termini (2009), the channel-length is 23.46 m, and the ratio R_c/B (R_c = radius of curvature at centreline of the apex, B = width of the channel) is 2.31. The bed of the flume is quartz sand with D₅₀ = 0.65 mm, and geometric standard deviation is δ_g = 1.3. The critical boundary shear stress for entrainment of the median sediment diameter is 0.35 N/m². Two straight channels are constructed at the upstream and downstream ends of the meandering flume for transition.

The pertinent parameters of their flow and plain-geometry are summarized in Table 1.

Previous research had pointed out that a small value of width to depth ratio (B/H = 2.68) can represent the flow situation in mountain rivers, particularly within flood events (Blanckaert and De Vriend, 2004; Blanckaert, 2010; Abad and Garcia, 2009a, 2009b). Hooke et al. (2011) have also pointed out that the experiment of Termini and Piraino (2011) is closer to many natural meandering rivers, as it has large amplitude meander bends with slowly varying channel curvature and two different values of the width to depth ratio.

The maximum streamwise velocity occurs at the free surface regardless of curvature at high values of (B/H), and its variation in a river bend with a small aspect ratio (B/H) is due to the effect of the walls (Afzalimehr and Singh, 2009; Ferro, 2003). The range of width to depth ratios (B/H) in these two experimental sets is 9.1-13.3. Thus, these two experiments can represent the flow situation in natural meandering rivers, and the maximum streamwise velocity occurs at the free surface.

The ratio of curvature radius to river width (relative curvature) is a very important factor which plays the main role in morphological changes of river meander (Esfahani and Keshavarzi, 2011). On this basis, river bends can be classified into 2 classes: strongly curved bends with relative curvature smaller than 3, and mild bends which have relative curvature larger than 3 (Leschziner and Rodi, 1979; Rozovskii, 1961). Odgaard and Bergs (1988) performed some experiments inside a mild (R_c/B=5.4) 180° alluvial curved bend. They reported that velocity components, bed topography and flow structure are affected by changes in the curvature. The contribution to probability of events for strongly curved meanders with relative curvature (R_c/B) of 2.6 was found to be higher than for mild curved meanders with relative curvature (R_c/B) of 4.43 (Esfahani and Keshavarzi, 2011). The relative curvature of the flume in Termini (2009) is 2.31, representing strongly curved bends.

Whiting and Dietrich (1993) examined the impacts of topography-induced secondary flow on depth-averaged main flow based on experiments in curved flumes with aspect ratios between 5 and 17.2. Da Silva et al. (2006) pointed out that the convective structure of the depth-averaged flow can be used to predict the features of the bed topography in meandering channels with aspect ratios of 12.5 < B/H < 13.3. Experiments by Termini (2009) were conducted in a sine-generated flume with aspect ratios ranging from 9.1 to 16.7, which can be referred to as 'wide' channels based on the definition of Bolla Pittaluga and Seminara (2011).

Model calibration

The model of CCHE2D was verified using a dataset obtained from physical experiments to get proper parameters.

The performance was evaluated using the bias (BIAS), Nash-Sutcliffe (NS) statistics of the residuals, mean-absolute-error (MAE), and percentage difference (PD) defined as:

where O_mean is the mean value of observed value; S_i and O_i are the simulated and observed value, respectively; subscript I represents each cross section, and I is the total amount of evaluated points. BIAS measures the tendency of the simulated flows to be larger or smaller than their observed counterparts; the optimal value is 0.0, positive values indicate a tendency to overestimation, and negative values indicate a tendency to underestimation. NS measures the fraction of the variance of the observed flows explained by the model in terms of the relative magnitude of the residual variance ('noise') to the variance of the flows ('information'); the optimal value is unity and values should be larger than 0.0 to indicate 'minimally acceptable' performance. NS could be used to evaluate the degree of conformity. A smaller value for MAE indicates better simulation. PD measures the difference for total amount and peak values between simulated and observed. The units of BIAS and MAE are the same as that of the evaluated value, while NS and PD are dimensionless.

Figures 2 and 3 and Table 2 show the calibration results of water surface elevations and depth-averaged flow velocities, respectively. The calibration is satisfactory, in general, except for the overestimated water surface elevations at the centreline. The values for wall slip during simulation are 0.88 (flume with deflection angle of 30°) and 0.9 (flume with deflection angle of 110°), respectively. The values for the roughness coefficient are 0.017 (flume with deflection angle of 30°) and 0.0155 (flume with deflection angle of 110°), respectively.

The calibration of measured and simulated steady bed profile at the channel banks is shown in Table 3 and Figure 4. The model calibration is satisfactory in general. It shows that estimation of the steady bed profile around the apex section and inflection section is not very good, e.g., Sections 25 and 37. The deposition at the left bank of Section 37 is overestimated by 3.1 cm, and the erosion at the right bank is underestimated by 3.4 cm. The parabolic eddy viscosity model and 0.9 wall slip coefficient are selected. The bed roughness is estimated using the formula of Wu et al. (1998).

 

 

REDISTRIBUTION OF PRIMARY FLOW

The flow structure inside the river meanders is complicated and is influenced by various properties and conditions, for example, the curvature and properties of bends (multi-bend or single bend) (Esfahani and Keshavarzi, 2011). Then, the influence of curvature-driven and topography-driven secondary flow on the redistribution of primary flow are analysed separately. Finally, the temporal variation of the shifting of primary flow is analysed.

Influence of curvature

The curvature-induced secondary flow is the result of a local imbalance between the vertically varying centrifugal force and the cross-stream pressure gradient, and it gives rise to the typical motion of helical flow. Streamline curvatures of river meanders exert significant influence on mean flow, secondary currents, and turbulence characteristics (Ghamry and Steffler, 2005; Anwar, 1986; Odgaard and Bergs, 1988; Blanckaert and De Vriend, 2005). The hydrodynamics of sharp bends may differ from those for bends with moderate or mild curvature (Bagnold, 1960; Leeder and Bridges, 1975; Hickin, 1978; Nanson, 2010), as the velocity components, bed topography and flow structure are affected by changes in the curvature (Da Silva, 1995). The findings of Termini (2009) also confirmed that changing river curvature has a significant influence on sediment transport and bed topography and showed that Termini's results were consistent with those of Solari et al. (1999) and Da Silva et al. (2006).

The geometries of the channels are based on Da Silva's (1995) experiments and summarized in Table 1. In Figs 5 and 6, sub-graphs (a) and (b) plot the intensities of primary flows and secondary flows, respectively. These channels have flat beds. Therefore, the secondary flows shown in Figs 5(b) and 6(b) are caused by channel curvature only. Figures 5(c) and 6(c) show the variation of main flow with different discharges. The core area of θU_s/θ_n may enlarge with increasing discharge (Figs 5(d) and 6(d); Table 4). With increasing sinuosity, the core area may move upward and cross the apex section. This indicates that the value of θU_s/θ_n may increase with increasing discharge and sinuosity, which can also be observed in Xu et al. (2017). Based on Figs 5 and 6, the core of maximum primary flow remains at the inner bank until reaching crossover sections. Da Silva (1995) also stated that, at the inner bank of ingoing river meanders and along the flow direction, the flow accelerates from the entrance to the apex, whereas it decelerates from the apex to the bend exit. The location of the high-flow core tends to migrate towards upstream in the high-sinuosity channel. Velocity around the apex section in the next bend is larger than that in the previous bends, and the location of core of the velocity is moving upward, especially in the channel with larger sinuosity.

 

 

By contrast, the secondary flows are stronger around the transition sections with maximum velocity being about 2%~5% of that of primary flows. With comparable hydraulic parameters, including inflow discharge and depth-averaged velocity, the secondary flow in a channel with small sinuosity is about 2.4 to 5 times that in a channel with large sinuosity. The main reason is that the flow in the channel with small sinuosity runs approximate in a straight line, which leads to a large angle between flow direction and the s axis of the curvilinear coordinate. However, the flow in a channel with large sinuosity runs approximately along the bend, which leads to a small angle between flow direction and the s axis of the curvilinear coordinate. The magnitude of secondary currents increases in the next bend. Siebert and Goetz (1975) also found that measurements of the secondary flow in two subsequent 180° bends showed that the strength of secondary flow decreased in the second bend. The reason is that the secondary motion is reversed in subsequent bends so that the residual motion from the previous bend counteracts the setting up of a secondary current in the next bend (Siebert and Goetz, 1975).

Influence of topography

The detailed flow and geometry characteristics are given in Table 2. The influence of bed deformation on redistribution of primary flow is compared by simulation of mobile bed and flat bed (Figs 7 and 8). It shows that the core of maximum primary flow moves to the outer bank, and the core area moves upward slightly. Scouring in the bend leads to deep sections at the toe of the outer bank, and the presence of secondary currents and the greater depths at the outer bank cause high velocity along the outer bank (Ghodsian and Mousavi, 2006). Declining bed shear stress and sediment transport rates along the inner bank cause net sediment deposition and point bar development in curved channels, and the point bar in turn influences the flow field around a bend as the bar forces high‐velocity fluid toward the outer bank (Dietrich and Smith, 1983). The sediment erosion/deposition has a limited contribution to the magnitude of depth-averaged velocity.

The core area of the secondary current moves upward, apparently, in the mobile bed, and the secondary currents in the mobile run are much larger than in the immobile run (about 2 to 4.5 times).

In Fig. 9, the black arrows demonstrate the initial primary flows with a flat bed and the red arrows demonstrate the primary flows at time t = 51.4 min with a deformed channel bed. With the two overlapping flow fields, Fig. 9(b) also shows the intensity of secondary flow (curvature-driven and topography-driven) at t = 51.4 min. In contrast, Fig. 9(a) shows the curvature-driven secondary flow only with a flat bed. Based on Figs 9(a) and 9(b), the re-distribution of primary flow mainly occurs in the upstream reach with a strong topography-driven secondary current. It is difficult to find the relationship between the re-distribution of primary flow with the curvature-driven secondary current in Fig. 9(a), although in theory it should work in a similar way to the topography-driven secondary current. The topography-driven current is about 10 times stronger than the curvature-driven current in the experiments by Termini (2009).

Changes with time

The equilibrium bed topography configuration was reached after about 150 min in the experiment of Termini (2009) and numerical simulation. However, numerical simulation shows that the primary flow remains after about 52 min. So, the analysis focuses on the first 52 min of the experiment. Besides, numerical simulation shows that the changing of flow characteristics in Section 7-19 and Section 31-43 continue when the bed profile reaches a steady state after 150 min. So, the variations of secondary current and primary flow in Section 19-31 between 52 min are analysed.

The transverse bed slope in Bend Section 25 is selected to analyse the variation of transverse bed slope (Fig. 10). At the beginning (about 0.1 min), bed deformation consists of erosion in the inner bank and deposition in the outer bank. At that time, the primary flow stays at the inner bank, and the core of secondary flow appears around the apex section (Fig. 11). At around 7.3 min, the bed deformation only consists of deposition in the inner bank. So, the area with erosion shifts from the inner bank to outer bank during 7.3 min. After 7.3 min, erosion stays at the outer bank, and deposition stays at the inner bank. Besides, the core of secondary flow moves to the upstream section, and the primary flow shifts to the outer bank with topography changing after 7.3 min (Fig. 11). The primary flow moves with the area of erosion in general, which indicates that the shift of primary flow may primarily be driven by topography.

The outer bank will be protected against the effect of the centre region cell and therefore against erosion, since the outer bank cell produces an obstruction between the outer bank and the centre region cell (Blanckaert and De Vriend, 2004; Blanckaert and Graf, 2001).

In the literature, the dimensionless 'scour factor' which represents the effect of momentum redistribution exerted by the topography-driven current, has often been assumed to be constant during channel evolution (Engelund, 1974; Kikkawa et al., 1976; Zimmerman and Kennedy, 1978; Ikeda et al., 1981; Parker and Andrews, 1986; Odgaard, 1989). It is convenient to calculate the parameter A with the numerical simulation. The coefficient which quantified the transverse bed slope can be calculated as for Chen and Tang (2012).

where A is the parameter, H is the reach-averaged flow depth (m), and n is the transverse direction, η is the channel bed elevation (m), and C is the channel centreline curvature defined in the following expression:

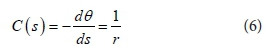
where θ is the deflection angle between the down-channel direction and the x axis, and r is the local radius of the curvature.

Figure 12 shows the variance of Parameter A and A_s at Section 25. Duan and Julien (2010) pointed out that in flat-bed channels the transverse slope and the plan form sinuosity increase with the evolution of a meandering channel; the core of maximum velocity will gradually shift to the outer bank, and the maximum transverse bed slope will be reached when the channel evolution reach an equilibrium state. The variation of parameter A agrees well with the development of a transverse bed slope. At the beginning, A = 0, indicating that the channel is flat in the transverse direction. Johannesson and Parker (1989) also pointed out that Parameter A vanishes when the channel bed is flat in the transverse direction. Parameter A increases gradually with the evolution of a meandering channel, and reaches its maximum of 1.6 at 1.5 h, when the equilibrium bed topography was reached. Numerical simulations of the evolution of the plan form of meandering rivers indicate that it is more realistic to treat A as a variable obtained from a slowly varying eddy viscosity approach (Camporeale et al. 2007).

 

 

As the amplitude of meanders increases, the most pronounced regions of erosion or deposition shift gradually to the vicinities of apexes (Yalin, 1992; Da Silva, 1995; Duan, 1998).

The values of Parameter A_s, which represents the effects of momentum redistribution exerted by the curvature-driven secondary currents (Johannesson and Parker, 1989), are as small as a tenth of the values of A, which intuitively indicates the insignificance of curvature-driven flow (Chen and Tang, 2012). A similar conclusion was obtained by Abad and Garcia (2009a, 2009b) by comparing the locations of the core of maximum velocity in flat-bed and deformed-bed laboratory bend flumes. According to Fig. 12, the parameter A_s around the inner bank is negligible, with a maximum value of 0.16.

 

DISCUSSION AND CONCLUSIONS

The curvature and bed topography of a curved river play an important role in the analysis of various aspects of river engineering problems, such as river regulation, navigability, bank protection, and dispersion of heat and pollutants. So, the sine-generated curves were selected to analyse the influence of curvature and bed topography on the shifting of the primary flow.

Two published laboratory experiments, including flat bed and mobile bed, are selected to investigate the influence of secondary flow on the shift of primary flow. Firstly, the CCHE2D experimental data were used to verify the results of the numerical model. Then, the simulated results were used to analyse the influence of two kinds of second currents on the shifting of primary flow. It compared the difference of primary flow in rigid and mobile experiments by CCHE2D. Calculated results indicated that:

• The shifting of primary flow from inner to outer bank in the curved channels is dominated by topography-induced current rather than the secondary flow driven by curvature

• Secondary currents in a flume with small amplitude are larger than those in a flume with large amplitude

• Sediment movement may lead to increased secondary currents

• In flat-bed channels, the transverse slope and the parameter A increase with the evolution of a meandering channel, and the parameter A reaches its maximum value as maximum transverse bed slope is reached when channel evolution reaches an equilibrium state.

The analysis of this paper is based on the simulation of a depth-averaged model. However, two-dimensional models cannot sufficiently present the influence of curvature on turbulent characteristics in meanders (Blanckaert and De Vriend, 2005). The distribution of velocity may differ in various bends, and the situation of maximum tangential velocity moves in depth from near-bed to near the water surface by decreasing the curvature (Esfahani and Keshavarzi, 2011). In strongly curved bends with small values of width/depth ratio (B/H), contour lines with the highest tangential velocity are located near the bed (or intermediate region and near the bed) in sharp multi-bends (Blanckaert and Graf, 2001; Blanckaert and De Vriend, 2004, 2005; Tilston et al., 2009; Esfahani, 2009; Esfahani and Keshavarzi, 2011). The maximum streamwise velocity is located in the intermediate region near the free surface region in mild multi-bends, and this result for mild bends is similar to a straight open channel (Esfahani, 2009; Esfahani and Keshavarzi, 2011; Jung and Yoon, 2000). Jung and Yoon (2000) conducted laboratory experiments in a mild 180° curved bend with different bed materials and found that, in the upper part of the bend, a situation of maximum streamwise velocity is not changed by the effect of bed materials and is skewed inwards. This indicated that the location of the highest tangential velocity in the vertical direction may be influenced by relative curvature and width/depth ratio. So, analysis of three-dimensional velocity is necessary in further research.

 

NOTATION

A and A_s are parameters

B = channel width, for rectangular, it is also the flow width

C = channel central line curvature (m^-1)

D₅₀ = mean diameter of grain size (mm)

F_r = Froude number

H = channel-averaged flow depth (m)

h = flow depth (m)

I = total amount of evaluated points

L = length of a meandering channel (in plan view)

O_mean = mean value of observed value

Q = flow rate

r = local radius of the curvature (m)

R_c = radius of curvature at centreline of the apex

R_e = Reynolds number

s and n are the two axes of curvilinear coordinate

S_bc = bed slope of a straight channel

S_i and O_i are the simulated and observed value, respectively

t = time

U = channel-averaged velocity

u_s = velocity

u_s,ma = maximum value of u_s

v_* = shear velocity

Z = changed bed elevation (cm)

θ₀ = deflection angle of sine-generated flume

Λ = meander wavelength

η = channel bed elevation (m)

σ = sinuosity

δ_g = geometric standard deviation

subscript i represents each evaluating point

 

ACKNOWLEDGEMENTS

This research was supported by (1) the National Key Research and Development Program of China (2016YFC0402303); (2) National Natural Science Foundation of China (51579230,51779242, 41330751,51509234, 51109198); (3) National Key Technology Research and Development Program (2012BAB02B02); and (4) National Program on Key Basic Research Project (2011CB403305). The authors are grateful for constructive comments provided by Dr Dong Chen and Dr Shiyan Zhang; the reviewers and Editor also provide invaluable suggestions to improve the paper.

 

REFERENCES

ABAD JD and GARCIA MH (2009a) Experiments in a high-amplitude Kinoshita meandering channel 1: Implications of bend orientation on mean and turbulent flow structure. Water Resour. Res. 45 W02401.         [ Links ]

ABAD JD and GARCIA MH (2009b) Experiments in a high-amplitude Kinoshita meandering channel 2: Implications of bend orientation on bed morphodynamics. Water Resour. Res. 45 W02402.         [ Links ]

AFZALIMEHR H and SINGH VP (2009) Influence of meandering on the estimation of velocity and shear velocity in cobble-bed channels. J. Hydraul. Eng. 4 (10) 1126-1135. https://doi.org/10.1061/(ASCE)HE.1943-5584.0000105        [ Links ]

ANWAR HO (1986) Turbulent structure in a river bends. J. Hydraul. Eng. 112 657-669. https://doi.org/10.1061/(ASCE)0733-9429(1986)112:8(657)        [ Links ]

BAGNOLD RA (1960) Some aspects of the shape of river meanders. U.S. Geological Survey Professional Paper 282‐E. United States Geological Survey, Washington, D.C.         [ Links ]

BLANCKAERT K (2010) Topographic steering, flow recirculation, velocity redistribution, and bed topography in sharp meander bends. Water Resour. Res. 46 W09506.         [ Links ]

BLANCKAERT K and DE VRIEND HJ (2004) Secondary flow in sharp open-channel bends. J. Fluid Mech. 498 353-380. https://doi.org/10.1017/S0022112003006979        [ Links ]

BLANCKAERT K and DE VRIEND HJ (2005) Turbulence structure in sharp open-channel bends. J. Fluid Mech. 536 27-48. https://doi.org/10.1017/S0022112005004787        [ Links ]

BLANCKAERT K and GRAF WH (2001) Mean flow and turbulence in open-channel bend. J. Hydraul. Eng. 127 (10) 835-847. https://doi.org/10.1061/(ASCE)0733-9429(2001)127:10(835)        [ Links ]

BOLLA PITTALUGA M and SEMINARA G (2011) Nonlinearity and unsteadiness in river meandering: a review of progress in theory and modeling. Earth Surf. Proc. Land. 36 (1) 20-38. https://doi.org/10.1002/esp.2089        [ Links ]

CAMPOREALE C, PERONA P, PORPORATO A and RIDOLFI L (2007) Hierarchy of models for meandering rivers and related morphodynamic processes. Rev. Geophys. 45 (28) RG1001. https://doi.org/10.1029/2005RG000185        [ Links ]

CHEN D (2005) Computational modeling of meandering channel evolution and width adjustment. Dissertation, Program of Hydrologic Science, University of Nevada, Reno.         [ Links ]

CHEN D and DUAN JG (2006) Simulating sine-generated meandering channel evolution with an analytical model. J. Hydraul. Res. 44 (3) 363-373. https://doi.org/10.1080/00221686.2006.9521688        [ Links ]

CHEN D and TANG CL (2012) Evaluating secondary flows in the evolution of sine-generated meanders. Geomorphology 163 (SI) 37-44. https://doi.org/10.1016/j.geomorph.2012.04.010        [ Links ]

DA SILVA AMF (1995) Turbulent flow in sine-generated meandering channels. PhD thesis, Queen's University. https://doi.org/10.1061/(ASCE)0733-9429(2006)132:10(1003)        [ Links ]

DA SILVA AMF, EI-TAHAWY T and TAPE WD (2006) Variation of flow pattern with sinuosity in sine-generated meandering streams. J. Hydraul. Eng. 132 (10) 1003-1014.         [ Links ]

DIETRICH WE and SMITH JD (1983) Influence of the point bar on flow through curved channels. Water Resour. Res. 19 (5) 1173-1192. https://doi.org/10.1029/WR019i005p01173        [ Links ]

DIETRICH WE and WHITING P (1989) Boundary shear stress and sediment transport in river meanders of sand and gravel. In: Ikeda S and Parker G (eds) River Meandering. American Geophysical Union. Water Resources Monograph. 1-50. https://doi.org/10.1029/WM012p0001        [ Links ]

DUAN JG and JULIEN PY (2010) Numerical simulation of meandering evolution. J. Hydrol. 391 (1-2) 36-48. https://doi.org/10.1016/j.jhydrol.2010.07.005        [ Links ]

DUAN JG, WANG SSY and JIA YF (2001) The applications of the enhanced CCHE2D model to study the alluvial channel migration processes. J. Hydraul. Res. 39 (5) 469-480. https://doi.org/10.1080/00221686.2001.9628272        [ Links ]

DUAN GH (1998) Simulation of alluvial channel migration processes with a two-dimensional numerical model. PhD thesis, University of Mississippi.         [ Links ]

ENGELUND F (1974) Flow and bed topography in channel bends. J. Hydraul. Div. 102 (3) 416-418.         [ Links ]

ESFAHANI FS (2009) Experimental investigation of erosion and deposition in river meanders. MSc thesis, Shiraz University.         [ Links ]

ESFAHANI FS and KESHAVARZI A (2011) Effect of different meander curvatures on spatial variation of coherent turbulent flow structure inside ingoing multi-bend river meanders. Stoch. Env. Res. A. 25 913-928. https://doi.org/10.1007/s00477-011-0506-4        [ Links ]

FERRO V (2003) ADV measurements of velocity distributions in a gravel-bed flume. Earth Surf. Proc. Land. 28 (7) 707-722. https://doi.org/10.1002/esp.467        [ Links ]

GHAMRY HK and STEFFLER PM (2005) Two-dimensional depth-averaged modeling of flow in curved open channels. J. Hydraul. Res. 43 (1) 44-55. https://doi.org/10.1080/00221680509500110        [ Links ]

GHODSIAN M and MOUSAVI SK (2006) Experimental study on bed scour in a 90° channel bend. Int. J. Sediment Res. 21 (4) 324-328.         [ Links ]

HE L and CHEN D (2013) Modeling curvature- and topography-driven secondary currents in sine-generated meandering channels. In: World Environmental and Water Resources Congress 2013: Showcasing the future - Proceedings of the 2013 Congress. 19-23 May, American Society of Civil Engineers (ASCE). 1727-1735. https://doi.org/10.1061/9780784412947.170        [ Links ]

HICKIN EJ (1978) Mean flow‐structure in meanders of the Squamish River, British Columbia. Can. J. Earth Sci. 15 (11) 1833-1849. https://doi.org/10.1139/e78-191        [ Links ]

HOOKE RLEB (1975) Distribution of sediment transport and shear stress in a meander bend. J. Geol. 83 (5) 543-566. https://doi.org/10.1086/628140        [ Links ]

HOOKE JM, GAUTIER E and ZOLEZZI G (2011) River meander dynamics: developments in meandering and empirical analysis. Earth Surf. Proc. Land. 36 (11) 1550-1553. https://doi.org/10.1002/esp.2185        [ Links ]

HUANG SL and NG CO (2007) Hydraulics of a submerged weir and applicability in navigational channels: Basic flow structures. Int. J. Numer. Meth. Eng. 69 (11) 2264-2278. https://doi.org/10.1002/nme.1849        [ Links ]

HUANG SL, JIA YF, GAO GH, CHEN QW and WANG SSY (2013) Numerical comparison of three- and two-dimensional model for modeling meandering channel flow. In: Proceedings of the 35th IAHR World Congress, 08-13 September 2013, China. 106-113.         [ Links ]

IKEDA S, PARKER G and SAWAI K (1981) Bend theory of river meanders, Pate I, Linear development. J. Fluid Mech. 112 (NOV) 363-377. https://doi.org/10.1017/S0022112081000451        [ Links ]

JIA Y and WANG SSY (1999) Numerical model for channel flow and morphological change studies. J. Hydraul. Eng. 125 (9) 924-933. https://doi.org/10.1061/(ASCE)0733-9429(1999)125:9(924)        [ Links ]

JIA Y, KITAMURA T and WANG SSY (2001) Simulation of scour process in plunging pool of loose bed-material. J. Hydraul. Eng. 127 (3) 219-229. https://doi.org/10.1061/(ASCE)0733-9429(2001)127:3(219)        [ Links ]

JIA Y, WANG SYY and XU YC (2002) Validation and application of a 2D model to channels with complex geometry. Int. J. Comput. Eng. Sci. 3 (1) 57-71. https://doi.org/10.1142/S146587630200054X        [ Links ]

JOHANNESSON H and PARKER G (1989) Velocity redistribution in meandering rivers. J. Hydraul. Eng. 115 (8) 1019-1039. https://doi.org/10.1061/(ASCE)0733-9429(1989)115:8(1019)        [ Links ]

JUNG JW and YOON SE (2000) Flow and bed topography in a 180-degree curved channel. In: 4^th International Conference on Hydroscience and Engineering. Korea Water Resources Association.         [ Links ]

KANTOUSH SA, BOLLAERT E and SCHLEISS AJ (2008) Experimental and numerical modeling of sedimentation in a rectangular shallow basin. Int. J. Sediment Res. 23 (3) 212-232. https://doi.org/10.1016/S1001-6279(08)60020-7        [ Links ]

KIKKAWA H, IKEDA S and KITAGAWA A (1976) Flow and bed topography in curved open channels. J. Hydraul. Div. 102 (9) 1327-1342.         [ Links ]

LEEDER MR and BRIDGES PH (1975) Flow separation in meander bends. Nature 253 (5490) 338-339. https://doi.org/10.1038/253338a0        [ Links ]

LESCHZINER M and RODI W (1979) Calculation of strongly curved open channel flow. J. Hydraul. Div. 105 (7) 1111-1112.         [ Links ]

MISIURA K and CZECHOWSKI L (2015) Numerical modeling of sedimentary structures in rivers on Earth and Titan. Geol. Q. 59 (3) 565-580.         [ Links ]

NASSAR MA (2011) Multi-parametric sensitivity analysis of CCHE2D for channel flow simulations in Nile River. J. Hydro-environ. Res. 5 (3) 187-195. https://doi.org/10.1016/j.jher.2010.12.002        [ Links ]

NANSON RA (2010) Flow fields in tightly curving meander bends of low width‐depth ratio. Earth Surf. Proc. Land. 35 (2) 119-135.         [ Links ]

NELSON JM and SMITH JD (1989) Flow in meandering channels with natural topography, In: Ikeda S, Parker G (eds) River Meandering. Water Resour. Monogr. Ser. vol. 12. AGU, Washington, DC. 69-102. https://doi.org/10.1029/WM012p0069        [ Links ]

ODGAARD AJ and BERGS MA (1988) Flow processes in a curved alluvial channel. Water Resour. Res. 24 (1) 45-56. https://doi.org/10.1029/WR024i001p00045        [ Links ]

ODGAARD AJ (1989) River meander model. I: development. J. Hydraul. Eng. 115 (11) 1433-1450.         [ Links ]

PARKER G and ANDREWS ED (1986) On the time development of meander bends. J. Fluid Mech. 162 139-156. https://doi.org/10.1017/S0022112086001970        [ Links ]

ROZOVSKII IL (1961) Flow of water in bends of open channels. Academy of Sciences of the Ukrainian SSR, Kiev, Israel Program for Scientific Translation, Jerusalem 1963.         [ Links ]

ROSTAMI M and HABIBI S (2014) Numerical simulation of local tributary widening impacts on hydro-morphological processes of river confluence using CCHE2D. In: Proceedings of the International Conference on Fluvial Hydraulics, River Flow 2014, 3-5 September, CRC Press/Balkema. 1015-1023. https://doi.org/10.1201/b17133-137        [ Links ]

SIEBERT W and GOETZ W (1975) Study on the deformation of secondary flow in models of rectangular meandering channels. In: Proceedings of the 16^th Congress of the IAHR, 27 July - 1 August 1975, IAHR, São Paulo, Brazil. Volume 2. 141-149.         [ Links ]

SMITH JD and MCLEAN SR (1984) A model for flow in meandering streams. Water Resour. Res. 20 (9) 1301-1315. https://doi.org/10.1029/WR020i009p01301        [ Links ]

SOLARI L, ZOLEZZI G and SEMINARA G (1999) Curvature driven distortion of free bars in river bends, In: Proceedings of the IAHR symposium on river, coastal and estuarine morphodynamics, 6-10 September 1999, Genova, Italy, 563-573.         [ Links ]

TERMINI D and PIRAINO M (2011) Experimental analysis of cross‐sectional flow motion in a large amplitude meandering bend. Earth Surf. Proc. Land. 36 (2) 244-256. https://doi.org/10.1002/esp.2095        [ Links ]

TERMINI D (2015) Momentum transport and bed shear stress distribution in a meandering bend: Experimental analysis in a laboratory flume. Adv. Water Resour. 81 128-141. https://doi.org/10.1016/j.advwatres.2015.01.005        [ Links ]

TERMINI D (2009) Experimental observations of flow and bed processes in large-amplitude meandering flume. J. Hydraul. Eng. 135 (7) 575-587. https://doi.org/10.1061/(ASCE)HY.1943-7900.0000046        [ Links ]

TILSTON MC, RENNIE R, ARNOTT WC and POST G (2009) On the nature of coherent turbulent structures in channel bends: burst-sweep orientations in three-dimensional flow fields. In: 33^rd IAHR Congress: Water Engineering for a Sustainable Environment, 9-14 August, ASCE, Vancouver, Canada. ISBN: 978-94-90365-01-1.         [ Links ]

TENA A, KSIAZEK L, VERICAT D and BATALLA RJ (2013) Assessing the geomorphic effects of a flushing flow in a large regulated river. River Res. Appl. 29 (7) 876-890. https://doi.org/10.1002/rra.2572        [ Links ]

WU WM, WANG SSY and JIA YF (1998) A 2-D non-equilibrium approach for nonuniform sediment transport modeling. Water Resour. Eng. 98 (1-2) 1392-1397.         [ Links ]

XU D, JI CN, BAI YC and SONG XL (2017) Three-dimensional numerical investigation on the influence of geometric shape on flow in river bends. J. Hydroinform. 19 (5) 666-685. https://doi.org/10.2166/hydro.2017.074        [ Links ]

YALIN MS (1992) River Mechanics. Pergamon Press, Oxford.         [ Links ]

ZHUANG J, ZHANG J, HUANG D, ZHENG GD and LAI GW (2009) On the characteristics of flow movement in the bending and bifurcated river. Adv. Water Resour. Hydraul. Eng. 1-6 859-864. https://doi.org/10.1007/978-3-540-89465-0_151        [ Links ]

ZIMMERMAN C and KENNEDY JF (1978) Transverse bed slopes in curved alluvial streams. J. Hydraul. Div. 104 (HY1) 33-48.         [ Links ]

 

 

Received 2 November 2016
Accepted in revised form 13 December 2017

 

 

* To whom all correspondence should be addressed. 86-10-64888151; e-mail: heli@ignrr.ac.cn