Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
Water SA
versión On-line ISSN 1816-7950
versión impresa ISSN 0378-4738
Water SA vol.44 no.1 Pretoria ene. 2018
http://dx.doi.org/10.4314/wsa.v44i1.11
http://dx.doi.org/10.4314/wsa.v44i1.11
Development and assessment of rules to parameterise the ACRU model for design flood estimation
JC SmithersI, II, III, IV, *; TJ RoweI; MJC HoranI; RE SchulzeI
ICentre for Water Resources Research, University of KwaZulu-Natal, Pietermaritzburg Campus, Private Bag X01, Scottsville, 3209, South Africa
IIBioresources Engineering, School of Engineering, University of KwaZulu-Natal, Pietermaritzburg Campus, Private Bag X01, Scottsville, 3209, South Africa
IIIJG Afrika (Pty) Ltd, 6 Pin Oak Avenue, Hilton, Pietermaritzburg, 3201, South Africa
IVNational Centre for Engineering in Agriculture, University of Southern Queensland, Toowoomba, Australia
ABSTRACT
Design flood estimation (DFE) is essential in the planning and design of hydraulic structures. In South Africa, outdated methods are widely applied for DFE. In this paper the potential of a continuous simulation modelling (CSM) approach to DFE in South Africa, using the daily time-step ACRU agrohydrological model, is investigated. The paper focuses on the links and similarities between the SCS-SA and ACRU models and the subsequent preliminary investigations that were undertaken to account for and incorporate the land cover classes, including land management practices and hydrological condition, of the SCS-SA model into the ACRU CSM approach. The approach to this study was to investigate how design volumes simulated by the SCS-SA model for various land management practices or conditions could be simulated by the ACRU model. Since peak discharge estimation in both models is directly dependent on simulated volumes, this preliminary study focused only on design runoff volumes, with subsequent investigations on peak discharge required in future research. In the absence of observed data, design runoff volumes and changes in design runoff volumes, as simulated by the SCS-SA model, were used as a substitute for observed data, i.e., as a reference, to achieve similar design runoff volumes and changes in design volumes in the ACRU model. This was achieved by adjusting relevant input parameters in the ACRU model to represent the change in management practice or hydrological condition, as represented in the SCS-SA model. Following a sensitivity analysis of relevant ACRU parameters, calibration of 2 selected parameters against SCS-SA CN values for selected land cover classes was performed. A strong linear relationship (R2 = 0.94) between these ACRU parameters and SCS-SA CNs for selected land cover classes was found and consequently specific rules and equations were developed to represent SCS-SA land cover classes in ACRU. Recommendations are made to further validate and verify the approach and to further the development of a CSM system for DFE in South Africa.
Keywords: Design flood estimation (DFE), continuous simulation modelling (CSM), SCS-SA and ACRU models, land cover, land management practice, hydrological condition
INTRODUCTION
Design flood estimation (DFE) is essential in the planning and design of hydraulic structures such as culverts, dams and canals. This involves the assessment of flood risk by associating a flood event with a probability of exceedance or return period (Smithers, 2012; Kang et al., 2013). Alexander (2002) and Smithers and Schulze (2003) highlighted the need for alternative approaches to DFE, or the development and improvement of conventional DFE techniques, after severe flooding in Southern Africa in 1999 and 2000. Smithers (2012) supports the comments of Alexander (2002) after flooding in the Western Cape in 2005 and the Free State and Eastern Cape in 2011. Alterations in rainfall patterns are generally attributed to climate change or, more recently, termed global changes (Kusangaya et al., 2014), which will impact on the estimation of design floods and reinforce the need for improved approaches to DFE. In addition, after a review of flood frequency estimation techniques and approaches in Europe, The European Cooperation in Science and Technology (COST, 2013) highlighted that in most countries flood frequency estimation is currently being undertaken using models which assume that historical records of flood flows or rainfall are stationary, i.e., the statistics of the distributions do not change with time. This emphasises the need to consider the effects of environmental change when estimating design floods.
DFE techniques for most countries can be grouped into two broad categories, which generally include approaches based on the statistical analysis of observed peak discharges and approaches based on event-modelling or continuous simulation modelling (CSM) using rainfall-runoff techniques (Boughton and Droop, 2003; Pathiraja et al., 2012; Smithers, 2012). Approaches to DFE in South Africa are similarly classified into two groups based on: (i) the analysis of observed flood peaks, and (ii) rainfall-runoff based techniques (Smithers and Schulze, 2002; Smithers, 2012), as depicted in Figure 1.
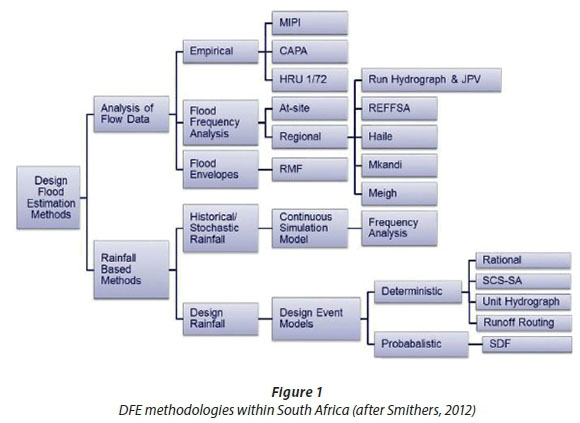
The numerous benefits of the rainfall-runoff CSM approaches to DFE have been highlighted within much of the literature both locally and internationally, including, inter alia: Calver and Lamb (1995); Cameron et al. (1999); Smithers and Schulze (2002); Boughton and Droop (2003); Chetty and Smithers (2005); Brocca et al. (2011); Pathiraja et al. (2012); Smithers (2012); Smithers et al. (2013); Cu (2016); Lamb et al. (2016) and Smithers et al. (2016). Examples of these benefits include the fact that actual climate information is input into a model which simulates the major processes which convert rainfall into runoff and therefore the antecedent soil moisture is accounted for and not estimated or averaged. Furthermore, direct calibration of the CSM may not be necessary given an increased understanding of hydrological processes and catchment conditions, e.g., with reference to the ACRU model, parameters are linked to physical catchment characteristics and therefore no direct calibration is performed; however, the simulated results may then be verified against observed data. Subsequently, simulations in ungauged catchments are more specific, reliable and scientific, i.e., since model parameters are linked to catchment characteristics they may be more easily transferred to ungauged catchments in a more scientifically justifiable manner (Hrachowitz et al., 2013). Finally, the method can account for the non-stationarity of the environment, i.e., in terms of land use change as well as changes in climate. Therefore, as alluded to by COST (2013), the non-stationarity of data can be accommodated.
In identifying the benefits and potential of CSM, this paper focuses on the preliminary developments towards a CSM approach to DFE in South Africa. The model selected is the Agricultural Catchments Research Unit (ACRU) model (Schulze, 1995) since it is adapted to South African conditions and has been successfully used in pilot studies for DFE by Smithers et al. (1997); Smithers et al. (2001); Chetty and Smithers (2005); Smithers et al. (2007); and Smithers et al. (2013). Currently, however, a widely-used rainfall-runoff technique used in practise is the event-based Soil Conservation Service - South African (SCS-SA) model which is an adaptation of the international SCS (1956) model (Schmidt and Schulze, 1987a).
A brief review of both the SCS-SA and ACRU models highlights some of the major similarities and differences between the models. The review identifies that in terms of land cover information, the land cover classification used in the SCS-SA model accounts for different land management practices and hydrological conditions, which are not accounted for in the ACRU land cover classification schemes. Since the runoff response parameters used in the original SCS model were derived from observations, and the SCS-SA model is an accepted method of DFE in small catchments in South Africa (Schmidt and Schulze, 1987a; Schulze et al., 2004; SANRAL, 2013; Van Vuuren et al., 2013), it was assumed in this study that the design runoff volumes simulated by the SCS-SA model are reasonable, and that the relative changes in design runoff volumes simulated by the SCS-SA model as a consequence of changes in land management practices or conditions are also reasonable. Based on these assumptions, the aim of the study by Rowe (2015) was to investigate how design volumes simulated by the SCS-SA model for various land management practices or conditions can be simulated by the ACRU model, and to derive classes in the ACRU classification schemes to account for land management practices and hydrological conditions. To achieve this several attempts were initially performed to link the ACRU soil textural inputs to SCS-SA soil inputs, i.e., soil response groups. These initial attempts, however, were unsuccessful and therefore a sensitivity analysis of simulated runoff volumes to relevant ACRU input parameters was conducted. This was performed in order to identify which parameters the ACRU model is most sensitive to in terms of DFE, and subsequently relevant parameters in the ACRU model were adjusted to represent the change in management practice or condition, as simulated by the SCS-SA model for SCS-SA soil response groups. Since peak discharge estimation in both models is directly dependent on simulated volumes, this preliminary study focused only on design runoff volumes, with subsequent investigations on peak discharge required in future research.
The objectives of the study reported in this paper are to: (i) review both the SCS-SA and ACRU models, (ii) discuss the attempts made to represent SCS-SA soil groups and land cover classes in the ACRU model, and (iii) present and assess trends, rules and equations that were developed in order to consistently simulate the relative hydrological impacts of management practices and hydrological conditions in the ACRU model, for selected land covers, which are similar to those estimated using the SCS-SA model.
HYDROLOGICAL MODELLING, RUNOFF PROCESSES IN THE SCS-SA AND ACRU MODELS AND UNCERTAINTIES
Two rainfall-runoff models, namely the SCS-SA and ACRU models, have received noticeable attention within South Africa. The similarities and differences between the two models are investigated in this section. In addition, the uncertainties associated with hydrological modelling are briefly discussed and noted.
The most striking similarity between the SCS-SA and ACRU models is that they both use the SCS (1956) runoff equation, as represented in Eq. 1 (Schulze, 1995), to estimate stormflow:
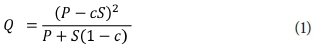
where Q is stormflow depth (mm); P is gross daily precipitation amount (mm); S is potential maximum soil water retention (mm), or the soil water deficit; and c is a regression coefficient, commonly referred to as the coefficient of initial abstraction.
The SCS-SA method, however, uses Eq. 1 to estimate stormflow for a single event, while the ACRU model uses Eq. 1 to simulate daily stormflow events. In addition, the manner in which S is computed differs considerably between the models. The SCS-SA model uses a simplified approach based on the soil and land cover, while the ACRU model disaggregates the soil water budget into its conceptual components in order to explicitly represent the processes that influence the soil moisture deficit prior to a daily rainfall event. These differences are detailed below, distinguishing between the runoff processes within both the SCS-SA and ACRU models.
Extensive effort has been expended on refining and developing the SCS-SA model for application in South Africa, by, inter alia, Schulze and Arnold (1979); Dunsmore et al. (1986); Schmidt and Schulze (1987a); Schmidt and Schulze (1987b); Schulze et al. (1992); and Schulze et al. (2004). The model, which has been verified and accepted as a suitable method to estimate design flood volumes and peak discharges for small catchments (≤ 15 km2) in South Africa, is widely applied in practice (Schmidt and Schulze, 1987a; Schulze et al., 2004; SANRAL, 2013). As with the original SCS (1956) model, S in the SCS-SA model is dependent on the soil type represented by soil response groups A - D, with Group A soils characterised by the highest infiltration and permeability rates and therefore the lowest stormflow potential, and vice versa for Group D soils, land cover, land management practices, hydrological condition and soil moisture status of the catchment (Schmidt and Schulze, 1987a). Theoretically, the value of S can vary from zero to infinity; however, practical upper and lower limits of S have been defined as the permanent wilting point and porosity of the soil within a catchment. A catchment response index to rainfall, termed the runoff curve number (CN), was therefore introduced in order to transform the maximum soil water retention (S) into a CN value that varies within a more logical range of 0 to 100 (Schmidt and Schulze, 1987a). The derivation of CNs in South Africa was based on the determination of CNs by the Soil Conservation Service (SCS, 1972), with adaptations to South African conditions. The original SCS CNs (SCS, 1972) were obtained through calibration and interpolation from observed data. More details on the derivation of CNs and the adaptation of CNs for South Africa are available from Schmidt and Schulze (1987a) and Rowe (2015). A table of CNs for selected agricultural, suburban and urban land covers was derived for use with the SCS-SA model (Schmidt and Schulze, 1987a), an example ofan example of which is shown in Table 1.
Therefore, in terms of S in the SCS-SA model, catchment conditions are integrated into a single parameter, i.e., the catchment CN, which accounts for soil properties, land cover, land management, hydrological condition and antecedent soil moisture content. Initial CNs may be adjusted to account for the antecedent soil moisture conditions. The median condition and joint association methods (Schmidt and Schulze, 1987a), which used the ACRU soil moisture budgeting routines to estimate the antecedent conditions 30 days prior to large rainfall events, were a major improvement to the original moisture adjustment procedure introduced into the original SCS (1956) model. However, the estimation of S and the resultant stormflow remains highly dependent on the initial CN selected.
The daily time-step ACRU agrohydrological model (Schulze, 1995) is a well-established physical conceptual model, developed at the University of KwaZulu-Natal (UKZN), and applicable to a wide variety of water resource assessments within South Africa, including DFE. The model is conceptual since it is made up of idealised concepts and is physically based as physical processes are explicitly represented (Schulze et al., 1994). A national database of default input information required by the model, e.g., climate data, soils and land cover information, has been compiled and regularly updated over several years through continual research contributions from the staff and postgraduate students at UKZN (Smithers and Schulze, 2004; Schulze, 2013). Simultaneously, continual refinement to the ACRU modelling system has also been undertaken, in terms of how processes are conceptualised. The various components of the hydrological cycle, as conceptualised within the ACRU model, are depicted in Figure 2.
In the ACRU model the following conceptual and practical refinements to the SCS runoff equation used in the SCS-SA model were performed (Schulze, 1995):
• Interception of rainfall by vegetation is abstracted separately and before the commencement of potential stormflow producing rainfall. Therefore, it is not part of the initial abstractions as assumed in the SCS and SCS-SA model.
• The coefficient of initial abstraction may be altered month-by-month in the ACRU model, dependent on the characteristics of the vegetation and site, as well as the land management practices.
• S, conceived as a soil water deficit, is calculated by the multi-layer soil water budgeting techniques of ACRU, thus avoiding the need for the determination of a final catchment CN. S is calculated as the difference between water retention at porosity and the actual soil water content prior to a rainfall event, after the total evaporation for the day has been abstracted. Soil properties are therefore represented in far more detail in the ACRU model and will be elaborated on in the following section.
• S is calculated for a selected critical response depth of the soil (SMDDEP). SMDDEP is dependent on, inter alia, the climate, vegetation and soil properties (Smithers and Schulze, 2004). The runoff generated is therefore strongly influenced by the SMDDEP and the moisture content of the soil prior to a rainfall event. As an example, a low SMDDEP value results in a smaller S and therefore more runoff since the runoff generating soil store is smaller.
• In addition, the daily Q at a catchment outlet is controlled by a quick flow response coefficient (QFRESP) which partitions the stormflow generated from a rainfall event, i.e., Q in Eq. 1, into a same day response fraction and a subsequent delayed stormflow response. QFRESP ranges from 0-1, if QFRESP = 1 all stormflow (Q) generated from a rainfall event exits the catchment on that day. If QFRESP is less than 1, only that fraction of Q exits the catchment on the same day and the remainder is added to the stormflow for the following day, and a faction (QFRESP) of this exits the catchment on the day.
The residual rainfall, i.e., the rainfall that is not initially abstracted and is not intercepted and does not contribute to stormflow, infiltrates into the topsoil (A horizon) and replenishes the soil water store and eventually contributes to baseflow via a set of processes detailed by Smithers and Schulze (2004). This contribution to the soil moisture store has a direct impact on S and consequently has a large influence on the amount of runoff generated on subsequent days. Total evaporation from the soil profile (Figure 2) also impacts on S and options and algorithms have been developed within the ACRU model to account for the contribution of total evaporation to the water balance and the associated S value (Smithers and Schulze, 2004). Vegetation properties for 5 land-cover categories, namely, urban land uses, agricultural crops, natural vegetation, aquatic systems and commercial forests, as classified by Schulze and Hohls (1993), have been developed and incorporated into a database called COMPOVEG, built into the ACRU model (Smithers and Schulze, 2004). The COMPOVEG database contains land cover specific ACRU parameters, at differing levels of detail, which is continually updated as new research findings are obtained. The land cover classification developed by Schulze and Hohls (1993) does not account for land management practice and hydrological condition. Clark (2014) is developing a standardised land cover/land use hierarchical classification system. This classification aims to improve on and update the classification of Schulze and Hohls (1993) and includes the current information derived from research results and the expert knowledge of Schulze (2013). The Clark (2014) classification, however, also does not account for land management practices and does not adequately account for hydrological conditions, as accounted for in the SCS-SA model. The hierarchical classification of Clark (2014), however, is adaptable and has been set-up to easily accommodate the addition of new classes as they are developed. More details on the current ACRU land cover classification, developed by Schulze and Hohls (1993), and the new hierarchical classification, are available from Schulze (1995) and Clark (2014), respectively.
Uncertainties are inherent in all forms of hydrological modelling, including both the SCS-SA and ACRU models. Consequently, it is important to comment on the uncertainties associated with hydrological modelling. Hughes et al. (2015) emphasise this reality, stating that it is essential for all role players involved in water resource management and assessment to understand the key concepts of uncertainty and to remember that virtually all of the information used to make decisions is uncertain. Hrachowitz et al. (2013) and Pomeroy et al. (2013) comment on the Predictions in Ungauged Basins (PUB) initiative and refer to the uncertainties involved in hydrological modelling. In their comments, they state that the aim of the PUB decade has been to reduce the uncertainties in hydrological modelling and parameter estimation through increased understanding of the complex processes and interactions associated with the hydrological cycle. Hughes (2013) reviewed putting PUB into practice within South Africa and commented on the historical reliance of most hydrological models on calibration from observed streamflow data and rainfall data, i.e., where the data are often patched (in-filled) to generate complete time series. According to Hughes (2013), current hydrological simulation models are still reliant on calibration to estimate model parameters, and these calibrated parameters are often subjectively transferred from gauged catchments to ungauged catchments based on catchment similarity. Hughes (2013) also highlights the inconsistency in parameter estimation across South Africa, with different regions calibrating model parameters slightly differently, which adds to the uncertainties in hydrological modelling. Hughes (2013), therefore, states that improved communication between scientists and organisations is needed to collectively select and determine the most appropriate parameter values based on sound scientific knowledge and experience. These issues are extremely valuable to this study, where links between the ACRU and SCS-SA model parameters are investigated. It is therefore important to note that these concerns and comments regarding parameter estimation and uncertainties have been noted within this study and that every effort has been made to ensure that parameter estimations and adjustments are based on acceptable scientific theory and realistic conceptualisation of hydrological processes.
METHODOLOGY
This section contains a brief outline of the general methodology that was applied in this study. As reviewed in the previous section on hydrological modelling, the links and similarities between the SCS-SA and ACRU models were identified. It was highlighted that the land cover classification of the SCS-SA model accounts for differences in runoff responses that result from differences in land management practices and hydrological conditions ( ). This is not accounted for in the ACRU land use/land cover classification, as well as the classification being developed by Clark (2014). In the ACRU hierarchical classification, for example, a common row crop such as maize is represented by a single general class, i.e., 'Agriculture Commercial Maize Dryland Summer Rainfall Region'. Therefore, as a starting point, a decision was made to use the SCS-SA land cover classes to derive equivalent classes in the hierarchical classification for use in ACRU. By way of example, contains information for a row crop land cover class in the SCS-SA classification and indicates that there are several subclasses based on different land management practices and hydrological conditions, i.e., straight or contoured rows, conservation practices, and conservation structures. Hydrological condition is represented by stormflow potential, i.e., high stormflow potential is representative of poor hydrological condition. Figure 3 summarises the general methodology and procedure followed in the study.
The following sections summarise the results of the study in a step-wise manner, starting with the various attempts made to achieve equivalence between the ACRU and SCS-SA soils inputs.
RESULTS
The objective of the soil translation is to identify and set values for the ACRU soil input parameters to represent each of the SCS-SA soil groups that will produce similar hydrological responses to those obtained for the SCS-SA model. By way of example, Figure 4 illustrates the trends in runoff volume calculated by the SCS-SA model for a Veld land cover, in fair hydrological condition, and shows the increasing runoff trend from an A to D soil in the SCS-SA model for different return period events. The 1-day design rainfall used is also depicted in Figure 4.
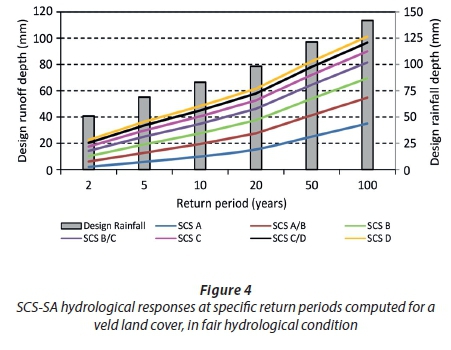
The aim was to use these trends as a guide to which ACRU parameters may be used, to represent A to D soils in ACRU in order to achieve similar runoff responses for a similar veld/grassland land cover in the ACRU hierarchical classification. The land cover information used in the ACRU model is derived from research and the expert knowledge of Schulze (2013). It is important to note that in this assessment a hypothetical catchment area of 1 km2 was used in both the SCS-SA and ACRU model simulations, for comparison, assuming climatic and physical catchment conditions for a randomly selected quinary catchment in KwaZulu-Natal (KZN), Quinary V11L3, i.e., Quinary Number 4854, in the Quinary Catchments Database (QCD) (Schulze, 2013). The daily rainfall file assigned to Quinary 4854 was used as the input into the ACRU model and the same daily rainfall file was used to calculate the 1-day design rainfall input values for the SCS-SA model. It is important to note that the design runoff volumes calculated by the SCS-SA model are obtained directly from the design rainfall values inputted to the model, i.e., based on the assumption that the return period of the design runoff volume simulated is the same as the return period of the input design rainfall. In contrast, the design runoff volumes output by the ACRU model are obtained by performing a frequency analysis on the daily simulated flows.
Initial approach
Initially three attempts were made to link SCS-SA soil groups to soil textural properties in the ACRU model. The first attempt (land type approach) involved analysis of the soil textural properties and SCS-SA soil groups assigned per Land Type (SIRI, 1987) by Schulze (2012). Schulze (2012) identified a need to map SCS-SA soil response groups for South Africa, to enable more rapid determination of these response groups when using the SCS-SA model to determine stormflow responses for any catchment in South Africa. Schulze (2012) used PWP values already mapped for South Africa by Pike and Schulze (1995) and Schulze and Horan (2005) from the Land Type databases, i.e., the most detailed soil maps available for South Africa, to derive a map of SCS-SA soil groups for South Africa. The PWP values and assigned SCS-SA soil groups for all Land Type polygons defined within the Land Type database, along with the additional soil properties required by the ACRU model, also assigned per Land Type Polygon, were arranged by SCS-SA soil group. Simple statistics, such as the median, minimum, maximum and 25th and 75th percentiles, were performed on all of the soil-related properties (PO, PWP, DUL and redistribution rates) required by the ACRU model, per SCS-SA soil group, and box and whisker diagrams were plotted. The median values of the soil-related properties were used as input into the ACRU model to represent each SCS-SA soil group, and simulations were performed. The simulations from the ACRU model were then compared to the corresponding simulations from the SCS-SA model. The analysis did not produce highly comparable results between the SCS-SA and ACRU model simulations, as shown in Figure 5.
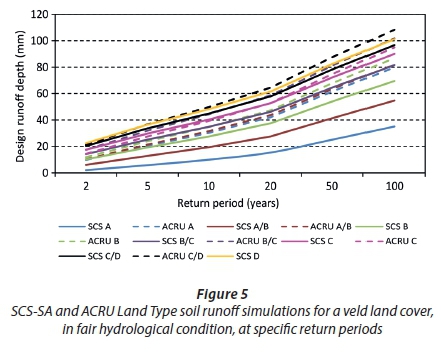
Furthermore, an inconsistent runoff trend was obtained for the ACRU simulations where runoff did not increase consistently from SCS-SA Soil Groups A to C/D, i.e., with no SCS-SA D soil group obtainable for the land type approach. Additionally, the relative differences in runoff responses between SCS-SA soil groups for the land type approach are significantly different to those of the SCS-SA results, as shown in Figure 5.
In order to quantify and compare the significance of the comparison between the SCS-SA and ACRU simulation results for the various attempts from this point on, the following general classification rules were developed:
(i) Highly comparable: the average absolute runoff depth difference ≤ 2 mm
(ii) Comparable: 2 mm < average absolute runoff depth difference ≤ 6 mm
(iii) Poorly comparable: 6 mm < average absolute runoff depth difference ≤ 10 mm
(iv) Incomparable: the average absolute runoff depth difference > 10 mm
The average absolute differences, i.e., the differences in the actual runoff simulation depths, between simulated SCS-SA and ACRU design runoff volumes (averaged for all return periods from 2-100 years) were calculated for each SCS-SA Soil Group A to D, for each of the soil translation attempts.
The second attempt (binomial approach) was similar to the first attempt, and involved a review of the Binomial Soil Classification (MacVicar et al., 1977) and the texture classes and SCS-SA soil groups assigned per soil form and series, as reported by Smithers and Schulze (2004). The soils in the Binomial Soil Classification were arranged by SCS-SA soil groups and the distribution of each soil texture class that made-up a SCS-SA soil group was tabulated. Furthermore, in the ACRU Theory Manual (Schulze, 1995) and ACRU User Manual (Smithers and Schulze, 2004), default soil-related properties required as input into the ACRU model have been assigned to soil texture classes, when only the soil texture class is known. Subsequently, the default soil-related properties were used with the distribution of texture percentages as weights to derive soil-related input values required by the ACRU model to represent each SCS-SA soil group. An inconsistent runoff trend was also identified for this attempt, i.e., with runoff not increasing consistently from assigned SCS-SA Soil Group A to D in the ACRU model. In addition, the analysis, although an improvement on the first attempt, did not produce highly comparable results between the SCS-SA and ACRU models.
The third attempt (calibration approach), which is the simplest of the three approaches, involved: (i) simulating runoff responses for each of the soil textural classes (sand - clay) available as input into the ACRU model, i.e., using default assigned soil-related properties built into the ACRU model, available as an option when inadequate soils information is available and only the soil texture class is known; (ii) arranging the simulated runoff volumes for each soil textural class in order of increasing runoff; and (iii) through selection/calibration assigning a soil textural class to each SCS-SA soil group. The objective of this approach was to generate representative texture classes for each SCS-SA soil group which would produce the correct runoff trend of increasing runoff from assigned SCS-SA Soil Groups A to D. Through this approach, the inconsistencies in the runoff trends were overcome; however, the SCS-SA and ACRU runoff comparisons remained poor, as depicted in Figure 6.
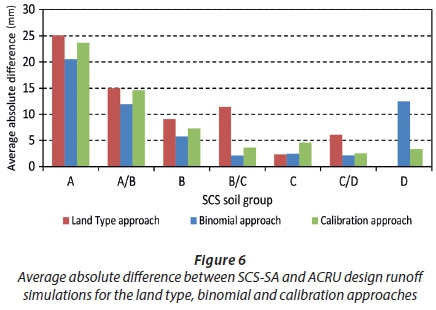
In summary and as depicted in Figure 6 for all three attempts, incomparable results were obtained for SCS-SA Soil Groups A and A/B and poorly comparable results obtained for SCS-SA Soil Group B. Incomparable results were also obtained for SCS-SA Soil Group B/C and D for the land type and binomial approaches, respectively. The results revealed that correlation of ACRU soil textural properties to SCS-SA soil groups alone is not adequate to obtain comparable responses.
Based on the above findings, it was necessary to perform a sensitivity analysis of ACRU model input parameters, in order to identify which ACRU parameters the model is most sensitive to in terms of design flood estimates, with the objective being to identify additional ACRU parameters, i.e., in addition to the soil textural properties, that may be used to represent SCS-SA soil groups, hydrological conditions and management practices more adequately in the ACRU model. The following section elaborates on the sensitivity analyses conducted.
ACRU sensitivity analysis
The sensitivity analysis procedure described in the ACRU Theory Manual (Schulze, 1995) was applied in this study to investigate the sensitivity of the ACRU model to selected parameters in terms of design flood estimates. Based on previous sensitivity analyses presented in the ACRU Theory Manual and consideration of model parameters that are likely to influence runoff responses, the parameters as summarised in Table 2 were investigated.

The sensitivity analysis identified two model parameters that impact on design runoff estimates. The parameters are: (i) the QFRESP coefficient, which partitions stormflow generated from a daily rainfall event into a same-day response fraction and a subsequent delayed stormflow response; and (ii) the SMDDEP, which determines the critical response depth of the soil. It is important to note that adjusting the QFRESP parameter does not change the accumulated volume of surface runoff generated, but only influences the timing and magnitude of the daily runoff volumes. In contrast, adjustment of the SMDDEP parameter influences the volume of stormflow simulated. These parameters were used to investigate if they could be calibrated to represent SCS-SA soil groups/CNs. The sensitivity of the CAY, PCSUCO, VEGINT and COIAM parameters were also investigated but, as seen from Table 2, these parameters were found to be insensitive, with the exception of the COIAM parameter which was found to be slightly sensitive.
The following section reports on the subsequent attempts made to represent SCS-SA soil groups/CNs in the ACRU model using the QFRESP and SMDDEP parameters.
Revised approach
For selected land cover classes, a manual calibration procedure was implemented to identify the most appropriate QFRESP and SMDDEP combination to be used, in addition to the soil textural properties assigned via the binomial classification approach, to represent each SCS-SA soil group. A veld land cover in fair hydrological condition was once again initially investigated for the same hypothetical 1 km2 study catchment. The design runoff volume results simulated by the SCS-SA model and the ACRU model, i.e., with the optimised QFRESP and SMDDEP combination obtained from the calibration procedure, were highly comparable or just out of the highly comparable range, as seen in Figure 7. Using the same approach, additional attempts were made to achieve comparable results for a veld in both fair and poor hydrological condition for the same hypothetical catchment, with predominantly highly comparable results being obtained (Figure 7).
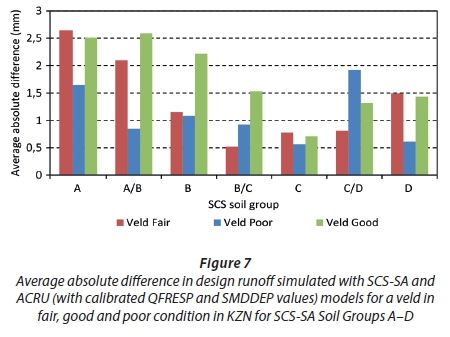
Although design flood volumes estimated using the ACRU model were found to be insensitive to the vegetation-related parameters (VEGINT, CAY, COIAM and PCSUCO), these were adjusted to account for land cover condition as recommended by Schulze (2013) for degraded veld in poor hydrological condition, with additional rules developed to represent a veld in good hydrological condition. These changes were made since, in reality, these parameters would be influenced by a change in management practice or hydrological condition. Since the changes, however, have a negligible influence on the design runoff volumes simulated in the ACRU model, adjustments to QFRESP and SMDDEP were once again performed to represent changes in the CN for hydrological condition.
The same calibration procedure and development of rules, as described above, was performed for a row crop/maize land cover, i.e., calibrating QFRESP and SMDDEP values to represent each of the SCS-SA row crop classes and soil groups within each class ( ). The default ACRU model input values for a general maize crop planted in November, in all feasible locations within South Africa (COMPOVEG crop number 3120102), was used to represent a row crop/maize land cover in good hydrological condition and rules were developed to represent a row crop/maize land cover in poor hydrological condition. The results, similar to the results for a veld land cover (Figure 7), revealed that in all cases the average absolute differences between the SCS-SA and ACRU design runoff volumes were small and were generally less than 2 mm, i.e., highly comparable, with a few exceptions where averages were greater than 2 mm but less than 6 mm, i.e., comparable.
To confirm that the calibrated values may be consistently applied at a different geographical location, the calibrated QFRESP and SMDDEP parameters found to represent SCS-SA soil groups best for a veld land cover in the KZN catchment, were then directly transferred and used to estimate design runoff volumes in Mpumalanga, i.e., with contrasting climatic and local conditions.
This was repeated for the Western Cape where a veld land cover was again tested for consistency. In both cases the results, although not as good as the calibrated results from the KZN simulations, were all within the comparable range, with several still falling within the highly comparable range. The results therefore supported the general applicability of the calibrated results to different locations, when attempting to obtain similar hydrological responses to those obtained from the SCS-SA model. An additional calibration was conducted for a wheat/small grain land cover in the Western Cape, i.e., as an equivalent to maize in KZN. The calibrated results were once again in the comparable and highly comparable range.
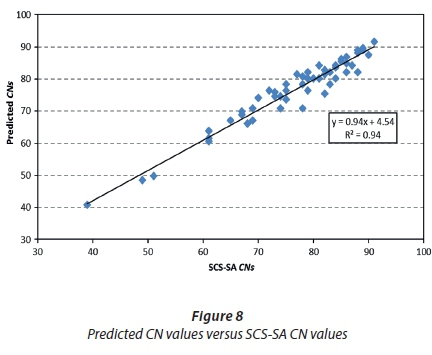
The calibration results for the various land cover classes investigated were tabulated for each SCS-SA soil group. A multiple linear regression analysis was initially performed to identify any trends between SCS-SA CNs and ACRU QFRESP and SMDDEP parameters. The regression analysis, performed in Microsoft Excel, revealed a strong linear relationship between SCS-SA CNs and the QFRESP and SMDDEP values calibrated to represent SCS-SA soil groups/CNs best, with a coefficient of determination of 0.94 and a standard error of 2.66. A CN predictor equation, similar to Eqs 2 and 3 below, was generated and used with the calibrated QFRESP and SMMDEP values to calculate 'predicted CN' values corresponding to each of the SCS-SA CN values.

The SCS-SA CNs and predicted CNs were plotted graphically, as depicted in Figure 8, which visually emphasises the high correlation between SCS-SA CNs and ACRU-calibrated QFRESP and SMDDEP parameters. In addition, a t-test was performed on the SCS-SA and predicted CN values. The t-test confirmed, at the 95% confidence interval, that there is no significant difference between the two datasets, further emphasising the high correlation between the SCS-SA and ACRU calibrated results.
Regression results, and generated equations and rules, similar to those presented in Eqs 2 and 3 and Table 3 to Table 6, were then used to assist in the analysis of the design runoff results from a sugarcane land cover, to test the applicability of the regression results on a land cover class not used in the calibration procedure. The objective was to assess if the regression equation and initial rules generated would produce ACRU simulation results similar to those of the SCS-SA model for a sugarcane land cover class. The SMDDEP and QFRESP input values required to represent a SCS-SA sugarcane land cover class in the ACRU model, for each SCS-SA soil group, were obtained using an equation and rules, similar to Eqs 2 and 3 and Table 4 and Table 6, i.e., which are the revised rules and equations as detailed in the following section. A CN predictor equation, similar to Eqs 2 and 3, was used with rules, similar to those presented in Table 4 and Table 6, to determine the QFRESP and SMDDEP input values from the SCS-SA CN values.
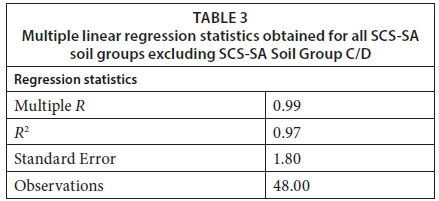
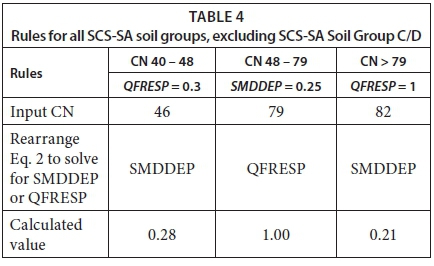
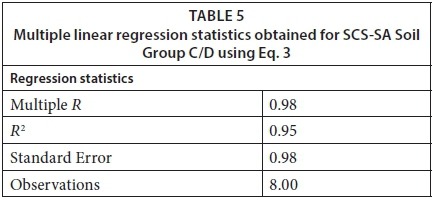
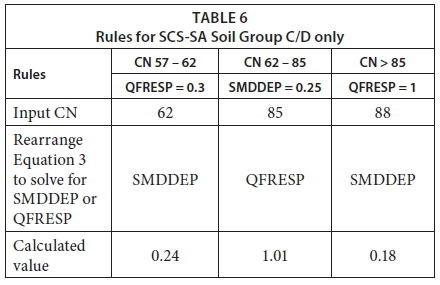
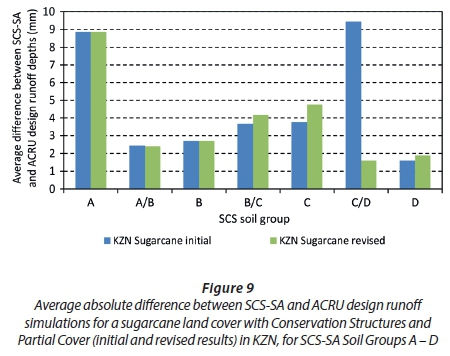
Some difficulty in simulating design runoff for a sugarcane land cover in the ACRU model was encountered; however, some additional rules were developed and the regression equation obtained was used to estimate parameter values in the ACRU model. The results were compared to those from the SCS-SA model and a discrepancy in the results was identified for SCS-SA Soil Groups A and C/D (Figure 9 - KZN Sugarcane initial). The poorly comparable results obtained for SCS-SA Soil Group A, however, were expected and can be explained by briefly commenting on the difficulties encountered when attempting to represent CNs lower than 40 in the ACRU model. SCS-SA Soil Group A for a sugarcane land cover with conservation structures and partial cover has a CN value of 25. From the assessments performed and rules developed, CN values lower than 40 are not recommended since erroneous results are obtained. Consequently, a CN value of 40 was used to represent SCS-SA Soil Group A in ACRU and explains the poorly comparable results. The discrepancy related to SCS-SA Soil Group C/D was identified to be as a result of the anomalous soil textural properties assigned to this group, through the binomial approach. This discrepancy was addressed by repeating the above multiple linear regression analysis performed on the CNs of all the SCS-SA land cover classes investigated and the calibrated QFRESP and SMDDEP values that were obtained. In this case, however, two separate multiple linear regression analyses were performed on: (i) all SCS-SA soil groups excluding SCS-SA Soil Group C/D; and (ii) SCS-SA Soil Group C/D alone. Revised regression equations and rules were then developed for the former (Eq. 2 and Table 4) and the latter (Eq. 3 and Table 6). These rules and equations are applicable to all the land cover classes investigated within this study, with further validation and investigation needed to justify their use on additional land cover classes. For more details on the statistical analyses and the rules and equations derived refer to Rowe (2015). The statistics listed in Table 3 were obtained for multiple linear regression (i) and Eq. 2 was derived to estimate 'predicted' CN values for given QFRESP and SMDDEP combinations for all SCS-SA soil groups, excluding SCS-SA Soil Group C/D.
The results presented in Table 3 show that the relationship is even stronger when omitting the results for SCS-SA Soil Group C/D. This is identified by the higher coefficient of determination (R2 = 0.97) compared to the initial coefficient of determination of 0.94, as well as the smaller standard error of 1.80 compared to 2.66. In addition, the statistics for SCS-SA Soil Group C/D, as presented in Table 5, also show a stronger relationship compared to the initial results for all SCS-SA soil groups.
Revised rules were determined for all SCS-SA soil groups, excluding SCS-SA Soil Group C/D, as shown in Table 4. The rules as summarised in Table 4 are explained as follows. Rules were developed for different CN ranges, with the first range of CN values being those ranging from 40-48. It is recommended that CN values lower than 40 should not be simulated due to erroneous results obtained below this value. For this range of CN values, the rules state that a fixed QFRESP value of 0.3 must be used in Eq. 2 to solve for SMDDEP. An example is shown in Table 4 where an estimated SMDDEP value of 0.28 is calculated for an input CN value of 46, after rearranging Eq. 2 to solve for SMDDEP. For CNs ranging from 48-79, the rules state that SMDDEP must remain fixed at a value of 0.25 and Eq. 2 must be rearranged in order to solve for QFRESP. An example is shown for a CN value of 79, where the QFRESP value is calculated to be 1.00. For CN values greater than 79, the rules state that QFRESP must remain fixed at 1.00 and Eq. 2 must be rearranged in order to once again solve for SMDDEP.
The statistics listed in Table 5 were obtained for multiple linear regression (ii) and Eq. 3 was derived to estimate 'predicted' CN values for given QFRESP and SMDDEP combinations for SCS-SA Soil Group C/D.
In addition, the rules presented in Table 6 were determined for SCS-SA Soil Group C/D and are interpreted in the same manner as the results from Table 4. This corrected the discrepancy in the results for SCS-SA Soil Group C/D (Figure 9 - KZN Sugarcane revised) and produced comparable results between the ACRU and SCS-SA models for a sugarcane land cover, with the exception of SCS-SA Soil Group A for the reasons detailed above.
A summary table of the preliminary rules and equations recommended for use with the ACRU model to simulate design runoff results and trends similar to those simulated by the SCS-SA model, for the specific land cover classes investigated, are detailed in Rowe (2015).
DISCUSSION AND CONCLUSIONS
Several severe flooding events across South Africa in recent years and the potential impacts of climate change have highlighted the need for updating and refining DFE methods used in South Africa. The focus of this study was on the initial development of a CSM approach to DFE in South Africa using the daily time-step ACRU agrohydrological model. Following a review on hydrological modelling and the links and similarities between the SCS-SA and ACRU models, it was identified that in terms of land cover information, the land cover classification used in the SCS-SA model accounts for more detailed land management practices and hydrological conditions, which are not accounted for in the current ACRU land cover classification, as well as the standardised hierarchical classification system developed by Clark (2014).
Since the CNs used in the original SCS model were derived from observations, and the SCS-SA model is an accepted method of DFE in small catchments in South Africa (Schmidt and Schulze, 1987a; Schulze et al., 2004; SANRAL, 2013), it was assumed in this study that the design volumes simulated by the SCS-SA model are reasonable, and the differences in design volumes simulated by the SCS-SA model as a consequence of changes in land management practice or condition are also reasonable. Based on these assumptions, the general approach to the study was to investigate how design volumes simulated by the SCS-SA model for various land management practices or conditions could be simulated by the ACRU model, and to derive rules and equations that may be applied to achieve this goal.
A summary of the procedures applied, results obtained and preliminary rules and equations derived from this study are presented in this paper. Further details, including a comprehensive summary table on how to implement the approach, are available from Rowe (2015). The rules and equations derived in this study are best preliminary estimates based on the results obtained in this initial study. Further investigation and validation of the approach is needed and recommended, including the analysis of additional land cover classes, further independent verification at different geographical locations, assessment of the approach for a range of catchment sizes and conditions, as well as verification of the simulated results against observed data. An additional critical step required for design flood estimation is an investigation and assessment of the simulated peak discharge, i.e., translation of flood volume to peak discharge, as both peaks and volumes are essential to DFE.
REFERENCES
ALEXANDER W (2002) Statistical analysis of extreme floods. J. S. Afr. Inst. Civ. Eng. 44 (1) 20-25. [ Links ]
BOUGHTON W and DROOP O (2003) Continuous simulation for design flood estimation-a review. Environ. Model. Softw. 18 309-318. https://doi.org/10.1016/S1364-8152(03)00004-5 [ Links ]
BROCCA L, MELONE F and MORAMARCO T (2011) Distributed rainfall-runoff modelling for flood frequency estimation and flood forecasting. Hydrol. Process. 25 (18) 2801-2813. https://doi.org/10.1002/hyp.8042 [ Links ]
CALVER A and LAMB R (1995) Flood frequency estimation using continuous rainfall-runoff modelling. Phys. Chem. Earth 20 (5-6) 479-483. https://doi.org/10.1016/S0079-1946(96)00010-9 [ Links ]
CAMERON D, BEVEN K, TAWN J, BLAZKOVA S and NADEN P (1999) Flood frequency estimation by continuous simulation for a gauged upland catchment (with uncertainty). J. Hydrol. 219 169-187. https://doi.org/10.1016/S0022-1694(99)00057-8 [ Links ]
CHETTY K and SMITHERS J (2005) Continuous simulation modelling for design flood estimation in South Africa: Preliminary investigations in the Thukela catchment. Phys. Chem. Earth Parts A/B/C 30 (11-16) 634-638. https://doi.org/10.1016/j.pce.2005.08.002 [ Links ]
CLARK D (2015) Development and assessment of an integrated water resources accounting methodology for South Africa. WRC Report No. K5/2205. Water Research Commission, Pretoria. [ Links ]
COST (2013) A review of applied methods in europe for flood-frequency analysis in a changing environment. WG4: Flood frequency estimation methods and environmental change. COST Action ES0901, Centre for Ecology & Hydrology, Wallingford, United Kingdom. [ Links ]
CU T (2016) Enhancement of design flood estimation using continuous simulation. PhD thesis, School of Civil and Environmental Engineering, Faculty of Engineering and Information Technology, University of Technology, Sydney, Australia. [ Links ]
DUNSMORE S, SCHULZE R and SCHMIDT E (1986) Antecedent soil moisture in design runoff volume estimation. ACRU Report No. 23, Department of Agricultural Engineering, University of Natal, Pietermaritzburg, South Africa. [ Links ]
HRACHOWITZ M, SAVENIJE H, BLÖSCHL G, MCDONNELL J, SIVAPALAN M, POMEROY J, ARHEIMER B, BLUME T, CLARK M, EHRET U, FENICIA F, FREER J, GELFAN A, GUPTA H, HUGHES D, HUT R, MONTANARI A, PANDE S, TETZLAFF D, TROCH P, UHLENBROOK S, WAGENER T, WINSEMIUS H, WOODS R, ZEHE E and CUDENNEC C (2013) A decade of predictions in ungauged basins (PUB)-a review. Hydrol. Sci. J. 58 (6) 1198-1255. https://doi.org/10.1080/02626667.2013.803183 [ Links ]
HUGHES D (2013) PUB in practice at the national scale: The case of South Africa, In: Pomeroy J, Whitfield P and Spence C (eds) Putting Prediction in Ungauged Basins into Practice. Canadian Water Resources Association, Canmore, Alberta, Canada. 175-184. [ Links ]
HUGHES D, MOHOBANE T and MALLORY S (2015) Implementing uncertainty analysis in water resources assessment and planning. WRC Report No. 2056/1/14. Water Research Commission, Pretoria. [ Links ]
KANG M, GOO J, SONG I, CHUN J, HER Y, HWANG S and PARK S (2013) Estimating design floods based on the critical storm duration for small watersheds. J. Hydro-environ. Res. 7 209-218. [ Links ]
KUSANGAYA S, WARBURTON M, ARCHER VAN GARDEREN E and JEWITT G (2014) Impacts of climate change on water resources in southern Africa: A review. Phys. Chem. Earth Parts A/B/C 67-69 47-54. https://doi.org/10.1016/j.pce.2013.09.014 [ Links ]
LAMB R, FAULKNER D, WASS P and CAMERON D (2016) Have applications of continuous rainfall-runoff simulation realized the vision for process-based flood frequency analysis? Hydrol. Process. 30 2463-2481. https://doi.org/10.1002/hyp.10882 [ Links ]
MACVICAR C, DE VILLIERS J, LOXTON R, VERSTER E, LAMBRECHTS J, MERRYWEATHER F, LE ROUX J, VAN ROOYEN T and HARMSE HVM (1977) Soil Classification - A Binomial System for South Africa. Department of Agricultural Technical Services, Soil and Irrigation Research Institute, Pretoria, South Africa. [ Links ]
PATHIRAJA S, WESTRA S and SHARMA A (2012) Why continuous simulation? The role of antecedent moisture in design flood estimation. Water Resour. Res. 48 (6) W06534 (06531-06515). [ Links ]
PIKE A and SCHULZE R (1995) AUTOSOILS: A program to convert ISCW soils attributes to variables usable in hydrological models. Department of Agricultural Engineering, University of Natal, Pietermaritzburg, South Africa. [ Links ]
POMEROY J, WHITFIELD P and SPENCE C (2013) Putting Prediction in Ungauged Basins into Practice. Canadian Water Resources Association, Canmore, Alberta, Canada. [ Links ]
ROWE T (2015) Development and assessment of rules to parameterise the ACRU model for design flood estimation. MSc Dissertation, Centre for Water Resources Research, University of KwaZulu-Natal, Pietermaritzburg, South Africa. [ Links ]
SANRAL (2013) Drainage Manual (Sixth Edition). SANRAL, Pretoria. [ Links ]
SCHMIDT E and SCHULZE R (1987a) Flood volume and peak discharge from small catchments in Southern Africa, based on the SCS technique. WRC Report No. TT 31/87. Water Research Commission, Pretoria. [ Links ]
SCHMIDT E and SCHULZE R (1987b) User manual for SCS-based design runoff estimation in southern Africa. WRC Report No. TT 33/87. Water Research Commission, Pretoria. [ Links ]
SCHULZE R (1995) Hydrology and agrohydrology: a text to accompany the ACRU 3.00 Agrohydrological Modelling System. WRC Report No. TT 69/95. Water Research Commission, Pretoria. [ Links ]
SCHULZE R (2012) Mapping hydrological soil groups over South Africa for use with the SCS -SA design hydrograph technique: methodology and results. Sixteenth SANCIAHS National Hydrology Symposium 2012, 1-3 October 2012, Pretoria. [ Links ]
SCHULZE R (2013) Modelling impacts of land use on hydrological responses in South Africa with the ACRU model by sub-delineation of quinary catchments into land use dependent hydrological response units. Internal Report, School of Agricultural, Earth and Environmental Science, University of KwaZulu-Natal, Pietermaritzburg, South Africa. [ Links ]
SCHULZE R, ANGUS G, LYNCH S and SMITHERS J (1994) ACRU: Concepts and Structure. ACRU Theory Manual, Department of Agricultural Engineering, University of Natal, Pietermaritzburg, South Africa. [ Links ]
SCHULZE R and ARNOLD H (1979) Estimation of volume and rate of runoff in small catchments in South Africa, based on the SCS technique. ACRU Report No. 8, Department of Agricultural Engineering, University of Natal, Pietermaritzburg, South Africa. [ Links ]
SCHULZE R and HOHLS B (1993) A generic hydrological land cover and land use classification with decision support systems for use in models. Proceedings of the Sixth South African National Hydrology Symposium, 8-10 September 1993, Pietermaritzburg, South Africa. [ Links ]
SCHULZE R and HORAN M (2005) AUTOSOILS revised. School of Bioresources Engineering and Environmental Hydrology, University of KwaZulu-Natal, Pietermaritzburg, South Africa. [ Links ]
SCHULZE R, SCHMIDT E and SMITHERS J (1992) PC-based SCS design flood estimates for small catchments in Southern Africa. ACRU Report No. 40 - SCS-SA User Manual, Department of Agricultural Engineering, University of Natal, Pietermaritzburg, South Africa. [ Links ]
SCHULZE R, SCHMIDT E and SMITHERS J (2004) PC-based SCS design flood estimates for small catchments in Southern Africa. ACRUcons Report No. 52 - Visual SCS-SA User Manual, Version 1. University of KwaZulu-Natal, Pietermaritzburg, South Africa. [ Links ]
SCS (Soil Conservation Service) (1956) Hydrology National Engineering Handbook, Supplement A, Section 4. Soil Conservation Service, US Department of Agriculture, Washington, DC. [ Links ]
SCS (Soil Conservation Service) (1972) National Engineering Handbook, Section 4. Soil Conservation Service, US Department of Agriculture, Washington, DC, [ Links ].
SIRI (Soil and Irrigation Research Institute) (1987) Land Type Series. Memoirs on the Agricultural Natural Resources of South Africa. Department of Agriculture and Water Supply, Soil and Irrigation Research Institute, Pretoria. [ Links ]
SMITHERS J (2012) Review methods for design flood estimation in South Africa. Water SA 38 (4) 633-646. https://doi.org/10.4314/wsa.v38i4.19 [ Links ]
SMITHERS J, CHETTY K, FREZGHI M, KNOESEN D and TEWOLDE M (2007) Development and assessment of a continuous simulation modelling system for design flood estimation. WRC Report No. 1318/1/07. Water Research Commission, Pretoria. [ Links ]
SMITHERS J, CHETTY K, FREZGHI M, KNOESEN D and TEWOLDE M (2013) Development and assessment of a daily time-step continuous simulation modelling approach for design flood estimation at ungauged locations: ACRU model and Thukela Catchment case study. Water SA 30 (4) 467-476. https://doi.org/10.4314/wsa.v39i4.4 [ Links ]
SMITHERS J, GÖRGENS A, GERICKE J, JONKER V and ROBERTS C (2016) The initiation of a national flood studies programme for South Africa. South African National Committee on Large Dams, Pretoria, South Africa. [ Links ]
SMITHERS J and SCHULZE R (2002) Design rainfall and flood estimation in South Africa. WRC Project No. K5/1060. Water Research Commission, Pretoria. [ Links ]
SMITHERS J and SCHULZE R (2004) ACRU Agrohydrological Modelling System. User Manual Version 4, School of Bioresources Engineering and Environmental Hydrology, University of KwaZulu-Natal, Pietermaritzburg, South Africa. [ Links ]
SMITHERS J, SCHULZE R and KIENZLE S (1997) Design flood estimation using a modelling approach. In: Rosbjerg D, Boutayeb N, Gustard A, Kundzewicz ZW, Rasmussen PF (eds) Sustainability of Water Resources Under Increasing Uncertainty. Int. Assoc. Hydrol. Sci. Publ. 240 365-376. [ Links ]
SMITHERS J, SCHULZE R, PIKE A and JEWITT G (2001) A hydrological perspective of the February 2000 floods: A case study in the Sabie River catchment. Water SA 27 (3) 325-332. https://doi.org/10.4314/wsa.v27i3.4975 [ Links ]
VAN VUUREN S, VAN DIJK M and COETZEE G (2013) Status review and requirements of overhauling flood determination methods in South Africa. WRC Report No. TT 563/13. Water Research Commission, Pretoria. [ Links ]
Received 22 September 2016
Accepted in revised form 10 January 2018
* To whom all correspondence should be addressed. +27332605490; e-mail: smithers@ukzn.ac.za














