Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
Water SA
versión On-line ISSN 1816-7950
versión impresa ISSN 0378-4738
Water SA vol.44 no.1 Pretoria ene. 2018
http://dx.doi.org/10.4314/wsa.v44i1.05
http://dx.doi.org/10.4314/wsa.v44i1.05
Evaluation of the effectiveness of the National Benchmarking Initiative (NBI) in improving the productivity of water services authorities in South Africa
Warren Brettenny*; Gary Sharp
Department of Statistics, Nelson Mandela Metropolitan University, PO Box 77000, Port Elizabeth, 6031
ABSTRACT
Water shortages, public demonstrations and lack of service delivery have plagued many South African water services authorities (WSAs) for a number of years. From 2004-2007 the National Benchmarking Initiative (NBI) was implemented to improve the performance, efficiency and sustainability of WSAs. The current study demonstrates the use of data envelopment analysis (DEA) and the Malmquist productivity index (MPI) for the assessment of the effectiveness of the NBI in achieving these goals. Furthermore, the MPI is used to assess the impact that the termination of the NBI had on the efficiency of the WSAs in the years that followed. In conclusion, the MPI is identified as a valuable tool for regulators and policy makers that wish to assess the performance of their benchmarking initiatives.
Keywords: water service provision, productivity, benchmarking, Malmquist index, DEA
INTRODUCTION
South Africa is a water-scarce country and the effective management of water resources is essential for the continued provision of services to the public (Fisher-Jeffes et al., 2015). There is an important need for Government to constantly assess the performance of water services authorities (WSAs) as poor performances in this regard can lead reduced provision of water services to their constituents. Assessments of this nature often take the form of a benchmarking scheme or initiative (OMBI, 2011; Braadbaart, 2007), which seeks to compare WSAs against each other or against predetermined target levels in an effort to ascertain the level of relative or absolute performance for each.
Performance benchmarking was initially used in the private sector and not considered for the public sector because government officials maintained that their organisations were unique and any comparisons would ultimately be of no use (Ammons, 1999). However, the success of benchmarking practices in the corporate world began challenging this argument. While there are many instances of benchmarking practices in the private sector, the most prominent is the successful use of benchmarking by the Xerox Corporation in the early 1980s which showed that organisations need not be alike for them to be able to learn from each other (Ammons et al., 2001). In this case, the Xerox Corporation learnt valuable warehousing and distribution lessons from a benchmarking project undertaken with the catalogue merchant L. L. Bean (Dorsch and Yasin, 1998). The disparity in the two business types in this case did not preclude them from learning valuable practices from each other (Ammons, 1999). The use of performance benchmarking in this manner undermined the 'uniqueness argument' (Ammons et al., 2001) used by public sector officials to rule out their involvement. As such, performance benchmarking and measurement in the public sector began gaining ground rapidly in the early 1990s (Bruder and Gray, 1994). Tillema (2010) provides examples of public sector organisations which have used benchmarking for performance assessments and the creation of accountability. These examples include, but are not limited to, local authorities where performance was assessed by the ability of the authorities to provide 'best value' services, i.e., to raise standards while limiting costs (Bowerman and Ball, 2000), and police forces, where reduction in crime and increase in public confidence were top performance objectives (Collier, 2006).
The water services sector in South Africa is not unfamiliar with performance benchmarking initiatives. In fact, over the past 15 years three separate benchmarking initiatives have been implemented. Initially the National Benchmarking Initiative (NBI), which included the 2004/05 to 2006/07 municipal years, sought to compare the performance of municipalities in South Africa. Performance assessment which focused on the provision and quality of potable water and the removal of wastewater was introduced by the Blue and Green Drop certification processes, respectively, in 2008. Most recently, a second benchmarking initiative, the Municipal Benchmarking Initiative (MBI), began in 2012. While the Blue and Green Drop initiatives focused on the quality of services, the NBI (and subsequently MBI) sought to use benchmarking to address the main challenges faced by the South African water sector, namely to (SALGA, DWAF and WRC, 2005):
•Increase public access to sanitation and water services while maintaining their affordability.
•Ensure that all processes and services provided were sustainable.
•Create the capacity to ensure that the above two challenges were met.
•Enhance the performance of the water service providers so that the above challenges were met in the most efficient manner.
The current study seeks to assess the effectiveness of the NBI in achieving the final challenges indicated above. In so doing, this study aims to establish whether the return to benchmarking in the form of the MBI was justified and to propose a tool for the continued assessment of the MBI. This is achieved through the use of data envelopment analysis (DEA) to assess the efficiency of water service delivery, and the Malmquist productivity index (MPI) which assesses the efficiency change over time.
METHODOLOGY OF DEA AND THE MPI
Econometric efficiency analysis as it is used today is based on the seminal work and approach proposed by Farrell (1957). Efficiency analysis assesses the ability of a firm to convert inputs (e.g. resources, labour) into outputs (e.g. items produced, water delivered) by comparing each to a constructed frontier. The frontier represents the set of the input and output combinations that indicate best practice among the observed firms. Firms which are closer to the frontier are adjudged to be more efficient than those further from the frontier. An efficiency estimate in this context is thus a numerical measure of a firm's ability to convert inputs into outputs relative to firms with similar operations. The two predominant methods used to estimate the efficiency of firms are stochastic frontier analysis (SFA) and DEA. The former (SFA) is a parametric approach and requires the specification of a functional form for the production function against which the efficiencies of specific firms are determined. This method also requires the specification of the distribution (typically half-normal, exponential or truncated-normal) of the inefficiency term prior to the implementation of the estimation routines. For a more thorough discussion of this method the interested reader is referred to Khumbhakar and Knox Lovell (2003) and Greene (2008). Unlike SFA, DEA is a nonparametric approach to the evaluation of econometric efficiencies and, as such, does not require the pre-specification of any functions or distributions. The DEA method uses a linear programming technique to construct the frontier against which the firms are compared to determine the relative efficiency of each. Owing to the flexibility of the DEA procedure and its prominence in the related literature, this method is selected for use in the current study.
The terminology used to present the DEA method is used with reference to Brettenny and Sharp (2016). Firstly, each of the n WSAs which are included in the analysis are considered to be decision-making units which are responsible for converting a set of l inputs, denoted Xi where i = 1,2, … , l, to produce a set of m outputs, denoted Yj where j = 1,2, … , m where all inputs and outputs are identical. Since the decision-making units in this case are WSAs, the outputs (water delivered, etc.) can be considered a predetermined and fixed value while the inputs used to achieve these specified outputs should be minimised to achieve econometric efficiency. The DEA procedure in this scenario thus takes on an input orientation.
The set of inputs and outputs used by WSA k, where k = 1, …, n, for a given time period t, can be expressed as (xtk, ytk) where xtk = (x1tk,... xtlk) and ytk = (yt1k,... ytmk) represent the input and output vectors, respectively. The original DEA model, as developed by Charnes et al. (1978) (the Charnes-Cooper-Rhodes or CCR-DEA model), was developed under the assumption of constant returns to scale (CRS) and the efficiency estimate, θ*k, for WSA k in time period t using this model is determined as the solution to the following (Cooper et al., 2007):

subject to:
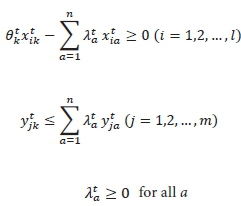
where the λta (a = 1, …, n) values indicate the degree to which each WSA contributes to the construction of the frontier for each evaluation (Gupta et al., 2006) and the constraints on the inputs and outputs ensure that no WSA can produce an input-output combination which is beyond the frontier. For each WSA k = 1, … , n, the solution, θ*k, to the linear programming problem in Eq. 1 measures the relative efficiency of WSA k relative to all of the WSAs included in the assessment. The kth WSA is considered to be efficient if θ*k = 1 and all associated slacks are equal to zero (Cooper et al., 2007). Slacks in this case are any shortfalls in the outputs or surpluses of the inputs for each assessed WSA, k, which are observed once the inputs have been reduced by a factor of θ*k (Singh et al., 2011). Banker et al. (1984) relaxed the assumption of CRS and developed a DEA model (the Banker-Charnes-Cooper or BCC-DEA model) which accounts for variable returns to scale (VRS) by including an additional convexity constraint ∑na=1 λa = 1 into Eq. 1. The evaluation of efficiencies under both the CRS and VRS assumptions allows for the determination of the scale inefficiencies present in the WSAs (see Murillo-Zamorano, 2004).
The method for DEA presented above provides a cross-sectional assessment of the WSAs for a given fixed time period t. As such, the frontier and associated efficiencies are fixed in time. To assess the change experienced by the WSAs from one time period to the next, the change in efficiencies as well as the change in the position of the frontier between the two time periods must be assessed. In a DEA framework, this is typically achieved through the use of the MPI. Less common approaches to assess this change, such as window analysis, are possible, but are not presented in this study, see Cooper et al. (2007) for details. Suppose that two time periods t1 and t2 are considered such that t2 > t1 and let δt2 (xt1k, yt1k) be defined as the efficiency estimate of WSA k using inputs and outputs from time period t1, evaluated against the DEA frontier formed by the observations in time period t2. Using this notation, the DEA efficiency estimate for WSA k as determined using Eq. 1 for time period t1 is θkt1 = δt2 (xt1k, yt1k). The MPI for productivity change between time periods t1 and t2 is now defined as (Cooper et al., 2007):
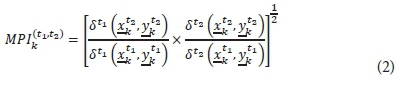
where efficiency estimates are determined under the CRS assumption. The index in Eq. 2 was decomposed by Färe et al. (1992) into a component for technical efficiency change (TEC) and technical progress (TP) as (Kleynhans and Pradeep, 2013):
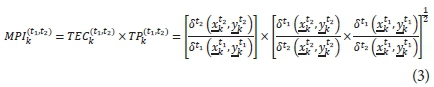
where TEC measures the change in the CRS efficiency estimate and TP measures the shift in the frontier between time periods t1 and t2. Let δt2v (xt1k, yt1k) denote the efficiency estimate calculated under VRS assumption. Using the VRS formulation, Färe et al. (1994) show that the TEC component in Eq. 3 can be decomposed into factors which are attributed to changes in scale efficiency (SEC) and changes in pure technical efficiency (PTEC). The TEC component is thus represented as TECk(t1, t2) = PTECk(t1, t2) x SECk(t1, t2) where:
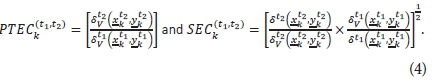
The MPI is thus the product of three components or factors, the PTEC, SEC and TP, with each component measuring a different and distinct element of the productivity change from one time period to the next. The PTEC value is a basic ratio of the BCC-DEA estimated relative technical efficiencies of a WSA from one period to the next, and the SEC value is a ratio of the scale efficiencies of a WSA from one period to the next. Values greater than 1 indicate an increase in the relative technical and scale efficiency between time periods, while values below 1 indicate a decrease in these categories. Improvements in relative technical efficiency (PTEC > 1) indicate that a WSA is moving closer to the frontier. Similarly SEC > 1 indicates an improvement in scale efficiency which is characterised by a WSA which moves towards production levels which are most suitable to the size of their operation. The opposite holds for PTEC < 1 and SEC < 1. TP measures the movement of the frontier, or the change in technology, from one time period to the next. Technical progress is observed when TP > 1, that is, from one time period to the next, less inputs are required to produce the same outputs and the technology has improved in the region of the WSA. Technical regress is indicated if TP < 1.
Table 1 provides a description of each component and is used for interpretative purposes according to the value of each component.
Using the results of the MPI technique, the effectiveness and value of benchmarking initiatives can be established and quantified by assessing the changes in productivity, efficiency and technology over the period in which the initiative is implemented. This information is critical to those implementing the benchmarking initiative as progress and regress can be established for each participating WSA for each year of the initiative. This allows for the identification of both the strengths and shortcomings of the initiative. Such knowledge can be used to enhance the initiative and provide direction for interventions to improve service delivery.
Literature review
The assessment of efficiency in the public sector, particularly the water sector, is not uncommon in the literature. Worthington (2014), Singh et al. (2011), De Witte and Marques (2010) and Abbot and Cohen (2009) provide thorough summaries of the studies that have assessed efficiency in the water services sector. Brettenny and Sharp (2016) discuss a number of studies which use DEA to analyse efficiencies in the water sector and provide a summary of the use of efficiency analysis in the South African public services sector. The review in the current study focuses on the literature pertaining to the use of the MPI to assess the change in efficiencies over time in the water services sector.
Urban water utilities in the Australian states of New South Wales and Victoria were subject to an efficiency assessment using DEA and the MPI by Byrnes et al. (2010). A total of 52 water utilities from these provinces were assessed over the 2000 to 2004 period. It was found that the utilities included in the assessment exhibited declines in both efficiency and technology. In fact, a yearly average decrease of 10% was observed in the total factor productivity for the utilities, with 70% of this attributed to declines in the productive capacity of the utilities.
Hon and Lee (2009) used the MPI to assess and quantify the efficiency change and technical change experienced by private and public water companies in Malaysia. The study assessed technological and efficiency changes for the 7-year period between 1999 and 2005. Hon and Lee (2009) found that the overall mean level of productivity in the Malaysian water services sector declined by 2.9% during this period. This observation was decomposed into a regress in the technology of the operations of 7.1% on average over the years assessed, and technical and scale efficiency increases over the same period. Hon and Lee (2009) noted that none of the state water utilities exhibited technological progress over the years included in the assessment.
In Portugal, Marques (2008) assessed 43 water and sewerage services (WSS) over the time period of 1994 to 2001. Marques (2008) utilised 4 different DEA models to determine the MPI, each distinguished from the other through the use of different input and output combinations. The results indicated that the average productivity decreased in each of the models and that this loss in productivity was largely as a result of a decrease in the production technology. This result echoes the findings of Byrnes et al. (2010).
Coelli and Lawrence (2006) assessed 18 large water services businesses in Australia over the period of 1996 to 2003, using the MPI to gauge productivity growth among these businesses. The MPI was assessed using 4 different models, taking into account capital and price deflators. As with Byrnes et al. (2010), an average decrease in productivity was observed. The results of Coelli and Lawrence (2006), however, indicated average yearly declines of between 0.6% and 1.7%, depending on the model used. Coelli and Lawrence (2006) concluded that the choice of the data used in the studies is important and that, in particular, the data available on the capital of each business require improvement.
Woodbury and Dollery (2004) investigated 73 municipal water services in New South Wales for a 3-year period (1998 to 2000). It was found that the productivity increased marginally (0.2%) over the time period assessed. This increase was attributed to a 2.2% increase due to a change in technology being all but cancelled out by a 1.9% decrease in efficiency, which suggested that the staff may still be adjusting to new technologies. A longer time period for assessment was suggested by the researchers, as this would provide additional clarity on the findings. This, however, would have resulted in fewer water services being included in the assessment owing to data limitations.
There have been several studies which use SFA to assess the productivity change of water service utilities; however, this discussion is limited to the studies which were conducted on the African continent. Estache and Kouassi (2002) assessed a sample of 21 African water utilities between 1995 and 1997 using SFA. The study found that, in general, African water utilities operate at relatively low efficiency levels. In Uganda, Mugisha (2007) assessed 15 Ugandan water sub-utilities to determine whether financial incentive applications reduce inefficiencies of the firms. The assessment used data for the 2000-2006 time period. It was found that financial incentives have positive effects in reducing firm inefficiency.
From a South African perspective there have been limited published studies which assess the efficiency of public services, most notably Mahabir (2014), Monkam (2014) and Van der Westhuizen and Dollery (2009), which assess the efficiency of municipalities considering all their operations and Brettenny and Sharp (2016) which focus on the South African water services sector. These studies all used cross-sectional data, and efficiency analysis over time using the MPI was not considered. Recently Mienie et al. (2017) used the MPI to assess the efficiency of port operations on the African continent, with particular attention being paid to the South African ports. Other than this, research of this kind in South Africa, and in the water services sector in particular, is absent. The current study addresses this gap in the literature by providing such an assessment, and using it to evaluate the effectiveness of the NBI in improving the efficiency of WSAs.
The South African metropolitan and local municipal structure
South Africa is split into non-overlapping geographical regions, with each region being classified and run by metropolitan (A) or local (B) municipalities. Local (B) municipalities are categorised, according to their size and population characteristics, into 4 sub-categories, namely, B1, B2, B3 and B4. District municipalities, which are made up of a collection of local municipalities, are not considered for this study owing to the poor quality of the data available for these entities. The characteristics of local and metropolitan municipalities in South Africa are provided in Table 2.
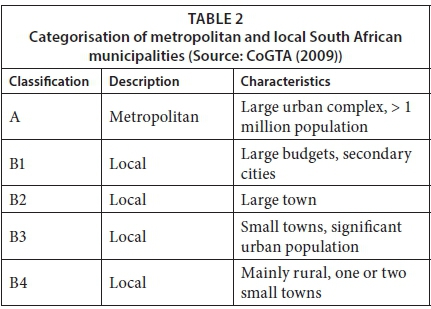
Each local and metropolitan municipality can be categorised according to whether it is a WSA or not. Only municipalities which are WSAs are considered in this study.
Data and variable selection
The choice of input and output variables in a DEA model is of utmost importance. These variables need to be chosen such that they provide sufficient information regarding the operations of the assessed WSAs, while at the same time the number of variables included in the model should be chosen to satisfy n ≥ max{2 x l x m, 3 x (l + m)} (Banker et al., 1989; Dyson et al., 2001). The variables chosen for use in the current study were based upon their prevalence in the related literature and their availability for the time period in question. Table 3 provides the input and output variables used in the current study.
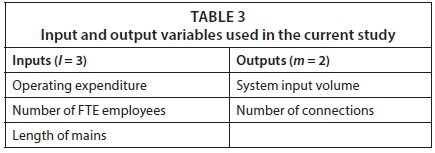
The use of multiple input and output variables is one of the key benefits of using the DEA methodology and, as such, does not present a problem in this study. Operating expenditure is a fundamental input of any water service provider. This variable provides an indication of the financial commitment of each WSA to achieve their level of output. The number of full-time equivalent (FTE) staff provides information regarding the labour force of each WSA which, again, is fundamental to the operations of the WSA. Lastly, the 'length of mains' variable, which indicates the physical length of the main water line, is included as a proxy for the capital costs of the WSA. This is in line with the use of the 'length of mains' variable for this purpose by Coelli and Lawrence (2006) and De Witte and Marques (2010). The outputs used are the system input volume, which indicates the volume of water delivered by the WSA, and the number of connections served by the WSA, which indicates the total number of metered or unmetered connections to the supply system. These (or similar) variables are the most common output variables used in studies which assess the efficiency of water service provision as indicated from the literature reviews of De Witte and Marques (2010) and Brettenny (2017). Lastly, an input-orientated DEA model is used to assess the efficiency of the South African WSAs. This is most appropriate as South African WSAs are required to meet a demand in the community (making the outputs exogenous) (Berg and Lin, 2008). Thus, efficiency studies in the water services sector typically aim at minimising the inputs used to achieve a desired, or predetermined, level of output.
The data required for the DEA and MPI assessments were gathered from the StatsSA - P9115 Financial Census of Municipalities document (StatsSA, 2011a), a report published by the WRC (TT522/12) entitled 'The State of Non-Revenue Water in South Africa', by Mckenzie et al. (2012), as well as the StatsSA - P9114 Non-Financial Audit of Municipalities document (StatsSA, 2011b).
Annual data were collected for each variable for the 2005/06 to the 2009/10 municipal years, as these were the most recent data available. For a WSA to be included in the assessment it would have to report data for all input and output variables, for every year of assessment. This presented a considerable challenge as the standard of record-keeping at municipal level in South Africa is often poor (Mckenzie et al., 2012). As such, only 36 municipalities reported sufficient data to be included in the study. Although this is a small number of WSAs it is considered to be a large enough sample to provide an indication of the effect of the NBI on water service efficiency.
RESULTS AND DISCUSSION
The DEA and MPI analyses were performed using the open-source statistical software R 3.3 (R Core Team, 2017) with the FEAR (Wilson, 2008) package. The DEA and MPI analytical routines solved within seconds and encountered no problems. Data were captured and sorted in Microsoft Excel 2016.
The NBI was implemented for the 2004/05 to 2009/10 municipal years. The data available to this study included the final 2 years of the NBI (2005/06 and 2006/07) and 3 subsequent years, i.e., the 2005/06 to 2009/10 municipal years. This data is sufficient to provide information regarding the success or failure of the NBI with respect to the efficiency of service delivery (2005/06-2006/07), as well as the effect of the termination of this initiative (2007/08-2009/10). Since this analysis is conducted over time, any variables which were measured in monetary terms (South African Rand) were standardised to the value of the most recent data, i.e., 2010, using the South African consumer price index (CPI).
To assess the change in efficiency for these time periods, the MPI and its components, namely, the pure technical efficiency change (PTEC), the scale efficiency change (SEC) and the technological progress (TP), were calculated for each year of the assessment. The geometric mean was then calculated for each WSA over the 2005-2007 and 2007-2010 time periods, separately. This value indicates the average yearly change for each WSA over each of these two periods. The geometric mean was used as it provides appropriate results in this setting as the MPI values indicate percentage growth/decline from one year to the next. The full set of results for each of the 36 WSAs are provided in the Appendix. For ease of interpretation and simplification of the findings, a summary is provided in Table 4.
Table 4 indicates the average MPI values (including its components), where the average is taken over all 36 municipalities and over each municipal category. No Category B4 local municipality reported sufficient data to be included in the study. This is a drawback, as there is thus no information regarding the effect of the NBI on the most rural of WSAs. However, sufficient detail is available for the remaining WSA categories to provide insight into the effectiveness of the NBI and the impact of its termination.
The results of the MPI analysis indicate that during the implementation of the NBI there was an average yearly increase in productivity of 4.6%. This provides evidence that the NBI was meeting its objectives of enhancing the provision of water service delivery in South Africa. The increase is mainly due to technological advances (TP = 1.036). This indicates that during the course of the NBI, there was an improvement in the productive capacity of the WSAs. That is, the relative best-practice frontier was shifting towards higher (or equivalent) output from lower input. That being said, marginal decreases (less than 0.5%) in PTEC (or managerial efficiency) and small increases (just above 1%) in scale efficiency are observed for this period. This indicates that, for this time period, the operational or managerial efficiencies of the WSAs decreased slightly, while the operating size of the WSAs improved. Most notable, however, is the increase in technology, which is associated with improved infrastructure and technological capacity. This observation is consistent through all categories of WSAs, with Category B3 WSAs showing the largest technological improvements. Minor decreases in scale efficiency are observed for Category B2 and B3 WSAs which service smaller towns and more rural areas. This, along with slightly lower MPI values for these categories, suggests that the NBI might have benefited urbanised WSAs more than their more rural counterparts. This, however, is of little consequence as the net result, for all WSA categories, is a considerable improvement in productivity during the implementation of the NBI.
The NBI was terminated following the 2006/07 municipal year. The MPI and its components for the 3 years following the termination (2007-2010) are presented in Table 4. The results of the MPI analysis for the years after the NBI stand in stark contrast to those observed during the NBI. For this period, there was an average yearly decline in productivity of approximately 3.7% when all of the assessed WSAs are considered. This decline is mainly due to a considerable average yearly regress in technological change (0.956). Hon and Lee (2009) claim that this regress could be as a consequence of poor maintenance and/or an increase in non-revenue water. The decrease observed in technological progress indicates that the production capacity of the WSAs was declining over the period observed. In its simplest form this means that, in general, additional resources are required to deliver the same service to the consumers. This provides compelling evidence that the NBI effectively increased the productivity of WSAs during its implementation. The negligible average annual increases observed for technical efficiency are outweighed by the significant decline in technology. Category B2 WSAs, those that benefitted most from the NBI, are, unsurprisingly, those that are most adversely affected by the termination of the NBI, with annual average decreases in productivity of around 4.8% observed for this category. The best performing category, according to the MPI, is Category A WSAs. Category A municipalities experienced an average yearly decrease in productivity of approximately 2.4% subsequent to the cessation of the NBI. Table A1 (Appendix) indicates that less than a third of the 36 WSAs assessed in this study exhibited average yearly technological progress during this time. This provides a strong indication that the termination of the NBI had an adverse effect on the technological progress of WSAs in South Africa.
The Blue and Green Drop systems began in 2008, subsequent to the cancellation of the NBI. The initiatives focused on the improvement in the quality of the products supplied by WSAs. The implementation of these initiatives may have affected the productivity of WSAs in the years following the NBI, as WSAs may focus additional resources on satisfying the requirements of the Blue and Green Drop assessments. This, however, cannot be established without more data. Nevertheless, the MPI has been demonstrated to be an effective tool for the assessment of the impact of these initiatives on the productivity of water services authorities in South Africa.
CONCLUSIONS, LIMITATIONS AND FURTHER WORK
Performance benchmarking of public services is an important tool for policy makers and regulators. It allows for peer comparison and evaluation which, in turn, can lead to improved performance over time. Equally important is a means to evaluate the effectiveness of the benchmarking initiatives which are undertaken. The current study demonstrates that the Malmquist productivity index (MPI) can provide important information on the performance of benchmarking initiatives in South Africa and the impact that the termination of these initiatives can have on productivity. The results of this study show that the National Benchmarking Initiative (NBI), which ran from 2004-2007, appears to have had a positive impact on the productivity of the water service industry in South Africa. Subsequently, the termination of this initiative coincides with notable decreases in productivity in the years that followed. The MPI thus provides a tool which is effective for the assessment of the impact of interventions and programmes in the water services (and other) sectors. As such, this is a method which can be used on an annual basis to assess ongoing benchmarking initiatives (namely the Municipal Benchmarking Initiative (MBI)) and the impacts thereof.
The main limitation of the current study is the fairly small sample size used. Although the sample is big enough to provide valuable insight into the productivity of WSAs in South Africa, a larger sample would provide more compelling evidence. A further limitation of the study was the lack of sufficient data to include district municipalities in the assessment. This analysis would have allowed for a more comprehensive investigation into the effect of the NBI, and its subsequent termination, on the productivity of all WSAs in South Africa. The continuing assessment of the productivity of South African WSAs using a larger sample is the primary area for future research into this topic. Added to this, the use of a bootstrapping technique to provide inferences regarding the MPI values is a further area for future research.
In conclusion, this study demonstrates that the MPI can be used to assess the effectiveness of South African benchmarking initiatives in achieving their goal of efficient and improved service delivery. Owing to the usefulness of this procedure it is envisioned that this can be used to assess the MBI which is currently underway in South Africa, provided the necessary data are made available.
REFERENCES
AMMONS DN (1999) A proper mentality for benchmarking. Public Admin. Rev. 59 (2) 105-109. https://doi.org/10.2307/977630 [ Links ]
AMMONS DN, COE C and LOMBARDO M (2001) Performance-comparison projects in local government: Participants' perspectives. Public Admin. Rev. 61 (1) 100-110. [ Links ]
BANKER R, CHARNES A and COOPER W (1984) Some models for estimating technical and scale inefficiencies in data envelopment analysis. Manage. Sci. 30 (9) 1078-1092. https://doi.org/10.1287/mnsc.30.9.1078 [ Links ]
BANKER R, CHARNES A, COOPER W, SWARTS J and THOMAS D (1989) An introduction to data envelopment analysis with some of its models and their uses. Res. Gov. Nonprofit Account. 5 125-163. [ Links ]
BERG S and LIN C (2008) Consistency in performance rankings: the Peru water sector. Appl. Econ. 40 (6) 793-805. https://doi.org/10.1080/00036840600749409 [ Links ]
BRAADBAART O (2007) Collaborative benchmarking, transparency and performance: Evidence from The Netherlands water supply industry. Benchmarking: An International Journal 14 (6) 677-692. https://doi.org/10.1108/14635770710834482 [ Links ]
BRETTENNY W (2017) Efficiency evaluation of South African water service provision. PhD thesis, Nelson Mandela Metropolitan University. [ Links ]
BRETTENNY W and SHARP G (2016) Efficiency evaluation of urban and rural municipal water service authorities in South Africa: A data envelopment analysis approach. Water SA 42 (1) 11-19. https://doi.org/10.4314/wsa.v42i1.02 [ Links ]
BRUDER KA and GRAY EM (1994) Public-sector benchmarking: A practical approach. Public Manage. 76 (9) S9-S14. [ Links ]
BOWERMAN M and BALL A (2000) The modernisation and importance of government and public services: Great expectations: Benchmarking for best value. Public Money Manage. 20 (2) 21-26. https://doi.org/10.1111/1467-9302.00207 [ Links ]
BYRNES J, CRASE L, DOLLERY B and VILLANO R (2010) The relative economic efficiency of urban water utilities in regional New South Wales and Victoria. Resour. Energ. Econ. 32 (3) 439-455. https://doi.org/10.1016/j.reseneeco.2009.08.001 [ Links ]
CHARNES A, COOPER W and RHODES E (1978) Measuring the efficiency of decision making units. Eur. J. Oper. Res. 2 (6) 429-444. https://doi.org/10.1016/0377-2217(78)90138-8 [ Links ]
COELLI T and WALDING S (2006) Performance measurement in the Australian water supply industry: A preliminary analysis. In: Coelli T and Lawrence DA (eds). Performance Measurement and Regulation of Network Utilities. Edward Elgar, Cheltenham, UK. [ Links ]
CoGTA (Department of Cooperative Governance and Traditional Affairs, South Africa) (2009) State of Local Government in South Africa, Overview Report: National State of Local Government Assessments. Cooperative Governance and Traditional Affairs. Working Paper. [ Links ]
COLLIER PM (2006) In search of purpose and priorities: Police performance indicators in England and Wales. Public Money Manage. 26 (3) 165-172. https://doi.org/10.1111/j.1467-9302.2006.00518.x [ Links ]
COOPER WW, SEIFORD, LM and TONE K (2007) Data Envelopment Analysis: A Comprehensive Text with Models, Applications, References and DEA-Solver Software, 2nd Edition. Springer, New York. [ Links ]
DE WITTE K and MARQUES RC (2010) Designing performance incentives, an international benchmark study in the water sector. Cent. Eur. J. Oper. Res. 18 (2) 189-220. https://doi.org/10.1007/s10100-009-0108-0 [ Links ]
DORSCH JJ and YASIN MM (1998) A framework for benchmarking in the public sector: Literature review and directions for future research. Int. J. Public Sector Manage. 11 (2) 91-115. https://doi.org/10.1108/09513559810216410 [ Links ]
DWAF, SALGA and WRC (Department of Water Affairs and Forestry, South African Local Government Association and Water Research Commission) (2005) National Water Services Benchmarking Initiative: Promoting best practice. Benchmarking outcomes for 2004/5. [ Links ]
DYSON R, ALLEN R, CAMANHO A, PODINOVSKI V, SARRICO C and SHALE E (2001) Pitfalls and protocols in DEA. Eur. J. Oper. Res. 132 (2) 245-259. https://doi.org/10.1016/S0377-2217(00)00149-1 [ Links ]
ESTACHE A and KOUASSI E (2002) Sector Organization, Governance, and the Inefficiency of African Water Utilities. Policy Research Working Paper 2890. World Bank, Washington, D.C. [ Links ]
FÄRE R, GROSSKOPF S, LINDGREN B and ROOS P (1992) Productivity changes in Swedish pharmacies 1980-1989: A non-parametric Malmquist approach. J. Productivity Anal. 3 (1) 85-101. https://doi.org/10.1007/BF00158770 [ Links ]
FÄRE R, GROSSKOPF S and NORRIS M (1994) Productivity Growth, Technical Progress, and Efficiency Change in Industrialized Countries. The Am. Econ. Rev. 84 (1) 66-83. [ Links ]
FARRELL MJ (1957) The measurement of productive efficiency. J. R. Stat. Soc. Series A (General) 120 (3) 253-290. https://doi.org/10.2307/2343100 [ Links ]
FISHER-JEFFES L, GERTSE G and ARMITAGE NP (2015) Mitigating the impact of swimming pools on domestic water demand. Water SA 41 (2) 238-246. https://doi.org/10.4314/wsa.v41i2.09 [ Links ]
GREENE WH (2008) The economic approach to efficiency analysis. In Fried HO, Knox Lovell CA and Schmidt SS (eds) The Measurement of Productive Efficiency and Productivity Growth. Oxford University Press, New York. https://doi.org/10.1093/acprof:oso/9780195183528.003.0002 [ Links ]
GUPTA S, KUMAR Sand SARANGI, GK (2006) Measuring the Performance of Water Service Providers in Urban India: Implications for Managing Water Utilities. National Institute of Urban Affairs, New Delhi. NIUA WP 06-0. [ Links ]
HON LY and LEE C (2009) Efficiency in the Malaysian water industry: A DEA and regression analysis. URL: http://www.webmeets.com/files/papers/EAERE/2009/9/WaterPaper EAERE 2009.pdf (Accessed 14 June 2017). [ Links ]
KLEYNHANS E and PRADEEP V (2013) Productivity, technical progress and scale efficiency in Indian manufacturing: post-reform performance. J. Econ. Fin. Sci. 6 (2) 479-494. [ Links ]
KUMBHAKAR S and KNOX LOVELL C (2003) Stochastic Frontier Analysis. Cambridge University Press, Cambridge, United Kingdom. [ Links ]
MAHABIR J (2014) Quantifying inefficient expenditure in local government: a disposal free hull analysis of a sample of South African municipalities. S. Afr. J. Econ. 82 (4) 493-517. https://doi.org/10.1111/saje.12050 [ Links ]
MARQUES RC (2008) Measuring the total factor productivity of the Portuguese water and sewerage services. Economia Aplicada 12 (2) 215-237. https://doi.org/10.1590/S1413-80502008000200003 [ Links ]
MCKENZIE R, SIQALABA ZN and WEGELIM WA (2012) The State of non-revenue water in South Africa (2012). WRC Report No. TT 522/12. Water Research Commission, Pretoria. [ Links ]
MIENIE BJ, SHARP, G and BRETTENNY W (2017) Ranking selected container terminals in Africa using data envelopment analysis. Manage. Dyn. J. South. Afr. Inst. Manage. Sci. 26 (1) 16-29. [ Links ]
MONKAM NF (2014) Local municipality productive efficiency and its determinants in South Africa. Dev. South. Afr. 31 (2) 275-298. https://doi.org/10.1080/0376835X.2013.875888 [ Links ]
MUGISHA S (2007) Effects of incentive applications on technical efficiencies: Empirical evidence from Ugandan water utilities. Utilities Polic. 15 (4) 225-233. https://doi.org/10.1016/j.jup.2006.11.001 [ Links ]
MURILLO-ZAMORANO LR (2004) Economic efficiency and frontier techniques. J. Econ. Surv. 18 (1) 33-77. https://doi.org/10.1111/j.1467-6419.2004.00215.x [ Links ]
OMBI (ONTARIO MUNICIPAL BENCHMARKING INITIATIVE) (2011). About: The Ontario Municipal Benchmarking Initiative. URL: http://www.ombi.ca (Accessed 20 June 2012). [ Links ]
R CORE TEAM (2017) R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing. Vienna, Austria. URL: http://www.R-project.org/ (Accessed 13 March 2017). [ Links ]
SINGH MR, MITTAL AK and UPADHYAY V (2011) Benchmarking of North Indian urban water utilities. Benchmarking: An International Journal 18 (1) 86-106. https://doi.org/10.1108/14635771111109832 [ Links ]
StatsSA (2011a) P9114 - Financial Census of Municipalities 2010/2011. URL: http://www.statssa.gov.za/publications/statspastfuture.asp?PPN=P9114 (Accessed 27 February 2013). [ Links ]
StatsSA (2011b) P9115 - Non-Financial Census of Municipalities 2010/2011. URL: http://www.statssa.gov.za/publications/statspastfuture.asp?PPN=P9115 (Accessed 27 February 2013). [ Links ]
TILLEMA S (2010) Public sector benchmarking and performance improvement: what is the link and can it be improved? Public Money Manage. 30 (1) 69-75. https://doi.org/10.1080/09540960903492414 [ Links ]
VAN DER WESTHUIZEN G and DOLLERY B (2009) Efficiency measurement of basic service delivery at South African district and local municipalities. TD: J. Transdisc. Res. South. Afr. 5 (2) 162-174. [ Links ]
WILSON PW (2008) FEAR 1.0: A software package for frontier efficiency analysis with R. Socio-Econ. Plann. Sci. 42 (4) 247-254. https://doi.org/10.1016/j.seps.2007.02.001APPENDIX [ Links ]
Received 22 June 2017
Accepted in revised form 1 December 2017
* To whom all correspondence should be addressed. +27415042895; e-mail: warren.brettenny@nmmu.ac.za















