Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Water SA
On-line version ISSN 1816-7950
Print version ISSN 0378-4738
Water SA vol.43 n.3 Pretoria Jul. 2017
http://dx.doi.org/10.4314/wsa.v43i3.08
Discharge coefficient of semi-circular labyrinth side weir in subcritical flow
M Khalili*; T Honar
Department of Water Engineering, Shiraz University, Shiraz, 71441-65186, Iran
ABSTRACT
Side weirs are flow diversion or intake devices that are widely used in irrigation and drainage networks and urban sewage systems. Labyrinth weirs have a proven hydraulic advantage due to their increased discharge rate at the same head for a given design condition. A labyrinth weir is defined as a weir crest that is not straight in plan-form. The increased sill length provided by labyrinth weirs effectively reduces upstream head to the particular discharge. In this study, a comprehensive laboratory study was conducted in a physical model of a semi-circular labyrinth side weir and the model is evaluated for three heights and three radii. In this particular study, the hydraulic effects of this shape of side weir in increasing discharge capacity was investigated. The discharge coefficient of semi-circular labyrinth side weirs was determined and the results were analysed to find the influence of the dimensionless parameters of weir height (w/b), weir length (r/b), nape height ((y1−w)/r), and upstream Froude number (Fr1) on discharge coefficient (Cd), based on the experimental conditions and previous studies. It was found that the discharge coefficient of the semi-circular labyrinth side weir gives a relatively high discharge coefficient value compared to other types of classic side weir positioned on a straight channel. Additionally, reliable equations for calculating the discharge coefficient (Cd) of semi-circular labyrinth side weirs are proposed. According to the proposed equation, Cd depends on dimensionless parameters, which are the ratios of r/b, r/w, (y1−w)/r, (y2−w)/r and Fr1.
Keywords: side-weir, discharge coefficient, semi-circular labyrinth side weir, subcritical flow.
INTRODUCTION
A side weir is an overflow weir set into the side of a main channel. Side weirs have been extensively used in hydraulic and environmental engineering applications. They typically are used for water level control in canal systems, diverting excess water into relief channels during floods, as storm overflows from urban sewage systems, and as a head regulator of distributaries.
A review of literature on side weirs indicates that their discharge coefficient has been extensively studied, due to its importance. Rectangular sharp-crested side weirs have been investigated extensively, including work for example by Ackers (1957), Collings (1957), Frazer (1957), Subramanya and Awasthy (1972), El-Khashab and Smith (1976), Uyumaz and Muslu (1985). The analyses of Ranga Raju et al. (1979) and Ramamurthy and Carballada (1980) indicated that bed slope and friction highly affect side weir outflow. Borghei et al. (1999) discussed the application of spatially varied flow in sharp-crested rectangular side weirs. The hydraulic behaviour and discharge coefficient of side weirs for the different types of weirs, main channels and flow conditions have been studied by many researchers, for example, Nandesamoorthy and Thomson (1972), Yu-Tech (1972), Cheong (1991), and Singh et al. (1994). Ghodsian (2003) studied supercritical flow in rectangular side weirs. Cosar and Agaccioglu (2004) studied the discharge coefficient of a triangular side weir, for weirs on both straight and curved channels. Aghayari et al. (2009) experimentally investigated the effect of height, width and side weir crest slope on the spatial discharge coefficient over broad-crested inclined side weirs under subcritical flow conditions in a rectangular channel. To study the discharge coefficient variation along a side weir, Swamee et al. (1994) used an elementary analysis approach to estimate the discharge coefficient in smooth side weirs through an elementary strip along the side weir.
Some of the proposed formulas for the estimation of discharge coefficient in rectangular side weirs are presented in Table 1.
Most of the presented equations for Cd depend on the Froude number of flow at the upstream section of the side weir. In addition, the majority of previous researchers have concentrated on investigating rectangular and triangular side weirs in straight channels. However, triangular and circular types of side weirs are also used in hydraulic and environmental engineering applications.
Labyrinth side weirs have different shapes, such as triangular, trapezoidal and semi-circular, in plan view. A labyrinth side weir provides a longer effective length for a given overall side weir opening. In fact, the effective length is the weir crest length that is denoted by l. The increased sill length provided by the labyrinth side weirs effectively reduces upstream head to the particular discharge. They can therefore be used to particular advantage where the width of a channel is restricted and a weir is required to pass a range of discharges with a limited variation in upstream water level. Emiroglu et al. (2010 a, b) studied the discharge coefficient of sharp-crested triangular labyrinth side weirs on a straight channel. They proposed dimensionless parameters for triangular labyrinth side weir discharge coefficients on a straight channel as:

where: Fr1, Cd, w, L, b and y1 are defined earlier, l is overflow length of the side weir, θ is the included angle of the triangular labyrinth side weir. The water nape deviation or deflection angle ψ, is defined the deflection of the side-weir nape from the water surface toward the weir side and is given as follows (Subramanya and Awasthy, 1972):

where: Vs is velocity of flow dQs over the brink. The water nape deviation ψ takes different values for each fluid particle and varies with the Froude number, which changes along the side weir due to spilling over the side weir. The deviation angle increases towards the side weir when the Froude number in the main channel decreases in the downstream direction. Some researchers have also mentioned that the dimensionless length of the side weir (L/b) includes the effect of the deviation angle on the discharge coefficient (Subramanya and Awasthy, 1972; El-Khashab, 1975; El-Khashab and Smith, 1976; Agaccioglu and Yüksel, 1998; Borghei et al. 1999). Therefore, the deviation angle ψ is not included in the side weir discharge coefficient equations in the literature. Emiroglu et al. (2010 a) reported that the discharge coefficient of the triangular labyrinth side weirs is 1.5-4.5 times higher than that of the rectangular side weir.
Unlike labyrinth spillways, one or two cycles are mostly sufficient for the labyrinth side weirs to deliver the required discharge. Therefore, there is a need to study different shapes of labyrinth side weirs in order to obtain comprehensive knowledge on this subject. Undoubtedly, an accurate and useful equation for semi-circular labyrinth side weirs with one cycle is required by hydraulic and environmental engineers. This study mainly aimed to evaluate various hydraulic characteristics of a semi-circular labyrinth side weir in one cycle by conducting experiments across a wide range of values for important parameters and to develop a useful and reliable equation for them in practical applications. This paper investigates the discharge coefficient of semi-circular labyrinth side weirs under subcritical flow condition and, in particular, the effect of the upstream Froude number Fr1 and dimensionless parameters (w/b), (r/b), (w/y1) on the discharge coefficient, given the experimental conditions and results of previous studies. The discharge coefficient of semi-circular labyrinth side weirs was determined based on dimensionless parameters, which are the ratios of r/b, r/w, b/y2, (y1−w)/r, (y2−w)/r and Fr1. Also, the longitudinal velocity of semi-circular labyrinth side weirs has been studied for the subcritical flow in detail.
DISCHARGE COEFFICIENT FUNCTION
The flow over a side weir is categorized as a spatially varied flow condition. The present study dealt mainly with the application of the energy principle in the analysis of flow over side weirs. The concept of constant specific energy (De Marchi, 1934) is quite often adopted in studying the flow characteristics of side weirs (Emiroglu et al., 2010a, b; Singh et al., 1994; Hager, 1987; Subramanya and Awasthy, 1972). De Marchi (1934) was one of the first researchers to provide equations for flow over side weirs. He assumed that the discharge over the side weir per unit length, q, is:

where: Q = discharge in the main channel at section s; s = distance from the beginning of the side weir; q (or = dQ/ds) = discharge spilling for per unit length of the side weir; g = acceleration due to gravity; w = height of the side weir; y = depth of flow at section s; and Cd = discharge coefficient of the rectangular side weir (Fig. 1). Thus the side weir discharge equation can be written as:


where: Qw is total flow over side weir, Cd is the discharge coefficient and is dimensionless, L is the width of side-weir, and y and w are main channel depth and height of weir crest, respectively.
Understanding the physical relationship between discharge coefficient and independent non-dimensional variables is very important to be able to construct an appropriate function. In this study, a dimensionless analysis based on Buckingham's theorem was used to find non-dimensional variables. After the determination of dimensionless variables and elimination of some of the parameters, the functional discharge coefficient can be obtained by:
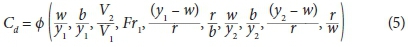
where: Fr1 is approach Froude number upstream of the side weir, w is side weir height, l is the effective side weir length, r is the radius of semi-circular labyrinth side weir, b is the main channel width, V1 and V2 are the mean velocities in the upstream and downstream sections of the weir crest, respectively, y1 and y2 are the depth of flow at the upstream and downstream end of the side weir in the centreline of the main channel. A longitudinal section and plan of a semi-circular labyrinth side weir with different variables are presented in Fig. 2.
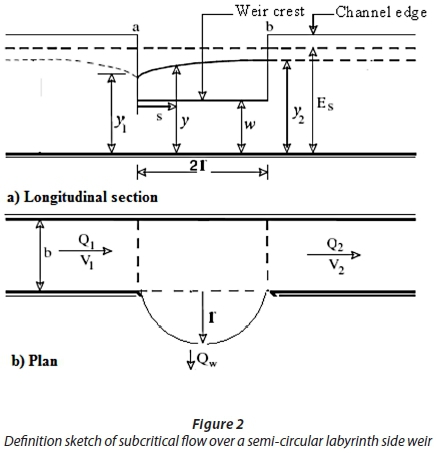
EXPERIMENTAL SET-UP
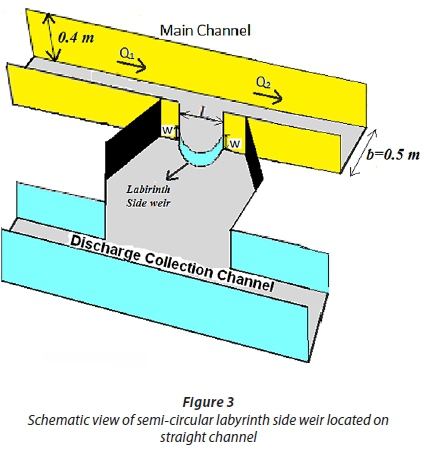
Semi-circular labyrinth side weir experiments were conducted at the hydraulic laboratory of Shiraz University, Shiraz, Iran. The experimental set-up consisted of a main channel and the discharge collection channel. The main channel was 15 m long with a rectangular cross-section. The main channel had internal width b = 0.50 m and 0.40 m depth with the bed slope at 1/1 000. The length of the channel from the inlet section to the beginning of the side weir was 7 m. A sluice gate is fitted at the end of the main channel to control flow depth. The lateral channel was parallel to the main channel and was 8 m long, 0.60 m wide and 0.40 m deep with a horizontal invert. A schematic representation of the semi-circular labyrinth side weir set-up is shown in Fig. 3. The main and lateral channels were made of brick masonry and plastered with cement. Two pre-calibrated standard V-notches were used to measure the discharge of the downstream end of the lateral and main channels. The side weirs were made of mild steel plate, the top edge being suitably bevelled to get a sharp crest. The side weir was installed flush with the main channel wall. To measure the water depth, a point gauge with an accuracy of ± 0.1 mm was used. Water depth was measured in the centreline axis of the channel length. Water depth measurements were made using a handmade type of frame, which can move in both x and y directions on a rail. Velocity was measured by using an electromagnetic velocity meter with an accuracy of 1 mm/s (model LP1100). To understand the hydraulic behaviour of the semi-circular labyrinth side weir, two sets of velocity measurements are taken at the side weir sections of the flume. The first set was taken with low overflow condition (Qw = 0.2 Q1). The second was taken with the high overflow condition (Qw= 0.65 Q1). Longitudinal velocities are measured at the point showed in Fig. 4. Experiments were conducted for open-end and semi-closed-end conditions. These experiments were conducted for subcritical flow, stable and free overflow conditions. Coleman and Smith (1923) pointed out that minimum nape height should be less than 19 mm because of the surface tension over the weir crest. Therefore, minimum nape height was taken as 20 mm. The experiments were conducted for 3 heights and 3 radii of semi-circular labyrinth side weir (w = 0.05, 0.10, 0.15 m and r = 0.18, 0.29, 0.40 m). In case of semi-circular labyrinth side weir with radius and height of 0.29 m and 0.10 m, respectively, the equivalent classical rectangular side weir was also tested and measured discharge coefficients were compared. The range of parameters is given in Table 2.
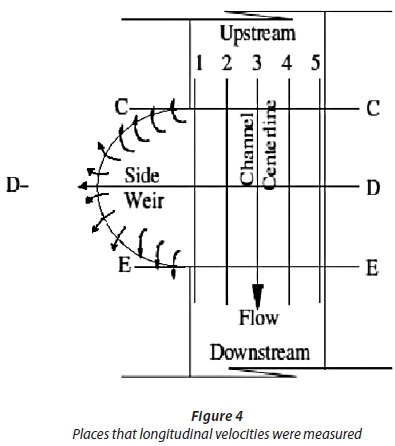
EXPERIMENTAL RESULTS AND ANALYSIS
Vertical profiles of longitudinal velocities in the main channel
Although this study did not anticipate investigating the velocity distribution in detail, an important feature was to observe the shape of the curve for maximum longitudinal velocity in order to know the effect of overflow on the main channel flow. Velocity measurements were conducted for both high and low overflow conditions (Qw = 0.65Q1 and Qw = 0.2 Q1) for the semi-circular labyrinth side weir with radius of r = 0.29 m (weir length of L = 0.58 m), weir height of w = 0.10 m and, discharge of main channel of Q1 = 30 L/s.
Vertical velocity profiles at the point of C1, C2, C3, C4 and C5; D1, D2, D3, D4 and D5; E1, E2, E3, E4 and E5 were measured. As can be seen in Fig. 4, velocity profiles at the C-C, D-D and E-E sections of the straight channel (v/vm ) are plotted versus z/z0. The velocities are normalized by dividing them with the maximum longitudinal velocity, which is measured along the channel, and the depth is normalized by dividing the measured height with the depth of flow in the same run of velocity measurements, in which vm is maximum velocity, and z and z0 are depths where z0 is equal to y (depth of flow).
Typical vertical profiles of longitudinal velocities along the semi-circular labyrinth side weir are shown in Fig. 5. Comparing the results of this study with those of Emiroglu et al. (2010 a), the same findings can be observed. The v/vm ratio decreases towards the inner bank due to lateral flow; the v/vm ratio for the inner bank is lower than that of outer bank. The inner bank has been delineated by Longitudinal Profile 5 of the flow through the main channel and the outer bank has been delineated by Longitudinal Profile 1, where the side weir is set in Fig. 4. In section E-E, velocity in the main channel decreases due to lateral flow at the downstream end of the side weir and thus flow depth at the downstream end become higher than that of the upstream end. The velocity value tends towards zero at the downstream end of the side weir. The effect of lateral flow is significant, especially for high overflow conditions.
Cd coefficient
Experiments were conducted to determine the discharge coefficient of semi-circular labyrinth side weirs. The discharge coefficient was computed using the De-Marchi equation (Eq. 4):

where:
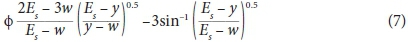
and: b is the main channel width, L is the weir crest width, y is the depth of flow, w is side weir height and ES is the specific energy that is assumed to be constant along the length of the side weir.
The crest length of the semi-circular labyrinth side weir is always longer than that of the classical rectangular side weir. In other words, if the crest length of the rectangular side weir is considered as L and the crest length of the semi-circular labyrinth side weir with one cycle is considered as l = π·r = π·L/2, then l/L = 1.57 can be calculated for the semi-circular labyrinth side weir. As we are obliged to use the length (width) of side weir (L) in Eq. 6, whereas the real length crest of a semi-circular labyrinth side weir is l and is 1.57 times longer than width of side weir (L), then it is expected to obtain a higher discharge coefficient (Cd) in comparison with classic side weirs. Since the weir length is excessive, more intensive secondary flow occurs. Thus, intensive secondary flow can also result with higher flow rate (Kaya et al., 2011). Therefore, the main purpose of a labyrinth side weir is to create a higher crest length as well as other hydraulic effects such as more severe secondary flow (secondary considerations).
Dimensional analysis allows description of all important factors involved in the phenomenon expressed in dimensionless components. A multicollinearity test was used to analyse the data (variable). Results showed that for a sharp-crested semi-circular labyrinth side weir, the discharge coefficient is a function of:
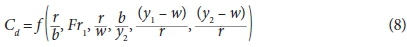
or
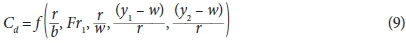
with regard to linear or non-linear regressions, respectively.
The discharge coefficient values for a semi-circular labyrinth side weir with r = 0.29 m and w = 0.10 m are compared with those of the equivalent classical rectangular side weir in Fig. 6. The values of Cd were plotted against Fr1. It can be seen in Fig. 6 that the values of Cd for the semi-circular labyrinth side weir with L/b = 1.16 and w/b = 0.2, are significantly higher than those of the rectangular side weir that was measured in this study. The primary reason for the increase in the discharge capacity of the semi-circular labyrinth side weir can be attributed to the increase in the overflow length of the side weir.

The discharge coefficient values for the semi-circular labyrinth side weir (r/b =0.36, 0.58, 0.80) are compared with those of Ranga Raju et al. (1979), Subramanya and Awasthy (1972) and Nandesamoorthy (1972) for rectangular side weirs. As can be seen in Fig. 7, the values of Cd for the semi-circular labyrinth side weirs are significantly higher than those suggested in previous studies. Based on the literature and dimensional analysis results, semi-circular labyrinth side weirs were tested for three different heights and radii, to investigate the effect of different heights and radii on discharge coefficient. To study the effect of parameter upstream Froude Number (Fr1) and dimensionless parameter of the nape height ((y1−w)/r) on the discharge coefficient, the values of Cd are plotted against Fr1 and (y1−w)/r in Figs 8 and 9, respectively, for all of the experimental data.
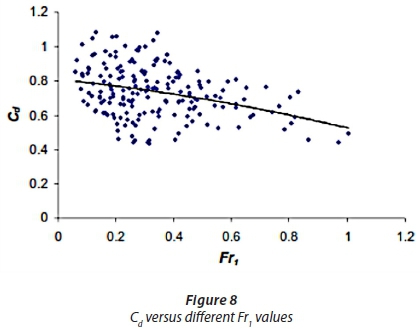

As can be seen in Fig. 8, the discharge coefficient decreases when the Froude number increases. This decreasing trend is counter to that reported by Emiroglu et al. (2010 a) for triangular labyrinth side weirs, but is similar to the recent study about semi-elliptical labyrinth side weirs reported by Kaya et al. (2011). Scattering of the data is attributed the influence of the effective parameters, such as r/b. Fig. 9 reveals that Cd almost has an indistinct trend versus the dimensionless parameter of the nape height (y1−w)/r. Although the scattering of data is very apparent, it shows a moderate descending trend in Cd values as (y1−w)/r increases. Figure 10 shows the effect of weir height on discharge coefficient of a semi-circular labyrinth side weir in different ratios of w/b and the ratio of r/b = 0.8. As can be seen in Fig. 10, Cd takes higher values when the dimensionless parameter of the weir's height w/b increases. Kaya et al. (2011) pointed out that the effect of exerting different heights (in the form of dimensionless parameters w/b or w/y1) on Cd can be explained by the existence of a discontinuity region. This discontinuity region has a strong secondary motion next to the boundary of the weir-side. The intensity of this secondary motion next to the boundary depends on the crest height of the side weir and decreases with an increase in height, due to the friction of the weir surface.

The variation of discharge coefficient of the semi-circular labyrinth side weir is presented for a ratio of w/b =0.3 for r/b =0.36 and r/b =0.8 (dimensionless parameter of weir's length) in Fig. 11. It is clearly observed from Fig. 11 that discharge coefficients of the semi-circular labyrinth side weirs have higher values at higher ratios of r/b. In other words, higher Cd values are obtained at high r/b ratios due to an increase in the intensity of secondary flow created by lateral flow. El-Khashab and Smith (1976) also pointed out that the secondary flow condition due to lateral flow is dominant when a side weir is relatively long (i.e. L/b > 1). A secondary flow is a relatively minor flow superimposed on the main flow which can be explained by the existence of a discontinuity region. The intensity of this secondary motion next to the boundary of the weir side depends on the crest height of the side weir and decreases with the crest height increase of the side weir due to the friction of the weir surface (Kaya et al., 2011).

Empirical correlations to predict discharge coefficient Cd were developed for semi-circular labyrinth side weirs, according to the result of dimensionless analysis that contains linear and non-linear equations. The resulting correlations are given in Eqs. 10 and 11.

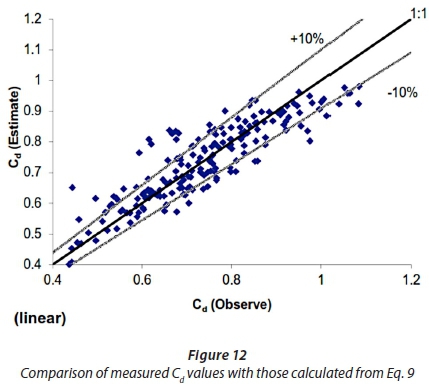
It should be noted that the discharge coefficient of the semi-circular labyrinth side weir is calculated for a single cycle. To compare the computed Cd values with the measured values, using Eqs 10, and 11, Figs 12 and 13 are presented, respectively. From Figs 12 and 13, it is evident that the majority of the data points fall in the error band of 10%. Therefore, very good agreements between the measured values and those computed from the predictive equations are obtained.

To evaluate the accuracy of the estimates produced using the obtained equations, the relative error (RE), root mean square error (RMSE) and index of agreement (d) criteria were used. These accuracy criteria are defined as:
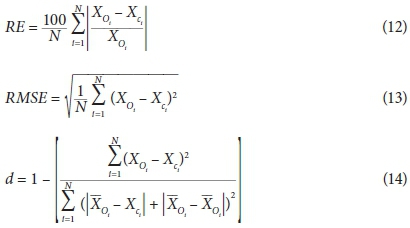
where: N is the number of data points and Xo and Xc are the observed and computed values of discharge coefficient, respectively. Also __ Xo is the mean of the observed values of the discharge coefficient. The computed values of RE, RMSE and d for the obtained Cd equations are presented in Table 3.

CONCLUSIONS
Laboratory experiments of the semi-circular labyrinth side weir located on a straight channel were carried out to investigate the effect of different dimensionless parameters on the discharge coefficient. Empirical equations predicting the discharge coefficient of the semi-circular labyrinth side weirs were developed. According to the suggested equation (non-linear equation), Cd depends on dimensionless parameters that are r/b, Fr1, r/w, (y1−w)/r and (y2−w)/r. The following conclusions can be drawn based on these findings:
•The longitudinal velocity of water moving in active overflow condition from the inner bank towards the outer bank increases due to lateral flow
•The discharge coefficient of the semi-circular labyrinth side weir is higher than that of the rectangular side weir
•The discharge coefficient increases with increasing r/b ratio
•The discharge coefficient increases with increasing w/b ratio
•The proposed equations for Cd, the De-Marchi Coefficient, were shown to be reliable for the subcritical flow condition in this study. Although a non-linear equation is suggested to predict the values of Cd, the linear equation generates similar predictions for Cd.
NOTATION
b width of channel
Cd side-weir discharge coefficient
Fr1 Froude number at upstream end of side weir
y main channel depth
y1 flow depth at upstream end of side weir at channel center
y2 flow depth at downstream end of side weir at channel center
L length (width) of side weir
l weir crest length
w height of weir crest
r radius of semi-circular labyrinth side weir
Q discharge in the main channel
Q1 discharge at the upstream end of the side weir in the main channel
Q2 discharge at the downstream end of the side weir in the main channel
Qw total discharge overflowed the side weir
ES specific energy
s distance alongside weir measured from upstream end of side weir (m)
V mean velocity in any section of channel
Vm maximum velocity of spiral flow along channel
V1 mean velocity of flow at upstream end of side weir
V/Vm dimensionless velocity at any point
z local vertical coordinate
z0 is equal to y
z/z0 dimensionless depth at any point
ψ deviation angle of flow
REFERENCES
ACKERS P (1957) A theoretical consideration of side-weirs as storm water overflows. Proc. Inst. Civ. Eng. 6 250-269. [ Links ]
AGACCIOGLU H and YÜKSEL Y (1998) Side-weir flow in curved channels. J. Irrig. Drain. Eng. 124(3) 163-175. https://doi.org/10.1061/(ASCE)0733-9437(1998)124:3(163) [ Links ]
AGHAYARI F, HONAR T and KESHAVARZI A (2009) A study of spatial variation of discharge efficient in broad-crested inclined side weirs. J. Irrig. Drain. Eng. 58 246-254. https://doi.org/10.1002/ird.416 [ Links ]
BORGHEI M, JALILI MR and GHODSIAN M (1999) Discharge coefficient for sharp-crested side weir in subcritical flow. J. Hydraul. Eng. 125 (10) 1051-1056. https://doi.org/10.1061/(ASCE)0733-9429(1999)125:10(1051) [ Links ]
CHEONG HF (1991) Discharge coefficient of lateral diversion from trapezoidal channel. J. Irrig. Drain. Eng. 117 (4) 321-333. https://doi.org/10.1061/(asce)0733-9437(1991)117:4(461) [ Links ]
COLEMAN GS and SMITH D (1923) The discharging capacity of side weirs. Proc. Inst. Civ. Eng. 6 288-304. [ Links ]
COLLINGS VK (1957) The discharge capacity of side weirs. Proc. Inst. Civ. Eng. 6 288-304. [ Links ]
COSAR A and AGACCIOGLU H (2004) Discharge coefficient of a triangular side weir located on a curved channel. J. Irrig. Drain. Eng. 130 (5) 321-333. https://doi.org/10.1061/(ASCE)0733-9437(2004)130:5(410) [ Links ]
DE MARCHI G, Saggio di teoria de funzionamente degli stramazzi letarali (1934) La Energ. Elet. 11 849-860. [ Links ]
EL-KHASHAB AMM (1975) Hydraulics of flow over side-weirs. PhD thesis, University of Southampton, England. [ Links ]
EL-KHASHAB AMM and SMITH KVH (1976) Experimental investigation of flow over side weirs. J. Hydraul. Eng. 102 (9) 1255-1268. [ Links ]
EMIROGLU ME, KAYA N and AGACCIOGLU H (2010a) Discharge capacity of labyrinth side weir located on a straight channel. J. Irrig. Drain. Eng. 136 (1) 37-46. https://doi.org/10.1061/(ASCE)IR.1943-4774.0000112 [ Links ]
EMIROGLU ME, KISI O and BILHAN O (2010b) Predicting discharge capacity of triangular labyrinth side weir located on a straight channel by using an adaptive neuro-fuzzy technique. Adv. Eng. Softw. 41 (2) 154-160. https://doi.org/10.1016/j.advengsoft.2009.09.006 [ Links ]
FRAZER W (1957) The behavior of side weirs in prismatic rectangular channels. Proc. Inst. Civ. Eng. 6 305-327. [ Links ]
GHODSIAN M (2003) Supercritical flow over rectangular side weir. Can. J. Civ. Eng. 30 (3) 596-600. https://doi.org/10.1139/l03-004 [ Links ]
HAGER WH (1987) Lateral outflow over side weirs. J. Irrig. Drain. Eng. 113 (4) 491-504. https://doi.org/10.1061/(asce)0733-9429(1987)113:4(491) [ Links ]
KAYA N, EMIROGLU ME and AGACCIOGLU H (2011) Discharge coefficient of a semi-elliptical side weir in subcritical flow. J. Flow Meas. Instrum. 22 25-32. https://doi.org/10.1016/j.flowmeasinst.2010.11.002 [ Links ]
KUMAR CP and PATHAK SK (1987) Triangular side weirs. J. Irrig. Drain. Eng. 113 (1) 98-105. https://doi.org/10.1061/(ASCE)0733-9437(1987)113:1(98) [ Links ]
NANDESOMOORTHY T and THOMSON A (1972) Discussion of spatially varied flow over side weir. J. Hydraul. Eng. 98 (12) 2234-2235. [ Links ]
RAMAMURTHY AS and CARBALLADA L (1980) Lateral weir flow model. J. Irrig. Drain. Eng. 106 (1) 9-25. [ Links ]
RANGA RKG, PRASAD B and GRUPTA SK (1979) Side weir in rectangular channels. J. Hydraul. Eng. 105 (5) 547-554. [ Links ]
SINGH R, MANIVANNAN D and SATYANARAYANA T (1994) Discharge coefficient of rectangular side weirs. J. Irrig. Drain. Eng. 120 (4) 814-819. https://doi.org/10.1061/(ASCE)0733-9437(1994)120:4(814) [ Links ]
SUBRAMANYA K and AWASTHY SC (1972) Spatially varied flow over side weirs. J. Hydraul. Eng. 98 (1) 1-10. [ Links ]
SWAMEE PK, SANTOSH KP and MASOUD SA (1994) Side weir analysis using elementary discharge coefficient. J. Irrig. Drain. Eng. 120 (4) 742-755. https://doi.org/10.1061/(ASCE)0733-9437(1994)120:4(742) [ Links ]
UYUMAZ A and MUSLU Y (1985) Flow over side weir in circular channels. J. Hydraul. Eng. 111 (1) 144-160. https://doi.org/10.1061/(ASCE)0733-9429(1985)111:1(144) [ Links ]
YU-TECH L (1972) Discussion of spatially varied flow over side weir. J. Hydraul. Eng. 98 (11) 2046-2048. [ Links ]
Received 26 July 2016
Accepted in revised form 20 June 2017
* To whom all correspondence should be addressed. e -mail: Khalili10@yahoo.com














