Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
Water SA
versión On-line ISSN 1816-7950
versión impresa ISSN 0378-4738
Water SA vol.43 no.2 Pretoria abr. 2017
http://dx.doi.org/10.4314/wsa.v43i2.05
Calibration and testing of AquaCrop for selected sorghum genotypes
Sandile T Hadebe*; Albert T Modi; Tafadzwanashe Mabhaudhi
Crop Science, School of Agricultural, Earth and Environmental Sciences, University of KwaZulu-Natal, Private Bag X01, Scottsville 3209, Pietermaritzburg, South Africa
ABSTRACT
Predicting yield response to water is important in rainfed agriculture. The objective of this study was to calibrate and test AquaCrop for simulating yield of 3 sorghum genotypes (PAN8816, a hybrid; Macia, an open-pollinated variety; and Ujiba, a landrace) grown during the 2013/14 and 2014/15 planting seasons (early, optimal and late planting dates). Variables considered during model evaluation included canopy cover (CC), biomass (B) and yield (Y). The model was able to simulate CC (R2 ≥ 0.710; root mean square error (RMSE) ≤ 22.73%; Willmott's d-index (d) ≥ 0.998), biomass accumulation (R2 ≥ 0.900; RMSE ≤ 10.45%; d ≥ 0.850), harvest index (R2 ≥ 0.902; RMSE ≤ 7.17%; d ≥ 0.987) and yield (R2 ≥ 0.945; RMSE ≤ 3.53%; d ≥ 0.783) well for all genotypes and planting dates after calibration. AquaCrop over-estimated biomass and crop yield. The relatively good simulations produced by the minimum data input calibration confirm AquaCrop's simplicity and suitability for use in places where extensive datasets may be unavailable. Biomass and yield overestimation resulting from the use of the minimum data input calibration suggests that other parameters (water productivity, canopy sensitivity to water stress and water stress coefficient) are required to improve canopy and yield predictions for sorghum genotypes.
Keywords: modelling, parameterization, minimum data input calibration, sorghum, water availability.
INTRODUCTION
High seasonal rainfall variability, delays in onset and irregular distribution of rainfall, and occasional dry spells within seasons negatively impact cereal yields and household livelihoods in sub-Saharan Africa (SSA) (Fjelde and Von Uexkull, 2012). The impact is exacerbated under rainfed agriculture, where rainfall is the sole water input into the agriculture system. Variability in rainfall affects timing and location of planting, as onset, cessation and amount of rainfall affect farmers' planting decisions. Cereal crops are a major contributor to food security and economy in arid and semi-arid regions. In SSA, a region where 95% of agriculture is rainfed (Singh et al., 2011), and arid and semi-arid areas account for 43% of total area (FAO, 2008), rainfall is a major limitation to cereal yields. Sorghum is predominantly grown in semi-arid and arid agro-ecologies of SSA, under rainfed conditions. This makes sorghum production highly susceptible to rainfall amount and distribution.
Examining yield response to rainfall amount and distribution under rainfed environments is both laborious and expensive. In consideration of such limitations, the use of crop models is useful. Crop models are valuable prediction tools where environments, soils, genotypes and climatic conditions vary. For increased accuracy of model predictions, models have to be parameterized, calibrated and tested before use. For model calibration, one changes model parameters and even coding in order to obtain accurate prediction versus observed data. On the other hand, testing is the process whereby the model is run against independent data, without any modification of model parameters or code. AquaCrop is a crop water productivity model developed by the Land and Water Division of FAO that simulates crop yield response to water (Raes et al., 2009b; Steduto et al., 2009). AquaCrop predicts crop productivity, water requirement, and water use efficiency and is particularly suited to address conditions where water is a key limiting factor in crop production.
Application of models by non-research end users (farmers, policy makers and extension services) remains a key challenge as models usually require extensive and difficult to obtain datasets for calibration (Hoogenboom et al., 2012). A major distinguishing feature of AquaCrop is its simplicity, the ability to use minimum data inputs during calibration to produce reliable estimates of crop growth and yield response to water availability (Raes et al., 2009b; Steduto et al., 2009). This procedure is termed 'minimum data input calibration'. It requires a relatively low number of intuitive, easy-to-obtain parameters and can be used when a crop has previously been calibrated for AquaCrop (Hsiao et al., 2012). The use of the minimum data input for calibration was an attempt to improve uptake and use of crop models, particularly in developing countries where access to extensive datasets is limited.
AquaCrop has been parameterized and tested for a wide range of crops (Farahani et al., 2009; Geerts et al., 2009; Hsiao et al 2009; Karunaratne et al., 2011; Steduto et al., 2009) under different environmental conditions, illustrating that the model could accurately simulate yield response to water. AquaCrop has already been parameterized for sorghum using data from Bushland, Texas, field trials in 1993 (FAO, 2012). However, there is a need to perform a local calibration for sorghum genotypes under production in SSA. This study aimed to calibrate and test AquaCrop for hybrid, open-pollinated and landrace sorghum genotypes. In this study, the minimum data input calibration procedure was used to calibrate sorghum genotypes, and subsequently test model performance under variable climatic conditions. In part, this study aimed to investigate whether minimum data input calibration (Hsiao et al., 2012) proposed for non-research AquaCrop users was sufficient in predictions of sorghum yield response to water. To our knowledge, no published materials exist on the effectiveness of minimum data input calibration, making this the first study to do so. The choice of genotypes used is explained in the materials and methods section.
MATERIALS AND METHODS
Model description
The FAO AquaCrop crop model is a water-driven simulation model (generic crop water productivity model) (Raes et al., 2009a; Steduto et al., 2009). It requires relatively few input parameters to simulate yield response to water of most major field and vegetable crops. Its parameters are explicit and mostly intuitive and the model maintains a sufficient balance between accuracy, simplicity and robustness (Raes et al., 2009a; Steduto et al., 2009).
The features that distinguish AquaCrop from other crop models are its focus on water, the use of canopy ground cover instead of leaf area index, and the use of water productivity values normalized for climate (atmospheric evaporative demand and carbon dioxide concentration). This confers the model an extended extrapolation capacity to diverse locations and seasons (Steduto et al., 2007), including future climate scenarios. The model uses canopy ground cover (CC) instead of leaf area index (LAI) as the basis to calculate transpiration and to separate soil evaporation from transpiration. Biomass is then calculated as the product of transpiration and a water productivity parameter (Eq. 1).

where: B = aboveground biomass (t·ha-1), WP = water productivity (biomass per unit of cumulative transpiration), and Tr = crop transpiration.
Crop yield is then calculated as the product of above-ground dry biomass and harvest index (HI):

where: Y = crop yield, HI = harvest index.
Although the model is simple, it gives particular attention to the fundamental processes involved in crop productivity and in the responses to water, from a physiological and agronomic perspective (Raes et al., 2009a). The FAO AquaCrop model predicts crop productivity, water requirement, and water use efficiency under water-limiting conditions (Raes et al., 2009a). AquaCrop considers the soil, with its water balance; the plant, with its development, growth and yield processes; and the atmosphere, with its thermal regime, rainfall, evaporative demand and carbon dioxide concentration.
Minimum data input calibration requires a relatively low number of parameters compared to full calibration, and is used when a particular crop has previously been calibrated for AquaCrop. These are fairly intuitive input variables, either widely used or largely requiring simple methods for their determination. Minimum input data consist of weather data, crop and soil characteristics, and management practices that define the environment in which the crop was cultivated, and are described in Hsiao et al. (2012). In this study, user-defined model inputs were used to describe soil physical and hydraulic properties, and daily weather, and user-specific crop parameters for each sorghum genotype obtained from field trials were used to describe crop growth and development. The crop description parameters (Table 2) were taken from Hsiao et al. (2012), in which minimum datasets required for calibration were described. Additionally, the model also considers some management aspects such as irrigation and fertility, as they affect the soil water balance, crop development and therefore final yield. Pests, diseases, and weeds are not considered (Raes et al., 2009b).
Plant material
Three sorghum genotypes, a hybrid (PAN8816), an open-pollinated variety (Macia) and a landrace (Ujiba), were selected for this study. This reflected the range of germplasm typically used by farmers for sorghum production in southern Africa. PAN8816 and Ujiba are grown in South Africa in sorghum-growing regions. Macia, was developed by the International Crop Research Institute for the Semi-Arid Tropics (ICRISAT), and is produced in most sorghum-growing regions across SSA (Charyulu et al., 2014; Takele and Farrant, 2013). Additional information on genotype characterisation is as defined in Table 1.
Site description
Field trials were planted at Ukulinga Research Farm (30°24'S, 29°24'E, 805 m amsl) over 2 planting seasons (2013/14 and 2014/15). The farm is situated in Pietermaritzburg in the subtropical hinterland of KwaZulu-Natal Province and represents a semi-arid environment characterized by clay-loam soils (USDA taxonomic system). Rain falls mostly in summer, between September and April. Rainfall distribution varies during the growing season (Swemmer et al., 2007) with the bulk of rain falling in November, December and early January. Occasionally light to moderate frost occurs in winter (May - July).
Trial layout and design
Field trials planted at Ukulinga on 17 January during the 2013/14 planting season were used for model calibration. The experimental design used was a randomized complete block design with 3 replications. Independent field trials planted during the 2014/15 planting season were used to test model performance. The experimental design was a split-plot design with planting date as the main factor and genotype as the sub-factor laid out in randomised complete blocks with 3 replications. The planting dates (3 November 2014, 17 November 2014, and 26 January 2015) represented early, optimal and late planting dates for sorghum. Early planting reflected onset of rainfall at Ukulinga in the 2014/15 season. The early planting date can be defined as the first rainfall event capable of supporting germination. In this study the early planting date was defined according to the Agricultural Research and Extension (AREX) criterion (Raes et al., 2004) which defines a planting date as the occurrence of 25 mm rainfall in 7 days before planting. This ensures there is enough soil water, not only for germination but also to sustain the crop through the early development stage (Moeletsi and Walker, 2012). Optimal planting date was based on Department of Agriculture, Forestry and Fisheries (DAFF) (2010) recommendations and historical weather data at Ukulinga. Late planting date represented latest planting from which seasonal rainfall can sustain 120-140 day growing season (Table 3). This was determined from historical weather data, where onset of winter season and cessation of rainfall usually occurs in May at Ukulinga.
All trials comprised of 3 sorghum cultivars, namely: PAN8816, Macia and Ujiba. The trials measured 310 m2, with individual plot size of 6 m x 4.5 m (18 m2), with 1 m interplot spacing between the plots. Final inter-row spacing was 0.75 m with 0.30 m intra-row spacing, amounting to 21 plants per row and 63 experimental plants per plot. Each individual plot had 7 rows with the 3 innermost rows as the experimental plants, and the remaining rows reserved for destructive sampling.
Agronomic practices
Soil samples were collected and analysed for fertility before land preparation. Before planting, fallow land was mechanically ploughed, disked and rotovated. A pre-emergence herbicide, Round-up (glyphosate at 10 mL·L-1 water) was applied to control weeds 2 weeks before planting. A deficit of fertilizer requirements (Smith, 2006) was applied using Gromor Accelerator (30 g·kg-1 N, 15 g·kg-1 P and 15 g·kg-1 K), a slow release organic fertilizer, at 14 days after sowing (DAS). Planting rows were opened by hand 25 mm deep and seeds were hand-sown in the ground. Planting was conducted by drilling sorghum seeds. Thereafter, at crop establishment (14 DAS), seedlings were thinned to the required spacing. Scouting for pests and diseases was done weekly. Cypermethrin (15 mL per 10 L knapsack) was applied to control insect pests 1 month after planting. Weeding was done using hand-hoes at frequent intervals.
Input data
Soil
Important soil input parameters required by AquaCrop model are: soil texture, volumetric water content at field capacity (FC), at permanent wilting point (PWP), and at saturation (SAT), saturated hydraulic conductivity (Ksat), and soil thickness (depth of soil profile). The soil textural class was described as clay (USDA Taxonomic System). Soil physical and hydraulic properties were obtained from classification and characterisation of experimental site soils by Mabhaudhi (2012). Soil hydraulic and physical properties were used to develop a soil (.SOL) file in the model. The soil was classified as clay, with 0.6 m soil depth. Other values used to describe the soil file were: PWP = 28.3%, FC = 40.6%, SAT = 48.1%, TAW = 123.0 mm·m-1, and Ksat = 25.0 mm·d-1.
Meteorological data
The climate file in AquaCrop is defined using maximum temperature (°C), minimum temperature (°C), rainfall (mm) and reference evapotranspiration (mm). Meteorological data for Ukulinga were obtained from an automatic weather station (within 100 m radius), courtesy of the Agricultural Research Council - Institute for Soil, Climate and Water (ARC-ISCW). Reference evapotranspiration was obtained from the weather station and was based on the FAO Penman-Monteith equation from full daily weather datasets, as described by Allen et al. (1998). Carbon dioxide concentration was obtained from AquaCrop's default Maunalua file. Daily meteorological data from 1 January 2014 until 31 August 2015 were used to develop the climate (.CLI) file in the model.
Crop growth and development parameters
Crop parameters were used to calibrate AquaCrop's default sorghum file (Raes et al, , 2012) for the three sorghum genotypes as part of the minimum data input calibration procedure. The minimum data input procedure includes providing input data for the following: planting date, planting density, time to crop establishment, time to flowering, flowering duration, maximum canopy cover, time to maximum canopy cover, time to senescence, time to physiological maturity, and harvest index (Table 2). The minimum data input calibration procedure includes rooting depth; however, in this study, we used the default depth in the default sorghum file.
Date of planting was recorded as the actual day when seeds were sown in the soil. Planting density was calculated as number of plants per given area based on row spacing and plant spacing. Area measurements were converted from m2 to hectares and planting density was reported in plants·ha-1. Time taken to reach phenological stages was recorded in days until ≥ 50% of planting population exhibited diagnostic signs of that particular stage. Canopy cover was measured using the LAI2200 canopy analyser (Li-Cor, USA) at midday (12:00 - 14:00), and calculated as described by Mabhaudhi et al. (2014). Maximum canopy cover was recorded as the highest recorded canopy cover measurement over the growing season. Time to maximum canopy cover was taken as time from sowing until maximum canopy cover was observed for each genotype. Flowering duration described time from when at least half the experimental population exhibited flower inflorescence to the time when at least half the experimental population exhibited anthesis.
To quantify effective rooting depth, an area around a plant root zone was dug out 1 m deep and 0.5 m from the main stem at physiological maturity, after which the soil around the roots was brushed off, and root length was measured from exposed roots. The model is capable of simulating the presence of an impeding layer. Soil profiling at the experimental site revealed that the effective rooting depth of the soil was 0.6 m which was then inputted to the soil file, while for the crop it was maintained as the default 2 m. During model runs, root growth will be limited by the depth of the soil profile, while the value of 2 m represents the crop's potential in the absence of an impeding layer or a shallow soil. This feature then allows for the same crop file to be used for different soils without the need to change the crops' effective rooting depth whenever the soil file is changed. Soil water content was measured weekly using a PR2/6 profile probe (Delta-T, UK), and used test model estimation of soil moisture.
Flowering was observed as time taken for 50% of experimental plant population to panicle bloom. Duration of flowering was recorded as time taken from flowering until 50% of experimental population exhibited anthesis. Physiological maturity was observed when a dark spot appeared on the opposite side of the kernel from the embryo, signalling completion of dry matter accumulation. However, physiological maturity in model simulations was observed when dry matter accumulation (biomass and yield) ceased. Since all trials were under sub-optimal rainfall, reference harvest index could not be calculated for sorghum genotypes. Therefore, the default harvest index was used for all genotypes. Crop growth and development parameters were specified as inputs in genotype crop (.CRO) in the model.
Model calibration
Observations from field trials planted at Ukulinga on 17 January during 2013/14 were used to calibrate each of the three sorghum genotypes. Minimum data input calibration was used, using parameters outlined in Table 2. Simulations were performed with the AquaCrop model (Version 4.0) as described by Raes et al. (2009a) and Steduto et al. (2009). Key inputs in the model included: climate file, soil file, and crop files (2 crop files, 1 file per genotype, which were calibrated using minimum data input calibration). Calibration of the model was conducted using 2013/14 data from rainfed trials conducted at Ukulinga. Since AquaCrop is a canopy-level model where biomass and yield are calculated based on transpired water from the canopy, simulated canopy cover values first needed to be matched to observed values. Upon good agreement between simulated and observed canopy cover, agreement in soil water content, biomass, yield and harvest index were then compared. Data used for calibration were not used for testing.
Model testing
Testing is an important step of model verification. It involves a comparison between independent field measurements (data) and simulated output created by the model. Testing confirms whether or not results obtained from the model can be relied on and if they compare well with experimental results. Model testing in this study was done by comparing canopy cover, biomass, yield and harvest index simulated by the model with that from the observed field experiments planted at different planting dates during the 2014/15 season.
Statistical analysis
Different statistical indices, including coefficient of determination (R2), root mean square error (RMSE) and its systematic (RMSES) and unsystematic components (RMSEU), as well as the index of agreement (d-index), were used for comparison of simulated against observed data. Systematic RMSE was calculated (Loague and Green, 1991) as follows:
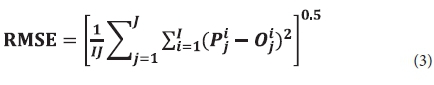
where: n is the number of observations, Pi and Oi refer to simulated and observed values of the study variables, respectively.
The RMSE is a good overall measure of model performance. It indicates the absolute fit of a model to observed field data, and evaluates the closeness between the two values. The RMSE was normalized by expressing it as a percentage of data range to remove scale dependency. The simulation is considered excellent with a normalized RMSE less than 10%, good if the normalized RMSE is greater than 10% and less than 20%, fair if normalized RMSE is greater than 20% and less than 30%, and poor if the normalized RMSE is greater than 30% (Jamieson et al., 1991).
Systematic root mean square error (RMSES) was calculated as the square root of the mean squared difference in regressed prediction-observation pairings within a given analysis region and for a given period (Loague and Green, 1991).
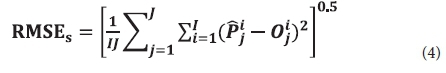
where: Pij is the individual predicted quantity at site i and time j, is the least square aggression, Oij is the individual quantity at site i and time j, and the summations are over all sites (I) and over time periods (J). And the least square aggression () is:

where: a is the y-intercept, and b is the slope of the resulting straight-line fit.
The RMSES estimates the model's linear (or systematic) error; hence, the better the regression between predictions and observations, the smaller the systematic error.
Unsystematic root mean square error (RMSEU) was calculated as the square root of the mean squared difference in prediction-regressed prediction pairings within a given analysis region and for a given time period.
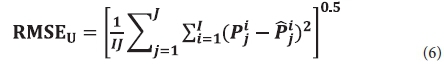
The unsystematic difference is a measure of how much of the discrepancy between estimates and observations is due to random processes or influences outside the legitimate range of the model.
The index of agreement (d-index) proposed by Willmott et al. (1985) was estimated using Eq. 7. The d-index condenses all of the differences between model estimates and observations within a given analysis region and for a given time period (hourly and daily) into one statistical quantity. It is the ratio of the total RMSE to the sum of 2 differences - between each prediction and the observed mean, and each observation and the observed mean. Viewed from another perspective, the index of agreement is a measure of the match between the departure of each prediction from the observed mean and the departure of each observation from the observed mean. Thus, the correspondence between predicted and observed values across the domain at a given time may be quantified in a single metric and displayed as a time series. The index of agreement has a theoretical range of 0 to 1. According to the d-index, the closer the index value is to 1, the better the agreement between the two variables that are being compared and vice versa.
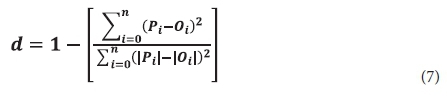
where: n is the number of observations, Pi the predicted observation, Oi is a measured observation, ΙPiΙ = Pi − M and ΙOiΙ = Oi− M (M is the mean of the observed variable). The simulated model results were compared statistically to observe experimental measurements using Microsoft Excel.
RESULTS AND DISCUSSION
Calibration
Since AquaCrop simulates crop growth and yield response to water availability, it is important to establish a good goodness of fit between model simulated and field observed soil water content. AquaCrop simulated soil water content (R2 ≥ 0.901; RMSE ≤ 13.32%; d ≥ 1.000) very well (Fig. 1), which gave confidence that other water-based crop processes were simulated based on good water availability prediction.
AquaCrop is a canopy level model (Mabhaudhi et al. (2014). As such, the canopy, through its expansion, ageing, conductance and senescence, is central to the model as it determines the amount of water transpired, which in turn determines the amount of biomass produced (Raes et al., 2009b). AquaCrop simulated canopy cover (R2 ≥ 0.659; RMSE ≤ 14.35%; d ≥ 0.999), biomass (R2 ≥ 0.79; RMSE ≤ 10.14%; d ≥ 0.908), harvest index (R2 ≥ 0.967; RMSE ≤ 3.55%; d ≥ 0.998) and yield (R2 ≥ 0.923; RMSE ≤ 3.82%; d ≥ 0.770) satisfactorily for all three genotypes during calibration (Fig. 2). Root mean-square error was low, with high goodness of fit (n = 16), and Willmot's d-index values were close to 1 implying that model-predicted values were close to observed values. This gave confidence in calibration of the model and allowed model testing using independent data.
Testing
There was good agreement between observed and simulated soil water content (R2 ≥ 0.710; RMSE ≤ 22.73%; d ≥ 0.998) and crop canopy cover (R2 ≥ 0.710; RMSE ≤ 22.73%; d ≥ 0.998) for all genotypes and planting dates. This showed that the model was capable of simulating water availability and canopy development under different environments (Fig. 3). This implies that the separation of soil evaporation from crop transpiration was captured well by the model. The result confirmed model robustness and consistency across environments. Once canopy senescence was triggered, the model simulated rapid canopy decline whereas in reality sorghum's canopy decline was moderate. This is because sorghum genotypes evaluated in the study employed osmotic adjustment and quiescence strategies which allowed for moderate canopy decline. The limitations of the model in capturing this aspect of sorghum resulted in a low goodness of fit between model simulated and observed values, especially under water stress.
With respect to the planting dates, the model simulated canopy cover well for early planting (R2 ≥ 0.843; RMSE ≤ 13.91%; d ≥ 0.999) and late planting (R2 ≥ 0.873; RMSE ≤ 12.07%; d ≥ 0.999) (Fig. 3). Model performance was satisfactory (R2 ≥ 0.710; RMSE ≤ 22.73%; d ≥ 0.998) for the optimal planting. Model performance for the optimal planting date was affected by observed low emergence at optimal planting due to low soil water availability during and shortly after sowing. This resulted in observed low canopy cover compared to model-simulated canopy cover (Fig. 3). In this instance, the model could be used to assess gaps between actual and potential canopy cover under field conditions.
In field trials, time to physiological maturity was observed when a dark spot appeared on the opposite side of the kernel from the embryo, signalling completion of dry matter accumulation (Eastin et al., 1973). However, physiological maturity in model simulations was observed when dry matter accumulation ceased. Under field conditions, physiological maturity occurred when canopy cover was relatively high, while for model simulations it coincided with relatively low or zero canopy cover. This resulted in a slight overestimation (≤ 7.8%) of time to physiological maturity in the model (Table 3). Since AquaCrop uses canopy cover to estimate transpiration and calculate biomass accumulation, this potentially led to a carry-over error in simulated biomass and yield. This would account for the overestimation of the two parameters. Adjusting canopy sensitivity to water stress (canopy expansion, stomatal closure, early senescence and harvest index) could potentially improve model simulation, especially during canopy senescence where model simulations were less than satisfactory. However, the relatively satisfactory performance of the model with minimum data input calibration confirms model simplicity and robustness and its suitability for use in areas with limited datasets.
AquaCrop separates the yield into biomass and harvest index (Raes et al., 2009b), where harvest index is the ratio of economic yield over total aboveground biomass. Biomass accumulation is calculated as a product of WP and transpiration. Thereafter, biomass partitioning into yield is a function of harvest index. Prediction of biomass (R2 ≥ 0.900; RMSE ≤ 10.45%; d ≥ 0.850) and yield (R2 ≥ 0.945; RMSE ≤ 3.53%; d ≥ 0.783) was very good (Figs 4 and 5). However, the model significantly over-estimated both biomass and yield, to generally be twice the observed values. On average, total biomass simulated by the model was 24.04, 20.68 and 20.70 t·ha-1, whereas observed biomass was 10.82, 10.36 and 6.09 t·ha-1, for early, optimal and late planting dates, respectively. Total yield simulated by AquaCrop was 12.24, 9.8 and 10.79 t·ha-1, whereas observed yield was 5.25, 5.31 and 3.16 t·ha-1, for early, optimal and late planting dates, respectively (Table 3). Expected sorghum yields are 3-8 t·ha-1 for genotypes used in the study. This implies that observed biomass and yield were within expected yields, whilst confirming that the model simulations over-estimated these variables. Good canopy simulation by the model resulted in confidence in transpiration predictions used in biomass calculation. Model simulations exhibited differential water stress levels across planting dates, with highest water stress levels during the late planting date for all genotypes. This implies that water stress played a major role in biomass and yield determination. Determining the genotype-specific water stress coefficients (Ks) could potentially improve model yield simulations. A default sorghum WP parameter (33.3 g·m-2) was used in simulations. Water productivity for C4 cereal crops is generally accepted to be 30-35 g·m-2 (Raes et al., 2010). However, this conservative parameter may need to be determined for local genotypes, as it is a potential source of error in model overestimation of yield.
In the interest of comparison with previous work, simulations obtained from experimental sorghum genotypes were compared to those obtained from simulations using the AquaCrop default sorghum file. In comparison, simulations using the default file instead of three study genotypes exhibited excellent predictions of yield (R2 ≥ 0.816; RMSE ≤ 1.90%; d ≥ 0.900) with relatively high overestimation error (23.0-109.2%). Yield overestimation error was low (23.0% and 27.2%) for early and optimal planting dates, respectively, where rainfall was relatively high and well distributed across planting season. For the late planting date, when relatively low, highly irregularly distributed rainfall was observed, yield overestimation was high (109.2%). Canopy cover was poorly simulated (R2 ≥ 0.11; RMSE ≤ 41.03%; d ≥ 0.995) suggesting that canopy characteristics of local genotypes differ significantly from those of the AquaCrop default crop file. This highlights the need to perform additional experiments to determine canopy sensitivity to water stress for calibration of the three genotypes used. Since AquaCrop is a canopy-level, yield response to water model, it is of primary importance to accurately predict canopy cover in order to predict biomass and yield. Therefore, improved yield and biomass estimations by the default file are pointless without a corresponding improvement in canopy cover predictions.
Despite the limitations in calculating biomass, the model was able to capture the build-up of harvest index (Fig. 6) very well (R2 ≥ 0.902; RMSE ≤ 7.17%; d ≥ 0.987). This implies that the contribution of harvest index as a source of error in over-estimation of yield was minimal. Model over-estimation of biomass and yield increased for late-planted sorghum genotypes, where water stress was observed to be relatively high in comparison to other planting dates under experimental field trials and simulations. This suggests that canopy sensitivity to water stress should also be accurately described when calibrating the model for local sorghum genotypes. Developing genotype specific Ks values for the sorghum genotypes used in this study could improve model simulations of biomass and yield. Overall, canopy cover, biomass, harvest index and yield model simulations were very good for all genotypes and planting date environments.
CONCLUSION
The model was able to simulate canopy cover, biomass accumulation, harvest index and yield relatively well for all sorghum genotypes and planting dates. The model did not accurately capture sorghum canopy decline as it did not consider sorghum's quiescence growth habit which allows for delayed canopy senescence under water-limited conditions. Conservative parameters in the default sorghum crop may not necessarily represent those of local genotypes, and this potentially contributes to overestimation of biomass and yield in the model. Despite model calibration simulating canopy cover relatively well, overestimation of biomass and yield suggests that conservative parameters, such as water productivity (WP), canopy sensitivity to water stress and water stress coefficient, additionally require calibration for local genotypes in order to improve calibration. Where water conservation and crop growth characteristics are of primary importance, the use of minimum data input calibrated files is recommended due to very good simulations of crop canopy and phenological development. In cases where biomass and yield simulation is important, the use of the default file is recommended to reduce overestimation error. The results of this study suggest that where local sorghum genotypes differ significantly in growth and development characteristics from the default file, the use of minimal data input calibration potentially compromises prediction of crop yield. In terms of model application where extensive data is absent, it is recommended that users add the parameters (WP, canopy sensitivity to water stress, and water stress coefficient) that are suggested in this study to improve calibration. For new sorghum cultivars that differ significantly in growth and development characteristics from the default crop file, it may be necessary to do a full calibration where possible to achieve good overall predictions of crop response to water availability.
ACKNOWLEDGEMENTS
The Water Research Commission (WRC) of South Africa is acknowledged for initiating, funding and directing the study through WRC Project No. K5/2274//4 'Determining water use of indigenous grain and legume food crops' (WRC, 2014).
REFERENCES
ALLEN R, PEREIRA L, RAES D and SMITH M (1998) Crop evapotranspiration (Guidelines for computing crop water requirements). FAO Irrigation and Drainage Paper, No. 56. FAO, Rome. 297 pp. [ Links ]
CHARYULU CD, BANTILAN MCS, REDDY BV, KUMAR AA, AHMED I and DAVIS J (2014) Estimation of ICRISAT sorghum research spillover benefits - strategies for research prioritization and resource allocation. ICRISAT, Patancheru. [ Links ]
DAFF (Department of Agriculture, Forestry and Fisheries, South Africa) (2010) Sorghum production guidelines. DAFF, Pretoria. [ Links ]
EASTIN JD, HULTQUIST JH and SULLIVAN CY (1973) Physiological maturity in grain sorghum. Crop Sci. 13 175-178. https://doi.org/10.2135/cropsci1973.0011183X001300020008x [ Links ]
FARAHANI HJ, IZZI G and OWEIS TY (2009) Parameterization and evaluation of the AquaCrop model for full and deficit irrigated cotton. Agron. J. 101 469-476. https://doi.org/10.2134/agronj2008.0182s [ Links ]
FAO (Food and Agriculture Organization of the United Nations) (2008) The state of food and agriculture. Biofuels: prospects, risks and opportunities. FAO, Rome. [ Links ]
FAO (Food and Agriculture Organization of the United Nations) (2012) Reference Manual, Annex I - AquaCrop, Version 4.0. FAO, Rome. [ Links ]
FJELDE H and VON UEXKULL N (2012) Climate triggers: Rainfall anomalies, vulnerability, and communal conflict in Sub-Saharan Africa. Polit. Geogr. 31 444-453. https://doi.org/10.1016/j.polgeo.2012.08.004 [ Links ]
GEERTS S, RAES D, GRACIA M, MIRANDA R, CUSICANQUI JA, TABOADA C, MENDOZA J, HUANCA R, MAMANI A, CONDORI O, MAMANI J, MORALES B, OSCO V and STEDUTO P (2009) Simulating yield response of Quinoa to water availability with AquaCrop. Agron. J. 101 499-508. https://doi.org/10.2134/agronj2008.0137s [ Links ]
HOOGENBOOM G, JONES JW, TRAORE PCS and BOOTE KJ (2012) Experiments and data for model evaluation and application. In: Kihara J, Fatondji D, Jones JW, Hoogenboom G, Tabo R and Bationo A (eds). Improving Soil Fertility Recommendations in Africa using the Decision Support System for Agrotechnology Transfer (DSSAT). Springer, Dordrecht. 9-18. https://doi.org/10.1007/978-94-007-2960-5_2 [ Links ]
HSIAO TC, HENG LK, STEDUTO P, ROJAS-LARA B, RAES D and FERERES E (2009) AquaCrop - the FAO crop model to simulate yield response to water III parameterization and testing for maize. Agron. J. 101 448-459. https://doi.org/10.2134/agronj2008.0218s [ Links ]
HSIAO TC, FERERES E, STEDUTO P and RAES D (2012) AquaCrop parameterization, calibration, and validation guide. In: Steduto P, Hsiao TC, Fereres E and Raes D (eds) Crop Yield Response to Water. FAO Irrigation and Drainage Paper 66. FAO, Rome. 70-87. [ Links ]
JAMIESON PD, PORTER JR and WILSON DR (1991) A test of computer simulation model ARC-WHEAT1 on wheat crops grown in New Zealand. Field Crops Res. 27 337-350. https://doi.org/10.1016/0378-4290(91)90040-3 [ Links ]
LOAGUE K and GREEN RE (1991) Statistical and graphical methods for evaluating solute transport models; overview and application. J. Contam. Hydrol. 7 51-73. https://doi.org/10.1016/0169-7722(91)90038-3 [ Links ]
KARUNARATNE AS, AZAM-ALI SN, AL-SHARREF I, SESAY A, JORGENSEN ST, and CROUT NM (2011) Modeling canopy development of bambara groundnut. Agric. For. Meteorol. 150 1007-1015. https://doi.org/10.1016/j.agrformet.2010.03.006 [ Links ]
MABHAUDHI T (2012) Drought tolerance and water-use of selected South African landraces of taro (Colocasia esculenta L. Schott) and bambara groundnut (Vigna subterranea L. Verdc). PhD thesis, University of KwaZulu-Natal, Pietermaritzburg, South Africa. [ Links ]
MABHAUDHI T, MODI AT and BELETSE YG (2014) Parameterisation and testing of AquaCrop for a South African bambara groundnut landrace. Agron. J. 106 243-251. https://doi.org/10.2134/agronj2013.0355 [ Links ]
MOELETSI ME and WALKER S (2012) Rainy season characteristics of the Free State Province of South Africa with reference to rain-fed maize production. Water SA 38 (5) 775-782. https://doi.org/10.4314/wsa.v38i5.17 [ Links ]
RAES D, SITHOLE A, MAKARU A and MILLFORD J (2004) Evaluation of first planting dates recommended by criteria currently used in Zimbabwe. Agric. For. Meteorol. 125 177-185. https://doi.org/10.1016/j.agrformet.2004.05.001 [ Links ]
RAES D, STEDUTO P, HSIAO TC and FERERES E (2009a) AquaCrop-The FAO crop model to simulate yield response to water: II. Main algorithms and soft ware description. Agron. J. 101 438-447. https://doi.org/10.2134/agronj2008.0140s [ Links ]
RAES D, STEDUTO P, HSIAO TC and FERERES E (2009b) AquaCrop-The FAO crop model to simulate yield response to water: Reference Manual Annexes. URL: www.fao.org/nr/water/aquacrop.html (Accessed 18 October 2016). [ Links ]
RAES D, STEDUTO P, HSIAO TC and FERERES E (2010) Reference manual, Chapter 3 - Calculation procedures. AquaCrop version 3.1. FAO, Land and Water Division. Rome, Italy. [ Links ]
RAES D, STEDUTO P, HSIAO TC and FERERES E (2012) Reference manual, Chapter 2 - AquaCrop version 4.0. FAO Land and Water Division, Rome. [ Links ]
STEDUTO P, HSIAO TC and FERERES E (2007) On the conservative behaviour of biomass water productivity. Irrig. Sci. 25 189-207. https://doi.org/10.1007/s00271-007-0064-1 [ Links ]
STEDUTO P, HSIAO TC, RAES D and FERERES E (2009) AquaCrop-The FAO crop model to simulate yield response to water: I. Concepts and underlying principles. Agron. J. 101 426 -437. https://doi.org/10.2134/agronj2008.0139s [ Links ]
SINGH P, WANI SP, PATHAK P, SAHRAWAT KL and SINGH AK (2011) Increasing crop productivity and effective use of water in rainfed agriculture. In: Integrated Watershed Management in Rainfed Agriculture. CRC Press, London. 315-347. https://doi.org/10.1201/b11424-11 [ Links ]
SMITH B (2006) The Farming Handbook. University of KwaZulu-Natal Press, Durban. 220-226. [ Links ]
SWEMMER AM, KNAPP AK and SNYMAN HA (2007) Intra-seasonal precipitation patterns and above-ground productivity in three perennial grasslands. J. Ecol. 95 780-788. https://doi.org/10.1111/j.1365-2745.2007.01237.x [ Links ]
TAKELE A and FARRANT J (2013) Water relations, gas exchange characteristics and water use efficiency in maize and sorghum after exposure to and recovery from pre and post-flowering dehydration. Afr. J. Agric. Res. 8 6468-6478. [ Links ]
WRC (Water Research Commission) (2014) WRC Knowledge Review 2013/14. Water Research Commission, Pretoria. [ Links ]
WILLMOTT CJ, AKLESON GS, DAVIS RE, FEDDEMA JJ, KLINK KM, LEGATES DR, ODONNELL J and ROWE CM (1985) Statistic for the evaluation and comparison of models. J. Geophys. Res. 90 8995-9005. https://doi.org/10.1029/JC090iC05p08995 [ Links ]
Received 8 July 2016
Accepted in revised form 3 March 2017
* To whom all correspondence should be addressed. Tel: +27 (33) 260-5447; Fax: +27 (33) 260-6094; e-mail: hadebesta@gmail.com.














