Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
Water SA
versión On-line ISSN 1816-7950
versión impresa ISSN 0378-4738
Water SA vol.43 no.1 Pretoria ene. 2017
http://dx.doi.org/10.4314/wsa.v43i1.06
Circulation induced by diffused aeration in a shallow lake
Arthur JA Toné; Carlos HA Pacheco; Iran E Lima Neto*
'Department of Hydraulic and Environmental Engineering - DEHA, Federal University of Ceará - UFC, Campus do Pici, bl. 713,60.451-970, Fortaleza, Brazil
ABSTRACT
Field surveys were carried out to investigate the surface jet flows and the resulting circulation patterns generated by diffused aeration in a shallow lake. In conrast to previous studies, the experimental conditions included point-source bubble plumes with very high air flow rates (100-400 L/min) relative to the shallow water depth (1.5 m). The results indicate that the surface jet velocity can be described by linear profiles. The decay of this velocity with distance displayed a similar behaviour to that reported in the literature, but the surface jet spread much faster under the present conditions. Combining our results with published data allowed for the generation of dimensionless correlations for the velocity and depth of the surface jet. A good agreement between the total circulation flow rates predicted by using the proposed correlations and integral modelling was also obtained. Lastly, a simple returning flow model was proposed to describe the circulation flow patterns induced by the bubble plumes. The results were also applied to assess the impact of circulation on vertical algae migration, which is important for water quality management.
Keywords: aeration, algae migration, bubbles, jets, plumes
INTRODUCTION
Bubble plumes generated by diffused aeration are widely used for treating wastewater and ameliorating water quality problems in lakes and reservoirs (Bombardelli et al., 2007; Socolofsky et al., 2008; Lima Neto, 2012a,b; Lima Neto and Parente, 2016). In addition to supplementing the dissolved oxygen levels and reducing internal phosphorus loading in water bodies, bubble plumes also generate water circulation patterns that can prevent or destroy stratification (Wüest et al., 1992; Singleton et al., 2010; Lima Neto et al., 2016). The behaviour of these circulation patterns must be well understood in order to promote positive effects such as the elimination of undesired algae, as well as to avoid negative effects such as resuspension of bottom sediments and nutrients (Imteaz and Asaeda, 2000; Jungo et al., 2001).
The rational use of point-source (axisymmetric) bubble plumes in the vicinity of water supply intakes has also been proposed as a measure to minimize the local impacts of eutroph-ication and reduce water treatment costs, particularly in the Brazilian semiarid region, where thousands of eutrophic reservoirs are used for human water supply (Campos et al., 2016). Bubble plumes have also been proposed to minimize water evaporation losses from reservoirs (Van Dijk and Van Vuuren, 2009; Helfer et al., 2011).
Several researchers have investigated the liquid flow induced by axisymmetric bubble plumes in unstratified environments (Milgram, 1983; Bombardelli et al., 2007; Lima Neto et al., 2008). However, their studies focused on the rising plume hydrodynamics, without giving details of the surface jet flow and circulation patterns produced by the bubble plumes. To the authors' knowledge, only Goossens (1979) has performed experimental studies involving measurement of the circulation flows generated by axisymmetric bubble plumes, which is the focus of the present investigation (see Fig. 1), while Wen and Torrest (1987), Fannel0p et al. (1991) and Riess and Fannel0p (1998) have studied the flows generated by line-source or plane bubble plumes. More recently, Brevik and Kristiansen (2002) have proposed theories to describe the circulation flows induced by both axisymmetric and plane bubble plumes.

The aims of the present paper are: (i) to investigate the surface flows generated by axisymmetric bubble plumes with relatively high air flow rates in a shallow lake, (ii) to propose a method to describe the circulation patterns induced by the bubble plumes, and (iii) to apply the results to assess the impact of circulation on vertical algae migration.
METHODS
The experiments were performed in the Santo Anastácio Lake, located in Fortaleza, Ceará, Brazil. This equatorial lake is very shallow (water depth < 4 m) and presents negligible thermal stratification (temperature difference < 1°C). The air injection system consisted of a 10 HP compressor which provided atmospheric air flow rates Q ranging from 115 to 450 L/min to a hose that fed a point-source diffuser placed at the bottom of the lake (water head of H = 1.5 m), approx. 30 m from the shore. The air flow rates were measured with a rotameter (ECR, model 440). The diffuser consisted of an array of 1" PVC pipes with a total of 160 holes of 1 mm, which was designed to promote high mixing efficiency and prevent clogging, as suggested by Lima Neto et al. (2008). The air flow rates per orifice were similar to those of Lima Neto et al. (2008), in which bubbles with diameters ranging from about 6 to 8 mm were formed. This agrees well with the values of 6.6-8.1 mm estimated from the correlation given by Lima Neto (2015). For such bubble sizes and the above air flow rate/water depth conditions, the effect of gas-liquid mass transfer on bubble plume hydrodynamics is expected to be negligible (see Lima Neto and Parente, 2016). An electromagnetic propeller anemometer (Omni Instruments, MiniWater20) with an internal diameter of 22 mm was used to measure the mean horizontal water velocity u in the surface flow induced by the bubble plumes, as shown schematically in Fig. 1. The same device has been used by Lima Neto et al. (2008) to measure the water velocity in vertical bubble plumes. The propeller anemometer was mounted on a stem connected to a thoroughly anchored boat.
The mean horizontal water velocity u was measured at different distances r from the centreline (0.3-1.5 m) and at different distances z from the water surface (0-0.85 m). This allowed generating velocity profiles along the radial direction. Note that the velocity u decreases from uo (at the water surface) to zero (at the stagnation line) (see Fig. 1). Hence, the depth of the surface jet hw(i.e., the outflowing layer) for each specific distance r could be obtained by gradually lowering the anemometer until it displayed a null velocity. Therefore, if we assume that the velocity profiles are linear, as one of the options suggested by Brevik and Kristiansen (2002), the surface jet flow becomes fully described by uo(r) and hw(r). The minimum distance of r = 0.3 m was adopted here because the radius observed for the fountains formed by the impingement of the vertical flow at the water surface reached up to about 0.2 m, which was larger than the values predicted by using the model of Friedl and Fannel0p (2000). Thus, we expect that at r = 0.3 m the vertical flow had totally turned into the horizontal surface jet flow. On the other hand, measurements for r > 1.5 m were not taken because the surface jet velocities u approached the minimum velocities that can be accurately measured by the anemometer (around 0.01 m/s).
Preliminary tests were conducted on 11 and 18 March 2014, and the complete set of experiments was carried out on 4 April 2014. The results shown herein refer to the data of 4 April 2014, but the March data were also used to verify the repeatability of the velocity measurements (deviations < 30%). Both air and water temperatures were about 25-30°C and the wind speed was lower than 3 m/s for all of the tests.
Dimensional analysis was conducted in order to normalize the test results and make them applicable to other experimental conditions. Therefore, assuming that air bubble plumes in water are fully turbulent flows dominated by buoyancy forces, the following function can be used to express the general behaviour of the maximum velocity uo and depth of the surface jet hw:

In the present study, we combined our data for strong bubble plumes (i.e., for 0.03 < L/H < 0.06) with that of Goossens (1979) for weaker bubble plumes (i.e., for L/H < 0.02), and tested different combinations for the parameters in Eq. 1 to obtain the dimensionless correlations that better described the surface jet flow induced by axisymmetric bubble plumes. Note that L is a length scale defined as L = Q2/5 g-1/5. A comparison of the total water flow rates obtained by using the proposed correlations with those estimated from the integral model of Lima Neto (2012a) is also presented. Furthermore, the dimensionless correlations for the surface jet flow are coupled with a simple returning flow model, similar to that of Brevik and Kristiansen (2002), in order to assess the impact of circulation on vertical algae migration through the water column. This combined model is implemented in Matlab (MathWorks).
RESULTS AND DISCUSSION
Figure 2 shows the profiles of mean horizontal water velocity at the surface jet flow obtained in the present study for different atmospheric air flow rates Q and distances r from the centreline. The filled circles represent experimental data while the dashed lines represent fitted linear curves, which were adjusted to the data with a coefficient of determination R2 ranging from 0.94 to 0.99. This confirms that, for the sake of simplicity, the surface jet flow induced by axisymmetric bubble plumes can be described by linear velocity profiles. Note that the data shown in Fig. 2 correspond to the maximum velocity of the surface jet uo, its half value uo/2 (which coincides with the depth-averaged velocity of the surface jet uavg, assuming linear velocity profiles), and the null value of u that occurred at the stagnation line (i.e., at z = hw) (see Fig. 1). It is clearly seen that both uo and hwincrease with Q. On the other hand, uodecreases with r while hw increases. Similar behaviours have been reported by Goossens (1979) and Brevik and Kristiansen (2002). Figure 3 also shows that the decay of uo with r follows approximately a power law of the type uo ~ rα, in which α is a coefficient that increases from about 0.6 to 0.9 as Q increases. These values of α are within the range of 0.4-0.9 obtained experimentally by Goossens (1979) and close to the value of 0.67 proposed in the model of Brevik and Kristiansen (2002). Moreover, the spreading of the surface jets follows approximately a linear curve of the type hw ~ βr, in which β increases from about 0.15 to 0.34 as Q increases. It is interesting to observe that these values of β are much higher than those (0.03-0.05) obtained by Goossens (1979) and Brevik and Kristiansen (2002). This faster spreading probably occurred because the axisymmetric bubble plumes investigated in the present study were stronger (with L/H > 0.03) than those studied previously (with L/H < 0.02).
Dimensional analysis was carried out to normalize the relevant bubble plume parameters and obtain general correlations by combining our results with the lab and field data of Goossens (1979). His study considered bubble diameters of about 3-10 mm, water depths of 4-15 m, and atmospheric air flow rates of 50-10 000 L/min. For such flow conditions, the effect of gas-liquid mass transfer on bubble plume hydrodynamics is estimated from Lima Neto and Parente (2016) to be smaller than 10%. Therefore, neglecting this effect and assuming that the above-mentioned bubble plumes were fully turbulent/buoyancy-driven flows, the functional relationship given by Eq. 1 can be used. Hence, the following dimensionless correlations could be obtained by least-square fitting of the data:

As mentioned earlier, L is a length scale defined as L = Q2/5g-1/5, while U is a velocity scale defined as U = Q1/5g2/5. Figures 3(a) and 3(b) show comparisons between the experimental data and the values predicted by using the correlations given by Eqs 2 and 3, which resulted in standard deviations of 18% and 8%, respectively. This indicates that uo/ U and hw/L can be described by the proposed functions of r/H and L/H. Consistently, uodecreases with r but increases with both Q and H, while hwincreases with the three parameters (r, Q and H). It is worthwhile to mention that the model of Brevik and Kristiansen (2002) provided standard deviations of up to about 50%, as compared to our experimental data. Therefore, the proposed correlations can be seen as a simplified method that can predict the surface jet flow induced by axisymmetric bubble plumes under a wider range of flow conditions (i.e., for 0.01 < L/H < 0.06).
The correlations given by Eqs 2 and 3 can also be used to estimate the total water circulation flow rates induced by axisym-metric bubble plumes through the following equation:

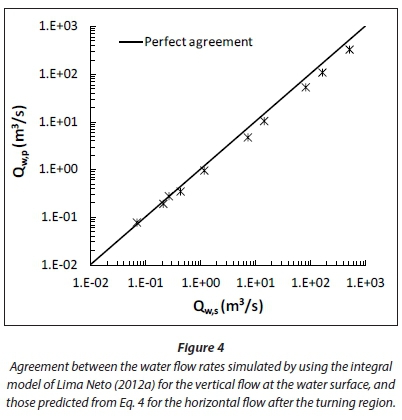
where: r is a characteristic radius of the vertical plume at the water surface, which can be taken as the starting value of r for the surface jet flow. Note that the estimation of Qwusing Eq. 4 assumes that there is no entrainment/detrainment in the turning flow region (from the vertical upwards flow to the radially outwards horizontal flow). In the present study, r was calculated from the integral model of Lima Neto (2012a) as the radial distance from the vertical plume centreline where the velocity is equal to 1/e of the maximum (centreline) value. Figure 4 shows the agreement between the water flow rates simulated by using the model of Lima Neto (2012a) for the vertical flow at the water surface and those predicted from the proposed equation (Eq. 4) for the horizontal flow after the turning region (at r = ro). The simulations included water depths H ranging from 2 to 50 m and atmospheric air flow rates Q ranging from 50 to 200 000 L/min, which resulted in values of L/H varying from 0.01 to 0.06. For all the tests, large bubbles of 8 mm diameter (common in coarse bubble aeration) were used, so that the effect of mass transfer on bubble plume hydrodynamics could be neglected. A good agreement between the two methods can be seen in Fig. 4, resulting in standard deviations of 22%. This suggests that the correlations proposed herein can also be used to assess the circulation patterns generated by axisymmetric bubble plumes.
Assuming linear velocity profiles, the following equations can be used to describe the surface jet and the returning flow in a 2D framework:

Thus, the complete circulation flow model consists of Eqs 2, 3, 5, 6 and 7, which are solved using Matlab (MathWorks). In the present study, several simulations were performed to analyse the circulation patterns induced in the water column. As an example, Fig. 5 shows the velocity field simulated for a bubble plume with Q = 200 L/min and H = 4 m. The stagnation line clearly indicates the limit between the surface jet and the returning flow.

It is possible now to study the impact of circulation on algae migration by superimposition of the flow field given by Fig. 5 (for example) and a maximum vertical velocity of the algae of va = ± 3 mm/s (see Kromkamp and Walsby, 1990; Visser et al., 1997). The results of this superimposition are shown in Fig. 6 in the form of streamlines, which were generated using Matlab (MathWorks). Figure 6(a.I) shows the downward migration of algae for nutrients in the absence of ambient flow, while Fig. 6 (a.II) shows the effect of artificial circulation on this migration. It can be seen that circulation can prevent the algae from reaching the lake bottom nutrients and also remove them from the vicinity of the bubble plume. On the other hand, Fig. 6(b.I) shows the upward migration of algae for light in the absence of ambient flow, while Fig. 6(b.II) shows the impact of circulation on this migration. It is seen that circulation can drag the algae into the bubble plume and spread them radially away from the site. Note that similar migration patterns as those depicted in Figs 6(a.II) and 6(b.II) have been observed for other values of Q, H and va. Therefore, it can be inferred that artificial circulation can promote shortage of light and/or nutrients in addition to displacement of algae from the bubble plume surroundings (although not investigated here, turbulence may also promote algal cell rupture). This suggests that such devices can be used as a measure to reduce the negative effects of eutrophication, at least near the intakes for water supply. It is important to observe, however, that the proper air flow rate Q must be selected as a function of H and va, not only to reduce the concentration of algae by means of the lowest possible electricity cost, but also to avoid resuspension of bottom sediments/nutrients, which may lead to water quality deterioration.
CONCLUSIONS
The results obtained in the present investigation indicate that the surface jet velocity can be described by linear profiles. The decay of this velocity with radial distance showed similar behaviour to that reported previously for weaker bubble plumes, but the surface jet spread much faster under the present experimental conditions. Combination of our data with that available in the literature allowed for the generation of dimensionless correlations for the velocity and depth of the surface jet as a function of the radial distance, air flow rate, and head above the diffuser. Consistently, the correlations indicate that the surface jet velocity decreases with an increase in radial distance but increases with both the air flow rate and head above the diffuser, while the depth of the surface jet increases with these three parameters. A validation of the proposed correlations with the data for total water flow rates obtained by using integral modelling was also presented. Therefore, our simple approach can be used to assess not only the surface jet flow but also the circulation flow patterns induced by axisymmetric bubble plumes for a wide range of flow conditions. Moreover, a simple returning flow model was proposed to predict the circulation flow patterns induced by the bubble plumes. Model simulations showed that circulation can clearly prevent algae migration, in addition to displacing algae away from the aeration site. This implies that bubble plumes can be used not only to minimize the impacts of lake eutrophication but also to potentially reduce algae concentrations at water supply intakes in reservoirs.
ACKNOWLEDGMENTS
This work has been financially supported by the Brazilian National Council for Scientific and Technological Development -CNPq (Project 476430/2011-9).
REFERENCES
BOMBARDELLI FA, BUSCAGLIA GC, REHMANN CR, RINCÓN LE and GARCÍA MH (2007) Modeling and scaling of aeration bubble plumes: A two-phase flow analysis. J. Hydraul. Res. 45 (5) 617-630. https://doi.org/10.1080/00221686.2007.9521798 [ Links ]
BREVIK I AND KRISTIANSEN 0 (2002) The flow in and around air-bubble plumes. Int. J. Multiphase Flow 28 617-634. https://doi.org/10.1016/S0301-9322(01)00077-5 [ Links ]
CAMPOS JNB, LIMA NETO IE, STUDART TMC and NASCIMENTO LSV (2016) Trade-off between reservoir yield and evaporation losses as a function of lake morphology in semi-arid Brazil. Ann. Braz. Acad. Sci. 88 (2) 1113-1126. https://doi.org/10.1590/0001-3765201620150124 [ Links ]
FANNEL0P TK, HIRSCHBERG S and KÜFFER J (1991) Surface current and recirculating cells generated by bubble curtains and jets. J. Fluid. Mech. 229 626-657. https://doi.org/10.1017/S0022112091003208 [ Links ]
FRIEDL MJ and FANNEL0P TK (2000) Bubble plumes and their interaction with the water surface. Appl. Ocean Res. 22 119-128. https://doi.org/10.1016/S0141-1187(99)00022-X [ Links ]
GOOSSENS L (1979) Reservoir destratification with bubble columns. Ph.D. Thesis, Department of Physics, Delft University of Technology, Holland. [ Links ]
HELFER F, ZHANG H and LEMCKERT C (2011) Modelling of lake mixing induced by air-bubble plumes and the effects on evaporation. J. Hydrol. 406 182-198. https://doi.org/10.1016/j.jhydrol.2011.06.020 [ Links ]
IMTEAZ MA and ASAEDA T (2000) Artificial mixing of lake water by bubble plume and effects of bubbling operations on algal bloom. Water Res. 34 (6) 1919-1929. https://doi.org/10.1016/S0043-1354(99)00341-3 [ Links ]
JUNGO E, VISSER PM, STROOM J and MUR LR (2001) Artificial mixing to reduce growth of the blue-green alga Microcystis in Lake Nieuwe Meer, Amsterdam: an evaluation of 7 years of experience. Water Sci. Technol. Water Supply 1 (1) 17-23. [ Links ]
KROMKAMP J AND WALSBY AE (1990) A computer model of buoyancy and vertical migration in cyanobacteria. J. Plankton Res. 12 (1) 161-183. https://doi.org/10.1093/plankt/12.L161 [ Links ]
LIMA NETO IE (2012a) Bubble plume modelling with new functional relationships. J. Hydraul. Res. 50 (1) 134-137. https://doi.org/10.1080/00221686.2011.651278 [ Links ]
LIMA NETO IE (2012b) Modeling the liquid volume flux in bubbly jets using a simple integral approach. J. Hydraul. Eng. 138 (2) 210-215. https://doi.org/10.1061/(ASCE)HY.1943-7900.0000499 [ Links ]
LIMA NETO IE (2015) Size of air bubbles formed from non-porous diffusers in water. Eng. Sanit. Ambient. 20 (2) 175-180 (in Portuguese). https://doi.org/10.1590/S1413-41522015020000119054 [ Links ]
LIMA NETO IE, CARDOSO SSS and WOODS AW (2016) On mixing a density interface by a bubble plume. J. Fluid Mech. 802 R3. https://doi.org/10.1017/jfm.2016.454 [ Links ]
LIMA NETO IE and PARENTE PAB (2016) Influence of mass transfer on bubble plume hydrodynamics. Ann. Braz. Acad. Sci. 88 (1) 411-422. https://doi.org/10.1590/0001-3765201520140453 [ Links ]
LIMA NETO IE, ZHU DZ and RAJARATNAM N (2008) Air injection in water with different nozzles. J. Environ. Eng. 134 (4) 283-294. https://doi.org/10.1061/(ASCE)0733-9372(2008)134:4(283) [ Links ]
MILGRAM HJ (1983) Mean flow in round bubble plumes. J. Fluid. Mech. 133 345-376. https://doi.org/10.1017/S0022112083001950 [ Links ]
RIESS IR and FANNEL0P TK (1998) Recirculating flow generated by line-source bubble plumes. J. Hydraul. Eng. 124 (9) 932-940. https://doi.org/10.1061/(ASCE)0733-9429(1998)124:9(932) [ Links ]
SINGLETON VL, RUEDA FJ and LITTLE JC (2010) A coupled bubble plume-reservoir model for hypolimnetic oxygenation. Water Resour. Res. 46 WR009012. https://doi.org/10.1029/2009WR009012 [ Links ]
SOCOLOFSKY SA, BHAUMIK T and SEOL DG (2008) Double-plume integral models for near-field mixing in multiphase plumes. J. Hydraul. Eng. 134 (6) 772-783. https://doi.org/10.1061/(ASCE)0733-9429(2008)134:6(772) [ Links ]
VAN DIJK M and VAN VUUREN SJ (2009) Destratification induced by bubble plumes as a means to reduce evaporation from open impoundments. Water SA 35 (2) 158-167. [ Links ]
VISSER PM, PASSARGE J and MUR LR (1997) Modelling vertical migration of the cyanobacterium Microcystis. Hydrobiologia 349 99-109. https://doi.org/10.1023/A:1003001713560 [ Links ]
WEN J and TORREST RS (1987) Aeration-induced circulation from line sources. I: Channel flows J. Environ. Eng. 113 (1) 82-98. https://doi.org/10.1061/(ASCE)0733-9372(1987)113:1(82) [ Links ]
WÜEST A, BROOKS NH and IMBODEN DM (1992) Bubble plume modeling for lake restoration. Water Resour. Res. 28 (12) 3235-3250. https://doi.org/10.1029/92WR01681 [ Links ]
Received 4 December 2015
Accepted in revised form 18 November 2016
* To whom all correspondence should be addressed. e-mail: iran@deha.ufc.br
















