Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Water SA
On-line version ISSN 1816-7950
Print version ISSN 0378-4738
Water SA vol.42 n.4 Pretoria Oct. 2016
http://dx.doi.org/10.4314/wsa.v42i4.19
Improving the understanding of rainfall distribution and characterisation in the Cathedral Peak catchments using a geo-statistical technique
F MorrisI, *; ML Warburton ToucherI; A ClulowI; S KusangayaI; C MorrisII; H BulcockI
ICentre for Water Resources Research, University of KwaZulu-Natal, Private Bag X01, Scottsville 3209, South Africa
IIAgricultural Research Council-Animal Production Institute (ARC-API), c/o School of Life Sciences, University of KwaZulu-Natal, Private Bag X0I, Scottsville 3209, South Africa
ABSTRACT
The characterisation of rainfall variability, spatially and temporally, is essential for hydrological and ecological analyses. Inherently, this variability is distinctly more obvious in mountainous areas compared to lowlands. The objective of this study was to ascertain if the use of the regression-Kriging technique would provide improved estimates and understanding of the rainfall distribution across the Cathedral Peak catchments in the Drakensberg escarpment region, South Africa. Findings showed longitude and altitude to be the overall best predictors of the distribution of rainfall for the annual period, wet season and dry season, with longitude explaining 72% and altitude explaining 26% of the rainfall variability for mean annual precipitation, 73% and 26% for the wet season and 50% and 22% for the dry season, respectively. The combination of both longitude and altitude showed a larger coefficient of determination, of 0.73, 0.74 and 0.51, for the annual, wet season and dry season, respectively. Long-term mean annual rainfall patterns showed an overall strong directional distribution from west to east with a distinct pattern observed during the dry season. It was concluded that regression-Kriging is a useful alternative method for characterising rainfall distribution as well as prediction errors for mountainous areas.
Keywords: Cathedral Peak, rainfall variability, regression-Kriging, mountainous areas
INTRODUCTION
The characterisation of spatial and temporal rainfall variability is essential for hydrological and ecological analyses (Tao, 2009; Aghakouchak et al., 2011; Vogel et aL, 2012; Masson and Frei, 2014). Inherently, this variability is distinctly more apparent in mountainous areas compared to lowlands (Cegnar, 2005; Thompson et al., 2009; Chang et al., 2014). This rainfall characteristic is mainly attributed to the interaction between atmospheric circulation and topographic features of the landscape, particularly altitudinal variation or orography (Prudhomme and Reed, 1998; Mair and Fares, 2010; Tan et al., 2012; Roe, 2005). Orographic effects influence the local distribution and intensity of rainfall when forced upward movements of moisture-filled air, due to topographic barriers, result in more precipitation on the windward side and less precipitation on the leeward side (Chang et al., 2014; Arora et al., 2006; Houze Jr and Medina, 2005).
Despite the above understanding, however, a precise understanding of the spatial distribution of rainfall in mountainous areas is still hindered by the typically sparse rain-gauge networks at higher altitudes (Ranhao et al., 2008, Masson and Frei, 2014, Roe, 2005). Generally, rain-gauge networks cover mainly valley and low-lying areas, where the weather-generating systems and resultant spatial patterns of rainfall are different to those at higher elevations (Prudhomme and Reed, 1998). In South Africa, Pegram et al. (2014) mention both a decrease in the cover of rain-gauge networks since the year 2000, as well as the lack of rain-gauges located at high altitudes.
Rainfall interpolation using data from a limited number of rain-gauges is one method that hydrologists use to derive the spatial distribution of precipitation in mountainous areas (Groisman et al., 2005, Masson and Frei, 2014, Vogel et al., 2012, Duethmann et al., 2013, Jacquin and Soto-Sandoval, 2013). Numerous interpolation methods have been proposed to interpolate rainfall from rain-gauge observations (Guan et al., 2005, Putthividhya and Tanaka). Several studies have reported that conventional techniques such as Thiessen polygon, inverse distance weighting, isoheytal methods and splines do not fully account for both climatological and spatio-statistical properties of rainfall fields ( e.g. Prudhomme and Reed, 1998; Guan et al., 2005; Vogel et al., 2012). Nevertheless, improved computing facilities and development of robust methods, especially geosta-tistically-based methods, have the potential of increasing our understanding of rainfall characteristics in mountainous areas (Hengl et al., 2007)2007.
Geostatistical methods such as Kriging are capable and have been shown to produce better estimates than traditional interpolation approaches (Goovaerts, 2000; Mair and Fares, 2010; Meng et al., 2013; Omran, 2012; Saffari et al., 2009). Additionally, they also provide some measures of accuracy and certainty in the predictions (Ly et al., 2013). Another advantage of geostatisti-cal methods is the use of auxiliary variables to improve rainfall estimates (Mair and Fares, 2010). According to Ly et al. (2013), the use of multivariate geostatistical methods has shown more accurate interpolations compared to deterministic interpolation methods. Geostatistical methods (such as regression-Kriging) for the estimation of rainfall are flexible, comprehensive, robust and free from serious bias (Hengl et al., 2007). Regression-Kriging is a spatial prediction method that combines a regression analysis of the dependent variable on auxiliary variables with the interpolation of the residuals from that regression (Hengl et al., 2007).
Regression-Kriging has been applied widely in various fields such as climatology (Bajat et al., 2013; Tadic, 2010), soil science (Hengl et al., 2004; Omuto and Vargas, 2015; Zhu and Lin, 2010), and species distribution modelling (Meng, 2006; Hengl et al., 2009).
This work builds on previous work done by Schulze (1976), who used deterministic methods such as trend surface analysis for rainfall estimation in the Cathedral Peak catchments. Trend surfaces of long-term annual precipitation and the use of the weighted average method for two short-term precipitation events were analysed. A 46-year data record is now available for the catchments compared to the 20-year record used by Schulze in 1976, and there have been recent advancements in interpolation methods which have the ability to provide error surfaces together with the rainfall prediction surfaces. Additionally, consideration of the increasing pressure on water resources, and the environmental, social and economic importance of high-altitude catchments such as Cathedral Peak compels immediate attention to provide accurate estimations of rainfall for the Cathedral Peak research catchments. The objective of this research was to ascertain if the use of a contemporary geostatistical interpolation method called regression-Kriging provided any improved estimates and understanding of the rainfall distribution across the high-altitude Cathedral Peak catchments in the Drakensberg escarpment region.
MATERIALS AND METHODS
Study area
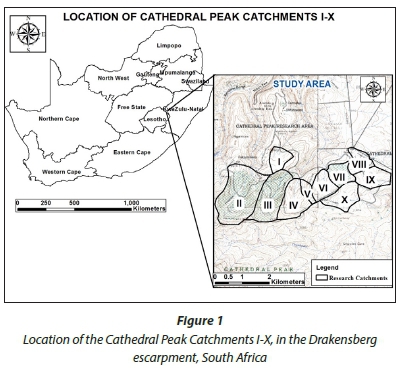
The Cathedral Peak research catchments (29° 00' S; 29° 15' E) are located on the Little Berg sandstone plateau in the northern part of the uKhahlamba Drakensberg area (Fig. 1). The uKhahlamba Drakensberg area constitutes one of South Africa's most important watersheds (Sycholt, 2002; Briggs, 2008) as it is the source of a major river - the Thukela River. The Thukela-Vaal (TUVA) transfer scheme is an inter-basin transfer scheme that has its upper catchments in the Cathedral Peak area and feeds the drier interior of South Africa (Nel and Sumner, 2008). The research catchments are situated at the head of three isolated Little Berg spurs, and range in altitude from 1 820 m amsl to 2 463 m amsl (Fig. 2). The Little Berg is a plateau below the basaltic cliffs of the main uKhahlamba Drakensberg range that is dissected by deep ravines (Scott et al., 2000; Briggs, 2008). The Cathedral Peak research catchments fall within the summer rainfall region of South Africa, thus the area experiences wet, humid summers and cold, dry winters (Everson et al., 1998).The mean annual precipitation (MAP) for the area is approximately 1 400 mm, with 84% of the MAP occurring between the months of October and March.
Data and processing
Historical rainfall data were obtained for the rain-gauge network of the Cathedral Peak catchments (I-X). The data were obtained from various historical sources, but these data are now available from the South African Environmental Observation Network (SAEON). The catchments are considered to have a fairly dense rain-gauge network (1 gauge per 0.352 km2; Schulze, 1976), with the highest density of rain-gauges in the eastern catchments (VIII-X). The dataset consisted of a time-series with hourly, daily, weekly and/or monthly rainfall totals at 22 stations during the 46-year research period stretching from August 1948 to March 1994. Various types of rain-gauges have been used in the catchments (Table 1). Not all of the rain-gauges were active for the full 46-year period and during the monitoring period some rain-gauges that were read manually were replaced by automatic logging rain-gauges (Schulze, 1974). Although rainfall measurements were available at hourly and daily time steps for some rain-gauges, the shortest common recording period for all rain-gauges was monthly; hence data were analysed on a monthly basis for this study.
In order to exclude the most obvious errors from the Cathedral Peak historical rainfall dataset, quality control procedures included checking for the completeness of the dataset and the detection of outliers or physically impossible values, as outlined by Einfalt and Michaelides (2008). Varying periods of records at individual gauges required the adjustment of rainfall to a standard base period. The 20 -year period from October 1965 to October 1985 was one during which most gauges recorded simultaneously; thus it was chosen as the base period. Although the World Meteorological Organization (WMO) recommends the use of 30-year means, several authors (e.g. Marquinez et al., 2003; Arora et al., 2006) have used shorter time periods for data analysis.
Five rainfall patching methods were tried to infill the missing monthly rainfall data: nearest neighbour by distance; nearest neighbour by correlation; inverse distance weighted; average of gauges selected by correlation and multiple linear regression analysis. The performance of all methods was compared using three error statistics: root mean square error (RMSE); mean bias (MB); and a correlation coefficient (R2). Of these, multiple linear regression had the least error based on the above error statistics evaluation and thus was used to infill gaps in the monthly rainfall data for 21 of the 23 gauges. The remaining two rain-gauges were excluded from further analysis due to insufficient data lengths during the 20-year base period and also their increased distance from the catchments.
Seasonal analysis
Analysis of the mean annual, wet and dry season rainfall confirmed a strong wet and dry season trend. On average, 83% of the annual rainfall occurs during the wet season (September to February) with the north-facing gauges receiving the most rainfall during both wet and dry seasons (Table 2). This finding is reported in Schulze (1974). This analysis was expected considering the altitudinal differences between the rain-gauges with different aspects, where north-facing rain-gauges average 2 007 m amsl and east- and west-facing rain-gauges average 1 932 m amsl and 1 895 m amsl, respectively. Rainfall data for the area is strongly seasonal, therefore mean rainfall for both the dry season (March to August) and wet season (September to February) was calculated for further analysis. Based on previously considered auxiliary variables (altitude, longitude and latitude) for the area (Schulze, 1976) and a comprehensive literature review, it was therefore hypothesized that factors such as altitude (m amsl), slope angle, slope orientation (aspect), latitude and longitude could be used to predict rainfall for the ungauged sites.
Regression analysis
Regression analysis was used to determine if the considered predictor variables (altitude, aspect, latitude and longitude) showed any significance in explaining the variation in the annual, wet and dry season rainfall. Utilizing the above predictor variables as independent variables, and rainfall (annual, wet or dry period) as the dependent variable, the regression equation (Eq. 1) was used:

where:
Y = dependent variable (rainfall for annual, wet or dry period)
X. = independent variable (altitude, aspect, latitude and longitude)
β= beta weights (slopes of each independent variable)
α= Y intercept
Regression-Kriging
Kriging is an interpolation method that uses values of a variable at known geographical locations to estimate values at unknown locations. Kriging relies on the fact that observations are not independent (Hengl et al., 2007)2007. Regression-Kriging is a type of Kriging that uses secondary variables for more accurate predictions (Karl, 2010). The method uses multiple regressions to explain the relationship between the observed variable and the secondary variables considered. The regression and Kriging results are combined to produce not only a prediction surface, but also an error surface. Regression-Kriging is therefore essentially a spatial prediction method that combines regression of the dependent variable on auxiliary variables (altitude, aspect, latitude and longitude) with the interpolation of the residuals from that regression (Hengl et al., 2007). With fitted parameters of the regression model and of the residual variogram, regression-Kriging was used to derive rainfall predictions at all locations. All subsets regression' was used in regression-Kriging to select predictor variables with regression slopes statistically significant at p < 0.05. The coefficient of determination (R2) was used as a measure of the goodness of fit of the model. Additionally, the Akaike Information Criterion (AIC), which is a measure of the relative quality of a statistical model for a given dataset, was also used to assess the predictive power of the developed model. The combination of both the regression and Kriging methods are illustrated below (Eq. 2):
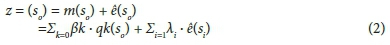
where:
z = predicted value of the target variable at an unknown location
m(so ) = the fitted deterministic part
ê(so ) = interpolated residual
ßk = the estimated regression model coefficients
λ.i = the Kriging weights determined by the spatial dependence structure of the residual
ê(si) = the residual at location si.
RESULTS AND DISCUSSION
Predictor variables from regression analysis
The best predictor models were selected based on the criteria that the p-value of each predictor variable be less than 0.05 and the AIC value the smallest. All-subsets regressions (Tables 3 to 5) indicate that the overall best predictors of the distribution of rainfall, for the annual, wet season and dry season, are longitude and altitude. Longitude shows greater significance than altitude, explaining 72% of the rainfall variability, with altitude explaining only 26% of the rainfall variability for MAP (Table 3). Longitude and altitude explained 73% and 26% of variability for the wet season (Table 4) and 50% and 22% for the dry season (Table 5), respectively. The significant negative effect for the MAP (Table 3) and wet season (Table 4) indicates that an increase in longitudinal direction (east-west) relates to an increase in rainfall, which was also reported by Schulze (1974). A small positive effect in the dry season (Table 5) indicates that there may be different rainfall variability patterns.
The high R2 and small AIC values for longitude alone indicate that the overall distribution is strongly directional with an east-west directional gradient. The combination of both longitude and altitude had a larger R2, of 0.73, 0.74 and 0.51, for the annual, wet season and dry season, respectively. However, when combined with longitude, altitude had a significant influence for all periods (p < 0.05). Aspect alone was shown to be significant for the annual and dry seasons, explaining 18% and 19% of the rainfall variability, respectively.
The 3-subsets model of longitude, altitude and aspect indicated a slight decrease in R2, with altitude and aspect being statistically insignificant for all rainfall periods. These results cannot be applied throughout the Drakensberg as the orientation of the Drakensberg range changes. Relationships may be different due to different aspects. Although there are latitudinal differences in the station positions, latitude is found to play no significant role in influencing the rainfall distribution for the area and neither does slope.
The regression analysis reveals that, based on the R2 values and small AIC values, a simple linear regression, with longitude alone, altitude alone or the combination of both longitude and altitude, can be used to satisfactorily characterise the rainfall variability for the Cathedral Peak area. However, the use of longitude alone may be applicable only to local conditions and not in other areas of the Drakensberg. Regression models selected for each rainfall period are shown in Table 6.
Rainfall spatial variability estimation from Kriging
The annual, wet season and dry season rainfall data suggested higher autocorrelation in a west to east direction compared to a north-south direction. Semi-variogram models were therefore chosen based on their ability to depict the anisotropic behaviour of the target variables. Both manual and automatic methods of fitting the semi-variogram models were used. Empirical model variograms (spherical, Gaussian, exponential and circular models) were visually compared to the automated fitted models. Residual semi-variograms were then derived based on the semi-variograms of the target variables. The Gaussian empirical models were selected to model the covariance structure of both the target variables and the regression residuals.
The rainfall patterns for the long-term mean annual data show an overall strong directional distribution ranging from over 1 531 mm/a in the north and south-west to under 020 mm/a in the east (Fig. 3). The influence of altitude appears significant in the spatial patterns of rainfall only in the two steepest catchments (namely, II and III). A similar pattern is observed for the wet season where the rainfall amounts range from over 1 286 mm/a in the north to south-west to under 836 mm in the east. A distinct pattern is observed during the dry season where rainfall ranges from 285 mm in the north-west to approximately 240 mm in the east and under 206 mm in the south-east (Fig. 3). The rainfall distribution during the dry season indicates the typical west to east frontal movement over South Africa.
Cross validation and error analysis
Unlike deterministic interpolation methods, for each prediction map generated with regression-Kriging a prediction error or standard deviation map is generated using the same Kriging method. Prediction error maps of standard deviations were used to assess the accuracy of the predicted rainfall maps. Standard deviations for the wet season have the same pattern as the MAP; however, lower standard deviations in areas with few rain-gauges were observed (Fig. 4). The lowest standard deviations were observed for the dry season, especially in the north-west and east. The high standard deviations at the high altitude catchments II III and IV are due to artefacts within the Kriging processes, specifically the algorithm involved. Since the high-altitude rain-gauges are fewer in number compared to those in the lower altitude catchments in the east, the algorithm works best for the lower altitude catchments. In regression-Kriging, a suitable number of point-pairs must be available at different spacings for variogram estimations (Hengl et al., 2007). To avoid overfitting, the minimal number of point pairs is recommended to be 10 (Hengl et al., 2007). The algorithm then estimates very high values due to the lack of point pairs in the high altitudes, and works well for areas that are well represented and collapses or overestimates at high altitudes.
Cross-validation results indicated a high root mean square error (RMSE) for the MAP and wet season, of 163.89 and 137.62, respectively, and a low RMSE for the dry season. Plots of observed and predicted rainfall indicated a high R2 for the MAP and wet season (78% and 79.7%, respectively) and low R2 (55%) values for the dry season (Fig. 5). The consideration of more frontal-related variables for the dry season, such as wind and distance to sea, may assist in better characterisation of the rainfall variability.
DISCUSSION
The regression-Kriging method was shown to be a useful tool in characterising the rainfall distribution for the Cathedral Peak catchments. The method was able to use auxiliary information, available in the form of maps of covariates (altitude, longitude, aspect and slope), to explain variations in rainfall for the area as well as provide prediction errors. Predictions indicated that the overall rainfall distribution for the area is strongly directional, particularly for the long-term mean annual rainfall and for the wet season, as well as a significant effect on rainfall distribution due to altitude. The results are comparable to what was obtained by Schulze (1976).
The main difference between the methods used, however, was that the deterministic interpolation method used in Schulze (1976) did not allow for the production of error maps compared to the regression-Kriging technique. However, what must be noted is the shortfalls of the technique, specifically with regards to the Cathedral Peak catchments. These include the issues of data quality, under-sampling of rain-gauges at altitudes above 2 000 m amsl and predictors with uneven relation to the rainfall for the area (Hengl et al., 2007). Results by Nel and Sumner (2006) and Nel and Sumner (2007) were also comparable to results from this study, indicating the role of altitude in characterising rainfall for catchments and the insignificance of the positions of the rain-gauges (latitude) compared to eastward distance from the escarpment.
Lower rainfall amounts were predicted for all rainfall periods in this study, with different rainfall patterns observed in the dry season. Rainfall estimates were lower by approximately 260 mm in the south-west and approximately 220 mm in the east, compared to the rainfall surfaces produced by Schulze (1976). This may be attributable to the different record period used in the Schulze (1976) study (1950-1969), as well as the higher long-term means compared to this study. The major rainfall-producing systems are attributed to large-scale line thunderstorms and orographically-induced thunderstorms in summer (Nel and Sumner, 2007), which are driven inland from an easterly direction, while approximately 43 mid-latitude cold fronts originating from the western Atlantic move across South Africa in a west to east direction each year, resulting in winter rainfall (Grab and Simpson, 2000; Nel, 2008).
Estimations clearly represented the spatial distribution of rainfall for the annual and wet season from east to west as well as the west-northeast to east-southeast spatial distribution for the dry season. According to Houze (2012), convective systems are enhanced by upslope flow and therefore higher rainfall is observed in the two steepest catchments during the annual and wet season. Convective systems moving in from the east are therefore enhanced in the high-altitude catchments. In the dry season, frontal systems, on the other hand, may rise easily over the terrain resulting in maximal rainfall on ridges and minimal rainfall in valleys (Houze, 2012). This spatial pattern is observed for the dry season where the crests of the catchments receive higher rainfall than the valleys in the catchments. These assumptions are however inconclusive considering the size of these precipitating mechanisms relative to the overall size of the catchments.
Longitude and altitude were shown to have lower significance in explaining the dry season rainfall variability, which may be due to the different effect of topography on frontal systems compared to convective rainfall.
However, the use of long-term means to characterise rainfall for an area which receives predominantly sub-daily short-duration events is not fully representative of the nature of rainfall in the area and can also explain the high RMSEs. Both a temporal and spatial analysis of rain-event properties for the area will allow for better understanding and characterisations of the type and distribution of rainfall received in the area. The high standard deviations at the high-altitude catchments, II III and IV, are due to artefacts within the Kriging process, the algorithm estimates very high values due to the lack of rain-gauges at the high altitudes but works well for lower altitude catchments in the east that are well represented.
CONCLUSION
Overall, the findings of the study at Cathedral Peak indicate that improved computing facilities and the recent advancements in interpolation methods has allowed easier methods for satisfactorily characterising rainfall variability for the area with the least amount of variables. The proposed interpolation technique (regression-Kriging) determines the spatial precipitation distribution just as well as previously-used methods with the ability of finding the same east-west directional decrease in rainfall across the catchment as demonstrated in previous studies. Nevertheless, the models obtained so far have a modest degree of explanation for the spatial distribution of rainfall for the Cathedral Peak catchments. These results, however, were shown to be specific for the Cathedral Peak catchments and not for the rest of the Drakensberg area.
ACKNOWLEDGEMENTS
The authors would like to acknowledge the Water Research Commission (WRC) and the Applied Centre for Climate and Earth Systems Science (ACCESS) for the financial support of this research. We would also like to thank the South African Environmental Observation Network (SAEON) for the data provision required to undertake this research.
REFERENCES
AGHAKOUCHAK A, NASROLLAHI N, LI J, IMAM B and SOROOSHIAN S (2011) Geometrical characterization of precipitation patterns. J. Hydrometeorol. 12 (2) 274-285. http://dx.doi.org/10.1175/2010JHM1298.1 [ Links ]
ARORA M, SING P, GOEL N and SINGH R (2006) Spatial distribution and seasonal variability of rainfall in a mountainous basin in the Himalayan region. Water Resour. Manage. 20 (4) 489-508. http://dx.doi.org/10.1007/s11269-006-8773-4 [ Links ]
BAJAT B, PEJOVIC M, LUKOVIC J, MANOJLOVIC P, DUCIC, V and MUSTAFIC S (2013) Mapping average annual precipitation in Serbia (1961-1990) by using regression Kriging. Theor. Appl. Climatol. 112 (1-2) 1-13. http://dx.doi.org/10.1007/s00704-012-0702-2 [ Links ]
BRIGGS P (2006) Ukhahlamba-Drakensberg Park: World Heritage Sites of South Africa. 30 Degrees South Publishers, Johannesburg. 176 pp. [ Links ]
CEGNAR T (2005) Mountain weather and climate in the media. Hrvatski Meteorol. Casopis 40 119-122. [ Links ]
CHANG H, JOHNSON G, HINKLEY T and JUNG IW (2014) spatial analysis of annual runoff ratios and their variability across the contiguous us. J. Hydrol. 511 387-402. http://dx.doi.org/10.1016/j.jhydrol.2014.01.066 [ Links ]
DUETHMANN D, ZIMMER J, GAFUROV A, GÜNTNER A, KRIEGEL D, MERZ B and VOROGUSHYN S (2013) Evaluation of areal precipitation estimates based on downscaled reanalysis and station data by hydrological modelling. Hydrol. Earth Syst. Sci. 17 (7) 2415-2434. http://dx.doi.org/10.5194/hess-17-2415-2013 [ Links ]
EINFALT T and MICHAELIDES S (2008) Quality control of precipitation data. In: Michaelides S (ed.) Precipitation: Advances in Measurement, Estimation and Prediction. Springer, Berlin. http://dx.doi.org/10.1007/978-3-540-77655-0_5 [ Links ]
EVERSON CS, MOLEFE G and EVERSON TM (1998) Monitoring and modelling components of the water balance in a grassland catchment in the summer rainfall area of South Africa. WRC Report No. 493/1/98. Water Research Commission, Pretoria. [ Links ]
GOOVAERTS P (2000) Geostatistical approaches for incorporating elevation into the spatial interpolation of rainfall. J. Hydrol. 228 113-129. http://dx.doi.org/10.1016/S0022-1694(00)00144-X [ Links ]
GRAB SW and SIMPSON AJ (2000) Climatic and environmental impacts of cold fronts over Kwazulu- Natal and the adjacent interior of South Africa. S. Afr. J. Sci. 96 (106) 602-608. [ Links ]
GROISMAN PY, KNIGHT RW, EASTERLING DR, KARL TR, HEGERL GC and RAZUVAEV VN (2005) Trends in intense precipitation in the climate record. J. Clim. 18 (9) 1326-1350. http://dx.doi.org/10.1175/JCLI3339.1 [ Links ]
GUAN H, WILSON JL and MAKHNIN O (2005) Geostatistical mapping of mountain precipitation incorporating autosearched effects of terrain and climatic characteristics. J. Hydrometeorol. 6 (6) 1018-1031. http://dx.doi.org/10.1175/JHM448.1 [ Links ]
HENGL T, HEUVELINK G and ROSSITER DG (2007) About regression-Kriging: From equations to case studies. Comput. Geosci. 33 (10) 1301-1315. http://dx.doi.org/10.1016/jxageo.2007.05.001 [ Links ]
HENGL T, HEUVELINK GB and STEIN A (2004) A generic framework for spatial prediction of soil variables based on regression- Kriging. Geoderma 120 (1) 75-93. http://dx.doi.org/10.1016/j.geoderma.2003.08.018 [ Links ]
HENGL T, SIERDSEMA H, RADOVIC A and DILO A (2009) spatial prediction of species' distributions from occurrence-only records: combining point pattern analysis, ENFA and regression-Kriging. Ecol. Model. 220 (24) 3499-3511. http://dx.doi.org/10.1016/j.ecolmodel.2009.06.038 [ Links ]
HOUZE JR RA and MEDINA S (2005) Turbulence as a mechanism for orographic precipitation enhancement. J. Atmos. Sci. 62 (10) 3599-3623. http://dx.doi.org/10.1175/JAS3555. [ Links ]!
HOUZE RA (2012) Orographic effects on precipitating clouds. Rev. Geophys. 50 (1) 1-47. http://dx.doi.org/10.1029/2011rg000365 [ Links ]
JACQUIN AP and SOTO-SANDOVAL JC (2013) Interpolation of monthly precipitation amounts in mountainous catchments with sparse precipitation networks. Chil. J. Agric. Res. 73 (4) 406-413. http://dx.doi.org/10.4067/S0718-58392013000400012 [ Links ]
KARL JW (2010) Spatial predictions of cover attributes of range land ecosystems using regression Kriging and remote sensing. Rangeland Ecol. Manage. 63 (3) 335-349. http://dx.doi.org/10.2111/REM-D-09-00074.1 [ Links ]
LY S, CHARLES C and DEGRÉ A (2013) Different methods for spatial interpolation of rainfall data for operational hydrology and hydrological modeling at watershed scale: A review. Biotechnol. Agron. Soc. Environ. 17 (2) 392-406. [ Links ]
MAIR A and FARES A (2010) Comparison of rainfall interpolation methods in a mountainous region of a tropical island. J. Hydrol. Eng. 16 (4) 371-383. http://dx.doi.org/10.1061/(ASCE)HE.1943-5584.0000330 [ Links ]
MARQUÍNEZ J, LASTRA J and GARCIA P (2003) estimation models for precipitation in mountainous regions: The use of GIS and multivariate analysis. J. Hydrol. 270 (1) 1-11. http://dx.doi.org/10.1016/S0022-1694(02)00110-5 [ Links ]
MASSON D and FREI C (2014) Spatial analysis of precipitation in a high-mountain region: Exploring methods with multi-scale topographic predictors and circulation types. Hydrol. Earth Syst. Sci. Discuss. 11 (5) 4639-4694. http://dx.doi.org/10.5194/hessd-11-4639-2014 [ Links ]
MENG Q (2006) Geostatistical prediction and mapping for large area forest inventory using remote sensing data. In: UCGIS Summer Symposium, 3 July 2006, Washington [ Links ]
MENG Q, LIU Z and BORDERS BE (2013) Assessment of regression Kriging for spatial interpolation-comparisons of seven GIS interpolation methods. Cartogr. Geogr. Inf. Sci. 401 28-39. http://dx.doi.org/10.1080/15230406.2013.762138 [ Links ]
NEL W (2008) Observations on daily rainfall events in the KwaZulu- Natal Drakensberg. Water SA 34 (2) 271-274. [ Links ]
NEL W and SUMNER P (2006) Trends in rainfall total and variability (1970-2000) along the KwaZulu-Natal Drakensberg foothills. S. Afr. Geogr. J. 88 (2) 130-137. http://dx.doi.org/10.1080/03736245.2006.9713855 [ Links ]
NEL W and SUMNER P (2007) Intensity, energy and erosivity attributes of rainstorms in the KwaZulu-Natal Drakensberg, South Africa. S. Afr. J. Sci. 103 (9-10) 398-402. [ Links ]
NEL W and SUMNER P (2008) Rainfall and temperature attributes on the Lesotho-Drakensberg escarpment edge, Southern Africa. S. Afr. J. Sci. 103 399-402. http://dx.doi.org/10.1111/j.1468-0459.2008.00337.x [ Links ]
OMRAN EL-SE (2012) Improving the prediction accuracy of soil mapping through geostatistics. Int. J. Geosci. 3 (3) 1-17. [ Links ]
OMUTO CT and VARGAS RR (2015) Re-tooling of regression Kriging in R for improved digital mapping of soil properties. Geosci. J. 19 (1) 157-165. http://dx.doi.org/10.1007/s12303-014-0023-9 [ Links ]
PEGRAM GGS, SINCLAIR S and BARDOSSY A (2014) Accounting for uncertainty in the repair of daily rain gauge records. 17th South African National Hydrological Symposium, 1 September 2014 - 4 September 2016, Cape Town, South Africa. [ Links ]
PRUDHOMME C and REED DW (1998) Relationships between extreme daily precipitation and topography in a mountainous region: A case study in Scotland. Int. J. Climatol. 18 (13) 1439-1453. http://dx.doi.org/10.1002/(SICI)1097-0088(19981115)18:13<1439::AID-JOC320>3.0.CO;2-7 [ Links ]
PUTTHIVIDHYA A and TANAKA K (2013) Optimal rain gauge network design and spatial precipitation mapping based on geostatistical analysis from colocated elevation and humidity data. Chiang Mai J. Sci. 40 (2) 187-197. [ Links ]
RANHAO S, BAIPING Z and JING T (2008) A multivariate regression model for predicting precipitation in the Daqing Mountains. Mt. Res. Dev. 28 (3)) 318-325. http://dx.doi.org/10.1659/mrd.0944 [ Links ]
ROE GH (2005) Orographic precipitation. Annu. Rev. Earth Planet. Sci 33 645-671. http://dx.doi.org/10.1146/annurev.earth.33.092203.122541 [ Links ]
SAFFARI M, YASREBI J, FATHI H, KARIMIAN N, MOAZALLAHI M and GAZNI R (2009) Evaluation and comparison of ordinary Kriging and inverse distance weighting methods for prediction of spatial variability of some soil chemical parameters. Res. J. Biol. Sci. 4 (1) 93-102. [ Links ]
SCHULZE RE (1974) Catchment Evapotranspiration in the Natal Drakensberg. Unpublished PhD thesis, University of Natal, South Africa. [ Links ]
SCHULZE RE (1976) On the application of trend surfaces of precipitation to mountainous areas. Water SA 2 110-118. [ Links ]
SCOTT DF, PRINSLOO FW, MOSES G, MEHLOMAKULU M and SIMMERS ADA (2000) A re-analysis of the South African catchment afforestation experimental data. WRC Report No. 810/1/00. Water Reasearch Commission, Pretoria. [ Links ]
SYCHOLT A (2002) A Guide to the Drakensberg. Struik, Cape Town. 200 pp. [ Links ]
TADIC MP (2010) Gridded Croatian climatology for 1961-1990. Theor. Appl. Climatol. 102 (1-2) 87-103. http://dx.doi.org/10.1007/s00704-009-0237-3 [ Links ]
TAN F, LIM H and ABDULLAH K (2012) The effects of orography in Indochina on wind, cloud, and rainfall patterns during Typhoon Ketsana (2009). Asia-Pacific J. Atmos. Sci. 48 (3) 295-314. [ Links ]
TAO T (2009) Uncertainty Analysis of Interpolation Methods in Rainfall Spatial Distribution-a Case of Small Catchment in Lyon. J. Environ. Prot. 1 (1) 50. http://dx.doi.org/10.4236/jwarp.2009.12018 [ Links ]
THOMPSON R, VENTURA M and CAMARERO L (2009) On the climate and weather of mountain and sub-Arctic lakes in Europe and their susceptibility to future climate change. Freshwater Biol. 541 (2) 2433-2451. http://dx.doi.org/10.1111/j.1365-2427.2009.02236.x [ Links ]
VOGEL H, MEYER-JACOB C, MELLES M, BRIGHAM-GRETTE J, ANDREEV A, WENNRICH V and ROSÉN P (2012) Detailed insight into Arctic climatic variability during Mis 11 at Lake El'gygytgyn, Ne Russia. Clim. Past Discuss. 8 (6) 6309-6339. http://dx.doi.org/10.5194/cpd-8-6309-2012 [ Links ]
ZHU Q and LIN H (2010) Comparing ordinary Kriging and regression Kriging for soil properties in contrasting landscapes. Pedosphere 20 (5) 594-606. http://dx.doi.org/10.1016/S1002-0160(10)60049-5 [ Links ]
Received 15 September 2015
Accepted in revised form 5 October 2016
* To whom all correspondence should be addressed. e-mail: rozymorris@yahoo.com














