Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Water SA
On-line version ISSN 1816-7950
Print version ISSN 0378-4738
Water SA vol.42 n.4 Pretoria Oct. 2016
http://dx.doi.org/10.4314/wsa.v42i4.15
Estimating runoff from ungauged catchments for reservoir water balance in the Lower Middle Zambezi Basin
W GumindogaI, *; H MakuriraII; M PhiriI, II; I NhapiIII
IDepartment of Civil Engineering, University of Zimbabwe, P.O. Box MP167, Mt. Pleasant, Harare, Zimbabwe
IIMinistry of Agriculture, PO Box 630161 Choma, Zambia
IIIDepartment of Environmental Engineering, Chinhoyi University of Technology, P. Bag 7724, Chinhoyi, Zimbabwe
ABSTRACT
The Lower Middle Zambezi Basin is sandwiched between three hydropower dams; Kariba, Kafue (Itezhi-tezhi) and Cahora Bassa. The operation of the upstream dams impacts on the inflows into the downstream Cahora Bassa Dam which, in turn, affects the area inundated upstream of the Cahora Bassa Dam. This study applied a rainfall-runoff model (HEC-HMS) and GIS techniques to estimate both the gauged and ungauged runoff contribution to the water balance of Cahora Bassa. The rivers considered in the study are the Zambezi, Kafue, Luangwa, Chongwe, Musengezi and Manyame. Missing data were generated using the mean value infilling method. The DEM hydro-processing technique was used to determine the spatial extent of the ungauged area. A hydrological model, HEC- HMS, was used to simulate runoff from the ungauged catchments. Results from the study show that the ungauged catchment contributes about 12% of the total estimated inflows into the Cahora Bassa Dam. Averaged results over 30 years show total inflows of 71.73 x 109 m3/yr, total outflows of 52.25 x 109 m3/ yr and a residual storage of 20 x 109 m3/yr. The study successfully estimated the water balance of the Middle Zambezi Basin which, in turn, may help to inform the operation of the Cahora Bassa Dam and management of artificial floods in the basin.
Keywords: Cahora Bassa, DEM hydroprocessing, HEC-HMS, remote sensing, reservoir operation, runoff simulation
INTRODUCTION
The increased water demands in the Zambezi Basin have led to the construction of dams to store excess flows for release during periods of low flows and to be used for hydropower generation, irrigation and other requirements (Tumbare, 2005; Magadza, 2006). In addition to these uses, the dams have also benefitted the inland fishing industry and hydro-tourism (Chenje et al., 1998; IFRC, 2007). However, negative effects such as flooding of settled and cultivated areas have also been associated with the operation of these reservoirs. The middle Zambezi River watercourse system, which stretches from the Victoria Falls up to the Cahora Bassa Dam wall, currently has three large hydroelectric dams namely, Kafue (Itezhi tezhi), Kariba and Cahora Bassa. These dams have full supply capacities of 5.6 km3, 180 km3 and 55.8 km3 respectively. The Kariba and Cahora Bassa dams lie on the Zambezi while the third lies on the Kafue River, a major tributary of the Zambezi. As these reservoirs were constructed in the Zambezi Basin primarily for hydropower production purposes, they maintain a high hydraulic head in order to maximise power production.
Natural floods in the basin are caused by high-intensity and short-duration rainfall from upstream catchments while artificial floods are due to the operation of the reservoirs whose main objective is power generation. Parts of Mbire and Muzarabani districts in Zimbabwe and Luangwa District (Zambia) extend into the low-lying Zambezi Valley. Muzarabani District has experienced at least one flood every year since 2000 (IFRC, 2007). The frequency and intensity of these floods is a source of concern especially when contrasted with the human and livestock population increases in these areas (Beilfuss and Dos Santos, 2001). Luangwa and Kanyemba have a lower flood frequency with the most severe flood in Luangwa realised in 2001 when an estimated 30 000 people were affected (Du Toit, 1993;IFRC, 2007).
In addition, the biggest challenge faced in trying to understand the hydrological and environmental conditions in this basin is the lack of hydrological data since some of the catchments are ungauged. Examples of these ungauged catchments are Angwa, Rukomechi and Lower Manyame. Hydrometric measurements are fundamental for the understanding of water balances of hydrological systems. For the middle Zambezi Basin, it is important to understand water balances as this informs the operation of reservoirs and management of floods. Many catchments have inadequate measurements of hydrologic variables to facilitate comprehensive water resource assessments. In some cases where data are available they are very limited and of questionable quality thus rendering many catchments ungauged (Beven, 2001; Sivapalan, 2003). Attempts at improving some traditional hydrologic tools such as the unit hydrograph and flow duration curves for ungauged basins have resulted in unnecessary sophistication of the tools (Sivapalan, 2003; Wale et al., 2009). The quest to assess water resources and stream flows in such ungauged catchments remains at the centre of hydrologic sciences and water resources planning and management in the Middle Zambezi Basin.
The integration of remote-sensing data into hydrological studies and water balance studies has progressed over the past decades (Kite and Pietroniro, 1996; Weissling and Xie, 2008; Delrieu et al., 2009; Gumindoga et al., 2011; Silvestro et al., 2013). Remote sensing can provide land surface data relevant to specific hydrologic problems such as streamflow or runoff modeling. In several studies, remotely-sensed data have served as input variables to semi-distributed and distributed hydrological models (Beven, 1997; Beven, 2001; Biftu and Gan, 2004; Gumindoga et al., 2014). At various spatial and temporal scales, remote sensing has provided numerous solutions and convenience to characterizing biophysical and geophysical land surface processes and properties, many of which relate to hydrological science (Schmugge et al., 2002; Santillan et al., 2012). Satellite data have emerged as a viable alternative or supplement to in-situ observations (Gumindoga et al., 2014) due to their easier accessibility and applicability over vast ungauged parts of the Middle Zambezi basin.
This study therefore sought to establish the applicability of a combination of in-situ measurements and remotely-sensed data to predict ungauged runoff from Middle Zambezi Basin using the Hydrologic Engineering Centre Hydrologic Modelling System (HEC-HMS) rainfall-runoff model, with the aim of improving water balance estimation.
MATERIALS AND METHODS
Study area
The study area lies almost entirely within the Middle Zambezi valley from 28.27°E to 32.75°E and 14.83°S to 17.08°S at an elevation range of approx. 145 m amsl at Cahora Bassa Dam to 1 700 m amsl in the plateau areas of the Angwa catchment. The area is shared by three countries Zambia, Mozambique and Zimbabwe (Fig. 1). The study area provides runoff into the Cahora Bassa Dam and is an area that is either ungauged or the gauging stations are located further upstream of the main Zambezi River.
This research focused on the contributing catchment into Cahora Bassa Dam covering the Zambezi, Luangwa, Chongwe, Kafue, Musengezi and Manyame rivers. The vegetation of the study area is predominantly savanna and perennial forest,and falls within the miombo woodland ecoregion that occurs across Zambia, Zimbabwe and Mozambique (Du Toit, 1993).
The climate is influenced by the Congo air masses, north easterlies and the Inter-Tropical Convergence Zone (ITCZ). The tropical cyclones from the Indian Ocean also affect the Zambezi basin, bringing large storms which, of late, have caused destruction of property and loss of lives through flooding. The local climate of the basin is also affected by the presence of large water bodies such as Lake Kariba, Lake Malawi and Cabora Bassa (Madamombe, 2004). The rainy season is largely dependent on the low-pressure system of the ITCZ, which moves southwards across Zambia in November and reaches its peak between January and February. The ITCZ peak period also coincides with the period when river flows are maximum thus making the basin more prone to flooding at this time of the year (Madamombe, 2004). Because of high temperatures during this period, convec-tional rainfall is also common. Although, on average, the area receives rainfall of about 650 mm/yr, the basin is characterized by extreme variations in rainfall, both spatially and temporally. For example, the Lower Manyame river catchment has a mean annual precipitation (MAP) of 836 mm, an evaporation rate of 2 092 mm/yr and a mean annual runoff (MAR) of 96 mm. The Musengezi river catchment has a MAP of 816 mm, evaporation rate of 2 094 mm/yr and a MAR of 102 mm (Garedondo, 2015). Maximum rainfall is recorded from December to February averaging approximately 200 mm in Luangwa river catchment with a long dry period extending from April to October across the whole basin. The rainfall season extends from October to March. Average daily temperatures in places such as Chongwe river catchment range from 24°C to 32°C, with the highest temperatures recorded in the Zambezi Valley (Mbire and Muzarabani districts) reaching as high as 40°C (Baudron et al., 2011). Such high temperatures, in particular those recorded across Southern Africa in the 2015/2016 rainfall season, are associated with droughts. Floods of unprecedented magnitudes experienced in the years 2000 and 2003 were mainly caused by tropical cyclones.
Data collection and filling
Observed flow data at Kafue, Chongwe, Luangwa, Manyame, Dande and Musengezi Rivers were used to analyse gauged flow contributions. Releases from Kariba and Kafue Dams were also considered as inflow with the main assumption here being that there are no transmission losses in between. This is logical given the rocky terrain traversed by the Zambezi River between these dams and Cahora Bassa Dam.
The daily time-step rainfall and runoff data used in this study had missing values of, on average, 1-3 days per month. Therefore, the mean value infilling method was employed after the data was divided into wet and dry seasons. Winsorised values were substituted for missing values to dampen the effects of outliers by estimating the mean and standard deviation of the symmetric distribution (Gilbert, 1987). This method was used because it is easy to apply and because it provides accuracy equal to the standard error of the mean (Shih and Cheng, 1989). The mean value infilling method was validated using the Pearson correlation coefficient method whereby the original time series with gaps was correlated with the filled time series for all the rainfall and runoff gauging stations.
Determination of the flow contribution from the ungauged catchments
In addition to the gauged flows, a component of the inflows into the Cahora Bassa comes from ungauged areas. According to Winsemius et al. (2009), a large portion of the Lower Middle Zambezi is ungauged. For hydrologists, it is always a considerable challenge to extrapolate information from gauged to ungauged basins (Sivapalan, 2003), yet contributions of ungauged systems may be significant (Ibrahim and Cordery, 1995). In order to estimate the ungauged component of the water balance and so determine its significance, GIS and remote sensing were used to extract the ungauged areal extent through the DEM hydroprocessing tool in the Integrated Water and Land Information System (ILWIS) software. Therefore, the extent of the ungauged area was extracted using a Hydro-IK DEM (1 km spatial resolution) of the Middle Zambezi Basin with the boundary of the ungauged area being determined by the locations of the most upstream gauging stations.
Simulation of flow contributions
The HEC-HMS rainfall runoff model of the US Army Corps of Engineers was used to simulate flows in both the gauged and ungauged catchments. In the absence of input data for the catchments under study, neighbouring catchments with similar characteristics were used to generate the input aided by the GIS ILWIS software. The similarity between the gauged and ungauged catchments was established through a physical parameter comparison (Adib et al., 2010; Wale et al., 2009). A similar approach was used in the Upper Manyame Basin (Gumindoga et al., 2016).
After conducting the physical parameter comparison, the HEC-HMS was then used to simulate flows based on inputs of rainfall, evaporation, soil type, hydrologic group, total flows from the gauged rivers and the managed releases from the Kariba Dam. Additional model inputs are catchment area, lag time, peaking coefficient and runoff coefficient. Simulation was conducted on a daily time step. The HEC-HMS model was selected because it has the Snyder Unit Hydrograph transformation subroutine specifically designed for ungauged catchments (Scharffenberg, 2015), making it more suitable for use in this study. The Snyder Unit Hydrograph was used to calculate the basin lag time and the runoff coefficient as it is the most documented analysis for ungauged catchments using HEC-HMS (Adib et al., 2010) which solves the Soil Conservation Service (SCS) unit hydrograph to get the time of concentration (tc based on the California Culverts Practice (US Army Corps of Engineers, 2015). The time of concentration is given by Eq. 1:

where: L = length of longest watercourse, miles and H = elevation difference between divide and outlet (in feet) (US SCS, 1986). The standard lag was obtained using Eq. 2:

where: tl = standard lag in minutes.
The peaking coefficient (cfs) is also used in the model. This value represents the peak flow for the unit at the point of analysis. The peaking coefficient was calculated by using historical data for rainfall-runoff events.
Meteorological inputs into HEC-HMS model
Weather data was obtained from Hidro Electrica de Cahora Bassa (HCB) and the meteorology departments of Zambia and Zimbabwe for stations in Kanyemba, Muzarabani, Luangwa, Petauke, Marongora and Rukomechi, for a period ranging from 1990 to2007. Pan evaporation (cumulated to monthly time step from available daily values) from HCB for the same time period was used, and was multiplied by a factor of 0.8 so that it closely reflected plant water use (Lidén et al. 2001; Gumindoga et al. 2016). The average monthly evaporation rates as required in the model were calculated from the daily pan evaporation obtained. All the simulation results of runoff were converted into yearly time units for consistency with the other datasets.
Model calibration, validation and parameter optimization
The model was calibrated with flow data from the Upper Musengezi Catchment at Station C68 for the period 1990 to 1994 and the Upper Luangwa Catchment at the Luangwa Bridge station for the period 1995 to 2000. The model was then validated with flow data for the Upper Musengezi for the period 1998 to 1999 and the Upper Luangwa catchment for the period 2004 to 2007. Selection of these periods was dictated by availability of common data. In order to improve the model performance, the parameter optimisation function in the model was then applied to come up with optimal parameter values for calibration.
Assessing model efficiency
The evaluation of hydrological model behaviour and performance is commonly made and reported through comparisons of simulated and observed variables (Krause et al., 2005). In this study, the flows were both simulated and observed at the gauged Upper Musengezi and Upper Luangwa catchments. The Nash-Sutcliffe Efficiency (NSE) for model efficiency was used to determine the goodness of fit of the simulated to the observed values (Krause et al., 2005; Sharad and Sudheer, 2007). The efficiency is calculated using Eq. 3:

where:
E = Nash-Sutcliffe model coefficient [-]
Qo= observed discharge (m3/s)
Qm= modelled discharge (m3/s)
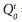 = observed discharge (m3/s) at time t
= observed discharge (m3/s) at time t
 = the mean of observed data (m3/s)
= the mean of observed data (m3/s)
Catchment parameter comparison
One method of estimating runoff from an ungauged area is through the application of the catchment parameter comparison approach where a catchment is paired with another of similar characteristics. In order to come up with a sound hydrological basis for transferring the parameters obtained after the validation process (Snyder Unit Hydrograph parameters) from the gauged catchment to the ungauged catchments, a similarity in catchment hydrological response needed to be established as described by Sreenivasulu and Bhaskar (2010). This was done through a comparison of the physical catchment characteristics based on data obtained from the hydro-processing of a DEM of the study area in GIS software. The hydro-processing results yielded the catchment area, the drainage network, the drainage density, upstream and downstream elevation, catchment perimeter and the longest flow length. The land cover and the soil types of the different sub-catchments were also compared so as to understand the hydrological response of the different watersheds. Rainfall from 7 different stations in the study area was also compared to see if it varied significantly between stations. This comparison of the above parameters gave the authors confidence to apply the similarity of catchments approach that was eventually used in estimating ungauged flows.
Runoff simulation for the ungauged catchments
After assessing model efficiency from the Upper Musengezi and Upper Luangwa catchments, the simulation of runoff was done for the ungauged catchments. This was also based on the changes made in catchment area, soil types, rainfall, initial soil moisture deficit and the maximum deficit from the catchment parameter comparison results. An established similarity between the gauged Musengezi and Luangwa and the ungauged catchments based on catchment characteristics and peak discharge resulted in the average of these two gauged catchment runoff coefficients being transferred to the ungauged catchments. Finally, the model was run for the ungauged catchments based on the Snyder Unit Hydrograph method with the basin lag time and the runoff coefficient as key parameters in the HEC-HMS (Adib et al., 2010)
Determination of the Cahora Bassa Dam water balance
The water balance of the lake is described by Eq. 4.

where:
P = lake's areal rainfall (Mm3/t)
Qgauged = gauged surface water inflow into the reservoir (Mm3/t)
Qungauged , = ungauged surface water contribution (Mm3/t) Eo= open water evaporation (Mm3/t)
Qout = outflow (Mm3/t) consisting of normal releases, releases for power generation and spillage
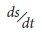 = change in storage (Mm3) over a given time interval t
= change in storage (Mm3) over a given time interval t
The demarcations between the gauged and ungauged portions of these rivers were determined by the location of gauging stations. The flow data were collected from the Department of Water Affairs in Zambia, the Zimbabwe National Water Authority (ZINWA), the Zambezi River Authority (ZRA) which operates the Kariba Dam and the Zambia Electricity Supply Corporation (ZESCO) which operates the Kafue Gorge Dam hydro-electric scheme. Inflow and outflow hydrographs were then plotted to determine the attenuation effects of the Cahora Bassa Dam on flows.
The direct contribution of rainfall into the lake was based on the rainfall data provided by the HCB for the Cahora Bassa Dam.
Reservoir releases from Cahora Bassa as a result of power generation, spillage and evaporation were considered as outflow variables. Records of releases from the dam based on reservoir operations combined with estimated evaporation were obtained from HCB, the operator of the reservoir.
Catchment area ratio method
The area ratio method is used in hydrological modelling to transfer the parameter set of gauged catchments to ungauged catchments of comparable area based on the assumption that the runoff coefficient is similar (Wale et al. 2009). In this study, the results of the HEC-HMS model simulation were then compared with the results of the catchment area ratio method. The catchment area was obtained by GIS hydro-processing of the study area DEM while the gauged catchment used was the Upper Musengezi with the outlet at Station C68 as shown in Fig. 2.

RESULTS and DISCUSSION
Validation of the data infilling method
Table 1 shows the correlation coefficients performed on the rainfall and runoff datasets after the mean value infilling method was performed. The original time series with gaps was compared with filled-in time series using the Pearson correlation coefficient method. The results show that the mean value infilling method is reliable to apply as a data quality checking method since all of the correlation coefficient values are above 0.85.

Extent of ungauged area
According to the results of DEM hydro-processing down in ILWIS using the 1 km Hydro IK DEM of the study area, the spatial extent of the ungauged area is just over 71 000 km2 with a perimeter of 2 171 km. The ungauged catchment covers parts of the Lower Luangwa, Lower Chongwe, the Mombasha, the Kafue River downstream of the Kafue Gorge dam, Chewore, Rukomechi, Sapi, Runese, Mwanza Mtanda, Angwa, Lower Manyame, Kadzi, Mkumbura and the Lower Musengezi (Refer to Fig. 1).
The spatial distribution of rainfall in the study area
The rainfall data as input into the HEC-HMS model were averaged through the Thiessen polygons, as shown in Fig. 3, from the seven stations in Kanyemba, Muzarabani, Luangwa, Petauke, Marongora, Rukomechi and HCB.

Results of HEC-HMS Model Calibration and Validation
Model calibration for the Upper Musengezi gave an average outflow of 70.5 mm3/yr against an observed outflow of 68 mm3/yr with a relative volume error (RVe) of 1.54%. This error is within the acceptable range of -10 to 10% (Janssen and Heuberger, 1995); hence the model was considered to perform satisfactorily, and using this performance indicator provided enough justification to transfer model parameters to ungauged parts of the basin. However, the model efficiency, as given by Nash Sutcliffe efficiency (NSE), was 0.47, which is not considered satisfactory since a value of 1 (perfect fit) would have been desirable. The performance of the model using the NSE performance indicator for the Upper Musengezi catchment may have been affected by the large number of impoundments in the upper catchment. The attenuation effect of these dams causes a time lag resulting in observed and simulated graphs being out of sync. The effect of the many dams in the catchment produced the equivalent of a 2-month lag time between the observed and simulated hydrograph peaks. Because of a lack of rating curves for these numerous dams, they were not included in the simulation. For the Luangwa catchment, model simulation gave an RVe of 8.42 and an NSE of 0.69 after parameter optimisation, indicating that the model was able to better simulate the catchment response.
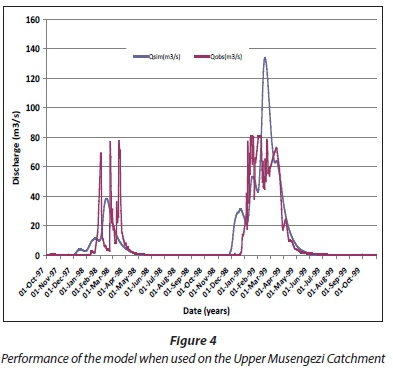
Model validation for the Upper Musengezi gave an RVe of 2.71% and a NSE of 0.41 which is interpreted as satisfactory (Fig. 4). Model validation for the Luangwa Catchment gave a RVe of -8.11 and a Nash-Sutcliffe coefficient of 0.61 which is also satisfactory.
The model was then further validated with one season's flow data from the Manyame at Mapomha Village station, set up as part of this projects objective of gauging ungauged catchments. The results of the validation with the Manyame Mapomha station flows give the hydrograph presented in Fig. 5. This gave an RVe of 3.20% while the Nash-Sutcliffe coefficient was 0.66 suggesting a good fit between simulated and observed flows at the gauging station. Even though the simulation for Manyame catchment was for a short season (1 year only) when most of the flows were low, the fact that the model efficiency is satisfactory in an additional catchment is justification that HEC-HMS can be used for the ungauged catchment simulations.
Catchment comparison and transfer
The catchment comparison based on the physical catchment parameters from the results of DEM hydro-processing in ILWIS shows the catchment area, drainage length, drainage density, longest drainage length and the elevation of the various sub-catchments. These parameters are most important in influencing the catchment runoff and other hydrological processes. One of the most important comparison parameters is the drainage density which shows how well drained an area is. The drainage density in the study area ranges between 32 m/km2 and 88 m/ km2. Both the ungauged area and the Luangwa and Musengezi are predominantly flat terrain with more than half of the catchment area below 600 m amsl (Fig. 6).
The comparison of the catchments showed that the predominant soils in the study area have similar hydrologic properties as given by the Hydrological Soil Group. Over 66% of the soils are in groups C and D indicating soils that are of a clayey nature or sandy but shallow and so tend to promote runoff rather than infiltration (Fig. 7).
As rainfall is another important determinant of runoff from any catchment, the rainfall pattern for seven different stations was compared. The stations at Nyamepi Camp (Mana Pools), Muzarabani, Kanyemba and Luangwa showed a similar trend. Figure 8 shows the rainfall pattern in the study area. Based on correlation coefficient analysis, there was a positive correlation (p<0.05) between the gauged (Musengezi and the Luangwa) catchment parameters and the ungauged catchments. Significant correlation was shown for the parameters: catchment area, drainage length, drainage density, longest drainage length, elevation of the various sub-catchments. Thus it was confirmed that runoff is influenced by catchment parameters besides rainfall distribution.

Ungauged area simulation results
Before simulating discharge from the ungauged catchments, parameters from the gauged catchments were transferred through the Snyder Unit Hydrograph transformation technique using the calculated values of catchment lag time and peaking coefficient. Based on the parameters from the Upper Musengezi and the Luangwa, stream flows were simulated for the remaining ungauged rivers in the catchment to come up with the ungauged contributions to the flows into the Cahora Bassa Dam. Figure 9 shows the delineation of the outline of the basin model of the HEC-HMS used to model runoff so as to come up with discharge figures for the different sub-catchments and a total for the whole ungauged area. Averaged runoff from these catchments using a 7-year simulation run gave a mean outflow of 8 760 x109 mm3/yr which is 11. 8% of the total inflows into the Cahora Bassa Dam.

Cahora Bassa Dam water balance
Direct rainfall on lake surface
The contribution from direct rainfall on the lake surface was calculated based on the average areal rainfall and the average lake surface area during the rainy season. The rainfall pattern on the lake surface was given by Thiessen polygons with data from the four rainfall stations at Luangwa, Kanyemba and Mzarabani and HCB which are shown in Fig. 3. The calculation of areal rainfall based on the average surface area of the lake during the rainy season and the total annual rainfall for the period under consideration gave a rainfall contribution directly on the lake surface as 1.637 x 109 m3, a value representing about 2.5% of the total Cahora Bassa Dam inflows.
Gauged inflows
The total inflow into Cahora Bassa Dam is based on the contribution from all the rivers flowing into the dam's catchment. However, the absence of gauging stations on some of the smaller rivers resulted in the initial inflow series being based on a summation of the gauged flows from the Upper Luangwa, Upper Musengezi, Upper Manyame and Upper Chongwe with the releases from the Kariba and Kafue Dams. Figure 10 shows the total flows from the gauged portions of the Luangwa River, Chongwe River and Musengezi River and the managed releases from the Kariba Dam from 1980 to 2005. Because the Luangwa is unregulated, the hydrograph of the Luangwa River gives a very good indication of the catchment response to rainfall activity. The contribution from Musengezi and Chongwe Rivers is much less; hence the use of a secondary axis. However, despite the Chongwe River being regulated and of a smaller magnitude than the Luangwa, it shows a similar trend of flow with similar peaks and troughs.

Figure 11 shows the relative contribution of the various gauged rivers to the total inflows into the Cahora Bassa Dam, showing that the managed releases from the Kariba Dam constitute the largest source of water entering the Cahora Bassa followed by the Luangwa and the Kafue Rivers. These three sources contribute about 97% of the gauged flows entering the Cahora Bassa Dam.

Outflows
The outflow from the Cahora Bassa Dam was determined based on discharge recorded at the Cahora Bassa Dam outlet. For the period from 1980 to 2010, the outflow from the Cahora Bassa ranged from a minimum of 19 x 109 m3/yr to a maximum of 137 x 109 m3/yr, with an average of 48 x 109 m3/yr. Evaporation data provided by the HCB adds up to 3.8 x 109 m3/yr thus contributing 7.32 % of the total outflows.
The improved water balance
With rainfall contribution directly on the lake surface estimated at 1.64 x 109 m3/yr, this contributed to about 2.5% of the total Cahora Bassa inflows. After simulating flows a refined water balance that incorporates both the ungauged and gauged flow was developed and is presented in Table 2. In hydrological modelling, each time contributions from ungauged catchments are considered in water balance and runoff estimations, water balance simulations improve (Ibrahim and Cordery, 1995; Wale et al. 2009; Odiyo et al., 2012). Overall, the study sought to use improved techniques such as hydrological modelling, GIS and remote sensing techniques to estimate the water balance of the Lower Middle Zambezi Basin, thus rendering the new surface water balance estimates improved.

The improved surface water balance of the Cahora Bassa shows an average inflow over the 30-year period of 7 110 x 109 m3/yr, an average annual outflow of 5 200 mm3/yr and a residual storage of 20 680 mm3/yr. A contribution of 86% of the inflows comes from gauged catchments while 11.78% comes from the local ungauged catchment.
CONCLUSIONS
In largely ungauged systems such as the tributaries of the Zambezi River, GIS and remote sensing techniques can provide significant information and analytical capability to water resource assessment of the given basin. This study has confirmed the complementary approaches of remote sensing, hydrological modelling techniques and observed in-situ data to refine the water balance of the Middle Zambezi Basin. Through the application of these techniques, it has been established that about 12% of the inflow into Cahorra Bassa Dam is generated from the ungauged basins.
The improved water balance estimates facilitate easy water management in the basin as they inform the Cahora Bassa Dam operators of the peak flows to expect and their timing. This is important for flood prediction especially in this study area where artificial or natural flooding can occur either separately or simultaneously.
Although the simulations estimate flow contributions reasonably well, even at monthly time-steps, a more refined analysis at daily time-steps would capture some peaks which may have significant impacts on communities in the basin.
ACKNOWLEDGEMENTS
The authors would like to acknowledge the Eco-Hydro Project and WaterNet for sponsoring this study through the Integrated Water Resources Management Capacity Building Programme at the University of Zimbabwe. The US Army Corps of Engineers, Hydrologic Engineering Center (HEC) are gratefully acknowledged for provision of the HEC-HMS software and manuals. Special thanks to METI and NASA for the ASTER GDEM.
REFERENCES
ADIB A, SALARIJAZI M and NAJAFPOUR K (2010) Evaluation of synthetic outlet runoff assessment models. J. Appl. Sci. Environ. Manage. 14 (3) 13-18. http://dx.doi.org/10.4314/jasem.v14i3.61450 [ Links ]
BAUDRON F, CORBEELS M, ANDERSON J A, SIBANDA M and GILLER KE (2011) Delineating the drivers of waning wildlife habitat: The predomonance of cotton farming on the fringe of protected areas in Mid-Zambezi Valley, Zimbabwe. Biol. Conserv. 144 1481-1493. http://dx.doi.org/10.1016/j.biocon.2011.01.017 [ Links ]
BEILFUSS R and DOS SANTOS D (2001) Patterns of hydrological change in the Zambezi Delta, Mozambique. Working Paper #2. Program for the Sustainable Management of Cahora Bassa Dam and the Lower Zambezi Valley. URL: http://www.xitizap.com/zambeze-hydrochanges.pdf (Accessed 7 Sept 2016). [ Links ]
BEVEN KJ (1997) Distributed Hydrological Modelling: Applications of the TOPMODEL concept. John Wiley and Sons Ltd, Chichester, UK. [ Links ]
BEVEN KJ (2001) Rainfall-Runoff Modelling: The Primer. John Wiley & Sons, Lancaster, UK. [ Links ]
BIFTU GF and GAN TY (2004) A semi-distributed, physics-based hydrologic model using remotely sensed and Digital Terrain Elevation Data for semi-arid catchments. Int. J. Remote Sens. 25 (20) 4351-4379. http://dx.doi.org/10.1080/01431160310001654374 [ Links ]
CHENJE M, PALECZY D and SOLOA L (1998) The State of Zimbabwe's Environment. Ministy of Mines, Environment and Tourism, Government of the Republic of Zimbabwe, Harare. [ Links ]
DELRIEU G, BRAUD I, BERNE A, BORGA M, BOUDEVILLAIN B, FABRY F, FREER J, GAUME E, NAKAKITA E, SEED A, TABARY P and UIJLENHOET R (2009) Weather radar and hydrology. Adv. Water Resour. 32 (7) 969-974. http://dx.doi.org/10.1016/j.advwatres.2009.03.006 [ Links ]
DU TOIT R (1993) Reconnaissance vegetation survey of the Chewore-Angwa-Kanyemba areas of the Zambezi Valley, Zimbabwe. Kirkia 14 (1) 61-17. [ Links ]
GILBERT RO (1987) Statistical Methods for Environmental Pollution Monitoring. John Wiley and Sons Ltd, New York, USA. [ Links ]
GAREDONDO B (2015) Impacts of land use and land cover changes on streamflows in data scarce catchments: a case of the Middle Zambezi Catchment within Zimbabwe. MSc Thesis, University of Zimbabwe. [ Links ]
GUMINDOGA W, RIENTJES HTM, SHEKEDE MD, RWASOKA DT, NHAPI I and HAILE AT (2014) Hydrological impacts of urbanisation of two catchments in Harare, Zimbabwe. Remote Sens. 6 (12) 12544-12574 doi:12510.13390/rs61212544. http://dx.doi.org/10.1016/j.pce.2014.11.012 [ Links ]
GUMINDOGA W, RIENTJES THM, HAILE AT and DUBE T (2014) Predicting streamflow for land cover changes in the Upper Gilgel Abay River Basin, Ethiopia: A TOPMODEL based approach. Phys. Chem. Earth, Parts A/B/C 76-78 3-15. [ Links ]
GUMINDOGA W, RWASOKA DT and MURWIRA A (2011) Simulation of streamflow using TOPMODEL in the Upper Save River catchment of Zimbabwe. Phys. Chem. Earth, Parts A/B/C 36 (14-15) 806-813. http://dx.doi.org/10.1016/j.pce.2011.07.054 [ Links ]
GUMINDOGA W, RWASOKA DT, NHAPI I and DUBE T (2016) Ungauged runoff simulation in Upper Manyame Catchment, Zimbabwe: Application of the HEC-HMS model. In press, corrected proof. Phys. Chem. Earth. http://dx.doi.org/10.1016/j.pce.2016.05.002. [ Links ]
IBRAHIM AB and CORDERY IAN (1995) Estimation of recharge and runoff volumes from ungauged catchments in eastern Australia. Hydrol. Sci. J. 40 (4) 499-515. http://dx.doi.org/10.1080/02626669509491435 [ Links ]
IFRC (International Federation of the Red Cross and Red Crescent Societies, Zimbabwe) (2007) Muzarabani Floods, DREF Operation No MDRZW002 GLIDE No FL-2007-000227-ZWE, December 2007. The International Federation's Disaster Relief Emergency Fund (REF). [ Links ]
JANSSEN PHM and HEUBERGER PSC (1995) Calibration of process-oriented models. Ecol. Model. 83 (1-2) 55-66. http://dx.doi.org/10.1016/0304-3800(95)00084-9 [ Links ]
KITE GW and PIETRONIRO A (1996) Remote sensing application in hydrological modeling. Hydrol. Sci. J. 41563-591. http://dx.doi.org/10.1080/02626669609491526 [ Links ]
KRAUSE P, BOYLE DP and BASE F (2005) Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 5 89-97. http://dx.doi.org/10.5194/adgeo-5-89-2005 [ Links ]
LIDÉN R, HARLIN J, KARISSON M and RAHMBERG M (2001) Hydrological modelling of fine sediments in the Odzi River, Zimbabwe. Water SA 27 (3) 303-314. http://dx.doi.org/10.4314/wsa.v27i3.4973 [ Links ]
MADAMOMBE EK (2004) Zimbabwe: Flood Management Practices - Selected Flood Prone Areas, Zambezi Basin. The Associated Programme on Flood Management, Integrated Flood Management, World Meteorological Organisation. URL: http://www.apfm.info/pdf/case_studies/cs_zimbabwe.pdf/ (Accessed 7 September 2016). [ Links ]
MAGADZA CHD (2006) Kariba Reservoir: Experience and lessons learned. Lakes & Reservoirs: Res. Manage. 11 (4) 271-286. http://dx.doi.org/10.1111/j.1440-1770.2006.00308.x [ Links ]
ODIYO JO, PHANGISA JI and MAKUNGO R (2012) Rainfall-runoff modelling for estimating Latonyanda River flow contributions to Luvuvhu River downstream of Albasini Dam. Phys. Chem. Earth, Parts A/B/C 50-52 5-13. http://dx.doi.org/10.1016/j.pce.2012.09.007 [ Links ]
SANTILLAN J, PARINGIT E, RAMOS R, MENDOZA R, ESPANOLA N and ALCONIS J (2012) Near real-time flood flood extent monitoring in Marikina River, Philippines: Model parameterization using remotely-sensed data and field measurements. In: Proceedings of the 33'd Asian Conference on Remote Sensing, ACRS 2012 - Aiming Smart Space Sensing, 26-30 November 2012, Ambassador City Jomtien Hotel, Pattaya, Thailand. [ Links ]
SCHARFFENBERG W (2015) Hydrologic Modeling System HEC-HMS User's Manual. U.S. Army Corps of Engineers, Hydrologic Engineering Center, Davis, CA. [ Links ]
SCHMUGGE TJ, KUSTAS WP, RITCHIE JC, JACKSON TJ and RANGO A (2002) Remote sensing in hydrology. Adv. Water Resour. 25 1367-1385. http://dx.doi.org/10.1016/S0309-1708(02)00065-9 [ Links ]
SHARAD KJ and SUDHEER KP (2007) Fitting of hydrologic models: A close look at the Nash- Sutcliffe Index. J. Hydrol. Eng. 13 (10) 981-986. [ Links ]
SHIH SF and CHENG KS (1989) GENERATION OF SYNTHETIC AND MISSING CLIMATIC DATA FOR PUERTO RICO1. J. Am. Water Resour. Assess. 25 (4) 829-836. http://dx.doi.org/10.1111/j.1752-1688.1989.tb05398.x [ Links ]
SILVESTRO F, GABELLANI S, DELOGU F, RUDARI R and BONI G (2013) Exploiting remote sensing land surface temperature in distributed hydrological modelling: the example of the Continuum model. Hydrol. Earth Syst. Sci. 17 39-62. http://dx.doi.org/10.5194/hess-17-39-2013 [ Links ]
SIVAPALAN M (2003) Prediction in ungauged basins: a grand challenge for theoretical hydrology. Hydrol. Process. 17 (15) 3163-3170. http://dx.doi.org/10.1002/hyp.5155 [ Links ]
SREENIVASULU V and BHASKAR PU (2010) Estimation of Catchment Characteristics using Remote Sensing and GIS Techniques International Journal of Engineering Science and Technology 2 (12) 7763-7770. [ Links ]
TUMBARE MJ (2005) The Management of the Zambezi River Basin and Kariba Dam, Bookworld Publishers, Lusaka. [ Links ]
US ARMY CORPS OF ENGINEERS (2015) Hydrologic Modeling System HEC-HMS Applications Guide. US Army Corps of Engineers, Hydrologic Engineering Center,Davis, CA. [ Links ]
US SCS (United States Department of Agriculture, Soil Conservation Service) (1986) Urban Hydrology for Small Watersheds. Technical Release No. 55. Second Edition. US SCS, Washington, D.C. [ Links ]
WALE A, RIENTJES THM, GIESKE ASM and GETACHEW HA (2009) Ungauged catchment contributions to Lake Tana's water balance. Hydrol. Process. 23 (26) 3682-3693. [ Links ]
WEISSLING BP and XIE H (2008) Proximal watershed validation of a remote sensingbased streamflow estimation model. J Appl. Remote Sens. 2 (023549). [ Links ]
WINSEMIUS HC, SCHAEFLI B, MONTANARI A and SAVENIJE HHG (2009) On the calibration of hydrological models in ungauged basins: A framework for integrating hard and soft hydrological information. Water Resour. Res. 45 (12) W12422. http://dx.doi.org/10.1029/2009wr007706 [ Links ]
Received 5 January 2016
Accepted in revised form 6 September 2016
* To whom all correspondence should be addressed. ☎+ 26 377 435-6999; e-mail: wgumindoga@gmail.com














