Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
Water SA
versión On-line ISSN 1816-7950
versión impresa ISSN 0378-4738
Water SA vol.41 no.5 Pretoria oct. 2015
http://dx.doi.org/10.4314/WSA.V41I5.01
A conceptual theoretical framework to integrally assess the possible impacts of climate change on domestic irrigation water use
Chikondi MakwizaI; Musandji FuambaII; Fadoua HoussaII; Heinz Erasmus JacobsI
IDepartment of Civil Engineering, Stellenbosch University, Private Bag X1, Matieland, 7602, South Africa
IIDepartment of Civil, Geological and Mining (CGM) Engineering, Polytechnique Montréal, Canada, 2500, Chemin de Polytechnique, Montreal, Quebec, Canada H3T 'J4
ABSTRACT
Southern Africa is likely to experience higher evapotranspiration and altered rainfall characteristics due to global warming and climate change. Climate-driven water use may potentially stress water supply facilities due to increased demand and reduced surface water yield. This paper presents a conceptual theoretical framework for assessing impacts of climate change on domestic irrigation water use. The prediction of climatic conditions that may potentially influence future water use is reviewed together with regional capacity for downscaling global climate projections. The impact assessment of water use is based on the modification and adaptation of an existing end-use model for water demand to include parameters for climate change. The Penman-Monteith equation and the soil water balance equation are incorporated for the estimation of daily water needs of vegetated areas in residential properties. The paper also discusses data requirements and a calibration procedure to improve model fit to the observed domestic irrigation water use. The proposed approach could form a basis for constructing a detailed model for planning various adaption measures relating to climate-driven domestic irrigation water use.
Keywords: climate change, outdoor water use, end-use model, irrigation water use
INTRODUCTION
Research context
Domestic water use comprises indoor and outdoor components. Water is needed outdoors mainly for garden irrigation - to water vegetation such as lawns, flowerbeds and trees. Other outdoor water uses include pool top-ups, washing of cars, washing of hard surfaces, etc.. Water may also be used for small-scale urban agriculture - to grow edible plants like herbs, fruit and vegetables. Various climatic parameters impact outdoor water use, including, for example, rainfall, evapo-transpiration and ambient temperature (Balling et al., 2008; Praskievicz and Chang, 2009; Breyer and Chang, 2014). This climatically-driven water use profile is particularly true for edible plants with seasonal growth.
Climate change has been reported to affect parameters requisite for estimating irrigation requirements (Gutzler and Nims, 2005; Balling and Cubaque, 2009), and may thus have important implications for modelling residential outdoor water use. To study the impacts of climate change on residential outdoor water use, it is vital to incorporate biophysical interrelationships pertinent to outdoor water using features. In this regard, water end-use models are more likely to produce better results compared to models that are built on aggregated water use measurements (Bennett et al., 2013). Research is still needed to estimate the impact of climate change on water use at the end-use level, thereby augmenting other existing broad-scale efforts aimed at assessing the current and future capacity of water resources to meet domestic, agricultural and environmental water requirements.
Objectives
The main objective of this paper is to present a conceptual theoretical framework for a Climate Impact Water Use (CIWU) model that would integrate climate change impacts into a residential end-use model for estimating domestic irrigation water use. The goal is to present a framework or tool that could ultimately feed into a more complex model in future to predict long-term impacts of climate change on outdoor water use. In this paper, the focus is on lawn and garden irrigation which, when present on a residential property, contributes significantly to water use (Jacobs et al., 2007).
Pricing, technological change and other socio-economic factors have also been reported to influence water use (Howe and Lineweaver, 1967; Butler and Memon, 2006). While such factors may change over time and thereby impact domestic irrigation water use, they have been disregarded in the modelling framework presented. Instead, the proposed end-use model allows for the analysis of the impact of predicted changes in climatic parameters on domestic irrigation water use of a specific residential property in a 'static environment' wherein non-climatic parameters remain constant.
Motivation
On a global scale, impacts of climate change on the water cycle are mainly manifested in the increased intensity and frequency of extreme events (Rana et al., 2014; Niang et al., 2014). The Mediterranean and southern Africa regions are generally expected to experience a significant decline in water resources due to global warming (IPCC, 2007; Niang et al., 2014). Thus, sustainable management of water resources and implementation of action plans to deal with possible water shortages require a good understanding of water end-uses and their response to climate change.
Water supply utilities are already facing pressure to maintain supply in the face of increasing water use and uncertain supply (Danilenko et al., 2010). Outdoor water use restrictions have already been applied extensively in many cities to manage water supply shocks (Atwood et al., 2007; Jacobs et al., 2007; Survis and Root, 2012). Any future increase in domestic irrigation water requirements that may be brought about by climate change could potentially further stress water resources due to increased water use, possibly combined with reduced surface water yield (Kusangaya et al., 2014). Accurate modelling of water use in the context of climate change is essential to effectively plan and implement future water management strategies.
STATE-OF-THE-ART CONCEPTS IN CLIMATE CHANGE AND WATER END-USE MODELLING
Climate change
Global warming due to increasing concentrations of greenhouse gases (GHG) in the atmosphere is expected to cause significant changes in future climate. According to the IPCC (2013), global temperatures will continue to rise given the present levels of anthropogenic GHG emissions. The direct effect of higher temperatures is increased atmospheric water demand and the intensification of the hydrological cycle. The intensification of extreme events is expected even in areas that are bound to experience decreased rainfall due to global warming, such as the Mediterranean Basin and some parts of southern Africa (Niang et al., 2014).
Global circulation models (GCMs) are widely used to generate forecasts of future climate (Dufresne, 2006; Rana, 2014; Servat, 2014; André, 2014). Prediction of future climate is a complex undertaking involving many physical, chemical and biological processes. Confidence in the application of GCMs has been growing with improved computing capabilities that have made it possible to perform numerically-intensive simulations within reasonable lengths of time. There are now a large number of GCMs available from different institutions around the world. The results of the IPCC fifth assessment, made public for potential use by the scientific research community, are based on the analysis of 27 GCMs (IPCC, 2007; IPCC, 2013). It has now become the norm to assess future climate conditions from an ensemble of GCMs in order to reduce regional and seasonal bias exhibited by individual models (Graham et al., 2011; Faramarzi et al., 2013). Table 1 provides an inventory of 16 of the most sophisticated GCMs amongst the 27 GCMs used by IPCC.
Versatile as they are, GCMs can only give valid outputs at grid scales that are essentially too coarse for most impact studies, particularly when the focus is on water use of relatively small residential neighbourhoods. Working at grid sizes larger than around 350 km2 to 450 km2, GCMs fail to capture the spatial and temporal patterns of second-order processes, for example, rainfall, with the same level of consistency as first-order atmospheric processes (Hardy, 2003). Regional downs-caling is required to bring the GCM outputs to grid scales of about 10 km2 to 50 km2. Two basic approaches are available for downscaling. The first approach, known as dynamical down-scaling, links a regional climate model (RCM) of smaller grid size to the relevant GCM. RCMs are based on similar theoretical foundations to those used in GCMs and offer results with finer spatial resolution (Rana et al., 2014). However, the scope of RCMs is limited to their regions of validity. Alternatively, statistical downscaling can be used to transfer GCM projections to the area of interest by coupling the regional and local climate through available observations. Statistical downscaling has much fewer computational requirements than dynamical downscaling but the final results will inherit any anomalies in the available data (Graham et al., 2011). According to Maraun et al. (2010), consensus between results from dynamical down-scaling and statistical downscaling is a better indicator of validity of the results.
A key issue when using future climate projections is quantifying the uncertainty inherent in the successive stages of modelling. Some climate processes are not yet well understood in terms of climate modelling. Thus, errors can be introduced into the results leading to an over- or underestimation of future climate (Schulze, 2011). The anthropogenic GHG emission scenarios used in GCMs are based on assumptions of highly unpredictable socio-economic and technological statuses of the future. The GCMs themselves comprise parameterisations that oversimplify processes of many local climate phenomena they represent. Hence it is desirable to introduce as little additional uncertainty as possible in the downscaling or sequent modelling stages.
In the African context, climate change simulations are usually carried out by using GCMs suggested by the IPCC. The severe lack of observed climate data and credible studies conducted on spatial and temporal variation of climate across Africa preclude an accurate assessment of future regional climate scenarios of most African regions (Gbesso et al., 2014; Kling et al., 2014; Rana et al., 2014). Projections of extreme weather conditions, as of the IPCC report published in 2001, were not available for wide portions of Africa due to inadequacy of data (DFID, 2004). The case in South Africa, however, seems to be different from the rest of the continent. South Africa seems to have more active participation in global climate change programmes and a wealthier literature resource of work on climate change than the rest of the continent (Ziervogel et al., 2014). International efforts are underway to develop regional climate models, especially for the southern African part. The UK Department for International Development (DFID) had supported the development of a regional climate model called ACCURATE from the Hadley Centre (DFID, 2004). CORDEX-Africa is yet another joint programme meant to increase the availability and quality of downscaled climate projections for Africa. In addition, South Africa has implemented strategic actions to better understand the implications of climate change at national level. The Climate Systems Analysis Group (CSAG) affiliated to the University of Cape Town has generated future climate scenarios on a daily scale for national and local application using five GMCs, namely, CGCM3.1, CNRM-CM3, ECHAM5/MPI-OM, GISS-ER and IPSL-CM4 (Schultze, 2011).
Residential water end-use modelling methods
Reliable water use estimates are the basis for most decisions water utilities and practitioners have to make concerning the design, operation and management of water distribution systems (Donkor et al., 2012). If water use estimates are obtained precisely at the spatial scale of individual residential properties, a marked improvement is evident in the performance of various aspects of the corresponding water supply network models (Xu and Goulter, 1998; Garcia et al., 2004; Alvisi et al., 2014). End-use modelling has been recognised to be the key to enhancing the spatial and temporal resolution of water use estimates entered as inputs into water supply network models. Water conservation studies have also demonstrated the potential of end-use models to achieve future water savings through effective implementation of bottom-up water demand management measures as a supplement to the usual top-down approaches (Macy, 1999; Mayer et al., 2003; Willis et al., 2009).
Several residential water end-use models have been proposed (Buchberger and Wu, 1995; Alvisi et al., 2003; Jacobs and Haarhoff, 2004; Garcia et al., 2004; Blokker et al., 2009; Bennett et al., 2013) since the development of technologies for effectively disaggregating metered consumption into water end uses at individual plumbing fixtures. Buchberger and Wells (1996) first showed that water use events at a residential stand can be represented by rectangular pulses characterised by their intensity, duration and frequency. Subsequently, models for simulating residential water use estimates were based on regenerating the patterns of occurrence of the pulses observed at the residential stand connection in probabilistic functions (Buchberger and Wu, 1995; Alvisi et al., 2003; Garcia et al., 2004; Blokker et al., 2009; Alvisi et al., 2014). Although the earlier stochastic end-use models, once calibrated, reproduce the water use events reasonably well, they do not hypothetically relate the simulated water usage to the inherent characteristics of the residential stand concerned. Consequently, extrapolating the simulation models in time or transferring the models to other locations demands recalibration of the model parameters using a new set of end-use data.
The residential end-use model (REUM), however, was developed to estimate water use from parameters that define characteristics of the respective water-using fixtures (Jacobs and Haarrhoff, 2004). Multiple facets of residential water use were addressed in REUM, namely, indoor water use, outdoor water use, hot water use and wastewater flow. REUM was formulated to produce monthly averaged outputs from inputs of typical parameter values. Scheepers and Jacobs (2014) later increased the indoor model complexity by describing all indoor parameters stochastically and modifying this model component to output hourly water-use estimates.
The cost associated with collecting and processing end-use data is perhaps the major challenge to the application of stochastic water end-use models. Blokker et al. (2009) demonstrated in the Simulation of Demand and End-Use Model (SIMDEUM) that water use events can alternatively be generated from parameters derived from household characteristics of the residential stands. The advantage of SIMDEUM is that it avoids expensive data-logging exercises by utilizing household characteristics model inputs derived primarily from household survey data. SIMDEUM, however, does not consider parameters for outdoor water use and may therefore not perform equally well where outdoor water use features are dominant. Generally, the more versatile residential water end-use models remain confined to indoor water end uses.
The outdoor water use model proposed by Jacobs and Haarhoff (2004) estimated outdoor water consumption from pan evaporation and rainfall. A similar formulation was adopted by DeOreo et al. (2011) for estimating outdoor water use in an end-use study in California. Later work by Du Plessis and Jacobs (2014) applied the outdoor demand component of REUM to residential estates in South Africa. Unlike the original model, Du Plessis and Jacobs (2014) used separate parameters to model evapotranspiration from plant surfaces and evaporation from open water surfaces. In each case, outdoor water use was assumed to essentially result from replenishing of water lost from evaporating surfaces. Outdoor consumption was deduced from monthly averaged pan evaporation and effective rainfall data but temperature, which is an important component in climate projections, was not included. Pan evaporation is also known to be sensitive to local conditions and requires application of carefully chosen pan coefficients (Sumner and Jacobs, 2005).
The estimation of outdoor water use is a fundamental issue in modelling residential water demand in southern Africa. One factor that makes outdoor water demand modelling problematic is the large variation observed between seasons and geographical locations. Correlating water use estimates and measured consumption is further complicated by uncertain behavioural responses of consumers to landscape water needs (Du Plessis and Jacobs, 2014). Considerable variability in outdoor consumption often occurs amongst residential stands of similar characteristics (Jacobs and Fair, 2012). Nevertheless, there is a close association between residential water use and stand area (Jacobs et al., 2004; Van Zyl et al., 2008; Griffioen and Van Zyl, 2014).
ADAPTED DOMESTIC IRRIGATION WATER END-USE MODEL
Model development
The concept of the proposed CIWU model builds on the REUM outdoor demand model (Jacobs and Haarhoff, 2004) and extends the underlying concepts to include basic weather variables for the study of the impact of climate change on domestic irrigation water use. A set of equations for evapotranspiration and soil water balance were built into CIWU and used to model domestic irrigation water requirements on a daily time-step, in a similar manner to crop water use modelling in case studies by Kuo and Liu (2003) and Smith et al. (2012). A calibration scheme using end-use data is suggested for adjusting model parameters to attain best fit to the observed water use while fine-tuning the model to show good agreement with the incidence of irrigation water use events. Notable climate-driven outdoor water uses are pool filling, lawn irrigation and garden irrigation. Other residential water uses located outdoors may also be indirectly influenced by climatic factors and therefore portray seasonal patterns, for example, pool top-ups, car washing etc. The focus in the CIWU model, however, is on domestic irrigation water use. Therefore the other outdoor water end uses have not been included in the conceptual model presented. The resulting calibrated model is expected to give satisfactory outdoor water use estimates in areas where lawn and garden irrigation are predominant.
Estimation of daily domestic irrigation water needs
Modelling of domestic irrigation water use relies on conceptualizing atmospheric water demand and soil-plant-water interrelationships. Water applied to the landscape is normally lost into the atmosphere through evapotranspiration from the soil and plant surfaces. Atmospheric water demand is defined as water loss from a hypothetical crop growing in non-limiting conditions, conventionally referred to as reference crop evapotranspiration (Allen et al., 1998). Several methods exist for estimating reference crop evapotranspiration, each with unique advantages. The Hargreaves method, for example, models reference crop evapotranspiration accurately enough in certain regions from temperature data alone (Jensen et al., 1997). The Penman-Monteith method is chosen here because it has been shown to perform more consistently in different geographical regions than other methods (Sumner and Jacobs, 2005; Benli et al., 2010). According to Allen et al. (1998), reference crop evapotranspiration is given by:
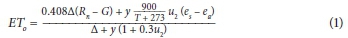
where:
ETois the reference evapotranspiration (mm/d)
Rnis the net radiation at the crop surface (MJ/m2-d)
G is the soil heat flux density (MJ/m2-d)
T is the mean daily air temperature at 2 m height (°C)
u2is the wind speed at 2 m height (m/s)
esis the saturation vapour pressure (kPa)
eais the actual vapour pressure (kPa)
A is the slope of the saturation vapour pressure curve at temperature T (kPa/°C)
g is the psychrometric constant (kPa/°C)
Crop evapotranspiration, ETc, is related to daily reference crop evapotranspiration by

where:
Kcis a crop coefficient
Ksis a reduction factor dependent on amount of water left in the soil
Some garden plants are seasonal and their crop coefficients vary within the year. The crop coefficient at each growth stage can be expressed as follows (Allen et al., 1998):
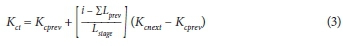
where:
i is the day number within the growing season
K c i is the crop coefficient on day i
Lstage is the length of the stage under consideration
Ʃ(Lstage) is the sum of the lengths of all previous stages
The reduction factor, Ks, is given by:

where:
Ksis the reduction factor dependent on available soil water
Dris the root zone depletion in mm
TAW is the total available soil moisture in the root zone in mm p is the fraction of TAW that a crop can extract from the root zone without suffering water stress.
Incorporating the soil water balance equation
Hypothetically, irrigation takes place to refill the root zone when a given fraction of the available water, p, has been depleted. The amount of water applied at a given event is assumed to be equal to the depth necessary to bring the soil moisture to field capacity. For a plant with an effective root zone, Zr(measured in mm), the total available water (TAW) at field capacity is:
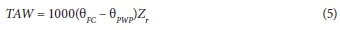
where:
0fc is the moisture content at field capacity
0PWP is the moisture content at permanent wilting point
The water stored in the soil at any time is tracked by maintaining a soil-water balance at a daily time-step (Kuo and Liu, 2003; Davis and Dukes, 2010) instead of monthly averages used in REUM. Groundwater contribution and effective rainfall are the two inputs of the water balance equation that are particularly difficult to measure or estimate. Since the water table is usually below 1 m in residential neighbourhoods, its effect on the root zone will be negligible. At a daily time-step, it is reasonable to assume that effective rainfall is limited to the amount that fills up the root zone (Davis and Dukes, 2010). Any rainfall in excess of this amount is assumed to be lost as runoff or deep percolation. The irrigation water use is given by the following simplified form of the soil-water balance equation:
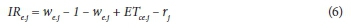
where:
IR is the net irrigation requirement
ETcis the crop evapotranspiration
r is effective rainfall
w is soil moisture depletion in the soil at a given time subscripts e and j denote end use and day of the year, respectively
The landscape is assumed to be divided into areas comprising plants of similar water use characteristics. Once suitable parameter values have been estimated for each type of feature, the landscape water use can be computed from the daily water requirement of each peculiar plant area. For any given period, n, the outdoor water use, is calculated from the summation of values of the irrigation requirement, IR, obtained at each time-step. Unlike monthly averaged water use estimates in REUM (Jacobs and Haarhoff, 2004), the monthly domestic irrigation usage is derived from the summation of the daily irrigation requirements as:
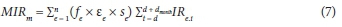
where:
MIR is the estimated monthly outdoor water use
ε represents the efficiency of the irrigation system
f relates to over-irrigation and under-irrigation
s is the surface area of the vegetation type
IR is the irrigation requirement
d is the number of days in the month
n is the number of types of vegetated surfaces
subscripts m and e denotes month and outdoor end use respectively.
Data requirements
As outdoor water use is estimated from outdoor water-using features, the presence and characteristics of the various features need to be determined as accurately as possible for the location of interest. End-use models typically have huge data requirements at their development stages. Populating parameters for each determinant of the domestic irrigation water use model requires, at minimum, data that describes the weather, the characteristics of landscape features and calendars of seasonal garden activities.
Weather data plays a central role in simulating atmospheric water demand. In some regions, acquiring weather data may not be a straightforward task. The model may not be effectively applied in regions where weather data of satisfactory quality is not available. The common issues are sparse networks of weather stations, or stations reporting only a subset of the desired weather variables or in some cases extended periods of missing values. The increased availability of automated weather stations, most of which are capable of continuous and remote data acquisition, is expected to help overcome these challenges.
Data required to populate parameters that characterise vegetated surfaces, including the cropping patterns of seasonal plants, can be sourced through household surveys, fixture audits and the use of geographical information systems (GIS). A number of case studies have demonstrated that landscape features can be demarcated, characterised and measured using aerial photographs or high-resolution satellite images (Mayer et al., 1999; Du Plessis and Jacobs, 2014; Hof and Wolf, 2014). DeOreo et al. (2011) have shown that the latter approach yields better results than measurements provided by survey respondents. For effective model calibration, a corresponding data set of actual irrigation water use is necessary.
Model calibration
Calibration is necessary to ensure that the irrigation water use model reproduces observed values reasonably well under the given climatic conditions. Some of the model biophysical parameters cannot be determined directly without elaborate laboratory analyses or experimentation. Soil properties in particular can be expensive and time consuming to measure. Even if the measurements were carried out, it is unlikely that the scale would be representative of the heterogeneity of the landscapes in all the neighbourhoods concerned (Wagener and Wheater, 2006). In addition, suitable over- and under-irrigation factors need to be identified considering the end users would not apply the exact amounts of water required by the plants. Likewise, the root zone depletion levels need to correspond with the end-user water application intervals. Similar challenges in parameter estimation are addressed through calibration in other water-related applications. Numerous case studies that utilise parametric calibration have been published in water distribution network modelling (Madsen, 2000; Van Vuuren, 2002; Van Dijk et al., 2008), rainfall-runoff modelling (Ndiritu and Daniell, 1999) of watersheds, etc. The calibration process involves the systematic adjustment of parameter values to achieve good agreement between model outputs and the observed values. The parameter values have to be maintained within their acceptable ranges, based on physical and mathematical constraints, while the model performance is evaluated by an objective function until an optima is reached. A common optimisation scheme is to minimise the sum of squares of deviations between simulated water use and observed consumption.
If end-use data is available, optimisation can focus on multiple facets of the observed outdoor water end uses. One such strategy would be to minimise the sums of squares of the total volumetric water use as well as the observed frequencies of water application events. The benefit realised from using the second objective function is that the final model will generate water application events that reflect the frequency of water application of the consumers. The use of multiple objectives on the other hand leads to computational complexity. The solution may not be a straightforward set of parameters but pareto-optimal solutions encapsulating the entire range of the feasible parameter values (Madsen, 2000). Solving the optimisation problem requires choice of an appropriate algorithm. The two broad classes are local and global optimisation algorithms (Duan et al., 1992). Global optimisation algorithms have the advantage of avoiding local minima by examining the entire search space to arrive at a global minima or maxima. Genetic algorithms are quite popular for solving global optimisation problems because of their simplicity, which nonetheless comes at the expense of processing time and computing resources (Koppel and Vassiljev, 2009).
INTEGRATING CLIMATE CHANGE IMPACTS INTO THE DOMESTIC IRRIGATION WATER-USE MODEL
The irrigation water end-use model, once properly calibrated to suit a given location, provides the means to assess potential impacts of future climatic conditions on irrigation water use in that location. Figure 1 shows a schematic of the CIWU modelling framework. Potential future water use is evaluated by inputting weather data sets generated from projections of climate models for a selected climate change scenario. It is then possible to make comparisons of the prevalent water use with the projected usage for selected future climate scenarios. The sensitivity of irrigation water use to geographical characteristics implies downscaling to smaller spatial scales applicable to cities.
The proposed CIWU model is a potential tool for planning of various adaptation measures under climate change relating to domestic irrigation water use. Several options for managing domestic irrigation water use are viable. The choice of the actual measures to implement would consider the savings attained by checking water use estimates predicted by the model as an appropriate variable is adjusted over its feasible range. For example, xeriscaping can be reflected in the model by reducing the size of irrigated areas in the model. Introduction of irrigation equipment that reduces water losses means a higher value of irrigation efficient becomes applicable in the model. A smaller crop coefficient would be used to represent a change to drought-tolerant landscaping plants.
CONCLUSIONS
This paper has discussed an integrated modelling approach for assessing impacts of climate change on domestic irrigation water use. Modifications to REUM outdoor water demand model associated with climatic parameters have been presented. The Penman-Monteith equation has been introduced into REUM for calculating potential evapotranspiration in the place of pan evaporation. The modified model is formulated to simulate water use at daily time-steps by maintaining a soil-moisture balance of the root zone. Weather data and information on landscape characteristics are the required inputs, whereas measured irrigation water use data is necessary for calibration. Calibration is required to select optimal values of some biophysical parameters which cannot be measured directly in a practical manner. Coupled with future climate projections from GCMs and relevant GHG emission scenarios, the proposed CIWU model can allow the quantification of uncertainty in the simulation of future domestic irrigation water use. The theoretical framework presented provides a potential tool for planning of various adaptation measures relating to climate-driven domestic irrigation water use.
ACKNOWLEDGEMENTS
The authors acknowledge the provision of funds made available through the Association of Universities and Colleges of Canada for the purpose of funding the project 'Expected Changes in Domestic Water Use in the Climate Change Context: Case of Southern Africa' as part of its funding of the Canada-Africa Research Exchange Grants.
REFERENCES
ALLEN RG, PEREIRA LS, RAES D and SMITH M (1998) Crop evapotranspiration. Guidelines for computing crop water requirements. FAO Irrigation and Drainage Paper No. 56. FAO, Rome. 300 pp. [ Links ]
ALVISI S, ANSALONI N, and FRANCHINI M (2014) Generation of synthetic water demand time series at different temporal and spatial aggregation levels. Urban Water J. 11 (4) 297-310. [ Links ]
ALVISI S, FRANCHINI M and MARINELLI A (2003) A stochastic model for representing drinking water demand at residential level. Water Resour. Manage. 17 (3) 197-222. [ Links ]
ANDRE JC (2014) Supercomputers and climate simulation: what vision for 2020? J. Meteorol. 84 49-53. [ Links ]
ATWOOD C, KREUTZWISER R and DE LOE R (2007) Residents' assessment of an urban outdoor water conservation program in Guelph, Ontario. J. Am. Water Resour. Assoc. 43 (2) 427-439. [ Links ]
BALLING RC and CUBAQUE HC (2009) Estimating future residential water consumption in Phoenix, Arizona based on simulated changes in climate. Phys. Geogr. 30 (4) 308-323. [ Links ]
BALLING RC, GOBER P and JONES N (2008) Sensitivity of residential water consumption to variations in climate: An intraurban analysis of Phoenix, Arizona. Water Resour. Res. 44 (10). [ Links ]
BENLI B, BRUGGEMAN A, OWEIS T and ÜSTÜN H (2010) Performance of Penman-Monteith FAO56 in a semiarid highland environment. J. Irrig. Drain. Eng. 136 (11) 757-765. [ Links ]
BENNETT C, STEWART RA and BEAL CD (2013) ANN-based residential water end-use demand forecasting model. Expert Syst. Appl. 40 1014-1023. [ Links ]
BLOKKER E, VREEBURG J and VAN DIJK J (2009) Simulating residential water demand with a stochastic end-use model. J. Water Resour. Plann. Manage. 136 (1) 19-26. [ Links ]
BREYER B and CHANG H (2014) Urban water consumption and weather variation in the Portland, Oregon metropolitan area. Urban Clim. 9 1-18. [ Links ]
BUCHBERGER S and WELLS G (1996) Intensity, duration, and frequency of residential water demands. J. Water Resour. Plann. Manage. 122 (1) 11-19. [ Links ]
BUCHBERGER S and WU L (1995) Model for instantaneous residential water demands. J. Hydraul. Eng. 121 (3) 232-246. [ Links ]
BUTLER D and MEMON FA (2006) Water Demand Management. IWA Publishing, London. [ Links ]
DANILENKO A, DICKSON E and JACOBSEN M (2010) Climate change and urban water utilities: challenges and opportunities. Water Working Notes No 24, Water Sector Board, Sustainable Development Network. World Bank, Washington DC. [ Links ]
DEOREO WB, MAYER PW, MARTIEN L, HAYDEN M, FUNK A, KRAMER- M, DAVIS R, HENDERSON J, RAUCHER B, GLEICK P and HEBERGER M (2011) California single family water use efficiency study. Report prepared for the California Dept. of Water Resources, Aquacraft Inc., Boulder, CO. 391 pp. [ Links ]
DFID (2004) Key sheet 7. Adaptation to climate change: The right information can help the poor to cope. URL: http://www.eldis.org/vfile/upload/1/document/0708/DOC15871.pdf (Accessed 18 August 2015). [ Links ]
DONKOR E, MAZZUCHI T, SOYER R and ALAN ROBERSON J (2012) Urban water demand forecasting: review of methods and models. J. Water Resour. Plann. Manage. 140 (2) 146-159. [ Links ]
DAVIS SL and DUKES MD (2010) Irrigation scheduling performance by evapotranspiration-based controllers. Agric. Water Manage. 98 (1) 19-28. [ Links ]
DU PLESSIS JL and JACOBS HE (2014) Model for estimating domestic outdoor water demand of properties in residential estates. 16th Water Distribution System Analysis Conference (WDSA 2014): Urban Hydroinformatics and Strategic Planning, 14-17 July 2014, Bari, Italy. Procedia Eng. 89 967- 974. [ Links ]
DUAN Q, SOROOSHIAN S and GUPTA VK (1992) Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res. 28 (4) 1015-1031. [ Links ]
DUFRESNE JL, SALAS Y MELIA D, DENVIL S, TYTECA S, ARZEL O, BONY S, BRACONNOT P, BROCKMANN P, CADULE P and CAUBEL A (2006) Simulation of recent and future climate using the CNRM and IPSL models. J. Meteorol. 55 45-59. [ Links ]
FARAMARZI M, ABBASPOUR KC, ASHRAF VAGHEFI S, FARZANEH MR, ZEHNDER AJB, SRINIVASAN R and YANG H (2013) Modeling impacts of climate change on freshwater availability in Africa. J. Hydrol. 480 85-101. [ Links ]
GARCIA VJ, GARCIA-BARTUAL R, CABRERA EM, ARREGUI F and GARCIA-SERRA J (2004) Stochastic model to evaluate residential water demands. J. Water Resour. Plann. Manage. 130 (5) 386-394. [ Links ]
GBESSO FHG, TENTE BHA, GOUWAKINNOU G and SINSIN BA (2014). Influence des changements climatiques sur la distribution géographique de Chrysophyllum albidum G. Don (Sapotaceae) au Benin. Int. J. Biol. Chem. Sci. 7 (5) 2007-2018. [ Links ]
GRAHAM LP, ANDERSSON L, HORAN M, KUNZ R, LUMSDEN T, SCHULZE R, WARBURTON M, WILK J and YANG W (2011) Using multiple climate projections for assessing hydrological response to climate change in the Thukela River Basin, South Africa. Phys. Chem. Earth Parts A/B/C. 36 (14-15) 727-735. [ Links ]
GRIFFIOEN ML and VAN ZYL JE (2014) Proposed guideline for modelling water demand by suburb. J. S. Afr. Inst. Civ. Eng. 56 (1) 63-68. [ Links ]
GUTZLER DS and NIMS JS (2005) Interannual variability of water demand and summer climate in Albuquerque, New Mexico. J. Appl. Meteorol. 44 (12) 1777-1787. [ Links ]
HARDY JT (2003) Climate Change: Causes, Effects, and Solutions. John Wiley & Sons, Chichester. 247 pp. [ Links ]
HOF A and WOLF N (2014) Estimating potential outdoor water consumption in private urban landscapes by coupling high-resolution image analysis, irrigation water needs and evaporation estimation in Spain. Landsc. Urban Plann. 123 61-72. [ Links ]
HOWE CW and LINEWEAVER FP (1967) The impact of price on residential water demand and its relation to system design and price structure. Water Resour. Res. 3 13-32. [ Links ]
IPCC (2013) Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Stocker FT, Qin D, Plattner G, Tignor MMB, Allen SK, Boschung J, Nauels A, Xia Y, Bex V, Pauline PM and Midgley PM (eds)]. Cambridge University Press, Cambridge and New York. 1 535 pp. [ Links ]
IPCC (2007) Climate Change 2007: Synthesis Report. Contribution of Working Groups I, II and III to the Fourth Assessement Report of the Intergovernmental Panel on Climate Change [Pachauri RK and Reisinger A (eds)]. IPCC, Geneva. 104 pp. [ Links ]
JACOBS HE, GEUSTYN L, FAIR KA, DANIELS J and DU PLESSUIS K (2007) Analysis of water savings: A case study during the 2004/05 water restrictions in Cape Town. J. S. Afr. Inst. Civ. Eng. 49 (3) 16-26. [ Links ]
JACOBS HE and HAARHOFF J (2004) Structure and data requirements of an end-use model for residential water demand and return flow. Water SA 30 (3) 293-304. [ Links ]
JACOBS HE, GEUSTYN LC, LOUBSER EBF and VAN DER MERWE B (2004) Estimating residential water demand in southern Africa. J. S. Afr. Inst. Civ. Eng. 46 (4) 2-13. [ Links ]
JACOBS HE and FAIR KA (2012) A tool to increase information-processing capacity for consumer water meter data. S. Afr. J. Inf. Manage. 14 (1) 7 pp. DOI: 10.4102/sajim.v14i1.500. [ Links ]
JENSEN DT, HARGREAVES GH, TEMESGEN B and ALLEN RG (1997) Computation of ETo under nonideal conditions. J. Irrig. Drain. Eng. 123 (5) 394-400. [ Links ]
KLING H, STANZEL P and PREISHUBER M (2014) Impact modelling of water resources development and climate scenarios on Zambezi River discharge. J. Hydrol.: Regional Studies 1 17-43. [ Links ]
KOPPEL T and VASSILJEV A (2009) Calibration of a model of an operational water distribution system containing pipes of different age. Adv. Eng. Softw. 40 (8) 659-664. [ Links ]
KUO S-F and LIU C-W (2003) Simulation and optimization model for irrigation planning and management. Hydrol. Process. 17 (15) 3141-3159. [ Links ]
KUSANGAYA S, WARBURTON ML, ARCHER VAN GARDEREN E and JEWITT GPW (2014) Impacts of climate change on water resources in southern Africa: A review. Phys. Chem. Earth, Parts A/B/C. 67-69 47-54. [ Links ]
MACY P (1999) Urban water demand management in Southern Africa: the conservation potential. SIDA Publications on Water Resources No. 13. SIDA, Harare. 52 pp. [ Links ]
MADSEN H (2000) Automatic calibration of a conceptual rainfall-runoff model using multiple objectives. J. Hydrol. 235 (3/4) 276-288. [ Links ]
MARAUN D, WETTERHALL F, IRESON AM, CHANDLER RE, KENDON EJ, WIDMANN M, BRIENEN S, RUST HW, SAUTER T, THEMESS M, VENEMA VKC, CHUN KP, GOODESS CM, JONES RG, ONOF C, VRAC M and THIELE-EICH I (2010) Precipitation downscaling under climate change: Recent developments to bridge the gap between dynamical models and the end user. Rev. Geophys. 48 (3) RG3003. [ Links ]
MAYER PW, DEOREO WB, OPITZ EM, KIEFER JC, DAVIS WY, DZIEGIELEWSKI B and NELSON JO (1999) Residential End Uses of Water. AWWA Research Foundation and American Water Works Association, University of Michigan. 310 pp. [ Links ]
MAYER PW, DEOREO WB, TOWLER E and LEWIS D (2003) Residential indoor water conservation study: evaluation of high efficiency indoor plumbing fixture retrofits in single-family homes in the East Bay Municipal Utility District Service Area. Boulder, Colorado. Prepared for and submitted to East Bay Municipal Utility District and the United States Environmental Protection Agency. Aquacraft Inc. Water Engineering and Management, Boulder, Colorado. [ Links ]
NDIRITU J and DANIELL T (1999) Assessing model calibration adequacy via global optimization. Water SA 25 (3) 317-326. [ Links ]
NIANG I, RUPPEL OC, ABDRABO MA, ESSEL A, LENNARD C, PADGHAM J and URQUHART P (2014) Africa. In: Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part B: Regional Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change [Barros VR, Field CB, Dokken DJ, Mastrandrea MD, Mach KJ, Bilir TE, Chatterjee M, Ebi KL, Estrada YO, Genova RC, Girma B, Kissel ES, Levy AN, MacCracken S, Mastrandrea PR and White LL (eds.)]. Cambridge University Press, Cambridge and New York. 1199-1265. [ Links ]
PRASKIEVICZ S and CHANG H (2009) Identifying the relationships between urban water consumption and weather variables in Seoul, Korea. Phys. Geogr. 30 (4) 324-337. [ Links ]
RANA A, FOSTER K, BOSSHARD T, OLSSON J and BENGTSSON L (2014) Impact of climate change on rainfall over Mumbai using Distribution-based Scaling of Global Climate Model projections. J. Hydrol.: Regional Studies 1 107-128. [ Links ]
SCHEEPERS HM and JACOBS HE (2014) Simulating residential indoor water demand by means of a probability based end-use model. J. Water Supply Res. Technol. 63 (6) 476-488. [ Links ]
SCHULZE RE (2011) Climate Change and the South African Water Sector: Setting the Scene on a 2011 Perspective. In: Schulze RE (ed.) A 2011 Perspective on Climate Change and the South African Water Sector. WRC Report No. TT 518/12, Chapter 1.1, 3-6. Water Research Commission, Pretoria. [ Links ]
SERVAT E, ARDOIN-BARDIN S, PATUREL JE, DEZETTER A and GIL M (2014). Climate models and possible evolution of pluviom-etry in the Medditerranean basin. J. LJEE (9&10) 14-25. [ Links ]
SMITH PC, CALANCA P and FUHRE J (2012) A Simple scheme for modeling irrigation water requirements at the regional scale applied to an Alpine River Catchment. Water 4 (4) 869-886. [ Links ]
SUMNER DM and JACOBS JM (2005) Utility of Penman-Monteith, Priestley-Taylor, reference evapotranspiration, and pan evaporation methods to estimate pasture evapotranspiration. J. Hydrol. 308 (1-4) 81-104. [ Links ]
SURVIS FD and ROOT TL (2012) Evaluating the effectiveness of water restrictions: A case study from Southeast Florida. J. Environ. Manage. 112 377-383. [ Links ]
VAN DIJK M, VAN VUUREN S and VAN ZYL J (2008) Optimising water distribution systems using a weighted penalty in a genetic algorithm. Water SA 34 (5) 537-548. [ Links ]
VAN VUUREN S (2002) Application of genetic algorithms -Determination of the optimal pipe diameters. Water SA 28 (2) 217-226. [ Links ]
VAN ZYL HJ, ILEMOBADE AA and VAN ZYL JE (2008) An improved area-based guideline for domestic water demand estimation in South Africa. Water SA 34 (3) 381-391. [ Links ]
WAGENER T and WHEATER HS (2006) Parameter estimation and regionalization for continuous rainfall-runoff models including uncertainty. J. Hydrol. 320 (1-2) 132-154. [ Links ]
WILLIS R, STEWART RA, PANUWATWANICH K, CAPATI B and GIURCO D (2009) Gold Coast domestic water end use study. Water J. Aust. Water Assoc. 36 (6) 79-85. [ Links ]
XU C and GOULTER I (1998) Probabilistic model for water distribution reliability. J. Water Resour. Plann. Manage. 124 (4) 218-228. [ Links ]
ZIERVOGEL G, NEW M, ARCHER VAN GARDEREN E, MIDGLEY G, TAYLOR A, HAMANN R, STUART-HILL S, MYERS J and WARBURTON M (2014) Climate change impacts and adaptation in South Africa. Wiley Interdiscip. Rev. Clim. Change 5 (5) 605-620. [ Links ]
Received: 23 October 2014
Accepted in revised form 17 August 2015
* To whom all correspondence should be addressed. 514 340-4711 ext. 4813; e-mail: musandji.fuamba@polymtl.ca














