Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Water SA
On-line version ISSN 1816-7950
Print version ISSN 0378-4738
Water SA vol.41 n.3 Pretoria Apr. 2015
http://dx.doi.org/10.4314/wsa.v41i3.10
Evaluation of an automated struvite reactor to recover phosphorus from source-separated urine collected at urine diversion toilets in eThekwini
Maximilian GP Grau; Sara L Rhoton; Chris J Brouckaert*; Chris A Buckley
Pollution Research Group, School of Chemical Engineering, University of KwaZulu-Natal, Durban 4041, South Africa
ABSTRACT
In the present study we attempted to develop a reactor system to recover phosphorus by struvite precipitation, and which can be installed anywhere in the field without access to a laboratory. A reactor was developed that can run fully automated and recover up to 93% of total phosphorus (total P). Turbidity and conductivity signals were investigated as automation proxies for magnesium dosage, thus making laboratory phosphate measurements to determine the exact magnesium dosage unnecessary. Conductivity is highly influenced by the dosing parameters (molarity and pump speed) and turbidity is affected by particle size distribution issues. Algorithms based on both conductivity and turbidity signals were not able to detect the precipitation endpoint in real time. However it proved possible to identify the endpoint retrospectively from the conductivity signal, and thereafter to dose an algorithm-calculated volume of urine to use up the excess magnesium dosed.
Keywords: struvite precipitation, human urine, turbidity, conductivity, automation, magnesium dose, VUNA
INTRODUCTION
Worldwide, 2.5 billion people lack access to improved sanitation, leading to waterborne diseases (UNICEF and WHO, 2012). In many countries water scarcity makes a waterborne sanitation solution nearly impossible. Thus dry sanitation systems, such as urine diversion dehydration toilets (UDDT), have been implemented in many cases to overcome the sanitation backlog. One example is the eThekwini Municipality where over 75 000 UDDT have been installed in the rural and peri-urban areas (Roma et al., 2011). The advantage of a UDDT is source separation of the urine from the faeces (Tilley et al., 2008). Source-separated human urine is an ideal source for fertilizer production, as the majority of nutrients found in wastewater streams originate from urine (Larsen et al., 1996). One way to extract nutrients from stored urine is by adding soluble magnesium to recover phosphate by precipitating struvite (magnesium ammonium phosphate hexahydrate; MgNH4PO4∙6H2O) (Tilley et al., 2008). This can be done in industrial processes such as OSTARA or Multiform Harvest. An important factor for struvite recovery in a reactor is the magnesium source itself, as it has an effect on operating costs (Etter et al., 2011). Low-cost magnesium sources have been widely studied, and include bittern, magnesite and seawater (Ye et al., 2011; Etter et al., 2011; Sakthivel et al., 2012; Dai et al., 2014). However, accurate dosage in a struvite reactor is problematic. Chemical analysis has to be undertaken to measure phosphate concentration beforehand and the right overdosage with magnesium has to be determined experimentally to reach maximum phosphate recovery. To overcome this, on the one hand, other methods, such as electrical conductivity, have been tested to estimate phosphate concentrations by correlation to measurements (Etter et al., 2011), with attempts to develop an automated feedback control system (Shepherd et al., 2009). On the other hand, turbidity has been successfully used to analyse the struvite crystallization kinetics in urine (Triger et al., 2012). However, no known method exists, to the authors' knowledge, to dose magnesium accurately in a struvite reactor without prior phosphate measurement of the urine.
In the present study, the aim was to develop a fully-automated struvite reactor that incorporates an automated feedback control system to determine the magnesium dosage rate and time, given a certain molarity of dosing solution. Electrical conductivity and turbidity were investigated for this purpose.
MATERIALS AND METHODS
Urine source
Urine was collected at UDDTs of around 700 households in the rural and peri-urban areas of eThekwini, KwaZulu-Natal, South Africa. Plastic containers (25 ℓ) were connected to the urine pipe on the back of the toilet and brought to storage tanks. Collection was done by staff of the eThekwini Municipality Water and Sanitation unit at regular intervals. The collected urine was transported to a central collection point at Newlands Research Site with a total storage capacity of around 15 000 ℓ and brought to storage tanks (2 200 ℓ) at the university, close to the laboratory used for reactor trials. Storage time was at least 1 month.
Urine analysis
Prior to analysis, urine was filtered using a glass-fibre filter with an average pore size of 0.4 µm (Machery-Nagel, Düren, Germany) and diluted with distilled water. Dissolved phosphate in the stored urine was measured using a Merck NOVA 60 spectrophotometer (Ammonium molybdate spectrometric method, Merck, Darmstadt, Germany). Total phosphate was measured using Merck test kits without filtering.
Struvite precipitation model
An ionic speciation model was developed to predict conductivity and suspended solids, which are further interpreted as turbidity, during struvite precipitation. The model describes aqueous ionic reactions using an algebraic equilibrium speciation and electrical conductivity model. The speciation model was the same as that described by Westergreen et al. (2013) and is included in the plant-wide wastewater treatment model of Ikumi et al. (2014). To this was added a kinetic formulation of struvite precipitation driven by supersaturation, based on Ronteltap et al. (2007). Conductivity was calculated from the speciated ionic composition using a model similar to that of McCleskey et al. (2012). This involves a sum of contributions from each charged species calculated at infinite dilution, plus a correction term for ionic strength. An empirical correction term was used, which was calibrated on a series of made-up solutions, based on a recipe for synthetic urine (Wilsenach et al., 2007). The model was used to guide the experiments on the reactor. The form of the expression for the rate of precipitation followed that of Koutsoukos et al. (1980). The empirical constant in this expression was adjusted to fit the experimental conductivity curves, giving rate constants of between 10 and 15 h-1 depending on the magnesium concentration, and similar to the results of Le Corre et al. (2007).
Struvite reactor
A stirred batch reactor (volume of 50 ℓ) made of PVC was set up as shown in Fig. 1. Urine supply and magnesium dosing pumps, an overhead stirrer and the air-actuated ball valve are fully automated using a National Instruments control system (compact RIO-9075 system; National Instruments, Austin, Texas, USA). Level sensors (Model KQ6001; IFM, Essen, Germany) were attached to the level meter on the reactor wall and the filter housing and were used to indicate the filling level and measure filtration times.
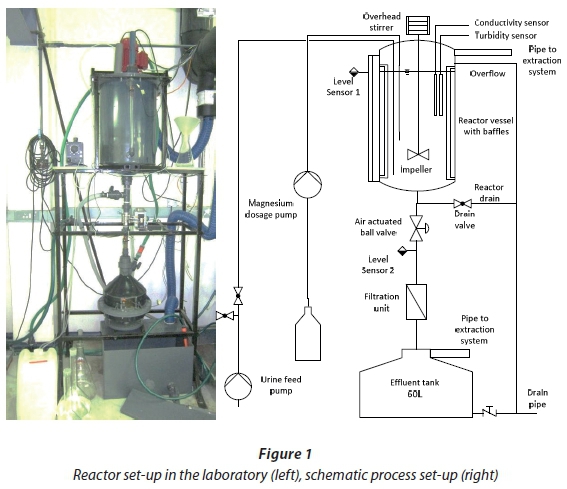
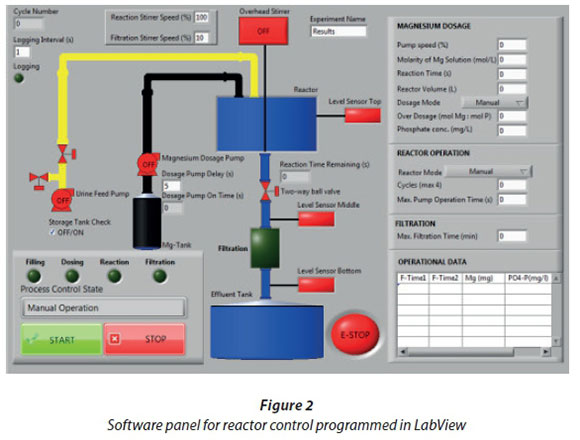
Reactor sequence control logic was used in these tests to automate fill, mix, dose, react, and drain to filter. The software control panel has been programmed using LabView (National Instruments, Austin, Texas, USA). A view of the software control panel is shown in Fig. 2. Industrial conductivity (Model D3727E2T; Hach, Loveland, Colorado, USA) and turbidity (Solitax HS-Line; Hach, Loveland, Colorado, USA) sensors connected to a transmitter (SC200; Hach, Loveland, Colorado, USA) were submersed from the top into the reactor to measure both parameters online. Data were collected from each process sequence for analysis that included reaction time, turbidity, conductivity, dosing pump status, and filter time. Industrial grade MgCl2 and BP grade MgSO4 were used to initiate the precipitation reaction. Struvite crystals were filtered from the liquid using cotton fibre discs, about 1 mm thick, placed in between PVC flanges in the filtration unit at the bottom. The reactor vessel and effluent tank were connected to an extraction system to reduce odour. For estimation of the reactor performance magnesium was added in a molar ratio of 1.1:1 (mol Mg : mol P). To calculate the theoretical endpoint for the struvite precipitation against which to compare the automated algorithm determined endpoint, at least two laboratory Total P (TP) measurements of the feed urine were taken and the required dose of magnesium calculated using a molar ratio of 1:1 (mol Mg : mol P).
Dosing experiments and algorithm
To investigate the potential of using turbidity and conductivity for endpoint determination, magnesium was dosed in different ways. In the first experiments the dosing pump was run continuously, adding a constant rate of magnesium into the reactor. In further experiments the dosing pump was switched on and off at intervals. Different dosing parameters, i.e., molarities and dosing rates, were studied in both operation modes of the dosing pump. An algorithm to detect the endpoint was developed. It calculates two 10-point moving averages one time-step (10 s) apart and determines the slope between these values. Two adjustable threshold slope values were implemented. The first detects and neglects the change of signal after dosing start. The second aims to detect the endpoint. The dosing pump switches off when the slope value is less than the second threshold value.
RESULTS AND DISCUSSION
Urine source
The long storage time in the containers guarantees full hydrolysis of the urine, converting the urea into ammonia and leading to a high pH. The measured pH was around 8.9, which is in the ideal range for effective struvite precipitation (Munch and Barr, 2001). The average phosphate concentration in the storage tank at the university was 242 ± 14 mg P/ℓ. The phosphorus content was typical of the urine collected from various areas in eThekwini (125 to 350 mg P/ℓ).
Reactor operation
The control logic incorporated 3 different reactor control modes: completely manual, semiautomatic or fully automatic. In semi-automatic mode each operation step - filling, magnesium addition and filtration - could be started individually; whereas in full automation all steps were started automatically in sequence by the software. The reactor can process several batches of urine automatically in sequence. In some experiments up to 7 cycles were processed, treating 350 ℓ urine in total. During such operations the filter was not changed. Measured phosphate recovery with the used cotton fibre filter was up to 93% total P (down to 7% in the filtrate). The build-up of filtration cake after several cycles (see Fig. 3) even increased recovery slightly through enhancing the filtration properties, as observed by Etter et al. (2011). But filtration times after several cycles increased by up to several hours and sometimes filtration did not take place at all, resulting in a lengthy overall operation time (Fig. 3).
Continuous dosing experiments
For first trials with MgCl2, the model was used to predict the conductivity response for dosing solutions of different molarities added at the same pump rate of 2 mℓ/s. In Fig. 4, a study with only minor changes of molarity from 0.2 to 0.26 mol/ℓ is shown. It can be seen that conductivity is affected by small changes in molarity. On the one hand, lower concentrations of around 0.21 mol/ℓ lead to dilution of the urine and a continuous decrease in conductivity. The endpoint can only be seen by a slight change in slope. On the other hand, with higher molarities of around 0.25 mol/ℓ, the conductivity starts to rise after the endpoint, making it easier to detect. The curves showed a trade-off between the magnitude of response and the change in slope at the endpoint. The clearest indication of the endpoint appears to be between 0.23 and 0.25 mol/ℓ for the particular urine batch, which had a conductivity of 31.5 mS/cm. Experimental data, as seen in Fig. 4, confirmed the model results. The overall change of conductivity from start to endpoint is very small - only about 0.5 mS/cm in most experiments. The precision of the sensor, given by the manufacturer as 0.5% of reading (which translates to 0.145 - 0.165 mS/cm for the tested urine samples), is not much smaller than the range of the measurements, which leads to difficulties in detecting the endpoint.
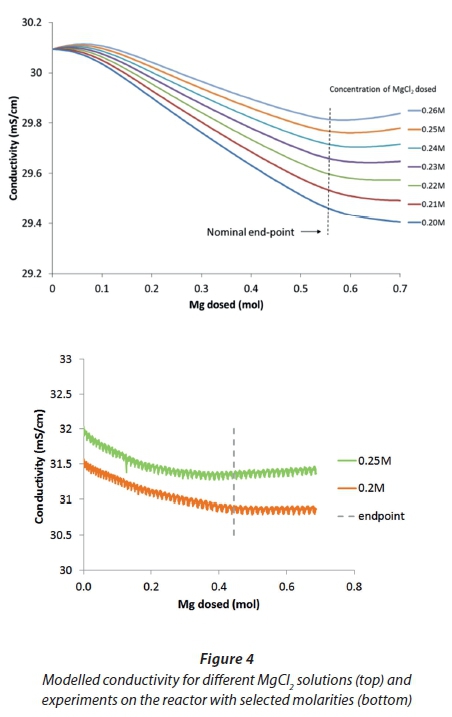
Experiments with MgSO4 showed similar trends, except that, because the MgSO4 has a lower contribution to conductivity than MgCl2, a higher molarity of MgSO4 is required to match the conductivity of the urine and generate similar curves. With 0.5 mol/ℓ MgSO4 solution dosed at the same rate, the conductivity starts to rise after the endpoint (Fig. 5).
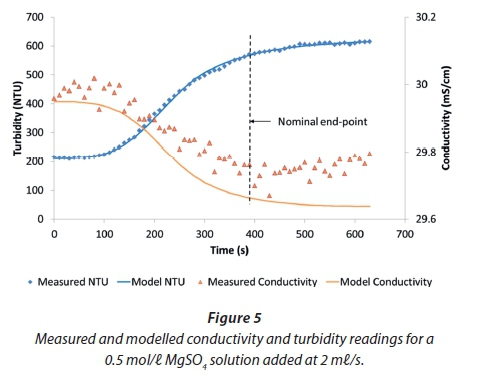
Figure 5 shows that the turbidity signal gives a stronger response to the crystallisation process. The model curve for turbidity was obtained from the modelled concentration of precipitated struvite scaled linearly according to the initial and final turbidity readings. This procedure gave a close correspondence between the model and the data; however, this was fortuitous. The relationship between suspended solids concentration and turbidity is complex, depending on the crystal size distribution, which in turn depends on the crystallisation reaction conditions, so that the scaling parameters vary from run to run.
Further experiments indicated that the turbidity is less sensitive to changes in the dosing parameters than the conductivity. In Fig. 6, it can be seen that a switch of dosing parameters (molarity and flow rate), while keeping the actual magnesium dosing rate constant, hardly affects the change of turbidity, whereas the conductivity signal behaves very differently. Turbidity reaches its maximum shortly after the theoretical endpoint.
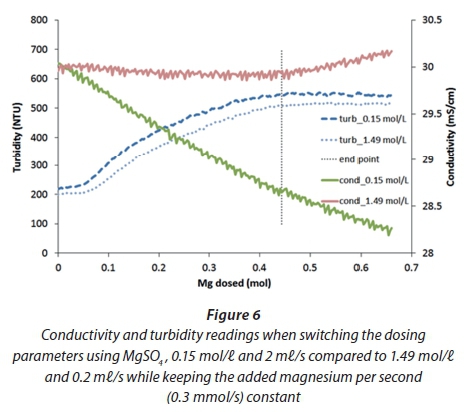
As the turbidity showed a less sensitive behaviour for endpoint detection when changing dosing parameters, the first tests with the algorithm used this signal. For the data shown in Fig. 6, a threshold value for the slope of the milliamp signal from the turbidity meter was found such that the dosing pump stopped about 3% later then the theoretically calculated time. However when the method was applied to new batches of urine the algorithm stopped the dosing far too early because the measured turbidity fluctuated strongly (Fig. 7). The algorithm for endpoint detection stopped the pump when the first plateau in the curve was encountered. Increasing the smoothing did not lead to better results. When running the reactor under fully automatic control, the detection always stopped the magnesium dosing too early because of fluctuations in the signal.
Step-wise dosing experiments
A further problem was revealed during attempts to model the process, namely, that the precipitation is not yet complete when the magnesium dose reaches the endpoint. Thus it is necessary to anticipate the endpoint from the indicator curves. To investigate this, tests were conducted with intermittent dosing, which allowed the precipitation process to continue during non-dosing periods.
In Fig. 8, the conductivity trace appears to be more informative than the turbidity. The continued precipitation during the periods when the dosing is off is evident from the slow decline in conductivity, which cannot be detected from the turbidity. Furthermore, as the endpoint is approached, there is a clear change in behaviour in the conductivity curve, with a slight increase before a slight decrease, whereas the turbidity shows no apparent response. A further advantage of the conductivity signal is that smoothing appears to be very effective, and so a smoothed signal should be effective for control purposes. However, the behaviour at the endpoint, while forming an easily recognisable visual pattern, is difficult to formulate as an automatic control algorithm.
Back-titration with urine
The difficulties in identifying the endpoint in real time are evident from Fig. 7. However, the endpoint is relatively easy to identify after the event, as the point where the slope of the smoothed conductivity curve changes, but the magnitude of the noise in the signal makes it impossible to identify this point until a significant overdose of magnesium has occurred. From Fig. 7, the change in slope should be clearly established by the time that a 10% overdose has occurred. It is relatively simple to hold back 10% of a batch of urine, and then add it to the batch after the magnesium dosing has been completed, to use up the excess. Figures 9 and 10 illustrate how an accurate endpoint detection algorithm works. Figure 9 is a heavily smoothed (3-min moving average) conductivity curve, derived from the same data as presented in Fig. 7. The marked endpoint corresponds to the measured phosphate concentration in the urine feed, and corresponds very well with the change in slope of the curve. Note that this could not have been identified in real time, because the average includes values measured after the theoretical end-point time.
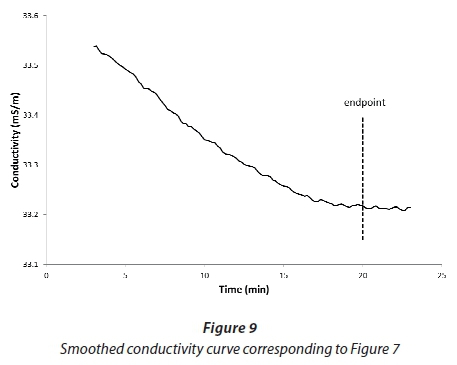
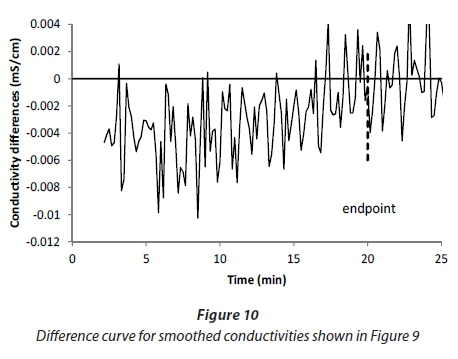
Although identifying the endpoint by eye from the shape of the smoothed curve seems relatively easy, it still relies on ignoring the residual irregularities, which are problematic for an automatic algorithm that relies on evaluating the slope. Figure 10 is a plot of differences between consecutive smoothed values presented in Fig. 9. Although one can identify the endpoint by eye as the point where the average curve goes through zero, the signal is very noisy.
If a 3-min moving average is applied to the differences (Fig. 11), the scatter is reduced sufficiently to locate the endpoint accurately. The double application of 3-min moving average smoothing requires that the dosing must have continued for at least 3 min beyond the endpoint. In general, a correction should also be applied to compensate for the inherent lag in the sensor response; however this was only 0.5 s for the conductivity sensor in question, which was negligible in comparison to the smoothing time.
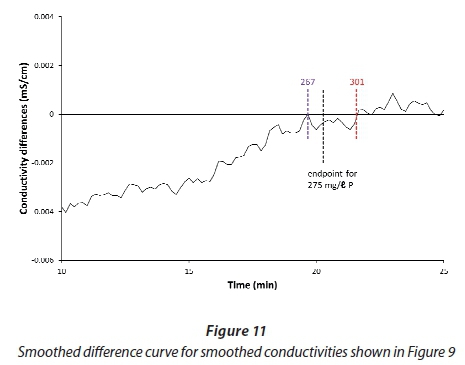
Once the endpoint time has been found, the 'overdose time' is the total dosing time less the endpoint time. The volume of urine to add to the batch is the original volume fed to the reactor multiplied by the overdose time and divided by the endpoint time. All of this can easily be programmed into a supervisory control algorithm.
The possibility of back-titrating with urine was only explored after the reactor had been dismantled, and the available data were not ideal for examining the reproducibility of the technique. Some information can be gleaned from Fig. 11. The nominal endpoint shown corresponds to the 275 mg/ℓ P content of the urine batch. The two coloured markers show where the curve touches the zero line, thus marking the range of uncertainty for the titration endpoint. The corresponding range of P values is 267 to 301 mg/ℓ, or ± 6.2%. An experimental run conducted with 0.25 mol/ℓ MgCl2 instead of 0.5 mol/ℓ MgSO4 yielded a P estimate of 302 mg/ℓ, which supports this range of uncertainty.
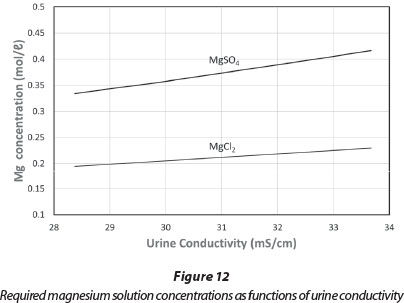
This technique will work best when the concentration of the dosing solution is set to cause the conductivity to increase slightly when no precipitation is taking place. This concentration depends on the conductivity of the urine. The conductivity model was used to prepare Fig. 12, which shows the dosing solution concentrations which just cause a conductivity increase with different initial values of the urine conductivity. It could be used to adjust the dosing concentration to compensate for variations in the urine being treated. However, the dependence is not very strong, and a given dosing solution should give adequate results over a range of urine conductivities.
CONCLUSIONS
An automated reactor was successfully operated with real human urine collected at urine diversion dehydrating toilets (UDDT) in the rural area of eThekwini. The reactor could operate on its own, process several batches of urine and achieve recovery rates of up to 93% total P. Filtration is still the critical part of the operation as the struvite crystals lead to clogging of the filter after several cycles. Conductivity and turbidity were studied as automation proxies for controlling the dosing. Molarities around 0.25 mol/ℓ for MgCl2 and 0.5 mol/ℓ MgSO4 at 2 mℓ/s showed good results enabling detection of the endpoint in urine with a conductivity of 31.5 mS/cm. Continuous and intermittent dosing strategies were investigated.
The following points are relevant in the formulation of the eventual dosing control system:
- Conductivity sensors are less expensive than turbidity sensors, and require less maintenance.
- Turbidity gives a much stronger response to precipitation than conductivity; however, the conductivity signal is more predictable and informative.
- Both signals are subject to noisy fluctuations; however, the conductivity signal can be smoothed more successfully.
- The relationship between turbidity and mass concentration of crystals appears to be complex, probably due the variations in the crystal size distribution that occur during precipitation.
- Intermittent dosing provides information about the precipitation kinetics that is masked during continuous dosing. A dosing control strategy might be able to take advantage of this to improve the accuracy of endpoint detection. However, the algorithm to implement this will be relatively complex, and requires further investigation.
- Although the conductivity noise to signal ratio prevents detection of the precipitation endpoint in real time, it can be identified retrospectively after overdosing with magnesium. The excess magnesium can then be utilised by adding a calculated quantity of urine to the batch determined by the automation algorithm.
ACKNOWLEDGMENTS
This study was undertaken in the framework of the Valorisation of Urine Nutrients in Africa (VUNA) project funded by the Bill & Melinda Gates Foundation (www.vuna.ch). The funding is obtained by the Swiss Federal Institute of Aquatic Science and Technology (Eawag). The support from Markus Nowotny from CheckIT Systems was essential to get the reactors running and find the right algorithms for automation. The support from Kai Udert and Bastian Etter from Eawag is highly appreciated. Without the strong support of the eThekwini Municipality, namely Teddy Gounden and his team, this study would not have been possible, without the collection and provision of so much urine. Final thanks belong to the workshop team around Ken Jack at the School of Chemical Engineering to help build the reactor set-ups.
REFERENCES
DAI J, TANG WT, ZHENG YS, MACKEY HR, CHUI HK, VAN LOOSDRECHT MCM and CHEN GH (2014) An exploratory study on seawater-catalysed urine phosphorus recovery (SUPR). Water Res. 66 75-84. [ Links ] Etter B, Tilley E, Khadka R and Udert KM (2011) Low-cost struvite production using source-separated urine in Nepal. Water Res. 45 (2) 852-862. [ Links ]
IKUMI DS, HARDING TH, VOGTS M, LAKAY MT, MAFUNGWA HZ, BROUCKAERT CJ and EKAMA GA (2014) Mass balances modelling over wastewater treatment plants III. Final Report submitted for WRC Project K5/1822 (23 December 2014). Water Research Commission, Pretoria. [ Links ]
KOUTSOUKOS P, AMJAD Z, TOMSON MB and NANCOLLAS GH (1980) Crystallisation of calcium phosphates. A constant composition study. J. Am. Chem. Soc. 102 (5) 1553-1557. [ Links ]
LARSEN TA and GUJER W (1996) Separate management of anthropogenic nutrient solutions (human urine). Water Sci. Technol. 34 (3-4) 87-94. [ Links ]
MCCLESKEY RB, NORDSTROM DK, RYAN JN and BALL JW (2012) A new method of calculating electrical conductivity with applications to natural waters. Geochim. Cosmochim. Acta 77 369-382. [ Links ]
MUNCH EV and BARR K (2001) Controlled struvite crystallisation for removing phosphorus from anaerobic digester sidestreams. Water Res. 35 151-159. [ Links ]
ROMA E, HOLZWARTH S and BUCKLEY CA (2011) Large-scale peri-urban and rural sanitation with UDDTs, eThekwini (Durban), South Africa. URL: http://www.susana.org/en/resources/case-studies/details/791 (Accessed 2 March 2015). [ Links ]
RONTELTAP M, MAURER M and GUJER W (2007) Struvite precipitation thermodynamics in source-separated urine. Water Res. 41 977-984. [ Links ]
SAKTHIVEL SR, TILLEY E and UDERT KM (2012). Wood ash as a magnesium source for phosphorus recovery from source-separated urine. Sci. Total Environ. 419 (0) 68-75 [ Links ]
SHEPHERD TA, BURNS RT, MOODY LB, RAMAN DR and STALDER KJ (2009) Investigating conductivity to predict magnesium addition requirements for struvite precipitation in swine manure slurries. Am. Soc. Agric. Biol. Eng. 25 (1) 103-108. [ Links ]
TILLEY E, ATWATER J and MAVINIC D (2008) Recovery of struvite from stored human urine. Environ. Technol. 29 (7) 797-806. [ Links ]
TILLEY E, LÜTHI C, MOREL A, ZURBRÜGG C and SCHERTENLEIB R. (2008) Compendium of sanitation systems and technologies. Swiss Federal Institute of Aquatic Science and Technology (Eawag). Dübendorf. Switzerland, URL: http://www.eawag.ch/forschung/sandec/publikationen/sesp/dl/compendium_high.pdf (Accessed 2 March 2015). [ Links ]
TRIGER A, PIC JS and CABASSUD C (2012) Determination of struvite crystallization mechanisms in urine using turbidity measurement. Water Res. 46 6084-6094. [ Links ]
UNICEF and WHO (2012) Progress on drinking water and sanitation: 2012 Update. In: WHO/UNICEF Joint Monitoring Programme for Water Supply and Sanitation. UNICEF/WHO, New York. URL: http://www.unicef.org/media/files/JMPreport2012.pdf (Accessed 2 March 2015). [ Links ]
WESTERGREEN S, BROUCKAERT CJ and FOXON KM (2012) Modelling of ionic interactions with wastewater treatment biomass. Water Sci. Technol. 65 (6) 1014-1020. [ Links ]
WILSENACH JA, SCHUURBIERS CAH and VAN LOOSDRECHT MCM (2007) Phosphate and potassium recovery from source-separated urine through struvite precipitation. Water Res. 41 458-466. [ Links ]
YE ZL, CHEN SH, LU M, SHI JW, LIN LF and WANG SM (2011) Recovering phosphorus as struvite from the digested swine wastewater with bittern as a magnesium source. Water Sci. Technol. 64 (2) 334- 339. [ Links ]
Received 1 September 2014
Accepted in revised form 17 March 2015
* To whom all correspondence should be addressed. e-mail: brouckae@ukzn.ac.za














