Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Water SA
On-line version ISSN 1816-7950
Print version ISSN 0378-4738
Water SA vol.41 n.1 Pretoria Jan. 2015
http://dx.doi.org/10.4314/wsa.v41i1.10
Investigating a spatial approach to groundwater quantity management using radius of influence with a case study of South Africa
Paul SewardI, *; Yongxin XuI; Anthony TurtonII
IDepartment of Earth Sciences, University of the Western Cape, Private Bag X17, Bellville, 7535, South Africa
IIUniversity of the Free State, PO Box 339, Bloemfontein, 9300, South Africa
ABSTRACT
The purpose of this paper is to investigate whether a simple, spatially-based approach to groundwater sustainability using radius of influence should be used to replace the pervasive, yet deprecated, 'natural recharge water balance' volumetric method. Using South Africa as a case study, the radius of influence methodology was shown to be scientifically practical, to provide plausible results, and to be permissible under the country's water laws. The approach also provides better indicators for institutions involved in groundwater management, and remains conceptually correct at all scales. However, further research is recommended on more robust alternatives to the Cooper-Jacob equation for determining radius of influence.
Keywords: groundwater, sustainability, spatial, water balance, indicators, institutions
INTRODUCTION
Groundwater development creates a range of benefits and a range of consequences that depend on how intensively development occurs (Custodio, 2002; Pierce et al., 2013). Sustainable groundwater development (hereafter abbreviated to 'sustainability') represents a subjective, value-driven decision on the trade-off between these benefits and consequences for a given situation (Llamas et al., 2006). It is the job of hydrogeology to input objective information for the subjective decision-making process and to provide objective information to guide the implementation of the chosen sustainability scenario (Seward et al., 2006; Gleeson et al., 2012). The default information provided by hydrogeology is a 'pump-the-recharge' water balance (Balleau, 2013). This default creates serious problems because it (i) ignores the spatial and temporal aspects of sustainability (Theis, 1940; Bredehoeft, 2002); (ii) does not encompass the whole range of sustainability benefits and consequences (Kalf and Woolley, 2005; Pierce et al., 2013), (iii) is not even an indicator of the sustainability of any particular benefits/consequences option (Seward et al., 2006), and (iv) fuels the misconception that there is a single, numerical answer to sustainability (Balleau, 2013; Rudestam and Langridge, 2014).
Existing approaches to this problem are (i) attempting to solve it by using the capture principle instead of natural recharge as the conceptual basis for monitoring, modelling, and adaptive management (Bredehoeft, 2002; Maimone, 2004), (ii) disputing that there is a problem (Zhou, 2009), and (iii) ignoring it (Balleau, 2013). While monitoring, modelling and adaptive management might seem like a reasonable solution in principle, in practice many countries do not have the combination of scientific and institutional capacity to implement this solution. A management/governance approach is therefore needed that has a sound conceptual basis and is readily implementable in practice. Instead of simple, but dubious, approaches based on allocating natural recharge, or 'complicated' but correct approaches of incorporating capture using adaptive management, this paper proposes a simple spatial approach using well-spacing and radius of influence to ensure that any new abstraction is sited far enough away from what shouldn't be captured. The purpose of this paper is to test the proposed solution scientifically and legally using South Africa as a case study, and to test the solution institutionally using the generic concept of indicators.
CONTEXT
This investigation depends on concepts related to groundwater 'safe yield' and groundwater 'sustainability.' These concepts have been debated for a century (Lee, 1915; Gleeson et al, 2012; Pierce et al., 2013; Rudestam and Langridge, 2014). A thorough history of the evolution of these concepts and their associated problems is provided by Kalf and Woolley (2005). It is difficult to find any definition of groundwater safe yield or sustainability that does not include some subjectivity or ambiguity. Even the 'purely hydrological' definition of Lee (1915 p. 48) contains the term 'dangerous depletion of storage reserves.' The seemingly irreverent definition of Lohman (1972 p. 62): 'The amount of groundwater one can withdraw without getting into trouble 'where 'trouble may mean anything under the sun,' highlights the subjectivity of safe yield and could well be applied to the more modern concept of sustainability. It would appear that the ecological impacts were not considered as part of 'getting into trouble' in the early definitions of safe yield, but are included in sustainability (Alley and Leake, 2004). The position of this paper is that the lists (Pierce et al., 2013; Llamas et al., 2006), commonly attached to what groundwater safe yield or sustainability should include, are merely attempts to bring 'anything under the sun' down to manageable limits, and that 'sustaina-bility' is ultimately a subjective, value-driven, 'political' choice. The fact that it is subjective does not, however, detract from the importance of the concept of sustainability, nor does it abrogate physical science from providing the best possible inputs.
These scientific inputs include acknowledging that groundwater sustainability has strong spatial controls. Spacing between wells, depths of wells and proximity to the recharge zone will determine how much water can be taken out an aquifer (Thomas, 1951). Proximity to existing wells, wetlands and streams will determine the extent of the consequences of utilising new wells. These spatial effects are explained by the capture concept (Lohman et al., 1972), whereby water sustainably pumped from wells is matched by reduced discharge and/ or increased recharge (Theis, 1940).
The 'capture' concept or principle (Lohman et al., 1972) as used in basin yield and well-field yield determinations, is related to, but has a clearly distinct meaning from, the 'capture' zones as used in contaminant hydrogeology (Javandel and Tsang, 1986; Shafer, 1987; Zhou 2011, Asadi-Aghbolaghi et al., 2011). In order to prevent confusion, the meaning of the two different types of 'capture' will be briefly discussed. In both meanings of the term 'capture' a pumped well is involved and something is being captured. In contaminant hydrogeology, the capture zone refers to the zone from which contaminants could be drawn into a pumped well. From Fig. 1 it can be seen that the capture zone may extend beyond, or extend less than, the cone of depression. This is because the cone of depression does not delineate the extent of flow or transport to the pumped well.
However 'capture' as used by Bredehoeft (2002) and Lohman et al. (1972) for hydraulic yield and equilibrium assessments is not primarily concerned with where the water being pumped by a well came from, but with the journey to basin or aquifer-scale equilibrium. Capture in the 'equilibrium' sense is concerned with what part of existing recharge or discharge or storage will balance any new abstraction. Capture in this sense does not need to concern itself with flow paths and where the water is coming from, but whether water levels have reached an equilibrium or not. In this sense of the term capture, it is the cone of depression or radius of influence that is relevant, not the capture zone. This paper is concerned with capture in the equilibrium sense, and thus uses the term radius of influence, rather than capture zone, to prevent misunderstanding.
A spatial approach to groundwater management using well spacing is not uncommon in developing countries where local communities have chosen to manage their groundwater resources themselves (Foster et al., 2000; Van Steenbergen, 2006; Taher et al., 2012). Typical well-spacing distances can range from 250 m to 1 km. Spatial approaches are also used in developed countries. Nearly all the western states of the USA, where groundwater is treated as private property, have some form of well spacing regulation (Gardner et al., 1997), and the well spacing can range from 100 m or less in some counties in Texas to 6 km in parts of Dakota (Brozowic et al., 2006).
These spatial approaches are primarily focused on distances between wells rather than distances to natural recharge or discharge areas. These spatial approaches do however take capture into account by making estimates of the likely extent of the cone of depression. While well-spacing does not appear to be effective in addressing intensive groundwater use in the Great Plains Aquifer, USA (Gardner et al., 1997; Sophocleous, 2010), there are several examples from countries such as Yemen where local communities are effectively managing groundwater use using a well-spacing approach (Van Steenbergen, 2006; Taher et al., 2012). Indeed, current thinking on groundwater governance (Taher et al. 2012, Wijnen et al, 2012) advocates using simple rules that can be practically monitored, where rule violations can be practically detected and enforced, rather than using rules that are difficult to determine scientifically, difficult to monitor and difficult to enforce. Taher et al. (2012) rank spatial methods as the first and third most useful variables to meet these challenges while quantity allocations - the de facto approach in many countries - were ranked 19th out of 22.
According to Brozowic et al. (2006) well-spacing regulations have been entirely ignored in the economic literature, even though well-spacing, in some conditions, might be more effective and appropriate than (volumetric) quotas. Katic and Grafton (2012) argue that spatial regulations could also provide excellent controls either by themselves or in conjunction with extraction controls, and that well-spacing regulations could provide substantial welfare gains even if extraction rates are unregulated.
Thus there are some examples where well-spacing has been shown to be an effective management tool in practice, and there are some researchers who believe the topic requires more attention. However, the pervasive paradigm for groundwater management is direct volume control using quotas assigned by permits (Lopez-Gunn, 2003; Mukherji and Shah, 2005; Feitelson, 2006; Llamas and Garrido, 2007; Seward, 2011; Wester et al., 2011; Mechlem, 2012; Wijnen et al., 2012), with well spacing used as an adjunct, if at all. Well-spacing can be considered to be a form of indirect volume control. However, the primary purpose of well-spacing is to prevent unacceptable effects using spatial controls rather than limit volumes to a specific amount, so the distinction between volume and spatial will be retained for the sake of simplicity.
The yield-based approach almost invariably resorts to 'pumping the recharge' determinations (Balleau, 2013) rather than using the capture principle. A possible explanation for this could be that a large part of the hydrogeological community disagrees that there is anything wrong with using natural recharge for aquifer and hydrological sustainability. Zhou (2009) argues that it is a misconception that aquifer sustainability depends totally on either natural recharge or on capture, and that the reality is that aquifer sustainability depends on both processes. However, the basis for Zhou's (2009) argument is the special case where there is no induced recharge caused by pumping. In this case natural recharge to a basin equals the sum of all the discharges (natural or human-induced) and the total pumping from the basin cannot exceed the natural recharge. While this may be of value in theoretical comparisons of one basin with another, it gives no practical indication of aquifer sustainability for a particular well or well-field within a given basin. Aquifer sustainability could be considerably less than the natural recharge since local well-fields could dry up before their boundaries have responded to offset pumping. In addition, it is not clear how it can be known in advance that there will be no induced recharge caused by pumping within a certain basin, and that aquifer sustainability could not be greater than natural recharge. If the recharge zone(s) were located, wells drilled in these zones, and the water levels significantly lowered, it is difficult to see how recharge or discharge would not be affected.
Another argument is that even if using capture is theoretically preferred to natural recharge for determining aquifer sustainability, it is just too impractical to implement (Vivier, 2013). Indeed, Lohman et al. (1972) advocate not putting a number on aquifer sustainability in the early stages of development. The argument (Vivier, 2013) is that a water balance is needed to determine whether or not additional groundwater development is feasible, and to determine at least an initial pumping rate as part of an adaptive management strategy. The counter argument is that well densities based on radius of influence could provide as good, or a better, indication of the room for additional development, and that well yields derived from pumping tests provide a much better indicator of initial pumping rates than a percentage of natural recharge.
Another possible reason for the preference for managing groundwater volumetrically rather than spatially is because that is what legislators and water managers expect. Rudestam and Langridge (2014) describe how hydrogeologists and water managers in the state of California are essentially obligated to pin groundwater sustainability down to a specific number even though the nature of groundwater sustainability makes this impossible. This obligation does not appear to be restricted to California. A directive, for example, that pumping should be limited to 1 097 632 m3/year does seem a lot more authoritative, precise and scientific than a 'messy' directive not to pump in Zone A, not to pump in Zone B, or to stay more than 1 km from the nearest well, with no limits on pumping quantities in the remaining areas. However the 'messy' directive will actually be more effective in preventing unacceptable impacts than the 'precise' directive to limit pumping to 1 097 632 m3/year if it takes cognisance of the capture principle, and if the 'precise' directive is only based on a water balance.
METHODOLOGY
Overview
The feasibility of a spatial approach, using radius of influence, was investigated from a scientific, a legal, and an institutional perspective. The scientific perspective involved estimating radius of influence using South African data and using the results to estimate aquifer sustainability at catchment and national scales. The legal perspective involved investigating whether a spatial approach was possible under South African water law. The institutional perspective involved comparing the water balance approach and the radius of influence approach using the concept of indicators.
Aquifer sustainability estimates
After a 'sufficiently long' pumping time the Theis radial flow equation simplifies with reasonable accuracy to (Cooper and Jacob, 1946) s = (Q/4T)ln(2.25Tt/r2S), where s = drawdown, Q = pumping rate, T = transmissivity, r = radial distance, S= storage, t = time. In practice 'sufficiently long' may mean an hour of pumping or less (Kruseman and De Ridder, 1994). The radial distance at which the Cooper-Jacob equation equals zero, r = 1.5(Tt/S)a5, can be to used to calculate a so-called 'radius of influence.' However the 'radius of influence' will increase with time (Fig. 2) according to the Cooper-Jacob equation, addresses pumpage from storage only, and, according to the Theis equation (Theis, 1935), is infinite.
The radius of influence for a pumped well for each quaternary catchment in South Africa was estimated using the equation r = 1.5(Tt/S)0.5.
The average transmissivity for each quaternary catchment was determined by taking an estimate of average well yield (Haupt, 2001), and converting this to an estimated transmissivity (Meier et al., 1999) using T = cQ/s, where c is a constant ranging from 0.9 to 1.3, and is assumed to 1.2 for the purposes of the study. For drawdown (s) the average thickness of the weathered aquifer (DWAF), 2006) for each quaternary catchment is used. The weathered aquifer contains the most water strikes and the highest density of water strikes so it seems a reasonable assumption that a sustainable pumping regime would not draw down water significantly below the weathered aquifer.
An average specific yield value for each quaternary catchment (DWAF, 2006) is used for the storage value. Specific yield values were estimated (DWAF, 2006) from rock type and the depths where water was intercepted. All rock types are covered, but in the South African context this was primarily weathered and fractured bedrock.
The time (t) was set at 5 years. While this is a somewhat arbitrary selection, a sensitivity analysis showed that varying the time from 3 to 5 years made little difference, while varying the times between 6 months and 2 years made a significant difference. From a practical point of view, the choice of 5 years is conservative, since it is highly unlikely that wells will be pumped 24 hours a day, 365 days a year for 5 years. In addition, for much of South Africa, where aquifers are typically of the confined type and small, equilibrium conditions will be reached relatively quickly, thus adding to the argument that setting the time to 5 years is conservative.
The 'catchment yield' is estimated from the number of radii of influence that can be fitted into a catchment, multiplied by the average well yield for that catchment, the assumption being that the 5-year period is sufficiently conservative to prevent serious negative consequences of groundwater use. In practice, however, it is accepted that negative consequences could happen, including well interference and lowering of well yield. The 5-year period is essentially a screening process, a 'coarse sieve' to eliminate as large as possible percentage of the negative consequences, and thus should be seen as a probalistic approach to likely outcomes, and not totally deterministic.
Spatial approach using radius of influence versus South African water law
The salient points of the National Water Act (Republic of South Africa (RSA), 1998) that pertain to groundwater use were identified, and were then investigated to ascertain whether a spatial approach was permissible or not.
Using indicators to investigate the institutional implementability of a spatial approach to groundwater management
For the purposes of this investigation an institution can be a national government, a regional government, a catchment management agency, a water user association, or any voluntary or legally-mandated group involved in determining, monitoring and enforcing decisions regarding groundwater use. It was then assumed that the better the indicator the more likely that the institution would be able to manage groundwater using that indicator.
An indicator points to a condition, not with a 100% certainty, but with enough precision to allow the communication of useful information and for decisions to be made (Gutierrez-Espeleta, 1998; OECD, 2003; Vrba and Lipponen, 2007). The reason for not having 100% certainty might be because it is not possible - as with complex systems - or that it is not necessary. It is suggested that groundwater models are, in a sense, indicators - they cannot predict the future with 100% certainty but are still very useful (Bredehoeft and Durbin, 2009). From a distillation of selected literature on the subject (Gutierrez-Espeleta, 1998; Godfrey et al, 2002; OECD, 2003; Vrba and Lipponen, 2007; Juwana et al., 2012), the characteristics of good indicators can be defined as:
- RELEVANT: They point to something about the system that needs to be known.
- EASY TO UNDERSTAND: The meaning of the 'story' (Gutierrez-Espeleta, 1998) that the indicator is telling must be clear, even to people who are not experts on the subject.
- RELIABLE: The information provided can be trusted. It is responsive to change with a reasonable degree of accuracy. It must have a sound theoretical basis.
- BASED ON ACCESSIBLE INFORMATION: The information required is either available or not difficult to obtain.
The spatially-based radius of influence approach was then compared with the volumetrically-based water balance approach using these characteristics of good indicators.
RESULTS
Aquifer sustainability estimates for South Africa
Values for the radius of influence from 212 m to 16.3 km were obtained. The distribution curve (Fig. 3) shows that the highest number of cases occurs for a radius of influence of between 1 km and 3 km. The arithmetic mean for the radius of influence was 3 113 m and the median was 2 764 m. The reason for the change in distribution pattern from 7.5-8.0 km to greater distances is not known. It is speculated that cases from 7.5 to 15.5 km are anomalies related to erroneously high transmissivity values or erroneously low specific yield values.
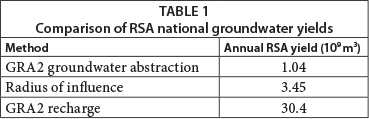
The annual yields determined using the radius of influence approach for all of South Africa (Table 1) are higher than the estimates of current abstraction (DWAF, 2006), but lower than estimates of annual recharge. While the comparison may seem meaningless because of the different parameters involved in the different computations, it is reassuring to note that the radius of influence method does not give results that are many orders of magnitude different from the recharge or abstraction methods. It is also reassuring to note that the radius of influence results are higher than current abstraction, but lower than recharge, which is consistent with it being a reasonable indicator of what might actually be abstracted.
The relevant mechanisms in the NWA (RSA, 1998) are:
- General authorisations - where impacts of water use are expected to be small to moderate, a 'blanket' authorisation permits use under certain conditions, such as within a specified annual quantity of water. This allows for moderate impact water use without placing an administrative burden on the users or regulators.
- Licensing - where water use exceeds the general authorisation, the user must apply for a licence.
Before a licence can be issued the regulator must determine the 'Reserve', defined as the quality and quantity of water required to: (1) satisfy basic human needs, and (2) protect aquatic ecosystems in order to secure ecologically sustainable development and use of the relevant water resource.
Conditions, which may be attached to the use of water under both a licence and a general authorisation, are given in section 29 of the NWA. Section 29 (1) (e) applies to the taking or storage of water, of which the first 4 conditions (RSA, 1998) are relevant to this discussion:
(i) Setting out the specific quantity of water or percentage of flow that may be taken
(ii) Setting out the rate of abstraction
(iii) Specifying the method of construction of a well and the method of abstraction from the well
(iv) Specifying the place from where water may be taken
The current, volumetric approach - the specific quantity of water - is thus an option rather than a requirement for licences and general authorisations. The option of a radius of influence approach is possible under bullet (iv) since the place from where water can be taken can be specified, and therefore the place from where water cannot be taken can also be specified, thus allowing groundwater use to be excluded according to a radius of influence determination. The Reserve is the only case where a quantity is required. However the quantity and quality of water required by the Reserve could be achieved using protection and exclusion zones, rather than an approach using volumetric limits on extraction.
Institutional implementability of a spatial approach to groundwater management
The water balance approach using natural recharge is compared with the spatial approach using radius of influence. The characteristics of good indicators are used to draw the comparison between the two approaches:
- RELEVANT: The water balance approach seems less relevant because it only provides a 'snapshot' (Bredehoeft and Durbin, 2009) of the situation at a given time, and cannot predict the spatial location of impacts. This 'snapshot' does not point to future conditions, whereas the radius of influence approach at least tries to do so, as well as differentiating between impacts at different locations.
- EASY TO UNDERSTAND: It is easy to imagine that a well close to a feature that needs to be protected could impact that feature. It is less easy to understand that there is a threshold of natural recharge that if exceeded could impact the resource.
- RELIABLE: The radius of influence approach used many approximations, for example the Cooper-Jacob equation was used as an approximation of the Theis equation, the Theis equation was used as an approximation for flow to a well, and so on. Despite all these approximations, the radius of influence approach has a sound conceptual basis. With more reliable data and more sophisticated radius of influence models, more reliable results could be obtained. The same cannot be said of the water balance approach using natural recharge because it will remain conceptually simplistic, no matter how good the data are that are used. For example: a water balance type volumetric indicator might 'reserve' 30% of the natural recharge to a catchment to 'protect' ecosystems. However, without any induced recharge caused by pumping - a decrease in rejected recharge - to compensate the pumping of 70% of the natural recharge, all that this reserve achieves is to ensure that the ecosystems will receive between 0% and 100% of their previous water requirements because it is not known what will be captured. However, a spatial approach that 'reserved' 30% of the spatial area of the catchment in the vicinity of the ecosystems, by prohibiting any pumping in this area, has a far greater probability of protecting the ecosystems, because capture of groundwater from the ecosystem area will be limited by the 'spatial reserve'. In addition, the South African approach of 'allocating' the natural recharge by first subtracting a portion for aquatic ecosystems, and then subdividing the remainder between users, is not grounded in reality. There is no scientific reason why any of the allocated recharge should be flowing beneath a particular property. There is no scientific reason why the quantity reserved for aquatic ecosystems should reach the aquatic ecosystem just because the total catchment yield is reduced by a certain percentage.
- BASED ON ACCESSIBLE INFORMATION: Even in developed countries regulating groundwater development successfully using water flow meters appears to be the exception rather than the norm (Sophocleous, 2010; Wester et al., 2011; Wijnen et al., 2012). Quantities of groundwater extracted, groundwater levels, and time of pumping are notoriously difficult to obtain. On the other hand, the presence or absence of a well is perhaps the easiest aspect of groundwater development to monitor, and is readily accessible or potentially accessible. A spatial approach to groundwater management, based on monitoring the presence of wells, therefore meets the accessible information requirements of good indicators, while volumetric monitoring via flow meters does not.
DISCUSSION
The radius of influence approach presented enables areas to be identified where groundwater extraction will probably have acceptable consequences, as well as areas where groundwater extractions will probably have unacceptable consequences. What is 'acceptable' and what is 'unacceptable' will be subjective, 'political' choices. The trade-off between what is acceptable and what is unacceptable will determine the groundwater 'sustainability' for a given area. Should legislators, water managers, or hydrogeologists require a groundwater extraction volume/ rate rather than a delimited extraction area, the production area can easily be converted to a production rate using the methodology presented.
This investigation has refuted arguments that the capture approach to groundwater management is too complicated to implement in practice. The simple spatial approach to approximate radius of influence used readily available aquifer parameter data, but even when no data are available, reasonable estimates could be made by estimating transmissivity and storativity from rock types. Where better data are available better radius of influence models and approximations can be used.
The results obtained were scientifically plausible when national scale comparisons were made. The results are also consistent with expert opinion (Van Tonder, 2010) on local-scale monitoring for well/surface water impacts based on radius of influence considerations: relatively intensive monitoring for wells closer than 1 km to a river, less intense monitoring between 1 km and 3 km, and no monitoring at distances further than 3 km away. However the extreme range in the values of radius of influence obtained raises some questions about the validity of these results. Variations in radius of influence by 2 orders of magnitude imply variations in transmissivity or specific yield by 4 orders of magnitude because of the square root in the equation: r = 1.5(Tt/S)°.5. While this is not impossible, given the extreme variations in the hydraulic parameters of rock types in South Africa, it does suggest that verification work is needed.
While using the Cooper-Jacob equation to estimate radius of influence is a step forward in utilising spatial approaches that are computationally straightforward, there is plenty of room for improvement. One such improvement would be to use the Glover equation for stream depletion by wells (Glover and Balmer, 1954). The Glover equation can be written in the form: q/Q = 1-erf(x/(4tT/S)0,5) where q = depletion rate at stream, Q = pumping rate at well, x = distance from well to stream, t = time, T = transmissivity, S = specific yield, and erf = the error function. This equation contains the same parameters as the Cooper-Jacob equation, and by setting q to zero instead of drawdown to zero, can be used to delineate radius of influence in a similarly straightforward way to that used for the Cooper-Jacob equation in this paper.
A shortcoming of the spatial approach to radius of influence is that the temporal effects have not been fully addressed. A somewhat arbitrary time span of 5 years was used in the estimates of the extent of the cones of depression. It has been argued that the approach used is so conservative that it does not matter that it is a transient approach, implying that it does not matter when or if a steady state is reached. However, this is a far from satisfactory assumption. Sooner or later the abstraction points will either dry up or reach equilibrium. It would be more satisfactory to resolve the temporal effects by using steady state rather than transient formulae. This aspect needs further research.
The case study has shown that a radius of influence approach is permissible under South Africa's NWA. From the perspective of indicators used by institutions for groundwater management, a spatially-based approach using radius of influence is preferable to a volumetric approach based on a water balance.
The spatially-based approach is also preferable when moving from one scale to another. The water balance approach essentially simplifies groundwater occurrence to a single cell or 'bath tub' model. Even if the numbers are correct for the overall 'bath tub' there is no way of sensibly down-scaling and determining what will happen at a point in the 'bath tub' because the bath tub does not allow for spatial variations. However the spatial approach does allow for transitioning between different scales. All the various impacts at various locations can be summed to sensibly predict what will happen at the next higher scale. It is suggested that aquifer sustainability for a catchment can be far more meaningfully appraised by summing all the actual and potential 'production facilities' for that catchment, rather than by estimating average natural recharge.
CONCLUSIONS
Groundwater sustainability has strong spatial controls. Globally, some examples of good groundwater governance being realised solely by spatial controls have been documented. This investigation has shown that the sustainability problems created by the 'pump-the-recharge water balance' approach can be solved by a simple spatial approach to radius of influence. The scientific methodology used was easily implemented and yielded plausible results. The spatial approach (i) is permissible in South Africa according to its NWA (RSA, 1998); (ii) provides much better indicators for groundwater management and governance than volumetric approach; and (iii) remains conceptually correct at all scales, unlike the 'pump-the-recharge' approach. However, there is scope for further research, specifically utilising the Glover equation (Glover and Balmer, 1954) for stream depletion by wells, and utilising more robust formulae than the Cooper-Jacob (Cooper and Jacob, 1946) equation to estimate future steady-state conditions.
REFERENCES
ALLEY WM and LEAKE SA (2004) The journey from safe yield to sustainability. Ground Water 42 (1) 12-16. [ Links ]
ASADI-AGHBOLAGHI M, RAKHSHANDEHROO GR, and KOMPANI-ZARE M (2011) Analytical solutions for the radius of influence of a pumping well near a stream. Hydrogeol. J. 19 (6) 1161-1168. [ Links ]
BALLEAU WP (2013) The policy of "pumping the recharge" is out of control. Eos 94 (1) 4-5. [ Links ]
BREDEHOEFT JD (2002) The water budget myth revisited: Why hydrogeologists model. Ground Water 40 (4) 340-345. [ Links ]
BREDEHOEFT JD and DURBIN TJ (2009) Ground water development-the time to full capture problem. Ground Water 47 (4) 506-514. [ Links ]
BROZOWIC N, SUNDING DL and ZILBERMAN D (2006) Optimal management of groundwater over space and time. In: Goetz RU and Berga D (eds) Frontiers in Water Resource Economics. Springer, New York. [ Links ]
COOPER HH and JACOB CE (1946) A generalized graphical method for evaluating formation constants and summarizing well field history. Trans Am. Geophys. Union. 27 (4) 526-534. [ Links ]
CUSTODIO E (2002) Aquifer overexploitation: what does it mean? Hydrogeol. J. 10 (2) 254-277. [ Links ]
DWAF (DEPARTMENT OF WATER AFFAIRS AND FORESTRY, SOUTH AFRICA) (2006) Groundwater Resource Assessment: Task 1D Groundwater Quantification. DWAF, Pretoria. [ Links ]
FEITELSON E (2006) Impediments to the management of shared aquifer: A political economy perspective. Hydrogeol. J. 14 (3) 319-329. [ Links ]
FOSTER S, CHILTON J, MOENCH M, CARDY F and SCHIFFLER M (2000) Groundwater in rural development - facing the challenges of supply and resource sustainability. World Bank Technical Paper No. 463. World Bank, Washington, D.C. [ Links ]
GARDNER R, MOORE MR and WALKER JM (1997) Governing a groundwater commons: A strategic and laboratory analysis of Western law. Econ. Inq. 35 (2) 218-234. [ Links ]
GLEESON T, ALLEY WM, ALLEN DN, SOPHOCLEOUS MA, ZHOU Y, TANIGUCHI M and VANDERSTEEN J (2012) Towards sustainable groundwater use: Setting long-term goals, backcasting, and managing adaptively. Ground Water 50 (1) 19-26. [ Links ]
GLOVER RE and BALMER GG (1954) River depletion resulting from pumping a well near a river. Trans. Am. Geophys. Union 35 (3) 468-470. [ Links ]
GODFREY L, CLAASSEN M, TODD C, SMAKHTIN V, DU PREEZ M and STASSEN R (2002) National Core Set Of Environmental Indicators Phase 3: Selection Of Indicators - Inland Waters. Department of Environmental Affairs and Tourism, Pretoria. [ Links ]
GUTIERREZ-ESPELETA EE (1998) Designing environmental indicators for decision makers. Joint Conference of the International Association of Survey Statisticians and the International Association of Official Statistics, 1-4 September 1998, Aguascalientes, Mexico. [ Links ]
HAUPT CJ (2001) Ground Water Resources of South Africa. Directorate of Water Resource Planning. Report No. 97128. Department of Water Affairs and Forestry, Pretoria. [ Links ]
JAVANDEL I and TSANG C (1986) Capture-zone type curves: A tool for aquifer cleanup. Ground Water 24 (5) 616-625. [ Links ]
JUWANA I, MUTTIL N and PERERA BJC (2012) Indicator-based water sustainability assessment - A review. Sci. Total Environ. 438 357-371. [ Links ]
KALF FRP and WOOLLEY DR (2005) Applicability and methodology of determining sustainable yield in groundwater systems. Hydrogeol. J. 13 (1) 295-312. [ Links ]
KATIC PG and GRAFTON RQ (2012) Economic and spatial modelling of groundwater extraction. Hydrogeol. J. 20 (5) 831-834. [ Links ]
KRUSEMAN GP and DE RIDDER NA (1994) Analysis and Evaluation of Pumping Test Data (2nd edn.) International Institute for Land Reclamation and Improvement, Wageningen, The Netherlands. 377 pp. [ Links ]
LEE CH (1915) The determination of safe yield of underground reservoirs of the closed basin type. Trans. Am. Soc. Civ. Eng. 78 148-251. [ Links ]
LLAMAS MR, MARTINEZ-SANTOS P and DE LA HERA A (2006) The manifold dimensions of groundwater sustainability: An overview. International Symposium of Groundwater Sustainability, 23-27 January 2006, Alicante, Spain. [ Links ]
LLAMAS MR and GARRIDO A (2007) Lessons from intensive groundwater use in Spain: Economic and social benefits and conflicts. In: Giordano M and Villholth KG (eds.) The Agricultural Groundwater Revolution: Opportunities and Threats to Development. CAB, Wallingford, UK. [ Links ]
LOHMAN SW (1972) Ground-water hydraulics. USGS Professional Paper 708.United States Geological Survey, Washington, D.C. [ Links ]
LOHMAN SW AND OTHERS (1972) Definitions of selected groundwater terms. USGS Water-Supply Paper 1988.United States Geological Survey, Washington, D.C. [ Links ]
LOPEZ-GUNN E (2003) The role of collective action in water governance: a comparative study of groundwater user associations in La Mancha aquifers in Spain. Water Int. 28 (3) 367-378. [ Links ]
MAIMONE M (2004) Defining and managing sustainable yield. Ground Water 42 (6) 809-814. [ Links ]
MECHLEM K (2012) Groundwater governance - a global framework for action. Thematic Paper 6. Legal and Institutional Frameworks. GEF, Rome. [ Links ]
MEIER PM, CARRERA J and SANCHEZ-VILA X (1999) A numerical study on the relationship between transmissivity and specific capacity in heterogeneous aquifers. Ground Water 37 (4) 611-617. [ Links ]
MUKHERJI A and SHAH T (2005) Groundwater socio-ecology and governance: a review of institutions and policies in selected countries. Hydrogeol. J. 13 (1) 328-345. [ Links ]
OECD (2003) OECD Environmental Indicators - Development, Measurement and Use. OECD, Paris. [ Links ]
PIERCE SA, SHARP JM, GUILLAUME JHA, MACE RE and EATON DJ (2013) Aquifer-yield continuum as a guide and typology for science-based groundwater management. Hydrogeol. J. 21 (2) 331-340. [ Links ]
RSA (REPUBLIC OF SOUTH AFRICA) (1998) National Water Act. Act No. 36 of 1998. Government Printer, Pretoria. [ Links ]
RUDESTAM K and LANGRIDGE R (2014) Sustainable yield in theory and practice: Bridging scientific and mainstream vernacular. Ground Water. Early view online version. URL: http://onlinelibrary.wiley.com/doi/10.1111/gwat.12160/pdf (Accessed: 1 March 2014). [ Links ]
SEWARD P, XU Y and BRENDONCK L (2006) Sustainable ground-water use, the capture principle, and adaptive management. Water SA 32 (4) 473-481. [ Links ]
SEWARD P (2011) Challenges facing environmentally sustainable ground water use in South Africa. Ground Water 48 (2) 239-245. [ Links ]
SHAFER JM (1987) Reverse pathline calculation of time-related radius of influence in nonuniform flow. Ground Water 25 (3) 283-289. [ Links ]
SOPHOCLEOUS M (2010) Review: groundwater management practices, challenges, and innovations in the High Plains aquifer, USA - lessons and recommended actions. Hydrogeol. J. 18 (3) 559-575. [ Links ]
TAHER T, BRUNS B, BAMAGA O, AL-WESHALI A and VAN STEENBERGEN F (2012) Local groundwater governance in Yemen: building on traditions and enabling communities to craft new rules. Hydrogeol. J. 20 (6) 1177-1188. [ Links ]
THEIS CV (1935) The relation between the lowering of the piezometric surface and the rate and duration of discharge of a well using groundwater storage. Trans. Amer. Geophys. Union Vol. 16 (2) 519-524. [ Links ]
THEIS CV (1940) The source of water derived from wells. Civ. Eng. 10 (5) 277-280. [ Links ]
THOMAS HE (1951) The Conservation of Groundwater. McGraw Hill, New York. [ Links ]
VAN STEENBERGEN F (2006) Promoting local management in groundwater. Hydrogeol. J. 14 (3) 380-391. [ Links ]
VIVIER JJP (2013) Determination of sustainable groundwater yield: A Systems management approach based on the minimum groundwa-ter balance. 13th Biennial Groundwater Division Conference, 17-19 September 2013, Durban. URL: http://gwd.org.za/sites/gwd.org.za/files/01JJP%20Vivier Groundwater%20Sustainable%20Yield%20 Systems%20Approach1.pdf (Accessed: 16 March 2014). [ Links ]
VAN TONDER G (2010) Quoted in: Coetsee J (2010) Boorgatlisensies 'n nagmerrie. Landbouweekblad 5 Nov 2010. [ Links ]
VRBA J and LIPPONEN A (2007) Groundwater Resources Sustain-ability Indicators. IHP-VI Series on Groundwater No. 14. UNESCO, Paris. [ Links ]
WESTER P, MINERO RS and HOOGESTEGER J (2011) Assessment of the development of aquifer management councils (COTAS) for sustainable groundwater management in Guanajuato, Mexico. Hydrogeol. J. 19 (4) 889-899. [ Links ]
WIJNEN M, AUGEARD B, HILLER B, WARD C and HUNTJENS P (2012) Managing the Invisible: Understanding and Improving Groundwater Governance. World Bank, Washington DC. [ Links ]
ZHOU Y (2009) A critical review of groundwater budget myth, safe yield and sustainability. J. Hydrol. 370 (1-4) 207-213. [ Links ]
ZHOU Y (2011) Sources of water, travel times and protection areas for wells in semi-confined aquifers. Hydrogeol. J. 19 (7) 1285-1291. [ Links ]
Received 28 April 2014
Accepted in revised form 17 December 2014
* To whom all correspondence should be addressed. +2721 959 2911; fax: +2721 959 3126; e-mail: sewardp@vodamail.co.za














