Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
Water SA
versión On-line ISSN 1816-7950
versión impresa ISSN 0378-4738
Water SA vol.40 no.4 Pretoria oct. 2014
Analytical solutions for the recovery tests after constant-discharge tests in confined aquifers
Abdon Atangana
Institute for Groundwater Studies, Faculty of Natural and Agricultural Sciences, University of the Free State, Bloemfontein, 9300, South Africa
ABSTRACT
A new analytical solution for residual drawdown during the recovery period after a constant rate pumping test is described. A comparison between the proposed solution, existing solutions and experimental data from field observation are presented. The proposed analytical solution is in perfect agreement with the experimental data for α = 0.01, in contrast to the Cooper-Jacob solution. A new analytical solution for the determination of the skin factor without any restriction on the variables t and t' is derived. An analytical solution for the drawdown response in a confined aquifer that is pumped step-wise or intermittently at a different discharge rate is suggested. On the basis of the suggested solution, a new analytical solution for the analysis of residual drawdown data after a pumping test with step-wise or intermittently changing discharge rates is provided.
Keywords: recovery equations, residual drawdown, skin effect, variable discharges
INTRODUCTION
As soon as the pump is closed up after a test, the water levels in the well and the piezometers will start to rise. This rise in water level is referred to as residual drawdown, s'. In groundwater studies, this is expressed as the difference between the initial water level prior to the start of pumping and the water level measured at a time t' after the termination of pumping. In a hydraulic test, it is very important to measure the residual drawdown during the recovery period. Recovery test measurements allow the transmissivity of the aquifer under investigation to be determined more accurately. The residual drawdown field data are more reliable than the pumping test data because recovery occurs at a constant rate, whereas in practise, a constant discharge during pumping is often difficult to achieve (Kruseman and Ridder, 1994). For any well-flow equations, an adequate recovery equation can be mathematically represented (Kruseman and Ridder, 1994).
The concept of a skin effect is derived from petroleum engineering, which uses the concept to account for the head losses in the vicinity of the well (Ramey, 1982). If the effective radius of the well r is larger than the real radius of the borehole rw in groundwater studies, this concept is referred to as a positive skin effect. If it is smaller, the well is usually poorly developed or its screen is clogged and this is referred to as a negative skin effect (De Marsily, 1986). In groundwater studies, the theory behind this concept is that the aquifer is assumed to be homogeneous up to the wall of the borehole, while all the head losses are assumed to be concentrated in a thin, resistant skin against the wall of the borehole. In groundwater hydraulics, the skin effect is defined as a difference between the total drawdown observed in a well and loss component, assuming that the non-linear well losses are negligible (Kruseman and Ridder, 1994; Atangana, 2014; Atangana and Vermeulen, 2014; Cloot and Botha, 2006; Barker, 1986; Bear, 1972; Boonstra and Kselik, 2002).
In this paper a new analytical solution to the Theis recovery equation for the confined aquifer and the skin effect will be provided. It is very important to point out that the flow equation does not always give aquifer parameters accurately, because the data collected during the pumping test are obtained when the aquifer is under stress. However, the data collected after the pump is shut down are natural. Therefore, rather than estimating the aquifer parameters with the drawdown, which is the solution of the flow equation, one will instead consider the estimation with the recovery solution, which gives us the data while the aquifer is not under stress.
Confined aquifers and Theis's recovery method
In 1935, Theis (Theis, 1935) was the first to develop an equation for unsteady state flow, which introduced the time factor and the storativity as:

and provided a solution to this equation as:

where:
T is the transmissivity
S the storativity
Q the constant discharge rate
On the basis of Eq. (2) Theis developed his recovery method for confined aquifers. The Theis recovery method is widely used for the analysis of recovery tests.
Analytical solutions
After a constant rate pumping test, the residual drawdown during the recovery period according to Theis is given by:

It is worth noting that the above solution was derived under the following assumptions:
- The aquifer is confined
- The aquifer has a seemingly infinite area extent
- The aquifer is homogeneous, isotropic, and of uniform thickness over the area influenced by the test
- Prior to pumping, the piezometric surface is horizontal (or nearly so) over the area that will be influenced by the test
- The aquifer is pumped at a constant rate
- The well penetrates the entire thickness of the aquifer and thus receives water by horizontal flow
However, at the time in history that Theis's equation was derived, the presence of the exponential integral in this solution rendered the solution very difficult to handle. To have an expression that could be used for this purpose, Cooper and Jacob (Jacob, 1940; Jacob, 1944; Jacob, 1947) proposed an approximated solution to the Theis equation recovery equation as:

Cooper noticed that for the residual drawdown observations made in the near vicinity of the well after a sufficiently long pumping time, the terms beyond ln(u) or ln (u) in Eq. (4) become very small and can then be ignored. Then, for small values of u, u' < 0.01, the drawdown residual can be approximated by:

The above solution is that most often used in recovery tests because it is very easy to handle. However the condition under which the above solution is derived is not always true in practise, because it does not take into account the events taking place at the near vicinity of the well for a short time period. In this paper, an analytical solution is proposed to the Theis drawdown equation based on the equation derived by Atangana (2014):

On the basis of the above equation, an analytical solution to the Theis recovery equation is derived as:

The new parameter introduced in this solution can be viewed as the uncertainty that the above analytical solution will fit the field data for a fixed storativity S, S' and transmissivity T. Since there is always a possibility that the analytical solution will fit the experimental data for a given set of transmissivity and storativity, the new parameter introduced here will also be greater than zero, on the one hand. On the other hand, since it is not possible for the analytical solution to predict the aquifer parameters exactly, because in practise even the experimental data from field observation cannot exactly reveal the actual aquifer parameters under investigation and thus one would expect the new parameter to be less than one. Therefore, from the definition of the new parameter, we have 0 < α < 1.
Comparison of solutions
In order to check the validity of this proposed solution a comparison with existing solutions, including Theis and Cooper-Jacob residual-drawdown equations, is presented in Figs 1 and 2. To do this, a set of theoretical aquifer parameters was used. The following figures show the numerical solutions for residual-drawdown using Theis-, proposed- and Cooper-Jacob equations.

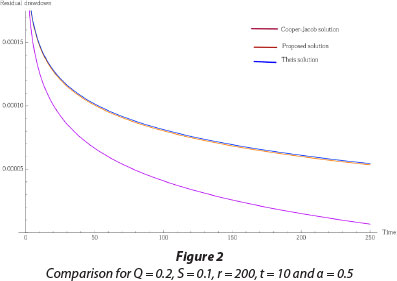
The above numerical comparison shows that the proposed solution predicts the same situation as Theis for any time and distance.
Comparison with experimental data
In order to test the accuracy of the proposed solution, a comparison with experimental data from field observation is presented in Fig. 3. To do this, experimental data from the pumping test performed by the Institute for Groundwater Studies, on one of their boreholes situated on the campus test site of the University of the Free State, were used. The test consisted of the pumping of the borehole at a constant discharge rate Q = 45.43 m3/h and monitoring the piezometric head at r = 50 m for 500 min. The pump was shut after 500 min and the residual drawdown was observed for 490 min. The aquifer test revealed a transmissivity of T =14. 6 and storativity of S = 0.0036. In order to find we fitted the analytical solution proposed in this paper to the observed data and a storativity of recovery or residual drawdown was determined. The experimental data are recorded in the table below.
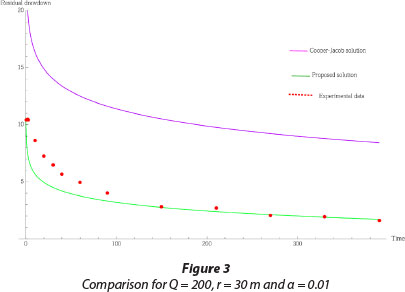

It is clear from Fig. 3 that the proposed solution is in good agreement with the observed residual drawdown for α = 0.01. It must be remembered, the Cooper-Jacob equation does not accurately predict the aquifer parameters, as can be seen in the figure below. The proposed solution is easier to handle and predicts more accurately the aquifer parameters, equivalent to the Theis equation. Here S' was revealed to be 0.00075. The red line in Fig. 3 corresponds to the solution as suggested by the Cooper-Jacob equation. The green line corresponds to the suggested solution, and the red dots correspond to the observed data from the real-world situation.
Recovery tests: determination of the skin effect
The concept of a skin effect originates from the discipline of petroleum engineering, which uses the skin effect to account for the head losses in the vicinity of the well (De Marsily, 1986). In groundwater studies, the aquifer is assumed to be homogeneous up to the wall of the borehole, while all the head losses are assumed to be concentrated in a thin, resistant skin against the wall of the borehole. In groundwater hydraulics, the skin effect is defined as a difference between the total drawdown observed in a well and loss component, assuming that the non-linear well losses are negligible (Kruseman and Ridder, 1994).
Addition of the skin effect to the Cooper and Jacob solution, and supposing that the non-linear well losses are so small that they can be neglected, a solution of the drawdown in a well that fully penetrates a confined aquifer and is pumped at a constant rate according to Cooper and Jacob is:
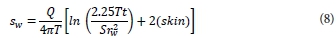
where:
skin 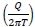 is the skin effect in meters skin is the skin factor with no units (dimensionless) and rw is in meters.
is the skin effect in meters skin is the skin factor with no units (dimensionless) and rw is in meters.
After the pump has been shut down, the residual drawdown at the well s'w according to the Cooper-Jacob equation, in a well for time 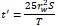 is given as:
is given as:

For time t = tp = total pumping time, Eq. (8) according to Cooper and Jacob becomes:

Here the difference sw(tp) and the residual drawdown s'w at any time t' according to Cooper and Jacob is:

Then for:
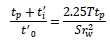
Thus Eq. (11) can be converted to the following:

The procedure for determining the skin factor has been investigated by many authors (Jacob, 1947).
Determination of the skin effect from the proposed solution
It is important to point out that the solution of Theis is an exact solution to the Theis equation, implying that this solution predicts more accurately the aquifer parameters and also the skin factor, than the Cooper-Jacob solution, although the Cooper-Jacob solution is much easier to work with. Therefore, adding the skin effect to the Theis equation and assuming that the non-linear well losses are so small that they can be ignored, and drawing on the work done by Atangana (2014) the following equation is obtained for drawdown in a well that fully penetrates a confined aquifer and is pumped at a constant rate:

The parameters involved remain the same as defined earlier. After the pump has been shut down, the residual drawdown in the well is given as:

It is very important to note that the above formula is derived without any restriction on the value of t and also t, as occurs in the case of that proposed by Cooper and Jacob (Eq. (5)). However, when t = t , which is the total time during which the water was taken out of the aquifer, then Eq. (13) can be converted to:
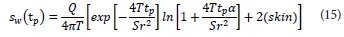
Nevertheless, by following the discussion presented earlier, one can obtain the difference between sw(tp) and at any given time according to the proposed solution is given as:
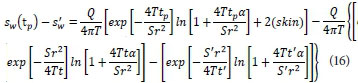
However for simphcity, one can put:

Such that:
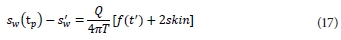
Therefore, with the above expression in hand, one can conclude that the skin effect can be given for any given time as:

The above formula is more practical since the skin effect can be calculated for any given time. The next concern now is to examine with care the recovery formula for variable-discharge rate.
Recovery tests for variable discharge rate
Variable discharge rate
In 1980 Birsoy and Summers presented an analytical solution for the drawdown response in a confined aquifer that is pumped step-wise or intermittently at different discharge rates (see Fig. 4). They obtained the expression for the drawdown in the aquifer at a time during the n-th pumping period of intermittent pumping by applying the principle of superposition to Jacob's approximation of the Theis equation (Eq. (1)) as:

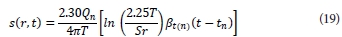
where:

where:
ti = time at which the i-th pumping period started
t-ti = time since the i-th pumping period started
t'. = time at which the i-th period ended
t_t'i = time since the i-th pumping period ended
Qi = constant well uninterrupted pumping
t'.i-1) = ti and the adjusted time βt(n)(t-tn) becomes:

is the discharge increment beginning at time ti.
Now, if the principle of superposition is applied to the proposed solution of the Theis groundwater flow equation (Eq. (1)), one obtains the following expression for the drawdown in the aquifer at time t during the n-th pumping period of intermittent pumping:
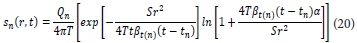
Dividing both sides of Eq. (20) by Q one obtains an expression for the specific drawdown:

The representative scheme underpinning the step-wise and intermittently changing discharge rates and resulting drawdown response is depicted in Fig. 4.
Recovery method for the test
To analyse the residual drawdown data after a pumping test with step-wise or intermittently changing discharge rates, the following expression based upon the proposed equation is suggested:

s' is therefore referred to as residual drawdown at t - t n> 0.
The assumptions used to derive the Birsoy and Summers analytical solution for the drawdown response in a confined aquifer that is pumped step-wise or intermittently at different discharge rates apply. This method is applicable if the assumptions listed earlier are satisfied in addition to the following which must be verified:
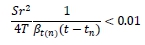
This is not always the case in practise. However the solution proposed in this paper for the same matter can be used under the assumption presented earlier and for any values of

which, as a matter of fact, gives more room for the possibility of prediction of aquifer parameters at any time and distance than the existing solution.
CONCLUSION
The rate of recovery is converted to a rate of flow into the well. The well is stressed by removing water (by pumping or bailing) until the available head in the well is reduced by at least 80%. Water levels are monitored as the well recovers and recorded, along with the time since pumping/bailing ceased. Monitoring of recovery can stop when water levels have recovered to 50% of the original available head. The volume of water produced from the well between the maximum drawdown and 50% drawdown level is calculated, taking into account storage within the well casing and within the filter-packed annulus. It is important to note that the aquifer parameters can be obtained more accurately during the recovery test, since the aquifer is not under stress. It is therefore important to provide a more accurate solution for the so-called residual drawdown.
This paper provides an analytical solution for residual drawdown during the recovery period after a constant rate pumping test. To test the accuracy of the proposed solution, the theoretical parameters were used and the proposed solution compared to the Theis and Cooper-Jacob solutions. The comparison revealed that the proposed solution is in better agreement with the Theis solution than the Cooper-Jacob solution. In order to assess the accuracy of the proposed theory, the solution was compared with experimental data from a pumping test performed by the Institute for Groundwater Studies. The test consisted of the pumping of a borehole at constant discharge rate Q = 45.43 m3/h and monitoring the piezometric head at r = 50 m for 500 min. The pump was shut down after 500 min. The residual drawdown was observed for 490 min. The aquifer test revealed a transmissivity of T =14. 6 and storativity of S = 0.0036. In order to find S', the proposed solution was fitted to the observed data and a storativity of recovery or residual drawdown was determined. A derivation of an analytical method in finding the skin factor was proposed. Finally the derivation of a solution for residual drawdown after a pumping test with step-wise or intermittently changing discharge rates was proposed.
REFERENCES
ATANGANA A (2014) Drawdown in prolate spheroidal-spherical coordinates obtained via Green's function and perturbation methods. Commun. Nonlinear Sci. Num. Simul. 19 (5) 1259-1269. [ Links ]
ATANGANA A and VERMEULEN PD (2014) Analytical solutions of a space-time fractional derivative of groundwater flow equation. Abstr. Appl. Anal.. Article ID 381753, 11 pp. DOI:10.1155/2014/381753. [ Links ]
BARKER JA (1988) A generalized radial flow model for hydraulic tests in fractured rock. Water Resour. Res. 24 (10) 1796-1804. [ Links ]
BEAR J (1972) Dynamics of Fluids in Porous Media. American Elsevier Environmental Science Series. Elsevier, New York. [ Links ]
BOONSTRA J and KSELIK RAL (2002) SATEM 2002: Software for Aquifer Test Evaluation. International Institute for Land Reclamation and Improvement, Wageningen. [ Links ]
BIRSOY VK and SUMMERS WK (1980) Determination of aquifer parameters from step tests and intermittent pumping data. Groundwater 18 137-146. [ Links ]
CLOOT A and BOTHA JF (2006) A generalised groundwater flow equation using the concept of non-integer order derivatives. Water SA 32 (1) 1-7. [ Links ]
DE MARSILY G (1986) Quantitative Hydrogeology. Groundwater Hydrology for Engineers. Academic Press Inc., San Diego. 440 pp. [ Links ]
KRUSEMAN GP and DE RIDDER NA (1994) Analysis and Evaluation of Pumping Test Data (2nd edn). International Institute for Land Reclamation and Improvement (ILRI), Wageningen. [ Links ]
JACOB CE (1940) On the flow of water in an elastic artesian aquifer. Trans. Am. Geophys. Union 21 574-586. [ Links ]
JACOB CE (1944) Notes on determining permeability by pumping tests under water table conditions. US Geological Survey, Reston. [ Links ]
JACOB CE (1947) Drawdown test to determine effective radius of artesian well. Trans. Am. Soc. Civ. Eng. 112 1047-1064. [ Links ]
MATTHEWS CS and RUSSELL DG (1967) Pressure build up and flow tests in wells. Soc. Petrol. Eng. Am. Inst. Min. Met. Eng. Monograph 1. 67 pp. [ Links ]
RAMEY HJ (1982) Well loss function and the skin effect: A review. In: Narasimhan TN (ed.) Recent Trends in Hydrogeology. Geological Society of America Special paper 189. 265-271. [ Links ]
THEIS CV (1935) The relation between the lowering of the piezometric surface and the rate and duration of discharge of well using groundwater storage. Trans. Am. Geophys. Union 16 519-524. [ Links ]
 Correspondence:
Correspondence:
Abdon Atangana
+27 78 294-8604
e-mail: abdonatangana@yahoo.fr
Received 11 April 2014
Accepted in revised form 3 September 2014














