Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
Water SA
versión On-line ISSN 1816-7950
versión impresa ISSN 0378-4738
Water SA vol.40 no.3 Pretoria jun. 2014
http://dx.doi.org/10.4314/wsa.v40i3.20
Determining hydraulic parameters of a karst aquifer using unique historical data from large-scale dewatering by deep level mining - a case study from South Africa
Aljoscha SchraderI, II; Ewald ErasmusII; Frank WindeII, *
IFaculty of Natural Sciences, Potchefstroom Campus, North-West University, Private Bag X6001, Potchefstroom 2520, South Africa
IIMine Water Research Group, Vaal Campus, North-West University, South Africa
ABSTRACT
Although karst aquifers constitute some of the most important water resources worldwide, generally accepted methods for reliably characterising their hydraulic properties are still elusive. This paper aims at contributing to the discussion by a first-ever attempt to utilise various sets of unique historical data derived from draining a large dolomitic karst aquifer by deep-level gold mines in South Africa. In contrast to conventional pumping tests which only penetrate thick aquifers to a limited extent from surface, this draining took place at the very bottom of the aquifer offering the rare opportunity to capture its entire thickness of nearly a kilometre. The datasets have been treated as analogies to conventional pumping tests applying various types of analytical methods designed for porous media. In order to increase the robustness of the results and to account for specific local conditions a total of four different analytical methods were applied to calculate (horizontal) transmissivity and storage coefficients. The obtained values, in general, compare favourably to previous studies in the area and values reported in literature for similar aquifer types confirming earlier findings that Darcy-based methods can be successfully applied to karst aquifers if the scale of investigation is large enough. Apart from improving the understanding of local karst hydrology the present study also aimed at retrieving and preserving valuable and unique historical datasets that otherwise would have been lost for scientific evaluation and the proactive preparation for mine closure.
Keywords: karst, dewatering, deep level mining, porous medium analytical methods, transmissivity, storage coefficient, Far West Rand
INTRODUCTION
The main purpose of this paper is to explore the usability of historical data gathered over 4 decades of deep-level gold mines dewatering an overlying dolomitic karst aquifer in the Far West Rand (FWR), South Africa, in order to determine hydrologi-cal parameters. Based on the conceptual understanding that the set-up under which these data were generated resembles an ultra-large pumping test covering the thickness of the entire karst aquifer, standard analytical methods typically used in pumping tests were applied.
At the same time the study attempts to preserve large sets of unique data that are regarded as most valuable for predicting hydraulic conditions after future mine closure. The latter is particularly important as mining-induced modifications of the natural hydrogeological setting in the FWR will, in all likelihood, have profound impacts on post-mining land use as well as on the long-term availability of surface and groundwater resources.
Hydrogeological conditions of the study area Geological setting
The karstified dolomites of the FWR goldfield, southwest of Johannesburg, host some of the largest groundwater resources in South Africa, as well as a range of strong associated karst springs. Gold-bearing reefs below the dolomite have been subject to extensive deep-level mining for many decades. Following a sudden and nearly catastrophic inrush of dolomitic groundwater to the Driefontein Mine in October 1968, it was found necessary to dewater the dolomitic aquifer above the mine void. Owing to the large-scale lowering of the regional groundwater table many of the karst springs dried up. Simultaneously, large quantities of hydrologic data were recorded, some of which are used in this study. The historical and hydrogeological context of the latter data is briefly outlined in this section.
The overall geological situation is depicted in Fig. 1, indicating a north to south cross-section in the FWR as well as the associated stratigraphy.
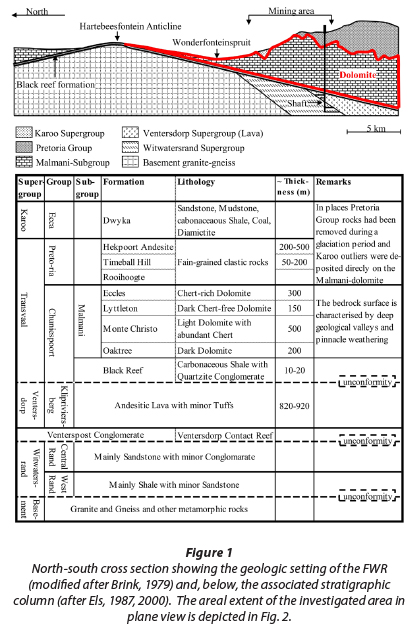
The dolomite is subdivided into several so called 'groundwater compartments' by approximately north to south-trending intrusive, nearly-vertical dykes, which act as groundwater flow barriers (De Kock, 1964; Brink, 1979). Compartments in the area concerned are the Venterspost, Bank, Oberholzer and, lastly, Boskop-Turffontein Compartments. Data analysed in this study exclusively refer to the Bank Compartment. The northern aquifer boundary is set by granites of the Hartebeesfontein Anticline (Fig. 1). To the south a gradual boundary forms where rocks of the Pretoria Group increasingly overlie the dolomite, preventing pronounced karstification through shielding the underlying dolomite from infiltrating rainfall (Enslin and Kriel, 1968; Brink, 1979). According to Swart et al. (2003), the shielding effect creates a boundary where the thickness of the Pretoria Rocks is at least 150 m. The Ventersdorp Supergroup Lava and Witwatersrand Supergroup Quartzites do not store significant volumes of groundwater (De Kock, 1964), and therefore constitute the lower flow boundary of the overlying dolomite. The storativity and transmissiv-ity of the dolomites decrease with depth. Figure 3 depicts the vertical zonation provided by Morgan and Brink (1984) and zones of storativity as listed by Winde et al. (2006).
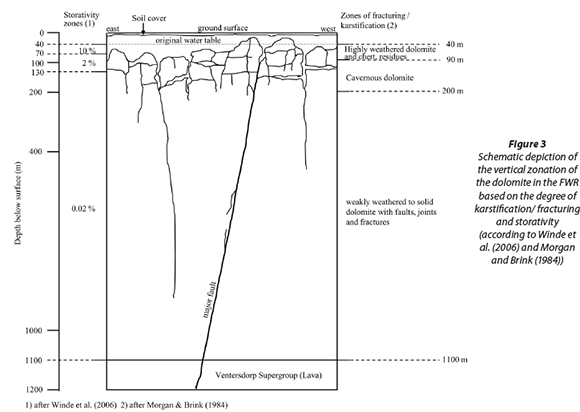
The zone just below the original water table (OWT) extends to a depth of about 70-90 m below surface (mbs) and has a thickness of up to 50 m. It consists mainly of the residues of leached and highly weathered dolomite (wad) as well as of chert and insoluble residues. Owing to the fine-grained nature of wad and the other sediments this zone resembles a porous layer. Below this zone water is stored in a network of large cavities, solution conduits and solution-widened fractures. This zone of 'cavernous dolomite' extends to depth of maximal 200 mbs. This is followed by a zone of weakly weathered to solid dolomite with intersecting vertical tectonic faults, joints and fractures that may in cases be widened by solution (Morgan and Brink, 1984). Based on estimates from various authors, Winde et al. (2006) identified 3 zones of storativity, as shown in Fig. 3. In accordance with the storativity of the various zones, the total volume of groundwater stored in the Bank Compartment has been estimated to be between 663 (derived from Winde et al, 2006) and 2 200 Mm3 (million m3) (Schwartz and Midgley, 1975). Values for the transmis-sivity of the dolomite differ within a broad range, which is typical for karst. Values between 1 000 and 25 000 m2/d have been recorded (Enslin and Kriel, 1959; Schwartz and Midgley, 1975; Bredenkamp et al, 1991).
Dewatering of the Bank Compartment
Dewatering of the Bank Compartment was implemented by West-Driefontein Mine from June 1969 onwards, after a hazardous inrush in October 1968, which occurred after mining operations encountered a major fault, namely, the so-called 'Big Boy fault' (Swart et al., 2003a). In this context the term 'dewatering' refers to the process of pumping ingress water from the mine void to surface and then discharging it outside the compartment boundaries at a rate that exceeds the natural groundwater recharge rate (Wolmarans, 1982). This results in gradual lowering of the water table reducing the water pressure above the mine void and thus the associated ingress volume. Dewatering is completed when the falling water table reaches a level at which the ingress rate equals the rate of the natural recharge of that particular compartment. Although the water table is lowered by several hundreds of meters in places, the compartment is not 'dewatered' in the true sense of the word but still contains significant volumes of groundwater (Wolmarans, 1982).
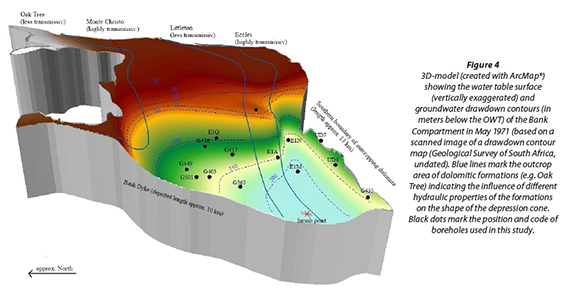
Most of the active drawdown of the groundwater table, which as a matter of policy commenced soon after the inrush, had been completed by 1974. By then the sustained groundwa-ter abstraction through the former inrush point had created a steep depression cone in the south-western corner of the Bank Compartment (Fig. 4). Swart et al. (2003) estimate that about 90% of all water pumped by West- and East Driefontein together still enters the mine void via the Big Boy fault.
Characterisation of the used historical data
The data used in this study consist of a variety of formats including diagrams, unpublished reports, maps at various scales, formats and age, pumping and drilling data from mine operators and water-level observations that were scattered over a multitude of sources including private collections, archives, mining companies, governmental departments, and academic institutions (Fig. 5). The data had been collected over decades by Professor EJ Stoch (Mine Water Research Group, North-West University), who prevented many of them from being irretrievably lost.
After retrieving the original data, most had to be converted manually into usable electronic formats for their subsequent compilation and collation in a dedicated database. Given the large amounts of funds spent at the time on generating these datasets and their uniqueness in terms of the scale and nature of associated events, which can never be repeated, their preservation was deemed imperative. Apart from possibly contributing to an improved understanding of karst hydrology in general, these data are also regarded to be of crucial importance for the proactive preparation for future mine closure in the FWR, as the largest and by far most water-rich active goldfield in South Africa. Preserving the data for future scientific use also counteracts the widespread 'loss of institutional memory' in South Africa where changing structures in Government as well as the mining industry often result in the loss of existing data, information, knowledge and expertise (Stoch and Winde, 2010).
This paper focuses exclusively on drawdown data and pumping figures associated with the Bank Compartment (Fig. 2). The total dataset can be subdivided into 3 distinctly different datasets which are briefly characterised.
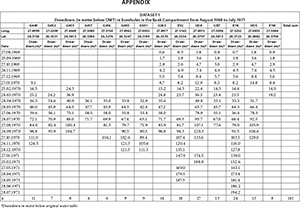
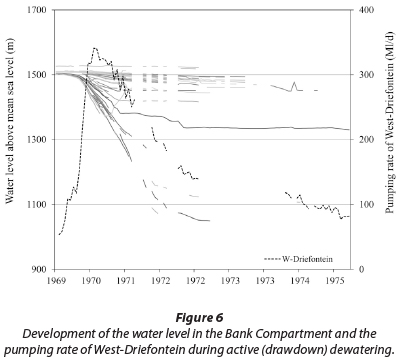
- Dataset 1 ('drawdown dewatering') originates from the dewatering of the Bank Compartment from 1969 to 1974, when the water table was actively lowered by mines pumping out up to 4 times more water than what naturally could be replenished. The pumping rate of West-Driefontein Mine that dewatered the compartment at the time is shown in Fig. 6. Also shown are drawdown observations as available for a total of 66 boreholes located in the Bank Compartment, mostly drilled by the gold mines for this specific purpose. For reasons discussed later, this study uses only observations from 14 boreholes within a distinct radius from the centre of the depression cone and a time period of 24 months, as listed in the Appendix. The geographical location of the used boreholes is shown in Figs 2 and 4.
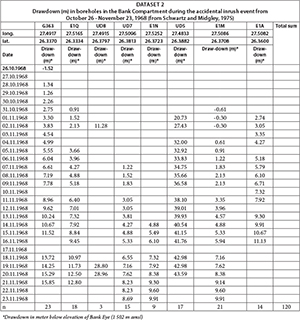
- Dataset 2 ('inrush event') originates from the accidental inrush of large volumes of dolomitic groundwater into the West-Driefontein Mine over a period of 4 weeks in October-November 1968. The event caused a water-level drawdown of up to 50 m in places, which was monitored by the mine in a total of 15 boreholes and led to the temporary drying up of the Bank Eye within a few days after the inrush started. This study uses drawdown data from 8 boreholes within the defined radius from the centre of the depression cone (see Appendix). The inrush volume was estimated at between 228 and 386 Ml/d (Anonymous, 2005, cited in Winde et al., 2006; Enslin et al., 1977). The latter volume, estimated 3 days after the beginning of the event (quoted in Cousens and Garrett, 1969) appears to be the most cited and more reliable one and is thus used in this study.
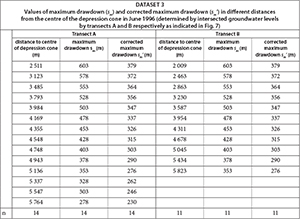
- Dataset 3 ('steady-state dewatering') consists of a snapshot of water-level data for the dewatered Bank Compartment from June 1996, representing the prevailing conditions after the active drawdown of the water table was achieved. Water level data (see Appendix) were digitised from the ground-water contour map shown in Fig. 7.
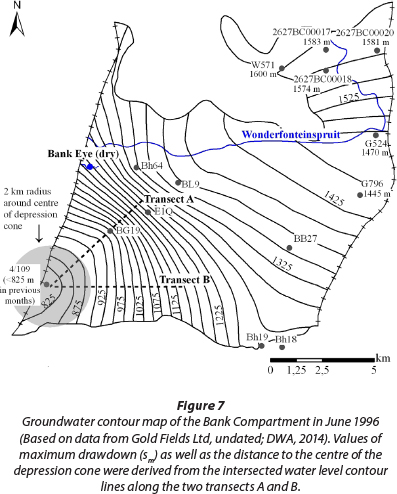
The data represent quasi steady-state conditions of the aquifer, which is characterised by a stable water table that is maintained by a constant pumping rate. Table 1 gives a condensed overview on the characteristics of the three datasets.
Pumping tests as an analogy to analyse historical data
As can be seen in Fig. 8, the hydrologic setting during dewatering of the Bank Compartment was very similar to a common pumping test setting except that the associated drawdown is much larger than commonly achieved.
The pumping well in the Bank Compartment is represented by the Big Boy fault, which in the following is called 'inrush point' (approx. coordinates: 27.477774, -26.361681; Fig. 8).Thus the above situation resembles an ultra-large pumping test, which allows the application of generalised analytical methods developed for pumping test analysis. Descriptions of these methods can, amongst others, be found in McWhorter and Sunada (1977) or Langguth and Voigt (2004).
Selecting appropriate analytical methods for the Bank Compartment
The first analytical method for the evaluation of (transient) pumping test data was developed by Theis (1935) for an aquifer with very specific conditions, as listed in Table 2. Today a wide range of those analytical methods exist, each applying to very specific aquifer conditions. Table 2 lists the methods applied in this study including required aquifer conditions in relation to conditions found in the Bank Compartment.
Given the large scale of the karst aquifer investigated in this study, it was found appropriate to apply porous-media analytical methods. While applying simple analytical methods comes with a number of limitations, this was regarded as acceptable given that the study aims at a first evaluation of the aquifer rather than developing a comprehensive (numerical) model. Consequently, 3 different porous-media analytical methods were applied as well as the analytical software tool MLU for Windows (Hemker and Post, 2012).
Treating the aquifer like a homogeneous porous medium is based on the assumption that the large area considered here represents a representative elementary volume (REV). The REV is defined as the smallest volume over which microscopic fluctuating parameters can be statistically meaningfully described by averaged parameters representative of the whole (Bear, 1972), i.e., that over a certain volume an average hydraulic conductivity can be determined that adequately describes the flow discharged from the block, despite the fact that the microscopic (local) hydraulic conductivity fluctuates within the block (due to different porosity types, i.e., porous matrix, fracture and conduit porosity).
Even though the aquifer shows characteristics of all major aquifer types (porous, fractured and karst), analytical methods for double-porosity (for fractured rocks) were deliberately ignored since assumptions underlying those methods hardly comply with the complex geological setting found in the Bank Compartment. Moreover, the application of double porosity methods is more complex and often requires rather detailed hydrogeological information that is not always available. The unusual drawdown curves as well as the uncertainty associated with the gathering of the data - this refers, for example, to the constantly changing pumping rate, dewatering of fractures and the fact that measurements in boreholes only started some time after the abstraction of water commenced - render the application of double-porosity methods problematic (e.g., obtaining a unique fit of drawdown and type curves) and would even hamper the interpretation of results by adding further vagueness.
In order to reduce the interference by double-porosity effects, this study considers only observation boreholes with a large distance (>2 000 m) from the inrush point. This is based on findings of Bourdet and Gringarten (1980), indicating that double-porosity effects are confined to a limited area surrounding the pumping well and can be neglected outside this area where drawdown is described by the type-curve of Theis. The above distance was determined from carefully observing drawdown data as well as preliminary calculations showing that boreholes closer to the inrush point are characterised by different drawdown behaviour.
For this particular case, a further advantage of porous-media analytical methods over double-porosity methods exists, as they allow for considering no-flow boundaries present in the aquifer (i.e. Bank Dyke). The analytical methods used in the study were that of Thiem (1906), Theis (1935) and Stallman (as quoted in Ferris et al., 1962) together with the software tool MLU (multi-layer unsteady state) for Windows (Hemker and Post, 2012).
The rather rigid requirements of the Theis methods are listed in Table 2. All other methods used here are, in essence, variations of the Theis method that try to overcome some of the limitations by introducing certain modifications. The Stallman method, for example, can be used if the depression cone reaches one or more aquifer boundaries, as is the case in the Bank Compartment (Fig. 4). The Thiem method, on the other hand, only applies to steady-state groundwater flow conditions in a pumped aquifer and is therefore limited to Dataset 3. MLU for Windows is a software tool for calculating drawdowns and analysing pumping test data. It combines an analytical solution technique with numeric applications (Stehfest's numerical method), the superposition principle and the Levenberg-Marquardt algorithm. Detailed information on the theoretical background is given by Hemker and Maas (1987) and Hemker (1999). Like other analytical methods, MLU assumes simplified aquifer conditions such as homogeneity, isotropy and the infinite horizontal extent of the aquifer (Carlson and Randall, 2012). However, despite making these assumptions MLU allows for analysing more complex aquifer conditions than the other methods applied in this study. For the case study at hand this is of particular importance as MLU is able to account for the variable pumping rate that affects the largest of the three datasets (Dataset 1, Fig. 6). All other analytical methods theoretically require at least a couple of drawdown observations during a period of stable pumping. MLU can also consider the influence of aquifer boundaries on the drawdown observations (as does the Stallman method) and thus considers the hydrogeologic setting more adequately, compared to the other methods used in this study.
Application of the selected analytical methods
Owing to the large drawdown observed in Datasets 1 and 3, the saturated thickness of the aquifer is significantly reduced, which creates unconfined (phreatic) water table conditions. However, the analytical methods applied require confined aquifer conditions. To overcome this obstacle the observed drawdown data had been adjusted by transferring values of observed drawdown (s) into the so-called corrected drawdown (s') data using the method of Jacob (1963).
The analytical methods applied in this study are well-established standard methods for analysing pumping test data. Therefore the technical details are only briefly touched on. For more information the original literature may be consulted (e.g. Theis, 1935; Kruseman and De Ridder, 1991).
Theis method
Drawdown curves of Datasets 1 and 2 as well as the Theis type curve are depicted in Fig. 9. Each data curve was brought to match with the type curve by shifting the curves parallel to the axes as illustrated in Fig. 10.
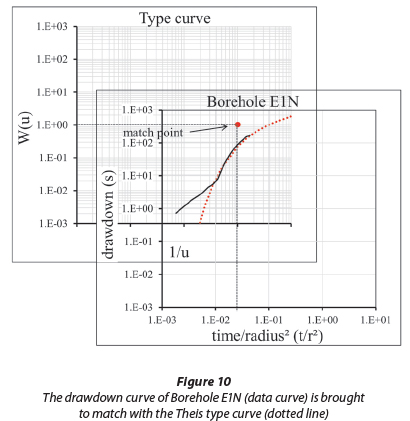
Following the advice of Kruseman and De Ridder (1991), more weight was given to data gathered towards the end of the pumping test while matching both curves. According to the authors the late-time data (Dataset 1) would reflect the combined fracture and matrix system and can be described by the Theis equation. The curves at early times show a deviation of the data from the Theis model, which is likely to be due to the ignoring of double porosity effects.
A match point was chosen, and corresponding values for W(u), 1/u, t/r2 and s were read from the axis. These values were inserted into the Theis equation (T =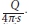 · W(u) and S =
· W(u) and S = 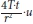 ) in order to calculate the transmissivity (T) and the storage coefficient (S). The calculation also requires the pumping rate (Q) at which the aquifer was pumped during the observed drawdown. In Dataset 1 the aquifer was pumped at a variable rate that cannot be accommodated in the Theis equation. Therefore an average pumping rate over the 24-month observation period had to be calculated (252 Mℓ/d). For Dataset 2 the pumping volume was 386 Mℓ/d.
) in order to calculate the transmissivity (T) and the storage coefficient (S). The calculation also requires the pumping rate (Q) at which the aquifer was pumped during the observed drawdown. In Dataset 1 the aquifer was pumped at a variable rate that cannot be accommodated in the Theis equation. Therefore an average pumping rate over the 24-month observation period had to be calculated (252 Mℓ/d). For Dataset 2 the pumping volume was 386 Mℓ/d.
Stallman method
The Stallman method (first quoted in Ferris et al., 1962) is used in the case when a pumping test is conducted close to an aquifer boundary. In such cases the assumption of the Theis method, i.e., the infinite extent of the aquifer, is no longer valid and the drawdown in the observation boreholes will be different from the drawdown that would occur in an (seemingly) infinite aquifer. In order to account for the resulting difference, the Stallman solution uses modified type curves while still employing the principle of curve matching (superposition). The method is based on the theory of 'image wells' described by Ferris (1959). The theory replaces the bounded aquifer with one pumping well by assuming a hypothetical infinite aquifer that is pumped at 2 wells as explained for Fig. 11.
MLU for Windows
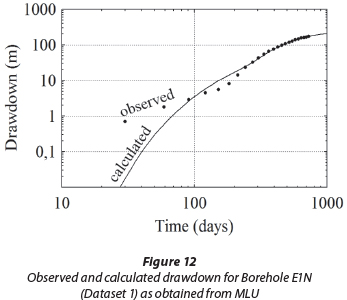
As a third method, MLU for Windows was applied to Datasets 1 and 2. For detailed information on the mode of operation of MLU the reader is referred to the software manual (i.e., Hemker and Post, 2012). The aquifer was treated as a single-layered aquifer of 810 m thickness. Each observation borehole was evaluated separately. An image well was set in order to account for the Bank dyke as no-flow boundary. MLU requires initial estimates for transmissivity and the storage coefficient. For that purpose values calculated from the Theis method were used. MLU was set to estimate both parameters, i.e., transmissivity and the storage coefficient, simultaneously. In order to optimise both parameters, MLU calculates the drawdown curve that fits the observed drawdown curve the best. Figure 12 displays the curve of calculated and observed drawdown of Borehole E1N (Dataset 1) as an example. Similar results were obtained for other boreholes. Figure 12 shows a good fit of observed and calculated values except for early time drawdown, which shows that the aquifer behaviour at early times differs from the model presumed by MLU.
Thiem method
The Thiem (1906) method was used to evaluate Dataset 3. It uses values of maximum drawdown (s ) measured at different distances from the centre of the depression cone to calculate the transmissivity. The pumping rate that maintained the depression cone was 61 Mℓ/d. Measurements of maximum drawdown were made in 2 directions to representatively cover the aquifer (Transects A and B, Fig. 7). Obtained values of maximum drawdown are listed in the Appendix (Dataset 3).
For both transects (A and B), values of corrected drawdown sm' are plotted against the corresponding distance (log-scale) to the centre of the depression cone (Fig. 13).
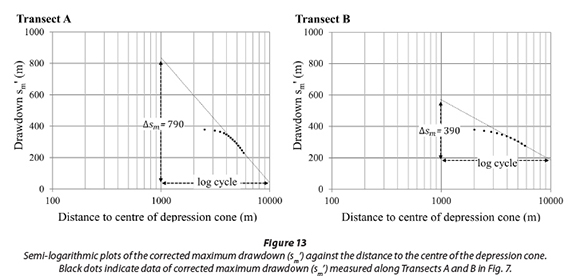
Then the best-fitting linear regression line and the slope As (maximum drawdown difference per one logarithmic unit of distance) are determined. The deviation of the observed drawdown from the regression line shows that drawdown towards the centre of the depression cone differs from what the method predicts for a homogeneous and porous aquifer. A reason for this could be that a vertical flow component increasingly impacts on the drawdown with decreasing distance to the inrush point. Therefore the values close to the inrush point were ignored while adjusting the best-fitting linear regression line.
Finally the Thiem equation (Q = 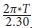 * Δsm ) is used to calculate the transmissivity. It is not po ssible t o determine the storage coefficient from the Thiem method.
* Δsm ) is used to calculate the transmissivity. It is not po ssible t o determine the storage coefficient from the Thiem method.
RESULTS AND DISCUSSION
Values of transmissivity and storage coefficients as derived from the four analytical methods are listed in Table 3.
Table 4 provides a condensed overview of the obtained T- and S-values for each analytical method and the associated dataset.
Values of transmissivity of individual boreholes show a high variability (relative standard deviation (SD) around 50%), which one would expect for a karstified aquifer. This indicates that the REV-concept is only applicable to a certain degree as expanding the investigated area (or adding additional observation boreholes) could significantly change the obtained average value. On the other hand, the fluctuations are small enough for deriving an order of magnitude for the transmissivity.
Sizable differences also exist between the results of the various analytical methods within a particular dataset.
For Dataset 1, transmissivities from the Theis and Stallman method are significantly lower than those for MLU. This difference is most probably attributable to the fact that both analytical methods (Theis and Stallman) do not consider the variable pumping rate, which affects Dataset 1 (Fig. 6). In contrast, in Dataset 2 the aquifer was pumped at a stable rate. Hence, values for the Stallman method differ only slightly from MLU. However, the average transmissivity received by the Theis method is still considerably below that of MLU. This is because MLU considers the influence of the no-flow boundary, i.e., the Bank Dyke, which the Theis method does not. Therefore, it is believed that for Dataset 1 MLU yields the most reliable results, while for Dataset 2 this is true for MLU and the Stallman method.
Results of transmissivity derived from inrush data (2 468 m2/d) are, on average, one order of magnitude higher than the dewatering data (285 rm/d). One possible explanation for this significant difference is that the two datasets represent very different thicknesses of water-filled (saturated) dolomite. The much higher T-value (2 468 m2/d) was derived from the completely water-filled aquifer, with all vertical zones of the dolomite being saturated (Fig. 3). In contrast, the 10-times lower transmissivity (285 m2/d) only represents the aquifer after the upper ~200 m below the OWT have already been dewatered. Therefore this value reflects only the zone of 'fractured and solid dolomite and does not consider the highly transmissive zone above it. In principle this is also true for the transmissivity obtained from the Thiem method. But since the latter does not take into account the no-flow boundary it is not considered in the following interpretation. Figure 14 summarises the calculated average values of hydraulic conductivity in relation to corresponding zones of karstification and storativity.
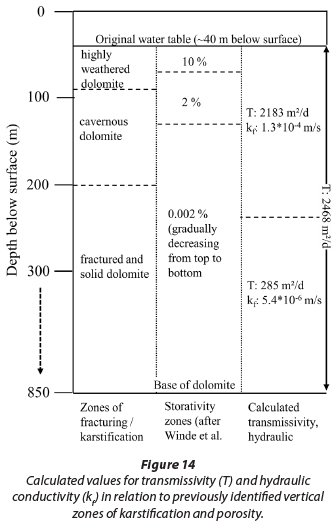
Values of hydraulic conductivity calculated for individual boreholes range from 7.0*10-5 to 3.1*10-4 m/s for the upper 200 m. For greater depths, values range from 2.9*10-6 to 1.0*10-5 m/s (Table 3). Figure 15 displays ranges of hydraulic conductivity in relation to values found in literature for similar aquifers.
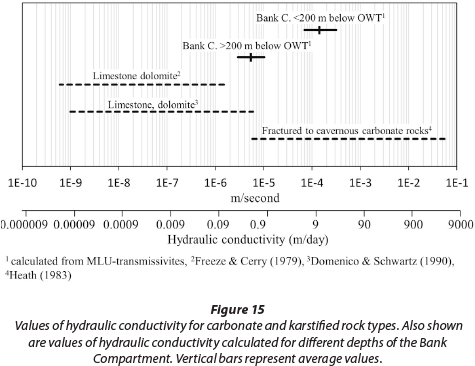
It can be seen that values from >200 m below the OWT concur with weakly fractured to solid dolomite. Values from above 200 m comply with moderately fractured to cavernous carbonate rocks. Thus values are in general agreement with what one would expect for the respective zones. The transmissivity of 2 468 m2/d calculated in this study is consistent with the value of 2 983 m2/d that Enslin and Kriel (1959) obtained for the similar nearby compartments (using an unspecified method), and the value of 1 818 m2/d that Bredenkamp (1991) obtained for the nearby Gemsbokfontein Compartment using the double-porosity model of Boulton and Streltsova (1977). Thus indications are that results of MLU and the Stallman method (in Dataset 2) have a realistic order of magnitude. To a certain degree this supports the argument that realistic results can be obtained from applying porous-media analytical methods to non-porous aquifers, provided the spatial scale of investigation is large enough (i.e., not considering a single karst channel or fracture, for example, but a large network of interconnected conduits with varying transmissivities). This, however, should not be seen as proof that those methods are in general applicable to all karst aquifers, given the deviation between the theoretical model of porous-media methods and the actual hydrogeologic situation as discussed in the section above.
Less reliable, however, are the calculated storage coefficients. Not much weight at all should be given to the storage coefficients obtained from Dataset 1 as these values display a so-called 'distance-dependency', as illustrated in double-logarithmic plots (Fig. 16).
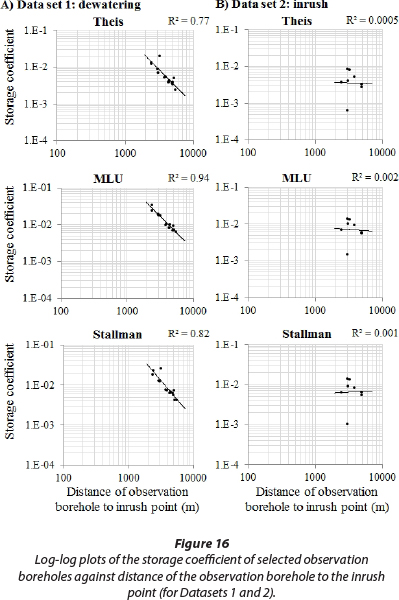
The plots show that the storage coefficient of individual boreholes increases with decreasing distance of the borehole to the pumping well (here: inrush point). This phenomenon was first recognised in South Africa by Bredenkamp et al. (1991), applying different analytical methods to a similar dolomitic aquifer. Later the same distance-dependency of storativity values was found in numerous fractured and karst aquifers throughout South Africa (Kirchner and Van Tonder, 1995). A possible explanation provided in literature is related to the concept of double-porosity. Porous-media analytical methods do not consider that the groundwater flow in fractured/karst aquifers is governed by different pressure gradients that develop between large fractures/conduits and the pore-matric/small fractures during drawdown. The generated pressure gradients are larger in close proximity to the pumping well and decrease with increasing distance, possibly explaining the distance-dependency of the associated storage coefficients (Neuman, 1994, personal communication quoted in Kirchner and Van Tonder, 1995). The problem of distance-dependency, however, is not restricted to porous-media analytical methods, as Van Tonder et al. (2002) showed that it also appears when applying double-porosity analytical methods that claim to account for the very double-porosity effects that are thought to cause the dependency.
For some reason the distance-dependency of the storage coefficient does not appear in values for Dataset 2 (Fig. 16), which warrants an interpretation. An average value of 0.0067 is derived from MLU and the Stallman method. This equals a storativity of 0.67 % (uniform over the entire thickness). Values of storativity for different zones quoted in Fig. 14 average to 0.5% if the dolomite is treated like a homogenous unit. Thus the value derived from MLU and Stallman is in the same order of magnitude as previous estimates even though it does not consider vertical changes in storativity.
Estimating the total volume of water stored in the dolomite of the Bank Compartment based on a porosity of 0.67% results in some 923 Mm3. (For this estimation the dolomite aquifer was assumed to extend approx. 1 070 m south of the southern border of the dolomite outcrop area, where the Pretoria Group rocks (dipping approx. 8°) reach a thickness of 150 m. This results in an areal extent of some 170 Mm2 The average depth of the dolomite was assumed to be 810 m. By this means the volume of the dolomite was estimated at 1.38*10+11 m3.) This falls between previous estimates for the Bank Compartment ranging from 663 Mm3 (following from Winde et al., 2006) to 2 200 Mm3 (Schwarz and Midgley, 1975), with Brink (1975) suggesting that the latter value probably represents an overestimation.
SUMMARY AND CONCLUSIONS
In the course of several decades of deep-level gold mining in the FWR, significant amounts of hydrogeological data were gathered relating to accidental as well as deliberate draining of a large overlying and highly karstified dolomitic aquifer.
Given the uniqueness of the situation, where an over 800 m-thick aquifer was dewatered literally by 'pulling the plug' at its very bottom - something only possible for deep-level mining operations - and the spatial and temporal scale of related events, it was deemed to be of scientific importance to preserve the associated data and prevent their irretrievable loss through diligent compilation in a dedicated database where they are available to scientists for further evaluation.
In total, 3 different datasets are analysed, all consisting of weekly to monthly groundwater-level measurements and associated daily pumping volumes that were generated during an accidental inrush event into the deep-level mine void and the subsequent dewatering of the overlying karst aquifer over the next 40+ years.
This paper is a first-ever attempt to use these data for characterising the hydraulic properties of the drained Bank aquifer, hoping that the unique situation and extreme scale of the associated events will provide new aspects for understanding the still challenging hydrology of karst aquifers in South Africa and perhaps even worldwide.
In applying the analogy of a pumping test, the 3 datasets were analysed by 4 porous-media -based analytical methods, differing mainly in the degree to which they are able to account for local conditions.
The obtained results are generally in good agreement with each other (exceptions are explained) as well as with previous estimates for the study area and values reported in general literature for similar rocks types. This is interpreted as confirming earlier suggestions that porous-medium analytical methods can indeed be applied to karst aquifers provided the spatial scale of investigation is large enough.
The study also shows that the accuracy of the obtained values was less affected by the fact that the applied analytical methods were actually developed for porous media and more by the degree to which the various requirements of the applied methods (such as constant pumping rates, no-flow boundaries, etc.) were met. Not surprisingly, MLU, as the one method that took most of the local peculiarities into account, yielded the best-fitting results for the largest of the three datasets.
The most pronounced limitations of the applied methods came from the fact that they all ignored vertical variations in permeability of the dolomite. This was revealed by comparing 2 different datasets pertaining to different vertical zones of the dolomitic column. The fact that the highly permeable zones in the dolomite were covered in one dataset, but not in the other, resulted in the respective transmissivity values differing by an order of magnitude. This, in turn, allowed for the first time quantification of the transmissivity of the different vertical zones of the dolomite in the Bank Compartment.
While obtained storage coefficients are generally less reliable than transmissivity values, their application yielded reasonable storage volumes that compare favourably with existing data and earlier estimates. However, no satisfactory explanation could be found why distance-dependency of the storage coefficients was observed in one dataset but not in the other. Thus storage values are to be interpreted cautiously.
Based on the obtained parameters, it is envisaged to investigate the effects that mining through dykes below the dolomite has on the future elevation of the recovered water table after mining and the associated dewatering ceases in the area. Given the large costs currently incurred by implementing emergency measures to address effects of haphazard mine closure in the East, Central and West Rand, a more pro-active and coordinated approach to mine closure in the FWR, as the most water-rich of all goldfields in South Africa, is deemed to be imperative.
ACKNOWLEDGEMENTS
The authors gratefully acknowledge the support and contribution of Prof EJ Stoch, who made his unique collection of hydro-logic, historical data available. Special gratitude is owed to Mrs Heather Erasmus for editing. Last, but not least, the authors wish to graciously thank the National Research Foundation (Grant No. 86331) for financial support.
REFERENCES
ANONYMOUS (2005) Salute this special mine. Ngonyama News (27) October 2005, 4-5. [ Links ]
BEAR J (1972) Dynamics of Fluids in Porous Media. American Elsevier, New York. 764 pp. [ Links ]
BOULTON NS and STELTSOVA TD (1977) Unsteady flow to a pumped well in a fissured water-bearing formation. J. Hydrol. 35 (3-4) 257-270. [ Links ]
BOURDET D and GRINGARTEN AC (1980) Determination of fissure volume and block size in fractured reservoirs by type-curve analysis. Paper SPE 9293 presented at the 1980 SPE Annual Fall Technical Conference and Exhibition, Dallas. 20 pp. [ Links ]
BREDENKAMP DB, FAYAZI M and BOTHA LJ (1991) Interpretation of pumping test in the Gemsbokfontein East Compartment - A typical heterogeneous karst system. DWAF Technical Report No. GH 3727. Department of Water Affairs and Forestry, Directorate of Geohydrology, Pretoria (unpublished). 13 pp. [ Links ]
BRINK ABA (1975) Discussion on evaluation of geohydrological constants for the Far West Rand dolomitic formations, by H. 1. Schwartz and D. C. Midgley. Trans. S. Afr. Inst. Civ. Eng. 17 178-180. [ Links ]
BRINK ABA (1979) Engineering Geology of South Africa, Vol. 1. Building Publications, Pretoria. 319 pp. [ Links ]
CARLSON F and RANDALL J (2012) MLU: A Windows application for the analysis of aquifer tests and the design of well fields in layered systems. Ground Water 50 (4) 504-510. [ Links ]
CARTWRIGHT AP (1969) West Driefontein - Ordeal by Water. Gold Fields of South Africa Ltd., JG Ince & Son Ltd., Johannesburg. 83 pp. [ Links ]
COUSENS RRM and GARRETT WS (1969) The flooding at the West Driefontein Mine. J S. Afr. Inst. Min. Met. 69 (9) 421-463. [ Links ]
DE KOCK WP (1964) The geology and economic significance of the West Wits Line. In: Houghton SH (ed.) The Geology of Some Ore Deposits in Southern Africa, Vol. 1. The Geological Society of South Africa, Johannesburg. 323-386. [ Links ]
DWA (DEPARTMENT OF WATER AFFAIRS, SOUTH AFRICA) (2014) National Groundwater Archive of South Africa. URL: http://www3.dwa.gov.za/NGANet/Security/WebLoginForm.aspx (Accessed 13 February 2014). [ Links ]
DOMENICO PA and SCHWARTZ FW (1990) Physical and Chemical Hydrogeology. John Wiley & Sons, New York. 824 pp. [ Links ]
ELS BG (1987) The auriferous Middelvlei Reef depositional system, West Wits Line, Witwatersrand Supergroup. Ph.D. thesis, Rand Afrikaans University, Johannesburg. 658 pp. [ Links ]
ELS BG (2000) Unconformities of the auriferous, Neoarchaan Central
Rand Group of South Africa: application to stratigraphy. J. Afr. Earth Sci. 30 (1) 47-62.
ENSLIN JF and KRIEL JP (1959) Some results obtained from a hydro-logical study of a dolomitic catchment area in the Transvaal, Union of South Africa. DWAF Technical Report No. GH 3727. Department of Water Affairs, Division of Hydrological Research, Pretoria (unpublished). 16 pp. [ Links ]
ENSLIN JF and KRIEL JP (1968) The assessment and possible future use of the dolomitic ground water resources of the Far West Rand, Transvaal, Republic of South Africa. International Conference on Water for Peace, Washington. 908-918. [ Links ]
ENSLIN JF, KLEYWEGT RJ, BEUKES JHT and GORDON-WELSH JF (1977) Artificial recharge of dolomitic ground-water compartments in the Far West Rand Gold Fields of South Africa. Proceedings of the Second International Symposium on Land Subsidence, Anaheim, California. IAHS Publ. 121 495-506. [ Links ]
FERRIS JG (1959) Ground water, Chapter 7. In: Wisler CO and Brater EF (ed.) Hydrology. John Wiley & Sons, New York. 198-272. [ Links ]
FERRIS JG, KNOWLES DB, BROWN RH and STALLMAN RW (1962) Theory of aquifer tests. U.S. Geological Survey Water-Supply Paper 1536-E. United States Government Printing Office, Washington. 174 pp. [ Links ]
FREEZE RA and CHERRY JA (1979) Groundwater. Prentice-Hall, Englewood Cliffs. 604 pp. [ Links ]
GEOLOGICAL SURVEY OF SOUTH AFRICA (undated) Drawdown Contour Map, 15 May 1971. Geological Survey of South Africa, Pretoria (unpublished). [ Links ]
GOLD FIELDS (2009) Driefontein Gold Mine technical short form report. Gold Fields Ltd. 11 pp. URL: https://www.goldfields.co.za/reports/rr2009/pdfs/Driefontein.pdf (Accessed 28 March 2011). [ Links ]
HARMONY GOLD MINING COMPANY (2010) Harmony Annual Report 2010. Harmony Gold Mining Company Ltd. 364 pp. URL:http://www.harmony.co.za/assets/investors/reporting/annual-reports/2010/f/HARAR2010.pdf (Accessed 18 April 2013). [ Links ]
HEATH RC (1983) Basic ground-water hydrology. U.S. Geological Survey Water-Supply Paper 2220. United States Government Printing Office, Washington. 83 pp. [ Links ]
HEMKER CJ and MAAS C (1987) Unsteady flow to wells in layered and fissured aquifer systems. J. Hydrol. 90 (3-4) 231-249. [ Links ]
HEMKER CJ (1999) Transient well flow in layered aquifer systems: the uniform well-face drawdown solution. J. Hydrol. 225 (1-2) 19-44. [ Links ]
HEMKER K and POST V (2012) MLU for Windows. Well flow modeling in multilayer aquifer systems. Amsterdam. 30 pp. URL: http://www.microfem.com/download/mlu-user.pdf (Accessed 13 February 2014). [ Links ]
JACOB CE (1963) Determining the permeability of water-table aquifers. In: Bentall R (ed.) Methods of Determining Permeability, Transmissibility and Drawdown. U.S. Geological Survey Water-Supply Paper 1536-I. United States Government Printing Office, Washington, 245-271. [ Links ]
JORDAAN JM, ENSLIN JF, KRIEL J, HAVEMANN A, KENT LE and CABLE WH (1960) Final report of the Interdepartmental Committee on Dolomitic Mine Water: Far West Rand. Department of Water Affairs and Forestry, Pretoria (unpublished). 38 pp. [ Links ]
KIRCHNER J and VAN TONDER GJ (1995) Proposed guidelines for the execution, evaluation and interpretation of pumping tests in fractured-rock formations. Water SA 21 (3) 187-200. [ Links ]
KRUSEMAN GP and DE RIDDER NA (1991) Analysis and Evaluation of Pumping Test Data. ILRI Publ. 47. International Institute for Land Reclamation and Improvement, Wageningen. 377 pp. [ Links ]
LANGGUTH RH and VOIGT R (2004) Hydrogeologische Methoden. Springer, Berlin, Heidelberg. 1005 pp. [ Links ]
McWHORTER DB and SUNADA DK (1977) Ground Water Hydrology and Hydraulics. Water Resources Publication, Littleton, Colorado. 290 pp. [ Links ]
MORGAN DJT and BRINK ABA (1984) The Far West Rand dolomites. Proc. Int. Conf. Groundwater Technology, 1984, Johannesburg, South Africa. National Water Well Association, Worthington, Ohio. 554-573. [ Links ]
SCHWARTZ HI and MIDGLEY DC (1975) Evaluation of geo-hydrologic constants for the Far West Rand dolomitic formations. Civ. Eng. S. Afr. 17 (2) 31-36. [ Links ]
STOCH EJ and WINDE F (2010) Threats and opportunities for post-closure development in dolomitic gold mining areas of the West Rand and Far West Rand (South Africa) - a hydraulic view. Part 3: Planning and uncertainty - lessons from history. Water SA 36 (1) 83-88. [ Links ]
SWART CJU, JAMES AR, KLEYWEGT RJ and STOCH EJ (2003) The future of the dolomitic springs after mine closure on the Far West Rand, Gauteng, RSA. Environ. Geol. 44 (7) 751-770. [ Links ]
SWART CJU, STOCH EJ, VAN JAARSVELD CF and BRINK ABA (2003a) The lower Wonderfontein Spruit: an expose. Environ. Geol. 43 (6) 635-653. [ Links ]
THEIS CV (1935) The relation between the lowering of the piezometric surface and the rate and duration of discharge of a well using ground-water storage. Trans. Am. Geophys. Union 16 (2) 519-524. [ Links ]
THIEM G (1906) Hydrologische Methoden. Gebhardt, Leipzig. 56 pp. [ Links ]
VAN TONDER G, BARDENHAGEN I, RIEMANN K, VAN BOSCH J, DZANGA P and XU Y (2002) Manual on pumping test analysis in fractured-rock aquifers. WRC Report No. 1116/1/02. Water Research Commission, Pretoria. 157 pp. [ Links ]
WINDE F, STOCH EJ and ERASMUS E (2006) Identification and quantification of water ingress into mine voids of the West Rand and Far West Rand Goldfields (Witwatersrand basin) with a view to long-term sustainable reduction thereof. Final report, Project No. 5512, Council for Geoscience, Pretoria (unpublished). 261 pp. [ Links ]
WOLMARANS JF (1982) The Least Unsafe Route, Vol. 1. Webb and Partners, Carletonville. 83 pp. [ Links ]
Received 29 July 2013
Accepted in revised form 15 July 2014.
* To whom all correspondence should be addressed.+27 /16 9103477; e-mail: Frank.Winde@nwu.ac.za