Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Water SA
On-line version ISSN 1816-7950
Print version ISSN 0378-4738
Water SA vol.40 n.2 Pretoria Apr. 2014
TECHNICAL NOTE
Dimensioning of aerated submerged fixed bed biofilm reactors based on a mathematical biofilm model applied to petrochemical wastewater - the link between theory and practice
Karol TrojanowiczI; Wtodzimierz WojcikII
IOil Refinery 'Glimar' S.A, ul. Michalusa 1,38-300 Gorlice, Poland
IIPWSZ Krosno, Polytechnic Institute; ul. Rynek 1,38-400 Krosno, Poland
ABSTRACT
The description of a biofilm mathematical model application for dimensioning an aerated fixed bed biofilm reactor (ASFBBR) for petrochemical wastewater polishing is presented. A simple one-dimensional model of biofilm, developed by P Harremöes, was chosen for this purpose. The model was calibrated and verified under conditions of oil-refinery effluent. The results of ASFBBR dimensioning on the basis of the biofilm model were compared with the bioreactor dimensions determined by application of load-based design rules for these systems (ATV standards). The differences resulting from two different approaches to ASFBBR design are analysed and discussed. The efficiency of the ASFBBR bioreactors, designed in two different ways, are then compared during dynamic simulation utilising the most advanced one-dimensional biofilm model developed by Wanner and Reichert (1996).
Keywords: Biofilm modelling; petrochemical wastewater; biofilm reactors
INTRODUCTION
Currently, applied aerated submerged fixed bed biofilm reactor (ASFBBR) design criteria are of an empirical nature. The design criteria have been developed on the basis of observations of many ASFBBR systems working under a variety of surface organic loading rates (SOL) and total Kjeldhal nitrogen loading rates (TKN-load). The results of these studies enabled the determination of the relationship between SOL or TKN-load and efficiency of organic contaminant removal or nitrification in ASFBBR reactors (Schlegel and Koeser, 2007; Chapanova et al., 2007; DWA/ATV-DVWK, 2002; DWA/ATV, 1997; DWA/ATV, 1991; Grady et al., 1999). In parallel, different types of mathematical models have been developed, taking into account their complexity and modelling objective (Mann and Stevenson, 1997; Henze et al., 2000; Morgenroth, 2000; Vanhooren, 2002; Wanner et al., 2006; Takacs at al., 2007). Authors such as Wilderer (2003), Harremöes (2003) and Rittmann (2007) emphasize the need to link theory with practice, for the transition from the design and operation of fixed bed biofilm reactors based on engineering pragmatism to the application of well-developed scientific theories. These authors indicate that this is a condition for the further development of biofilm technology and for meeting the future challenges of emerging contaminant removal from wastewater (Wuertz et al., 2003; Wanner et al., 2006; Rittmann, 2007).
Model-based ASFBBR system design is conducted by the calculation of organic matter or nitrogen removal rate per unit area of the reactor's bed, under the assumed technological conditions of the wastewater treatment process. The kinetics of contaminant removal is expressed in biofilm models in a mechanistic way, as a set of correlated mathematical equations, which describe basic (fundamental) processes and their relationships. Because of that, it might be assumed that this method of bioreactor dimensioning could be more accurate, precise and flexible in comparison to reactor design based solely on empirical criteria. Takacs et al. (2007) presented a new mathematical model of biofilm, developed for engineering purposes. In his publication, the results of simulations conducted with a calibrated model and data derived from other researchers' experiments on MBBR (moving bed bioreactors) and IFAS (integrated fixed film activated sludge) systems for municipal wastewater treatment were described. The results demonstrated that the model predicts the performance of these systems (nitrification) correctly. There is a lack of information in the available literature on model-based biofilm reactor dimensioning for industrial/petrochemical wastewater. The information presented in this paper concentrates on the application of a mathematical biofilm model to determine the minimum required area of bed media/minimum required bed media volume (the aim of biofilm reactor dimensioning) of an ASFBBR reactor for the final treatment of oil-refinery wastewater. Therefore, the process of organic carbon removal in ASFBBR was within the scope of all studies and simulations reported herein.
The aim of this article was to demonstrate how existing mathematical models of biofilm could be applied in engineering practice to ASFBBR reactor dimensioning. A simple, one-dimensional, mathematical model of biofilm (Harremoes, 1978) was chosen for this purpose, calibrated and verified under conditions of oil-refinery wastewater effluent. The assumed set of technological parameters utilised during reactor design was also derived from experimental studies on the full-scale wastewater treatment system of an oil-refinery. The results of ASFBBR dimensioning on the basis of the biofilms model were compared with the bioreactor dimensions determined by application of load-based design rules of these systems. Efficiency of the ASFBBR bioreactors, designed in two different ways, was then compared during dynamic simulation utilising the most advanced one-dimensional biofilm model, i.e. that developed by Wanner and Reichert (1996).
METHODS
Model chosen for ASFBBR system dimensioning
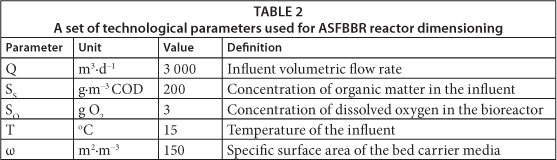
The model developed by Paul Harremoes in 1978, which is one of the earliest analytical one-dimensional models of biofilm, was selected for ASFBBR reactor design. It describes the kinetics of organic carbon conversion processes in biofilm and enables users to easily estimate the substrate removal rate in relation to the unit area of biological film (flux of substrate towards the biofilm). Model selection was conducted bearing in mind the aim for which it would be used after calibration and its practicality and ease of use. The Harremoes model describes the transport process of an organic substrate on the basis of molecular diffusion, from bulk-liquid perpendicularly into biofilm, for a steady-state. The main assumptions of the model are:
• Biofilm is flat and homogenous, the substrate removal (conversion) process is limited by one, soluble substrate: organic carbon or oxygen.
• Bioreactor is divided into 3 zones: bulk liquid, boundary layer between water and biofilm, and active biofilm.
• Description of substrate removal is based on combination of Fick's diffusion law with Monod-type bacterial growth model. Concentration of soluble organic substrate in the reactor's effluent is calculated from the mass balance (either for a completely mixed or a plug flow system).
• The growth process of microorganisms is only taken into account in the model, which affects only one parameter of the system (see Table 1).
• Biofilm depth and concentration of heterotrophs inside the biofilm is constant (steady-state conditions).
• Process of biofilm detachment is not included in the model.
In order to apply this model the following kinetics and stoi-chiometric parameters' values should be known: µπmax,Η, KS, KO, YH, XH, DO, DS and L. The model can be solved with a simple spreadsheet for steady-state conditions. The Petersen matrix of the Harremöes model, which describes substrate biochemical conversion processes and their influence on the system's components is presented in Table 1. A detailed description of the model is readily available in the literature (Harremoes, 1978; Vanhooren, 2002; Wanner et al., 2006).
Assumed set of operating conditions and the system being designed
The assumptions on which the ASFBBR reactor was designed, concerning influent volumetric flow rate (Q), and influent concentration of organic substrate (SS) and its biodegradable fraction (fB), resulted from thorough analysis of the wastewater treatment plant system of the Oil Refinery 'Glimar' S.A., Poland. In that wastewater treatment system, the pilot ASFBBR was installed. The pilot bioreactor was set up as a third-stage wastewater treatment following pre-treatment with gravity oil-water separation (API), coalescent separation (CPI) and the coagulation-flotation units (DAF). Studies and analysis of the performance of the pilot bioreactor, and the characteristics of biofilm and heterotrophic biomass, were the source of other necessary parameters for model-based dimensioning of the ASFBBR system. The assumed set of parameters for ASFBBR reactor design is presented in Table 2. Dissolved oxygen concentration in the bioreactor was assumed to be equal to 3 mg∙ℓ-1 O2, which is that recommended for ASFBBR systems, to enable deeper oxygen diffusion into biofilm (Schlegel and Koeser, 2007). The COD fractions (i.e. soluble biodegradable COD fraction, fB; Table 3) in the samples taken at bioreactor inlet and outlet were determined in dedicated experiments (Trojanowicz, 2009), the results of which will be published elsewhere. Additionally, the set of kinetic, stoichiometric and biofilm parameters were utilised for the calibration of the biofilm mathematical models. The values of most parameters of the model were compiled from pilot and laboratory experiments. The respirometric methods were chosen to determine: the heterotrophic growth rate (µmax,Η), decay coefficient (bH), half saturation coefficient (KS) and fraction of active heterotrophic biomass (fA,H). The method for heterotrophic yield (YH) determination was based directly on COD and the total suspended solids measurements during batch tests. Details concerning methods and results of kinetic and stoichiometric parameter determination for heterotrophic microorganisms under petrochemical wastewater conditions have been described in a separate paper (Trojanowicz et al., 2009). The values of some parameters, such as the half saturation coefficient for dissolved oxygen (KO), and the oxygen and organic matter diffusion coefficients in water (DO, DS) were taken from the literature (Wanner et al., 2006).
Model-based design of ASFBBR reactor
During model-based bioreactor design, characteristics of the influent and requirements concerning quality of the effluent are necessary input parameters for the calculation of minimum bioreactor volume (minimum volume of the reactor's bed). The volume of the bioreactor's bed (V) is calculated from the estimated value of the minimum required reactor's bed surface area (A) and assumed specific surface area of the biofilm carrier media (ω). The minimum reactor's bed surface area (A) at assumed ω value is calculated based on the known value of surface substrate removal rate, rA (substrate flux towards the biofilm). This parameter is determined from the model by finding its solution for a given set of input parameters. Substrate flux (rA) was estimated by fixing the bulk concentration of substrate (SS,bulk). The fixed concentration of the substrate in the reactor (equal to substrate concentration in the effluent for the steady state) is a function of the concentration of readily biodegradable substrate in the influent (SS,biod) and the bioreactor's assumed substrate removal efficiency (E).This parameter is determined from the model by finding its solution for a given set of input parameters.
Substrate flux (rA) was estimated by fixing the bulk concentration of substrate (SS,bu|k). The fixed concentration of the substrate in the reactor (equal to substrate concentration in the effluent for the steady state) is a function of the concentration ol readily biodegradable substrate in the influent (SS,biod) and the bioreactor's assumed substrate removal efficiency (E). Detailed description of the calculation principles during the model-based designing of ASFBBR reactor is presented below.
The required volume of the reactor's bed for removal of a given load of organic matter (expressed in COD units) was calculated with the following equation:

where:
TOL = total organic loading rate of the bioreactor (g∙d-1 COD)
rV = volumetric substrate removal rate of the bioreactor (g∙m-3∙d-1 COD)
The total organic loading rate (TOL) is defined as follows:
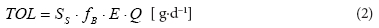
where:
SS = assumed value of COD in the influent (g∙m-3 COD)
Ss.fB = SS,biod (g∙m-3 COD)
fB = fraction of biodegradable substrate in total soluble COD
E = assumed efficiency of COD removal in bioreactor
Q = volumetric influent flow rate (m3∙d-1).
The volumetric substrate removal rate (rV) is calculated with the Harremoes biofilm model:

where:
rA = surface substrate removal rate of the bioreactor (g∙m-2∙d-1 COD)
ω = specific surface area of the reactor's bed media (m2∙m-3)
The general formula defining surface substrate removal rate (rA) is expressed as follows:

where:
kn,A,i = kinetic constant of the surface substrate removal process
Si,bulk = concentration of process-limiting substrate in the bulk liquid of the bioreactor (g∙m-3)
n = order of the substrate removal process
Additionally, the equation for rA value was modified by including the influence of temperature (T) on process rate:

The equations for calculation of kinetic constants of the substrate removal process at the level of bacterial cells (biochemical conversion processes) and biofilm are presented in Table 4.
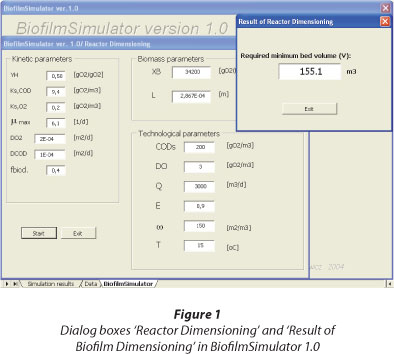
Dimensioning of ASFBBR reactors with the BiofilmSimulator 1.0 program
In the BiofilmSimulator 1.0 program, properties of the system being designed are specified in the dialog box 'Reactor Dimensioning' (Fig. 1). The user enters the input values in accordance with the terms set out in Table 5 and starts the calculation (Trojanowicz, 2009). The equations defining the rate of organic carbon removal in biofilm, transport of substrate into the biofilm, and the volume of the bed required to achieve the assumed efficiency of organic substrate removal in the reactor, are permanently set in the program and the user cannot change these relationships. The user, upon entering the input data, starts the calculation with the 'Start' button. The result is displayed in the dialog box 'Result of reactor dimensioning' (Fig. 1).
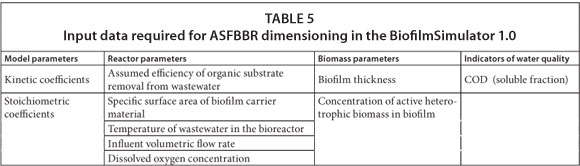
Dimensioning of ASFBBR reactors on the basis of empirical criteria specified in the DWA/ATV standard (1997/2002)
This kind of biofilm reactor dimensioning is based on the assumption that at a given surface organic loading rate (SOL), a given efficiency of the organic substrate removal from wastewater will be achieved. According to the DWA (German Association for Water, Wastewater and Waste) ASFBBRs will, at operating temperatures of 15 ± 5oC, consistently provide for municipal wastewater removal rates for BOD (biological oxygen demand) >95%, COD (chemical oxygen demand) >80% and TKN (Total Kjeldahl Nitrogen) >90%, if certain load-based design rules are followed (ATV, 1997). For BOD removal without nitrification, the specific BOD surface loading rate of the bioreactor should be <12 g-mr2∙d-1 (Schlegel and Koeser, 2007; Chapanova et al., 2007; DWA/ATV-DVWK, 2002; DWA/ATV, 1997; DWA /ATV, 1991).
Dynamic simulation with Wanner and Reichert biofilm model (1996) (Aquasim 2.1f) of the bioreactors designed with load- and model-based approaches
Dynamic simulations of the ASFBBR's performance were conducted in order to verify reliability of their calculated dimensions and identify potential differences in efficiency of organic carbon removal from wastewater between load- and model-based designed reactors. The dynamic simulation was carried out with Aquasim 2.1f - a program which allows the running of simulations on the basis of the most advanced, numerically-solved, one-dimensional biofilms model developed by Wanner and Reichert (Wanner and Reichert, 2006; Wanner and Morgenroth, 2004).
Input data concerning concentration of soluble organic substrate in the influent, influent volumetric flow rate, temperature and dissolved oxygen concentration in the bulk liquid of the bioreactor were generated as the set of random numbers from the range of values recorded during analysis of the pilot ASFBBR and wastewater treatment plant of the Oil Refinery 'Glimar' S.A.. Simulation was run for a 30-day period.
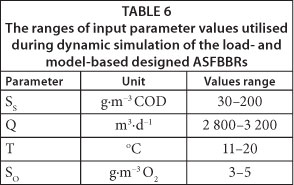
The equations describing the kinetics of growth and decay of the heterotrophs in biofilm were specified in compliance with the formulas of Wanner and Reichert's model's Petersen matrix (Wanner and Reichert, 1996; Reichert, 1998a, b; Vanhooren, 2002), whereas equations of transport processes and mass balance are an uneditable part of the program. The active processes were: growth and endogenous respiration of heterotrophs, which affect the concentration of organic substrate, heterotrophic biomass concentration in the biofilm and the biofilm thickness. Biofilm and model parameters utilised for the model calibration are shown in Table 3 (the same values were used for Harremoes model calibration in BiofilmSimulator 1.0). The ranges of input parameter values that were utilised to generate the input dataset used during dynamic simulation are presented in Table 6.
RESULTS
Results of load- and model-based ASFBBR dimensioning
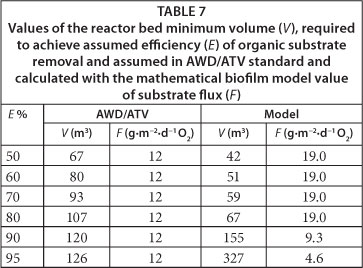
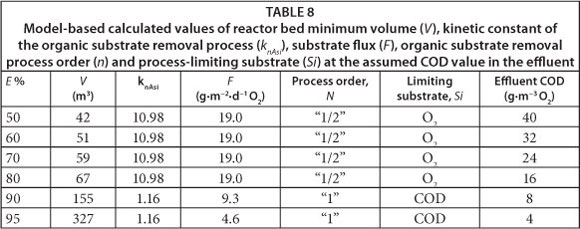
Values of the minimum required reactor bed volume (V) necessary to achieve assumed efficiency of organic matter removal (SS) from wastewater are shown in Table 7. These values were calculated for different assumed bioreactor efficiencies (E), utilising both empirical criteria (AWD/ATV standard) and a model-based approach. Additionally, Table 8 displays the values of the kinetic constant of organic substrate removal (knAsi), substrate flux (F), organic substrate removal process order (n) and process limiting substrate (Si). These values were calculated with the biofilm mathematical model.
Results of dynamic simulations of organic substrate removal in ASFBBRs designed on the basis of biofilm mathematical model and empirical criteria
The results of simulations for the two options are shown in Fig. 2.
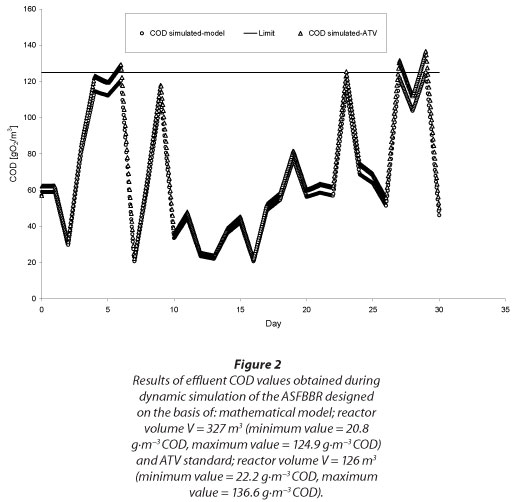
DISCUSSION AND CONCLUSIONS
The aim of the studies presented in this paper was to compare the volume of the ASFBBR designed on the basis of empirical criteria specified in AWD-ATV standard (Schlegel and Koeser, 2007; Chapanova, 2007; DWA/ATV, 2002; DWA/ATV, 1997; DWA/ATV, 1991) and utilising a one-dimensional, analytical, mathematical model of biofilm (Henze et al., 2000; Harremoes, 1978). Moreover, the efficiency of the designed ASFBBR reactors was to be verified with dynamic simulations conducted with the Wanner and Reichert model (1996). The parameter set used during dimensioning of the reactors is shown in Table 2. The determined value of biodegradable fraction of organic substrate in the influent (fB) was 0.4 and, because of this, the assumed daily biologically degradable COD loading was 240 000 g∙d-1. The value of biodegradable and total COD (at the assumed bioreactors efficiency (E) of 95%) in the effluent was 4 g∙m-3 and 124 g∙m-3, respectively. This is also the highest permissible value of this parameter specified in Polish regulations (125 g∙m-3 COD). The mean value of total and soluble COD determined in the wastewater at the influent to the pilot ASFBBR reactor was 130 g∙m-3 and 60 g∙m-3, respectively, so the assumed value of influent organic substrate concentration was higher than the actual value. The aim of such an assumption was to leave a safety margin for accidental shock organic loads to the reactor. In order to better illustrate the differences between the traditional approach towards ASFBBR dimensioning and model-based design, up-scaling was carried out, not only for the assumed organic carbon removal efficiency of 95% but also for 50%, 60%, 70%, 80% and 90%.
The results of the bioreactor bed volume calculations are presented in Table 7. For the assumed efficiency range from 50% to 90%, the calculated minimum bed volume was about 60% higher for the bioreactor dimensioned on the basis of the AWD-ATV standard. The minimum required bed volume calculated for the assumed efficiency (E) equal to 95% was 260% higher in the case of ASFBBR reactor designed based on the biofilm mathematical model. Where do these significant differences result from? Answering this question could be possible upon analysing values of the substrate flux values which were assumed in the AWD/ATV standards and those calculated with the biofilm mathematical model. In the case of the AWD/ATV standard, the substrate flux value is constant and equals about 12 g∙m-2∙d-1 COD. During ASFBBR design with the biofilm model, this value is calculated every time for the assumed set of model parameters. In the case being discussed, the values of all parameters have constant values except the assumed value of the biodegradable fraction of COD in the effluent, which is equal to biodegradable organic matter concentration in the bulk liquid of the reactor, because it may be considered as a fully-mixed system. This value depended on the assumed ASFBBR reactor efficiency (E).
The values of substrate flux calculated with the model varied significantly from those assumed in the AWD/ATV constant value of 12 g∙m-3 COD. This directly affected the calculated minimum required volume of the bioreactor's bed (see Table 7). Values of substrate flux (F) calculated with the mathematical model for a given assumed reactor's efficiency (E), as well as for other correlated model parameters, are shown in Table 8. For the range of E values from 50% to 80% the process rate limiting substrate was dissolved oxygen and the calculated kinetics of the reactor was half-order. The estimated substrate flux for this range was 19 g∙m-2∙d-1 COD and was constant, since the assumed dissolved oxygen concentration in the bulk liquid was also constant (3 g∙m-3 O2). The limiting substrate changed from oxygen to organic substrate at the assumed reactor efficiency value of 90%, which corresponded with biodegradable soluble organic substrate concentration in the effluent of 8 g∙m-3 COD. It also resulted in a change of the process kinetics from half- to first-order and a related change of substrate flux (F) for 9.3 g∙m-3 COD (at E=90%) and 4.6 g∙m-3 COD (at E=95%). It demonstrated the differences between the two presented ASFBBRs dimensioning approaches.
The traditional, load-based design approach treats the bioreactor as a 'black box' working with constant high efficiency. The second approach of reactor sizing based on a biofilm mathematical model takes into account several parameters that affect the rate of overall organic substrate removal process from wastewater in the bioreactor. Its foundation is understanding and mathematical representation of basic physical and biochemical processes that occur in biofilm. In order to examine how the differences in calculated minimum required bed volume would affect the achieved substrate removal efficiency, dynamic simulations of the designed ASFBBRs were conducted (Reichert 1998, Wanner and Reichert, 1996). The results of the dynamic simulations might appear to be surprising (see Fig. 2), because the significant differences of simulated effluent total COD values might be expected for the reactors with significant differences in bed volume (V=126 and 327 m3). As observed, the simulated values of total COD at the bioreactor outflow did not exceed the limit of 125 g∙m-3 COD in the case of model-based dimensioned reactors, whereas this occurred during simulations of the load-based designed bioreactor (maximum COD value of about 137 g∙m-3 COD). However, taking into account the simulation's uncertainty (Trojanowicz and Wojcik, 2011) those differences are negligible. The source of such small differences is that calculated values of biodegradable, soluble COD fractions in the reactor effluent were in the order of a few or a dozen COD units; because of this, values of total effluent COD were influenced to the most extent by the estimated inert fraction of COD. This suggests the conclusion that an increase in soluble COD removal from pre-treated oil-refinery wastewater may be achieved not by way of ASFBBR bed volume enlargement but by finding ways of increasing the biodegradable fraction of soluble COD in the influent. This is possible by the implementation of a bioaugmentation process which consists of enriching the biofilm with selected bacterial strains capable of degrading a wide spectrum of organic compounds from oil-refinery wastewater (Wuertz et al., 2003).
REFERENCES
CHAPANOVA G, JANK M, SCHLEGEL S and KOESER H (2007) Effect of temperature and salinity on the wastewater treatment performance of aerobic submerged fixed bed biofilm reactors. Water Sci. Technol. 55(8-9) 159-164. [ Links ]
DWA STANDARD ATV-A 122E (1991) Principles for Dimensioning, Construction and Operation of Small Sewage Treatment Plants with Aerobic Biological Purification Stage for Connection Values between 50 and 500 Total Number of Inhabitants and Population Equivalents. German Association for Water, Wastewater and Waste. Verlag, Hennef. [ Links ]
DWA/ATV (1997) Plants with Submerged Fixed Beds - ATV Manual for Biological and Advanced Wastewater Treatment (4th edn.) (in German). Ernst und Sohn, Berlin. [ Links ]
DWA/ATV-DVWK (2002) Trickling Filter and Submerged Carriers. Report of the Working Group Ka-6.3. German Association for Water, Wastewater and Waste, Hennef. [ Links ]
GRADY L, DAIGGER GT and LIM HC (1999) Biological Wastewater Treatment (2nd edn.). Marcel Dekker, New York. 1 079 pp. [ Links ]
HARREMOES P (1978) Biofilm kinetics. Water Pollut. Microbiol. 2 71-109. [ Links ]
HENZE M, HARREMOES P, JANSEN J and ARVIN E (2002) Waste-water treatment. Biological and Chemical Processes. Springer-Verlag, Berlin. 430 pp. [ Links ]
MANN AT and STEVENSON T (1997) Modelling biological aerated filters for wastewater treatment. Water Res. 31 (10) 2443-2448. [ Links ]
MENROTH E, VAN LOOSDRECHT MCM and WANNER O (2000) Biofilm model for the practitioner. Water Sci. Technol. 41 (4-5) 509-512. [ Links ]
REICHERT P (1998a) AQUASIM 2.0 - Tutorial. Computer Program for the Identification and Simulation of Aquatic Systems. Swiss Federal Institute for Environmental Science and Technology (EAWAG), Dübendor. [ Links ]
REICHERT P (1998b) AQUASIM2.0 - User Manual. Computer Program for the Identification and Simulation of Aquatic Systems. Swiss Federal Institute for Environmental Science and Technology (EAWAG), Dübendor. [ Links ]
RITTMANN BE (2007) Where are we with biofilms now? Where are we going? Water Sci. Technol. 55 (8-9) 1-7. [ Links ]
SCHEGEL S and KOESER H (2007) Wastewater treatment with submerged fixed bed biofilm reactor systems - design rules, operating experiences and ongoing developments. Water Sci. Technol. 55 (8-9) 83-89. [ Links ]
TAKACS I, BYE CM, CHAPMAN K, DOLD PL, FAIRLAMB PM and JONES RM (2007) A biofilm model for engineering design. Water Sci. Technol. 55 (8-9) 329-336. [ Links ]
TROJANOWICZ K (2009) The Final Treatment of Petrochemical Wastewater with ASFBBR Type Bioreactor. PhD Thesis, Krakow University of Technology, Poland. 209 pp. [ Links ]
TROJANOWICZ K, STYKA W and BACZYNSKI T (2009) Experimental determination of kinetic parameters for heterotrophic microorganisms in biofilm under petrochemical wastewater conditions. Pol. J. Environ. Stud. 2 913-921. [ Links ]
TROJANOWICZ K and WOJCIK W (2011) Calibration and verification of models of organic carbon removal kinetics in aerated submerged fixed-bed biofilm reactors (ASFBBR) - a case study of wastewater from an oil-refinery. Water Sci. Technol. 63 (10) 2446-2456. [ Links ]
VANHOOREN H (2002) Modelling for Optimization of Biofilm Wastewater Treatment Processes: a Complexity Compromise. PhD thesis, Universiteit Gent. 256 pp. [ Links ]
WANNER O, EBERL HJ, MORGENROTH E, NOGUERA D, PICIOREANU C, RITTMANN BE and VAN LOOSDRECHT MCM (IWA Task Group on Biofilm Modeling) (2006) Mathematical Modeling of Biofilms. IWA Scientific and Technical Report No. 18. IWA Publishing, London. 199 pp. [ Links ]
WANNER O and MOENROTH E (2004) Biofilm modeling with AQUASIM. Water Sci. Technol. 49 (11-12) 137-144. [ Links ]
WANNER O and REICHART P (1996) Mathematical modeling of mixed-culture biofilms. Biotechnol. Bioeng. 49 72-184. [ Links ]
WUERTZ S, BISHOP P and WILDERER P (2003) Biofilms in Wastewater Treatment. An Interdisciplinary Approach. IWA Publishing, London. 401 pp. [ Links ]
 Correspondence:
Correspondence:
Wtodzimierz Wojcik
+48602 520146
e-mail: wwojcik1@yahoo.com
Received 9 March 2013
Accepted in revised form 3 March 2014