Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
Water SA
versión On-line ISSN 1816-7950
versión impresa ISSN 0378-4738
Water SA vol.39 no.4 Pretoria ene. 2013
Unit Reference Value: Application in appraising inter-basin water transfer projects
PH van NiekerkI, *; JA du PlessisII
IDepartment of Water Affairs, Private Bag X313, Pretoria 0001, South Africa
IIDepartment of Civil Engineering, University of Stellenbosch, P/Bag X1, MATIELAND 7602, South Africa
ABSTRACT
Unit Reference Value (URV) is a common measure in South Africa to assess the economic efficiency of proposed water projects. This is a companion article to an earlier one establishing that the current approach of appraisal of inter-basin water transfer projects (IBTs) with significant pumping costs overestimates likely future water transfers and thereby variable operational costs. Those findings are taken further and it is established that the URV, as currently applied, fails as a suitable measure to appraise such IBTs. From rooting URVs in fundamental cost effectiveness analysis theory a revised URV approach is proposed that provides for a conceptual separation between water transfers affecting operating costs and water transfers used as a proxy measure for effectiveness. The prominent effect of the revised URV approach is demonstrated by means of the example of the proposed Thukela Water Project in South Africa.
Keywords: unit reference value, cost effectiveness analysis, inter-basin water transfers, project appraisal
INTRODUCTION
A preceding article by Van Niekerk et al. (2013; henceforth also called 'the companion article') reported on research showing that the actual experience of water transfers and life-cycle costs of inter-basin transfer (IBT) projects with significant variable costs does not correspond with the assumptions made originally at the planning stage. The deterministic method of appraisal, called the Incremental Approach, substantially overestimates the quantities of water to be transferred and thereby the life-cycle costs of the IBT. It does not take into account the uncertainty regarding the year-to-year future need for water transfers. A revised approach, called the Comprehensive Approach, is recommended to allow for the explicit consideration of the uncertainty of future water transfers and associated costs. This approach provides greater realism in predictions of likely water transfers and life-cycle costs.
This article now reports on further research (Van Niekerk, 2013) regarding the implication of the above findings on the application of the unit reference value (URV) measure, used in South Africa to assess, inter alia, IBT projects.
The URV measure has its origin in the South African Department of Water Affairs (DWA) in the 1980s. It was conceptualised for use by planners of Government water works, being public projects, to assess best sizes, layouts, and configurations of such schemes. For that purpose, the cash flow to construct, operate and maintain a particular scheme is projected over its economic life, usually 30 to 45 years. These costs are determined at constant prices, adjusted to exclude any taxes and subsidies, sometimes also shadow priced to allow for market distortions, e.g., the cost of unskilled workers in an environment of surplus labour but minimum wages. The value of such a cash flow stream at a specific point in time, usually present day, is determined using an economic discount rate, sometimes also called a 'social discount rate'. Any remaining value at the end of the discounted period is credited to the cost stream and accounted for in the discounting calculation.
To determine the URV of a particular scheme, the water supplied (i.e. the primary benefit derived from it) is projected over the same period and 'discounted' at the same rate to derive a 'present value' in cubic meters. In the Incremental Approach it is assumed that all of the demand exceeding the capability of the existing system has to be met from new resource development. Variable costs, i.e., costs that are directly related to the water quantities delivered, such as pumping (energy), water treatment (energy and chemical) and royalty (international payment) costs, would follow the same pattern.
The URV of the scheme is derived by dividing the PV of the costs with the PV of the water supplied, as shown in Eq. (1).
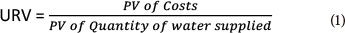
The URV measure should not be confused with tariffs. Tariffs are determined primarily for cost recovery purposes, i.e., to ensure that the actual monetary outlay to bring projects to fruition, and to run and maintain them, is recovered over a specified repayment period, usually between 10 and 20 years. Commercial (bank) lending rates apply and depend on the capital market situation and projections of interest rates that pertain at the time the calculations are made. Inflation has to be factored into the cash flow requirement over the construction period and beyond, when the project is in operation.
Water sales are projected over the repayment period and an associated unit tariff is determined (by iteration) that will lead to break-even exactly at the end of the period. The tariff is expressed in Rands per cubic meter (or kilolitre). The URV determination can be expected to lead to a lower figure than its calculated tariff. This is mainly due to the shorter discount period and the higher discount rates applied to the tariff calculation.
The URV measure has become entrenched as a component in South Africa's water sector appraisal arsenal and is currently widely used to assess the feasibility of water resource interventions, whether structural or non-structural (e.g. Kleynhans et al., 2011). Its use has also been extended to the evaluation feasibilities of measures such as water demand management and catchment management (e.g. Hoffman et al., 2008 and Van Wilgen et al., 1997). In a recent DWA report that considered scenarios of future water costs to the economy and society at large, URVs were also used in the forecasts of relative costs of new water supplies into the medium- and long-term (DWA, 2010).
METHODOLOGY
A conceptual model was firstly developed to identify the elements required for the derivation of the URV with the Incremental Approach. The model is then used to identify the elements affected by the Comprehensive Approach. Issues regarding the derivation of the URV in the situation of uncertainty regarding water transfers are probed and the need to investigate the theoretical roots of the URV measure established.
This is followed by a literature survey and fundamental philosophical analysis to root the URV measure in economic theory. From the economics of cost-effectiveness analysis (CEA) a revised approach for the derivation of the URV measure is proposed. The prevalence of the previous URV approach within the Incremental Approach is established by examining case studies used in the companion article. The impact of the revised approach as opposed to its predecessor is followed by a demonstration of its application in the example of the proposed Thukela Water Project.
RESULTS
The URV in the Incremental Approach
A conceptual model of the elements of the Incremental Approach, and the linkages with the URV measure, is provided in Fig. 1 for a typical IBT project.
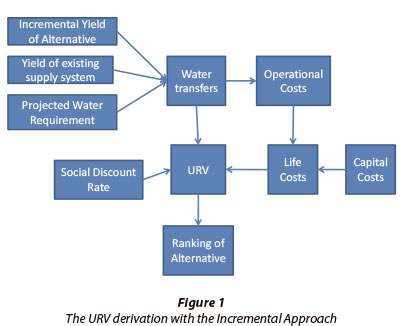
It is assumed that the annual water transfers can be derived from the difference between the projected water requirement and the yield of the existing supply system, capped by the incremental yield due to the new project. The annual water transfers feed into the life-cycle costing stream part of the URV equation via its direct impact on the operational costs. In addition the annual water transfer data feed directly into the URV derivation by means of its denominator. The same social discount rate is applied to the costing and water streams. The URV derived by means of Eq. (1) can then be compared against other alternatives in order to rank its acceptability from an economic perspective.
The Incremental Approach, as demonstrated in the companion article, overestimates the water transfers that can be realistically expected during the economic life of an IBT project with associated pumping costs of some significance. The new Comprehensive Approach is recommended to address this issue.
The URV and elements affected by the Comprehensive Approach
This approach requires stochastic analysis by means of simulation of the system, of which the proposed IBT project is an integral part, to obtain a probabilistic perspective of future water transfers. The elements of the above model that are affected are shown in Fig. 2.
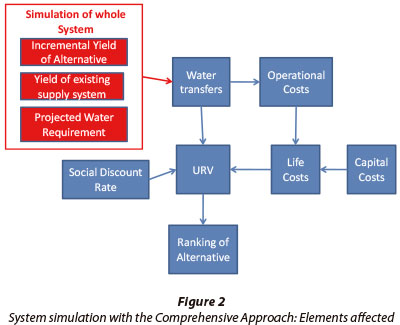
From the sequences of water transfers the expected present value of water transfers as well as associated variable operational costs are derived. With this as input, a more realistic present value of life-cycle costs is obtained.
The elements of the model in Fig. 1 affected by the improved water transfer data are shown in Fig. 3.

As water transfers influence the URV measure, both in the denominator as well as the nominator of its equation, the resulting effect is not unambiguous and raises a serious question as to the soundness of its derivation. As both life-cycle costs and water transfers are embedded in the way URVs are derived, further research was required to provide conceptual clarity about this measure and the way it is applied. A critical examination started with a literature search regarding the underlying theoretical basis of the URV measure.
The URV measure - its theoretical base
Implicit in the URV derivation is the assumption that the benefit that can be derived from such a project can directly be measured, or assessed, as the quantity of water delivered (Mullins, 2011).
The methodology to appraise water resource projects from an economic efficiency perspective has not changed significantly since early publications specific to the subject, such as Water Resources Projects Economics by Kuiper (1971). Many books written since have broadened the appraisal (sometimes also called evaluation: In some quarters, e.g. the World Bank, this term is reserved for an ex post facto review of the success of a project) methodologies with techniques such as multi-criteria decision analysis (MCDA), so as to include in the analysis environmental sustainability and social objectives such as equity and job creation. Kuiper distinguished between what he called cost comparison, cost comparison including risks, and benefit-cost analysis. The first is the most simplified appraisal technique and more often called the least-cost approach in the literature.
Least-cost approach is used to choose between projects with the same or very similar objectives, and when these objectives are difficult to quantify in monetary terms (Republic of South Africa, National Treasury, 2010). The Centre for International Economics of Australia described the least-cost approach as an analysis that assumes that an extra unit of water offers the same benefits, irrespective of the kind of intervention. Therefore, 'the focus of the analysis is on the costs of alternative projects given that all projects are assumed to deliver the same benefits' (CIE, 2009 p. 28).
The theory of cost-benefit analysis (CBA) is primarily used to assess economic efficiency of resource allocation. The Water Research Commission (WRC) publication A Manual for Cost Benefit Analysis in South Africa with Specific Reference to Water Resource Development (Conningarth Economists, 2007), provides the basis for applying CBA in the water sector in South Africa.
Recognising the difficulty of placing a monetary value on benefits, such as in public programmes, Boardman et al. (2011 p. 464) describe the application of cost effectiveness analysis (CEA) and state that 'if the effectiveness measure captures most of the benefits, then it may be reasonable to use CEA to avoid the burden of conducting a CBA'. While CEA can be used to assess the technical efficiency of undertaking a certain measure, a CBA is required to assess its allocative efficiency, i.e., 'whether something is worth doing'.
In the CBA the cost and benefit streams are discounted to their present value (using the real social discount rate of return) to determine net present benefit (NPB) and the internal rate of return (IRR). When undertaking a CEA the present value of the cost stream is the object of minimising for a specific output, usually a water supply figure.
As CEA 'compares (mutually exclusive) alternatives in terms of the ratio of their costs and a single quantified, but not monetised, effectiveness measure' (Boardman et al., 2011 p. 464), it is concluded that the URV measure is completely analogous to the CEA ratio in respect of methodology followed. The only difference between the two concepts is that the URV term is only used in relation to water management interventions in South Africa - to rank options and ascertain best configurations of projects. Similar to the CBA (or CEA), cash flows to construct, operate and maintain a particular scheme are discounted over its economic life, usually 30 to 45 years.
One of the constituent factors used in the CEA, as well as the CBA, method, and which has elicited much debate in the literature in the past (see e.g. Boardman et al., 2011), has been the choice of an appropriate rate for discounting costs and benefits. The debate seems to have converged to a consensus that a real social discount rate of return should be used. In the original CBA Manual (CEAS, 1989) the rate of 8% was proposed for capital investments and, more recently, Conningarth Economists (2007) found that this rate remained appropriate for South African conditions.
It is standard practice to also do a sensitivity analysis round the 8% discount rate, typically using discount rates of 6% and 10%.
Herrington (2006 p. 257-258) mentioned the need in Britain in the 1970s for a 'unique measure of the incremental cost of a given scheme so that options could be filtered out' and provided a definition for such a cost-effectiveness measure, called discounted unit cost (DUC), as 'the PV of supply costs over a suitable horizon divided by the present worth of water actually delivered to meet a deficit over that time'. The DUC used in Britain was therefore completely analogous to the URV measure used in South Africa.
Having established that the theoretical base for the URV measure is found in the CEA theory, the attention shifted to the appropriate estimation of effectiveness.
Reassessing the URV method in view of stochasticity of water transfers
In the application of the Incremental Approach it is also generally assumed that the PV of the water transfers is the appropriate denominator to obtain the URV of the project. This assumption needs to be questioned in the light of the stochastic nature of the water transfers and the effect that in practice, as was shown in the companion article, the actual transferred water turned out to be significantly less in quantity than predicted at the appraisal stage.
Appropriate denominator of the URV
As argued above, URVs are for all purposes completely analogous in application to the CEA ratio method. The assumption made in the Incremental Approach was to equate the present value of water transfers with effectiveness. It should be noted that this is typically the kind of assumption made in CEA -whether the measure is 'water actually delivered' (Herrington, 2006) or lives saved in the case of public health programmes (Boardman et al., 2011). The non-monetised measure of effectiveness is used as denominator in the cost-effectiveness ratio, e.g. Rands per m3 or Rands per life saved.
The Incremental Approach assumes that future water transfers can be treated as deterministic inputs into the appraisal process, but it has been demonstrated that these transfers are stochastic, i.e., non-deterministic. The question now arises whether it would be logical, in the situation of uncertainty regarding water transfers, to use the expected value of such transfers as the measure of effectiveness, therefore the denominator.
Before answering this question it is advisable first to consider what exactly is meant by 'effectiveness' when appraising the augmentation of an existing supply system. Fundamentally society and, by implication, the water resource manager, are interested in the availability of reliable water supplies into the future. Acceptable levels of reliability of water supply have to be established for a particular supply area before embarking on the process of planning an augmentation scheme.
In the RSA, priority tables that define required levels of security for categories of water users are employed as inputs into the Water Resources Yield Model (WRYM) and Water Resources Planning Model (WRPM) simulation tools (see Basson et al., 1994 for detail). Elsewhere the objectives have been described as levels of service (LOS) criteria. The Government of Queensland, Australia, for instance, set LOS criteria for water supply to the Brisbane area not only in terms of the frequency of different levels of restrictions, but also in terms of the maximum durations of these restrictions (Queensland Government, 2006).
It is argued that, provided the reliability criteria are satisfied, i.e., not violated, a project that would meet the projected water demand for a certain period into the future can be considered 'effective'. An appropriate measure of effectiveness would be the incremental demand that is secured by means of the augmentation scheme - as projected. The latter qualification is required as it is assumed that the additional security of supply afforded by a project over the initial period until the growth in demand has 'caught up' with the new system capacity (these projects typically being 'lumpy'), does not hold significant utility for the water users. If it had held significant utility, it could be reasoned, such utility would have found its way into the reliability criteria set a priori.
The conclusion from the above is that a good measure of the effectiveness of a project that will increase the system capacity of supply is the additional water assured into the future by the project. This, coincidentally, reflects the same quantities used in the Incremental Approach, which was based, erroneously as was shown in the companion paper, on the assumption that these quantities were actually to be transferred in the future.
URV reviewed
In determining the URV of a potential IBT project, using the Incremental Approach, the quantity of water used to calculate the PV of the life-cycle costs was also used in the denominator - as shown in Eq. (1). This approach, where variable operating costs are stochastic in nature, as is usually the case with IBT projects, will lead to the wrong URV derivations.
The improved URV method of the Comprehensive Approach has the following equation:
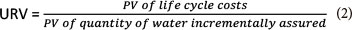
were:
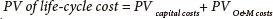
and

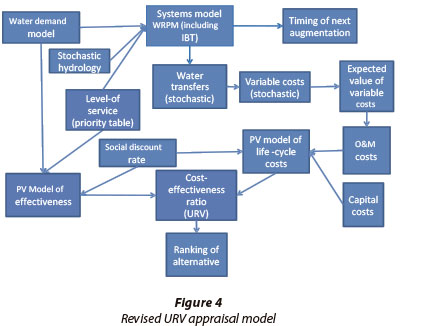
The elements and linkages of this approach to the URV determination are schematically depicted in Fig. 4. As can be seen by comparing this model to the one in Fig. 1, the new approach has widened the scope of appraisal to include the uncertainties produced by the stochasticity of the hydrological inputs regarding variable costs. In addition the issue of effectiveness was brought to the fore in the URV measure; a differentiation is made between the water transfers that are likely to occur during the life of an IBT and the assurance of water supplies sought from the proposed project.
Case studies on current URV application
Four South African case studies were researched regarding appraisal approaches followed (see companion article.) All four cases involved recent feasibility investigations by internationally recognised professional water resource planners. It was found that the Incremental Approach was followed in all cases - pointing to the current generality of that approach. The research also examined the measure used to rank projects. The results are summarised in Table 1.
Application of revised URV
The companion paper demonstrates the effect on the PV of the life-cycle costs when applying the Comprehensive Approach. The example used, that of the proposed Thukela Water Project (TWP), is also used here to demonstrate the application of the revised URV measure in combination with the Comprehensive Approach.
A description of the proposed TWP is provided in the companion paper. In brief it would comprise a large dam, the Jana Dam, in the Thukela River, and conveyance facilities to transfer water against an elevation difference of 1 030 m across the continental divide into the upper reaches of the Vaal River, to augment the existing Vaal River System that supplies water to the economically important industrial and mining areas of the Gauteng and Mpumalanga provinces in South Africa.
TWP example: URVs and the Incremental Approach
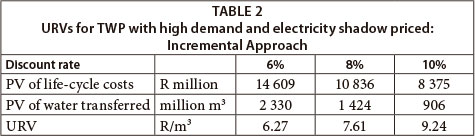
With the Incremental Approach the assumption is that all future water requirements greater than the existing Vaal System yield have to be sourced from Jana Dam and transferred to the Vaal River basin. The present values (PVs) of the costs associated with TWP during its economic life as well as the water transfers were discounted at 6%, 8% and 10% per year. The resultant PVs for life-cycle costs and water transfers, and resultants URVs, are shown in Table 2. (Note: currency is in South African Rand (R)).
TWP example: URVs and the Comprehensive Approach
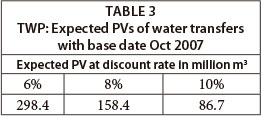
In the companion article it was shown that, by means of stochastic analysis of the system as a whole, i.e., inclusive of the source and receiving systems, using the South African WRPM simulation analysis tool, hydrological sequences of the transfers can be stochastically generated that have similar characteristics to water transfers actually experienced in South Africa. The expected PVs of water transfers were determined as shown in Table 3.
The commensurate expected PV of variable costs of the proposed TWP, and, by addition to the other costs, the expected PVs of life-cycle costs, are shown in Table 4. For the determination of the URV the effectiveness of the project is approximated by the quantity of water assured by the IBT, as discussed earlier.
The URVs were also determined, following the example in the companion article, for the stochastic range, being for the 10th and 90th percentile values of the state variable, the water transfer. The results are given in Table 5.
DISCUSSION
The results of the calculations, following the two approaches, are summarised in Table 6.
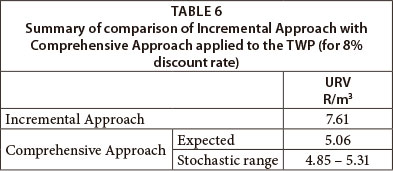
The sensitivity of the URV results become very apparent: for the 8% discount rate it moves from R7.61/m3 using the Incremental Approach to R5.06/m3 for the Comprehensive Approach - a significant change. The URV of the Incremental Approach lies completely outside the stochastic range of URVs with the Comprehensive Approach.
CONCLUSION AND RECOMMENDATIONS
Examination of the URV measure in view of its underlying CEA economic theory revealed that a good measure of effectiveness would be the incremental water availability assured by the expansion of a system and bounded by the projected demand curve until full capacity is reached. The PV of the annual quantities of water thus assured is used as denominator in the URV equation. It was shown that a conceptual separation is required between water transfers affecting operating costs and the water transfers used as a proxy measure for effectiveness.
This article provides clarity on the application of the URV measure in appraising water resource capacity expansion projects. In combination with the Comprehensive Approach in the companion paper (Van Niekerk et al., 2013) it introduces a new generalised approach that explicitly provides for the inclusion of uncertainty of input costs. This approach is recommended to ensure unbiased ranking of IBT projects and, accordingly, appropriate proposals for implementation.
ACKNOWLEDGEMENTS
The authors wish to thank the Department of Water Affairs, South Africa, for the use of its records and documents.
REFERENCES
BASSON MS, ALLEN RB, PEGRAM GGS and VAN ROOYEN JA (1994) Probabilistic Management of Water Resource and Hydropower Systems. Water Resource Publications, Colorado. [ Links ]
BOARDMAN AE, GREENBERG DH, VINING AR and WEIMER DL (2011) Cost-Benefit Analysis: Concepts and Practice (4th edn.) Pearson Education, New Jersey. [ Links ]
CEAS (CENTRAL ECONOMIC ADVISORY SERVICES, SOUTH AFRICA) (1989) A Manual for Cost-Benefit Analysis in South Africa. CEAS, Pretoria. [ Links ]
CIE (CENTRE FOR INTERNATIONAL ECONOMICS, AUSTRALIA) (2009) Review of economic aspects of Traveston Crossing Dam Environmental Impact Assessment documentation. Prepared for Department of Environment, Water, Heritage and the Arts. CIE, Canberra. URL: http://www.environment.gov.au/epbc/notices/assessments/ 2006/3150/pubs/traveston-dam-cie-report-part1.pdf (Accessed 10 May 2011). [ Links ]
CONNINGARTH ECONOMISTS (2007) A Manual for Cost Benefit Analysis in South Africa with Specific Reference to Water Resource Development (2nd edn.). WRC Report No. TT 305/07. Water Research Commission, Pretoria. [ Links ]
DWA (DEPARTMENT OF WATER AFFAIRS, SOUTH AFRICA) (2010f) Assessment of the ultimate potential and future marginal cost of water resources in South Africa. Report No P RSA 000/00/12610. Department of Water Affairs, Pretoria. URL: http://www.dwaf.gov.za/Documents/Other/Water%20Resources/ Assessment%20of%20Future%20Marginal%20Cost%20of %20Water%20in%20SA%20-%20FINALPDF (Accessed 6 June 2011). [ Links ]
HERRINGTON RH (2006) The economics of water demand management. In: Butler D and Memon FA (eds.) Water Demand Management. IWA Publishing, London. 236-279. [ Links ]
HOFFMAN JJ AND DU PLESSIS JA (2008) Water demand management: an economic viable option. URL: http://www.ewisa.co.za/literature/files/2008 147.pdf(Accessed 6 November 2012). [ Links ]
KUIPER E (1971) Water Resources Project Economics. London: Butterworths. [ Links ]
KLEYNHANS MT, ENGLISH G, BOTHA K and MUGUMO M (2011) Investigation of Future Surface Water Options to Augment the Western Cape Water Supply System. Paper presented at 15th SANCIAHS National Hydrology Symposium, Science and Practice for Sustainable Water Resources Management, 12-14 September 2011, Rhodes University, Grahamstown. URL: http://www.ru.ac.za/154E25C9-4489-4854-B9F2-011139F42A8A/FinalDownload/ DownloadId-7B32156731253A 7E0F14 054F61CF8B78/154E 25C9-4489-4854-B9F2-011139F42A8A/static/institutes/iwr/SANCIAHS/2011/the.pdffiles/MKleynhansPaper.pdf (Accessed 6 November 2012). [ Links ]
MULLINS D (2011) Personal communication, 22 June 2011. Dr D Mullins, Conningarth Economists, Pretoria, South Africa. [ Links ]
QUEENSLAND GOVERNMENT (2006) Water for South East Queensland - A Long Term Solution. August. URL: http://www.google.com/search?q=Queensland+Government %2C+2006%2C+ Water+for+South+East+Queensland+%E2%80%93+A+Long+Ter m+Solution%2C+August.&sourceid=ie7&rls=com.microsoft:en-US&ie=utf8&oe=utf8&rlz (Accessed 17 Oct 2011). [ Links ]
REPUBLIC OF SOUTH AFRICA, NATIONAL TREASURY (2010) 2011 MTEF Capital Expenditure Guidelines. URL: <http://www.treasury.gov.za/publications/guidelines/2011%20Capital%20 Expenditure%20Guidelines.pdf> (Accessed 17 May 2011). [ Links ]
VAN NIEKERK PH (2013) Hydrologic-economic appraisal of inter-basin water transfer projects. PhD thesis, Stellenbosch University. URL: http://hdl.handle.net/10019.1/79887. [ Links ]
VAN NIEKERK PH and DU PLESSIS JA (2013) Hydrologic-economic appraisal of life-cycle costs of inter-basin water transfer projects. Water SA 39 (4) 539-548. [ Links ]
VAN WILGEN BW, LITTLE PR, CHAPMAN RA, GÖRGENS AHM, WILLEMS T and MARAIS C (1997) The sustainable development of water resources: history, financial costs, and benefits of alien plant control programmes. S. Afr. J. Sci. 93 (9) 404-411. [ Links ]
Received 30 November 2012
Accepted in revised form 8 July 2013
* To whom all correspondence should be addressed. +27 82 807 4981; e-mail: peter.v.n@mweb.co.za














