Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Water SA
On-line version ISSN 1816-7950
Print version ISSN 0378-4738
Water SA vol.39 n.4 Pretoria Jan. 2013
Removal of copper(II) ion from aqueous solution by high-porosity activated carbon
Dragan D MilenkovićI; Milutin M MilosavljevićII; Aleksandar D MarinkovićIII; Veljko R ÐokićIII; Jelena Z MitrovićIV; Aleksandar Lj BojićIV, *
IHigh Chemical Technological School, Department of Chemical Technology, Kosančiceva 36,37000 Kruevac, Serbia
IIFaculty of Technical Science, University of Pritina, Kneza Miloa 7,38220 Kosovska Mitrovica, Serbia
IIIFaculty of Technology and Metallurgy, University of Belgrade, Karnegijeva 4,11120 Belgrade, Serbia
IVFaculty of Science and Mathematics, University of Ni, Viegradska 33, 18000 Ni, Serbia
ABSTRACT
The removal of copper(II) ion from aqueous solution by the granular activated carbon, obtained from hazelnut shells (ACHS) (Corylus avellana L. var. lunga istriana), was investigated. The ACHS was prepared from ground dried hazelnut shells by specific method carbonisation and water steam activation at 950oC for 2 h. The granular activated carbon produced from hazelnut shells has a high specific surface area (1 452 m2·g-1) and highly developed microporous structure (micropore volume: 0.615 cm3·g-1). In batch tests, the influences of solution pH, contact time, initial metal ion concentration and temperature on the sorption of copper(II) ion on ACHS were studied. The results indicate that sorption of copper(II) ion on ACHS strongly depends on pH values. The adsorption data can be well described by the Langmuir isotherm and Redlich-Peterson model. The monolayer adsorption capacity of the ACHS-copper(II) ion, calculated from the Langmuir isotherms, is 3.07 mmol·g-1. The time-dependent adsorption of copper(II) ion could be described by the pseudo second-order and Elovich kinetics, indicating that the rate-limiting step might be a chemical reaction. The intra-particle diffusion model indicates that adsorption of copper(II) ions on ACHS was diffusion controlled.
Keywords: Activated carbon, lunga istriana, copper, equilibrium, kinetics
INTRODUCTION
Materials of highly porous structure are widely used as adsorbents in industrial separation processes. These materials presently have a very important role in the purification of industrial wastewater for removal of heavy metals, coloured and other organic pollutants. A large number of works on this topic are available in the scientific literature. Generally, all of this research can be divided into two groups: first, those which use raw materials, with or without purification, of relatively small specific area; second, those dealing with thermallytreated raw materials, which therefore have different degrees of carbonisation.
A wide variety of raw materials have been used: aerobic activated sludge, sulphurised activated carbon prepared from nut shells, wheat bran, valonia tannin resin, spent tea leaves, etc. (Orozco et al., 2007; Nouri et al., 2007; Tajar et al., 2009; Sengil et al., 2009; Bajpai and Jain, 2010). In addition, different methods of thermal treatment and the subsequent processing (activation) produce adsorbents with different properties (El Qada et al., 2008). Obviously, structural and adsorption characteristics of these materials depend on the nature of raw material and methods of subsequent processing. Shells of various stone fruits are very suitable for production of adsorbents with favourable adsorption properties. Recently there has been growing interest in hazelnut shell, which has exceptional morphological characteristics suitable for the production of a high quality adsorbent.
This paper deals with the adsorption properties of active carbon obtained from the hazelnut shell, the specific regional variety lunga istriana, grown in the central part of Serbia (region Sumadija). Hazelnut shell was obtained from food industry waste. The aim was to investigate the use of hazelnut shell waste for wastewater treatment. Active carbon of hazelnut shell was prepared by specific carbonisation method and activated by water steam. High temperature carbonisation and activation (950oC) of purified shell for an extended time of 2 h was applied. Influence of experimental conditions, such as pH value, initial copper(II) ion concentration and temperature, on adsorption behaviour was investigated.
EXPERIMENTAL
Materials and methods of activation
Hazelnut (Corylus avellana L. var. lunga istriana) shell was harvested from the central part of Serbia. Raw hazelnut shell was washed several times with deionised water in order to remove surface impurities and dried at 100oC overnight. Afterward, dried material was crushed by a hammer mill, simultaneously carbonised and activated at 950oC for 2 h by water steam, in a rotating cylindrical oven. The temperature at the entrance to the rotary oven was 150oC and 950oC at exit. Activated material was washed 3 times with distilled water, dried at 110oC for 24 h and stored in desiccators. Copper(II) acetate (CuAc), analytical reagent grade, was purchased from Merck, Inc. Deionised water (18 Mfl-cm resistivity) was used to prepare aqueous solutions of CuAc.
Methods of characterisation of ACHS
Scanning electron microscopy (SEM) was performed on a JEOL JSM-6700 electron microscope. X-ray diffraction (XRD) data were obtained using a Bruker D8 Advance with Vario 1 focusing primary monochromator (Cu kα1 radiation, λ = 1.5405 x10-10 m). Recording was done in the field of 2θ = 5° to 70° with the step of 0.025°C, time τ = 1 s. For the characterisation of diffractograms, the database diffraction ICDD (International Centre for Diffraction Data 1996) was used. The specific surface area, pore specific volume and pore diameter were measured by nitrogen adsorption/desorption at 77.4 K using a Micromeritics ASAP 2020MP.
Batch adsorption experiments
Batch equilibrium adsorption experiments were performed by varying the initial copper(II) ions concentration in the range from 13 mmol·ℓ-1 to 260 mmol·ℓ-1, at constant temperature. An Erlenmeyer flask (250 ml), fixed on a swinger (90 oscillations per minute), was used as an adsorption vessel, containing 100 ml copper(II) ion solution and 1.0 g of the adsorbent. After reaching adsorption equilibrium (6 h) all samples were centri-fuged (1 500 r·min-1 for 5 min) to ensure separation of adsorbent particles. The adsorbed amount of copper(II) ions was calculated from the difference between initial and equilibrium Cu(II) ion concentration, as given by Eq. (1)

where:
q is the mass of copper(II) ion adsorbed at time τ per unit mass of adsorbent
C0 and C are the initial copper(II) ion concentration and the copper(II) ion concentration at appropriate time τ, respectively
V is the volume of CuAc solution (100 ml)
mACHS is the amount of adsorbent (1.0 g).
For each sample, the copper(II) ion concentration was measured in triplicate and the mean value was reported. The sorption of copper(II) on the Erlenmeyer flask surface, without sorbent addition, was negligible. Atomic absorption spectroscopy measurements of copper(II) ion concentrations were performed on a Perkin Elmer 1100B.
The influence of pH
In order to evaluate influence of pH on copper(II) sorption, the pH was varied in the range from 3.04 to 5.50, by adjustment with 0.01 mol·ℓ-1 NaOH and 0.01 mol·ℓ-1 HCl, at 25 ± 0.2oC. The optimal pH was found to be 5.0, and this pH was then used throughout all of the adsorption experiments. Initial concentration of copper(II) ion was 155 mmol·ℓ-1. After reaching adsorption equilibrium (6 h) a sample was centrifuged (1 500 r·min-1 for 5 min), following by copper(II) determination in supernatant solution.
The influence of temperature
Influence of temperature on adsorption of copper(II) ion was studied for the temperature range from 20oC to 80oC. Starting concentration of copper(II) ion and pH was 255 mmol·ℓ-1 and 5.0 ± 0.01, respectively.
Kinetic experiments
The effect of ACHS-copper(II) ion contact time was examined in the range 1 min to 6 h. In the kinetics experiments initial copper(II) ion concentration was 255 mmol·ℓ-1. The residual copper(II) ion concentration in the liquid phase was periodically measured during the adsorption by an ion-selective electrode (type GPE 201.801, IHTM, Belgrade, Serbia).
RESULTS AND DISCUSSION
Characterisation of granular activated carbon
The ACHS is prepared from hazelnut shell by carbonisation and steam activation at 950oC for 2 h. ACHS characterisation was performed using standard methods (Table 1; ASTM International, 2012; Beuth Verlag, 2012), and, according to particle size and SEM analysis, the prepared active carbon was granular. The specific surface area and iodine number were 1 452 m2·g-1 and 1 396 mg·g-1, respectively, which are the highest values thus far reported for activated carbon obtained from hazelnut shell. Alkali (Sayan, 2006), acid-treated (Demirbas et al., 2004) and salt-impregnated (ZnCl2) (Aygün et al., 2003) active carbons have been reported to have specific surface areas of 10.1 m2·g-1; 441 m2·g-1and 793 m2·g-1, respectively, while the specific surface areas of non-impregnated activated carbons were 825 m2·g-1 (Yalcin and Arol, 2002) and 786 m2·g-1 (Kazemipour et al., 2008). Therefore, applied long-term carbonisation/activation processes, at elevated temperature, do have significant influences on the development of high surface area and porosity of ACHS (Table 1).
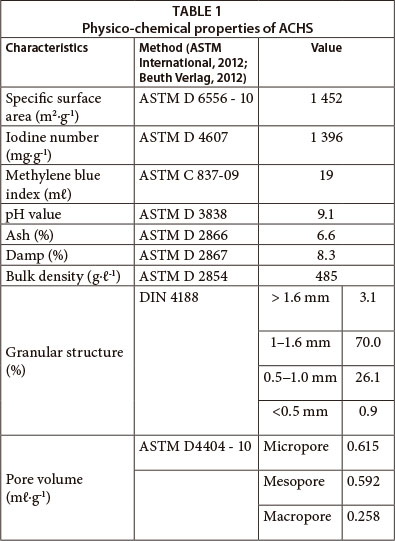
In Fig. 1, an X-ray diffraction (XRD) micrograph of an ACHS surface is presented. In the observed spectra a peak at 2θ ≈ 25° originates from the amorphous structure of carbon (Allaf et al., 2011). A different full width at half-maximum (FWHM) value of the 002 peak, indicating the presence of a different micropore wall structure, can also be observed.
A peak at 2θ = 44.33° and interplanar distance d = 2.0418 x 10-10 m results from the crystal lattice of iron present in the carrier sample.
Scanning electron microscopy (SEM) is a technique which can be used for the study of active carbon morphology (Mohanty, 2006). Figure 2 shows the SEM photographs, at 3 500 times magnification, of the hazelnut shell after carbonisation at the optimum operating condition. The large surface-area of activated carbon is revealed, and pores of different sizes and shapes can be observed. Cavities resulting from the evaporation of volatile organic compounds produced during carbonisation are observed. Some particles and degradation products could be trapped in the pores and possibly block the entrances to meso- and micropores. For this reason, water steam activation could be considered to increase porosity, and thus contribute to significantly increased adsorption capacity of the ACHS.

Equilibrium time
The removal of copper(II) ion from aqueous solution by ACHS at pH 5.0 as a function of contact time indicates that sorption of copper(II) ion is a slow process; 6 h was sufficient for the sorption equilibrium to be achieved. Adsorption time was fixed at 6 h in subsequent adsorption experiments.
Effect of pH
pH is an important parameter influencing heavy metal adsorption from aqueous solutions. It affects both the surface charge of the adsorbent and the degree of ionisation of the heavy metal in solution. The copper(II) cations in aqueous solution at different pH values give rise to soluble ionic forms or more and less insoluble products, due to hydrolysis. The dominant species of copper(II) ion in the pH range 3 to 4 are copper(II) ion and CuOH+, while the copper(II) ion at pH higher than 5.0 precipitates out as insoluble Cu(OH)2 (Antunes, 2003).
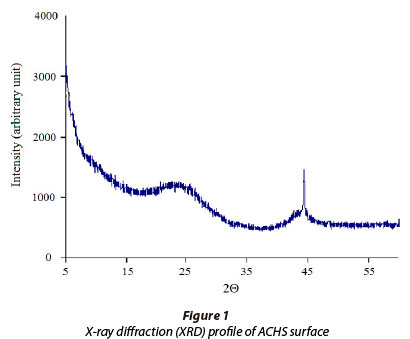
A significant effect of pH on copper(II) sorption on ACHS (Fig. 3) was demonstrated, using 255 mmolℓ-1 initial copper(II) ion concentration. A gradual increase in pH causes ACHS adsorption capacity to increase; optimum pH was found to be 5.0 (qe = 88.9 mg·g-1). At pH < 5, the dominant copper species is Cu2+, therefore, the lower Cu2+ sorption at low pH can be attributed mostly to the competition between H+and Cu2+ion. A decrease in ACHS adsorption capacity at pH values higher than 5, is a consequence of an increase in Cu(II) hydroxy species, which have a lower affinity towards the ACHS surface. At pH higher than 6, precipitation of copper(II) hydroxide begins as a concurrent process (Antunes, 2003).
Effect of temperature
Temperature has a significant impact on the sorption process, resulting in varying contributions of individual sorption mechanisms to the overall process, involving the co-existence of physisorption, i.e., ion exchange, electrostatic attraction and chemisorption, i.e., surface complexation. Seven characteristics which determine the adsorption mechanism, i.e., chemisorp-tion or physical adsorption, are described in the literature. Generally, chemisorption is favoured at increased temperature, and the opposite is true for physisorption (Sawalha et al., 2007).
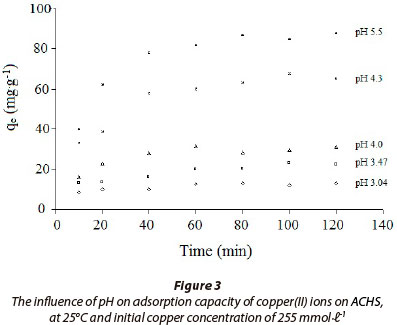
The influence of temperature on ACHS sorption capacity is presented on Fig. 4, for the temperature range 20oC to 80oC, and at 255 mmol·ℓ-1 initial copper(II) ion concentration. The removal of copper(II) ion increases in the temperature range 20oC to 60oC, and then starts decreasing rapidly at higher temperatures. Maximum sorption capacity, q = 93 mg·g-1, was obtained at 60oC. At higher temperatures adsorption capacity decreases, most likely due to desorption being the more favoured process. Because of the complexity of the copper(II) sorption process, unequivocal evidence of the sorption mechanism will require additional and more detailed investigation.
Adsorption mechanism
Generally, it is expected that copper(II) ions are able to attach on adsorbent particle surfaces both physically (via adsorption by Van der Waals, electrostatic or London dispersion forces) and chemically (via a chemical complexation). In both cases, intra-particle diffusion of copper(II) ions will occur and additionally complicate the removal process. Although, a pure carbon surface is considered to be non-polar, some carbon-oxygen complexes (CxO, COx, and CxO2) are usually present, which hydrolyse water molecules. Products of hydrolysis can react with copper(II) ions present in aqueous solution as shown in Eqs. (2) and (3) (Periasamy and Namasivayam, 1996):
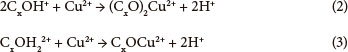
The contribution of the proposed adsorption mechanisms presented in Eqs. (2) and (3) requires investigation in further kinetic studies, which could help in understanding the rate-determining step of the overall process.
Adsorption isotherms
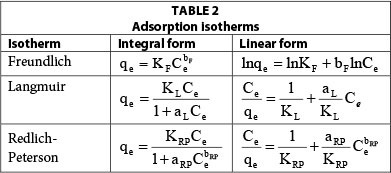
In general, sorption processes were found to be complex, consisting of different steps such as external mass transfer of solute, boundary layer diffusion, intra-particle diffusion and adsorption at the active centres. Unless extensive experimental data are available, it is impossible to determine the rate-determining step of the overall process. However, sorption isotherm equations, which explain the process at equilibrium conditions, provide some quantitative information on sorption process, the surface properties and sorbent affinity. In addition, isotherm equations do not consider the complex mechanisms (external mass transfer, pore diffusion, chelation, ion exchange and chemisorption) involved in the sorption process; scientists use the equilibrium equation for ease of design of sorption systems.
Some of the isotherm equations that could describe solid-liquid adsorption systems are Langmuir, Freundlcih, Sips, Toth isotherm, Redlich-Peterson, Dubinin-Raduskevich and Harins-Jura isotherm equations (Ho et al., 2002). Among of them, Langmuir (Langmuir, 1916), Freundlich (Freundlich, 1906), and Redlich-Peterson (Redlich and Peterson, 1959) isotherms are the most commonly used (Altenora et al., 2009).
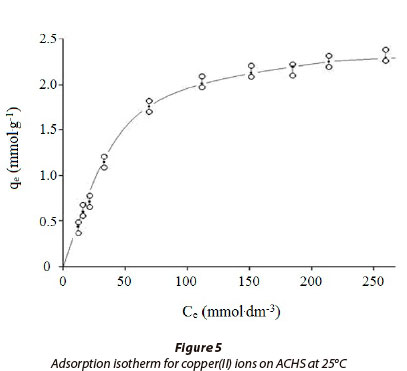
The adsorption data for copper(II) ion on ACHS is shown in Fig. 5., which is in agreement with the standard isotherm, Type 1 of the Brunauer, Deming, Deming and Teller classification (Brunauer et al., 1940). In the initial part of the curve, at low copper concentrations, the ratio of ACHS functional sites, which participate in sorption, to Cu(II) ions is relatively high, resulting in an efficient and fast sorption process. At higher concentrations of the solute, the change in ACHS sorption capacity, q , with increasing Cu(II) concentration is smaller, until maximum sorption capacity is reached. This type of curve is characteristic of high-porosity adsorbents, which is in accordance with the data presented in Table 1, as micro- and meso-pores make up 82.3% of the total pore volume.
Freundlich model
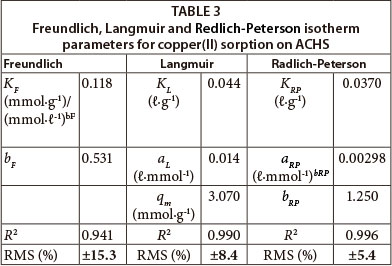
The integral and linear form of the Freundlich model adsorption isotherm (Freundlich, 1906) is presented in Table 2. The Freundlich isotherm assumes a heterogeneous surface with a non-uniform distribution of heat of adsorption and multilayer adsorption over the surface. When an adsorption process is well described by the Freundlich model, the calculated KF parameter is proportional to capacity and bF to intensity of adsorption. In this study, Freundlich constants were obtained by fitting the adsorption equilibrium data to the isotherm models, and are listed in Table 3. As there was some deviation of the experimental data from the linear form of the Freundlich adsorption isotherm this suggests that this model is not a good description of copper(II) ion sorption on ACHS, as indicated by the relatively low value of R2 and high value of RMS (±15.3) (Table 3).
Langmuir model
The integral and linear form of the Langmuir model adsorption isotherm (Langmuir, 1916) is presented in Table 2. This is the most widely used adsorption model, which assumes the following: monolayer adsorption; adsorption takes place at specific homogeneous sites within the adsorbent, and no further adsorption can take place at that site; adsorption energy is constant and does not depend on the degree of occupation of an adsorbent's active centres; the strength of the intermolecular attractive forces is believed to fall off rapidly with distance; the adsorbent has a finite capacity for the dye (at equilibrium, a saturation point is reached where no further adsorption can occur); all sites are identical and energetically equivalent; the adsorbent is structurally homogeneous; there is no interaction between molecules adsorbed on neighbouring sites.
In this study Langmuir constants were obtained by fitting the adsorption equilibrium data to the isotherm models (Fig. 6.); these are listed in Table 3. The R2 values (Table 3) for the Langmuir model are higher, and RMS values are lower, than those for the Freundlich model. This indicates that the Langmuir model better describes the adsorption of copper(II) ion onto ACHS, with a somewhat better fit at the higher concentration of copper(II) ion, of 50 mmol·g-1. Such results indicate a more homogeneous distribution of active sites on the ACHS surface and thus homogenous coverage by adsorb-ate, relative to copper(II) ion removal by raw hazelnut shells (Demirbas et al., 2008).
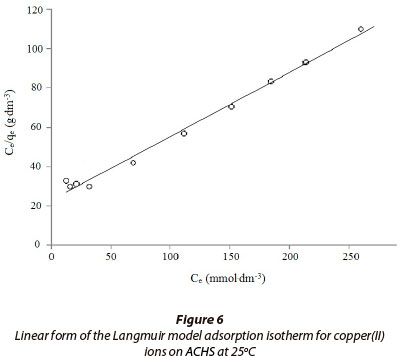
The maximum adsorption capacity for copper(II) ion from aqueous solution by ACHS is 3.07 mmol·g-1 (195 mg·g-1) (Langmuir model). Periasamy and Namasivayam (1996) reported the sorption capacity for copper(II) ion on active carbon obtained from peanut shell (Langmuir model) is 65.57 mg·g-1. The higher value for ACHS obtained in this study can be attributed to the greater specific surface area and pore volume of the ACHS.
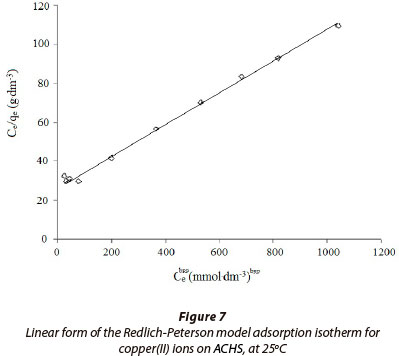
Redlich-Peterson model
Table 2 presents the integral and linear form of the Redlich-Peterson model (Redlich and Peterson, 1959). Redlich and Peterson have proposed an empirical equation incorporating three parameters more appropriate for the description of adsorption equilibrium over a wide range of concentrations (El Qada et al., 2008), which can be applied either in homogenous or heterogeneous systems. This isotherm combines elements from both the Langmuir and Freundlich equations, and the mechanism of adsorption proposed is a hybrid process, which does not follow ideal monolayer adsorption. The Redlich-Peterson equation is reduced to the Freundlich isotherm at low surface coverage and to the Langmuir isotherm at high adsorbate concentration.
In this study, Redlich-Peterson constants were obtained by fitting the adsorption equilibrium data to the isotherm models (Fig. 7.); these are listed in Table 3. It can be seen that the value of bRP tends to 1 (1.25), indicating that the applied model indeed approaches the Langmuir model. Values in Table 3 show that the maximum sorption capacity, qm, is larger than values reported previously. Based on the correlation coefficient (R2 = 0.996) and RMS (± 5.4%), the Redlich-Peterson model best describes the sorption process.
Adsorption kinetics
The removal of copper(II) ions by ACHS as a function of contact time was analysed by pseudo second-order, Elovich and intra-particle diffusion kinetic models. Kinetic studies have been performed to investigate the sorption mechanism, which is helpful for selecting optimum operating conditions for the full-scale batch process.
Pseudo second-order model
The pseudo second-order equation was used to correlate experimental data based on the proposed adsorption mechanism (Cheung et al., 2001):
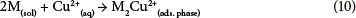
The corresponding pseudo second-order kinetic rate equation is expressed as:

where:
qe (mmol-g-1) and qτ (mmol-g-1) are the sorption capacity at equilibrium and at appropriate time τ (min), respectively constant k2 (g-mmoF-min-1) is the pseudo second-order rate constant.
For the boundary conditions τ = 0 → qτ = 0 at τ = τo → qr = q; the integrated form of Eq. (11) becomes:

and its linearised form:

The initial sorption rate, h, at t = 0 is defined as:

and half-adsorption time of the copper(II) ions t1/2, is:

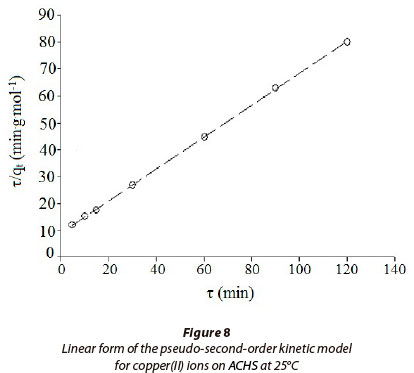
The plot of τ/qr against τ of Eq. (13) gave a linear relationship, and qe and k2 were determined from the slope and intercept of the plot (Fig. 8). Kinetic and statistical parameters of the pseudo-second-order model for the adsorption of copper(II) ion on ACHS are shown in Table 4. Among the three kinetic models, the pseudo-second-order model gave the best fit of experimental data, having the highest correlation coefficient (R2 = 0.999), and the lowest normalised root mean square value RMS (0.82%). According to some authors (Ho, 2003; Bulut and Tez, 2007), this result indicates a high prevalence of chemisorption in the overall sorption process.
Elovich model
The Elovich equation has been applied satisfactorily to some chemisorption data and has been found to cover a large range of slow adsorption processes (Feng-Chin et al., 2009). The Elovich equation is often valid for systems in which the adsorbing surface is heterogeneous. The equation is stated as:

or in integrated form:
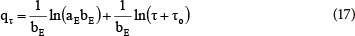
where:
aE (mmol-g-1-min-1) is the initial adsorption rate
bE (g-mmol-1) is the desorption constant during only one experiment
Teng and Hsieh (1999) proposed that the constant aE is related to the rate of chemisorption and the constant bE is related to the surface coverage. The parameter to (2.14 min) was (17) estimated by trial and error, to obtain a linear plot of qr against ln (τ+τo ); aE and bE are calculated from the intercept and the slope. According to Eq. (17), for τo = 0 at τ = 0, time constant τo can be calculated from Eq. (18):

The linear form of Eq. (17), on the basis of experimental data for the adsorption of copper(II) ions on ACHS, is shown in Fig. 9. The Elovich model parameters are shown in Table 3, confirming that the experimental kinetic data give a good fit to this equation and similar results previously published (Ho and McKay, 2000). The values of Elovich model parameters aE and bE are 0.184 mmol·g1·min-1 and 2.090 g·mmol-1, respectively, as previously found for similar systems (Cheung et al., 2001). Time constant τo, calculated according to Eq. (18) (τo = 2.09 min) is close to the value calculated using the trial-and-error method (τo = 2.14 min; error ±2.3%).
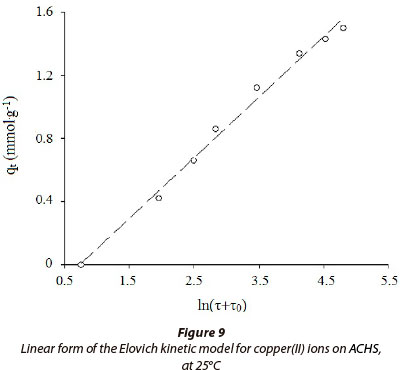
Intra-particle diffusion model
Adsorptive transfer from solution to adsorbent surface is highly complex. The most commonly used model for analysing the overall adsorption process is the intra-particle diffusion model, given by the following equation (Weber and Morris, 1963):

where:
qτ is amount of metal adsorbed at time τ (mmol·g-1)
Kd is the intra-particle diffusion rate constant (mmol·g-1-min0.5)
CI is the intercept (mmol·g-1).
If intra-particle diffusion occurs then qτ against √τ ill be linear and the line will pass through the origin, indicating that intra-particle diffusion was the only rate-limiting parameter controlling the process. Otherwise, some other mechanism is also involved. The value of the intercept gives an indication of the thickness of the boundary layer, i.e., the larger the intercept the greater is the boundary layer effect (Kannan and Sundaram, 2001).
In Fig. 10, a plot of adsorbed Cu(II) per unit mass of ACHS adsorbent, qt vs. t0.5, is presented; this indicates that the intra-particle diffusion model well describes the adsorption process. Two linear consecutive regions could be observed: Part (I), fast uptake, is attributed to intra-particle diffusion; and Part (II) is a slower process indicating the effect of pore diffusion, which could be attributed to the difference in rates of mass transfer in the initial and final stages of adsorption (Panday et al., 1986). This is attributed to the instantaneous adsorbate bonding at the most readily available adsorbing sites on ACHS. It is noteworthy that in Part (I) the line passes through the origin, indicating that the process is predominantly controlled by intra-particle diffusion, rather than film diffusion. Part (II) may be attributed to a slower diffusion of the adsorbate from the surface film into the meso- and micro-pores, which are less accessible sites of adsorption. This also stimulates a very slow rate of migration of adsorbate from the liquid phase on to the adsorbent surface. The values of kp,1 , and kp,2 ., as obtained from the slopes of the straight lines, are given in Table 4, and the data indicate that pore diffusion is not the sole rate-controlling step (Mane et al., 2007).
CONCLUSION
The granular activated carbon, ACHS, produced from hazelnut shells has a high specific surface area and highly developed meso- and micro-porous structure. The specific method of carbonisation and activation applied in this study favours the formation of meso- and micro-porous structure in ACHS. The sorption experimental data for copper(II) ion on ACHS follow the Langmuir and Radlich-Peterson adsorption isotherm models. The highest value of R2 and lowest value of normalised RMS are obtained using the Radlich-Peterson model. The kinetics of copper(II) ion removal on ACHS follow the pseudo-second-order model, indicating that chemical adsorption between the adsorbent and the adsorbate prevails rather than physical adsorption. As the intra-particle diffusion model fits the kinetic data well, adsorption of copper(II) ions on the granular activated carbon is also diffusion controlled. The prepared ACHS can be used as an effective adsorbent for batch adsorption of copper(II) ion from aqueous solution.
ACKNOWLEDGEMENTS
This work was supported by the Ministry of Education, Science and Technological Development of Serbia (Grant Number TR 34008).
REFERENCES
ALLAF RM, RIVERO IV, SPEARMAN SS and HOPE-WEEKS LJ (2011) On the preparation of As-produced and purified single-walled carbon nanotube samples for standardized X-ray diffraction character. Mater. Charact. 62 857-864.
ALTENORA S, CARENEA B, EMMANUELB E, LAMBERT J, EHRHARDTC JJ and GASPARDA S (2009) Adsorption studies of methylene blue and phenol onto vetiver roots activated carbon prepared by chemical activation. J. Hazardous Mater. 165 1029-1039. [ Links ]
ANTUNES WM, LUNA AS, HENRIQUES CA and COSTA AC (2003) An evaluation of copper biosorption by a brown seaweed under optimized conditions. Electron. J. Biotechnol. 6 174-184. ASTM INTERNATIONAL (2012) URL: http://www.astm.org/Standard/index.shtml. [ Links ]
AYGÜN A, YENISOY-KARAKAS S and DUMAN I (2003) Production of granular activated carbon from fruit stones and nutshells and evaluation of their physical, chemical and adsorption properties. Micropor. Mesopor. 66 189-195. [ Links ]
BAJPAI SK and JAIN A (2010) Removal of copper(II) from aqueous solution using spent tea leaves (STL) as a potential sorbent. Water SA 36 221-228. [ Links ]
BEUTH VERLAG (2012) URL: http://www.beuth.de/en [ Links ]
BRUNAUER S, DEMING LS and DEMING TELLER WS (1940) Types of adsorption isotherms. J. Am. Chem. Soc. 62 1723. [ Links ]
BULUT Y and TEZ Z (2007) Adsorption studies on ground shells of hazelnut and almond. J. Hazardous Mater. 149 35-41. [ Links ]
CHEUNG CW, PORTER JF and McKAY G (2001) Sorption kinetic analysis for the removal of cadmium ions from effluents using bone char. Water Res. 35 605-612. [ Links ]
DEMIRBAS Ö, KARADAĞ A, ALKAN M, DOGAN M, BULUT Y and TEZ Z (2008) Removal of copper ions from aqueous solutions by hazelnut shell. J. Hazardous Mater. 153 677-648. [ Links ]
FENG-CHIN W, RU-LING T and RUEY-SHIN J (2009) Characteristics of Elovich equation used for the analysis of adsorption kinetics in dye-chitosan systems. Chem. Eng. J. 150 366-373. [ Links ]
FREUNDLICH HMF (1906) Uber die adsorption in losungen. Z. Phys. Chem. 57A 385-470. [ Links ]
HO YS, McKAY G (2004) Sorption of copper(II) from aqueous solution by peat. Water Air Soil Pollut. 158 77-97. [ Links ]
HO YS, PORTER JF and McKAY G (2002) Equilibrium isotherm studies for the sorption of divalent metal ions onto peat: Copper, nickel and lead, single component systems. Water Air Soil Pollut. 141 1-33. [ Links ]
KANNAN K and SUNDARAM MM (2001) Kinetics and mechanism of removal of methylene blue by adsorption on various carbons -A comparative study. Dyes Pigments 51 25-40. [ Links ]
KAZEMIPOUR M, ANSARI M, TAJROBEHKAR S, MAJDZADEH M and KERMANI HR (2008) Removal of lead, cadmium, zinc, and copper from industrial wastewater by carbon developed from walnut, hazelnut, almond, pistachio shell, and apricot stone. J. Hazardous Mater. 150 322-327. [ Links ]
LANGMUIR I (1916) The constitution and fundamental properties of solids and liquids. J. Am. Chem. Soc. 38 2221-2295. [ Links ]
MANE VS, MALL ID and SRIVASTAVA VC (2007) Use of bagasse fly ash as an adsorbent for the removal of brilliant green dye from aqueous solution. Dyes Pigments 73 269-278. [ Links ]
MOHANTY K (2006) Preparation and characterization of activated carbons from Sterculia alata nutshell by chemical activation with zinc chloride to remove phenol from wastewater. Adsorption 12 119-132. [ Links ]
NOURI L, GHODBANE I, HAMDAOUI O and CHIHA M (2007) Batch sorption dynamics and equilibrium for for the removal of cadmium ion from aqueous phase using wheat bran. J. Hazardous Mater. 149 115-125. [ Links ]
OROZCO MF, CONTRERAS EM, BERTOLA N and ZARITZKY N (2007) Hexavalent chromium removal using aerobic activated sludge. Water SA 33 239-244. [ Links ]
PANDAY KK, PRASAD G and SINGH VN (1986) Mixed adsorbent for Cu(II) removal from aqueous solutions. Environ. Technol. Lett. 50 (7) 547-554. [ Links ]
PERIASAMY K and NAMASIVAYAM C (1996) Removal of copper(II) by adsorption onto peanut hull carbon from water and copper plating industry wastewater. Chemosphere 32 769-789. [ Links ]
EL QADA EN, ALLEN SJ and WALKER GM (2008) Adsorption of basic dyes from aqueous solution onto activated carbons. Chem. Eng. J. 135 174-184. [ Links ]
REDLICH O and PETERSON DL (1959) A useful adsorption isotherm. J. Phys. Chem. 63 1024. [ Links ]
SAWALHA MF, PERALTA-VIDEA JR, ROMERO-GONZALEZ J, DUARTE-GARDEA M, GARDEA-TORRESDEY JL (2007) Thermodynamic and isotherm studies of the biosorption of Cu(II), Pb(II) and Zn(II) by leaves of saltbush. J. Chem. Thermodynamics 39 488-492. [ Links ]
ŞAYAN E (2006) Ultrasound-assisted preparation of activated carbon from alkaline impregnated hazelnut shell: An optimization study on removal of Cu(II) from aqueous solution. Chem. Eng. J. 115 213-218. [ Links ]
SENGIL I, OZACAR M and TURKMENLER H (2009) Kinetic and isotherm studies of Cu(II) biosorption onto valonia tannin resin. J. Hazardous Mater. 162 1046-1052. [ Links ]
TAJAR AF, KAGHAZCHI T and SOLEIMANI M (2009) Adsorption of cadmium from aqueous solutions on sulfurized activated carbon prepared from nut shells. J. Hazardous Mater. 165 1159-1164. [ Links ]
TENG H and HSIEH C (1999) Activation energy for oxygen chemisorption on carbon at low temperatures. Ind. Eng. Chem. Res. 38 292-297. [ Links ]
WEBER WJ and MORRIS JC (1963) Kinetics of adsorption on carbon from solution. Am. Soc. Civ. Eng. 89 (SA2) 1-40. [ Links ]
YALCIN M and AROL AI (2002) Gold cyanide adsorption characteristics of activated carbon of non-coconut shell origin. Hydrometallurgy 63 201-206. [ Links ]
Received 1 April 2012
Accepted in revised form 27 June 2013
* To whom all correspondence should be addressed. +381 63 106 40 16; fax: +381 18 533 014; e-mail: bojica@pmf.ni.ac.rs














