Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Water SA
On-line version ISSN 1816-7950
Print version ISSN 0378-4738
Water SA vol.39 n.4 Pretoria Jan. 2013
Development and assessment of a daily time-step continuous simulation modelling approach for design flood estimation at ungauged locations: ACRU model and Thukela Catchment case study
JC Smithers*; KT Chetty; MS Frezghi; DM Knoesen; MH Tewolde
School of Bioresources Engineering and Environmental Hydrology, University of KwaZulu-Natal, Pietermaritzburg Campus, Private Bag X01, Scottsville 3209, South Africa
ABSTRACT
The estimation of design floods is necessary for the design of hydraulic structures. Commonly used event-based approaches to design flood estimation have several limitations, which include the estimation of antecedent soil moisture conditions and the assumption that the exceedance probability of the design flood is the same as the exceedance probability of the design rainfall. Many of the limitations of event-based approaches may be overcome by the use of continuous simulation modelling for design flood estimation. This paper contains a brief summary on the development and assessment of a continuous simulation modelling system for design flood estimation in ungauged catchments. These developments include an investigation into the appropriate spatial scale of model configuration for optimum performance of the system, the temporal disaggregation of daily rainfall for hydrograph generation, flood routing in ungauged catchments and the use of radar information and rain-gauge data to improve the estimation of catchment rainfall. Results from the application of the system for design flood estimation in the Thukela Catchment in South Africa are presented and discussed. The results from the study highlight the challenges of hydrological modelling in an operational catchment and the need for reliable rainfall and runoff data. From the results obtained, it is concluded that reasonable and consistent estimates of design floods in the Thukela Catchment, particularly in smaller sub-catchments, can be obtained using the ACRU model.
Keywords: Design flood estimation; continuous simulation modelling, Thukela Catchment
INTRODUCTION
Estimates of design floods, where the magnitude of a flood is associated with a level of risk (e.g. exceedance probability or return period), are necessary in the planning, design and operation of hydraulic structures (e.g. bridges, culverts, dam spillways, drainage canals) for the preservation of human life and property (Rahman et al., 1998; Smithers and Schulze, 2003; Pegram and Parak, 2004; Reis and Stedinger, 2005). Under or over-design of even small hydraulic structures can result in a considerable waste of resources. The choice of an acceptable and cost-effective engineering solution is dependent upon having reliable estimates of the frequency-magnitude relationship of floods, both in terms of peak flows and volumes of water. However, while flood frequency estimation in ungauged catchments is of great practical interest, it is a continuing challenge (Blazkova and Beven, 2002).
The situation which faces design engineers and hydrologists most frequently is when no, or inadequate, observed streamflow data are available at the site of interest, and then either regional approaches or rainfall-runoff models have to be used for design flood estimation. Standard techniques for flood estimation have been developed for most countries and procedures for design flood estimation may be broadly categorised as methods based on the analysis of observed floods and rainfall-based methods, as shown schematically in Fig. 1. Regionalisation, by developing regressions between the flow statistics from gauged catchments with catchment characteristics (e.g., catchment area, slope, shape, hydraulic length), has been the dominant methodology used in the past to estimate design floods at ungauged locations. Continuous hydrograph simulation, driven by either historical or stochastic rainfall as input, is an approach which utilises the more widely available rainfall records (Blazkova and Beven, 2002) and is a viable method for flood frequency estimation (Blazkova and Beven, 2004).
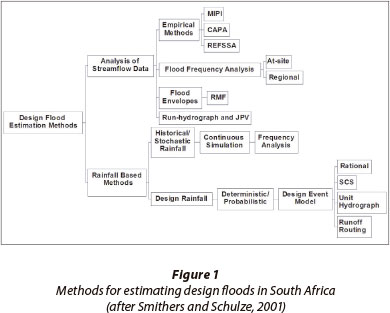
Most of the methods used for design flood estimation in South Africa were developed in the late 1960s and early 1970s, as summarised in HRU (1972), and are in need of updating, with more than 40 years of additional data currently available and with new approaches used internationally (Alexander, 2002b; Smithers and Schulze, 2003; Görgens, 2007; Van der Spuy and Rademeyer, 2010; Smithers, 2012). Software to implement design flood procedures currently used in South Africa has been developed (e.g. Schulze et al., 1992; Van Dijk, 2005; Gericke, 2010), but there is no universally applicable method for design flood estimation in South Africa (Van der Spuy and Rademeyer, 2010).
According to HRU (1972), design floods may be estimated using either a statistical approach, which is an ordering and transposition of past experience, or a deterministic approach, in which rainfall is translated into a flood. Methods used for design flood estimation in South Africa are based on empirical, deterministic and probabilistic approaches (Pegram and Parak, 2004; Van der Spuy and Rademeyer, 2010) and Pegram (1994) presents a decision tree for the selection of design flood estimation methods in South Africa. Alexander (1990; 2001) classifies the methods for design flood estimation in South Africa as direct statistical analysis, regional statistical analysis, deterministic and empirical methods. SANRAL (1986) identifies empirical and statistical, as well as the Rational, SCS, run-hydrograph and synthetic unit hydrograph approaches, as appropriate and promising methods for estimating design floods in South Africa. As reviewed by Smithers (2012), more recently developed methods for design flood estimation in South Africa include a probabilistically-based Rational Method, termed the Standard Design Flood (SDF), developed by Alexander (2002a; 2002c; 2002d), the Joint Peak-Volume (JPV) design flood methodology developed by Görgens (2007), and the Regional Estimation of Extreme Flood Peaks by Selective Statistical Analyses (REFSSA) method developed by Nortje (2010).
Rainfall data are far more abundant and have longer records than streamflow data in South Africa. Hence, rainfall-driven event-based approaches such as the Unit-Hydrograph, Rational Method and Soil Conservation Service (SCS) methods, which are generally simple to apply and which lump complex, heterogeneous catchment processes into a single process or index (Houghton-Carr, 1999), are currently widely used for design flood estimation in South Africa. The event-based approach greatly simplifies the estimation of catchment conditions prior to the occurrence of an extreme event, even when rainfall-runoff modelling is performed to estimate the flood hydrograph (Cameron et al., 1999).
One of the major limitations of design event based models is the assumption that, for representative inputs and model parameters, the frequency of the estimated flood is equal to the frequency of the input rainfall (Pilgrim and Cordery, 1993; Rahman et al., 2002). Numerous studies have shown that this is generally not the case and that the antecedent soil moisture conditions prior to a rainfall event are significant in determining the runoff response (Schulze and Arnold, 1979; Schulze, 1982; Schmidt and Schulze, 1984; Dunsmore et al., 1986; Pilgrim and Cordery, 1993). Another major limitation of event-based methods is the inability of most of the methods to account for antecedent soil moisture conditions prior to flood events, which may result in unrealistic estimates of runoff. These assumptions are likely to introduce significant bias in the frequency of flood estimates (Rahman et al., 1998). Considerable uncertainty is present in inputs such as storm duration, the spatial and temporal distribution of the design storm and model parameters (Rahman et al., 1998). Design event based approaches consider the probabilistic nature of rainfall, but generally ignore the probabilistic behaviour of other inputs and parameters (Rahman et al., 2002). Event-based methods are recommended for use in South Africa and are generally applied in a deterministic manner and hence suffer from the limitations of this approach.
Some of the limitations of event-based approaches to design flood estimation, which are widely used in South Africa, could possibly be overcome by adopting a continuous simulation approach to rainfall-runoff modelling. Continuous Simulation Models (CSM) strive to represent the major processes responsible for converting the input catchment rainfall into streamflow (Rahman et al., 1998) and numerous continuous simulation rainfall-runoff models with varying levels of complexity have been reported in the literature (Brocca et al., 2011). Hydrographs can be generated for long periods of time using the input historical rainfall series, potential evaporation and other climatological as well as catchment attributes (e.g. soils, land cover and topography). An important characteristic of these models is the use of a continuous water budget model for the catchment which enables the simulation of antecedent conditions prior to each rainfall event (Rahman et al., 1998; Lamb and Kay, 2004) and hence this approach can be used in ungauged or scarcely gauged catchments (Moretti and Montanari, 2008).
In practice, the entire design hydrograph, and not only the peak discharge, is frequently required when designing, for example, flood-reducing detention ponds and emergency spillways for dams. Design floods can be estimated directly from the simulated hydrographs from a continuous simulation model (Brocca et al., 2011), and hence the computed exceedance probability of a flood is not dependent on the exceedance probability of the input rainfall (Goel et al., 2000). Current or predicted (e.g. from climate change) patterns of rainfall and land use in the catchment can be modelled explicitly and thus influence the estimated design floods. Runoff from rainfall varying over multiple catchments can be simulated and analysed. Antecedent soil moisture conditions are modelled explicitly and hence realistic runoff responses to rainfall events can be estimated. An additional advantage of the continuous simulation modelling approach is that the flood attenuating effects of, for example, river reaches and dams can be directly accounted for by the model. These and other advantages and disadvantages of continuous simulation modelling for design flood estimation are widely reported in the literature (e.g. Boughton and Hill, 1997; Rahman et al., 1998; Cameron et al., 1999; Reed, 1999; Lamb and Kay, 2004) and CSM has been used for design flood estimation in a number of international studies (Calver and Lamb, 1995; Boughton and Hill, 1997; Rahman et al., 1998; Steel, 1998; Calver et al., 1999; Cameron et al., 1999; Houghton-Carr, 1999; Lamb, 1999; Reed, 1999; Steel et al., 1999; Calver et al., 2000; Calver et al., 2001; Blazkova and Beven, 2004; Calver et al., 2004; Lamb and Kay, 2004; Morettiand Montanari, 2008; Blazkova and Beven, 2009; Viviroli et al., 2009; Brocca et al., 2011) and has also been promoted and demonstrated in South Africa (Schulze, 1989; Smithers et al., 1997; Smithers et al., 2001; Smithers et al., 2006). The use of CSM for design flood estimation is receiving increasing interest and use in the USA (ASCE, 1997) and Calver et al. (2000) believe that CSM may form the basis for the next generation of flood frequency estimation in the UK. The validity of results from a CSM will depend on the accurate representation of both rainfall and of the rainfall-runoff processes within the model, and on the values of the parameters used in the model (Blazkova and Beven, 2004). Consequently, the extent to which CSM can provide reliable simulations over a wide range of spatial scales is questioned by Moretti and Montanari (2008), and Lamb and Kay (2004) believe that the ability of the CSM to perform well over a range of catchment scales and types is critical for the success of the CSM approach to design flood estimation.
In order to reduce uncertainties in the calibration and validation of hydrological models, it is necessary to derive model parameter values directly from field measured data or inferred directly from the catchment response data. The CSM needs to have a valid structure to represent physical processes in the catchment and needs to be applicable to the domain being simulated (Brocca et al., 2011).
The objectives of this paper are (i) to summarise both the development of a daily time step CSM for design flood estimation using the daily time-step ACRU agrohydrogical model (Schulze, 1995), (ii) to describe the application of the system to estimate design floods in the Thukela Catchment (29 036 km2) in South Africa as a test case, and (iii) to highlight some of the difficulties encountered when modelling an operational catchment with limited information and unreliable data records. Examples of the comparison between design floods estimated using the CSM approach and from observed floods are also presented. Full details of the study are contained in Smithers et al. (2006).
SUMMARY OF MODEL DEVELOPMENT AND METHODOLOGY
The ACRU model (Schulze, 1995) is described as a physical-conceptual model which operates on a daily time step and where the simulated streamflow and peak discharge are sensitive to rainfall, soils, land cover and catchment characteristics. The ACRU model has been used and verified on data from South Africa, Swaziland, Zimbabwe, Germany and the USA (Schulze, 1995). Schulze (1995) presents 11 verification studies on various components of the ACRU model, both on simulated output and internal state variables. Schulze and Pike (2004) list an additional 10 verification studies. The ACRU model has also been used and verified in Canada (Kienzle and Schmidt, 2008; Schmidt et al., 2009) and New Zealand (Kienzle, 2011; Kienzle et al., 2012). Further verifications of model output are performed in this study. Given that the ACRU model has shown potential to be used to estimate design floods (Smithers et al., 1997; Smithers et al., 2001) and was developed and has been widely verified in South Africa, it was selected as the continuous simulation model for this study.
The ACRU modelling system was developed and refined by Smithers et al. (2006) in a number of areas to improve simulated peak discharges and related design flood estimation. These included:
- An investigation into the scale of application and levels of soil and land cover information required to apply the ACRU model for continuous simulation modelling in order to estimate design floods. Results reported by Smithers et al. (2006) and Chetty and Smithers (2011) indicated that the larger quaternary catchments should not be modelled as lumped entities and should be discretised into sub-catchments and hydrological response units (HRUs) within the sub-catchments, as the best simulations were obtained using HRU catchment configurations. The use of area weighted and not modal soil information resulted in the best simulations and the critical importance of estimating rainfall over a catchment was highlighted.
- The development and evaluation of a method to disaggregate daily rainfall into hourly totals in South Africa. This was undertaken in order to improve the shape of simulated hydrographs and estimation of peak discharge. Knoesen (2005) developed a regionalised semi-stochastic daily rainfall disaggregation model which is capable of producing a range of different temporal patterns which reflect the regional characteristics of rainfall. The methodology was assessed independently at 15 sites in South Africa and moments, statistics and extreme rainfall events were analysed. The results indicated that the disaggregation model reproduced the general distribution of rainfall relatively well, both when observed short-duration data were available as well as when only daily rainfall data were used, but that the structure (sequencing) of the disaggregated rainfall requires additional refinements. The development, application and assessment of the daily rainfall disaggregation method is summarised in Knoesen and Smithers (2008; 2009).
- An assessment of procedures developed by Pegram and Sinclair (2004) to merge rain-gauge and radar data. This was performed by Frezghi (2005), and summarised in Frezghi and Smithers (2008), using data from raingauges used in the conditioning of the radar data and from rain-gauges not used in the merging process. The Leibenbergsvlei Catchment in South Africa was used as a study site as both radar and rainfall data from a dense network of gauges were available. For most sub-catchments reasonably good estimates of rainfall were obtained for the independent verifications, with R2 values generally > 0.70. It was noted that the rain-gauges selected to represent the areal rainfall of the sub-catchments when modelling generally over-estimated the mean areal merged rainfall values of the sub-catchments by between 5% and 50%. Based on the premise that merged rainfall fields are the best estimate of catchment rainfall, the short periods of available radar data were used by Frezghi (2005) to develop relationships between the merged rainfall fields for a catchment and rainfall data from a selected rain-gauge. This relationship was then used to adjust the much longer record of historical gauged daily rainfall data to better represent rainfall in the catchment.
- An assessment was performed by Frezghi (2005) of the stochastic, fine resolution space-time String-of-Beads model (SBM) developed by Clothier and Pegram (2002) to simulate long series of rainfall over a catchment. This was undertaken to enable long series of simulated streamflow to be generated in order to estimate design floods. The results indicated that the SBM reproduced the observed statistics at a daily time scale reasonably well and better than at monthly or annual time scales. This result was not unexpected as the SBM is a short-duration rainfall model designed to mimic rainfall values at a detailed temporal and spatial resolution. Consequently small errors at 5-minute durations accumulate over longer durations to the errors evident at the daily and longer time scales. Spatially, the SBM reproduced the statistics of the selected rain-gauges used in the study. Therefore, it was concluded by Frezghi (2005) that an appropriately calibrated SBM may be used in rainfall-runoff modelling which requires rainfall at detailed spatial and temporal resolutions and could be used as input to a CSM system in order to estimate design floods.
- The development and assessment of techniques for flood routing in ungauged catchments using streamflow data from the Thukela Catchment (Tewolde, 2005; Tewolde and Smithers, 2006). The results of these studies indicated that the Muskingum-Cunge method, both with empirically estimated parameters and parameters estimated from the cross-sections of the selected rivers, resulted in reasonable accuracy in the computed outflow hydrographs with respect to peak discharge, timing of peak flow and volume. Hence, it was concluded that the Muskingum-Cunge method, with parameters estimated using empirical relationships, can be applied to route floods in ungauged catchments in the Thukela Catchment.
These developments and refinements to the ACRU modelling system made by Smithers et al. (2006) were incorporated into the ACRU model and the Thukela Catchment in South Africa was used to assess the use of a CSM for design flood estimation.
The ACRU model is not a parameter-fitting model or a model which is calibrated to fit observed data, and input variables, rather than optimised parameters values, are generally estimated from physically-based characteristics of the catchment (Schulze and Smithers, 2004). Most of the flood frequency estimation studies using a CSM approach reported in the literature (e.g. Brath et al., 2006; Moretti and Montanari, 2008; Brocca et al., 2011) rely on the availability of short-duration (typically 1 h) observed flow data from relatively small catchments to calibrate the CSM. In this study the daily time-step CSM was not calibrated and was configured using input variables derived from available catchment information in an effort to provide a true test of the CSM approach to estimating design floods at ungauged locations.
APPLICATION IN THE THUKELA CATCHMENT
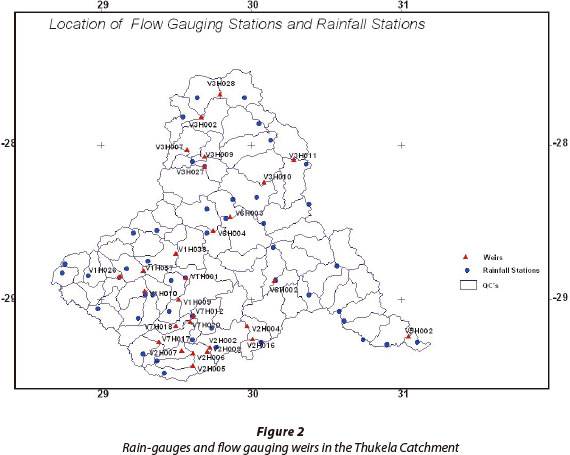
The Thukela Catchment (29 036 km2), located as shown in Fig. 2, was selected as a case study. As a consequence of the diverse hydrological responses within many of the 86 quaternary catchments (QCs) in the Thukela Catchment, Schulze et al. (2005) further sub-divided the 86 QCs into 235 sub-catchments based on natural heterogeneities (altitude, rainfall, temperature/evaporation), soils, natural vegetation, channel-based factors (location of streamflow gauging weirs and dams), environmental flow considerations (environmental flow requirement sites) and political history (degraded vegetation). Smithers et al. (2006) identified and modelled hydrologi-cal response units (HRUs) within each of the 235 sub-catchments, based on the land cover within each sub-catchment. The HRUs were modelled as 'homogenous spatial entities' with no fixed spatial location within the sub-catchment. The location of flow gauging weirs, identified by Joubert and Hurley (1994) as having good quality data and relatively un-impacted catchments, are shown in Fig. 2. Primary flow data was obtained from the South African Department of Water Affairs (DWA, 2012).
The configuration of the ACRU model for the Thukela Catchment by Schulze et al. (2005) was used as a basis for the configuration used in this study. A single daily rainfall station was selected to represent rainfall in each of the sub-catchments based on criteria such as distance from the rainfall station to the centroid of the catchment, available period of record, differences between the mean annual precipitation at the catchment centroid and station rainfall data, and the reliability of the data. Soils information was obtained from soils maps published by the Institute for Soil, Climate and Water (SIRI, 1987) at the 1:50 000 scale, and was translated into ACRU variables using a methodology developed by Pike and Schulze (1995). Land cover information was obtained from the National Land Cover Database (CSIR, 1999) at a resolution of 1:250 000 and which had been translated into ACRU variables by Schulze (2001).
As reported by Smithers et al. (2006), the application of the model proved challenging in an operational catchment where the observed data were not perfect, the network of daily rain-gauges was relatively sparse, flow depths at flow gauging weirs exceeded rating tables, transfers of water between catchments occurred, irrigation had been developed over time and other land cover changes have occurred. Some of the issues encountered include the following:
- The problems associated with estimating rainfall over a catchment using a single rain-gauge were evident in some results when the simulated and observed streamflow did not correspond for some events.
- A thorough investigation into the reliability of the observed streamflow data indicated that the data from many flow gauging stations were not suitable for verification studies.
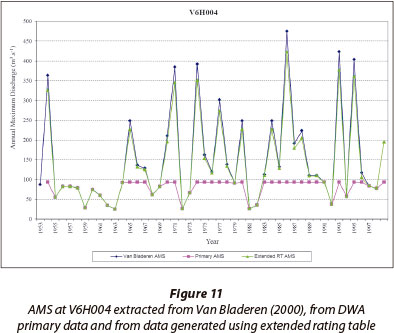
- The stages recorded at many of the flow gauges exceeded their rating tables during larger events. The moderate extension of the rating tables performed by Smithers et al. (2006), who used a simple log-log extension of the rating table as described by Van Rensburg (2005), is believed to add to the uncertainty of the accuracy of the observed flow data, but had a large impact on the volumes of observed flow and observed annual maximum series (AMS) of peak discharges.
- The AMS extracted from the DWA primary flow data generated using the extended rating tables generally corresponded well with AMS supplied by Van Bladeren (2000), although in some cases the AMS from Van Bladeren (2000) exceeded the extracted values.
- • No detailed information useful for a daily time-step model was available on the transfers of water between catchments, which limited the number of catchments which could be used for verification of the simulations.
- The areas irrigated in the sub-catchments were derived from the Water Use Licencing, Registration and Revenue Collection database (WARMS, dated 1 Dec 2005) developed by the Department of Water Affairs in South Africa. Without detailed information on irrigation management practices, 2 irrigation schedules were used to simulate irrigation demand. The first (ISCHED1) is dependent on the climate and soil, and irrigation was initiated when the soil water in the root zone fell below 50% of the plant available water, at which point an amount was irrigated to refill the soil profile to a level (5 mm) below the drained upper limit of the soil, in order to utilise any rainfall which may occur shortly after an irrigation event. The second irrigation schedule simulated (ISCHED2) was a fixed amount (15 mm) applied in a fixed cycle (7 days). The cycle was reset if 15 mm or more rainfall occurred.
- The development of irrigation in some sub-catchments impacted significantly on the streamflow simulated. This was evident in the results obtained from a number of catchments by the good correspondence between accumulated observed and simulated runoff in the early part of the record when irrigation was not simulated, and in the latter part when irrigation was simulated.
- The use of a static land cover in the simulations, which did not reflect temporal changes within a catchment, resulted in better simulations closer to the date on which the land cover information used in the simulations had been captured.
The results from the application of the CSM in the Thukela Catchment are reported in the following section.
RESULTS
Verification of the uncalibrated simulated streamflow (i.e. input variables determined as described above from catchment characteristics) was performed by Smithers et al. (2006) at selected gauging weirs located at the outlet of sub-catchments where the flow data were deemed to be of an acceptable quality, and which did not have significant periods of missing data. Generally, stations with more than 10% of the data missing in the rainy season were excluded and 10 flow gauging weirs (V1H009, V1H010, V1H026, V1H031, V1H038, V2H007, V2H016, V3H007, V3H009 and V6H004), with catchment areas ranging from 126 to 1916 km2, were used in the verifications. The log-Pearson Type 3 (LP3) probability distribution was subsequently used to estimate design floods from both the simulated series and observed data at those locations. Selected results are presented below.
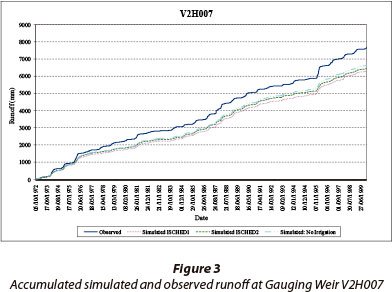
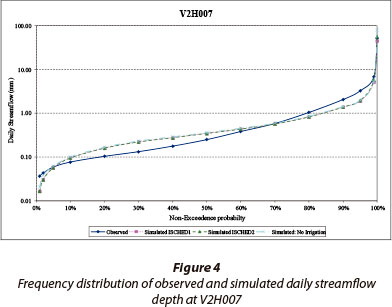
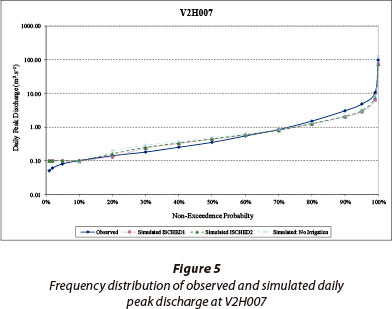
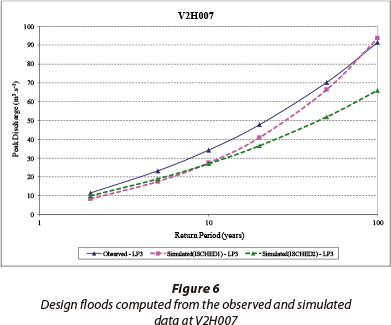
The accumulated observed and simulated runoff at Gauging Weir V2H007 (111.3 km2) for the period of available observed flow data (1972-2000) is shown in Fig. 3. The influence of irrigation in the catchment is shown by the results which did not simulate irrigation abstractions, and the development of irrigation in the catchment over time is evident by the trends in the observed and simulated values for the simulation with no irrigation. The simulated results generally agree better with the observed values for the latter part of the record. This is attributed to the fact that the model input variables increasingly reflected the actual land cover of the catchment as the capture date (1999) of the land cover database was approached. Frequency analyses of daily runoff depths indicate that the CSM, including the simulation of abstractions for irrigation, simulated the observed runoff depth reasonably well and there was little difference between the two irrigation scheduling scenarios considered (Fig. 4). The frequency distributions of daily peak discharge performed on the simulated and observed values are very similar over the entire range of flows (Fig. 5). Similarly, as shown in Fig. 6, the design flood peak discharges computed from the observed data and simulated values are similar, particularly for the ISCHED1 irrigation scheduling.
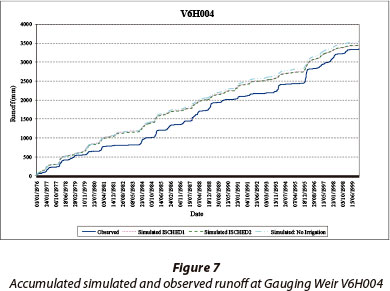
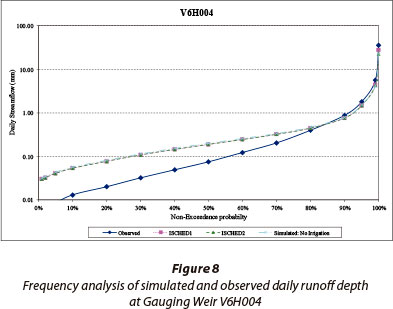
The accumulated simulated and observed runoff at Gauging Weir V6H004 (654.5 km2) for the period of available reliable observed flow data (1976-2000) is shown in Fig. 7 and a frequency analysis of daily runoff depth is shown in Fig. 8. These results indicate that the CSM slightly over-simulated the observed runoff volume up to approximately 1984. This could have been caused by the 1999 land cover information used in the simulation. The distribution of the observed and simulated runoff volumes are similar, particularly for larger events.
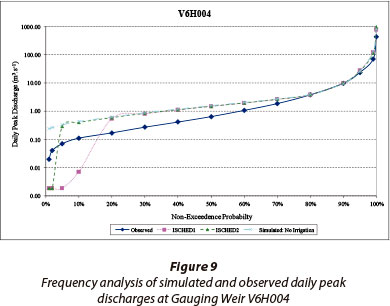
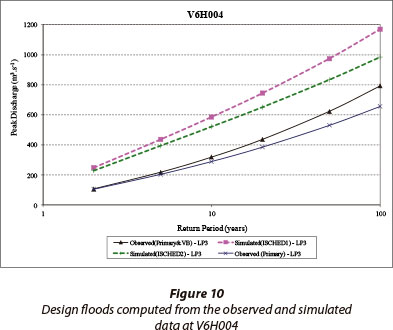
As shown in Fig. 9, the frequency distributions of daily peak discharges performed on the simulated and observed values indicate that the larger peaks are over-simulated. The design floods computed from the observed and simulated data are shown in Fig. 10 and include design peak discharges estimated using a combination of values from the DWA primary flow data and combined with data from Van Bladeren (2000). These are termed 'Primary' and 'Primary and VB' respectively. The impact on design peak discharges of curtailed rating tables is evident in Fig. 10, which contains design discharges computed using the AMS extracted from Van Bladeren (2000), extracted from the DWA primary data and extracted from flows generated using an extended rating table, as shown in Fig. 11. The results in Fig. 11 demonstrate potential improvements to the reliability of the AMS and confirm the validity of the method used in this study to extend the rating tables.
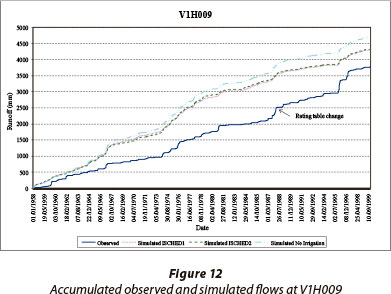
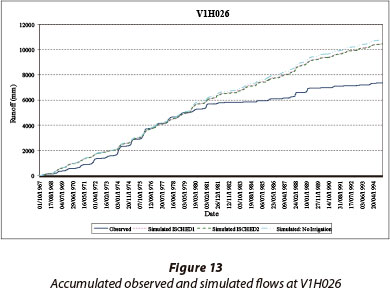
The impact of changes to the Rating Table (RT) during the period of available record is illustrated in Fig. 12 for Gauging Weir V1H009 (196.3 km2), where the apparent over-simulation prior to 1989 may be the result of errors and changes in flow gauging in this catchment. Similarly, the impacts of water transfers from the catchment are illustrated in Fig. 13 for Gauging Weir V1H026 (1 916.5 km2). The importance of using a physically-based, conceptual model is highlighted in Figs. 12 and 13 where the direct calibration of a model to these data, in the absence of further information on the gauging structure or abstractions, would result in erroneous simulations.
DISCUSSION AND CONCLUSIONS
The application of the CSM proved challenging in an operational catchment where the observed data are not perfect, the network of daily rain-gauges is relatively sparse, transfers of water between catchments occur, irrigation is developed over time and other land cover changes occur. In order to realistically simulate observed hydrological responses, the study highlighted the importance of improving the estimation of historical catchment rainfall and the need for detailed records of irrigation and land cover changes in a catchment and intercatchment transfers of water.
It is evident that flows measured by DWA may not be consistent over time at flow gauging weirs where the flow rating tables have been updated during the period of record. In addition, the limited maximum stage height used in the flow rating tables at some DWA flow-gauging weirs resulted in an underestimation of volumes and peak discharges for larger events. It was thus necessary to extend the flow rating tables to include all stages measured in order to improve the accuracy of flow measurement for large events.
From the results presented it is evident that the use of the ACRU model for design flood estimation was able to produce distributions of simulated daily volumes which generally reflected the observed distribution in catchments for a range of catchment areas in the Thukela Catchment. The distribution of the daily simulated peak discharges generally reflected the observed distribution in smaller catchments (e.g. < 150 km2). In larger catchments the good simulation of the distribution of streamflow volumes did not consistently translate into good distributions of daily peak discharge.
The potential of daily time-step continuous simulation modelling to provide consistent and reliable estimates of design floods has been highlighted in this study. This approach avoids the need for model calibration against observed flow data which may be compromised due to gauging limitations and/or non-stationary data resulting from changes in the catchment and/or climate change. In addition, the CSM is able to reflect current and future conditions in the catchments when estimating design floods.
The results from this study show the successful use of the ACRU model as a CSM to simulate the hydrological responses from an operational catchment and to estimate design peak discharges, despite the challenges related to data and operations in the catchment. The output from the CSM has been shown to produce reasonable and consistent estimates of design floods in the Thukela Catchment, particularly in smaller sub-catchments. Further development and verification of a continuous simulation modelling approach to design flood estimation in South Africa is recommended.
REFERENCES
ALEXANDER WJR (1990) Flood Hydrology for Southern Africa. SANCOLD, Pretoria. [ Links ]
ALEXANDER WJR (2001) Flood Risk Reduction Measures. University of Pretoria, Pretoria. [ Links ]
ALEXANDER WJR (2002a) The standard design flood. J. S. Afr. Inst. Civ. Eng. 44 (1) 26-31. [ Links ]
ALEXANDER WJR (2002b) Statistical analysis of extreme floods. URL: http://www.up.ac.za/academic/civil/divisions/water/upflood.html (Accessed 1 April 2002). [ Links ]
ALEXANDER WJR (2002c) The standard flood - theory and practice. URL: http://www.up.ac.za/academic/civil/divisions/water/upflood.html (Accessed 1 April 2002). [ Links ]
ALEXANDER WJR (2002d) Use manual: The standard flood - a new design philosophy. URL: http://www.up.ac.za/academic/civil/divi-sions/water/upflood.html (Accessed 1 April 2002). [ Links ]
ASCE (1997) Flood-Runoff Analysis. ASCE Press, New York. 176 pp. [ Links ]
BLAZKOVA S and BEVEN K (2002) Flood frequency estimation by continuous simulation for a catchment treated as ungauged (with uncertainty). Water Resour. Res. 38 (8) 14/11-14/14. [ Links ]
BLAZKOVA S and BEVEN K (2004) Flood frequency estimation by continuous simulation of subcatchment rainfalls and discharges with the aim of improving dam safety assessment in a large basin in the Czech Republic. J. Hydrol. (Amsterdam) 292 (1/4) 153-172. [ Links ]
BLAZKOVA S and BEVEN K (2009) A limits of acceptability approach to model evaluation and uncertainty estimation in flood frequency estimation by continuous simulation: Skalka Catchment, Czech Republic. Water Resour. Res. 45 (12) W00B16. [ Links ]
BOUGHTON W and HILL P (1997) A Design Flood Estimation Procedure Using Data Generation and a Daily Water Balance Model. Report 97/8. Cooperative Research Centre for Catchment Hydrology, Monash University, Clayton, Victoria, Australia. 39 pp. [ Links ]
BRATH A, MONTANARI A and MORETTI G (2006) Assessing the effect on flood frequency of land use change via hydrological simulation (with uncertainty). J. Hydrol. 324 (1/4) 141-153. [ Links ]
BROCCA L, MELONE F and MORAMARCO T (2011) Distributed Rainfall-runoff modelling for flood frequency estimation and flood forecasting. Hydrol. Proc. 25 (18) 2801-2813. [ Links ]
CALVER A and LAMB R (1995) Flood frequency estimation using continuous rainfall-runoff modelling. Phys. Chem. Earth 20 (5-6)479-483. [ Links ]
CALVER A, LAMB R and MORRIS SE (1999) River flood frequency estimation using continuous runoff modelling. Institution of Engineers, London, UK. Paper 11883, Proc. Instn Civ. Engrs Wat., Marit. & Energy, 136 (December), 225-234. [ Links ]
CALVER A, LAMB R and CREWETT J (2000) Generalised flood frequency estimation using continuous simulation. In: Bronstert A, C Bismuth and L Menzel (eds.) European Conference On Advances In Flood Research. PIK Report 65. Potsdam Institute for Climate Impact Research, Potsdam, Germany. 412-421. [ Links ]
CALVER A, LAMB R, KAY AL and CREWETT J (2001) The Continuous Simulation Method for River Flood Frequency Estimation. CEH Wallingford, Wallingford. 56 pp. [ Links ]
CALVER A, KAY AL, JONES DW, KJELDSEN TR, REYNARD NS and CROOKS S (2004) flood frequency quantification for ungauged sites using continuous simulation: A UK approach. In: Rizzoli AE and Jakeman AJ (eds.) Complexity and Integrated Resources Management, Transactions of the 2nd Biennial Meeting of the International Environmental Modelling and Software Society. International Environmental Modelling and Software Society, Manno, Switzerland. 5 pp. [ Links ]
CAMERON DS, BEVEN KJ, TAWN J, BLAZKOVA S and NADEN P (1999) Flood frequency estimation by continuous simulation for a gauged upland catchment (with uncertainty). J. Hydrol. 219 169-187. [ Links ]
CHETTY K and SMITHERS JC (2011) An assessment of scale issues related to the configuration of the ACRU model for design flood estimation. Hydrol. Res. 42 (5) 401-412. [ Links ]
CLOTHIER AN and PEGRAM GGS (2002) Space-Time Modelling of Rainfall Using the String of Beads Model: Integration of Radar and Raingauge Data. WRC Report No. 1010/1/02. Water Research Commission, Pretoria. [ Links ]
CSIR (1999) South African National Land Cover (NLC) Database Project. Environmentek, CSIR, Pretoria. [ Links ]
DUNSMORE SJ, SCHMIDT EJ and SCHULZE RE (1986) Antecedent Soil Moisture in Design Runoff Volume Estimation. WRC Report No. 155/1/86. Water Research Commission, Pretoria. [ Links ]
DWA (DEPARTMENT OF WATER AFFAIRS, SOUTH AFRICA) (2012) Hydrological Services - Surface Water (Data, Dams, Floods and Flows). URL: http://www.dwa.gov.za/Hydrology/hymain.aspx. Department of Water Affairs, Pretoria. [ Links ]
FREZGHI MS (2005) The Development and Assesment of a Methodology to Improve the Estimation of the Spatial Distribution of Rainfall. MSc Eng., dissertation, School of Bioresources Engineering and Environmental Hydrology, University of KwaZulu-Natal, Pietermartizburg, South Africa. [ Links ]
FREZGHI MS and SMITHERS JC (2008) Merged rainfall fields for continuous simulation modelling. Water SA 34 (5) 523-528. [ Links ]
GERICKE OJ (2010) Evaluation of the SDF Method Using a Customised Design Flood Estimation Tool. MSc dissertation, University of Stellenbosch, Stellenbosch, South Africa. 480 pp. [ Links ]
GOEL NK, KUROTHE RS, MATHUR BS and VOGEL RM (2000) A derived flood frequency distribution for correlated rainfall intensity and duration. J. Hydrol. 228 (1/2) 56-67. [ Links ]
GÖRGENS AHM (2007) Joint Peak-Volume (JPV) Design Flood Hydrographs for South Africa. WRC Report No. 1420/3/07. Water Research Commission, Pretoria. [ Links ]
HOUGHTON-CARR H (1999) Flood Estimation Handbook. Volume 4: Restatement of the Flood Studies Report Rainfall-Runoff Method. Institute of Hydrology, Wallingford. 288 pp. [ Links ]
HRU (HYDROLOGICAL RESEARCH UNIT) (1972) Design Flood Determination in South Africa. Report No. 1/72, Hydrological Research Unit, Department of Civil Engineering, University of the Witwatersrand, Johannesburg. [ Links ]
JOUBERT AR and HURLY PR (1994) The Use of Daily Flow Data to Classify South African Rivers. WRC Report No. 295/1/94. Water Research Commission, Pretoria. [ Links ]
KIENZLE SW and SCHMIDT J (2008) Hydrological impacts of irrigated agriculture in the Manuherikia Catchment Otago, New Zealand. J. Hydrol. NZ 47 (2) 67-84. [ Links ]
KIENZLE SW (2011) Effects of area under-estimations of sloped mountain terrain on simulated hydrological behaviour: A case study using the ACRU model. Hydrol. Proc. 25 (8) 1212-1227. [ Links ]
KIENZLE SW, NEMETH MW, BYRNE JM and MACDONALD RJ (2012) Simulating the hydrological impacts of climate change in the Upper North Saskatchewan River Basin, Alberta, Canada. J. Hydrol. 412-413 (0) 76-89. [ Links ]
KNOESEN DM (2005) The Development and Assessment of Techniques for Daily Rainfall Disaggregation in South Africa. MSc dissertation, School of Bioresources Engineering and Environmental Hydrology, University of KwaZulu-Natal, Pietermartizburg, South Africa. 91 pp. [ Links ]
KNOESEN DM and SMITHERS JC (2008) The development and assessment of a regionalised daily rainfall disaggregation model for South Africa. Water SA 34 (3) 323-330. [ Links ]
KNOESEN DM and SMITHERS JC (2009) The development and assessment of a daily rainfall disaggregation model for South Africa. Hydrol. Sci. J. 54 (2) 217-233. [ Links ]
LAMB R (1999) Calibration of a conceptual rainfall-runoff model for flood frequency estimation by continuous simulation. Water Resour. Res. 35 3103-3114. [ Links ]
LAMB R and KAY AL (2004) Confidence intervals for a spatially generalized, continuous simulation flood frequency model for Great Britain. Water Resour. Res. 40 (7) W07501. [ Links ]
MORETTI G and MONTANARI A (2008) Inferring the flood frequency distribution for an ungauged basin using a spatially distributed rainfall-runoff model. Hydrol. Earth Syst. Sci. 12 (4) 1141-1152. [ Links ]
NORTJE J (2010) Estimation of extreme flood peaks by selective statistical analyses of relevant flood peak data within similar hydrological regions. J. S. Afr. Inst. Civ. Eng. 52 (2) 48-57. [ Links ]
PEGRAM GGS (1994) Hydrologic Estimates (Chapter 2). In: CSRA Guidelines for the hydraulic design and maintenance of river crossings - Vol 1: Hydraulics, Hydrology and Ecology. Committee of State Road Authorities, Pretoria. 25 pp. [ Links ]
PEGRAM GGS and PARAK M (2004) A Review of the regional maximum flood and rational formula using geomorphological information and observed floods. Water SA 30 (3) 377-392. [ Links ]
PEGRAM GGS and SINCLAIR DS (2004) A Flood Nowcasting System for the Ethekwini Metro: Umgeni Nowcasting Using Radar - An Integrated Pilot Study. WRC Report No. 1217/2/04. Water Research Commission, Pretoria. [ Links ]
PIKE A and SCHULZE RE (1995) Autosoil Version 3: A Soils Decision Support System for South African Soils. Department of Agricultural Engineering, University of Natal, Pietermaritzburg. [ Links ]
PILGRIM DH and CORDERY I (1993) Chapter 9: Flood Runoff. In: Maidment DR (ed.) Handbook of Hydrology. Mcgraw-Hill, New York. [ Links ]
RAHMAN A, HOANG TMT, WEINMANN PE and LAURENSON EM (1998) Joint Probability Approaches to Design Flood Estimation: A Review. Report 98/8, Cooperative Research Centre for Catchment Hydrology, Monash University, Clayton, Victoria, Australia. 70 pp. [ Links ]
RAHMAN A, WEINMANN PE, HOANG TMT and LAURENSON EM (2002) Monte Carlo simulation of flood frequency curves from rainfall. J. Hydrol. 256 196-210. [ Links ]
REED D (1999) Flood Estimation Handbook. Volume 1: Overview. Institute of Hydrology, Wallingford. 108 pp. [ Links ]
REIS DS and STEDINGER JR (2005) Bayesian MCMC Flood frequency analysis with historical information. J. Hydrol. 313 97-116. [ Links ]
SANRAL (1986) Road Drainage Manual. The South African National Roads Agency Limited, Pretoria. [ Links ]
SCHMIDT EJ and SCHULZE RE (1984) Improved Estimates of Peak Flow Rates Using Modified SCS Lag Equations. WRC Report No. 63/1/84. Water Research Commission, Pretoria. [ Links ]
SCHMIDT J, KIENZLE SW and SRINIVASAN MS (2009) Estimating increased evapotranspiration losses caused by irrigated agriculture as part of the water balance of the Orari Catchment, Canterbury, New Zealand. J. Hydrol. NZ 48 (2) 73-94. [ Links ]
SCHULZE RE and ARNOLD H (1979) Estimation of Volume and Rate of Runoff in Small Catchments in South Africa. ACRU Report No. 8. Department of Agricultural Engineering, University of Natal, Pietermaritzburg. 79 pp. [ Links ]
SCHULZE RE (1982) Adapting the SCS stormflow equation for application to specific events by soil moisture budgeting. ACRU Report No. 15. Department of Agricultural Engineering, University of Natal, Pietermaritzburg. 63 pp. [ Links ]
SCHULZE RE (1989) Non-stationary catchment responses and other problems in determining flood series: A case for a simulation modelling approach. In: Kienzle SW and H Maaren (eds.) Proceedings of Fourth South African National Hydrological Symposium. SANCIAHS, Pretoria. 135-157. [ Links ]
SCHULZE RE, SCHMIDT EJ and SMITHERS JC (1992) PC-Based SCS Design Flood Estimates for Small Catchments in Southern Africa. ACRU Report 40. Department of Agricultural Engineering, University of Natal, Pietermaritzburg. 47 pp. [ Links ]
SCHULZE RE (1995) Hydrology and Agrohydrology: A Text to Accompany the ACRU 3.00 Agrohydrological Modelling System. WRC Report No. TT 69/95, Water Research Commission, Pretoria. 552 pp. [ Links ]
SCHULZE RE (2001) National Landcover Classification: Development of a Decision Support System for the ACRU Model. Internal Report, School of Bioresources Engineering and Environmental Hyrology, University of Natal, Pietermaritzburg. 25 pp. [ Links ]
SCHULZE RE and PIKE A (2004) Development and Evaluation of an Installed Hydrological Modelling System. WRC Report No. 1155/1/04. Water Research Commission, Pretoria. 179 pp. [ Links ]
SCHULZE RE and SMITHERS JC (2004) The ACRU agrohydrological modelling system as of 2002: Background, concepts, structure, output, typical applications and operations. In: Schulze RE (ed.) Modelling as a Tool in Integrated Water Resources Management: Conceptual Issues and Case Study Applications. WRC Report No. 749/1/04. Water Research Commission, Pretoria. 47-83. [ Links ]
SCHULZE RE, HORAN MJ and GRAY R (2005) Sensitivity studies of hydrological responses in the Thukela catchment to spatial and temporal representations when using a baseline and a projected future climate scenario. In: Schulze RE (ed.) Climate Change and Water Resources in Southern Africa. WRC Report No. 1430/1/05. Water Research Commission, Pretoria. 211-232. [ Links ]
SIRI (SOIL AND IRRIGATION RESEARCH INSTITUTE) (1987) Land Type Series. Memoirs on the Agricultural Natural Resources of South Africa. Soil and Irrigation Research Institute, Department of Agriculture and Water Supply, Pretoria. [ Links ]
SMITHERS JC, SCHULZE RE and KIENZLE SW (1997) Design flood estimation using a modelling approach. In: Rosbjerg D, Boutayeb N, Gustard A, Kundzewicz ZW and Rasmussen PF (eds.) Sustainability of Water Resources under Increasing Uncertainty. IAHS Publication 240. 365-376. [ Links ]
SMITHERS JC and SCHULZE RE (2001) Design runoff estimation: A review with reference to practices in South Africa. Proc. Tenth South Africa National Hydrology Symposium, 26-28 September 2001, School of BEEH, University of Natal, Pietermaritzburg. [ Links ]
SMITHERS JC, SCHULZE RE, PIKE A and JEWITT GPJ (2001) A hydrological perspective of the February 2000 floods: A case study in the Sabie River catchment. Water SA 27 (3) 325-332. [ Links ]
SMITHERS JC and SCHULZE RE (2003) Design Rainfall and Flood Estimation in South Africa. WRC Report No. 1060/01/03. Water Research Commission, Pretoria. 155 pp. [ Links ]
SMITHERS JC, CHETTY KT, FREZGHI MS, KNOESEN DM and TEWOLDE MH (2006) Development and Assessment of a Continuous Simulation Modelling System for Design Flood Estimation. WRC Report No. 1318/1/07. Water Research Commission, Pretoria. 210 pp. [ Links ]
SMITHERS JC (2012) Review of methods for design flood estimation in South Africa. Water SA 38 (4) 633-646. [ Links ]
STEEL ME (1998) Recent Scottish hydroclimatology: Evaluation of flood events using historical rainfall series. Proc. Second International Conference on Climate and Water, 17-20 August 1998, Espoo, Finland. Helsinki University of Technology, Finland. 400-409. [ Links ]
STEEL ME, BLACK AR, WERRITY A and LITTLEWOOD IG (1999) Reassessment of flood risk for Scottish rivers using runoff data. In: Gottschalk L, Reed D, Rosbjerg D and Olivery J (eds.) Hydrological Extremes: Understanding, Predicting, Mitigating. IAHS Publication 255. 209-215. [ Links ]
TEWOLDE MH (2005) Flood Routing in Ungauged Catchments Using Muskingum Methods. MSc Eng dissertation, School of Bioresources Engineering and Environmental Hydrology, University of KwaZulu-Natal, Pietermartizburg. [ Links ]
TEWOLDE MH and SMITHERS JC (2006) Flood routing in ungauged catchments using Muskingum methods. Water SA 32 (3) 379-388. [ Links ]
VAN BLADEREN D (2000) AMS Flood Data for RSA. SRK Consulting, Johannesburg. [ Links ]
VAN DER SPUY D and RADEMEYER PF (2010) Flood Frequency Estimation Methods as Applied in the Department of Water Affairs. Department of Water Affairs, Pretoria, South Africa. 98 pp. VAN DIJK M (2005) Upflood - Flood Analysis Programs. URL:http://www.sinotechcc.co.za/Software/UPFLOOD/upflood.html#Package (Accessed 1 July 2005). [ Links ]
VAN RENSBURG J (2005) First Interim Report on Improved Flood Hydrograph Generation Techniques. Progress Report on WRC Project No. K5/1420 (Updated Guidelines and Design Flood Hydrograph Techniques for Dam Safety) presented to Reference Group, 4 July 2005. Ninham Shand Consulting Services, Cape Town. 29 pp. [ Links ]
VIVIROLI D, MITTELBACH H, GURTZ J and WEINGARTNER R (2009) Continuous simulation for flood estimation in ungauged mesoscale catchments of Switzerland - Part II: Parameter regionalisation and flood estimation results. J. Hydrol. 377 208-225. [ Links ]
Received 19 October 2012
Accepted in revised form 25 June 2013
* To whom all correspondence should be addressed. +27 33 260-5490; e-mail: smithers@ukzn.ac.za














