Serviços Personalizados
Artigo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em Google
Similares em Google
Compartilhar
Water SA
versão On-line ISSN 1816-7950
versão impressa ISSN 0378-4738
Water SA vol.39 no.4 Pretoria Jan. 2013
Kinetic, equilibrium and thermodynamic modelling of the sorption of metals from aqueous solution by a silica polyamine composite
H TutuI, *; E BakatulaI; S DlaminiI; E RosenbergII; V KailasamII; EM CukrowskaI
IUniversity of the Witwatersrand, School of Chemistry, Private Bag X3, WITS 2050, Johannesburg, South Africa
IIUniversity of Montana, Department of Chemistry and Biology, Missoula, MT59812, USA
ABSTRACT
Batch sorption studies were conducted to assess the potential of a phosphonated silica polyamine composite (BPAP) to remove metals (Co, Cu, Fe, Mg, Mn, Ni, U and Zn) from mine waters. The metal adsorption showed a good Langmuir isotherm fit. Ni and Mn fitted both the Freundlich and Langmuir isotherms. The activation energies (Ea) of Co, Mg and Ni ranged between 5 and 40 kJ-mol-1, signifying physisorption while U showed a chemisorption type of adsorption (with Ea > 50 kJ-mol-1). Cu and Fe on the other hand gave negative Ea values, indicating their preference to bind to low-energy sites. The pseudo-second-order kinetic model provided the best correlation of the experimental data, except for Mg and Ni for which the pseudo-first-order model and the Elovich model gave a better fit, respectively. Adsorption was almost constant over a wide pH regime and increased with time. Adsorption increased with concentration of the metals with the exception of Co, Fe and Ni which displayed about a 40% drop at a concentration of 200 mg.l-1. Desorption experimental data gave poor results except for U which showed 99.9% desorption.
Keywords: silica polyamine composite, sorption, kinetics, isotherms, desorption
INTRODUCTION
The presence of trace metals in aquatic systems is of concern because of their toxicity and non-biodegradable nature. The sources of metals in the environment include sewage, mining, agricultural and industrial activities, with mining accounting for the larger proportion. Mining of certain minerals, including gold, copper, and nickel, is associated with acid mine drainage (AMD) problems that cause long-term impairment to waterways and biodiversity (Akcil and Koldas, 2006). There are several existing methods for the treatment of AMD, depending upon the volume of effluent, and the type and concentration of contaminants present (Chander and Mohan, 2001). These include chemical treatment (e.g. oxidation and neutralisation by lime), phytoremediation (i.e. phytoextraction, phytovolatilisation and phytostabilisation), ion exchange (e.g. use of activated carbon), polymers and biosorption, among others. There are some drawbacks associated with most of these methods: e.g., neutralisation leads to the formation of metal-containing solid waste that poses disposal problems; slow rates of biomass production in phytoremediation (Jiang et al., 2009); polymer adsorbents tend to have low selectivity of the metals and often swell and shrink due to their elastic nature.
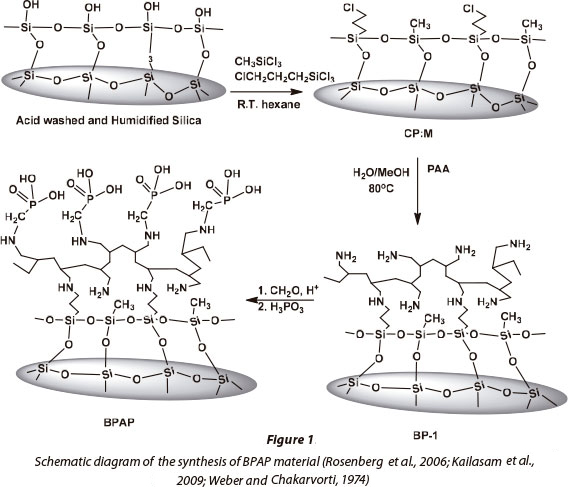
This study presents a silica-based polyamine composite, namely BPAP, as an alternative material for the adsorption of metals from acidic mine leachates and wastewaters. Generally, silica-based composites have polyamine chelating ligands which are bound to the silica gel layer covalently. The polyamine chelating ligands can be further modified with metal-selective functional groups, which is an advantage of these composites. In the case of BPAP, the Mannich reaction was used to convert the polyamine composite to an amino phosphonic acid-functionalised composite which has been used to immobilise high valent metals (Fig. 1) (Rosenberg et al., 2006). These materials do not shrink or swell; can be used at high temperatures (up to 110°C); have improved stability with regard to radiolytic decomposition; and have an elongated usable lifetime, unlike their polymer counterparts (Kailasam et al., 2009). The polar nature of their surfaces also makes for better mass-transfer kinetics in aqueous solutions. This study focused on the kinetic, equilibrium and thermodynamic processes related to metal sorption on BPAP, using metals commonly found in AMD.
Kinetics of metal ion sorption governs the rate, which determines the residence time and is one of the important characteristics defining the efficiency of an adsorbent (Kaur et al., 2012). The kinetic models used included the pseudo-first-order model, the pseudo-second-order model, the intraparticle diffusion model and the Elovich model.
The pseudo-first-order equation (Lagergren, 1898) has been widely used by many other researchers to study the kinetics of heavy metal adsorption (Qiu et al., 2009). The model has the following form:

where:
qe and qt are the amount of metal ions adsorbed (mg-g-1) at equilibrium and at any time t, respectively
k1 is the rate constant (min-1) of pseudo-first-order adsorption.
By applying the boundary conditions t = 0 to t = t and qt = 0 to qt = qt, the integration form is given by the equation below:
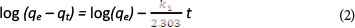
The plot of log (qe - qt) vs t should give a linear relationship from which k1 and qe can be determined from the slope and intercept of the plot, respectively.
The pseudo second-order equation is expressed as (Ho et al., 1999):

where:
k2 is the rate constant of the pseudo second-order adsorption (gm-g-1-min-1)
For the boundary conditions t = 0 to t = t and qt = 0 to qt = qt , the integrated form of Eq. (2) becomes:

The linear form of Eq. (3) is given by the following equation:

If the pseudo-second-order is applicable, the plot t/qt vs t should give a straight line. qe and k2 may be determined from the slope and intercept of the plot, respectively.
The Elovich model describes the chemical nature of the adsorption and is generally expressed as (Günay et al., 2007):

where:
α is the initial adsorption rate (mg-g-1-min-1) and
β is the Elovich constant related to the surface coverage (gmg-1)
By applying the boundary conditions qt = 0 at t = 0 and qt = qt at t = t, the integrated form of Eq. (6) is:

The plot of qt vs ln(t) should yield a linear relationship with a slope of (1/β) and an intercept of (1/β) ln(αβ).
The intraparticle diffusion model is characterised by a linear relationship between the amount adsorbed at time t (qt) and the square root of the time, and is expressed as (Allen et al., 1989):

where:
qt is the amount of metal ion adsorbed at time t (min) expressed (mg-g-1), kid is the initial rate constant (mg-g-1-min-1/2) of intraparticle diffusion, t is the time of sorption duration (min), and C gives information about the boundary layer thickness
A normalised standard deviation (Δq) was used in order to compare the validity of each model. Δq (%) is calculated by the following expression (Wang et al., 2007):
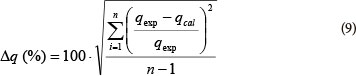
where:
qexp is the experimental metal ion uptake
qcal the calculated amount of metal ions adsorbed and n is the number of data points
The goodness-of-fit of the models to the experimental data was controlled by comparison of the correlation coefficients R and standard errors S. The CurveExpert 1.3 program was used to fit the experimental data with the confidence level set at 95%.
Adsorption equilibria provide fundamental physicochemical data for evaluating the applicability of the adsorption process as a unit operation (Srivastava and Rupainwar, 2011). In this study, the Langmuir and Freundlich isotherms expressions were used for the anaysis of the equilibrium data.
The linear form of the Langmuir equation is:

where:
qe (mg-g-1) is the equilibrium adsorption capacity,
KL is a constant related to the energy of adsorption,
Ce (mg.l-1) is the concentration at equilibrium and
qo (mg-g-1) is the maximum amount adsorbed required to saturate a unit mass of adsorbent.
b and qo are obtained from the slope of the plot Ce/qeversus Ce
A good fit of this equation reflects monolayer adsorption (Teng and Hsieh, 1998).
The Freundlich model is as follows:

where:
Kf and n are equilibrium constants indicative of adsorption capacity and adsorption intensity, respectively (Cozmuta et al., 2012; Teng and Hsieh, 1998)
The linearised form of the Freundlich equation can be used:
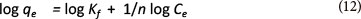
where:
Ce is the equilibrium phase ion concentration (mg-l-1) and qe is the adsorption capacity at equilibrium (mg-g-1)
The n and Kf values can be obtained from the slopes and intercepts of the isotherm. If the value of n is between 1 and 10, this refers to a beneficial isotherm. The linear regression analysis was carried out with the CurveExpert 1.3.
Zheng et al. (2009) stated that the essential characteristics of a Langmuir isotherm can be expressed in terms of a dimensionless separation factor, Rs, which is defined by the following equation:

where:
a is the Langmuir constant,
Co is the initial concentration (mg-l-1),
Rs indicates the shape of the isotherm as follows:
Rs > 1 Unfavourable
Rs = 1 Linear
0 < Rs < 1 Favourable
Rs = 0 Irreversible
EXPERIMENTAL PROTOCOL Materials
Synthesis of BPAP by the Mannich Reaction
The silica polyamine composite BP-1 is first synthesised and used as a precursor for making BPAP. The synthesis of BPAP is mentioned in detail in other work by co-authors of this study (Rosenberg et al., 2006; Kailasam et al., 2009). 10 g of BP-1 was mixed with a reagent solution of 30 ml of 2 mol.l-1 HCl and 10 g of phosphonic acid (H3PO3) in a 250 ml flask equipped with an overhead stirrer. The flask was heated to 95°C, and 9 ml of formaldehyde (CH2O) solution (37.7%) was gradually added with stirring. The reaction mixture was heated at 95°C for 24 h. The flask was cooled and the product was filtered. The resulting composite was washed three times with 40 ml of deionised water; once with 40 ml of 1 mol-l-1 NaOH; three times with 40 ml of deionised water; once with 40 ml of 0.5 mol-l -1 H2SO4; two more times with 40 ml of deionised water; twice with 40 ml of methanol; and dried to a constant mass at 65°C. A mass gain of 20% and 22% was obtained starting with BP-1.
The elemental composition of the BPAP made from BP-1 is 14.20% C, 3.03% H, 3.36% N, 4.34% P (Kailasam et al., 2009; Hughes et al., 2006).
Adsorption studies
Reagents used for the sorption studies were of analytical grade. Standards used for quantification were of high purity and were obtained from Merck, South Africa. The metal ion solutions (Co2+, Cu2+, Fe2+, Mg2+, Mn2+, Ni2+, U6+ (as UO22+) and Zn2+) were prepared by weighing appropriate amounts of the nitrate salts to make 1 000 mg-l-1stock solutions. Appropriate aliquots were taken from these standards for subsequent dilution to the desired concentration level. Adsorption for single-component solutions was done using an optimised solid: solution ratio of 1:50.
The effect of pH on adsorption was assessed over the pH range 2-10 and the thermodynamic parameters were calculated at 18 oC and 30oC. The effects of metal concentrations were assessed in the range 10-200 mg l-1 while contact time was in the range 0-180 min. The metal ion concentrations were measured using a Genesis Inductively Coupled Plasma Optical Emission Spectrometer (ICP-OES) (Spectro, Kleve, Germany).
The adsorption capacity was calculated using the general equation:

where:
qe is the amount of metal ions adsorbed (mg-g-1),
Co and Ct are metal ion concentrations in solution before and after adsorption (mg-l-1),
V the volume of the medium (l), and
M the amount of BPAP used in the reaction mixture (g)
Desorption studies
Batch desorption tests of metals (regeneration of BPAP) were conducted using H2SO4, ethylene diamine tetraacetic acid (EDTA) and Na2CO3 with concentrations ranging from 0.1-3.0 mol-l-1 with 1.0 g of BPAP sorbent containing the desired concentration of metal ions. The mixture was agitated in 250 ml bottles at 150 r.min-1 for 12 h using a mechanical automated shaker. The solution was then filtered using Whatman No. 41 filter paper. The concentration of the metal ions in the filtrate was measured using ICP-OES.
RESULTS AND DISCUSSION
Effect of pH
The results for the effect of pH on metal adsorption are shown in Fig. 2. Adsorption was based on a solution containing 5 mg-l-1 of each metal.
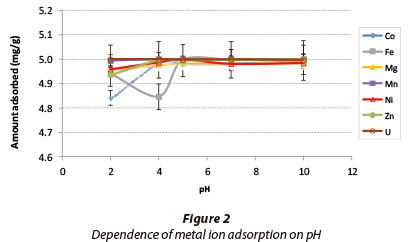
The adsorption for all the metals was in the range 99.9-100%. The elevated adsorption at low pH regimes shows that this adsorbent has potential to be applied in the remediation of AMD. Equilibrium is reached at pH 4, and the trend of increasing adsorption for all of the metals levels off beyond that, where equilibrium dominates. Metals such as uranium, manganese, nickel, zinc and magnesium were removed efficiently. As pH increases from 2-10, there is 99-100% adsorption for all of the abovementioned metals, which suggests that changes in pH do not affect the adsorption of these metals. Even in the low pH regime, where there is a higher concentration of hydrogen ions, competition between metal and hydrogen ions appears to play no significant role.
The high percentage adsorption of metals at high pH (6-10) could be a combination of adsorption and precipitation, because at high pH metals begin to hydrolyse, therefore precipitate out of solution forming hydroxides. It is thus difficult to deduce whether adsorption or precipitation is taking place at these pH ranges. Further studies will have to be conducted to establish the type of reaction happening within these pH ranges.
Effect of concentration
The results for the dependence of adsorption on metal ion concentration are presented in Fig. 3. A pH of 2.5 was chosen in order to assess how efficiently adsorption would occur in acidic mine leachates.
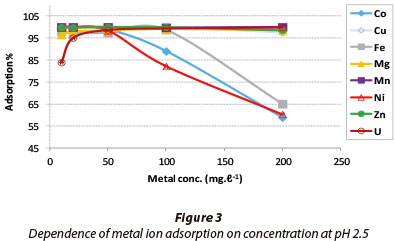
Cu, Mg, Mn, U and Zn showed a constant maximum adsorption as the feed concentration of each metal increased from 10 mg-l-1 to 200 mg-l-1. The adsorption of Co and Ni decreased beyond 60 mg-l-1, while that for Fe decreased beyond 90 mg-l-1. The trend is correlated to the activation energies obtained in Table 1. Ni had an Ea value of 0.76 kJ-mol1 (defining a diffusion mechanism) while Fe and Co had negative Ea values of -90.51 and -2.61 kJ-mol-1, respectively. The negative values depict preference for low energy sites during adsorption, which could have been exhausted at 60 and 90 mg-l-1.
Thermodynamic parameters
The thermodynamic criteria for sorption are well explained by evaluation of the three important thermodynamic parameters, namely: change in enthalpy (ΔH), Gibbs free energy change (ΔG) and entropy change (ΔS). Net enthalpy change (ΔH) is related to ΔG and ΔS as ΔG = ΔH - T (ΔS). The thermodynamic parameters calculated are given in Table 1.
In this process, changes in temperature (291 K and 303 K) did not have much effect on the adsorption of the metals. The adsorption percentage of the metals ranges from 99.84 to 100%, showing that this adsorbent efficiently removed the metal ions from the solution.
The trend in the Gibbs free energy shows negative values for all of the metals tested, which indicates that the adsorption process of these metals was spontaneous. A positive or a negative change in enthalpy indicates whether a reaction is endothermic or exothermic. ΔH° values for Cu, Fe and Zn are negative, implying that the process is exothermic for these ions. Most of the metals showed positive ΔHo values indicating that their adsorption was endothermic. The activation energy (Ea) values obtained in Table 1 show that most of the metals adsorb via physisorption , with the exception of U which adsorbs by chemisorption. A reaction is classified as physisorption when the Ea ranges between 5 and 40 kJ-mol-1, whereas chemisorption has an Ea value between 40 and 800 kJ-mol-1 (Boparai et al., 2010).
Fe and Cu had negative values for activation energy. This could be attributed to their preference to bind to active sites with low energy. As such, adsorption of these metals occurs without an energy barrier. Their adsorption mechanism could be a combination of physisorption, chemisorption and diffusion. The Ea for Ni adsorption falls outside that of either chemisorption or physisorption.
The high Ea for U is a result of ion complex formation between the uranyl ion and the phosphate ligand on the adsorbent, which occurs via the inner-sphere mechanism in which the adsorbate loses solvating water molecules (Taffet, 2004). Mg, Mn and Zn adsorption is of a physisorption type, which is due to ion pair formation of the metals occurring through the outer-sphere complexes and/or as complexes that lose part of their aqueous solvation spheres, hence the low Ea values (Bakatula, 2012).
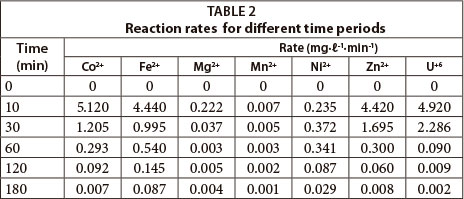
Effect of time
The rates of reaction for the different times studied in this experiment are given in Table 2. All of the metals displayed fast adsorption within the first 10 min (kinetic control), with a decrease beyond this time zone (equilibrium control). This is largely attributed to the availability of active reaction sites, which decreases with time.
Adsorption kinetics
The estimated model and related statistical parameters are reported in Table 3. Based on the linear regression (R2 > 0.95) values of the metal ions, the sorption of Fe, Mg and Mn was observed to follow the pseudo second-order kinetic model. The adsorption of Co, Zn, Ni and U also followed the pseudo second-order kinetic model with a correlation coefficient between 0.890 and 0.920. Pseudo second-order kinetics is based on the assumption that sorption follows a second-order mechanism, with chemisorption as the rate-limiting step. The rate of occupation of adsorption sites is proportional to the square of the number of unoccupied sites (Zan et al., 2012).
The experimental data for Mg showed good compliance with the pseudo first-order and the pseudo second-order kinetic models (R2 > 0.950).
The rate constants of pseudo-second-order (K2) were in the range 0.217-0.278 g-mg-1-min-1 and were found to be higher than those obtained for pseudo first-order kinetics, with the exception of Mg which had K1 (0.903) > K2 (0.241). This result correlated more closely with the best fit found for the pseudo first-order kinetic model.
The Elovich kinetic parameters, α, β and correlation coefficients, are also presented in Table 3. The correlation coefficients were in the range of 0.921-0.994. The Elovich kinetic model best defined the adsorption process for all of the metal ions studied. The coefficients α and β are related to chemisorption rate and surface coverage, respectively.
The values of kid were calculated from the slopes of plots for intraparticle diffusion (plots not shown here) and the R2 values suggest that the intraparticle diffusion process was not the rate-limiting step. This was further substantiated by the fact that the plot of qe vs. t1/2 did not pass through the origin. If the the plot of qe vs t1/2passes through the origin, then intraparticle diffusion is the rate-limiting step. When the plot does not pass through the origin, it is indicative of some degree of boundary layer control. This means intraparticle diffusion would not be the only rate-limiting step. Higher values of kid illustrate an enhancement in the rate of adsorption and a better adsorption mechanism, which is related to an improved bonding between metal ions and the adsorbent.
Adsorption isotherms
The values of adsorption constants and correlation coefficients obtained for both adsorption models are presented in Table 4. The Langmuir constant (b) values were found to be higher for Co, Fe, Mg and Ni. Although Mg had the highest value for b, its experimental data did not fit the Langmuir isotherm. The essential characteristics of the Langmuir isotherm expressed by a dimensionless constant separation factor Rs were in the range 0 to 1 for the adsorption of metal ions onto BPAP, thereby indicating favourable adsorption. The values for Rs are shown in Table 4.
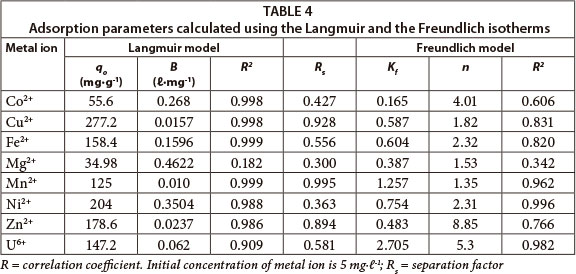
As seen from the table, the correlation coefficients for all the adsorbate-adsorbent systems were very high (> 95%) for the Langmuir model, except for Mg and U. The experimental data for Mn and Ni can also be described by the Freundlich model. The adsorption of U is defined by the Freundlich isotherm. The experimental data for Mg did not fit the Freundlich model either. A good fit of the Freundlich isotherm to an adsorption system means there is almost no limit to the amount which can be adsorbed. The magnitude of the Freundlich parameter Kf gives quantitative information on the relative adsorption affinity towards the adsorbed cation and the magnitude of the constant 1/n provides information about the linearity of adsorption. Nonlinear adsorption indicates that the adsorption energy barrier increases exponentially with an increasing fraction of filled sites on the adsorbent (Schwarzenbach et al., 2003).
The magnitude of Kf values indicate that for this adsorbent the adsorption of Ni and Mn is favoured over that of Fe, Mg, Zn and Cu.
The value of qo (i.e. maximum uptake) appears to be significantly higher for Cu, Ni, Zn, Fe and Mn. The value of 1/n less than unity is an indication that significant adsorption takes place at low concentrations, but that the increase in the amount adsorbed with concentration becomes less significant at higher concentrations, and vice versa (Vaishnav et al., 2011).
Desorption studies
Desorption studies help to elucidate the nature of adsorption and recycling of the spent adsorbent and the metal ions. The results for the desorption of U essentially showed an optimum desorption at about 0.8 mol-l-1 Na2CO3. This is expected as U tends to form strong complexes with carbonates (Tutu et al., 2009). The other metals were not released with this solution. Optimum desorption was achieved at 1 mol-l-1 EDTA concentration with 75% of Fe, 30% of Cu and 10% of Mg. The other metals displayed <5% desorption. At 1 mol-l-1 H2SO4 concentration, 45% of Cu and 20% of Mg were desorbed while the rest of the metals had <5% desorption.
CONCLUSIONS
The BPAP silica polyamine composite has been shown to be an effective adsorbent for the removal of metals from aqueous solution and particularly from acidic drainages such as AMD. Adsorption kinetics are important in establishing the time zones and effective lifespanss of adsorbents and provide information on the need for regeneration. The Langmuir isotherm best described the adsorption of the metal ions studied. The pseudo second-order kinetic model as well as the Elovich model best defined the kinetic adsorption process. Thermodynamic studies were shown to be important in determining the surfacemetal reaction mechanisms. The sorption process was found to be of a physiosorption type for most of the metals, as predicted by the activation energies. While desorption results for U were commendable, those for other metals were unsatisfactory, thus necessitating further exploitation of other desorbents.
ACKNOWLEDGEMENTS
The authors would like to thank the Carnegie Corporation and the Friedel Sellschop Foundation for financial support.
REFERENCES
AKCIL A and KOLDAS S (2006) Acid mine drainage (AMD): causes, treatment and case studies. J. Clean. Prod. 14 1139-1142. [ Links ]
ALLEN SJ, McKAY G and KHADER K (1989) Intraparticle diffusion of a basic dye during adsorption onto sphagnum peat. J. Environ. Pollut. 50 39-50. [ Links ]
BAKATULA EN (2012) Development of a biophysical system based on bentonite, zeolite and micro-organisms for remediating gold mine wastewaters and tailings ponds. PhD thesis, University of the Witwatersrand, Johannesburg. 465 pp. [ Links ]
BOPARAI HK, JOSEPH M and O'CARROLL DM (2010) Kinetics and thermodynamics of cadmium ion removal by adsorption onto nano zerovalent iron particles. J. Hazardous Mater. 186 458-465.
CHANDER S and MOHAN D (2001) Single component and multicomponent adsorption of metal ions by activated carbons. Colloids Surf. A 177 183-196. [ Links ]
COZMUTA ML, COZMUTA MA, PETER A, NICULA C, BAKATULA EN and TUTU H (2012) The influence of pH on the adsorption of lead by Na-clinoptilolite: Kinetic and equilibrium studies. Water SA 38 (2) 269-278. [ Links ]
GÜNAY A, ARSLANKAYA E and TOSUN I (2007) Lead removal from aqueous solution by natural and pretreated clinoptilolite: Adsorption equilibrium and kinetics. J. Hazardous Mater. 146 (1-2) 362-371. [ Links ]
HO YS, WASE DAJ and FORESTER CF (1999) Kinetic studies of competitive heavy metal adsorption by sphagnum peat. Environ Technol. 17 441-443. [ Links ]
HUGHES M, MIRANDA P, NIELSEN D and ROSENBERG E (2006) Silica polyamine composites: New supramolecular materials for cation and anion recovery and remediation. Macromol. Symp. 235 161-178. [ Links ]
JIANG J, WU L, LI N, LUO Y, LIU L, Q. ZHAO Q, ZHANG L and CHRISTIE P (2009) Effects of multiple heavy metals contamination and repeated phytoextraction by Sedum plumbizincicola on soil microbial properties. Eur. J. Soil Biol. 46 18-26. [ Links ]
KAILASAM V, ROSENBERG E and NIELSEN D (2009) Characterization of surface-bound Zr(IV) and its application to removal of As(V) and As(III) from aqueous systems using phosphonic acid modified nanoporous silica polyamine composites. Ind. Eng. Chem. Res. 48 3991-4001. [ Links ]
KAUR R, SINGH J, KHARE R and ALI A (2012) Biosorption the possible alternative to existing conventional technologies for sequestering heavy metal ions from aqueous streams: A Review. Univers. J. Environ. Res. Technol. 2 (4) 325-335. [ Links ]
LAGERGREN S (1898) Zur theorie der sogenannten adsorption gelöster stoffe. Kungliga Svenska Vetenskapsakademiens. Hand-lingar, Band 24 (4) 1-39. [ Links ]
QIU H, LV L, PAN B, ZHANG Q, ZHANG W and ZHANG Q (2009) Critical review in adsorption kinetic models. J. Zhejiang Univ. Sci. A 10 (6) 716-724. [ Links ]
ROSENBERG E, NIELSEN D, HUGHES MA, VIALE A, GOBETTO R, FEREL J and BURTON S (2006) Structural investigations of silica polyamine composites: Surface Coverage, metal ion coordination, and ligand modification. Ind. Eng. Res. 45 6538-6539. [ Links ]
SCHWARZENBACH RP, GSCHWEN MP and IMBODEN DM (2003) Environmental Organic Chemistry. John Wiley & Sons, Inc., Hoboken, NJ. 1313 pp. [ Links ]
SRIVASTAVA R and RUPAINWAR DC (2011) A comparative evaluation for adsorption of dye on Neem bark and Mango bark powder. Indian J. Technol. 18 67-75. [ Links ]
TAFFET M (2004) Study of the reactions controlling the mobility of uranium in ground and surface water systems in contact with apatite. Lawrence Livermore National Laboratory Report, UCRL-TR-203891. University of California, Livermore, CA. [ Links ]
TENG H and HSIEH C (1998) Influence of surface characteristics on liquid-phase adsorption of phenol by activated carbons prepared from bituminous coal. Ind. Eng. Chem. Res. 37 (9) 3618-3624. [ Links ]
TUTU H, McCARTHY TS, CUKROWSKA EM, CHIMUKA L and HART R (2009) Radioactive disequilibrium and geochemical modelling as evidence of uranium leaching from gold tailings dumps in the Witwatersrand Basin. Int. J. Environ. Anal. Chem. 89 687-703. [ Links ]
VAISHNAV V, CHANDRA S and DAGA K (2011) Adsorption studies of Zn (II) ions from wastewater using Calotropis procera as an adsorbent. Int. J. Sci. Eng. Res. 2 (12) 2229-5518. [ Links ]
WANG XS, HUANG J, HU HQ, WANG J and QUIN Y (2007) Determination of kinetic and equilibrium parameters of the batch adsorption of Ni(II) from aqueous solutions by Na-mordenite. J. Hazardous Mater. 142 (1-2) 468-476. [ Links ]
WEBER TW and CHAKARVORTI PK (1974) Pore and solid diffusion models for fixed bed adsorbers. Am. Inst. Chem. Eng. J. 20 228-237. [ Links ]
ZAN F, HUO S, XI B and ZHAO X (2012) Biosorption of Cd2+ and Cu2+ on immobilized Saccharomyces cerevisiae. Front. Environ. Sci. Eng. 6 (1) 51-58. [ Links ]
ZHENG H, LIU D, ZHENG Y, LIANG S and LIU Z (2009) Sorption isotherm and kinetic modeling of aniline on Cr-bentonite. J. Hazardous Mater. 167 141-147. [ Links ]
Received 22 March 2012
Accepted in revised form 24 June 2013
* To whom all correspondence should be addressed. +27 11 717 6771; e-mail: hlanganani.tutu@wits.ac.za














