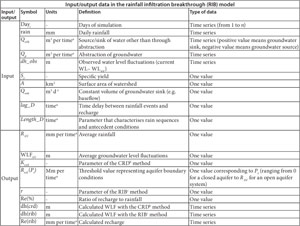
Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Water SA
On-line version ISSN 1816-7950
Print version ISSN 0378-4738
Water SA vol.39 n.2 Pretoria Jan. 2013
Application of the rainfall infiltration breakthrough (RIB) model for groundwater recharge estimation in west coastal South Africa
X SunI; Y XuI, II, *; NZ JovanovicIII; E KapangaziwiriIII; L BrendonckIV; RDH BuganIII
IDepartment of Earth Sciences, University of the Western Cape, Cape Town 7535, South Africa
IIInstitute of Karst Geology, Chinese Academy of Geological Sciences, Guilin, China
IIICSIR Natural Resources and the Environment, PO Box320 Stellenbosch 7599, South Africa IVDepartment of Biology, Katholieke Universiteit Leuven, Leuven 3000, Belgium
ABSTRACT
Recharge estimation in arid and semi-arid areas is very challenging. The chloride mass balance method applied in western South Africa fails to provide reliable recharge estimates near coastal areas. A relationship between rainfall events and water level fluctuations (WLF) on a monthly basis was proposed in the rainfall infiltration breakthrough (RIB) model for the purpose of groundwater recharge estimation. In this paper, the physical meaning of parameters in the CRD and previous RIB models is clarified, and the RIB model is reviewed with the algorithm improved to accommodate various time scales, namely, daily, monthly and annual scales. Recharge estimates on a daily and monthly basis using the revised RIB approach in 2 study areas, one in a sandy alluvial aquifer (Riverlands) and the other in the Table Mountain Group (TMG) shallow unconfined aquifer (Oudebosch), are presented, followed by sensitivity analysis. Correlation analysis between rainfall and observed WLF data at daily scale and monthly scale, together with recharge estimates obtained from other methods, demonstrates that the RIB results using monthly data are more realistic than those for daily data, when using long time series. Scenarios using the data from Oudebosch with different rainfall and groundwater abstraction inputs are simulated to explore individual effects on water levels as well as recharge rate estimated on a daily basis. The sensitivity analysis showed that the recharge rate by the RIB model is specifically sensitive to the parameter of specific yield; therefore, the accurate representative specific yield of the aquifer needs to be selected with caution. The RIB model demonstrated in these two cases can be used to estimate groundwater recharge with sufficiently long time series of groundwater level and rainfall available in similar regions. In summary, the RIB model is best suited for shallow unconfined aquifers with relatively lower transmissiv-ity; the utility of the RIB model for application in different climatic areas under different hydrogeological conditions needs to be further explored.
Keywords: RIB model, shallow unconfined aquifer, groundwater-level fluctuation, groundwater recharge, Table Mountain Group aquifer
INTRODUCTION
Estimation of groundwater recharge is a key challenge for determining sustainable groundwater development and management, especially in arid and semi-arid areas, where rainfall as well as recharge is low while evapotranspiration is high. Numerous studies have focused on groundwater recharge in Southern Africa over the past three decades (Xu and Beekman, 2003). Systematic recharge studies were carried out in Botswana and South Africa in the early 1970s (Verhagen et al., 1974; Mazor et al., 1977; Bredenkamp and Vogel, 1970; Bredenkamp et al., 1974; Smit, 1978). A co-operative programme entitled Groundwater Resources Monitoring and Recharge Study (GRES) was jointly launched by the governments of Botswana and The Netherlands, aimed at better understanding the recharge process in Botswana in 1987 (De Vries and Von Hoyer, 1988; De Vries et al., 2000). A manual entitled 'Preparation of a manual on Quantitative Estimation of Groundwater Recharge and Aquifer Storativity', published by the Water Research Commission of South Africa in 1995 (Bredenkamp et al., 1995), presents a great variety of well-tested (semi-empirical) methods that are widely employed in South Africa, and contains a wealth of recharge case studies and data covering the past 30 years. The Namibian Government has conducted large-scale groundwater recharge studies since the 1990s. The Namibian and German governments jointly launched programme of cooperation in 1992 for recharge studies in the north-eastern part of the country (Schmidt and Ploethner, 2000). Physical and tracer methods, the most commonly used approaches in these studies, were adapted to estimate recharge at local and national scales in Southern Africa. The validity of these methods in arid and semi-arid areas, in terms of the principles, advantages and limitations, and general rules governing the choice of different methods, have been summarised by several researchers (Scanlon et al., 2002; Beekman and Xu, 2003).
Several methods for the estimation of groundwater recharge have been applied in African countries in recent decades, with more or less success (Beekman and Xu, 2003). Results of applications of these methods showed that groundwater recharge estimates done by different practitioners varied widely when different methods and input data sets were used. Most of the groundwater recharge methodologies developed are applicable to the large scale, whilst little information is available describing processes at the local scale. Recharge estimation in coastal areas using the chloride mass balance method (CMB) can be problematic. Studies on chloride concentration- of groundwater as well as rainwater in South Africa imply that the variation in rainwater and groundwater chloride content in time and space could be significantly high (coefficient of variation is larger than 50%); therefore, the application of the CMB method in coastal areas should be applied with great caution and consideration (Van Wyk et al., 2011), and recharge estimates near coastal areas based on the CMB method need to be re-evaluated.
The rainfall infiltration breakthrough (RIB) method, one of the physical models for estimation of groundwater recharge, was developed based on the cumulative rainfall departure (CRD) method and then applied to dolomite and Karoo aquifers in South Africa using monthly rainfall and water-level data (Xu and Van Tonder, 2001). The CRD/RIB method has also been applied in America, Palestine, Iran, etc. (Fenelon, 2000; Baalousha, 2005; Rasoulzadeh and Moosavi, 2007); the RIB approach was proven to be a simple but promising tool for groundwater recharge estimation. However, the physical meaning of some parameters proposed in the RIB equation is not clear.
The purpose of this paper is to describe and demonstrate the RIB model, and to estimate the recharge under 2 extreme conditions (alluvial and fractured rock aquifers), with a revised algorithm of the RIB model developed to accommodate a wide variety of circumstances in terms of time scales, namely, daily, monthly and annual scales. Recharge estimations using the revised RIB programme, on a daily and monthly basis using existing information in two study areas, one a sandy alluvial aquifer (Riverlands) and the other a TMG shallow unconfined aquifer (Oudebosch), are presented, followed by sensitivity analyses. Scenarios using data from Oudebosch with different rainfall and groundwater abstraction inputs are simulated to explore their effects on water level as well as the recharge rate estimated on a daily basis.
METHODOLOGY
The concept of recharge
Groundwater recharge can be generally defined as an addition of water to a groundwater reservoir. Four types of recharge can be distinguished (Beekman and Xu, 2003):
- Water flow through the unsaturated zone reaching the water table
- Lateral and/or vertical inter-aquifer flow
- Artificial recharge, such as man-made infiltration ponds or water recharge from injection boreholes
- Induced recharge from nearby surface water bodies (such as rivers, lakes), resulting from groundwater abstraction
This paper focuses on the first situation, where recharge is the part of rainfall percolating through the unsaturated zone to the water table. The time that percolating rainfall takes to reach the water table is defined as the time lag. The time lag can be distinguished as:
- Rapid response: within hours or days of intensive rainfall; normally happens as preferential flow to the water table
- Intermediate response: over months, or a year or two
- Slow response: over years or longer; normally occurs as piston flow through porous matrix with low conductivity
The breakthrough recharge water reaching the water table does not necessarily result from a single rainfall event. Water level fluctuations may be caused by a series of preceding rainfall- events. The time lag and the length of related rainfall events depends on several factors, such as the thickness of the unsaturated zone, the soil texture, the type and size of vegetation and the geology of the aquifer.
The RIB method
Based on the cumulative rainfall departure (CRD) method in South Africa (Bredenkamp et al., 1995), the RIB method was developed by Xu and Van Tonder (2001). Both methods utilise the relationship between water level fluctuations and the departure of rainfall from the mean rainfall of a preceding time. The RIB formula is defined as:
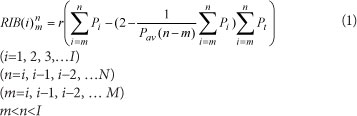
where:
RIB(i) is the cumulative recharge from rainfall event of m to n
I is the total length of rainfall series. r is a fraction of cumulative rainfall departure
P. is the rainfall amount at ith time scale (daily, monthly or annually)
Pav is the mean precipitation of the whole time series
Pt is a threshold value representing the boundary conditions (Pt, ranges from 0 to Pav)
Value of 0 represents a closed aquifer system, which means that the recharge at ith time scale only depends on preceding rainfall events from Pm to Pn; while value of Pav represents an open system, which means that the recharge at the ith time scale depends on the difference between the average rainfall of preceding rainfall events from Pm to Pn and the average rainfall of the whole time series). Both r and Pt values are determined during the simulation process.
It is assumed that groundwater recharge by the RIB method has a linear relationship with water level fluctuations under natural conditions. The relationship between natural rainfall and water level fluctuations can be described by Eq. (2):

where:
Δh. is the water-level fluctuation, which is equal to the difference between the observed water level at ith time scale and the mean water level of the whole time series; a positive value represents an increase of water level while a negative value implies a decrease of water level. Sy is the specific yield of the aquifer.
Equations (1) and (2) indicate that the water-level fluctuation at ith time scale (daily/monthly/annually) is affected by preceding rainfall events from Pm to Pn (m<n), with a weighting factor that is a function of the moving average of 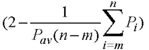 a rainfall time series. It is not necessarily constant and may be positive or negative depending on whether or not the amount of rainfall during the period of interest exceeds the moving average rainfall. The schematic of the RIB model is shown in Fig. 1.
a rainfall time series. It is not necessarily constant and may be positive or negative depending on whether or not the amount of rainfall during the period of interest exceeds the moving average rainfall. The schematic of the RIB model is shown in Fig. 1.
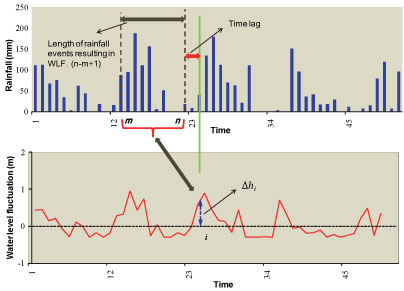
Figure 1
Schematic of the RIB process
Three rainfall percolation mechanisms can be distinguished on different time scales, the mechanisms are listed as follows in terms of the duration of the time lag:
• Mechanism a: water level fluctuations result from preceding rainfall events. This was often observed at places with relatively quick infiltration rates (range from hours to 1 day).
• Mechanism b: water level fluctuations result from the cumulative result of all previous rainfall. This often represents the combination of point and diffuse recharge mechanisms.
• Mechanism c: water level fluctuations are caused by limited rainfall series with a certain time lag; the length of the time lags varies from several days to months (range from 1 week to 12 months).
In reality, the water level fluctuations result from many factors besides rainfall, including groundwater abstraction, baseflow and water flow into/out of the aquifer, etc. The relationship between the RIB model and water level fluctuations can be expressed as:
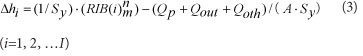
where:
A is area of the catchment, Qp, Qut and Qoth represent groundwater abstraction, outflow and groundwater volume changes resulting from other activities, respectively.
The relationship between RIB and recharge estimation
It is assumed that the water level fluctuations vary with the cumulative rainfall departure from the average rainfall series. However, the CRD and previous RIB methods fail to explain the condition where the continuous departures are negative and yet the observed water level may still rise, and the physical meaning of parameter r, representing the recharge percentage, in the CRD and previous RIB methods is problematic. The difference of contiguous departures should- be regarded as recharge instead of using the departure from average. The groundwater level will rise if the difference is positive and vice versa; recharge at the ith time scale can be calculated as:
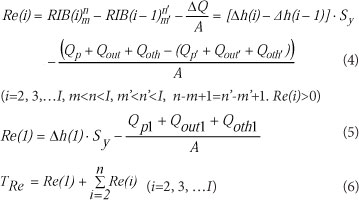
where:
Re(l) is the recharge for the first time step, and
Re(i) represents the recharge estimate at the ith time, which could be daily, monthly or annually.
TRe is the sum of the recharge in mm for the whole time series. If the value of Re(i) becomes negative in Equations
(4) and (5), no recharge on the ith time scale is assumed.
Software interface
The RIB programme is implemented in an Excel Spreadsheet (Microsoft 2007), and programmed using Visual Basic Application (VBA). The programme enables one to manipulate, analyse and display data, and calculates groundwater recharge based on observed groundwater levels (which must be transformed into WLF) and rainfall time series. A solver function is adopted to minimise the difference between observed WLF and the calculated values using the least squares method. With key parameters (like time lag, length of related rainfall events and r value) obtained from available rainfall and water level data, the program is also capable of filling gaps in groundwater-level data and predicting the water level fluctuations using rainfall and abstraction data. An example of the screen printout of the RIB user interface is shown in Fig. 2.
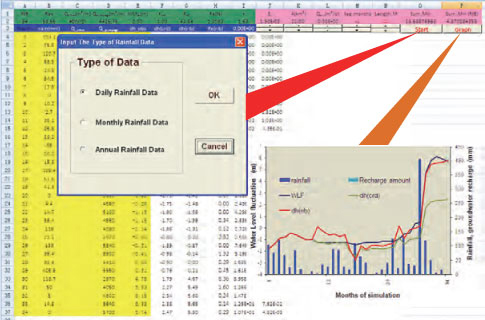
Figure 2
Screen printout of the RIB user interface
The definition of the symbols used in the RIB programme is given in Appendix A along with units and type of data (e.g. input/output, one value/time series etc.). Input data are time series of rainfall, sink/sources of groundwater, observed groundwater level fluctuations, specific yield (S), area of the catchment (A) and parameters for fitting the time lag between rainfall and recharge events. The sink/source terms (Qothet, Qout, Q ) can be left vacant if data are absent (in the areas where the groundwater abstraction is low, the effects of these variables on water-level changes can be considered negligible compared with rainfall input).
The time scale needs to be defined manually before starting data inputs. This depends on the type of rainfall and water level data available (daily, monthly or annual basis). The time scale can be activated by clicking the 'Start' button (Fig. 2).
Groundwater level fluctuations and recharge are calculated by pressing the 'Graph' button (Fig. 2). The chart is updated automatically and displays rainfall, observed/calculated groundwater level fluctuations (using RIB as well as CRD model) and recharge estimate with the RIB method. The time lag and length need to be adjusted to fit the curve of observed and calculated WLF value.
Critical assumptions
A series of assumptions and general rules for using the RIB method to estimate the recharge are highlighted as follows:
• The water level fluctuations from the monitoring borehole should be representative of the study area. For example, it is not recommended to use the data collected from pumping boreholes or boreholes close to surface water bodies (river, lake, etc.) unless these sources and sinks can be quantified accurately.
• The term (Qp+Qout+Qoth)/(A) of Eq. (5) could be ignored if the impact of pumping and/or outflow on WLF is not evident. The effect may, however, be large under certain conditions, for example, in fractured dolomite aquifers with relatively high hydraulic conductivity.
• The specific yield should be representative of the aquifer system. For determining the effect of long-term pumping of an aquifer, laboratory values of specific yield are appropriate, but for estimation of groundwater recharge with the RIB model, laboratory values of S are probably too large.
• The RIB method is usually applicable in unconfined aquifer systems with shallow water levels and relatively small trans-missivity, where the water level responds clearly to rainfall.
• The RIB model is applicable where suitable time series of rainfall and groundwater level are available.
Case studies
Site description and data collection
Two research sites characterised by two different types of geology were selected to simulate the water-level fluctuation and calculate groundwater recharge. These two systems represent two main modes of groundwater recharge, namely diffuse and localised. A site where the aquifer is a coastal plain sand with a diffuse recharge mechanism was selected in Riverlands Nature Reserve (Western Cape, South Africa), while another site was chosen in Oudebosch catchment in the Kogelberg Nature Reserve (Western Cape, South Africa), representing the Table Mountain Group aquifer (TMG).
The Riverlands Nature Reserve, located at about 10 km southwest of Malmesbury (Fig. 3), is in quaternary catchment G21D. A shallow unconfined sandy aquifer underlies deep, well-leached, generally acidic and coarse sandy soils of marine and aeolian origin. The recharge area used in the simulation is about 10 ha (0.1 km2) with S ranging from 0.05 to 0.15 for fine to medium sand cover, and water table depth ranging from 1.6 to 3.5 m. Mean annual precipitation (MAP) is about 450 mm, occurring mainly from May to August. Daily rainfall data were collected from a rain gauge (from May 2007 to September 2011). There are 13 piezometers in the study area, 3 of which were collapsed; 2 boreholes (RVLD 6 and RVLD 8) were selected to monitor the water level using a data logger installed in the borehole. More detailed information on the topography, and soil physical and chemical properties of the Riverlands Nature Reserve is given by Jovanovic et al. (2009).
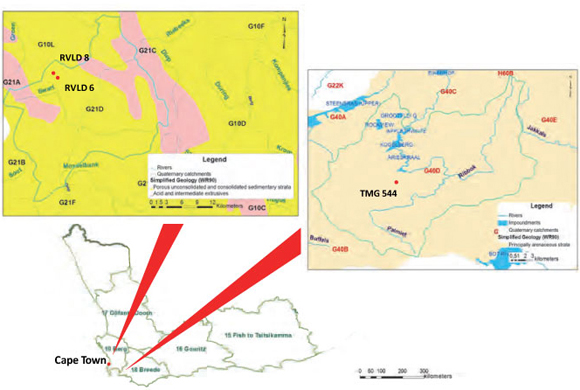
Figure 3
Location of Riverlands Nature Reserve and Oudebosch catchment
The Oudebosch catch m ent within the Palmiet River basin is located northeast of Betty's Bay (Fig. 3), where the geology is typically characterised by TMG, which mainly consists of a fractured rock aquifer. The Oudebosch stream passes through the catchment and the hydrological boundaries indicate that the site is located in quaternary catchment G40D. Three monitoring boreholes were considered in this study. Daily water level data over 3 years indicated that, due to the interaction between the stream and groundwater, the water level fluctuations in one borehole close to the stream were significant, while the water level in another borehole stayed very stable and did not show a clear relationship with rainfall series data. Water level data recorded from borehole TMG 544 were used to calculate the recharge. The catchment covers an area of 3.4 km2. Specific yield of the aquifer was estimated at 0.21 (Saayman et al., 2007). The mean annual precipitation (MAP) is approx. 800 mm (occurring mainly from May to October). Data recorded from a rain gauge (from January 2008 to July 2010) and borehole TMG 544 (Fig. 3) were used to calculate groundwater recharge for the catchment.
Groundwater recharge estimation and analysis
The simulations were carried out using daily time series of rainfall and groundwater levels. The length of simulation was 1 603 d for RVLD6 and RVLD8 (from 01/05/2007 to 19/09/2011; a gap in water level data occurred from 04/08/2008 to 18/03/2009, which is about 7 months) and 928 d for TMG544 (from 01/01/2008 to 16/07/2010; there is an approx. 300-day water-level data gap from January to March 2008, and no water-level data were available in June and July of 2010). The daily and monthly groundwater recharge estimates for the sandy and TMG aquifers, and observed groundwater level fluctuations calculated with the CRD method (dh(crd)) and the RIB method (dh(rib)), are shown in Fig. 4.
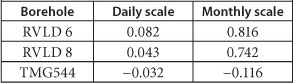
The graphs in Fig. 4 plot rainfall inputs and calculated groundwater recharge in mm as bars. Pearson's correlation between observed WLF and WLF simulated with the RIB and CRD models, which reflects the degree to which the variables are related, is listed in Table 1. The results demonstrate that the results of the RIB method show significant correlation to observed WLF. The simulated groundwater level fluctuations from the RIB model closely fit the observed values after calibrating the time lag (lag_Days) and length of related rainfall events (Length_D) on a daily basis. The term lag_Days varied from 0 days at Riverlands to 82 days at Oudebosch, i.e., it takes less than 1 day and 82 days for percolating rainwater to reach the water table in Riverlands and Oudebosch, respectively. The term Length_D was 82 d at Riverlands and 85 d at Oudebosch. The results for the time lag and length of related rainfall events on a daily and monthly basis for a range of specific yield are listed in Table 2.
TABLE 1
Pearson's correlation between observed WLF and simulated WLF by the RIB and CRD models

The results of the RIB model indicate that the time lag between rainfall infiltration and groundwater recharge for the sandy alluvial aquifer is much less than that for the TMG aquifer, which reflects the different characteristics of the two aquifer systems. It also indicates that the recharge estimate made using daily data is much higher than that made using monthly data.
The effects of factors other than rainfall, i.e, evapotran-spiration, atmospheric pressure and entrapped air, on water level fluctuations at short-term scales can be significant (Healy, 2010). Spearman's method was adopted to calculate the correlation coefficients between rainfall and observed WLF on a daily and monthly basis. The Spearman correlation coefficients listed in Table 3 indicate that the relationship between rainfall and observed WLF on a monthly basis is more significant than that on a daily basis. Therefore, the recharge rates estimated at monthly scale are more realistic than those estimated at daily scale, and the impacts of the factors mentioned above on WLF cannot be ignored at the daily scale. Several approaches can be used for correcting water-level data (Tamura et al., 1991; Toll and Rasumssen, 2007; Crosbie et al., 2005; Von Asmuth et al., 2008). For the monthly basis, water level fluctuations mainly occur in response to rainfall, pumping, evapotranspiration or other phenomena.
TABLE 3
The Spearman correlation coefficients between rainfall and observed WLF
From Table 2, the recharge in the G21D catchment is predicted to be 9.7-29.1% of MAP on a monthly basis, with Sy ranging between 0.05 and 0.15; the recharge in the G40D catchment is predicted to be about 15.7% of MAP on a monthly basis with 0.21 as specific yield of the aquifer. With regards to groundwater studies carried out in sandy aquifers, a number of recharge values have been estimated. A study in catchment G21D by DWAF (2006) provided a value of 15.4% of MAP using the chloride mass balance (CMB) approach, and a value of 5% using a GIS-based groundwater recharge algorithm, and a value of 13% in the vicinity of Riverlands (DWAF, 2006). Another study in the area reported recharge values of 26% of rainfall (380 mm/a) using a water balance method at Atlantis (20 km south of Riverlands) (Vandoolaeghe and Bertram, 1982). Bredenkamp (1982) modelled the conditions at Atlantis and came up with a recharge rate of 21% of total rainfall (350 mm/a). The recharge rate was reconsidered as 0.2-3.4% of MAP in Atlantis using the CMB approach (Conrad et al., 2004); however, this result needs to be re-evaluated. The main reason for this might be the different timeframes between the CMB and the RIB method (Crosbie et al., 2010). The CMB method provides an estimate of recharge over the residence time of the water in the aquifer, which can be many thousands of years, while the RIB method provides an estimate of recharge over the length of time that measurements of water levels were recorded; this can be days, months, or decades.
The recharge estimate on a monthly basis in Oudebosch is 15.7% of MAP (183.9 mm/a), with specific yield of 0.21, which is much higher than the average recharge value (29.7 mm/a) estimated in the TMG aquifer by Wu (2005). Because of the heterogeneous geology in the Table Mountain Group (TMG), the specific yield differs significantly from place to place (10-6-10-2 of specific yield is appropriate; Lin, 2007; Jia, 2007), and it is reasonable to expect high variability in recharge. Therefore, sensitivity analysis of specific yield is needed.
Sensitivity analysis
Parameters of monthly rainfall and water level, as well as specific yield value, were chosen as inputs to assess individual impacts on the estimated recharge rate. According to studies on specific yield of the TMG aquifer (Van Tonder et al., 2002), the specific yield of highly permeable fractures in the TMG aquifer is usually very low, in the order of 10-4 to 10-7, whilst that of the matrix can be much higher (i.e. 0.005 to 0.05). Considering the high uncertainty of specific yield in the TMG aquifer and the assumed linear relationship between recharge and specific yield in the RIB model (Eqs. (3)-(6)), a sensitivity analysis was carried out over a range of specific yields from 2.1 x 10-3 to 0.21. The corresponding change in the model output was observed.
A sensitivity analysis for rainfall and water level was also performed at the three borehole sites - RVLD6, RVLD8 (S = 0.05) and TMG544 (S = 0.21). A uniform distribution was adopted with perturbations of ±10% around the monitored rainfall and water level values; the two additional time series therefore represent the extremes/boundaries (minimum and maximum) of the uniform distribution. These minimum and maximum time series were run through the model. The model outputs gave a range of variability of recharge, and this range defined the sensitivity to the key model inputs. The simulation results are shown in Table 4.
TABLE 4
Summary of inputs of the sensitivity analysis of groundwater recharge calculated with the RIB model on a monthly basis
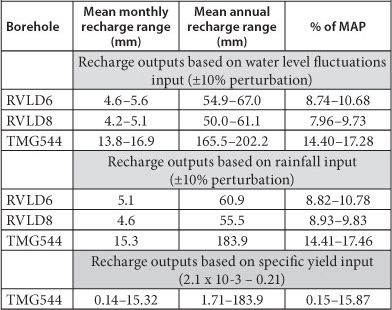
The results in Table 4 show that a perturbation of the water level time series data by a factor ±10% results in a range of recharge of 14.40-17.28% of MAP in Oudebosch, and 8.74-10.68% and 7.96-9.73% of MAP in Riverlands with RVLD 6 and RVLD 8, respectively. The results also show that for a perturbation of the rainfall time series data by a factor ±10%, the recharge percentage ranges from 14.41 to 17.46% of MAP in Oudebosch, and 8.82-10.78% and 8.93-9.83% of MAP in
Riverlands with RVLD 6 and RVLD 8, respectively. The mean annual recharge stays the same in all three cases. These results indicate the sensitivity of recharge estimated using the RIB model is higher for Oudebosch than for Riverlands.
As discussed above, the recharge rate in the RIB model has a linear relationship with specific yield. The recharge rate in Oudebosch can be calculated with any specific yield value ranging from 2.1 x 10-3 to 0.21; results are shown in Tables 2 and 4. Figure 5 refers to the relationship between recharge and specific yield from the data in Table 2. The results indicate that the RIB model is very sensitive to the specific yield. From this perspective, in a site where recharge rate has been estimated using other approaches, the RIB model could indicate the accuracy of the specific yield. As the recharge estimate using other methods in TMG aquifer is less than 10% (Wu, 2005), specific yield values for the aquifer in Oudebosch ranging from 0.021 to 0.042 (18.7-33.9 mm/a of groundwater recharge) are recommended.
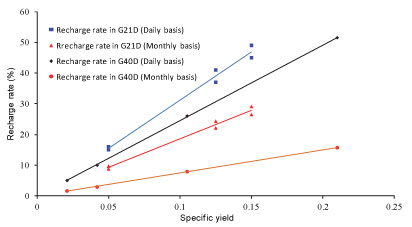
Figure 5
The relationship between specific yield and recharge rate in the RIB model
Scenario simulations
Abstraction scenarios
The Kogelberg Nature Reserve was identified as one of a set of sites that was suitable for a groundwater exploration programme carried out by the City of Cape Town (Hay et al., 2004). Simulations were therefore run with RIB in order to predict groundwater level trends under different abstraction scenarios. Borehole TMG544 was used for this purpose and 3 scenario simulations were run:
• Baseline conditions (without abstraction): Using recorded rainfall data from January 2008 to July 2010 as input; Sy is assumed to be 0.042, based on the discussion of the y relationship between recharge and specific yield above; aquifer area = 3.40 km2
• Abstraction of 3 M£-d-1: Same rainfall data input; Sy = 0.042; aquifer area = 3.40 km2
• Abstraction of 3 M£-d-1 from 1/10 of the aquifer area: Same rainfall input; Sy = 0.042; aquifer area = 0.34 km2
The resulting groundwater level predictions are plotted in Fig. 6. An abstraction of 3 Mℓ-d-1 did not affect the groundwater level drastically. The groundwater level with abstraction was 0.02 m lower than the baseline without abstraction. The effect of abstraction was small because of the relatively large area of the aquifer (3.40 km2). However, if the draining area for a borehole is reduced by 1/10 (i.e. 10 abstraction boreholes are used over the same area), the effect on the groundwater level was predicted to be much larger (0.21 m lower than the baseline). The result also indicates that the recharge rate, which is 7.99% of MAP for these three scenarios, is independent of abstraction.
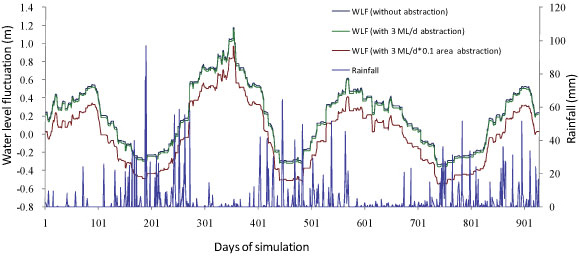
Figure 6
Measured rainfall and groundwater levels (baseline conditions, with 3 Mi-d' abstraction and with abstraction from '/'0 of the surface area of the aquifer) for borehole TMG544 in the Oudebosch catchment
Climate scenarios
Three simulations were run with the RIB model to predict groundwater level trends under climate change, in particular reductions in rainfall. The following scenarios applied at borehole TMG 544 were run:
• Baseline conditions: Using recorded rainfall data from January 2008 to July 2010; S =0.042; aquifer area = 3.40 km2
• Reduction in measured rainfall by 10%; Sy=0.042; aquifer area = 3.40 km2
• Reduction in measured rainfall by 20%; Sy=0.042; aquifer area = 3.40 km2
The predictions of groundwater level fluctuations are shown in Fig. 7; the average recharge rate for the baseline condition is about 93.9 mm/a from 2008 to 2010 (7.99% of MAP). The prediction shows that, in the initial period of simulation, reduced rainfall did not affect groundwater levels. However, the effects became increasingly visible over time, especially in the dry season. After about 1 year, the groundwater level dropped by 0.16 m with 10% rainfall reduction and by 0.32 m with 20% rainfall reduction compared to the baseline. It is interesting to notice that the ratio of recharge rate to precipitation did not change significantly; it was slightly higher than the baseline (mean recharge rate is 8.11% and 8.25% of corresponding rainfall with 10% and 20% rainfall reduction, respectively). However, the recharge amount with 10% and 20% rainfall reduction resulted in a drop of about 8.1 mm/a and 16.2 mm/a, respectively, relative to baseline condition.
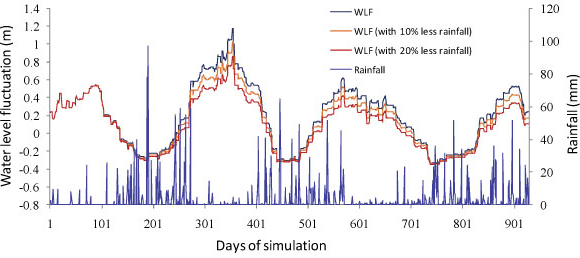
Figure 7
Measured rainfall and groundwater level fluctuations (baseline conditions, with '0% and 20% less rainfall) for borehole TMG544 in the Oudebosch catchment
DISCUSSION
The RIB model is capable of recharge estimation if specific yield is known and the critical assumptions listed in the previous section are met. Furthermore, it is important to note that the RIB model can be used only under certain conditions in shallow unconfined aquifers. According to Darcy's law, the recharge in a catchment can be simplified as:
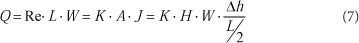
Then:

A dimensionless function based on Eq. (8) can be developed as:

where:
Q = flow rate (m3/d)
A = the area of radial cross-section (m2)
J = hydraulic gradient
Re = recharge rate per unit surface area (m/d)
W = the width of the catchment (m)
L = the average distance of groundwater flow away from groundwater mound (m)
Δh = water level fluctuations (m)
K = hydraulic conductivity of the aquifer (m/d)
H = the saturated thickness of the aquifer (m)
D = the depth to the water table (m)
From Equations (8) and (9), the RIB method is best applied in situations where the water level displays sharp rises and declines with recharge; i.e., the parameter Γ cannot be very small. The relationship among Γ and these factors, including annual rainfall (P), hydraulic conductivity of aquifer (K) and the depth to the water table (D), are discussed as follows:
• Theoretically, the RIB model is incapable of recharge estimation in extremely arid areas where rainfall (P) is less than 100 mm/a, as the recharge from rainfall is too small to cause water level rises, i.e., Γ ∞ 0.
• The hydraulic conductivity of the aquifer (K) cannot be extremely high. For instance, with high hydraulic conductivity, the outflow from the aquifer is greater than that reaching the aquifer. In other words, with significantly high value of K, recharge can still happen without producing water table rises. Hence, the application of the RIB model to fractured rock aquifers needs to be done with caution, as some fractures might be a primary conduit for water movement, and the recharge from rainfall could flow to the aquifer where water level changes might not take place. • The depth to the water table (D), referring to time lag, should be shallow. The larger the thickness of the unsaturated zone, the longer the time lag. For example, for water depths over 200 m in northern African countries, individual rainfall events could hardly play a significant role in water level fluctuations. The parameter of Γ approaches zero in such cases.
In summary, theoretically, the RIB model is best suited for shallow unconfined aquifers with relatively low transmissivity. The range of Γ under which the RIB model is capable of estimating recharge needs to be defined using more case studies.
Conclusion
Using the improved RIB model, with Sy ranging from 0.05 to 0.15, groundwater recharge was estimated to be 16-47% of MAP at the daily scale and 9.3-27.8% at monthly scale at Riverlands, while the recharge at Oudebosch was 51.5% and 15.7% of MAP at the daily and monthly scales, respectively. The Pearson correlation coefficients indicate that the results of the RIB model are more significantly correlated to observed values than those of the CRD method. The Spearman correlation coefficients between rainfall and observed WLF together with recharge estimates obtained from other methods in these areas demonstrate that the recharge estimates on a monthly basis are more realistic than those on a daily basis. Through sensitivity analysis, the model was found to be particularly sensitive to specific yield, particularly when applied to the TMG aquifer system; the estimated recharge rate may become unrealistic with a high specific yield value.
We conclude that the RIB model is a simple and efficient method to estimate groundwater recharge and fill water level data gaps in shallow unconfined aquifers where groundwater levels respond distinctly to rainfall. With different rainfall and/ or abstraction inputs, different scenarios can be simulated to estimate the water level fluctuations and calculate recharge, which could provide valuable information for water managers. It is not a data-intensive method but a good knowledge of the hydraulic properties of the aquifer is required.
There are ample opportunities for application of the RIB model in similar regions. In this paper, 2 case studies with 2 different types of geology were presented using this model. Discussion of the limitations of RIB indicates that the model is best suited for shallow unconfined aquifers with relatively low transmissivity. Due to limited available data, only recharge estimates at daily and monthly basis are simulated. The utility of the model could be further explored using more data collected in different climatic areas under different hydrogeological conditions.
Acknowledgements
The authors acknowledge funding by the Vlaamse Inter-universitaire Raad (VLIR) and the Water Research Commission (Pretoria, South Africa). Riverlands Nature Reserve and Kogelberg Biosphere Reserve are thanked for providing the experimental sites. Finally, we would like to thank two- anonymous reviewers for their helpful comments and very valuable suggestions.
References
BAALOUSHA H (2005) Using CRD method for quantification of groundwater recharge in the Gaza Strip, Palestine. Environ. Geol. 48 889-900. [ Links ]
BEEKMAN HE, XU Y (2003) Review of groundwater recharge estimation in arid and semi-arid southern Africa. In: Xu Y and Beekman HE (eds.) Groundwater Recharge Estimation in Southern Africa. UNESCO International Hydrological Programme, Paris. [ Links ]
BREDENKAMP DB and VOGEL JC (1970) Study of a dolomitic aquifer with carbon-14 and tritium. Isotope Hydrology, Proc. Symp. IAEA, 9-13 March 1970, Vienna. 349-372. [ Links ]
BREDENKAMP DB, SCHUTTE JM and DU TOIT GJ (1974) Recharge of a dolomitic aquifer as determined from tritium profiles. Isotope Techniques in Groundwater Hydrology 1974, IAEA, Vienna. 73-94. [ Links ]
BREDENKAMP DB, BOTHA LJ, VAN TONDER GJ and VAN RENSBURG HJ (1995) Manual on Quantitative Estimation of Groundwater Recharge and Aquifer Storativity. WRC Report No. TT 73/95. Water Research Commission, Pretoria. [ Links ]
BREDENKAMP DB and VANDOOLAEGHE MAC (1982) Die Ontginbare Grondwater Potensiaal van die Atlantis Gebied. Gh Report 3227. Department of Water Affairs and Forestry: Directorate of Geohydrology, Cape Town. [ Links ]
BREDENKAMP DB (1982) Evaluering van die Waterpotensiaal van die Kussande by Atlantis Volgens 'n Wiskundige Model van die Grondwaterstelsel en Beramings van die Interferensie tus-sen Boorgate. Gh Report 3233. Department of Water Affairs and Forestry: Directorate of Geohydrology, Pretoria. [ Links ]
CONRAD J, NEL J and WENTZEL J (2004) The challenges and implications of assessing groundwater recharge: A case study - northern Sandveld, Western Cape, South Africa. Water SA 30 (5) 75-81. [ Links ]
CROSBIE RS, BINNING P and KALMA JD (2005) A time series approach to inferring groundwater recharge using the water table fluctuation method. Water Resour. Res. 41 1-9. [ Links ]
CROSBIE RS, JOLLY ID, LEANEY FW and PETHERAM C (2010) Can the dataset of field based recharge estimates in Australia be used to predict recharge in data-poor areas? Hydrol. Earth Syst. Sci. 14 2023-2038. [ Links ]
DE VRIES JJ and VON HOYER M (1988) Groundwater recharge studies in semi-arid Botswana - a review. In: Simmers I (ed.) Estimation of Natural Groundwater Recharge. NATO ASI Series C222. Reidel, Dordrecht. 339-348. [ Links ]
DE VRIES JJ, SELAOLO ET and BEEKMAN HE (2000) Groundwater recharge in the Kalahari, with reference to paleo-hydrologic conditions. J. Hydrol. 238 1-2 110-123. [ Links ]
DWAF (2006) Groundwater resource assessment. Task 3aE recharge. Department of Water Affairs and Forestry, Pretoria, South Africa. [ Links ]
FENELON JM (2000) Quality assurance and analysis of water levels in wells on Pahute Mesa and vicinity, Nevada Test Site, Nye County, Nevada. USGS Water Resources Investigation Report 00-4014. United States Geological Survey, Reston. [ Links ]
HAY ER, RIEMANN K, BROWN C, COLVIN C and LUGER M (2004) TMG Aquifer feasibility study and pilot project ecological and environmental Report No. 3389F/9944 47-49. [ Links ]
HEALY RW (2010) Estimating Groundwater Recharge. Cambridge University Press, Cambridge. JIA HL (2007) Groundwater resource evaluation in Table Mountain Group Aquifer systems. Ph.D. thesis, University of the Western Cape. [ Links ]
JOVANOVIC NZ, ISRAEL S, TREDOUX G, SOLTAU L, LE MAITRE D, RUSINGA F, ROZANOV A and VAN DER MERWE N (2009) Nitrogen dynamics in land cleared of alien vegetation (Acacia saligna) and impacts on groundwater at Riverlands Nature Reserve (Western Cape, South Africa). Water SA 35 (1) 37-44. [ Links ]
LIN L (2007) Hydraulic properties of the Table Mountain Group (TMG) Aquifers. Ph.D. thesis, University of the Western Cape. [ Links ]
MAZOR E, VERHAGEN BTH, SELLSCHOP JPF, JONES MT, ROBINS NS, HUTTON L and JENNINGS CMH (1977) Northern Kalahari groundwaters: hydrologic, isotopic and chemical studies at Orapa, Botswana. J. Hydrol. 34 203-234. [ Links ]
RASOULZADEH A and MOOSAVI S AA (2007) Study of groundwater recharge in the vicinity of Tashk Lake area. Iran. J. Sci. Technol., Trans. B, Eng. 31 (B5) 509-521. [ Links ]
SAAYMAN IC, BEEKMAN HE, ADAMS S, CAMPBELL RB, CONRAD J, FEY MB, JOVANOVIC N, THOMOS A and USHER BH (2007) Assessment of Aquifer Vulnerability in South Africa. WRC Report No. 1432/1/07. Water Research Commission, Pretoria. [ Links ]
SCANLON BR, HEALY RW and COOK PG (2002) Choosing appropriate techniques for quantifying groundwater recharge. Hydrogeol. J. 10 18-39. [ Links ]
SCHMIDT G and PLOETHNER D (2000) Hydrogeological investigations in the Otavi Mountain land. Prof. XXXIAH Congress on Groundwater: Past Achievements and Future Challenges, 26 November - 1 December 2000, Cape Town. 419-424. [ Links ]
SMIT PJ (1978) Groundwater recharge in the dolomite of the Ghaap Plateau near Kuruman in the Northern Cape, Republic of South Africa. Water SA 4 (2) 81-92. [ Links ]
TAMURA Y, SATO T, OOE M and ISHIGURO M (1991) A procedure for tidal analysis with a Bayesian information criterion. Geophys. J. Int. 104 507-516. [ Links ]
TOLL NJ and RASMUSSEN TC (2007) Removal of barometric pressure effects and earth tides from observed water levels. Ground Water 45 101-105. [ Links ]
VANDOOLAEGHE MAC and BERTRAM E (1982) Atlantis Grond-water-sisteem: Herevaluasie van Versekerde Lewering. Gh Report 3222. Department of Water Affairs and Forestry: Directorate of Geohydrology, Cape Town. [ Links ]
VAN TONDER GJ, BARDENHAGEN I, RIEMANN K, BOSCH KRJ, DZNANGA P and XU Y (2002) Manual on Pumping Test Analysis in Fractured-Rock Aquifers. WRC Report No. 1116/1/02. Water Research Commission, Pretoria. [ Links ]
VAN WYK E, VAN TONDER GJ and VERMEULEN D (2011) Characteristics of local groundwater recharge cycles in South African semi-arid hard rock terrains-rainwater input. Water SA 37 (2) 147-154. [ Links ]
VERHAGEN B MAZOR E and SELLSCHOP J (1974) Radiocarbon and tritium evidence for direct rain recharge to groundwaters in the Northern Kalahari. Nature 249 343-644. [ Links ]
VON ASMUTH JR, MASS K, BAKKER M and PETERSEN J (2008) Modeling time series of ground water head fluctuations subjected to multiple stresses. Ground Water 46 30-40. [ Links ]
WU Y (2005) Groundwater recharge estimation in Table Mountain Group Aquifer systems with a case study of Kammanassie area. Ph.D. thesis, University of the Western Cape. [ Links ]
XU Y and BEEKMAN HE (2003) Groundwater Recharge Estimation in Southern Africa. UNESCO IHP Series No. 64. UNESCO, Paris. [ Links ]
XU Y and VAN TONDER GJ (2001) Estimation of recharge using a revised CRD method. Water SA 27 (3) 341-344. [ Links ]
Received 23 May 2012
Accepted in revised form 6 March 2013.
* To whom all correspondence should be addressed. +27 21 959-3882; fax: +27 21 959-3118; e-mail: yxu@uwc.ac.za
APPENDIX A
Input/output data in the rainfall infiltration breakthrough (RIB) model
ª Day, month or year
b Cumulative rainfall departure method
c Rainfall infiltration breakthrough method