Serviços Personalizados
Artigo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em Google
Similares em Google
Compartilhar
Water SA
versão On-line ISSN 1816-7950
versão impressa ISSN 0378-4738
Water SA vol.38 no.4 Pretoria Jan. 2012
Operational optimisation of water supply networks using a fuzzy system
Saulo de Tarso Marques BezerraI, *; Simplício Arnaud da SilvaII; Heber Pimentel GomesIII
IDepartment of Technology, Centre of Agreste Region, Federal University of Pernambuco, Caruaru, PE, Brazil
IIDepartment of Electrical Engineering, Federal University of Paraíba, João Pessoa, PB, Brazil
IIILaboratory of Power and Hydraulics Efficiency in Water Supply Systems, Department of Civil and Environmental Engineering, Federal University of Paraíba, João Pessoa, PB, Brazil
ABSTRACT
This paper presents a fuzzy system to control the pressure in a water distribution network, by using valves and controlling the rotor speed of the pumping systems. The variable frequency drive tracks the minimum head of the pumping system, while the control valves have the function of eliminating the excess pressure at various points of the network. The control system can track any reference pressure value and there is no limit for the number of monitored points. Experiments were carried out to demonstrate the fuzzy system's efficiency. By extrapolating the results achieved in the experimental setup to a real hydraulic network with leakages and no pressure control, the volumetric losses could be reduced by more than 56%. The experiments showed that the system is robust enough to control the pressure of an experimental setup of water distribution. Besides, the proposed system can be easily applied to similar water supply systems and would help to reduce the consumption of water and electricity, as well as to reduce the maintenance costs.
Keywords: water, power efficiency, water supply system, fuzzy logic
Introduction
Energy and water are two indispensable and interrelated commodities for life. Seven percent of the world's energy consumption in 2000 was used to pump and treat water for urban residents and industry (Ghimire and Barkdoll, 2007). During the lifetime of the water supply network, in the majority of cases, the energy cost of pumping surpasses the investment costs (Gomes et al., 2008).
Energy consumption of most of the water supply systems worldwide could be reduced by at least 25% through the use of power efficiency processes. Water supply companies have the potential to save more energy than the total consumption of Thailand (James et al., 2002). The optimisation of pumping operations may generate significant savings, especially in large systems, where these savings can reach millions of dollars per year. Several studies both in Europe and the United States of America indicate that many industrial processes have a saving potential of 30% to 50% in their pumping systems (Hovstadius, 2007).
An efficient alternative to reducing the electric power consumption of water distribution network pumping systems is the reduction of flows and pressures. The most effective way to decrease the volume of pumped water, without rationing, is to minimise the actual water losses (Bezerra, 2009). As a mid- or short-term measure, pressure management is the most practical and economical method among the various ways of controlling the losses from leakages (Germanopoulos and Jowitt, 1989; Tabesh and Hoomehr, 2009). It may be noted that the control of pressure in hydraulic networks has a direct bearing on the electric power and water consumption.
The most common automation systems, supervisory control and data acquisition - SCADA systems - enable the indirect control of pressure at the network points. However, decisions are linked to the experience of operators, since the supervisory control and data acquisition systems, as a rule, provide only assisted operation. You can monitor, control and interfere with several units of the system in real time, but not with the automatic and integrated control of processes. The larger the water distribution system, the more complex are the decisions to be taken. The large number of elements that may change their states complicates the procedure to obtain the best combination of operation status to be defined by operators (Bezerra, 2009). Due to this high complexity, the search for the most appropriate decisions in terms of operational processes should be done with the aid of appropriate computational tools.
The available equipment for pressure control in hydraulic networks is the variable frequency drive (VFD) and the control valves. Usually, the rotational speed control performed by the VFD coupled to the electric motor is based on a single-point measurement of the hydraulic network pressure. The control valves used to reduce pressure are called pressure-reducing valves and are placed at the entry points of the networks.
The larger the water supply network gets, the more significant will be the pressure variation within the hydraulic network. In these cases, to ensure pressure control at various points of the system there is a need for simultaneous application of control valves and variable frequency drives.
Thus, the main objective of this paper is to develop a fuzzy system control applied to a water supply system to minimise electric power consumption and the volume of water pumped. The variable frequency drive control system operates to keep the manometric height of the pumping system at an optimal value and the valve control system helps to reduce the pressure at several points of the water network.
Literature review: Fuzzy systems
With the technological advances of recent decades, more modern and efficient controllers are being designed for complex processes. Fuzzy systems have emerged as an alternative to the automatic control of nonlinear systems and with multiple inputs and outputs. This control system is based on fuzzy logic, which is an attempt at formalisation/ mechanisation of human capability to make rational decisions (Zadeh, 2008).
Fuzzy systems have demonstrated their ability to solve different kinds of problems in various application areas. Due to the great importance of environmental issues at present, there are several research publications dealing with the use of fuzzy controllers to improve renewable energy generation plants and increase the energy efficiency of industrial processes. An extensive collection of papers is found in the literature on this subject. Cirre et al. (2009) described the design and implementation of 2-layer hierarchical control strategies for a distributed solar collector field, and also provided significant experimental results, on the basis of which the benefits of using this approach were compared with those of current operation practices. The upper layer of the hierarchical strategy was implemented using two different approaches, fuzzy logic and physical model-based optimisation. Both determine the optimal plant operating point automatically, taking into account the operating constraints while maximizing the profit from the sale of the electricity generated. Lin et al. (2011) presented the design of an on-line training recurrent fuzzy neural network controller with a highperformance model reference adaptive system observer for the sensor-less control of an induction generator. The proposed output maximisation control is achieved without the mechanical sensors, such as the wind speed or position sensor, and the new control system will ensure the delivery of maximum electric power with light weight, high efficiency and high reliability. Sung et al. (2011) developed a robust observer-based fuzzy control for a variable-speed wind power system. In their work, an output-feedback control for stabilising the uncertain nonlinear system is proposed. For achieving a robust stability, they deal with the parametric uncertainties of the concerned system which is based on the Takagi-Sugeno fuzzy model. The simulation results for variable-speed wind power systems are demonstrated to visualise the feasibility of the proposed method.
Fuzzy systems are widely used in the control of variable rotation speeds, particularly in induction machines utilised in industrial processes. Lima (2007) developed a fuzzy system to control the soil water matrix potential, aiming at an optimal irrigation process, by varying the rotational speed of the pumping system. Souza et al. (2007) proposed an adaptive fuzzy controller for efficiency optimisation of adjustable-speed drives, with an emphasis on vector-controlled induction motor drives. The technique combines two distinct control methods, namely, online search of the optimal operating point and a model-based efficiency control. Yu et al. (2010) focused on the problem of position tracking control for field-oriented induction motors with parameter uncertainties and load torque disturbance. Traditionally, the controllers utilised for the motors use the PID controller. In practice, for a drive system, the parameters may vary during the operation, and, as a result, the system performance may deteriorate, resulting in instability during extreme conditions. This problem is minimised in the fuzzy system. As exemplified in some of the earlier works that have been cited, fuzzy logic systems are used to approximate the nonlinearities of control of induction motor drives. Several methods have been proposed in the literature for control of these motors, but applications for motor pumping systems that take into account the nature of the water distribution network for the design of fuzzy controllers are rarely found.
Fuzzy logic is also commonly used as a decision support system (DSS) in almost all areas of, for example, water supply systems. Sinske and Zietsman (2004) developed a DSS for pipe-break susceptibility analysis. The manager can apply the DSS to model the complex pipe-break phenomena in a water distribution system in order to identify the pipes that are susceptible. The DSS has already been successfully applied to the water distribution system of Paarl in South Africa. El-Baroudy and Simonovic (2006) explored the utility of adopting fuzzy performance measures for evaluating the performance of a complex water supply system, in terms of combined reliability-vulnerability, as well as, robustness and resilience.
System description
The study was conducted using an experimental setup for water distribution, consisting of a tank, pumping system, a variable frequency drive, 2 control valves (CVc and CVs), 2 pressure transducers, and 2 flow transducers, besides the hydraulic and electrical accessories (Fig. 1).
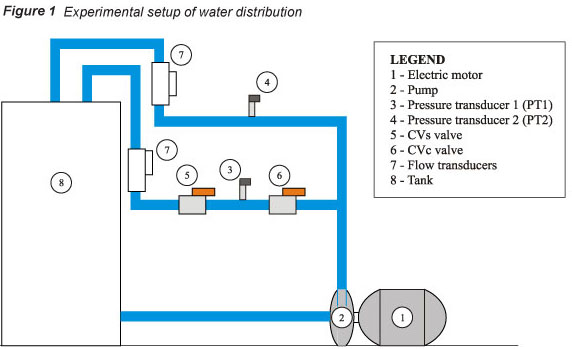
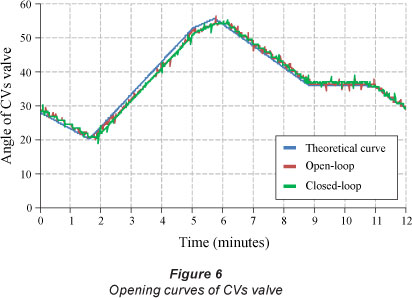
The experimental setup is composed of 2 branches to simulate 2 sectors in a real water distribution network. The CVs are used to change the system's operating conditions, emulating a demand variation. When CVs is closed, the flow decreases; consequently, the pressure upstream of the valve increases. The opening curve of the CVs curve was based on a profile of water consumption of a sector of the Metropolitan Region of Sao Paulo, Brazil.
The variable frequency drive (VFD) is intended to keep the pressure at the most critical point of the hydraulic network equal to the desired pressure (reference pressure), while the CVc valve eliminates the excess pressure at the point of measurement in Branch 1.
The data acquisition system comprises of a PC and USB data acquisition (DAQ). Two energy analysers were employed to measure and monitor the input and output electrical variables of the VFD + electric motor (electric current, electric voltage and power).
Proposed fuzzy system
The control system was developed in LabVIEW and consists of 2 fuzzy controllers: the first one is responsible for determining the frequency of the VFD, while the second one operates at the control valve CVc.
The use of fuzzy sets allows the development of the control system without prior knowledge of the mathematical model corresponding to the controlled plant. The fuzzy system uses 4 analogue inputs and 3 analogue outputs of the DAQ. The analogue inputs are the signals from the pressure transducers PT1 and PT2, and from the valves CVc and CVs. The analogue outputs are used to adjust the opening of the CVc and the activation frequency of the motor of the pump.
Inputs and outputs of the fuzzy system, and the linguistic variables, as well as the number and format of the membership functions, were selected as per literature recommendations, heuristic analysis and experimental tests. The crisp variables can be normalised, simplifying the universe of discourse or determined as a function of its application. In this work, the range of universe of discourse was defined based on real values.
The linguistic variables were selected in order to enable the pressure control at the 2 measurement points of the experimental setup. The input linguistic variables are:
- PRES - pressure at the most critical point of the hydraulic network
- FREQ - activation frequency of the motor-pump system
- DIF - deficit or excess of pressure downstream the CVc
- VALVE - angle position of CVc valve
The output linguistic terms of the fuzzy system are:
- AF - increase or decrease of the control signal of VFD
- AV - increase or decrease in the opening angle of CVc valve
The number of membership function sets recommended in the literature is between 2 and 7. The greater the number of sets, the greater the precision; however, according to Simoes and Shaw (2007), for values greater than 7 there are no significant improvements. Therefore, 7 fuzzy sets were adopted for each variable, except for AF, for which 9 terms were used in order to smooth the output signal. This smoothing is important to minimise peak currents in the electric motor caused by the VFD.
The formats of the most common membership functions are triangular and trapezoidal, and they are easily generated. In order to reduce the complexity of the fuzzy-logic inference system, membership functions with shapes found in typical process control literature were adopted, where border terms are trapezoidal and the remainder of the terms are triangular. The membership functions were determined based on recommendations in the literature and heuristic knowledge from simulations and experimental tests.
The inference method used was Mamdani's procedure based on min-max decision. There are two commonly used methods of defuzzification, namely, centre of area and mean of maximum. Here, the centre of area method was chosen as the universes of discourse for the output variables are continuous. With defuzzification, resultant fuzzy values of the fuzzy rules are converted into crisp values.
Fuzzy controller of VFD
Through a qualitative analysis of the behaviour of the pressure, depending on the change of speed of rotation of the pumping system, 2 entries were determined for the fuzzy controller of the variation frequency drive - PRES and FREQ. The first one represents the deficit or excess pressure in the critical point of the system, while the second indicates the value of the motor drive frequency.
The input linguistic variable PRES (Fig. 2) was defined to a set-point of 20, i.e., the controller was developed considering the value of 20 as an optimal value for the variable taken into consideration. The universe of discourse was based on the measuring range of the pressure transducers. The linguistic terms and the membership functions of the VFD controller are described in Fig. 2. For the variable FREQ these terms are very low (VL), low (LO), slightly low (SL), optimum (OP), slightly high (SH), high (HI), and very high (VH).
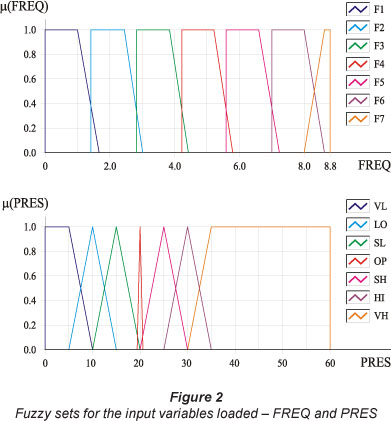
The first output of the fuzzy system is AF, which is directly related to the measurement of the system pressure and rotation speed. The heuristic search of the output variable is based on the following statement:
- If the pressure in the most critical point of the system is less than desired, the controller increases the rotational speed of the pumping system; if the pressure in the critical point of the system is higher than desired, the controller decreases the rotational speed of the rotational speed of the pumping system.
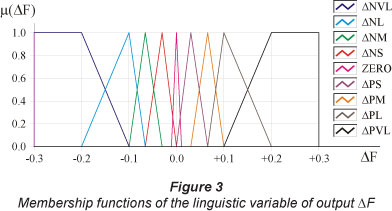
The universe of discourse of the variable AF is in the range [-0.30, 0.30], which corresponds to real values of electrical voltage. The sum of the value of AF and FREQ (which varies between 0 and 8.8) takes the value of the voltage sent to the converter through the DAQ. The membership functions are shown in Fig. 3.
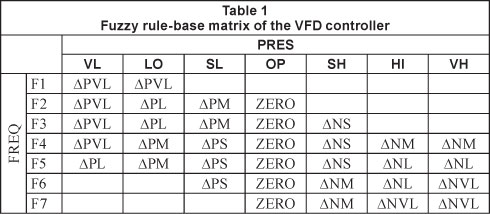
Thirty-four rules of fuzzy inference have been established to determine the output variable AF. Table 1 presents the fuzzy associative matrix of the VFD controller based on past experience with manual settings. The rule-base represents the knowledge of the controller; hence the formulations should be carefully considered.
Modeling of the fuzzy controller of CVc
For the modelling of the fuzzy controller of CVc, it is essential to define the input and output variables. Through a qualitative analysis of patterns of behaviour depending on the pressure and opening angle of the CVc valve, 2 inputs were established to the controller fuzzy of the control valve - DIF and VALVE. The linguistic input variable DIF is defined based on the pressure measurements and it establishes the opening angle of the CVc valve. The variable DIF is calculated by Eq. (1) and corresponds to the excess or deficit of pressure downstream of the CVc valve and its desired value is zero. The universe of discourse for these input functions was limited between -5 and 5, which corresponds to the range in real values measured in meters.
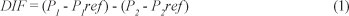
where:
Pi is the pressure at the point i
Piref is the reference value of the point i
The control valve used in the study is of proportional type and its opening angle varies linearly with the voltage imposed on it, ranging from 2 to 10 V. However, it was observed that the pressure variation occurs only in the range of 17° to 60°. Between 0° and 17°, the valve CVc is still closed, and in the range of 60° to 90° it is completely open (the pressure drop approaches zero). Therefore, the universe of discourse is adopted to be [17, 60].
The output language, called AV, refers to the increase or decrease in degrees of opening angle of the CVc valve installed upstream of the PT1. The form of heuristic search for the output variable AV is based on the concept:
If there is excessive pressure downstream of the control valve, it should decrease the opening angle. On other hand, if there is a deficit in the pressure downstream of control valve, it should increase the opening angle.
The membership functions of the input and output variables are presented in Figs. 4 and 5. For the variable DIF these are positive large (PL), positive middle (PM), positive small (PS), zero (ZE), negative small (NS), negative middle (NM), and negative large (NL).
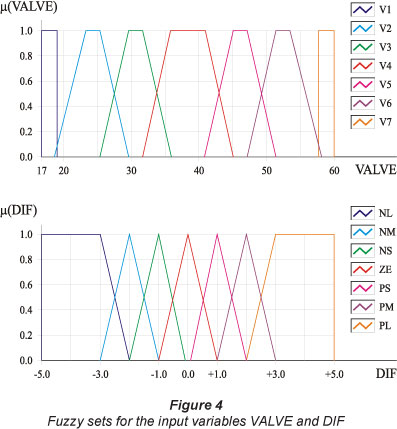
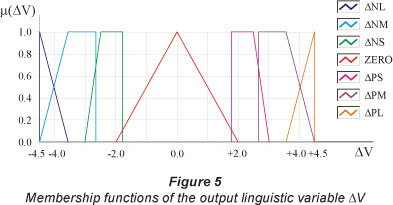
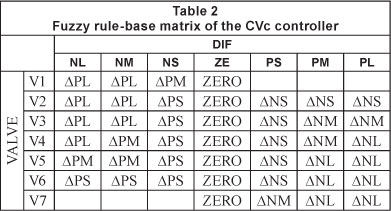
Forty-three rules of fuzzy interference have been established to determine the output variable AV, which relate the 7 membership functions of DIF with the 7 functions of variable VALVE. Table 2 presents the fuzzy associative matrix of the CVc controller.
Results and discussion
This section describes the experiments performed in the real plant (Fig. 1). Three experiments were performed in order to validate the proposed control system:
- Experiment 1: Test in an open-loop control (without control) with the valve downstream of the PT1 (CVs) varying its opening angle in order to emulate the inflow demand of a water system.
- Experiment 2: Test in a closed-loop control, with an input reference step of 20 for the variable PRES, using only fuzzy controller of VFD. This experiment is performed under the same operating conditions as Experiment 1. A virtual instrument to simulate demand for a real system through the remote operation of CVs was developed in the LabVIEW computational program. Fig. 6 shows the theoretical curve and the real curves of the CVs opening angle for Experiments 1 and 2.
- Experiment 3: Test in closed-loop control for an input reference step of 20 m for the 2 measurement points in which pressure was evaluated.
Experiment 1
Experiment 1 was conducted in an open-loop system to be later compared with Experiment 2. Fig. 7 shows the pressure and flow in Branches 1 and 2 in Experiment 1. As expected, the flow rate in Branch 1 follows the same pattern of the CVs opening angle.
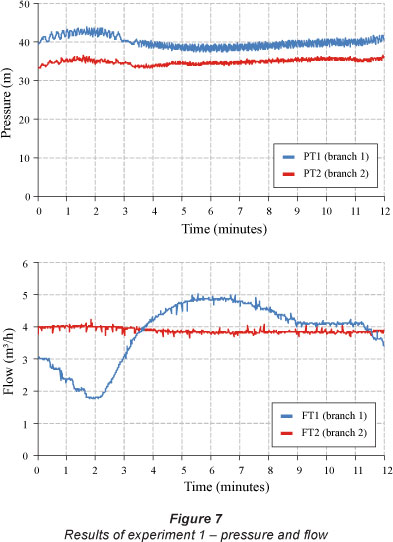
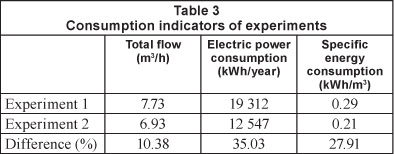
The average flow was 3.84 m3/h at Branch 1 and 3.89 m3/h at Branch 2, giving a total average flow of 7.73 m3/h. Considering the design pressure of 20 m, the mean pressure at PT1 (40.02 m) and PT2 (34.94 m) was 100% and 75%, respectively, which is higher than the ideal.
Experiment 2
Experiment 2 was conducted under the same operating conditions as Experiment 1, but with the operation of the fuzzy controller VFD. This is a closed-loop test with a step-type input of 20 m for the variable PRES. Initially, the frequency of the motor voltage was 50 Hz and CVc was fully open. The variation of the CVs opening angle was the same as in Experiment 2.
Figure 8 presents the pressure and flow in Branches 1 and 2 of Experiment 2. The FT2 flow has the same pattern of CVc opening angle, because the FT2 meter is located in the same branch of the valve. The average flow was 3.22 m3/h at Branch 1 and 3.71 m3/h at Branch 2, giving a total average flow of 6.93 m3/h. The mean pressures at the measuring points PT1 and PT2 were 27 and 20 m, respectively.
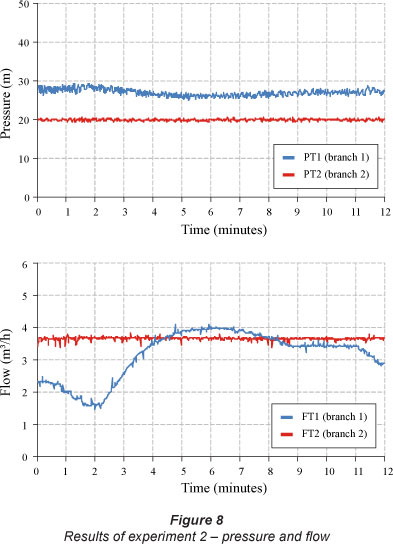
The control system showed a satisfactory response, and the steady-state error was 3.11% (0.62 m), with an average error of 1.02% (0.20 m).
Evaluation of electric power consumption
To evaluate the energy efficiency in the experimental setup the on-line power consumption was measured and the specific energy consumption was calculated. Specific energy consumption is widely used in the water supply sector and is defined as the ratio between energy consumption, in kWh, and the volume pumped, in m3, within a certain time interval.
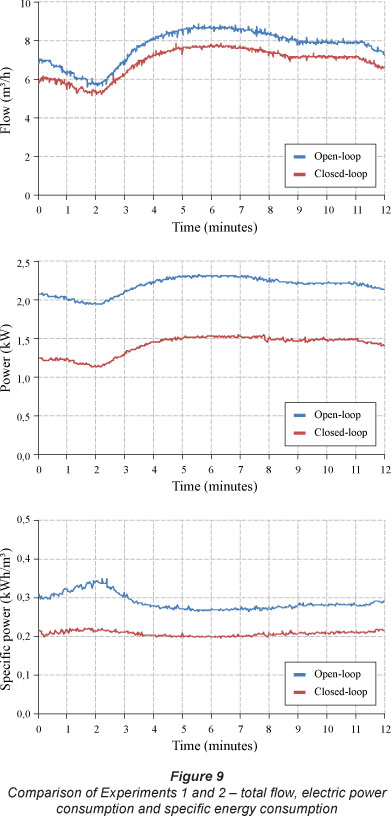
Despite the fact that the VFD consumes about 5% of total energy and causes a decrease in the motor-pump efficiency, it was found that control of the rotation speed provides a reduction in power consumption of 35.03%, with a decrease of 27.91% in specific energy consumption. The total flows achieved in Experiments 1 and 2, the power and the specific energy consumption are shown in Fig. 9. Table 3 presents the parameter values of the energy evaluation of Experiments 1 and 2.
Experiment 3
The VFD operating in isolation is not able to optimise the pressure at more than one point of a water distribution system, as can be seen at Measurement Point 1 (Branch 1), and there was an excess pressure of 7 m (see Fig. 8).
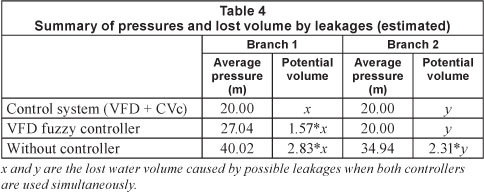
Using the equation suggested by the Fixed and Variable Area Discharge paths (FAVAD) theory (Eq. (2)), with N1 equal to 1.5 (background leakage typically), and extrapolating the results to a real network with leakages, the fuzzy system developed for the simultaneous control of the VFD and VC (Experiment 3) would provide a potential reduction of 64.67% (Branch 1) and 56.69% (Branch 2) in the amount of leakage, when compared with the control system with no pressure control. Table 4 presents a synopsis of the potential of leakage volumes and the network pressures for the various conditions mentioned.
The FAVAD theory (May, 1994) has greatly advanced the understanding of pressure-leakage relationships for networks. The theory takes into account the fact that certain types of leaks will follow variable leakage paths. The pressure leakage calculation can vary up to a power of 2.5 in such cases. Numerous field tests using the FAVAD theory have confirmed that the influence of pressure on the volume of leakage and frequency of new leaks is far greater than estimated previously.

where:
Q1 is the amount of leakage through a hole in a pipe whose pressure is P1.
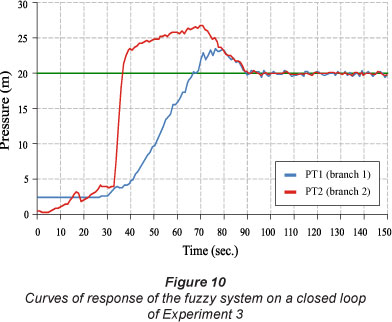
Therefore, Experiment 3 was performed for an input reference step of 20 m for the 2 measurement points. With this procedure, the performance indicators of the control system were obtained (overshoot, settling time and steady-state error). The settling time was 90 s, the steady-state error was 3.38% (0.68 m) and 3.47% (0.70 m), and the overshoot was 16.80% (3.36 m) and 33.91°% (6.78 m), for Measuring Points 1 and 2, respectively. Figure 10 shows the step response curves obtained at 2 points of pressure measurement.
Conclusion
This paper presents a fuzzy system applied to control the pressure of water distribution networks. The study aimed to design a robust controller for any pressure reference values. There is no limit for the number of monitored points to be controlled; moreover, the pressure reference values at these points could change over time.
The fuzzy system presented a satisfactory response; the error of maximum steady state in the experiments was 3.47% (0.70 m). The system's minimum pressure control, which is primarily done by the variable frequency drive (pump rotational speed), presented a quick response. However, due to the high response time of the control valve, the overall system response was relatively slow and with high overshoots. The settling time of about 90 s was considered to be appropriate for this type of application.
Despite the fact that the variable frequency drive consumes about 5% of total energy and causes a decrease in the motor-pump efficiency, it was found that the control of the rotational speed provides an overall reduction in power consumption of 35%, with a decrease of 28% in the specific electric power consumption (kWh/m3).
By extrapolating the results achieved in the experimental setup to a real hydraulic network with leakages and no pressure control, the volumetric losses could be reduced by more than 56%.
The performance of the control system proved to be satisfactory in the experimental setup. It is known that the main advantages of the fuzzy system are the absence of the need for modelling the plant, its adaptability to different operating conditions and its applicability for complex dynamic systems. Hence, it is expected that the fuzzy system developed here may be easily implemented in other similar water distribution networks.
Acknowledgement
The authors would like to thank the Brazilian Government for the financial support granted by Centrais Elétricas Brasileiras SA (ELETROBRÁS), through Financiadora de Estudos e Projetos (FINEP) and through the Brazilian Agency for Research and Development (CNPQ).
References
BEZERRA STM (2009) Sistema fuzzy para controle piezométrico de sistemas de distribuição de água visando à economia de água e energia. Ph.D. Thesis, Federal University of Paraíba, João Pessoa, Brazil. [ Links ]
CIRRE CM, BERENGUEL M, VALENZUELA L and KLEMPOUS R (2009) Reference governor optimization and control of a distributed solar collector field. Eur. J. Oper. Res. 193 (3) 709-717. [ Links ]
EL-BAROUDY I and SIMONOVIC SP (2006) Application of the fuzzy performance measures to the city of London water supply system. Can. J. Civil Engineering 33 (3) 255-265. [ Links ]
GERMANOPOULOS G and JOWITT PW (1989) Leakage reduction by excess pressure minimization in a water supply network. Institution of Civil Engineers 87 (2) 195-214. [ Links ]
GHIMIRE SR and BARKDOLL BD (2007) Incorporating environmental impact in decision making for municipal drinking water distribution systems through eco-efficiency analysis. Proc. World Environmental and Water Resources Congress 2007. Tampa, Florida, May. [ Links ]
GOMES HP, BEZERRA STM and SRINIVASAN VS (2008) An iterative optimisation procedure for the rehabilitation of water supply pipe networks. Water SA 34 (2) 225-236. [ Links ]
HOVSTADIUS G (2007) Tackling soaring energy costs in North America. World Pumps 492 38-40. [ Links ]
JAMES K, CAMPBELL SL and GODLOVE CE (2002) Agua y energía: Aprovechando las oportunidades de eficiencia de agua y energia aún no exploradas en los sistemas municipales de água. Alliance to Save Energy, Washington, USA. [ Links ]
LIMA FMC (2007) Desenvolvimento de um sistema de controle fuzzy do potencial matricial da água no solo visando à otimização de processos de irrigação. Ph.D. Thesis, Federal University of Paraíba, João Pessoa, Brazil. [ Links ]
LIN WM, HONG CM, OU TC and CHIU TM (2011) Hybrid intelligent control of PMSG wind generation system using pitch angle control with RBFN. Energy Conversion and Management 52 (2) 1244-1251. [ Links ]
MAY J (1994) Pressure dependent leakage. World Water and Environmental Engineering Management 17 (8) 10. [ Links ]
SIMÕES MG and SHAW IS (2007) Controle e modelagem fuzzy. 2rd ed. Edgard Blücher, São Paulo, Brazil. [ Links ]
SINSKE SA and ZIETSMAN HL (2004) A spatial decision support system for pipe-break susceptibility analysis of municipal water distribution systems. Water SA 30 (1) 71-80. [ Links ]
SOUZA DA, ARAGÃO FILHO WCP and SOUSA GCD (2007) Adaptive fuzzy controller for efficiency optimization of induction motors. IEEE Transactions on Industrial Electronics 54 (4) 2157-2164. [ Links ]
SUNG HC, PARK JB and JOO YH (2011) Robust observer-based fuzzy control for variable speed wind power system: LMI approach. International Journal of Control, Automation and Systems 9 (6) 1103-1110. [ Links ]
TABESH M and HOOMEHR S (2009) Consumption management in water distribution systems by optimizing pressure reducing valves' settings using genetic algorithm. Desalination and Water Treatment 2 95-100. [ Links ]
YU J, CHEN B and YU H (2010) Position tracking control of induction motors via adaptive fuzzy backstepping. Energy Conversion and Management 51 (11) 2345-2352. [ Links ]
ZADEH LA (2008) Is there a need for fuzzy logic? Information Sciences 178 (13) 2751-2779. [ Links ]
Received 16 June 2011; accepted in revised form 5 July 2012.
* To whom all correspondence should be addressed. ffi +55 81 3724 9022; fax: +55 81 3724 9022; e-mail: s.bezerra@yahoo.com.br














