Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Water SA
On-line version ISSN 1816-7950
Print version ISSN 0378-4738
Water SA vol.38 n.2 Pretoria Jan. 2012
ARTICLES
The influence of pH on the adsorption of lead by Na-clinoptilolite: Kinetic and equilibrium studies
L Mihaly CozmutaI, *; A Mihaly CozmutaI; A PeterI; C NiculaI; E Bakatula NsimbaII; H TutuII
ITech. Univ. Cluj Napoca, North Univ. Center Baia Mare, 76, Victoriei Street, 430122, Baia Mare Romania
IIMolecular Sciences Institute, School of Chemistry, University of the Witwatersrand, Private Bag X3, WITS 2050, Johannesburg, South Africa
ABSTRACT
The objectives of this study were, firstly, to establish the mechanism by which modified clinoptilolite (in Na form) adsorbs lead ions and, secondly, to assess the extent of influence of pH on the adsorption capacity. To this end, the experimental data have been fitted by adsorption isotherms, thermodynamic and kinetic models. Based on the standard errors obtained during experiments, it was determined that the accuracy of prediction of the isotherm models considered for adsorption decreases in the order: Dubinin-Raduschkevich (4.63%, average normalised standard deviation error); Langmuir (7.90%); and Freundlich (15.98%). For the kinetic models, the accuracy of prediction decreases in the order: intra-particle Weber-Morris (with an average normalised standard deviation error of 5.53%); heterogeneous diffusion (5.67%); pseudo-second order kinetic model (10.47%); diffusion through the particle surface (41.73%); and the pseudo-first kinetic model (47.51%). The mechanism of adsorption of lead ions by Na-clinoptilolite was found to occur in a monolayer and heterogeneous surface. The pH of contact solutions played an important role owing to competition by hydrogen ions. As the pH of the solution decreased, the maximum monolayer adsorption capacity established theoretically, based on the Langmuir isotherm, also decreased. Thus, if, for instance, the pH decreases from 4 to 1, the maximum adsorption capacity decreases from 0.3569 to 0.1604 mol-kg-1. At high pH of the contact solution, the adsorption process occurs by ion exchange and at low pH; i.e., it is physical. The variation of the Gibbs free energy demonstrates that adsorption occurs spontaneously. The process was also observed to occur at a higher rate at low acidity. Diffusion through the internal structure of macro- and micropores is the stage taking place with the lowest speed during the adsorption process and plays an important role in the mechanism of adsorption. The intra-particle diffusion coefficient depends on pH, which can modify the shape and concentrations of the hydrated metal complexes in solutions, thus affecting the adsorption process. The decrease of pH from 4 to 1 resulted in a decrease of the intra-particle diffusion coefficient from 4.0610-11 to 1.9610-11 m2min-1. The film diffusion coefficients were found to be 10 times larger than the intra-particle coefficients, suggesting that diffusion to the external surface cannot be the rate-limiting step in the adsorption mechanism.
Keywords: clinoptilolite, lead, isotherm of adsorption, distribution coefficient, kinetic model, ion exchange
Introduction
The utilisation of zeolite materials as adsorbents for different types of metallic ions and gases is widely mentioned in literature (Hernandez and Aguilar, 1999; Alvarez et al., 2003; Motsi et al., 2009; Jamil et al., 2010; Wang and Peng, 2010; Panagiotis, 2011). Due to their low cost and adsorbent properties, these materials offer major advantages in attempts to reduce environmental pollution, e.g., in the treatment of wastewaters contaminated with heavy metals or in the phytoremediation of polluted soils. Natural zeolites can be applied by combining adsorption and some biological methods. In this instance, active biomass is immobilised in the pores of zeolites through a combination of physical processes (Matis et al., 2004; Zamboulis et al., 2004). Other applications of zeolite involve the treatment of radioactive wastewaters (Faghihian et al., 1999; Rahman et al., 2010). Zeolites play a prominent role as catalysts in various industrial chemical processes (Liu et al., 2011). Natural zeolites belong to a class of hydrated aluminosilicates with a 3-dimensional structure, characterised by the association of SiO4 and AlO4 anionic tetraedras. The isomor- phous replacement of Si4+ by Al3+ produces negative charges in the structure which are balanced by the exchangeable cations (Na+, K+, Ca2+ and Mg2+). These counterbalancing cations can be easily exchanged in solution with other cations. The adsorption of various cations on zeolite is influenced by many parameters, among which the most important are:
- the concentrations of metal ions in solution and the ratio between the volume of solution and the mass of zeolite (the ratio between solid and liquid);
- the pH of the contact solution;
- the initial parameters of the zeolite, i.e., physico-chemical treatment, and the type and concentration of activated solutions used;
- temperature;
- the average diameter of the particle;
- the nature of the anion accompanying the cations;
- the hydrated radii of adsorbed ions and the magnitude of the dehydration energy.
In order to achieve high adsorption capacities, zeolites are often conditioned chemically. In general, natural zeolite is activated when the cations present in a solution substitute the cations in the zeolite structure. The substituting cations result in a uniform energy of adsorption on the surface of the zeolite because of their smaller volume, while they increase the adsorption capacity because of their higher mobility. The hydrated radii of NH4+, K+ and Na+ cations is smaller than the radii of Ca2+ and Mg2+ ions; and the hydration energies of the former are lower than the hydration energy of the latter (Trgo et al., 2006a; Coruh, 2008; Gorka et al., 2008). The activation cations which replace the Ca2+ and Mg2+ cations of the zeolite display a higher availability for ion exchange, thus explaining why the adsorption capacity of activated zeolite increases (Doula, 2006). In clinoptilolite conditioned with a NaCl solution, the concentration of Na+ increases and the concentration of Ca2+ decreases, subsequently leading to an increase of the Na+/Ca2+ ratio. The conditioning of zeolite with a HCl solution determines the growth of the Si/Al ratio to some extent, as well as the increase of the relative amount of K+ in clinoptilolite, subsequently decreasing the Na+/K+ ratio (Inglezakis et al., 2004; Gunay et al., 2007). The pH of the contact solution is an important parameter controlling the adsorption process. The adsorption capacity decreases as the acidity of the contact solution increases. These variations can be explained by the competition between metal ions and hydrogen ions and by the variation of hydrolysis products of metal ions with pH (in this study we only discuss adsorption of ions and not their precipitation at low pH) (Athanasiadis and Helmreich, 2005; Smiciklas and al., 2007; Wang et al., 2007; Sequeira et al., 2009).
The chemical composition and the porous internal structure of zeolite, as well as the experimental conditions for adsorption, influence the zeolite's selectivity for metallic ions (Erdem et al., 2004). In general, clinoptilolite has a well-known higher preference for Pb2+ and Cd2+ than for Cu2+, Co2+ and Ni2+. This happens because clinoptilolite prefers cations with lower dehydration energy, lower hydration radii and higher mobility.
Adsorption of heavy metals by clinoptilolite, the most used natural zeolite found in different types of volcanic tuff, has been the focus of many research studies (Mier et al., 2001; Petrus and Warchol, 2005; Sprynskyy et al., 2005; Karadag et al., 2006). The main research goals of most of these studies are to establish the adsorption mechanism, to find and explain the order of selectivity for different heavy metals and to compare, in quantitative terms, the influence of different factors on the adsorption capacity.
The mechanism of adsorption of heavy metals on clinoptilolite occurs in the following main steps:
(i) diffusion of ions from the mass of solution to the film surrounding the zeolite particle;
(ii) diffusion of ions through the external film;
(iii) diffusion through the macro-pores and micropores toward the adsorptive sites;
(iv) dehydration of ions in the proximity of adsorptive sites and hydration of the counterbalance cations;
(v) the inversion phenomenon between the ions and counterbalance cations (Sprynskyy et al., 2006);
(vi) binding of ions on the active sites and
(vii) diffusion of counter ions along the same path back to the external solution.
Under dynamic conditions, in heterogeneous systems, the diffusion of ions from the external solution into the film at the particle surface would not be the rate-limiting step. On the other hand, in solution, the ions exist only in the hydrated form. The volume of these hydrated ions depends on both the dehydrated ionic radius and the electric charge of ions. So, the ionic hydrated radius can affect mobility through the channels in the internal structures of zeolites, meaning the steps involving diffusion from the film, macro- and micropores can be the rate-limiting step of the mechanism. Also, the diffusion of different counter ions back into solution can affect the mobility of metal ions. Different hydrated ionic radii generate different dehydration energys. Cations with large hydrated ionic radii have high dehydration energy, thus affecting Step (iv). Generally, the rate-limiting step in the adsorption of heavy metal ions on zeolite can be: diffusion in the external film, diffusion in pores, dehydration of ions and the binding of ions on the active site. Step (vi) can be explained in correlation with the activated form of zeolite. Many research papers present different equations which can be useful for establishing the step of lowest speed in the mechanism of adsorption of heavy metal ions onto zeolite.
The objectives of this study, as stated above, sought to establish the mechanism of adsorption of lead onto Na-modified clinoptilolite and to assess the role of pH in the adsorption process.
The physical and chemical properties of zeolite
Clinoptilolite rock samples from the Stoiana Village deposit, Cluj County (Romania), containing 63% clinoptilolite, were used for the experiments described in the study. The main mineral and chemical characteristics of the samples are listed in Table 1. The chemical composition was obtained using wet chemical analysis while the mineral composition was obtained using a DRON X-ray powder difractometer connected to a data acquisition and processing unit to record the XRD patterns, which allowed for the determination of the parameters of the crystalline network of the zeolite. We used CuKa radiation (λ = 1.540598 Ǻ) and a graphite monochromator. The XRD diffraction analysis revealed the crystalline structure of zeolite, with average crystallite diameter of 75.74 nm.
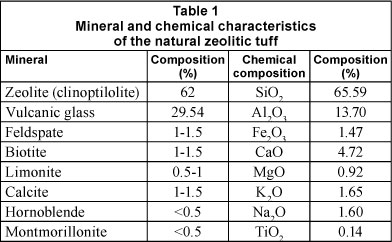
Clinoptilolite samples were ground in a mortar (Retsch RM 100, Germany) and divided by mechanical sieves (Retsch AS200 basic) into 0.5-1.0 mm size fractions. These zeolite fractions were then washed with distilled water to remove any turbidity and dried at 105°C for 24 h to remove any adsorbed water. Finally, the clinoptilolite samples were stored in a desiccator before performing the chemical activation to the Na-form.
The chemical treatment of zeolite (clinoptilolite) was performed by adding 1 ℓ of 2 M solutions of NaCl to the samples of clinoptilolite (100 g) at 25ºC in continuous movement (orbital shaker Heidolph Unimax 1010 Inkubator 1000, Germany). After 24 h, the solid phases were separated from the solutions, washed until all Cl- ions had been removed (controlled with AgNO3 solution). The samples were then dried at 105ºC using a Binder oven for 24 h.
Adsorption-desorption isotherms of the investigated samples were determined in order to obtain the specific surface area and the pore size distribution. The surface area of the clinoptilolite was determined by the Brunauer-Emmett-Teller (BET) method. A Sorptomatic, Thermo Electron Corporation system coupled with a Flatron L1718S computer system was used. The partial pressure range was 0.05 < P/P0 <0.3. Nitrogen adsorption was carried out at 77K. The basic parameters for the porous structure of natural and treated samples (Na-clinoptilolite) of the zeolite are presented in Table 2. The relative moisture content of natural clinoptilolite (7.27%) was determined by the thermometric method, drying the rock samples at 110ºC to constant mass.
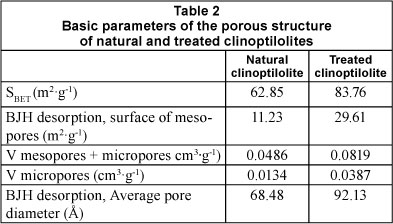
The specific gravity for natural clinoptilolite (2.1548 kg-ℓ-3) was determined by picnometric methods. The bulk density is 0.9402 kg.ℓ -3. By applying the NH4Ac method, the content of exchangeable cations (CEC) was found to be 64.85 meq-(100 g)-1 for natural clinoptilolite and 173.62 meq-(100 g)-1 for treated clinoptilolite.
Methods
The concentration of metal ions was determined in a filtered solution (the adsorbent was removed by filtration using Whatman paper no. 42, (7-9 μm retention particles)) by means of an atomic absorption spectrophotometer (Perkin Elmer Analyst 800, Shelton, USA), using the air-acetylene flame, 283.3 nm wavelength, 0.7 nm slit, with background correction. The standard deviation of the measurement was from 0.01 to 0.1%. The pH of the solution was determined using an Inolab pH 730 apparatus.
Mathematical modelling and statistical interpretation
The equilibrium isotherms were determined by mixing 1 g Na-clinoptilolite with 100 mℓ of a solution of lead ions in cylindrical flasks. The flasks were placed in a thermostatic stirrer (Heidolph Unimax 1010 Inkubator 1000, Germany) at 25ºC for 24 h at a fixed agitation speed of 200 rmin-1. At the end of the reaction (24 h), the concentration of the residual metal was determined by atomic absorption spec-trophotometry. Additionally, the concentration of lead in the aqueous phase was measured after pre-established periods of time.
All of the batch equilibrium and kinetic studies were performed in 3 replicates of dried Na-clinoptilolite. The standard reproducibility deviation was from 0.1%> to 4%.
In order to estimate the specific constants of the adsorption isotherm or of the adsorption kinetic models, a linear regression analysis (y = A + B . x) was adopted. The criterion considered was the minimisation of the squared sum of errors between the predicted values (qcalc) and experimental data (qexp).
In order to compare, in quantitative terms, the applicability of the models (i.e. the validity of each model), the value of the correlation coefficient (r) and the normalised standard deviation (Δq(%)) were calculated, as follows:
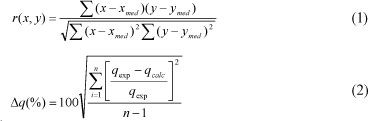
where:
x, y represent variables
xmed, ymed are the average (arithmetic mean) of the variables
n is the number of experimental data
The CurveExpert 1.37 freeware and Statistica 7.0 were used in all calculations with the confidence level set at 95%.
In order to evaluate the hydrochemical equilibrium species, Hydra and Medusa were used (freeware available from the Royal Institute of Technology, Sweden).
Results and discussion
The amount of lead ions adsorbed on clinoptilolite was calculated using the mass balance expression:

where:
V is the solution volume (ℓ)
M the amount of sorbent (kg)
Co and Ce (mol.ℓ-1) are the initial and equilibrium metal concentrations, respectively
Modelling of sorption equilibrium data
In this study, the adsorption isotherms have been described by 3 commonly-used models, namely: Langmuir, Freundlich and Dubinin-Radushkevich.
Langmuir isotherm
The Langmuir isotherm describes the ideal adsorption process by taking into consideration that:
- there are a limited number of active centres homogenously spread across the surface of the adsorbent;
- all active centres have exactly the same energy level;
- monolayer adsorption;
- the adsorption on an active centre has no influence on the adsorption on other active centres.
The Langmuir isotherm can be represented as:

where:
qe is the amount adsorbed at equilibrium (mol.kg-1)
Ce the equilibrium concentration (mol.ℓ-1)
b a constant related to the energy or net enthalpy of adsorption (ℓ.mol-1)
qm is the maximum adsorption capacity (mol.kg-1)
The Langmuir equation can be described by a linear equation as follows:
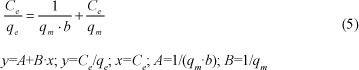
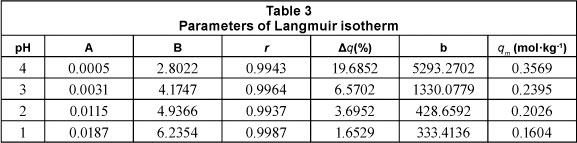
The constants qm and b were obtained from the slope and intercept of the plot of (Ce/qe) versus Ce. Table 3 includes the parameters of the Langmuir model for the adsorption of lead by Na-clinoptilolite.
Freundlich isotherm
The Freundlich isotherm is based on adsorption on a heterogeneous surface with a non- uniform distribution of energy of adsorption as follows:

where:
KF ((molkg-')/(mol-ℓ1/n) and
n are equilibrium constants indicative of the adsorption capacity and adsorption intensity, respectively.
If n > 1, adsorption is considered favourable. The linearised form of the Freundlich sorption isotherm is:
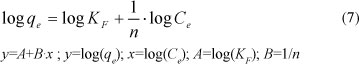
The constants KF and n were obtained from the slope and intercept of the plot of log(qe) versus log(Ce). Table 4 gives the parameters of the Freundlich model for the sorption of lead by Na-clinoptilolite.

adsorption. This model is based on the heterogeneity of the surface energies and can be written in the following linear form:
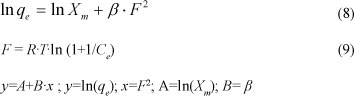
where:
Xm is the maximum sorption capacity of the sorbent (mol.kg-1)
β a constant (mol2.'kJ-2) related to the mean sorption energy
F the Polanyi potential
R the gas law constant (kJ.mol-1K-1)
T the absolute temperature (K).
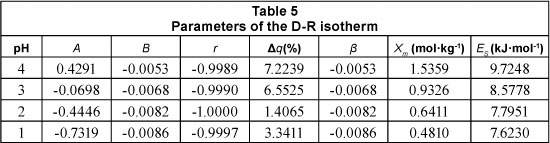
The constants β and Xm were obtained from the slope and intercept of the plot of ln(qe) versus F2. The parameters of the D-R model for the sorption of lead by Na-clinoptilolite are presented in Table 5.
The values of the sorption energy Es (kJmol-1) can be correlated to by using the following relationship:

If the magnitude of Es is between 8 and 16 kJ.mol-1, the adsorption process proceeds by ion exchange, while for values of Es < 8 kJ.mol-1, the adsorption process is of a physical nature (El-Kamash et al., 2005).
Comparison of isotherms
The experimental data are shown graphically in Fig. 1. The predictive precision of the isotherm models, considered as a function of their respective relative errors, was determined to be highest for the Dubinin-Raduschkevich model 4.63% (the average normalised standard deviation error) followed by the Langmuir model 7.90% and the Freundlich model 15.98%. This order shows that the mechanism which occurs is chem-isorption on a monolayer and heterogeneous surface (Garcia-Mendieta et al., 2009).
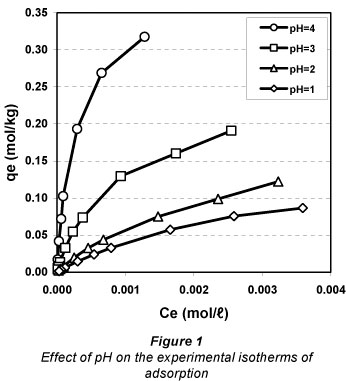
The theoretical maximum monolayer adsorption capacity, established based on the Langmuir isotherm (qm), decreases as the pH of the solution decreases (Inglezakis et al., 2002; Davila-Rangel and Solache-Rios, 2006; Taffarel, 2009).
Therefore, the decrease in pH between 4 and 1 induced a decrease in the maximum adsorption capacity from 0.3569 to 0.1604 mol.kg-1 (i.e. a 55.06% decrease). The maximum adsorption capacities calculated based on the D-R isotherm (Xm) are higher than those calculated using the Langmuir isotherm (qm), and as such cannot be used for the mathematical modelling of adsorption capacities. Other authors have observed differences of the same nature and magnitude between the 2 models (Gunay et al., 2007).
The importance of the D-R isotherm consists in the calculation of Es which offers information about the nature of the adsorption process. In the particular process researched, the value of the adsorption energy decreased from 9.72 to 7.62 kJ.mol-1 as the pH decreased from 4 to 1. The value indicates that, at low acidity (pH = 4), the adsorption mechanism is one of ionic exchange; while at high acidity (where the adsorption occurs slowly) the adsorption process is physical in nature, thus reducing the strength of the bond between metallic ions and the adsorbent substrate.
Modelling of thermodynamic data
The distribution coefficient, KD (ℓ.mol-1), was calculated as:

where:
Co and Ce (mol- ℓ-1) represent the initial and equilibrium concentrations, respectively
V/M (ℓ.kg-1) is the ratio of the volume of solution to the mass of adsorbent, namely, the batch factor
The distribution coefficient (KD) is a function of the initial concentration Co (or equilibrium concentration Ce)
The thermodynamic parameter, Gibbs free energy change AG° (kJmol-1) for the specific adsorption, was calculated as follows:

where:
KDo represents:
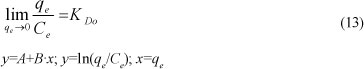
KDocan be obtained from the intercept of the plot of ln (qe/Ce) versus qe (as indicated in Table 6). The distribution coefficient (KDo) implicitly indicates the selectivity, capacity, and affinity of an ion for ion exchange (Inglezakis et al., 2004).

The interpretation of experimental results led us to conclude that the distribution coefficient (KD0) decreases as the pH decreases. This means the affinity and strength of the interaction between lead ions and zeolite decreases dramatically as the pH decreases.
The change of free energy (ΔG0) follows the same pattern. As the pH drops from 4 to 1, the change of free energy increases, suggesting the occurrence of a spontaneous adsorption process. The speed of this process is higher at lower acidity.
Modelling of sorption kinetics data
To examine the adsorption kinetics and mechanism, 5 kinetic models were applied: the pseudo-first and pseudo-second order (sorption kinetic models based on reaction order), the intra-particle diffusion Weber-Morris and models of diffusion through the particle surface (kinetic diffusion models used to check whether the sorption process occurs via an external or intra-particle diffusion mechanism), and the heterogeneous diffusion model (which assumes the variations of the diffusion rate through zeolite particles).
In each experiment, an aqueous solution with the same initial concentration of lead ions (namely 923.14 mg- ℓ-1) but different pH (variable between 1 and 4) was used.
Pseudo-first and pseudo-second order models are two of the most widely used models for the adsorption of a solute from aqueous solution.
The pseudo-first-order kinetic model is:

where:
qt (mol.kg-1) is the amount of metal ions adsorbed on the adsorbent at time t (min)
qe (mol.kg-1) is the amount adsorbed at equilibrium
k1 (min-1) is the rate constant of first-order adsorption
After integration between boundary conditions (t = 0 to t and qt = 0 to qe), the equation becomes:
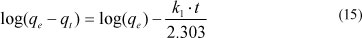
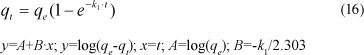
where:
qe and k1 can be determined from the intercept and slope of the plot, respectively.
The pseudo-second-order kinetic model is based on the sorption capacity of the solid phase and is expressed as:

where:
k2 (kg.mol-1.min-1) is the rate constant of second-order model.
For boundary conditions (t=0 to t and q, =0 to qe), this equation becomes:
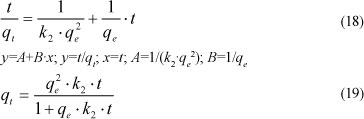
The plot of t/qt versus t should give a straight line if the pseudo second-order kinetic model is applicable, and qe and k2 can be determined from the slope and intercept of the plot, respectively.
Intra-particle diffusion Weber-Morris model
The intra-particle diffusion model can be formulated using the Morris-Weber equation. A linear relationship between the amount adsorbed (qt) and the square root of the time describes this model, which can be expressed as:
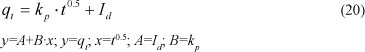
where:
kp is the initial rate of the intraparticle diffusion (mol.kg-1min-0.5)
Id is the constant (same units as qt)
The 2 parameters can be determined from the intercept of the plot of qt versus t0.5. The intercept (Id) is used to examine the relative significance of the 2 transport mechanisms of the solute, namely: intraparticle diffusion and external mass transfer (film or surface diffusion through the film surrounding a zeolite particle). If I = 0, the intraparticle diffusion is considered as the rate-limiting step, while, if I > 0, both the external mass transfer and intra-particle diffusion are considered as the rate-limiting steps. An increase of I translates to a higher resistance to ions of the layer of liquid surrounding the particle of zeolite.
The Weber-Morris model is of paramount importance as it enables the determination of the diffusion coefficient of ions inside the adsorbent material (Apiratikul and Pavasant, 2008).
By considering kp a constant it is possible to calculate the diffusion coefficient expressed as:

where:
De is the effective diffusion coefficient (m2.min-1) and d is the mean diameter of particles (m-1).
Diffusion through particle surface kinetic model
Diffusion through the surface of a particle can be expressed by the relation:

where:
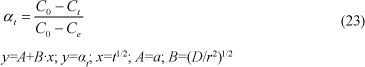
where:
Co, Ce and Ct are the initial, equilibrium and time concentrations
D is the diffusion coefficient (m2.min-1)
r is the mean diameter of the particles (m)
t is the time (min)
The slope of the linear part of the curves (D/r2)1/2 is proportional to the initial rate of sorption, and the intercept is proportional to the thickness of the boundary sorption layer. Using the slope (B) it is possible to calculate the diffusion coefficient through the external film surrounding the zeolite particle (r):

Heterogeneous diffusion model
At high values of pH of the solution, the formation of metal-complexe species can be possible (the main species being Me(OH)+). The mobility of ions in the external fluid, as well as in the internal channels, can be affected by these species, on the one hand, while an ion could be exchanged as a monovalent cation on the external or internal surface, on the other hand. The formation of these species could have an influence on the ion exchange process (Oren and Kaya, 2006; Inglezakis et al., 2007).
The heterogeneous diffusion model, which assumes variations of the diffusion rate through zeolite particles (internal chan-nels), is the most representative in the literature and is written as:

where:
αt=qt/qe is the fraction of metal ions bounded at time t,
p and C are dimensionless constants. The constants p and C were obtained from the slope and intercept of the plot of (αt) versus ln(t).
Comparison of adsorption kinetics
The adsorption of lead ions by Na-clinoptilolite increases with time and reaches equilibrium after 180 min (Fig. 2). The adsorption is faster during the first period of time and occurs more slowly afterwards. The pH of the contact solution has a negative impact on the adsorption capacity. When the solution pH decreases from 4 to 1, the experimental equilibrium adsorption capacity decreases from 0.3176 to 0.0866 mol.kg-1 (which means a decrease of 72.72%). This happens because during adsorption at lower pH values the hydrogen ions compete with the ions under investigation (Argun, 2008).

The predictive precision of the kinetic models, as a function of the relative errors, was found to be highest for the intra-particle Weber-Morris model, and decreases in the following order: heterogeneous diffusion > pseudo-second order kinetic model > diffusion through the particle surface > pseudo-first kinetic model (as indicated in Table 7). The average values of the normalised standard deviation for all the considered models in which the pH was modified were as follows: 5.53, 5.67, 10.47, 41.73, and 47.51%.
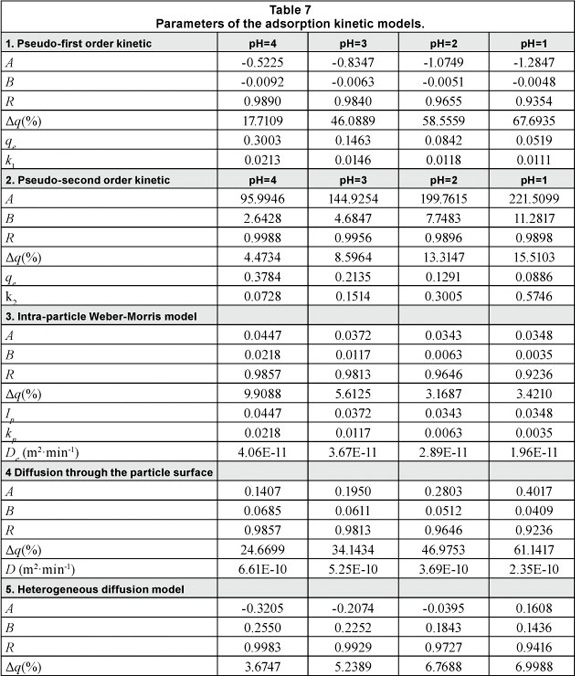
The pseudo-second order kinetic model described the experimental data better than the pseudo-first order model, which is in agreement with the conclusions of other authors (Sprynskyy et al., 2006). The calculated qe values using the pseudo-second order kinetic model are also close to the experimental data. Using the pseudo-first kinetic model, the equilibrium concentrations are smaller than the experimental data.
Regarding the intra-particle Weber-Morris diffusion model, the low values of Id had a relatively constant variation (the average of value was 0.0377 with a relative standard deviation of 12.72%), but with a decrease in pH from 4 to 1 the intra-particle diffusion coefficients (De) decrease between 4.0610-11 to 1.9610-11 m2min-1 (a 51.72% decrease). The diffusion coefficients from the external surface of particles (D) for the same pH range decrease from 6.6110-10 to 2.3510-10 m2min-1 (a 64.37% decrease). The film diffusion coefficient is 10 times higher than the intra-particle coefficient. This means that diffusion to the external surface cannot be the rate-limiting step in the adsorption mechanism; instead, diffusion through the internal porous structure is the rate-limiting step.
The order of magnitude for the calculated distribution coefficients is the same as the order of magnitude observed in other papers (Inglezakis et al., 2002, 2004). This suggests that 2 factors induce the reduction of the adsorption capacity as a function of the pH, namely: the mobility of hydrated lead ions decreases and hydrogen ions with a lower hydrated radius competitively adsorb the divalent hydrated ions of lead. At the same value of contact solution pH, the diffusion coefficient does not depend on the concentration of the adsorbent ions. This means that in acidic solutions an increase in the concentration of hydrogen ions affects the mobility of lead ions. In the internal porous structure of zeolite, the same phenomenon occurs.
The analysis of the normalised standard deviation revealed that the Weber-Morris diffusion model describes the experimental data better for decreasing values of pH of the contact solution. As pH decreases from 4 to 1, the relative standard deviation decreases from 9.91% to 3.42%.
An inverse variation between pH and standard deviation can be observed in the case of the heterogeneous diffusion model. The relative standard deviation increases from 3.67% to 6.99% as the pH decreases from 4 to 1.
The minimum values of relative standard deviation recorded at pH=1 for the intra-particle Weber-Morris diffusion model (3.42%) and at pH=4 for the heterogeneous diffusion model (3.67%) can be explained by considering the different hydro-chemical equilibrium species formed under different pH regimes of the contact solution.
Figure 3 presents the different species containing hydrated lead ions as a function of the pH of the contact solution for a solution with an initial concentration of 923.14 mg-ℓ-1. The spe-ciation diagram was obtained using Hydra and Medusa specia-tion modelling freeware versions.
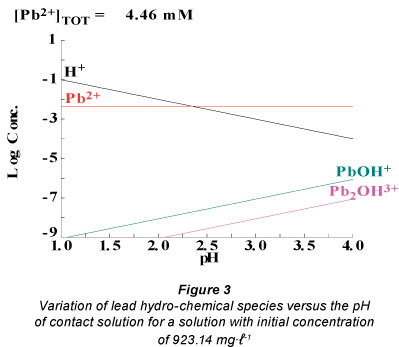
At different values of pH, different species containing hydrated lead ions are generated. The concentration of Pb(OH)+ depends on the pH of the solution. Thus, at pH = 4, the concentration of the complex is 10-6.02 M. At pH = 1, the concentration becomes 10-9 M.
The following equilibrium can be considered:

In low acidic media (pH = 4), the equilibrium presented in Reaction (26) shifts to the left and more highly charged metal complexes are formed as compared with those generated in high acidic media (pH=1). This behaviour is beneficial for adsorption. The hydrated radius of the lead complex ([Pb(H2O) x-1(OH)]+) is smaller than that of the hydrated radius of lead ion ([Pb(H2O)x]2+), meaning that the hydrated radius of the lead complex results in higher mobility than that of the hydrated lead ion. Moreover, the adsorption capacity of [Pb(H2O) x-1(OH)]+ is higher than that of [Pb(H2O)x]2+ because the adsorption capacity of monovalent ions is higher than that of the divalent ions.
Within the framework of the heterogeneous diffusion model, the fact that the normalised standard deviation decreases as the pH increases from 1 to 4 confirms these hypotheses. Because the concentration of the hydro-complexes in solution increases as the pH increases, they will behave in different ways depending on their volume, as follows:
- If the hydrated ionic radius of the hydro-complexes is small, the adsorption of monovalent ions is favoured (Stylianou et al., 2007); an example is the hydrated [Pb(OH)]+ complex
- A high hydrated ionic radius will affect the mobility of ions; this reduces the diffusion coefficient through the liquid film surrounding the zeolite particles or the internal micropores of the structure; the overall effect is a diminished adsorption capacity
- In some cases, given the inability of the ions to diffuse through the micropores of particles, there will be no adsorption at all.
Other researchers have also confirmed the existence of the equilibrium as in (26); the effects induced by this equilibrium suggest that either the adsorption process is not stoichiometric (Peric et al., 2004) or that the pH changes during the adsorption process (Trgo et al., 2006b).
By fitting experimental data to the kinetic and isothermic models, the correlation coefficients (r) of a number of representative parameters were calculated in order to validate the mechanism by which ions of lead are adsorbed by Na-clinoptilolite. Table 8 presents the values determined for the correlation coefficients obtained between parameters in the following models: Langmuir, Dubinin-Radushkevich, distribution coefficient, Weber-Morris, diffusion through the particle surface.
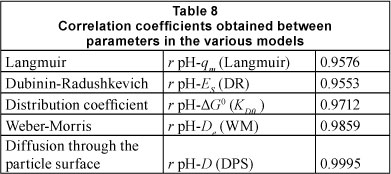
The best correlation seems to be between the pH of the contact solution and the diffusion coefficients (D and De), which substantiates the hypothesis that the diffusion process of hydrated lead ions through the pores of zeolite particles depends on the concentration of hydrogen. The variation of the Gibbs free energy (∆G°), the maximum adsorption capacity (qm) obtained from the Langmuir isotherm and the sorption energy (E) obtained from the D-R isotherm indicate a strong correlation with the pH. The values for the relative standard deviation (∆q%), as obtained by fitting the kinetic experimental data on the heterogeneous diffusion model reveal that the correlation coefficient is smallest at pH = 4.
Conclusion
Adsorption of lead onto Na-clinoptilolite has been found to be predominantly based on a monolayer mechanism in which the pH of the contact solution has an important influence on the way the hydrogen ions compete. The speed of diffusion of ions is higher on the external surface of the zeolite than in its internal structure. At high pH of the contact solution, adsorption occurs by ion exchange while at low pH, the process is physical. On the basis of free energy change, we can conclude that the process occurs spontaneously and is more pronounced at low acidity. The affinity between lead ions and zeolite (evaluated on the basis of the distribution coefficient) decreases with a decrease in pH. Diffusion through the internal structure of macro- and micropores plays an important role in the adsorption mechanism and is the slowest among all stages of the diffusion process. The intra-particle diffusion coefficient depends on pH which can modify the type and the concentration of the hydrated metal complexes in solution, thus affecting the adsorption process.
Acknowledgments
This research was undertaken within the ANCS, ZEMIP no. 82AS/2008 - Romania - South Africa bilateral project which is part of the Romanian National Plan of Interdisciplinary Research and Development Program PNCDI 2007-2013.
References
ALVAREZ A, GARCIA-SANCHEZ A and QUEROL X (2003) Purification of metal electroplating waste waters using zeolites. WaterRes. 37 4855-4862. [ Links ]
APIRATIKUL R and PAVASANT P (2008) Sorption of Cu2+, Cd2+, and Pb2+ using modified zeolite from coal fly ash. Chem. Eng. J. 144 245-258. [ Links ]
ARGUN M E (2008) Use of clinoptilolite for the removal of nickel ions from water: Kinetics and thermodynamics. J. Hazard. Mater. 150 587-595. [ Links ]
ATHANASIADIS K and HELMREICH B (2005) Influence of chemical conditioning on the ion exchange capacity and on kinetic of zinc uptake by clinoptilolite. WaterRes. 39 1527-1532. [ Links ]
CORUH S (2008) The removal of zinc ions by natural and conditioned clinoptilolites. Desalination 225 41-57. [ Links ]
DAVILA-RANGEL JI and SOLACHE-RIOS M (2006) Sorption of cobalt by two Mexican clinoptilolite rich tuffs zeolitic rocks and kaolinite. J. Radioanal. Nucl. Chem. 270 (2) 465-471. [ Links ]
DOULA M K (2006) Removal of Mn2+ ions from drinking water by using Clinoptilolite and a Clinoptilolite-Fe oxide system. Water Res. 40 3167-3176. [ Links ]
EL-KAMASH A, KAKI AA and EL-GELEEL MA (2005) Modeling batch kinetics and thermodynamics of zinc and cadmium ions removal from waste solutions using synthetic zeolite A. J. Hazard. Mater. B127 (2005) 211-220. [ Links ]
ERDEM E, KARAPINAR N and DONAT R (2004) The removal of heavy metal cations by natural zeolites. J. Colloid Interface Sci. 280 309-314. [ Links ]
FAGHIHIAN H, MARAGEH MG and KAZEMIAN H (1999) The use of clinoptilolite and its sodium form for removal of radioactive cesium, and strontium from nuclear wastewater and Pb2+, Ni2+, Cd2+, Ba2+ from municipal. Appl. Radiat. Isot. 50 655-660. [ Links ]
GARCIA-MENDIETA A, SOLACHE-RIOS M and OLGUIN MT (2009) Evaluation of the sorption properties of a Mexican clinop-tilolite-rich tuff for iron, manganese and iron-manganese systems. Microporous Mesoporous Mater. 118 489-495. [ Links ]
GORKA A, BOCHENEK R, WARCHOL J, KACZMARSKI K and ANTOSA D (2008) Ion exchange kinetics in removal of small ions. Effect of salt concentration on inter and intraparticle diffusion. Chem. Eng. Sci. 63 637-650. [ Links ]
GUNAY A, ERTAN A and TOSUN I (2007) Lead removal from aqueous solution by natural and pretreated clinoptilolite: Adsorption equilibrium and kinetics. J. Hazard. Mater. 146 362-371. [ Links ]
HERNANDEZ H R, DIAZ L and AGUILAR-ARMENTA G (1999) Adsorption equilibria and kinetics of CO2, CH4 and N2 in natural zeolites. Sep. Purif. Technol. 15 163-173. [ Links ]
INGLEZAKIS V J, LOIZIDOU MD and , GRIGOROPOULOU HP (2002) Equilibrium and kinetic ion exchange studies of Pb2+, Cr3+, Fe3+ and Cu2+ on natural clinoptilolite. Water Res. 36 2784-2792. [ Links ]
INGLEZAKIS V J, LOIZIDOU MD and GRIGOROPOULOU HP (2004) Ion exchange studies on natural and modified zeolites and the concept of exchange site accessibility. J. Colloid Interface Sci. 275 570-576. [ Links ]
INGLEZAKIS V J, STYLIANOU A, GKANTZOU D and LOIZIDOU MD (2007) Removal of Pb(II) from aqueous solutions by using clinoptilolite and bentonite as adsorbents. Desalination 210 248-256. [ Links ]
JAMIL T S, IBRAHIM HS, EL-MAKSOUD IHA and EL-WAKEEL ST (2010) Application of zeolite prepared from Egyptian kaolin for removal of heavy metals: I. Optimum conditions. Desalination 258 34-40. [ Links ]
KARADAG D, KOC Y, TURAN M and ARMAGAN B (2006) Removal of ammonium ion from aqueous solution using natural Turkish clinoptilolite. J. Hazard. Mater. B136 604-609. [ Links ]
LIU P, YAO Y, ZHANG X and WANG J (2011) Rare earth metals ion-exchanged β-zeolites as supports of platinum catalysts for hydroi-somerization of n-heptane. Catalysis kinetics and reactors. Chin. J. Chem. Eng. 19 (2) 278-284. [ Links ]
MATIS K A, ANASTASIOS I, ZOUBOULIS GALLIOS GP, ERWE T and BLOCHER C (2004) Application of flotation for the separation of metal-loaded zeolites. Chemosphere 55 65-72. [ Links ]
MIER M V, RAYMUNDO LC, GEHR R , CISNEROS BEJ and PEDRO JJA (2001) Heavy metal removal with Mexican clinoptilo-lite: multi-component ionic exchange. Water Res. 35 (2) 373-378. [ Links ]
MOTSI T, ROWSON NA and SIMMONS MJH (2009) Adsorption of heavy metals from acid mine drainage by natural zeolite. Int. J. Miner. Process. 92 42-48. [ Links ]
OREN H A and KAYA A (2006) Factors affecting adsorption characteristics of Zn2± on two natural zeolites. J. Hazard. Mater. B131 59-65. [ Links ]
PANAGIOTIS M (2011) Application of natural zeolites in environmental remediation: A short review. Microporous Mesoporous Mater. 144 15-18 [ Links ]
PERIC J, TRGO N and MEDVIDOVIC NV (2004) Removal of zinc, copper and lead by natural zeolite a comparison of adsorption isotherms. Water Res. 38 1893-1899. [ Links ]
PETRUS R and WARCHOL JK (2005) Heavy metal removal by clinoptilolite. An equilibrium study in multi-component systems. Water Res. 39 819-830. [ Links ]
RAHMAN A R, IBRAHIM HA, HANAFI M and MOMEN NM (2010) Assessment of synthetic zeolite Na A-X as sorbing barrier for strontium in a radioactive disposal facility. Chem. Eng. J. 157 100-112. [ Links ]
SEQUEIRA-TEUTLI A, RIOS R and OLGUIN MT (2009) Influence of Na+, Ca2+, Mg2+ and NH4+ on the sorption behavior of Cd2+ from aqueous solutions by a Mexican zeolitic material. Hydrometallurgy 97 46-52. [ Links ]
SMICIKLAS I, DIMOVIC S and PLECAS I (2007) Removal of Cs1+, Sr2+ and Co2+ from aqueous solutions by adsorption on natural clinoptilolite. Appl. Clay Sci. 35 139-144. [ Links ]
SPRYNSKYY M, LEBEDYNETS M, TERZYK AP, KOWALCZYK P, NAMIESNIK J and BUSZEWSKI B (2005) Ammonium sorp-tion from aqueous solutions by the natural zeolite Transcarpathian clinoptilolite studied under dynamic conditions. J. Colloid Interface Sci. 284 408-415. [ Links ]
SPRYNSKYY M, BUSZEWSKI B, TERZYK AP and NAMIESNIK J (2006) Study of the selection mechanism of heavy metal (Pb2+, Cu2+, Ni2+, and Cd2+) adsorption on clinoptilolite. J. Colloid Interface Sci. 304 21-28. [ Links ]
STYLIANOU M A, HADJICONSTANTINOU MP, INGLEZAKIS VJ, MOUSTAKAS KG and LOIZIDOU MD (2007) Use of natural clinoptilolite for the removal of lead, copper and zinc in fixed bed column. J. Hazard. Mater. 143 575-581. [ Links ]
TAFFAREL R and RUBIO J (2009) On the removal of Mn2+ ions by adsorption onto natural and activated Chilean zeolites. Miner. Eng. 22 336-343. [ Links ]
TRGO M, PERIK J and MEDVIDOVIC NV (2006a) A comparative study of ion exchange kinetics in zinc/lead-modified zeolite-clinoptilolite systems. J. Hazard. Mater. B136 938-945. [ Links ]
TRGO M, PERIK J and MEDVIDOVIC NV (2006b) Investigations of different kinetic models for zinc ions uptake by a natural zeolitic tuff. J. Environ. Manage. 79 298-304. [ Links ]
WANG S and PENG Y (2010) Natural zeolites as effective adsorbents in water and wastewater treatment. Chem. Eng. J. 156 11-24. [ Links ]
WANG X S, HUANG J, HU HQ, WANG J and QIN Y (2007) Determination of kinetic and equilibrium parameters of the batch adsorption of Ni(II) from aqueous solutions by Na-mordenite. J. Hazard. Mater. 142 468-476. [ Links ]
ZAMBOULIS D, PATAROUDI SI, ZOUBOULIS KA and MATIS A (2004) The application of sorptive flotation for removal of metal ions. Desalination 162 159-168. [ Links ]
Received 28 September 2011;
Accepted in revised form 2 April 2012.
* To whom all correspondence should be addressed. +40 742588575; fax: +40 0262276153 E-mail: mihalyl@yahoo.com














