Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Water SA
On-line version ISSN 1816-7950
Print version ISSN 0378-4738
Water SA vol.38 n.1 Pretoria Jan. 2012
TECHNICAL NOTE
On modifying the Arrhenius equation to compensate for temperature changes for reactions within biological systems
Craig SheridanI,*; Jochen PetersenII; Johann RohwerIII
ISchool of Chemical and Metallurgical Engineering, University of the Witwatersrand, Private Bag 3, Wits, 2050, South Africa
IICentre for Bioprocess Engineering Research (CeBER), Department for Chemical Engineering, University of Cape Town, Private Bag X6, Rondebosch 7701, South Africa
IIITriple-J Group for Molecular Cell Physiology, Department of Biochemistry, Stellenbosch University, Private Bag X1, Matieland 7602, South Africa
ABSTRACT
In this communiqué, we discuss the use of the Arrhenius relationship to describe the temperature dependence of reacting biological systems, such as those treating wastewater. We also discuss the use of the modified Arrhenius function, and those instances where its applicability is limited. We show that the error when using the modified relationship is 7% at 30ºC, 15% at 40ºC and 25% at 50ºC. We conclude that whilst the modified relationship is acceptable at lower temperatures, in those applications where higher temperatures are reached (above 25ºC) the error with using the relationship may not be acceptable. We present an Arrhenius equation for use in biological systems, which is applicable for all temperature ranges.
Keywords: kinetics, biological processes, Arrhenius equation
Introduction
The kinetics of a process are related to temperature through the Arrhenius relationship (Fogler, 2005). For a given catalytic or microbial system, with given chemical components, this relationship is shown in Eq. (1) with the temperature given in Kelvin:

where:
k(T) is the rate constant as a function of temperature
A is the pre-exponential factor
E is the activation energy in J/mol
R is the gas constant = 8.314 J/(mol·K)
T is the absolute temperature in K
This relationship is sometimes given in the differential form, as shown in Eq. (2):

The kinetics of the degradation processes occurring within many reacting biological systems, including municipal wastewater treatment (Benefield and Randall, 1980; Crites and Tchobanoglous, 1998; Nitisoravut and Klomjek, 2005), anaerobic lagoons (Oleszkiewicz and Koziarski, 1986), facultative lagoons (Mashauri and Kayombo, 2002) and constructed wetlands (Nitisoravut and Klomjek. 2005; Mashauri and Kayombo, 2002; Andreottola et al., 2007; Kadlec, 2009; Marsili-Libelli and Checchi, 2005; Rodgers and Dunn, 1995; Rousseau et al., 2004) are described using a modified form of this equation (denoted the Modified Arrhenius Function or MAF) given in Eq. (3), with temperature, T, given in degrees Celcius (Benefield and Randall, 1980; Haug, 1993; Kadlec and Knight, 1996; Kadlec et al., 2000).

The MAF is attractive as an experimental equation because of its ease of use; the temperature is given in degrees Celcius and the temperature correction factor, θ, is measurable. The derivation of this form of the Arrhenius Equation is based on the assumption that the operating temperature is close to or below 20ºC (Derivation Box 1). In countries with hot climates such as South Africa, and especially those with high humidity, where the effect of evaporative cooling is reduced, the MAF may not be applicable and could result in water treatment and other biological systems that do not perform to design specifications. For the temperature ranges where this assumption may not hold true, a new form of the Arrhenius Equation is proposed here that will not differ significantly from the current form of the MAF at lower temperatures, yet will follow the exponential form of the Arrhenius equation at higher temperatures.

The primary assumption to be considered when using the MAF is that the temperature is not much greater than 20ºC. This assumption allows the conversion of an exponential function into a power function, which has different mathematical properties, which are more pronounced with increasing temperature.
Methods and results of the investigation of the non-applicable temperature range of the MAF
To assess applicable and non-applicable temperature ranges for the MAF, we have used θ values related to the design of constructed wetlands. For this assessment θ has been assigned a value of 1.06 as recommended by the IWA Specialist Group on the Use of Macrophytes in Water Pollution Control (Kadlec et al., 2000) and the value of k20 is taken as 1.104/day as specified by the US EPA (US EPA, 2000), since the IWA does not recommend one single value. Using these parameters the rate constant can be calculated for a range of temperatures. If the log of Eq. (1) is taken, the following relation can be obtained:
(7)
where:
ln(A) is replaced by α and 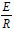 substituted by β
substituted by β
The value for k was calculated for the temperature range over which the data were most likely collected; i.e., 0ºC to 20ºC (273K to 293 K) using the MAF, and a plot of ln(k) vs. 1/T is shown in Fig. 1. The points are essentially reproduced data, and these 'data'; have been regressed (the line through the points) to determine the constants in Eq. (7).
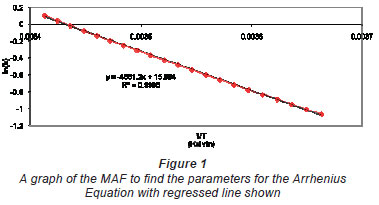
The y-intercept and the x-intercept of this plot correspond to α and β in Eq. (7). The twisting of the data around the regressed line is caused by the conversion of data found from a power function being presented as an exponential function.
These calculated values for α and β were then used to fit the Arrhenius function given by Eq. (1), such that A = 8.83·106 and 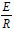 = 4600. Using these 'data';, a comparison of the Arrhenius equation and the MAF was performed and the results are presented in Fig. 2.
= 4600. Using these 'data';, a comparison of the Arrhenius equation and the MAF was performed and the results are presented in Fig. 2.
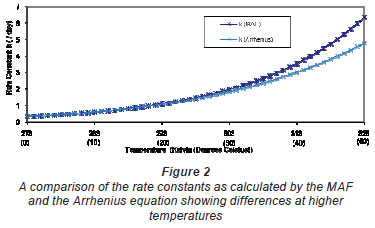
This analysis indicates that the difference between the 2 forms of rate constant is 7% at 30ºC, 15% at 40ºC and 25% at 50ºC. This difference would become greater at higher temperatures since the exponential law reaches an asymptote at the value for A at infinite temperature, whilst the MAF increases infinitely with increasing temperature. The analysis was halted at 50ºC since there are few reacting biological process that will operate temperatures higher than this (although some bio-metallurgical operations may occur at temperatures higher than 60ºC).
Discussion of the modified Arrhenius equation
In hot climes and for certain industries (such as distillery effluents) it is possible that the effluent temperature may rise above 30ºC and thus the assumptions upon which the MAF is based may not be valid. It is with this in mind that a new functional dependence of k on temperature, given by Eq. (8), is proposed (Derivation Box 2). In this derivation, the values of k20 as measured for the MAF will still be valid (shown as k(293)). It is, however, a simple modification to change the temperature to ºC.

Conclusion
Whilst the MAF is used substantially for the wastewater and other industries (Benefield and Randall, 1980; Haug, 1993; Kadlec et al., 2000), and is undoubtedly applicable to cooler and temperate climates, it should be used with caution at higher ambient or reaction temperatures since it may lead to the use of a rate constant which is greater than that which is occurring. At temperatures lower than 20ºC it is not important which equation is used, because the rate constants are small and the difference between the 2 functions is negligible. In countries with hot climates, and especially those with high humidity, where the effect of evaporative cooling is reduced, the MAF may not be applicable and could result in systems that do not perform to design specifications. The MAF may also overestimate the rate constant required for designing systems to treat warm effluents, such as distilleries or for use in hot biological reacting systems such as composting or heap leaching. It should also be relatively easy to reassess existing literature to calculate the values for A and β and these could be used, with the published values for k20 to find the rate constant at any temperature.
References
ANDREOTTOLA G, OLIVEIRA E, FOLADORI P and ZIGLIO R (2007) Respirometric techniques for assessment of biological kinetics in constructed wetlands. Water Sci. Technol. 56 (3) 255-261. [ Links ]
BENEFIELD LD and RANDALL CW ( 1980) Biological Design forWastewater Treatment. Prentice Hall, Engelwood Cliffs. [ Links ]
CRITES R and TCHOBANOGLOUS G ( 1998) Small and Decentralised Wastewater Management Systems. WCB McGraw Hill, Singapore. [ Links ]
FOGLER HS ( 2005) Elements of Chemical Reaction Engineering. Prentice Hall, USA. [ Links ]
HAUG RT ( 1993) The Practical Handbook of Compost Engineering. CRC Press, Boca Raton. [ Links ]
KADLEC RH (2009) Comparison of free water and horizontal subsurface treatment wetlands. Ecol. Eng. 35 159-174. [ Links ]
KADLEC RH and KNIGHT RL ( 1996) Treatment Wetlands. CRC Press, Boca Raton. [ Links ]
KADLEC RH, KNIGHT RL, VYMAZAL J, BRIX H, COOPER P and HABERL R (2000) Constructed Wetlands for Pollution Control.Processes, Performance, Design and Operation. IWA Specialist Group on the Use of Macrophytes in Water Pollution Control. IWA Scientific and Technical Report No 8, IWA Publishing, London. [ Links ]
MARSILI-LIBELLI S and CHECCHI N (2005) Identification of dynamic models for horizontal subsurface constructed wetlands. Ecol. Model. 187 201-218. [ Links ]
MASHAURI DA and KAYOMBO S (2002) Application of the two coupled models for water quality management: facultative pond cum constructed wetland models. Phys. Chem. Earth 27 773-781. [ Links ]
NITISORAVUT S and KLOMJEK P (2005) Inhibition kinetics of salt-affected wetland for municipal wastewater treatment. Water Res. 39 4413-4419. [ Links ]
OLESZKIEWICZ JA and KOZIARSKI S (1986) Kinetics of piggery wastes treatment in anaerobic lagoons. Agric. Wastes 16 13-25. [ Links ]
RODGERS JH and DUNN A (1995) Developing design guidelines for constructed wetlands to remove pesticides from agricultural runoff. Ecol. Eng. 1 83-95. [ Links ]
ROUSSEAU DPL, VANROLLEGHEM PA and DE PAUW N (2004) Model-based design of horizontal subsurface flow constructed treatment wetlands: a review. Water Res. 38 1484-1493. [ Links ]
US EPA (2000) Constructed Wetlands Treatment of Municipal Wastewaters. EPA/625/R-99/010. United States Environmental Protection Agency. [ Links ]
Received 28 February 2011; accepted in revised form 14 December 2011.
* To whom all correspondence should be addressed. +27 11 717-7592; fax: +27 86 211-8303; e-mail: craig.sheridan@wits.ac.za














