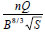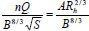Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Water SA
On-line version ISSN 1816-7950
Print version ISSN 0378-4738
Water SA vol.38 n.1 Pretoria Jan. 2012
TECHNICAL NOTE
Effects of free-surface on design charts for open channels
Majid Rahimpour*
Department of Water Engineering, Shahid Bahonar University of Kerman, Iran
ABSTRACT
Normal depth is an important parameter for the design of channels and canals. For rectangular, trapezoidal, and circular channel sections it is possible to express normal depth by a trial-and-error procedure or analytically. However, the effects of free-surface on the design charts for determination of the normal depth are not investigated. In this paper, graphical solutions of normal depth for the rectangular, trapezoidal, and circular cross-sections have been obtained in the non-dimensional form. To evaluate the resistance effects of the free-surface in the calculation of the normal depth, the dimensionless-form of Manning';s equation with free-surface weight factor is introduced herein. The design charts reported previously were modified.
Keywords: Open-channel flow; normal depth; free-surface effect
Introduction
In the design of channels, one is required to determine the normal depth. The calculation of normal depth is essential to the analysis of open-channel flows and is required even for non-uniform flows. The uniform flow in a channel is frequently determined by the use of a resistance equation such as the Manning';s equation:

where:
Q is the flow discharge
A is the flow area
R is the conventional hydraulic radius defined as R=A/P P is the wetted perimeter
S is the channel slope
n is the Manning';s roughness coefficient
Unfortunately Eq. (1) is implicit in the normal depth for the majority of cross-sections. To determine the normal depth, one has to apply time-consuming trial-and-error methods. Graphs and tables have been provided for some of the simpler cross-sections (e.g., rectangular, trapezoidal, triangular, and circular sections) by Chow (1958), Henderson (1966), and French (1986), among others. Swamee (1994) presented explicit equations for normal depth in rectangular, trapezoidal, triangular, and circular sections. Shirley and Lopes (1991) have reported an iterative procedure for quickly and accurately solving the implicit problem of determining the normal flow depth in complex channel sections. Babaeyan-Koopaei (2001) reported graphical solutions for normal depth in round-bottomed triangular, parabolic, and round-corner rectangular cross sections.
From the above literature search, it appears that a free-surface effect on the normal depth has not received any treatment yet. This research aims to present graphical solutions for the effects of free-surface on the design charts for determination of the normal depth.
Dimensionless-form of equation
Rectangular sections
Equation (1) is implicit and one has to resort to trial-and-error methods for the calculation of normal depth. In the following, graphical solutions are presented for the calculation of the normal depth with free-surface effects. In order to simplify the computation of the normal depth, with substitution of the new hydraulic radius (Rh) instead of conventional hydraulic radius (R) , the dimensionless form of the Manning';s equation, (Eq. 1), is suitable for the graphical solution:
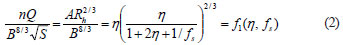
where:
η=y/B is the dimensionless depth
B is the bottom width
y is the flow depth
ƒs is the free-surface weight factor by which the free-surface is evaluated as a kind of weak wall
Generally, this parameter must be determined by experiment. If fs = 1, the free-surface is equivalent to the wall. If ƒs tends to ∞, there is no wall in the position of the free surface, and the third term in the denominator of Eq. (2) becomes zero and Rh tends to conventional hydraulic radius.
A family of dimensionless curves showing the relation between η and ƒ1( η, ƒs ) has been prepared in Fig. 1 for the rectangular cross-section with ƒs = 1, 2, 3, 4, 5,10, 20, 100 and ∞. To calculate normal depth using Fig. 1, one should take the following steps:
• Step 1: Knowing discharge Q, roughness coefficient n, bottom width B, and channel slope S, calculate
• Step 2: From Eq. (2) we know
• Step 3: Using Fig. 1, with
and fs , one can find
and, hence, normal depth yn
Circular sections
To incorporate the resistance effects of the free-surface into the calculation of the normal depth, in a circular cross section with diameter, D, and flow depth, y, the dimensionless form of the Manning';s equation suitable for graphical solution is:
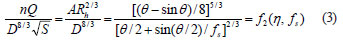
where:
θ = 2 cos-1(1-2 η)
η=y/D is the dimensionless depth
A family of dimensionless curves for circular cross-sections showing the relation between η and ƒ2(η, ƒs) is shown in Fig.1 for ƒs = 1, 2, 3, 4, 5, 10, 20, 100 and ∞. Using Eq. (3) and Fig. 1, one can find yn /D and, hence, normal depth yn. For high accuracy Fig. 1 is divided into 4 parts (Figs. 1b-e).
Trapezoidal sections
For carrying large discharges, rectangular sections are not preferred. This is on account of stability of the side slopes. Vertical side walls are required to be of a large thickness in order to resist the pressure of the earth. On the other hand, sloping side walls need less thickness. Thus, for trapezoidal channel sections, the dimensionless form of the Manning';s equation suitable for graphical solution is:
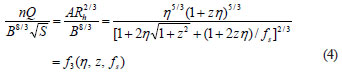
where:
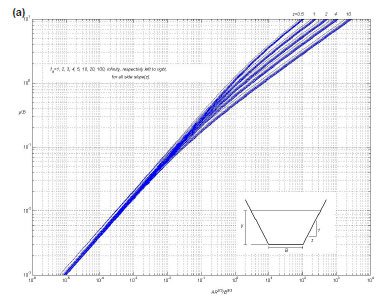
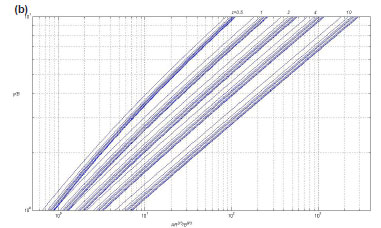
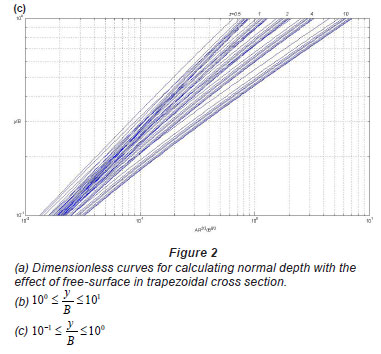
z is the side slope (zH:1V. A family of dimensionless curves shown in Fig. 2 for a trapezoidal cross-section with z = 0.5, 1, 2, 4 and 10 using the relation between η and ƒ3( η, z, ƒs) for ƒs = 1, 2, 3, 4, 5, 10, 20, 100 and ∞.
Using Eq. (4) and Fig. 2, one can find yn/B and, hence, normal depth yn. For high accuracy Fig. 2 is divided into 2 parts (Figs. 2b, c).
Example 1: Given a trapezoidal channel with a bottom width of 5 m, side slopes of 1:1, a longitudinal slope of 0.00035, and a resistance coefficient of n = 0.015, find the normal depth of flow for a discharge of 20 m3/s.
Solution: For the given data, the value of the section factor is:
With regard to Eq. (4),
By using Fig. 2, with z = 1, and ƒs = ∞ (free-surface not affecting the normal depth) the dimensionless depth (y/B) is 0.3898, thus the normal depth (yn) is 1.949 m.
Solutions of this example with effects of free-surface on the normal depth for various ƒs is 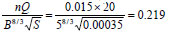 given in Table 1.
given in Table 1.
With regard to Eq.(4)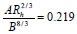
Limitation of the chart method
Figure 1(a) and Figure 2(a) have low accuracy but Figs. 1(b-e) and Figs. 2(b-c) have high accuracy. With the aid of a computer program, one can determine the normal depth using Eqs. (2), (3) and (4) for rectangular, circular and trapezoidal cross-sections, respectively, for effect of free surface on the normal depth.
Results and discussion
To allow a quantitative analysis, the difference between curves in Figs. 1 and 2 for different values of free-surface weight factor, the non-dimensional section factor (ξ) is defined as:
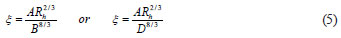
The percentage of difference in the between non-dimensional curves can be defined as:

Using Eqs. (6) and (7), the dimensionless depth vs. non-dimensional section factor for different values of ƒs is shown in Fig. 3 in rectangular and trapezoidal cross-sections. In Fig. 3, the effects of free-surface take lower values for larger y/B, for all values of ƒs. If ƒs = 1, the free-surface is equivalent to the wall (flow in duct). If ƒs tends to ∞, the effects of free-surface take lower values. In Fig. 3, it can be seen that the effects of free-surface do not provide a meaningful change for y/B < 0.01 in constant ƒs. In Fig. 4, the relative errors are indicated and the relative errors that were computed in Example 1 can be seen within this figure. In this figure, if ƒs is constant, it can be seen that the effects of free-surface on the normal depth take higher values for great values of side slopes. In these figures, the side slope is z = 0, 0.5, 1, 2, 4 and 10 for all values of free-surface weight factor.

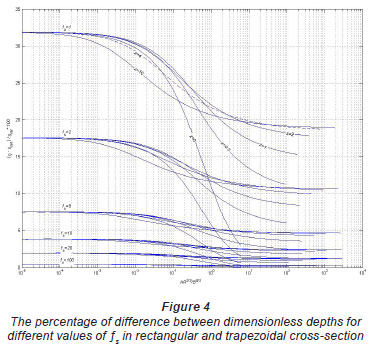
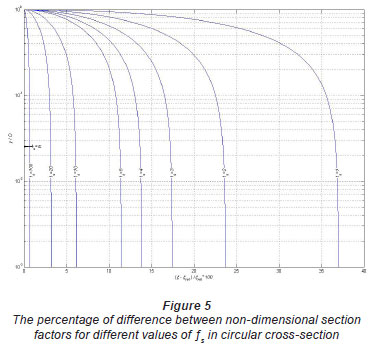
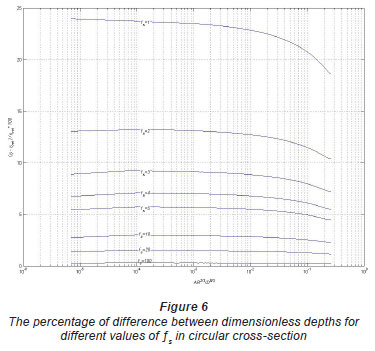
The same analysis described for the rectangular and trapezoidal cross-sections was also performed for the circular cross-section obtaining similar results, but with diameter of circle (D) instead of B. The behaviour of the curves shown in Fig. 5 and Fig. 6 is similar to that described in Figs. 3 and 4. Figure 5 shows that for all ƒs in y/D = 1 free surface does not affect the normal depth.
Summary and conclusions
The effects of free-surface on the design charts for determination of the normal depth are presented. A graphical solution of normal depth is proposed here that was used to calculate a design chart with the effect of free-surface for open channel flow. Figures 1 and 2 can be used to calculate normal depth in rectangular, circular, and trapezoidal cross-sections with the effect of free surface.
References
BABAEYAN-KOOPAEI K (2001) Dimensionless curves for normal-depth calculations in canal sections. J. Irrig. Drain. Eng. ASCE 127 (6) 386-389. [ Links ]
CHOW VT (1958) Open Channel Hydraulics. McGraw-Hill, New York. [ Links ]
FRENCH RH (1986) Open Channel Hydraulics. McGraw-Hill, New York. [ Links ]
HENDERSON FM (1966) Open Channel Flow. Macmillan, New York. [ Links ]
SHIRLEY ED and LOPES VL (1991) Normal-depth calculations in complex channel sections. J. Irrig. Drain. Eng. ASCE 117 (2) 220-232. [ Links ]
SWAMEE PK (1994) Normal-depth equation for irrigation canals. J. Irrig. Drain. Eng. ASCE 120 (5) 942-948. [ Links ]
Received 19 April 2011; accepted in revised form 14 December 2011.
* To whom all correspondence should be addressed.+98 913 199 0614; fax: +98 341 322 2043; e-mail: rahimpour@mail.uk.ac.ir