A simplified method to calculate the percentage of fresh effluents (PFE) in non-steady state reactors

 

 

Simona Consoli^I,*; Giuseppe Luigi Cirelli^I; Marcelo Juanicó^II

^IDepartment of Agro-Food and Environmental System Management, Faculty of Agriculture, University of Catania, Via S. Sofia, 100 -95123 Catania, Italy
^IIJuanicó-Environmental Consultants Ltd., Ram On 19205, Israel

 

 

---

ABSTRACT

Storage reservoirs are a key element in wastewater treatment trains for agricultural reuse; however, there is a need for further research on design criteria and operation rules for such reactors. The percentage of fresh effluents (PFE) is an important parameter for the design of perfectly-mixed reactors. PFE correlates better than mean residence time with the performance of the reactor. It allows for estimation of the removal of pollutants in non steady-state systems, such as seasonal wastewater storage reservoirs, and for forecasting the quality of the effluents released for irrigation. However, calculation of PFE is a difficult process requiring complex computer algorithms. A simplified analytical approach is developed to calculate the PFE for n days. The formulation is discussed, describing the relationships between the hydraulic variables, and then applied to a non-steady-state continuous-flow wastewater reservoir in Eastern Sicily (Italy).

Keywords: hydraulic age distribution, perfectly-mixed reactor, mean residence time, wastewater storage reservoirs

---

 

 

Introduction

Wastewater storage reservoirs are becoming common facilities in many wastewater reuse projects for agricultural purposes (Angelakis et al., 1999; Brissaud, 2002; Xu et al., 2002; Cirelli et al., 2009). The effectiveness of storage in terms of a change in water quality mainly depends on the characteristics of stored wastewater, climatic conditions and ecosystem characteristics (nutrient concentration, microorganism and algal population, etc.), as well as on reservoir design features and operational modalities (continuous flow versus batch storage) (Juanicó and Shelef 1991, 1994; Juanicó and Dor, 1999, Barbagallo et al., 2003a; Mancini and Vagliasindi, 2006; Cirelli et al., 2008). However, limited information on design criteria and operational procedures for such reactors is available, and the optimisation of reservoir design and operation requires a better understanding of the processes that affect the removal of selected contaminants in wastewater (Barbagallo et al., 2003b; Cirelli et al., 2009).

The observations on reservoir behaviour were initially focused on the effects of seasonal and intra-seasonal parameters (temperature, solar radiation, etc.) over wastewater quality changes (Funderburg et al., 1978; Weissman and Kott, 1979; Pearson et al., 1987). Several studies (Juanicó and Friedler, 1994; Juanicó and Shelef, 1994; Barbagallo et al., 2003a), carried out mainly for perfectly mixed reactors, addressed the importance of operational modalities, i.e., fluctuations in wastewater depth, inlet and outlet flow rate, volume/area relationship, etc. The use of wastewater storage reservoirs to regulate and transfer winter wastewater volume, satisfy agricultural water needs and improve the bacteriological quality of the effluent, requires the selection of appropriate procedures to combine the need for continuous wastewater disposal with the natural removal process dynamics (Friedler et al., 2003; Barbagallo et al., 2003b; Mancini and Vagliasindi, 2006; Cirelli et al., 2009).

Generally, completely mixed (unstratified) sewage treatment reactors (i.e. aerated lagoons, activated sludge, waste stabilisation ponds with long residence time, etc.) are assumed to be steady-state flow systems with constant flow rate, volume and mean hydraulic residence time, and the dynamics of water quality changes in these reactors are, generally, modelled using first-order kinetics by the Marais approach (Marais, 1974). These reactors do not actually fulfil the ideal steady-state flow assumption, because of differences in flow rate between day and night, weekdays and weekends, summer and winter, etc.

Juanicó and Friedler (1994) developed a mathematical tool to analyse the hydraulic age distribution (days of storage) in completely mixed reactors and demonstrated that the performance of these reactors is not determined by the whole volume of effluents within the reactor but by a small fraction of fresh effluents within it. These authors calculated this small fraction and called it PFE - percentage of fresh effluents. They concluded that the mean residence time (MRT) of the whole effluent can be used for the design of steady-state reactors because MRT and PFE have an absolute correlation under ideal steady-state conditions. As evidenced by several authors, the analysis of PFE may contribute to change the design geometry of the storage, affect the withdrawal point of the effluent for reuse, and affect the timing of effluent withdrawal for irrigation, which is mainly dictated by the type of crop (Juanicó and Friedler, 1994; Barbagallo et al., 2003a; Mancini and Vagliasindi, 2006).

Juanicó and Shelef (1994) developed an equation to calculate PFE2 (the percentage of fresh effluents having spent up to 2 days within the reactor). They then used a FORTRAN algorithm to calculate PFE for more days, in order to avoid timeconsuming iterations due to the high number of variables (i.e. inflow entering the reservoir, storage wastewater volume, outflow, etc.) to consider. The PFE is a measurement of the amount of fresh effluent within the reactor, where 'fresh' is defined in time units. i.e., PFE5 is the percentage of fresh effluents having spent 5 or less days (or hours, or minutes) within the reactor. In non-steady-state flow reactors, such as wastewater storage reservoirs, PFE is not constant, varying according to the change in inflow rate and reservoir volume. This variability deeply affects the performance of the reservoirs in terms of wastewater pollutant removal (Juanicó and Shelef, 1994; Barbagallo et al., 2003a; Mancini and Vagliasindi, 2006). In fact, in their publication, Cirelli et al. (2009) developed a new operational parameter, 'MRT%FE', which measures the mean residence time (MRT) of the freshest effluent percentage in a wastewater storage reservoir characterised by non-steady state flow conditions. The use of MRT%FE has provided evidence that E.coli removal is strongly influenced by the freshest 50% of effluent, with a MRT50%FE of about 8 days, and not by the whole stored volume (MRT=25 days).

In the present paper, a new simplified approach is proposed with the aim of simplifying the calculation of PFE proposed by Juanicó and Shelef in 1994. The application of this simplified formulation to a non-steady-state wastewater storage reservoir in Eastern Sicily (Italy) is also described. PFE values were related to microbiological concentrations of treated wastewater using regression analyses.

 

Calculation of PFE

To evaluate the percentages of fresh effluents that have been in a reactor for n time intervals or less, Juanicó and Shelef (1994) proposed the following formulation for PFEn on a generic day d:

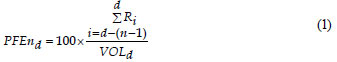
were

were:

R_i is the amount of inflow (m³) entering the reservoir on Day i and that still remains in the reservoir on Day d; VOLd is the stored wastewater volume (m³) on Day d; d-(n-1)> 0; IN_i is the amount of inflow (m³) entering the reservoir on Day i;

LIN_(i)j is the amount of inflow (m³) (entering on Day i) lost through outflow OUT_j on Day j;

n is the time interval of fresh effluents within the reactor.

For example, for n=2 Eq. (1) can be written as:

were

is the amount of inflow lost through outflow (OUT_d-1) on Day d-1;

is the amount of inflow lost through outflow (OUT_d-1) on Day d.

is the equation for 1-day old effluents PFE1_d-

The calculation of PFEn_d (Eq. (1)) is an extension of Eq. (4); it is much more complicated and therefore a FORTRAN algorithm has been proposed to calculate it (Juanicó and Friedler, 1994).

In the study herein presented, a simplified formulation was derived from the original calculation for PFEn_d:

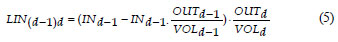
where:

is the amount of inflow N_i lost through outflow on Day i

Thus, Eq. (5) can be written as:

Equation (7) for PFE2_d can be written as:

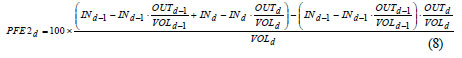
In the simplified formulation, the term (total amount of inflow lost through outflow) is neglected, with the exception of the loss related to the outflow during Day d.

The application of both general equations, Eqs. (1) and (5), to calculate the PFEn (n=1, 2, 5, 10, 20, 30) of a random data set characterising a continuous inflow/outflow reservoir operation led to an error ranging between 0 and 4%, with an average value of about 3%, increasing with an increase in n (Fig. 1).

 

 

Case-study

To evaluate the performance of the simplified approach (Eq. (5)), it was applied and compared to the original method (expressed by Eq. (1)) to calculate the PFEn (n= 1, 2, 3, 5) in a wastewater storage reservoir operating in Caltagirone, a municipality of about 35 000 PE in Eastern Sicily (Italy).

The wastewater treatment plant (WWTP) of the municipality consists of an activated sludge system. During the year 2000, an unlined earth reservoir (maximum capacity of 25 000 m³ and maximum depth of 5 m) was fed by the WWTP. The inflow/outflow system operations were discontinuous, with a daily input varying between 0 and 20 ℓ·s^-1, and a daily outflow rate between 0 and 5 ℓ·s^-1, apart from evaporation losses (mean daily value around 0.11 m). Reservoir operation started in late February 2000 and was concluded by late October of the same year (Fig. 2). Discontinuous discharges from the reservoir depend on the irrigation demand of citrus orchards (the main crop within the agricultural context under study), which is mostly concentrated during the May to September period. The study area is characterised by a semi-arid climate, with total rainfall during the monitoring period amounting to 380 mm, which contributed 1 900 m³ of water to the reservoir.

 

 

Water samples were collected within the reactor at intervals of 7 and 14 days at 3 selected sampling locations: near the reservoir embankment (about 10 m from the inlet) at a depth varying between 0.6 and 1.5 m; 0.2 m below the water surface; and 0.5 m above the bottom of the reservoir. Samples were analysed according to Standard Methods (APHA, 1999): SS (180ºC), BOD5, COD, total phosphorus, nitrogen, total coliforms (TC), faecal coliforms (FC), E.coli, faecal streptococci, Salmonella and helminth eggs (Barbagallo et al., 2003b). During the monitoring period, FC contents measured at the surface, bottom and near the embankment varied in the same manner with a few exceptions (Fig. 3). Differences between concomitant values were relatively low; thus FC content of the stored water can be represented by the mean of the 3 measured values. In general, during the entire study period a reduction in the concentration of microorganisms of about 2 to 3 orders of magnitude was observed after a few days of storage, with a further decrease of about 5 orders of magnitude after about 30 to 40 days of detection. This high removal efficiency was most likely due to the improvement in climatic conditions (increase in solar radiation and air temperature).

 

 

The maximum number of Salmonella detected in the influent was 1 100 MPN-100 mℓ^-1; the absence of Salmonella in the stored wastewater confirms the great efficiency of storage in removing pathogens.

During the monitoring period a prevailing south-west wind (mean speed of about 1.2 m·s^-1) allowed a fairly good circulation of wastewater within the reservoir, avoiding hydraulic shortcuts. However, the hydrodynamic behaviour of the reservoir was affected by changes in the operation procedure (inflow and outflow) and the climate (mainly temperature and solar radiation) (Barbagallo et al., 2003b). Behaviour changes were also evaluated by differences in temperature, EC, DO and pH profiles (Barbagallo et al., 2003b). However, owing to the relatively long period of observation for this reservoir, it was not feasible to attempt to relate FC content to operational and climatic conditions.

The experiment confirms that treated wastewater storage with continuous inflow represents a valuable option for FC removal. Inlet water had a mean concentration of 10⁵ CFU-100 ^-1. The average FC removal was of 2.3 Ulog. FC content seldom exceeded 10³ CFU-100 mℓ^-1 during the irrigation period (May-September).

 

Results and discussion

Table 1 shows a part of the operational data set of the Caltagirone Reservoir during the study period. The grey square indicates the variables required for the calculation of PFE5₆.

 

 

Both Eqs. (1) and (5) use the same variables describing the operation of the reservoir. Results can be summarised as follows:

• During the fill-up period no outflow from the reservoir took place; as a result the variable OUT. was zero and Eq. (1) and Eq. (5) offered the same results

• During the irrigation season the main term of water loss was different from zero, thus resulting in differences between the 2 formulations, with maximum values for PFE with up to 5 days within the reactor

Figure 4 reports the percentage of error on PFE5_d obtained using Eq. (5) rather than Eq. (1); the average error is about 0.65%. The percentage of error increases during the irrigation phase with the increase of the outflow rate. The values of PFEnd (n=1, 2, 3, 5), using the simplified Eq. (5) for the Caltagirone reservoir, are reported in Fig. 5.

 

 

 

 

By comparing PFEn_d with faecal coliform (FC) and E.coli removal in the reservoir (Fig. 5), it can be noted that removal was low in early spring when fresh wastewater entered the reservoir, reaching a minimum of 0.77 Ulog, and high during the end of the irrigation season, with an average removal of about 2.3 Ulog. The die-off coefficient, K_T, calculated by means of climatic variables (incident solar radiation and water temperature), showed a great variability during the observation period, with a mean value of 2.6 d^-1 (Barbagallo et al., 2003b).

Multiple regression analyses performed to identify the main parameters affecting the removal of faecal coliforms in the reservoir (Barbagallo et al., 2003a; Mancini and Vagliasindi, 2006) indicate that the dynamics of the process vary among locations in the same reservoir: at the surface and at the embankment edge PFEs calculated for a few days (PFE1 and PFE5) present the highest correlation with coliform (FC and E. coli) removal. At the bottom layer, PFE20 and PFE30 substitute PFE1 and PFE5 as parameters with highest correlation coefficients (Table 2). Therefore, PFE is the best parameter to be monitored and controlled in order to optimise coliform removal across the whole irrigation season.

 

 

Conclusions

The advantage of the simplified method herein presented is the use of an easy algebraic formulation for the calculation of PFEn_d, especially for n values of more than 3 days. An average error of about 3% is estimated when there is outflow from the reactor.

Results of the experimental activity carried out for Caltagirone Reservoir using the simplified formulation highlighted a close correlation between PFEn_d values and FC removal, thus confirming the importance of this parameter in the definition of operational modalities for the reactors.

The simplified method could contribute to solving problems of data elaboration for modelling the behaviour of reservoirs, and for determining set-up design criteria and operational rules. Finally, the analysis of PFE variability within a storage reservoir is important, not only to indirectly indicate the pathogen content level but (primarily) to suggest design and management criteria and rules.

 

References

APHA (1999) Standard Methods for the Examination of Water and Wastewater (20^th edn.) American Public Health Association, Washington D.C.        [ Links ]

ANGELAKIS AN, MARECOS DO MONTE MHF, BONTOUX L and ASANO T (1999) The status of wastewater reuse practice in the Mediterranean basin: need for guidelines. Water Res. 33 (19) 2201-2217.        [ Links ]

BARBAGALLO S, CIRELLI GL, CONSOLI S and SOMMA F (2003a) Wastewater quality improvement through storage: a case study in Sicily. Water Sci. Technol. 47 (7) 169-176.        [ Links ]

BARBAGALLO S, BRISSAUD F, CIRELLI GL, CONSOLI S and XU P (2003b) Modelling of bacterial removal in wastewater storage reservoir for irrigation purposes: a case study in Sicily, Italy. Water Sci. Technol.: Water Supply 3 (4) 169-175.        [ Links ]

BRISSAUD F (2002) Extensive reclamation technologies for irrigation reuse. In: Proc. Regional Symposium on Water Recycling in Mediterranean Region, 26-29 September 2002, Iraklio, Greece.        [ Links ]

CIRELLI GL, CONSOLI S and DI GRANDE V (2008) Long term storage of reclaimed water: the case studies in Sicily (Italy). Desalination 218 62-73.        [ Links ]

CIRELLI GL, CONSOLI S and JUANICÓ M (2009) Modelling Escherichia coli concentration in a wastewater reservoir using an operational parameter MRT%FE and first order kinetics. J. Environ. Manage. 90 604-614.         [ Links ]

FRIEDLER E, JUANICÓ M and SHELEF G (2003). Simulation model of wastewater stabilization reservoirs. Ecol. Eng. 20 (2) 121-145.        [ Links ]

FUNDERBURG S, MOORE B, SORBER C and SAGIK B (1978) Survival of polivirus in model wastewater holdings ponds. Prog. Water Technol. 10 (5-6) 619-629.        [ Links ]

JUANICÓ M and DOR I (1999) Reservoirs for Wastewater Storage and Reuse - Ecology, Performance and Engineering Design. Springer, Berlin. 394 pp.        [ Links ]

JUANICÓ M and FRIEDLER E (1994) Hydraulic age distribution in perfectly mixed nonsteady-state reactors. J. Environ. Eng. ASCE 120 (6) 1427-1445.        [ Links ]

JUANICÓ M and SHELEF G (1991) The performance of stabilization reservoirs as a function of design and operation parameters. Water Sci. Technol. 23(7-9) 1509-1516.        [ Links ]

JUANICÓ M and SHELEF G (1994) Design, Operation and Performance of Stabilization Reservoirs for Wastewater Irrigation in Israel. Water Res. 28 (1) 175-186.        [ Links ]

MANCINI G and VAGLIASINDI FGA (2006) Issues and guidelines for treated wastewater reservoirs design and operation. Int. J. Environ. Pollut. 28 (1/2) 128-143.        [ Links ]

MARAIS GvR (1974) Faecal bacterial kinetics in stabilisation ponds. J. Environ. Eng. Div. 100 (1) 119-139.        [ Links ]

PEARSON H, MARA D, MILLS S and SMALLMAN D (1987) Physico-chemical parameters influencing fecal bacteria survival in waste stabilization ponds. Water Sci. Technol. 19 (12) 145-152.        [ Links ]

WEISSMAN S and KOTT Y (1979) The effect of changing oxygen concentration on viability of bacteria. In: Proc. Symp. Israel Ecol. Soc. A-144.        [ Links ]

XU P, BRISSAUD F, MAIHOL JC, VALETTE F and LAZAROVA V (2002) Design of a climate-dependent water reuse project. Water Sci. Technol. 46 (6-7) 289-296.         [ Links ]

 

 

Received 25 February 2011; accepted in revised form 5 September 2011.

 

 

* To whom all correspondence should be addressed. +39 095 7147547; fax: +39 095 7147600; e-mail: simona.consoli@unict.it