Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Water SA
On-line version ISSN 1816-7950
Print version ISSN 0378-4738
Water SA vol.37 n.2 Pretoria Apr. 2011
Investigating the cooperative strategies between China and North Korea for the Tumen River Area Development Programme
S Lee*; W Park and H Park
Dept. of Civil and Environmental Engineering, KAIST (Korea Advanced Institute of Science and Technology), Daejeon, Korea
ABSTRACT
Addressing the equitable management of an international boundary river, this study aims to find the optimal strategy with regard to how to build multi-purpose dams and allocate the benefits and costs thereof. The interests of the riparian countries (North Korea and China) are defined in terms of the cooperative 2-person nonzero-sum game, and the Nash product is then calculated for various alternative strategies. The results reveal that the Kangkudong Dam and the Simpo Dam should be collaboratively constructed, and that the benefits of the 2 dams should be allocated according to relative demand in order to provide North Korea and China with sufficient benefits and to equitably address their conflicting interests. Furthermore, the suggested strategy was found to be optimal or at least quasi-optimal when the North Korean economy, which is regarded as a crucial source of uncertainty in this case, moved from a low-growth scenario to a high-growth scenario.
Keywords: Boundary river management, Tumen River, Nash bargaining solution, cooperative game theory
Introduction
The Tumen River passes through the international boundary between China, North Korea, and Russia, as depicted in Fig. 1. The river originates from a basaltic plateau, which surrounds Baekdu Mountain, with an altitude of 2 750 m, and then flows into the East Sea. The abundant water, which averages 6.8 billion m3/yr, has huge potential as a water resource as well as an electricity source for the riparian countries. As China, Russia, and South Korea have recognised the economic value of developing the Tumen River, a joint team, comprising members from these nations and supported by the United Nations Development Program (UNDP), recently investigated the geographical and hydrological characteristics of the river, as summarised in Table 1. As a result, the joint team recommended that 2 multi-purpose dams be constructed. The Kanggudong Dam and the Simpo Dam were estimated to enable a water supply of 845 million and 940 millionm3/yr, and electricity supply of 350 and 275 GWh/yr, respectively (the plan is often referred to as the Tumen River Area Development Programme, hereafter simply referred to as TRADP). Furthermore, the river is known for its huge coefficient of river regime, i.e. the ratio between the maximum and minimum amount of flow, of 300. Owing to this feature of extreme seasonality, people in the riparian area have frequently suffered the consequences of floods and droughts. The 2 proposed dams are expected to effectively relieve these problems. Note that specific actions to implement this plan have yet to be taken.
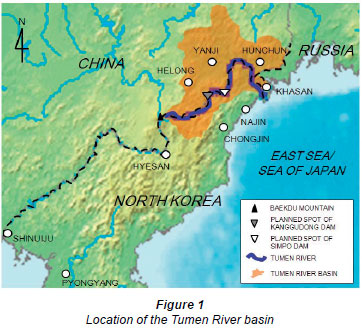
Indeed, North Korea and China have on a number of occasions attempted to develop water resource infrastructures in this river basin. At each occasion, however, they could not reach mutual agreement on the specified strategies (hereafter, the term strategy implies the definite course of action concerning how the 2 dams should be built and how the benefits and the costs should be allocated). According to Kim (2002), China preferred building and operating each dam individually by mutual consent, whereas North Korea insisted upon building the dams collaboratively and allocating the benefits according to their contributions. In addition to this, as pointed out by Lee et al. (2008), planning the strategies is often hampered by the economic situation of North Korea, which has stagnated since the 1990s. To sum up the above arguments, more efforts should be made to resolve the conflicting interests between China and North Korea, and to reflect the economic situation of North Korea, in order to expedite the TRADP.
This study begins with the results of a preliminary investigation by a UNDP joint team (K-Water, 2004), and therefore takes it as given that the planned dams will effectively lead to improved urban living standards, will stimulate economic growth, raise agricultural productivity, and help manage droughts and floods in the river basin. Hence, the aim of this study is to recommend specified strategies for the TRADP.In order to do this, the TRADP case is defined as a cooperative 2-person nonzero-sum game, with the following considerations: First, it is assumed that the TRADP is only related to China and North Korea, not Russia. As shown in Table 1, the Russian territory accounts for merely 0.3 % of the total area of the river basin, and this part of Russia is also sparsely populated. As such, in comparison to the other 2 countries, Russia does not have significant interests in the Tumen River. Secondly, gains in a country are not always linked to losses in another country, considering the abundant water resources of the river. Thus, it seems more likely to be a nonzero-sum game. Thirdly, the possibilities are excluded where a country decides upon non-cooperative strategies to satisfy its urgent demands for water and electricity. It has been almost 20 years since the UNDP launched discussions on the TRADP. However, neither of the 2 countries has hastened to individually develop water resource infrastructure. This is not merely based on empirical findings that cooperative strategies offer larger benefits to all riparian countries than non-cooperative strategies. Rather, it is mainly because, on the basis of the border treaty, they have thus far realised that the Tumen River is common property. Despite the vast economic values of the river basin, both countries are concerned that conflict over river management will harm political relations and lead to a border dispute (K-Water, 2004). Furthermore, the economic feasibility of the TRADP was examined by Shim and Lee (2001), who contended that non-cooperative strategies will yield negative outcomes where the 2 countries do not have sufficient development funds to individually invest in the undeveloped area. The study concluded that the TRADP is achievable only with cooperative strategies, which are advantageous for attracting external funds from international financial institutions or other northeast Asian countries (However, it should also be noted that people are not always willing to cooperate in using common-pool resources).
Figure 2 depicts the general approach to identifying the optimal strategy for the TRADP. Based on current discussions on the TRADP and on socio-economic indicators of the river basin, water and electricity demands are predicted up to the year 2050 (Step B). Thereafter, possible strategies to implement the 2 dam projects are presented (Step C). The final choice among the cooperative strategies will affect benefit and cost allocations, and thus the 2 countries' payoffs. For every strategy, hence, payoffs are calculated, based on water and electricity demands as well as the way that the relevant strategy allocates resources (Step D). The Nash bargaining solution, the methodological merits of which are discussed in the following section, is used to decide upon the strategy, adjusting the interests of the 2 countries in an equitable manner (Step E). The selected strategy cannot be said to always be optimal for the TRADP, because the estimation does not take into account that the future of the North Korean economy is known to be highly uncertain, and because some data are inevitably assumed as being identical for the 2 countries. The sensitivities of the optimal strategy are therefore tested over a wide range of growth rates of the North Korean economy (Step F) and over a wide range of the assumed data (Step G).
This study does not focus on pursuing a methodological contribution. During the past few decades, many researchers have tried to mediate conflicts originating from ill-defined water rights in boundary or transboundary river basins. Some proved conclusively that game theory is useful to define conflicting interests between riparian areas, and also derived optimal solutions. Instead, the aim of this study is to contribute to more practical application. First, the game model is applied to special cases where data are not sufficient. Despite having an urgent need to further develop water resource infrastructure, North Korea is rarely discussed in the scientific community in this regard, and thus this study should help to shed light on the complicated situation surrounding water resources in North Korea. Secondly, this study attempts to address the uncertainty in the North Korean economy before suggesting the optimal strategy for the TRADP. Addressing uncertainty as such is imperative when planning in any country where there is a probability that the national economy may fluctuate violently, and where the economic situation affects water or electricity demand, and ultimately the benefits from the water resource projects. Thirdly, this study illustratively shows that the optimal solution, which offers satisfactory benefits to both riparian countries, is indeed collaborative in nature. This can be another lesson on how to deal with conflicting interests due to shared water resources.
Cooperative 2-person nonzero-sum game
Applications of game theory to shared water resource management
Since Von Neumann and Morgenstern published the book Theory of Games and Economic Behavior (Von Neumann and Morgenstern, 1944), game theory has been recognised and used as a quantitative and rigorous method to predict strategic behaviours of economically rational players. With respect to improving water resource management, its applications are vast, differing from areas of conflict to identifying the kinds of available strategies. Meanwhile, water resource management scholars who have previously applied game theory commonly noted its potential as a unique systems method that is readily applicable to problems that conventional systems methods cannot solve (Madani, 2010). The prevailing methods in water resource planning and management, for example, mathematical programming, specialise in deriving solutions for mechanical or machine-like systems. When confronted with system failures or system design problems, system boundaries and objec tive functions of the whole system are first postulated. It is then expected that all the parts within the boundaries will interact together such that the defined objective functions are maximised. However, in handling many water resource problems, and especially with growing interest in the integrated water resource management principle, parts of the system are often decision-makers or 'players', i.e. individuals or organisations who decide upon strategies to achieve self-interests. The conventional system method, as described above, forces optimisation of the whole system on the players. If any of the players are unwilling to contribute to the whole system, the optimised outcomes cannot help to settle real water resource problems. Such cases are easily found in workshops or public hearings. In contrast, game theory focuses heavily on the rationality of an individual player or grouped players (it is generally accepted that a strategy is rational when a player chooses the best strategy according to their preferences), not on the objectives of the whole system. The levels at which all objectives are achieved result from the set of all strategies. It thus leads to realistic insights about why the players are willing or unwilling to contribute to the whole system, what strategies the players will select to attain larger interests under situations of competition or negotiation, and sometimes how the rules of the game should be improved to accomplish the objectives of the whole system (Madani, 2010).
The game theory is classified chiefly depending on whether a game is viewed as non-cooperative or cooperative. A noncooperative game is used to predict or evaluate the strategies of players who, under strong competition, can gain more payoffs by cheating other players. Consequently, these games end in all players' failures, as in the Prisoner's Dilemma game, or a large loss to players who are not familiar with the competition situation, as in the Chicken game. When water resources management conflicts are treated as non-cooperative games (for the state-of-art, see Carraro et al. (2005)), the following is generally illustrated: water resource users select strategies maximising their urgent self-interests, for example, a pumping rate exceeding agreements previously made to maintain the groundwater table; the set of those strategies causes the shared water resources to be seriously depleted or deteriorated; and, eventually, the benefits from water resources cease or become extremely restricted to all users. In order to avoid such negative situations, it is suggested that third party organisations and binding regulations be established, which play an important role in punishing water resource users for violation of the agreement.
The cooperative game theory is used to handle the strategies of players who are very likely to collaborate rather than compete with each other. The collaboration is justified when players gain more payoffs by devising a cooperative strategy or acting as a coalition. Even in these games conflicts can arise, because the cooperative strategies do not always allocate the same payoffs among the players. When water resource management conflicts are treated as cooperative games (for the stateof-art, see Parrachino et al. (2006)), it is generally illustrated that cooperation is impeded as long as water resource users adhere to strategies for self-interest. To advance cooperation, water resource users should reach mutual agreement upon the Pareto-efficient strategy.
Since the TRADP case is treated as a cooperative game, it is necessary to note other cases in which the cooperative game theory was applied in shared water resources management. Netanyahu et al. (1998) examined the water resource allocation of the Mountain Aquifer between Israel and the Palestinian Authority. Based on the projection that the aquifer would be threatened by over-pumping and degradation unless the 2 countries cooperated, the Mountain Aquifer case was defined as a cooperative game. The authors then used the Nash bargaining solution in analysing mutual interests served by the various strategies. As a result, it was concluded that Israel, the sole manager at that time, should cooperate with Palestine in managing the aquifer, and the cooperative strategy was anticipated to be robust. Frisvold and Caswell (2000) tackled the allocation problem of the costs and benefits involved in pollution control projects in the Colorado River. Based on the International Boundary and Water Commission (IBWC) framework ensuring binding commitments between Mexico and the USA, the Colorado River case was defined as a cooperative game. By means of the Nash bargaining solution, the case demonstrated how the costs and benefits should be allocated between the 2 countries, and why the equal cost-sharing rule was an obstruction to their cooperation. Recently, Choi and Lee (2008) examined the Imnam Dam project in the Imjin River flowing from North Korea into South Korea. Similarly, the Nash bargaining solution revealed that cooperation of the 2 countries could be sustained if North Korea guaranteed 50% of the total flow to South Korea, and South Korea compensated the North with a joint aggregate harvest project.
Water resource conflicts have been addressed by the cooperative game theory, rather than the non-cooperative game theory. This is mainly due to the existence of large economies of scale, owing to which water users prefer construction and operation of large-sized water resource infrastructures, and also because water resource usage often uncovers reciprocal externalities (Parrachino et al., 2006). It is thus easy to find that cooperative strategies dominate non-cooperative strategies, and there are strong incentives to cooperate in resolving water resource management conflicts (Becker and Easter, 1999). As a well-known case, Rogers (1969) applied game theory to devise a water resource project in a downstream region of the Ganges River, along the border between India and Pakistan. To deal with water issues related to the growing demands of hydroelectricity and water resources, as well as flood control, the study presented 6 strategies, where one was the status quo, three were non-cooperative, and two were cooperative. After examining the net benefits from the 6 strategies, the study proved that unless a joint project was cooperatively developed, the benefits to the 2 countries would be far from the Pareto efficiency.
Nash bargaining solution for the TRADP
Previous studies provide 2 important insights into the TRADP case. First, it is expected that this case can be effectively analysed with the Nash bargaining solution from the viewpoint of the cooperative game. This case is very similar to the cost allocation problem presented in Frisvold and Caswell (2000). As with Mexico and the USA, who are bound together by the IBWC framework, China and North Korea are very unlikely to act separately in developing the river basin, in light of the aforementioned institutional, political, and economic situation. Furthermore, the 2 countries have continuously shown a type of sequential bargaining game. Although the UNDP strived to advance the project, China and North Korea have simply exchanged proposals, and very slow progress has been made over the past 20 years. Keeping in mind that UNDP aid and other external finance is inevitable for the project, it seems likely that the delays in resolving the conflict decrease opportunities to use external funds. Regarding this, Binmore et al. (1986) theoretically proved that the Nash bargaining solution approximates the outcomes of the sequential bargaining game well. Therefore, the Nash bargaining solution appears to provide the TRADP with appropriate cooperative game concepts.
Secondly, it is ascertained that the model for the bargaining solution needs to be further unpacked to consider uncertainties. Choi and Lee (2008) assumed the benefits from the Imnam Dam project and the aggregate harvest project to be certain. However, the North Korean economy is relatively unstable, which can affect the demands for water resources and aggregates (Park and Lee, 2005; Park et al., 2005). The validity of the assumption for these benefits thus seems doubtful. Likewise, it is anticipated that in the TRADP case large uncertainties will be propagated through the North Korean economy. As an effort to handle the uncertainties, it is possible to consider 2 scenarios, i.e. a low-growth scenario (LGS) and a high-growth scenario (HGS), according to the recent prospects for the North Korean economy. Subsequently, the scenarios are endowed with probabilities so that the Nash bargaining solution can reveal how the North Korean economy alters the optimal strategy.
The model employed for the Nash bargaining game is briefly explained here. For the cooperative game, the Nash bargaining solution (1953) represents an axiomatic unique allocation between 2 players, in particular because 'the alloca tion is feasible, fulfils individual rationality, is Pareto optimal, symmetric, not related to non-relevant alternatives and to a specific presentation of the von-Neumann Morgensten utility function (Dinar, 2001 p. 478).' In addition to conceptual richness, the Nash bargaining solution requires a clear description and simple calculation. That is, the cooperative strategy of 2 players is optimal when the Nash Product, N, is maximised as follows (the Nash bargaining solution was later generalised for n players with n > 2 by Harsanyi (1959; 1963): Similarly, the Pareto optimal strategy maximises the product Z = 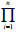 (ui -ui0)).
(ui -ui0)).
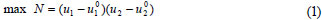
where:
ui is the payoff that player i derives from cooperation, and
ui0 is the payoff of player i that reflects the status quo (it is assumed that i = 1 for North Korea and i = 2 for China).
The term payoff is a description used in economics; hereafter the more familiar term 'net economic benefits' will be used instead of 'payoff'. Because neither of the 2 dams will be constructed before cooperation, ui0 is regarded as zero.
To calculate the net benefits to the ith country, the total benefits and the total costs were presumed as follows: it was roughly assumed that the total benefits arise from supplies of water resources ƒi1 and electricity ƒi2 to each respective country, and profits from water trade ƒi5 or electricity trade ƒi6; the total costs also include dam construction cost ƒi3, dam maintenance cost ƒi4, and expenses of water trade ƒi5 or electricity trade ƒi6. If ƒi5 and ƒi6 have negative values when the country exports water resources or electricity to another country, the net benefits of the ith country are thus,
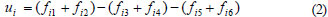
Each function in Eq. (2) can be simply described, as follows:
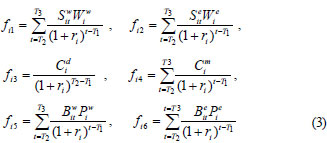
where:
Suw and Sue are the total amounts of water resources (m3/yr) and electricity (kWh/yr) that the 2 dams actually supply to the ith country in the year t (i.e. produced amounts - exported amounts + imported amounts);
Wiw and Wie are the willingness to pay for water resources (USD/m3) and electricity (USD/kWh);
Piw and Pie denote the market price of water resources (USD/m3) and electricity (USD/kWh);
Biw and Bie are the traded amount of water resources (m3/yr) and electricity (kWh/yr) in the year t, and are set at negative values when the ith country is the exporter, in the same way as ƒi5 and ƒi6·
Cid and Cim denote the construction cost (USD) and maintenance cost (USD/yr);
ri, T1, T2, and T3 are, respectively, the discount rate (%), the base year, the operation year, and the last year in time horizon (years), which are all needed to calculate all costs and all benefits in the monetary value of T1.
If the market price closely reflects the real benefits of each service, Eq. (2) can be simplified as:
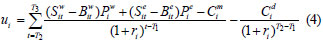
Furthermore, let us assume that p is the LGS probability, and uij is the net benefit of ith country under the jth scenario ( j = 1for the LGS, and 2 for the HGS). From Eq.(1) and Eq.(4), the expected value of the Nash product can be defined again, as:
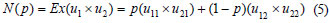
where
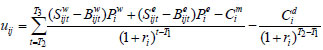
Most variables in Eq. (5) largely depend on the way the 2 dams are constructed and operated as well as on service demands.
Data
The data applied to Eq. (5) were calculated, inferred, or assumed in some instances, as follows:
• Time parameters (Table 2[1]): The base year T1 was set at 2010, meaning that the net benefits were converted to monetary values for the year 2010. The proposed dams were also regarded as being operated from the year 2020, under the supposition that it will take at least 10 years for negotiations, preliminary investigations, design, and construction. The last year in the time horizon T3 was set to be 2050, taking into account that water resource infrastructures are typically endowed with life-spans of approximately 30 years. The discount rates were also considered as 3.24% for China and 2.96% for North Korea, as stated by the Bank of Korea.
• Scenarios for the North Korean economy (Table 2[2]): based on the predictions of Jung et al. (2001), the LGS and the HGS were regarded as having economic growth rates of 6.67%/yr and 10.70%/yr, respectively
• Unit cost and unit benefit (Table 2[3]): it is speculated that the 2 countries will not make some data available and that they do not officially calculate some other necessary data. Alternatively, it was commonly assumed that the construction cost is 0.274 USD/m3, the annual maintenance cost is 1% of the construction cost, and market prices are 0.587 USD/m3 for water service and 6.43×10-2 USD/kWh for electricity service, based on dam design standards and market information for South Korea (Korea Energy Economics Institute, 2007; Yun, 2003). The assumption that the 2 countries have the same unit cost and unit benefit is not easily accepted, and thus sensitivity tests are later conducted concerning the cases where unit cost and unit benefit for North Korea are not equal to those of China.
• Water and electricity supply capacity of the 2 proposed dams (Table 2[4]): according to the work by the UNDP joint team (K-Water, 2004), it was presumed that the total water supply capacity is 845 + 940 = 1 785 million m3/yr, whereas the total electricity supply capacity is 350 + 275 = 625 GWh/yr.
• Water demand (Table 3): because North Korea has not officially calculated water consumption in recent years, it is impossible to use typical econometric models to estimate water demand. This study thus utilises the trend curves of Park et al. (2005), who inferred the water demand of North Korea until 2020, after having analysed water intake data announced before the 1990s and then having adjusted the data through interviews and questionnaire surveys with more than 100 refugees. The trend curves were classified into residential demand, industrial demand, or agricultural demand, which significantly change according to patterns such as population (for residential demand), land use (for industrial and agricultural demands), and economic growth rate (for industrial demand). When the trend curves were applied to the Tumen River basin and then extended to cover the period from 2020 to 2050, it was projected that:
_ The residential demand will increase constantly from 29.7 million m3/yr in 2020 to 48.7 million m3/yr in 2050
_ The agricultural demand will be constant at 255 million m3/yr, because the area of farmland was expected to follow an invariant pattern
_ The industrial demand will reach 717 million m3/yr or 2 912 million m3/yr, depending on whether the LGS or the HGS occurs in reality. The results seem to be reasonable, given that the river basin not only contains largescale industrial complexes, such as the Musan mine and the Hoeryong paper factory, but also adjoins the Najin-Sunbong special economic zone.
• For China, there are more reliable data available to predict water demand. Among available data, data from the US Department of Commerce (2005), National Bureau of Statistics of China (2009), and K-Water (2004) were used to develop trend curves. It was projected that:
_ The residential demand will increase constantly from 41 million in 2020 to 86 million m3/yr in 2050
_ The agricultural demand will decrease slightly to 1 619 million m3/yr in 2050
_ The industrial demand will eventually increase to higher than 3 400 million m3/yr, largely due to the Hunchun development plan (Sim and Lee, 2001), a large-scale master-plan including the economic cooperation zone and the relevant infrastructures.
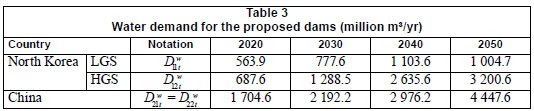
North Korea and China were found to have current water supply capacity of 16 million and 673 million m3/yr in the river basin, respectively. If there are no other plans to expand water supply capacity in the river basin, water demand for the proposed dams can be regarded as the difference between the total demand and the existing supply capacity (for example, the amount of water that China requires from the 2 reservoirs in the year 2050 is 86 + 1 619 + 3 416 - 673 = 4 448 million m3/yr).
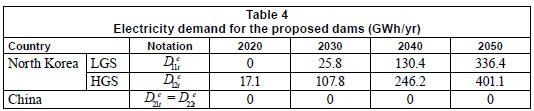
Electricity demand (Table 4): for North Korea, Jung et al. (2001) calculated the existing electricity supply capability and predicted the long-term trend curves of demand, which was also considered to depend on population and the economic growth rate. When data for the river basin were applied to the trend curves, it was projected that the additional demand will be small in 2020, because the existing supply capacity can almost cover the total electricity demand, but the demand will grow exponentially and reach 336 or 401 GWh/yr in 2050 depending on the scenarios. For China, many experts (e.g. Lee, 2003; Korea Energy Economics Institute, 2008) pointed out that the growth rate of demand has been dampened since 2006, and the current supply capacity is sufficient to meet the demand into the distant future. In this regard, it was assumed that China will not have electricity demand for the proposed dams.
Strategies for the TRADP
To sum up the results presented in Tables 3 and 4, water demand is urgent to both countries, but generating electricity is meaningful only to North Korea. For equitable management of the TRADP, 8 cooperative strategies were examined and are presented in Fig. 3:
• Protection of water rights: these strategies imply that one country develops both dams and then provides the other country with electricity or a certain amount of water in light of permitting water rights. Strategy 1 is the case where China develops both dams, and passes the exclusive right to all electricity over to North Korea. For China, there will be no electricity demand, yet there will be higher water demand than the total supply capacity in the long run. Therefore, Fig. 3(a) shows that Strategy 1 does not include any trade. In contrast, Strategy 2 is the case where North Korea develops both dams, and passes the exclusive right to 50% of available water resources over to China. As water demand for North Korea is predicted to reach less than half of the total water supply capacity in 2050, the 2 countries can increase the mutual benefits by trading water resources from North Korea to China. Hence, Strategy 2 involves water trade, as shown in Fig. 3(b).
• Individual dam construction: these strategies are that each country constructs a dam individually, and then trades surplus water or electricity to increase the benefits to itself. Strategy 3 assumes that North Korea and China individually develop the Kanggudong Dam and the Simpo Dam, and Strategy 4 presents the opposite case. For both strategies, there are opportunities to increase the benefits by making use of the unused supply capacity of each country. That is, China exports electricity while North Korea exports water resources, as depicted in Figs. 3(c) and (d).
• Individual dam construction by support from South Korea: Strategies 5 and 6 are similar to Strategies 3 and 4, respectively, except that South Korea supports construction costs for North Korea. These strategies were added to assess the suitability of participation of South Korea, which is very interested in the water resource project of North Korea, from both a humanitarian and strategic standpoint. These strategies differ from Strategies 3 and 4, in that they do not require that North Korea bears any initial construction costs. The requirement for China and North Korea to respectively export electricity and water resources, as in Figs. 3(e) and (f), is unchanged.
• Collaborative dam construction: Strategy 7 implies that the 2 countries collaboratively construct 2 dams with each country paying 50% of the costs. North Korea can be provided with all available electricity, and with an upper limit of 50% of available water resources (since it was previously anticipated that the water demand of North Korea would not be overly large in the near future). Instead, China can be supplied with a large amount of water from the begin ning. For an agreement on this strategy, China has no right to electricity and North Korea has a right to water resources corresponding to its demand. Therefore, Strategy 7 does not involve any trade, as shown in Fig.3g. For Strategy 8, the 2 dams are collaboratively built with North Korea pay ing 100 α% and China 100(1-α)% of the costs, the produced water and electricity being allocated according to contribu tion α, and each country then trading surplus water and electricity. If the 2 countries agree on Strategy 8, the rights to water and electricity are proportional to the contribution that each country makes toward developing the 2 dams. Therefore, while comparing unused supply capacities (i.e. exclusive rights - their own demands) and unsatisfied demands of the other country, the 2 countries are expected to trade water resources and electricity so as to further increase their benefits, as depicted in Fig. 3(h).
Results
Table 5 shows the benefits allocated to the riparian countries according to each strategy. Most conspicuous is that the sum of the net benefits of the 2 countries, i.e. u11 + u21 or u12 + u22, is roughly constant at around 14 billion USD irrespective of which strategy is chosen. In other words, for the economics of the entire river basin, it is not critical which of the 8 strategies is selected. However, it was found that individual net benefits vary across the strategies: under the conditions of the LGS for North Korea, 0.1<u11<13.6 and -4.7<u21<14.0; under the conditions of the HGS, 0.2<u12<13.7 and -1.0<u21<14.0. This reveals that the choice made among the 8 cooperative strategies can cause serious inequity in the benefits that the TRADP offers to each country. For example, if Strategy 1 is selected, the sum of the net benefits, 14.1 or 14.2 billion USD, is not relatively small. However, the benefit to North Korea is less than 1% of the benefit to China: i.e. u11/u21<0.01 and u12/u22<0.01. It is, therefore, anticipated that if China proposes Strategy 1, North Korea cannot accept it, and their cooperation will be perpetually delayed.
Contrary to the sum of the benefits, the Nash product is known to present the strategy that can optimally lead to collaboration and simultaneously result in large benefits to both countries. Let us first suppose that the possibility of each scenario is 50% (p = 0.5), which implies that the economic growth rate of North Korea will be the median between 6.67 and 10.7 %. As summarised in Table 6, the Nash product shows that Strategy 7, i.e. constructing 2 dams collaboratively and allocat ing the benefits according to demand, is optimal in adjusting the interests of the 2 countries for the TRADP. In this case, the expected benefits to North Korea are u1= 0.5 x 6.7 + (1-0.5) x 7.9 = 6.8 billion USD while those to China amount to u2 = 0.5 x 7.9 + (1-0.5) x 7.2 = 7.6 billion USD. It should also be noted that the benefit to North Korea reaches 90% of that to China, and Strategy 7 simultaneously guarantees relatively large benefits to both countries.
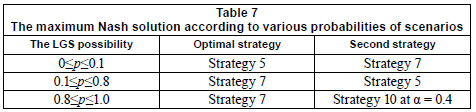
Furthermore, the Nash product was calculated over the full range of LGS possibilities (0<p<1). As shown in Table 7, Strategy 7 was estimated to be at least quasi-optimal even when the North Korean economy is close to the high growth scenario (0<p<0.1).
Discussion
Kim (2002) and K-Water (2004) noted that North Korea wanted to construct the dams through a joint project, and then allocate the benefits according to investment costs, whereas China wished to construct the dams individually under mutual agreement. Therefore, it is not unreasonable to consider that Strategy 8 speaks for the preference of North Korea while Strategy 3 or 4 speaks for that of China. Table 5 offers a chance to interpret these preferences. If Strategy 8 is implemented as North Korea insists, North Korea can obtain maximum benefits of about 13.7 billion USD for 30 years, which exceeds that yielded by the other strategies; in this case, however, the costs borne by China outweigh the benefits. North Korea is thus regarded as a rational economic agent trying to maximise its benefits under the gaming situation. On the contrary, if Strategy 3 or 4 is implemented, as China wishes, China is expected to obtain benefits of 5.6 to 7.3 billion USD for 30 years, or no more than half of the benefits from Strategy 1. Meanwhile, the benefit obtained by North Korea ranges from 7.2 to 8.0 billion USD for the same period, mean ing that the benefits to North Korea can be moderately satisfied, compared to the yields of other strategies. Therefore, China is not viewed as a rational economic agent, because it does not exert effort to maximise its own benefits. The authors speculate that this can be attributed to China's greater enthusiasm for the TRADP due to urgent water demand.
This study finally considers Strategy 7 to be appropriate for the TRADP. Firstly, Strategy 7 can optimally adjust the interests of North Korea and China under most conditions, including that in which the North Korean economy changes from the LGS to the HGS. Indeed, Strategy 5, which means that North Korea develops the Kanggudong Dam with financial aid from South Korea and China develops the Simpo Dam, was expected to be better than Strategy 7 if the North Korean economy approaches the HGS. However, Strategy 5 appears to be vulnerable to political conflicts. According to Park et al. (2005), North Korea is unwilling to accept direct aid from South Korea for water resource projects. Furthermore, if North Korea and China own the upstream dam and the downstream dam, respectively, a serious problem can occur in the dry season. Because North Korea does not have incentive to release the stored water to the downstream dam, Strategy 5 again leads to conflict over the transboundary river. In this regard, it is concluded that the optimal strategy for the TRADP is to construct the proposed dam collaboratively and allocate the benefits according to the demands.
In this study, the same data for unit cost and unit benefit were applied to the 2 countries. Because this assumption is not generally accepted, it is necessary to assess whether the dif ferences in unit cost and unit benefit between the 2 countries will lead to different outcomes: i.e. sensitivity analyses must be performed. To this end, it was supposed that the market prices and the unit costs for China are a and b times those of North Korea, respectively, as follows:

where:
a is the ratio of market prices of water or electricity between North Korea and China, and
b is the ratio of construction costs or maintenance costs between North Korea and China.
As a and b changed along a range of 0.5 to 2.0, the Nash product was calculated again. These tests revealed that Strategy 7 is still optimal or quasi-optimal over the various conditions of the North Korean economy in the given range of a and b. Therefore, the assumption that the 2 countries have the same unit cost and unit benefit was found not to significantly affect the conclusion.
Conclusion
This study sought to find the cooperative strategy for 2 multi purpose dams on the Tumen River, i.e., how the 2 dams should be built and how the benefits and the costs should be allocated. Although the riparian areas urgently require water resources and electricity, and often suffer from droughts and floods, appropriate action has not been undertaken because of conflicting interests. In this light, their interests were regarded as part of a cooperative 2-person nonzero-sum game. After the net benefits were calculated over the various cooperative strategies that the 2 countries had already suggested or that should be considered in promoting the project, it was found that the sum of the benefits to the 2 countries did not vary significantly between the strategies. More specially, the proposed dam projects will provide the whole river basin with benefits of roughly 14 billion USD over 30 years, regardless of which strategy is selected. However, the benefits to each country are expected to vary from a negative value to around 14 billion USD, depending on selection of the strategy. This shows that a serious inequity in the benefits can arise if the strategy is improperly chosen. After calculating the Nash Product, however, it was found to be possible to guarantee large benefits to both parties and to adjust the conflicting interests very well: i.e. if the Kangkudong Dam and the Simpo Dam are collaboratively constructed, and the benefits of the 2 dams are allocated according to related demand, North Korea and China are respectively expected to receive benefits of 6.8 billion and 7.6 billion USD. Moreover, it was ascertained that the suggested strategy was optimal or at least quasi-optimal when the North Korean economy varied from a low growth scenario to a high growth scenario (though noting that different results may be obtained if other cooperative game theory solution concepts are used).
Finally, it should be noted that much of the data regarding North Korea were inferred or assumed, in the absence of officially documented data. Notwithstanding the limitations of the data, however, the results are thought to be meaningful. This is partly because the assumptions for unit costs and unit benefits were evaluated to be insignificant through sensitivity analyses, and mostly because decisions are inevitably made under highly uncertain conditions when any infrastructure project is in the planning stage, as is the case with the TRADP.
Acknowledgements
This research was supported by a grant (07-UR-B04) from the High-tech Urban Development Program funded by the Korean Ministry of Land, Transport and Maritime Affairs. The authors acknowledge the helpful comments of the reviewers.
References
BECKER N and EASTER KW (1999) Conflict and cooperation in managing international water resources such as the Great Lakes. Land Econ. 52 (2) 233-245. [ Links ]
BINMORE K, RUBINSTEIN A and WOLINSKY A (1986) The Nash bargaining solution in economic modeling. Rand J. Econ. 17 (2) 176-188. [ Links ]
CARRORO C, MARCHIORI C and SGOBBI A (2005) Applications of negotiation theory to water issues. The World Bank Policy Research Working Paper 3641. [ Links ]
CHOI D and LEE M (2008) Applying game theory for strategy transboundary river: the case of the Han River in North and South Korea. J. Korean Water Resour. Assoc. 41 (4) 353-363 (in Korean). [ Links ]
DINAR A (2001) Scale and equity in water resource development: a Nash Bargaining model. Nat. Resour. Model. 14 (4) 477-494. [ Links ]
FRISVOLD GB and CASWELL MF (2000) Transboundary water management game-theoretic lessons for projects on the US-Mexico border. Agric. Econ. 24 (1) 101-111. [ Links ]
HARSANYI JC (1959) A bargaining model for the cooperative n-person game. In: Tucker AW and Luce RD (eds.) Contributions to the Theory of Games 1-4. Princeton University Press. 325-355. [ Links ]
HARSANYI JC (1963) A simplified bargaining model for the n-person cooperative game. Int. Econ. Rev. 4 194-220. [ Links ]
JUNG W (2001) Planning of the South's Support of Electricity to the North Korea: The Final Report. Korea Energy Economics Institute. (In Korean). [ Links ]
KIM W (2002) Utilization and management of water resources in the Tumen River Basin. J. Korean Water Resour. Assoc. 35 (3) 86-90. (In Korean). [ Links ]
K-WATER (2004) The Measures for Utilization and Management of Water Resources of the Tumen River: the Final Report. The United Nations Development Program. (In Korean). [ Links ]
KOREA ENERGY ECONOMICS INSTITUTE (2007) Yearbook of Energy Statistics: the 26th Edition. Korean Ministry of Commerce, Industry and Energy. (In Korean). [ Links ]
KOREA ENERGY ECONOMICS INSTITUTE (2008) An Analysis of Energy Markets in the Northeast Asia: the Final Report. Korean Ministry of Knowledge Economics. [ Links ]
LEE D (2003) The status and problems of the Chinese power industry. China Weekly 15. POSCO Research Institute. (In Korean). [ Links ]
LEE G, KANG B and JEONG G (2008) North and South Korean cooperation for water resources and economy development projects. Water for Future. Korean Water Resour. Assoc. 41 (8) 79-87. (In Korean). [ Links ]
MADANI K (2010) Game theory and water resources. J. Hydrol. 381 (3/4) 225-238. [ Links ]
NASH J (1953) Two-Person Cooperative Games. Econometrica 21 (1) 128-140. [ Links ]
NATIONAL BUREAU OF STATISTICS OF CHINA (2009) Website Database. URL: www.stats.gov.cn/english/statisticaldata/yearly-data (Accessed 30 Jan 2009). [ Links ]
NETANYAHU S, JUST R, and HOROWITZ JK (1998) Bargaining over shared aquifers: the case of Israel and the Palestinians. In: Just R and Netanyahu S (eds.) Conflict and Cooperation on Trans-Boundary Water Resources. Kluwer Academic Publishers. 41-60. [ Links ]
PARK H and LEE S (2005) Suggestion on the collaboration of the water supply projects with North Korea: establishment of the North Korea water corporation. J. Water Ind. 4 30-44. (In Korean). [ Links ]
PARK H, LEE C, HYUN I, CHOI S, LEE D, CHOI T, KIM J, LEE S, YUN B and LEE J (2005) An Investigation into the Current Status of Water Supply Systems of North Korea: The Final Report. Korean Ministry of Construction and Transportation and K-water (in Korean). [ Links ]
PARRACHINO I, DINAR A, and PATRONE F (2006) Cooperative game theory and its application to natural environmental and water resource issues: 3. Application to water resources. The World Bank Policy Research Working Paper 4074. [ Links ]
ROGERS P (1969) A game theory approach to the problems of international river basins. Water Resour. Res. 5 (4) 749-760. [ Links ]
SHIM U and LEE GX (2001) Estimations and Problems of the Tumen River Development Project. Korea Institute for International Economic Policy. (In Korean). [ Links ]
THE PEOPLE'S BANK OF CHINA (2009) Website Database. URL: www.pbc.gov.cn/ (Accessed 30 Jan 2009). [ Links ]
US DEPARTMENT OF COMMERCE (2006) Water Supply and Wastewater Treatment Market in China. United States Department of Commerce. [ Links ]
VON NEUMANN J and MORGENSTERN O (1944) Theory of Games and Economic Behavior. Princeton University Press. [ Links ]
YUN Y (2003) An Investigation into the Prospects and Participation in the Water Resources Project of North Korea: The Final Report. K-water. (In Korean). [ Links ]
Received 12 April 2010; accepted in revised form 6 April 2011.
* To whomall correspondence should be addressed. +82-42-350-3660; fax: +82-42-350-3610; e-mail: peregian78@gmail.com














