Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
Water SA
versión On-line ISSN 1816-7950
versión impresa ISSN 0378-4738
Water SA vol.37 no.2 Pretoria abr. 2011
Experimental and numerical investigations of flow through free double baffled gates
Ahmed M Helmi; Mohamed H El-Gamal*
Irrigation and Hydraulics Dept., Faculty of Engineering, Cairo University, Orman, Giza, Egypt
ABSTRACT
Studying the flow patterns and behaviour of double baffled gates under different flow heads is important to improve their performance, which could help in widening the range of their application. In the present study, physical and numerical investigations were conducted on the double baffled gate. A 3D Acoustic Doppler Velocity Meter (ADV) was used for laboratory measurements of the instantaneous velocity fields in the physical gate model. In parallel with this, the CFD Fluent package was adopted to carry out a sensitivity analysis for a matrix of geometric parameters of the double baffled gate. The outcomes of the laboratory and CFD numerical investigations were incorporated in a spreadsheet with the purpose of informing the design of double baffled gates under conditions of non-submergence.
Keywords: Control structures, irrigation, baffled gates, computational fluid dynamics, Fluent
Introduction and literature review
Flow control structures have long been used to control the water levels and flow discharge in rivers, open channels and waterways. On the one hand, huge research effort has been directed towards the study of the hydraulics of flow underneath single controlling gates (whether the traditional sluice type, the flap type or the radial gate type). Examples of such early experimental research studies are that of Henry (1950), Binnie (1952) and Rajaratnam and Subramanya (1968). Fangmier and Strelkoof (1968) have applied the conformal mapping theory to the flow underneath a sluice gate. McCorquodale and Li (1970), Isaacs (1977) and Diersch et al. (1977) were among the first researchers to apply the finite element numerical approach to sluice gate flow. Recently, many researchers have carried out different numerical techniques including that of finite volume to solve the Reynolds time-averaged Navier-Stokes equations such as Kim (2007). On the other hand, significantly less research effort has been directed to experimental and numeri cal investigation of multiple gates or multiple baffled gates. Despite the fact that double baffled gates (as an example of constant flow structures) are classic solutions that have been used for the past four decades to control outflows from channels (Kraatz, 1975), literature on this topic is quite incomplete and relevant expertise is not well reported.
In 1990, Larsen and Mishra experimentally and analytically investigated the hydraulic behaviours of a constant discharge module for field irrigation. The proposed module consisted of triple straight baffles and the module was designed to accommodate a design discharge in the range of 2 to 7 ℓ/s, which is suitable for small-scale field applications.
This study presents an experimental investigation and numerical analysis of the flow through the free double baffled gate. The gate investigated was quite similar to Nyrepic Module Gates, currently widely used as constant flow controlling structures. The typical design discharge of this sys tem is significantly larger than that used by Larsen and Mishra (1990).
The study was divided into 3 main stages. The first stage, the experimental stage, involved a number of experiments car ried out at the Irrigation and Hydraulics Laboratory of Cairo University's Faculty of Engineering. These were carried out in a closed-circuit rectangular glass- sided tilting flume, 12 m in length. A downscaled physical model of a typical double baf fled gate was constructed about mid-length with the tail water depth controlled via a tail gate. Velocity measurements were conducted using a Sontek Acoustic Doppler Velocity Meter (ADV) 16 Mhz. In the laboratory experiments different shapes of baffled gates were investigated and measurements including instantaneous velocity, water level, and turbulence intensity were recorded.
The second research stage focused on the use of computational fluid dynamics (CFD) Fluent package (ANSYS, 2006) to numerically simulate the hydraulic performance and flow structure throughout the double baffled gate distributors. The final stage involved the analysis of the experimental and simulated data and the production of a user-friendly spreadsheet to assist in the design and evaluation of baffled gates.
Experimental work
Flume set-up
All laboratory experiments were conducted in a glass-sided tilting Arm-Field flume with a fabricated stainless steel bed. The typical flow section is rectangular in shape with working dimensions of 300 mm in width, 450 mm in depth and 12 m in length. The flume is provided with a closed flow circulating system with a series of water sump tanks located on the floor and connected with each other. The last sump is provided with a centrifugal pump that lifts water to the upstream section of the flume. The flume is provided with a small manual moving cart that works as a carriage to move the point gauge and to hold the ADV probe along the entire length of the flume; the flume is marked with a millimetre scale to help in identifying the location of the carriage and the measuring devices. Operating tail water levels are maintained by a tail gate located at the downstream end of the flume. Both end tanks are made from glass-fibre reinforcement plastic (GRP). Water circulation is carried out by the centrifugal pump mounted beneath the flume channel, drawing water from the series of interconnected sump tanks mounted on the floor and running alongside the flow channel. The flow is regulated using a manual control valve. Flow rate is measured using a 90 mm orifice meter with a differential manometer located on the control console (Fig. 1).
Velocity measuring device
The Nortek Micro-ADV was used in this study and is based on the acoustic Doppler principle for measuring velocity. Nortek Micro-ADV is an efficient measurement tool that is widely used to obtain instantaneous 3-dimensional velocity measure ments with high-resolution (Gordon and Cox, 2000). The ADV Velocimeter consists of 3 modules: the measuring probe, the conditioning module, cable (Fig. 2), and the processing module (P.C.). The acoustic sensor consists of 1 transmitting transducer and 3 receiving transducers. The water sampling volume is located away from the sensor to provide undisturbed measurements. The pulses emitted from the transmitter are scattered by the colloidal particles which exist in natural water ways (streams, lakes, rivers, oceans, etc.), and the receivers receive the reflected echoes. The natural occurrence of particles is sufficient for proper operation. To check if the water is properly seeded, the Nortek ADV provides a read-out of the signal to noise ratio (SNR), an indicator of how well the flow is seeded: the higher the SNR, the better the seeding, and the more reli able the velocity measurements are. The Acoustic Doppler Velocimeter (ADV) operates by the principle of Doppler shift. This shift in frequency can be calculated using Eq. (1):

where:
FDoppler = change in received frequency (Doppler shift)
FSource = frequency of transmitted sound
V = velocity of source relative to receiver
C = speed of sound
Sampling time and frequency
The reliability of turbulence measurements depends on the sampling frequency and sampling time. Sampling time is defined as the period of time (seconds or minutes) over which the velocity is recorded at each of the measurement loca tions. Sampling frequency is the number of velocity readings to be recorded in each second at the measured point. The discrepancies in velocity measurements with low frequency are attributed to the inadequate recording time and the discrepancies with high frequency measurements are due to the spatial averaging by the sensor (Soulsby and Dyer, 1981). The spatial averaging by the sensor is considered insignificant with respect to the mean flow turbulence (Kim and Lim, 2000). Voulgaris and Trowdridge (1998) used approximately 6 min as the sampling time, as recommended by Trowbridge et al. (1989), to estimate the mean velocity at the measurement point. As limited guidance is available in the literature regarding the choice of sampling time, a preliminary investigation was performed in this study to choose the appropriate sampling time. Velocity measurements were taken at the same point, near the bottom and in the main body of the flow, for the same flow conditions using different sampling times ranging from 0.5 to 25 min for a sampling frequency of 25 Hz. The near-bottom point is located at 0.05 d from the bottom and the point in the main body of the flow is located at 0.7 d, where d is the flow depth (Salaheldin, 2003). Figures 3 to 6 show the effect of changing the sampling time on the velocity components along the axes Ox, Oy and O z, respectively, u, v and w, and on the turbulence parameters w'w', u'w' and TKE where u', v', and w' are the fluctuations of u, v and w, respectively and the TKE is the turbulence kinetic energy.
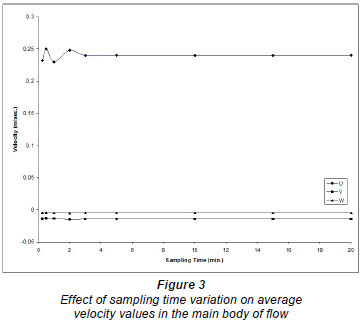
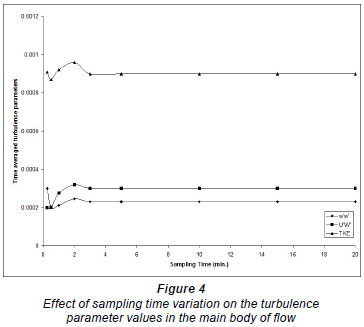
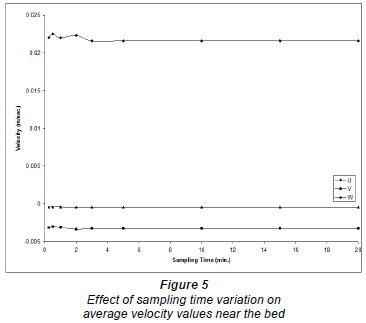
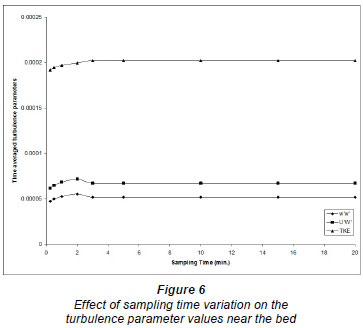
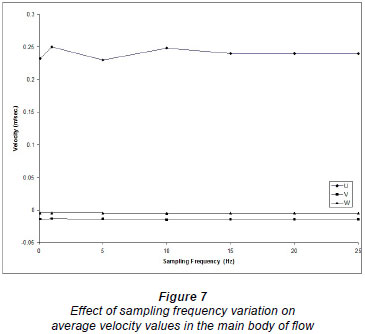
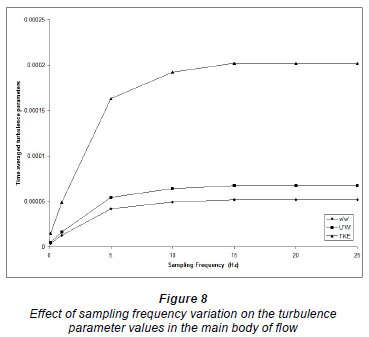
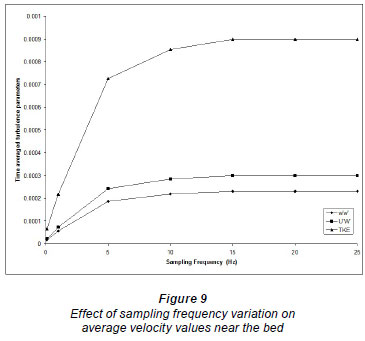
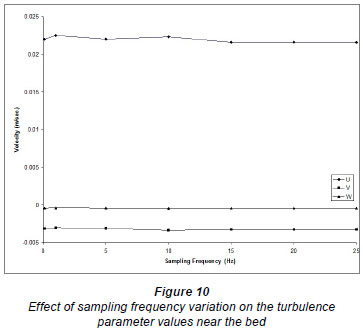
As there is no general guidance in the literature for choos ing the sampling frequency, another preliminary investigation was performed in this study to choose the appropriate sam pling frequency. Velocity measurements at the same points, near the bottom and in the main water body of the flow, for the same flow conditions, were taken by using different sampling frequencies from 0.1 (1 measurement every 10 se) to 25 Hz (25 measurements every 1 s). The point near the bottom is located at 0.02 d from the bottom and the point in the main body of the flow is at 0.7 d, where d is the flow depth. Figures 7 through 10 show the effect of sampling frequency on velocity components u, v, and w and on the turbulence parameters, w'w', u'w' and TKE. It should be mentioned that no significant lateral variations are expected (especially at the centreline of the flume) due to the 2-dimensional nature of the problem, and thus the lateral components of the Reynolds turbulence stresses are expected to be insignificant. The velocity measurements reported and used in this study were recorded with a sampling frequency of 20 Hz, and sampling time of 3.0 min, which was considered to be sufficient for capturing the velocity fluctuations and average values.
Laboratory experiments
The main purpose of the laboratory experiments was to vali date the results obtained using the Fluent program for the following parameters:
• Water surface profile
• Q-H relation (flow-head relation)
• Velocity component distribution
• Turbulence intensity distribution
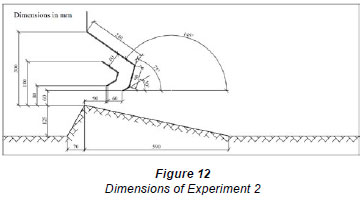
Two sets of laboratory experiments were carried out: the first was to validate the Q-H relation while keeping free-flow downstream conditions constant with regard to sill formation, as previously simulated using Fluent program (Fig. 11). The second set of laboratory experiments were conducted with high tail water depth downstream of the gate (i.e. submerged flow conditions) (Fig. 12). The study reported herein focused on the first set of experiments only. It should be noted that having submerged flow conditions will enable velocity measurements of the emerged flow (using the ADV) from the gate since the ADV cannot measure the velocities within the upper 5.0 cm surface layer of the flow depth.
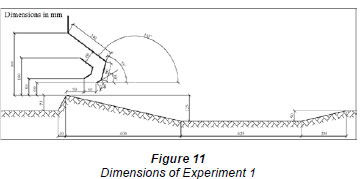
The first set of experiments assumed a free gate condition and the downstream tail gate was kept totally open. For the high head points on the gate curve, it was necessary to use an external pump in addition to the flume's built-in centrifugal pump. An additional submerged pump with a calibrated maximum discharge of (13 ℓ/s) was therefore used in addition to the flume's built \-in centrifugal pump (with a maximum value of 27 ℓ/s).
The head upstream from the gate was measured using the point gauge with a 0.1 mm vernier. The head corresponding to each discharge was measured twice; once at the rising stage and once during the falling stage.
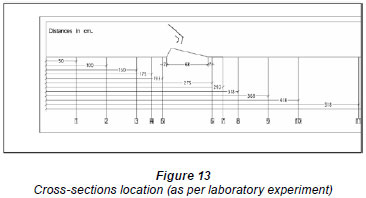
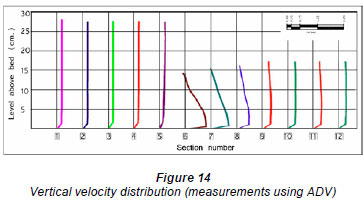
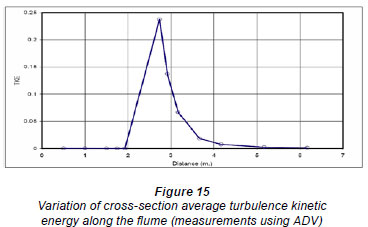
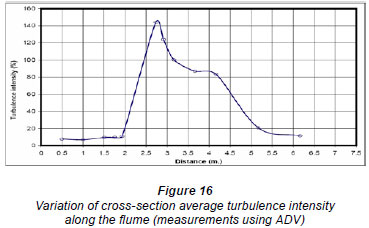
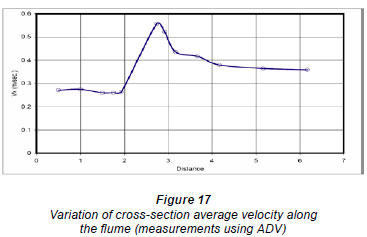
The flume was divided into 12 cross-sections; 5 crosssections were located upstream of the gate and 7 cross-sections were located downstream of the gate. The distances and locations of the cross-sections are shown in Fig. 13. The vertical velocity profile at each section is shown in Fig. 14, and the typical cross-section average turbulence kinetic energy, turbulence intensity, and velocity are shown as a longitudinal profile along the flume length in Figs. 15 through 17. The data obtained from the experiments give full details of the flow structure upstream and downstream of the gate; these data were used to calibrate the numerical model and to ensure the accuracy of its results.
Flow stages in double baffled gates
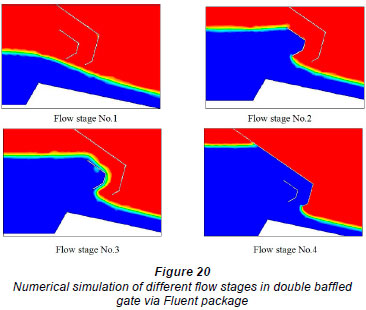
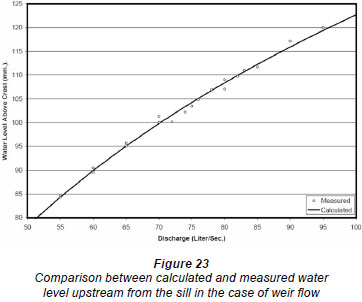
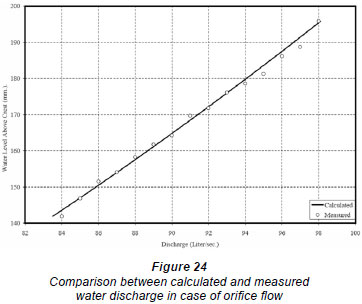
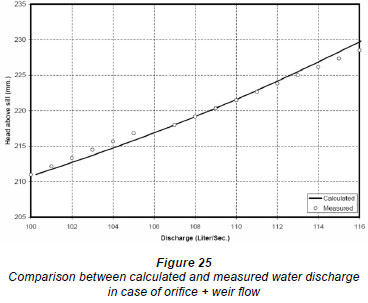
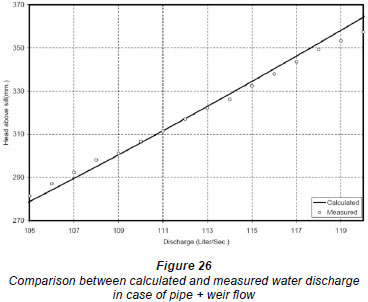
The flow through double baffled gates can be divided into 4 main flow stages. The first stage is the free (pure) weir flow case. In this case, the upstream water surface did not reach the lower tip of the upstream baffle (Fig. 18, Shot 1). The second stage is the free orifice flow case (Fig. 18, Shot 2). In this flow case, the upstream water surface submerges the upstream gate opening and the gate acts as an orifice. The third stage exists when the upstream water level starts spilling freely from the crest of the upstream baffle (Fig. 18, Shot 3). In such a flow case, a combination of weir flow (over the upstream baffle) and orifice flow takes place. The fourth and last flow stage exists when the upstream water level increases, causing the gap between the 2 baffle gates to be full of water, causing it to act as a pipe or conduit (Fig. 18, Shot 4). Therefore, in the last flow stage there is a combination of orifice flow (existing underneath) and pipe flow (existing between the 2 baffles).
Numerical simulation
Computational fluid dynamics (CFD) is one of the branches of fluid mechanics that uses numerical methods and algorithms to solve and analyse problems that involve fluid flows. Computers are used to perform the millions of calculations required to simulate the interaction of fluids and gases with the complex surfaces used in engineering. Even with simplified equations and high-speed supercomputers , only approximate solutions can be achieved in many cases. Ongoing research, however, may yield software that improves the accuracy and speed of complex simula tion scenarios such as turbulent flows. Fluent is a state-of-the-art computer program for modelling fluid flow in complex geometrics. Fluent provides complete mesh flexibility including the ability to solve the flow problems using unstructured meshes that can be generated about complex geometrics with relative ease.
Fluent package
Fluent (ANSYS, 2006) is one of the CFD programs which provide comprehensive modelling capabilities for a wide range of incompressible and comprisable, laminar and turbulent fluid flow problems. Steady state or transient analyses can be performed. In Fluent, a broad range of mathematical models for transport phenomena is combined with the ability to model complex geometrics. For all flows, Fluent solves conservation equations for mass and momentum. Fluent is written in the C computer programming language and makes full use of the flexibility and power offered by the language. Consequently, true dynamic memory allocation, efficient data structures, and flexible solver control are all possible. All functions required to compute a solution and display the result are accessible in Fluent through an interactive, menu-driven interface. Both single-precision and double-precision versions of Fluent are available and, for most cases, the single-precision solver will be sufficiently accurate, as was the case for this study.
Multi-phase volume of fluid (VOF) model
The VOF model is a surface tracking technique. It is designed for two or more immiscible fluids where the position of the interface between the fluids is of interest (in our case water and air at the free surface, and in bubbles formed in the hydraulic jump location). In the VOF model, a single set of momentum equations is shared by the fluids, and the volume fraction of each of the fluids in each computational cell is tracked throughout the domain. Applications of the VOF model include stratified flows, free-surface flows, filling, sloshing, the motion of large bubbles in a liquid, the motion of liquid after a dam break, the prediction of jet breakup (surface tension), and the steady or transient tracking of any liquid-gas interface. The VOF formulation relies on the fact that two or more fluids (or phases) are not inter-penetrating. For each additional phase which is added to the model, a variable describing the volume fraction for that phase is introduced. In each control volume, the volume fractions of all phases sum to unity. The fields for all variables and properties are shared by the phases and represent volume-averaged values, as long as the volume fraction of each of the phases is known at each location. Thus the variables and properties in any given cell are either purely representative of one of the phases, or representative of a mixture of the phases, depending upon the volume fraction values. In other words, if the qth fluid's volume fraction in the cell is denoted as αq, then the following 3 conditions are possible:
| Case (1) : | α q=0 | The cell is empty (of the qth fluid) | ||
| Case (2) : | α q=1 | The cell is full (of the qth fluid) | ||
| Case (3) : | 0<αq<1 | The cell contains the interface between the fluids |
Based on the local value of α q, the appropriate properties and variables will be assigned to each control volume within the domain.
Volume fraction equation
The tracking of the interface(s) between the phases is accomplished by the solution of a continuity equation for the volume fraction of one (or more) of the phases. For the qth phase, this equation has the following form:
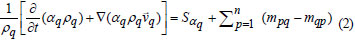
where:
mqp is the mass transfer from phase q to phase p, and
mpq is the mass transfer from phase p to phase q.
By default the source term on the right-hand side of Eq. (2) [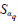 ] is zero, but a user-defined mass source for each phase can be specified. The volume fraction equation will not be solved for the primary phase; the primary-phase volume fraction will be computed based on the following constraint:
] is zero, but a user-defined mass source for each phase can be specified. The volume fraction equation will not be solved for the primary phase; the primary-phase volume fraction will be computed based on the following constraint:

Properties
The properties appearing in the transport equations are determined by the presence of the component phases in each control volume. In a 2-phase system, for example, if the phases are represented by subscripts 1 and 2, and if the volume fraction of the second of these is being tracked, the density in each cell is given by:

In general, for an N-phase system, the volume-fraction-aver aged density takes on the following form:

All other properties (e.g., viscosity) are computed in this manner.
The momentum equation
A single momentum equation is solved throughout the domain, and the resulting velocity field is shared among the phases. The momentum equation, shown below, depends on the volume fractions of all phases through the properties ρ and µ.
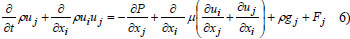
One limitation of the shared-fields approximation is that in cases where large velocity differences exist between the phases, the accuracy of the velocities computed near the interface can be adversely affected.
Boundary conditions
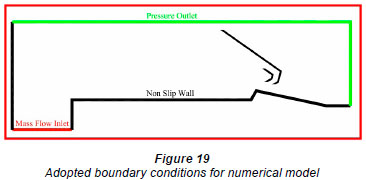
The boundary conditions in case of open channel flow are critical for good simulation since the flow is 2-phase flow. The inlet can be modelled as a mass flow inlet or velocity inlet since the flow is incompressible. The pressure outlet condition is imposed at the outlet with zero gauge pressure. This is acceptable since for incompressible flows the pressure gradient is required for solving the Navier-Stokes equation and not the absolute pressure. The top of the domain is considered a pressure outlet, either to allow the air to exit from the domain without changing its density or without affecting the water flow underneath it. A no-slip velocity condition is applied for all remaining surfaces (Fig. 19).
Sensitivity analysis for mesh size
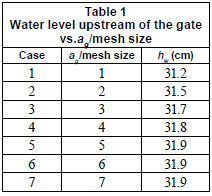
In CFD simulations, the mesh should be fine enough to capture the flow gradients and also to reduce numerical errors. In general, this is achieved by meshing with a different number of grid elements and observing the change in the quantity of interest. Since the water level upstream of the gate (hw) is one of the most important quantities that affects the conveyed flow through the double baffled gate, in this study it was selected for the process of checking the grid dependence. A mesh sensitivity analysis was conducted where 7 different grids were tested and meshed with different grid spacing. All simulations were performed via the standard K-e model while keeping all of the other variables unchanged. Table 1 gives the results of the mesh sensitivity study on the estimated upstream water depth (hw). It was noted that discretising the gate opening into at least 5 elements is the accepted minimum, so as to avoid the effect of coarse mesh sizing on the numerical estimation of the upstream water depth.
Effect of the chosen turbulence model
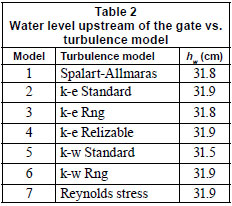
Several turbulent closure models are available in the Fluent package. Thus it is crucial to investigate the dependence of the numerical model predictions on the selected turbulence model. The proper mesh size obtained from the previous step was adopted and the numerical runs were repeated using different turbulence models. Table 2 summarises the results. It was noted that 6 out of 7 of the turbulence closure models (including the default k-ε model) used produced almost the same results, while the k-ω model gave the outlier value. Accordingly, the default k-ε model was adopted for all the runs that followed.
Model calibration
The numerical model has been calibrated by selecting a relevant roughness height of the flume boundaries. Figure 20 presents the numerical simulation of the 4 flow stages using the Fluent package. It was noted that there is a very good match between the numerical results as shown in Fig. 20 and the laboratory results given in Fig. 18. Figure 21 also compares the results of the numerical and physical experiments for the flow at Stage 3, when part of the gap between the 2 baffles started to be partially full. A good match between the numerical and laboratory results was also obtained.
Simulation cases
In order to evaluate the effect of each design parameter related to the baffled gate distributors, several simulations were done using Fluent. Typical dimensions of the double baffled control gate have been proposed and considered as a base run, called the reference gate dimensions. For sake of comparison, all of the other runs were compared to the results produced from the reference gate dimensions, shown in Fig. 22.
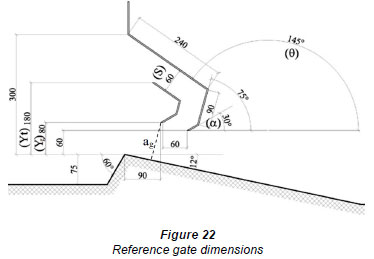
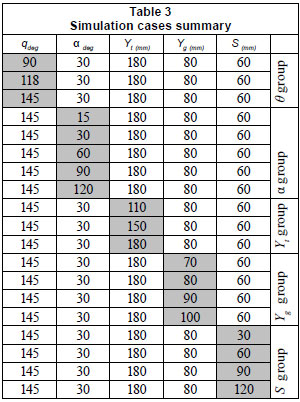
As a first step, the geometric elements of 5 gates have been selected for further examination. These geometric elements include: yt, yg, θ, S and α (refer to Fig. 22 for definitions). Secondly, a set of numerical experiments have been carried out to study the sensitivity of each one of the aforementioned geometric elements on the gate rating curve. For this regard, a matrix of numerical runs has been developed with a total number of 19 runs as shown in Table 3. In each run, a number of sub-runs were performed in order to cover the full range of the gate rating curve. In other words, the numerical simulations were divided into 5 groups as indicated in Table 3, to simulate the effect of a specific geometric parameter on the gate rating curve while keeping the other geometric elements constant.
Analysis of data
The outcome of the 19 numerical experiments is presented in detail in Helmy (2008). Based on these results, the following equations were developed to describe the H-Q behaviour for each flow stage based on the numeri cal simulation results. Each equation has been given in its canonical form. Figures 23 through 26 show the comparison between calculated and measured flow values versus different head values.
Stage (1):

Stage (2):

Stage (3):
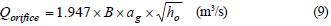
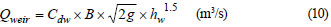
Stage (4):
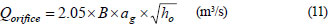
where:
Q is the discharge throughout the gate (m3/s)
B is the channel width (m)
ag is the upstream baffle gate opening measured perpendicular to the bed (m)
h is the upstream head of the gate measured vertically from the crest (in the case of pure weir flow) (m)
ho is the upstream head (for all cases excluding the pure weir flow case)
hw is the head over the weir (hw =ho-yt)
Cdw is the coefficient of discharge for the upper flow weir
Design example
Design problem: A baffled gate distributor must be designed to deliver an average discharge of 1 m3/s. Determine gate dimensions, the gate operating head, and the maximum upstream head variation to give a maximum discharge variation of 10%. Compare the results with those for an ordinary sluice gate.
Solution: Using the design spreadsheet, the gate rating curve (as given in Fig. 27) and the required gate dimensions (as shown in Fig. 28) can be obtained. The gate dimensions and hydraulic parameters can be summarised as follows:
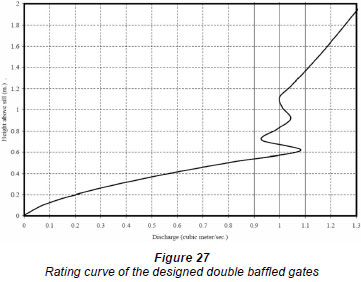
• Required sill height = 8 cm
• Vertical upstream gate opening (yg) = 39 cm
• Maximum downstream baffle gate height = 303 cm
• Nominal (working head) = 95 cm
• Maximum upstream head variation around the nominal head value = 55 to 135 cm
For ordinary sluice gate the head variation corresponding to 10% variation in discharge = 21% but in double baffled gate distributor the variation in head = 45%.
Conclusion
The flow through the double baffled gate has been investigated experimentally and numerically. The study has shown that the discharge of open channels can be significantly controlled by using such a controlling module. The studied cases revealed that ± 45% variation in nominal upstream head can be achieved with ± 10% variation in the nominal design discharge. It was also found that the gate inclination angle (α, refer to Fig. 22) and the gate spacing (S) are the most effective parameters in controlling the H-Q relation. The study has shown that the optimum value of α is about 30º, and of the gate spacing (S) is 60 to 70% of the gate opening.
A new design methodology was formulated and developed in an Excel spreadsheet for the double baffled gate distributors (commercially known as 'NYRPIC' gates) based on the verified numerical results. The required data for using the achieved equations are an approximate value for the gate opening and the nominal upstream head. The output will contain the rating curve of the gate, the allowable head variation, and the dimensions of the gate.
The study indicated the power of CFD models (such as Fluent) in revealing the fine flow structure details for the different flow regime and flow stages.
References
ANSYS (2006) Fluent User Manual. [ Links ] BINNIE AM (1952) The flow of water under a sluice-gate. Quart. J. Mech. Appl. Math. V 4 395-407. [ Links ]
DIERSCH HJ, SCHIRMER A and BUSCH KF (1977) Analysis of flow with initially unknown discharge. J. Hydraul. Div. Proc. ASCE 103 213-232. [ Links ]
FANGMEIR DD and STRELKOFF T (1968) Solution for gravity flow under a sluice gate. J. Eng. Mech. Div. Proc. ASCE 94 153-176. [ Links ]
GORDON L and COX J (2000) Acoustic Doppler Velocimeter performance in a laboratory flume. Nortek USA Technical Rep., Nortek USA, San Diego. [ Links ]
HELMY AM (2008) Experimental and Numerical Investigation of Flow Schemes at Constant Discharge Baffled Irrigation Gates. Ph.D. Thesis, Faculty of Engineering, Cairo University. 163 pp. [ Links ]
HENRY H (1950) Discussion on diffusion of submerged jets. Trans. ASCE 115 687-697. [ Links ]
ISAACS LT (1977) Numerical solution for flow under sluice gates. J. Hydraul. Div. Proc. ASCE 103 473-482. [ Links ]
JOHN K and JUNWOO L (2000) A liner process in wall bounded turbulent shear flows. J. Phys. Fluids 12 (8) 1885-1888. [ Links ]
KIM DG (2007) Numerical analysis of free flow past a sluice gate. KSCE J. Civ. Eng. 11 (2) 127-132. [ Links ]
KRAATZ DB and MAHAJAN IK (1975) Small hydraulic structures. In: Irrigation and Drainage Paper (FAO) No. 26 (v.1). Land and Water Development Div. FAO, Rome (Italy). 422 pp. [ Links ]
LARSEN AP and MISHRA PK (1990) Constant discharge device for field irrigation. J. Hydraul. Res. 28 (4) 482-489 [ Links ]
RAJARATNAM N and SUBRAMANYA K (1967) Flow equation for the sluice gate. J. Irrig. Drain. Div. Proc. ASCE 93 (IR3) 167-186. [ Links ]
SALAHELDIN T (2003) Experimental Modeling of Local Scour in Cohesive Soil. Ph.D. Thesis, University of South Carolina. [ Links ]
SOULSBY RL and DYER KR (1981) The form of the near bed velocity profile in a tidally accelerated flow. J. Geophys. Res. 86 8037-8074. [ Links ]
VOULGARIS G and TROWBRIDGE JH (1998) Evaluation of the Acoustic Doppler Velocimeter (ADV) for turbulence measurements. J. Atmos. Ocean Technol. 15 272-289. [ Links ]
Received 5 June 2010; accepted in revised form 1 February 2011.
* To whomall correspondence should be addressed. 02-010-3388-986; fax: 02-3573-2948; e-mail: mohamedelgamal@yahoo.com














