Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
Water SA
versión On-line ISSN 1816-7950
versión impresa ISSN 0378-4738
Water SA vol.36 no.3 Pretoria abr. 2010
Revisiting the stream-aquifer flow problem with a flux-based Green element model
AE Taigbenu*; E Nyirenda
School of Civil and Environmental Engineering, University of the Witwatersrand, Private Bag 3, WITS 2050, Johannesburg
ABSTRACT
This revisit of the stream-aquifer problem is based on a recent flux-based Green element formulation which offers more accurate solutions than previous formulations presented in Taigbenu (2003). Its accuracy also surpasses those provided by finite element and finite difference methods using grids that are coarser. As in all Green element formulations, the current formulation is predicated on the singular boundary integral theory that is implemented in an element-by-element fashion. What is new in the current formulation is that it calculates the fluxes at all nodes and not only at external nodes. While this approach exhibits much improved accuracy, its drawback lies with handling an increased number of unknowns. This drawback is, however, compensated for by the fewer elements required to achieve accuracies comparable to other conventional numerical methods. In this paper, it is demonstrated that with between 20% and 30% of elements used in finite element and finite difference models, comparable accuracy is achieved with this formulation. The main significance of the current computational technique is that it preserves the flux calculations in a manner that is consistent with the stream-aquifer interaction problem.
Keywords: stream-aquifer interaction, The Green element method
Introduction
While the estimation of stream-aquifer fluxes continues to attract the attention of hydrologists who understand that the fluxes are different manifestations of a unitary water system (the hydrological cycle), arid and semi-arid areas present the most critical areas where the fluxes are the life-line of streams and rivers (Butterworth et al., 1999). The traditional approach to estimating these fluxes is through classical hydrological methodology of hydrograph separation using the distinguishing characteristics in time scales between surface runoff and baseflow (Chow et al., 1988). The baseflow, comprising interflow and groundwater contribution to the adjoining stream, can be related to the hydraulic conductivity of the adjoining aquifer and the interface characteristics between the aquifer and the surface water body, although most published works rarely explicitly provide this linkage (Hughes et al., 2003; Priest and Clarke, 2003; Smakhtin, 2001). The second approach that is sometimes followed calculates the fluxes from the solution of the flow differential equation (the Laplacian) and explicitly incorporates the non-linear free-surface equation (Bear, 1979). This approach, referred to as the hydrodynamic one, best approximates the aquifer-streamflow problem, but is rarely followed because of the difficulties associated with its solution process (affecting the non-linear free surface condition of which the free surface is part of the solution that is sought) and the fact that available field hydrogeological data, which are usually depth-averaged, are not sufficiently detailed enough to support it. The few solutions of the hydrodynamic model have been carried out on a 2-D vertical section of the aquifer and stream, and assumed that variation of fluxes in the stream-wise direction is negligibly small. The earliest solution of the 2-D hydrodynamic model was based on the Hele-Shaw apparatus which served a useful purpose of providing a physical realisation of the stream-aquifer interaction problem (Ibrahim and Brutsaert, 1965; Rochester and Kriz, 1968). Attempts have also been made to solve the 2-D hydrodynamic model by analytical techniques for idealised aquifer parameters and geometries in which the region is of infinite extent (Jeng et al., 2005a; b; Serrano, 2003; Teo et al., 2003; Schmitz and Edenhofer, 2000; Parlange and Brutsaert, 1987). The analytical solutions are of limited application and can rarely be extended to aquifer geometries that are finite and irregular or cases where the aquifer is heterogeneous. It is these limitations that are overcome by numerical methods of which the boundary-conforming formulation of the boundary element method (BEM) has shown a lot of promise, especially in its ability to track the moving free-surface (Liggett and Liu, 1983; Dillon and Liggett, 1983). A recent solution by the finite difference method has been carried out by Singh and Jaiswal (2006), who incorporated the effect of recharge and depth-dependent evapotranspiration on the water table fluctuation.
Because aquifers generally have large lateral dimensions in relation to the water table elevation, the hydrodynamic flow equations can be depth-averaged so that the modelling is simplified. This is generally referred to as the hydraulic approach which is most widely pursued in addressing the stream-aquifer problem, and provides reliable estimates of the interaction fluxes except at interfaces of the stream and aquifer where significant gradients of the water table occur. It incorporates the Dupuit-Forchheimer approximation, neglects flow velocities in the vertical direction, and effectively assumes the nonexistence of a seepage face at the interface between the stream and the aquifer. Apart from the computational simplification achieved by the approach, hydrogeological field data are readily obtained to support it, and in addition regional groundwater flow and its interaction with the stream along its length are more readily obtained. The hydraulic model involves solving the non-linear Boussinesq equation, which still presents considerable challenges to analytical techniques. One of the earliest analytical solutions using similarity considerations was obtained by Boussinesq (1904). Other analytical solutions have been achieved through some form of simplification or linearisation to the non-linear differential equation and/or imposition of some idealised boundary/initial conditions (Serrano et al., 2007; Telykovskiy and Allen, 2006; Hunt, 2003; Lockington, 1997; Guo, 1997; Serrano, 1995; Streltsova, 1975; Desai, 1973). Although most of the analytical solutions are in the form of a series, with some perturbation parameter that indicates their range of validity, their usefulness lies mainly in validating numerical models. All these solutions have been obtained for flow in one spatial direction and as such do not address the regional groundwater-surface water flow problem. Numerical solutions of the regional groundwater-surface water flow problem abound in the literature. The finite difference method (FDM) has been widely applied (Hornberger et al., 1970) and is currently embedded in a commercially-available package like MODFLOW (McDonald and Harbaugh, 1988; Rodriguez et al., 2006; Fox 2003).
The finite element method (FEM) has also been widely applied to the regional stream-aquifer problem (Huyakorn and Pinder, 1983). One of the primary motivations for the use of a singular integral-based method for the solution of the stream-aquifer problem is its second-order accuracy in calculating the interaction fluxes. The Green element method (GEM) is an integral-based method that uses the singular fundamental solution to a unit forcing function to achieve an integral realisation of the flow equation that is then discretely implemented in an element-by-element fashion (Taigbenu, 1995; 1999). The earlier formulation of GEM (Taigbenu, 2003) that was applied retained the fluxes only on external boundaries but approximated them in terms of the water table elevation at internal nodes. That approximation introduced some errors, which are herein overcome by retaining the fluxes at all nodes in the computational domain. In essence, the current formulation exhibits considerably improved accuracy over the previous one, but at a price of escalation in the number of unknowns. Whereas this drawback is undesirable, it is counteracted by the fact that the enhanced solution accuracy of the current formulation is obtained with a very coarse grid. In other words, it requires a minimal number of elements to achieve very accurate solutions. It is demonstrated with numerical examples that, with between 20 to 30% of the discretisation grid of FEM and FDM, superior solutions are obtained with the current flux-correct GEM. It is this advantage of the method that makes it most appealing in addressing the stream-aquifer problem.
Flow equation
The flow equation in an unconfined aquifer adjoining a river is obtained by integrating the mass conservation equation and Darcy law over the flow thickness of the aquifer. It is commonly known as the non-linear Boussinesq equation (Bear, 1979):
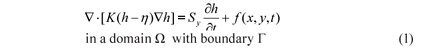
in which:
h ≡ h(x, y, t) is the hydraulic head or water table elevation above a datum
∇ is the two-dimensional gradient operator
K ≡ K(x, y) is the hydraulic conductivity
η ≡ η (x,y) is the bedrock elevation about the datum
Sy is the specific yield of the aquifer
f accounts for distributed recharge from natural and artificial sources and as well as point sources/sinks due to pumping or recharge wells
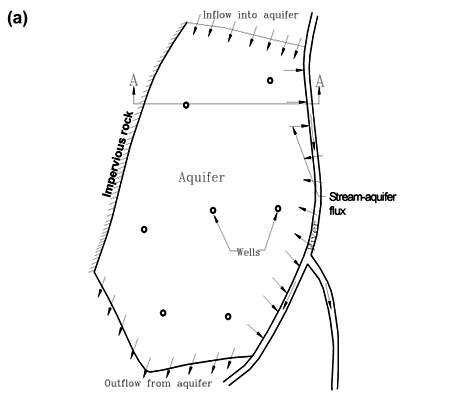
Adapted from Taigbenu (2003), the flow problem is illustrated in plan and section in Figs. 1a and 1b. In general the hydrogeological parameters of the aquifer vary spatially (heterogeneous aquifer), and similarly for the bedrock elevation. When the aquifer is confined or leaky-confined, the governing equation is generally easier to solve because it is linear. Being a time-dependent problem, the distribution of the water table elevation has to be specified everywhere in the aquifer at the initial time t0, that is
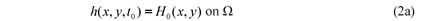
At every time, appropriate conditions have to be specified for the water table and/or the flux on the boundary in order to have unique solutions to Eq. (1). These conditions are a combination of the Dirichlet-type boundary condition that specifies the water table along a part of the boundary Γ1,

and the Neumann-type boundary condition that specifies the normal flux q across another segment of the boundary Γ2,

in which n is the outward pointing unit normal vector on the boundary.
Of interest in the stream-aquifer interaction problem is estimating the normal flux q along a boundary which is common to the aquifer and the stream. Eq. (1) is re-expressed as a Poisson-type equation

in which:
Ψ = ln k and Φ= 1/K (h-η)
When the bedrock of the aquifer is along the horizontal datum, then η = 0 and Eq. (3) simplifies to
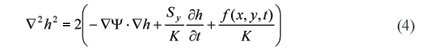
Although Eq. (3) is simpler than Eq. (4), both are still non-linear and potentially challenging to any solution strategy. In most instances, analytical solution strategies fail. The first term on the right hand side of both equations accounts for the heterogeneity of the medium which falls off when the medium is homogeneous. The flux GEM is presented here for the more general case, which is Eq. (3); it is understood that the method is coded appropriately when Eq. (4) applies.
To avoid re-introducing GEM, this paper will focus mainly on the aspects of the current formulation, referred to as the flux GEM, which are different from previous formulations. In this regard, it is assumed that the reader has a fair appreciation of GEM that is presented in such references as Taigbenu (1995; 1999). GEM uses the second Green's identity to transform the flow differential Eq. (3) into an integral one that is singular because of its fundamental solution, which is the response function of an infinitely extensive aquifer to an instantaneous unit pumping rate. The integral equation is solved for each element that is used to discretise the flow region. Suitable elements are, in general, polygons (rectangles for regular flow regions and triangles for irregular geometries). The outcome of this discretisation process is a system of discrete equations that are in terms of the water table h and the flux q. In previous formulations, the flux q at internal nodes is expressed in terms of h, but in the current formulation the flux is retained at every node. The system of discrete equations, still non-linear, is linearised by the Newton-Raphson technique.
Flux Green element formulation
Eq. (3), treated as a Poisson equation, is complemented by an auxiliary equation ∇2 G = δ(r - ri) that applies to an infinite space. With the known singular fundamental solution to the auxiliary equation, that is G = ln(r - ri ), Green's second identity is used to derive the integral representation of Eq. (3). It is
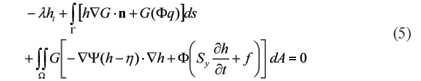
where:
subscript i denotes the source point ri = (xi, yi)
λ is the nodal angle at ri that is obtained from a Cauchy integration of the Dirac delta function δ about the source point
The integral Eq. (5) is implemented in each element used to discretise the flow domain Ω. With the use of Lagrange-type linear interpolations for h, q, Φ and Ψ (h – η), those quantities are then expressed in terms of their nodal values. Denoting Nj as the interpolation function applicable to node j, the discrete equation resulting from evaluating the integrals in Eq. (5) on the boundary and within each element denoted as Ωe is

where Λ = Ψ (h – η) and the matrices are defined as:

All the integrals in Eq. (7) are evaluated in an exact manner when rectangular and triangular elements are used to discretise the flow region, thereby enhancing the accuracy of the numerical scheme. An aggregation of the discrete element, Eq. (6), is done for all elements that are used to discretise the flow region to obtain a matrix equation of the form

It should be realised that the matrices and the force vector Fi in Eq. (8) depend on the water table h, making it non-linear. Using a differencing approximation for the time derivative, dh/dt ≈ (h(2) - h(1))/ Δt, in conjunction with a weighting parameter θ that accounts for the position in which differencing is done within the time step Δt, Eq. (8) becomes

where the superscripts 2 and 1, respectively, denote the current time t2 = t1 + Δt and previous time t1 and ω = 1 – θ. A more compact form of Eq. (9) is

where  is a mixed vector of the unknowns at every node at the current time, and Ri is a vector of known quantities comprising the initial data, forcing term, and prescribed boundary conditions. Equation (10) is non-linear and is amenable to linearisation by the Newton-Raphson (N-R) algorithm (Ypma, 1995; Taigbenu and Onyejekwe, 1999).
is a mixed vector of the unknowns at every node at the current time, and Ri is a vector of known quantities comprising the initial data, forcing term, and prescribed boundary conditions. Equation (10) is non-linear and is amenable to linearisation by the Newton-Raphson (N-R) algorithm (Ypma, 1995; Taigbenu and Onyejekwe, 1999).
Without elaborating on the N-R algorithm, its main goal is to iteratively solve for h and q by making use of the Jacobian matrix that is derived from Eq. (10). The Jacobian matrix is:

where the additional index m represents the iteration number. The solution for the vector of unknowns is then obtained from:

where:
 is a known estimate of the solution at the previous iterate
is a known estimate of the solution at the previous iterate
 is the increment which is used to refine the previous iterate
is the increment which is used to refine the previous iterate
 to obtain the current iterate in the following manner:
to obtain the current iterate in the following manner:
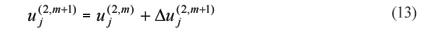
The iteration process takes place at each time step till the increment becomes acceptably small according to a convergence criterion based on either the absolute or relative error. We have found the N-R algorithm to converge very quickly, requiring usually no more than 6 iterations in most of the examples.
The calculation of the water table elevation and the normal flux at every node presents a new challenge of having fewer generated integral equations than unknowns at internal nodes. This is a closure problem that does not exist at external nodes where the prescribed boundary conditions make up for the shortfall in the number of generated integral equations. By using Stokes theorem a compatibility relationship for the fluxes is derived that resolves the closure problem at internal nodes (Taigbenu, 2009).
Reviewing the current formulation shows that, apart from round-off errors that are inevitable with finite precision machines, the only other major sources of error associated with the formulation are the linear interpolation and the differencing of the time derivative. That means that when the unknowns are fairly well approximated by the interpolation functions, very high accuracy can be expected with the current formulation. It is this feature that allows the flow region to be coarsely discretised, as demonstrated in the next section with a few numerical examples. On the downside, there is considerable increase in the number of unknowns because of the fluxes that are calculated at every node, but this is compensated by the fewer elements that are required to generate accurate results.
Examples
Four examples of stream-unconfined flow are solved by the current formulation. Three of these examples were addressed previously in Taigbenu (2003). The results are not only benchmarked with analytical solutions, where they are available, but with other numerical solutions. As will be observed in the comparisons, a higher level of accuracy is achieved with the current formulation using as little as 20% of the grid of other numerical methods. For large-scale problems, such as that demonstrated in Example 4, this means tremendous savings in computing resources.
Example 1
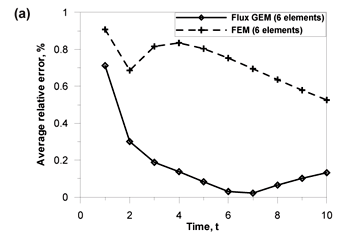
In this example, a semi-infinite unconfined aquifer lies between 2 rivers whose water levels are maintained at 33 m and 21 m elevations above the bedrock of the aquifer. The rivers are separated by a distance of 300 m, while the aquifer receives uniform recharge of 8 mm/h along its entire length. The initial water table distribution is h = 33 – 0.04x. The transient evolution of the water table distribution is sought as a result of the head difference between the rivers and the recharge from precipitation. The aquifer is assumed to be homogeneous and isotropic with hydraulic conductivity of 0.6 m/h and specific yield of 0.2. The steady state scenario of this example is widely reported in the groundwater literature as the Dupuit problem which has an exact solution. That solution is compared with that obtained by the previous Green element method (Model 1 – Taigbenu, 2003), using 10 linear rectangular elements each with a length of 30 m in the x direction, and a time step of 30 h for the first 600 h and 60 h thereafter till 1 200 h. The steady-state solution was simulated by FEFLOW (a finite element model) and MODFLOW (finite difference model) and the results supplied by Freeternity Rusinga. Using the same time discretisation as the previous GEM, the current formulation simulates this example with 10, 5 and 3 linear rectangular elements. The results are presented in Fig. 2, in terms of relative error as a percentage for the flux GEM, FEM and FDM. At first, it looks improbable that a formulation that uses only 30% of the grid of FEM and FDM will give more accurate results. As indicated earlier, this should not come as a surprise; as long as the interpolation function correctly captures the distribution of the water table and the flux, high accuracy is bound to be achieved with the flux GEM.

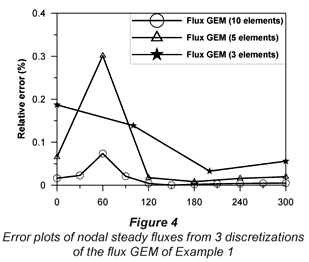
As the main thrust of this paper is assessing the predictive capability of the current GEM for the stream-aquifer fluxes, we now make comparison of the hydrograph from the previous and current Green element formulations. These are presented in Fig. 3. Because the exact solution for the flux is available only at steady state, we are unable to make accuracy comparisons of the numerical solutions during the transient phase. However, judging from the fact that the hydrographs from the flux GEM with 3 and 10 elements are virtually the same and both give better predictions of the steady fluxes at the rivers, we are confident in stating that the current formulation gives a better prediction of the stream-aquifer fluxes. What this example illustrates, as with other works of ours on the current formulation (Taigbenu, 2008), is that no useful purpose is served in terms of accuracy enhancement by using a more refined grid. One more analysis with this example compares the steady-state fluxes at every node when the flux GEM is discretised with 10, 5 and 3 elements. This comparison is possible because of the additional information on the nodal fluxes that this formulation provides. This kind of information is particularly useful when a groundwater flow model is coupled with a contaminant transport model, where the latter model receives input of the fluxes from the former model at every node. The results, presented as relative error plots in Fig. 4, are remarkably good, considering that the highest relative error of about 0.3% occurs at the mound of the water table where the flux is negligibly small.

Example 2
This example is that of a stream-aquifer problem arising from a flood wave passing through the river. It is assumed that before flooding conditions occurred, the river and aquifer are in hydraulic equilibrium with the water table and river stage at the same elevation of 16 m above the bedrock of the aquifer. The flood stage has a sinusoidal variation for the first 6 h, and maintains a crest of 2 m for the next 4 h after which it decays exponentially with a depletion rate of 0.1/h. This is represented mathematically as:

The flow in the aquifer takes place along its 200 m length, and is considered infinite in extent in the other direction. With a no-flux condition at one end of the aquifer, the flow in the aquifer is triggered by the imbalance in head due to the flood wave in the river. The hydraulic conductivity and specific yield of the aquifer are, respectively, 3.6 m/h and 0.35. Two scenarios are considered; one with no recharge on the unconfined aquifer and the other with a uniform recharge of 10 mm/h per unit length of the aquifer. The previous GEM used a uniform spatial discretisation of 50 square elements and a uniform time step of 0.25 h. In the current flux GEM, a time step of 0.5 h is used, while the region is discretised into 10 and 5 uniform elements, representing 20% and 10% of the grid of the previous GEM.
The results for the water table distribution at different times are presented in Fig. 5a, when there is no recharge, and Fig. 5b with recharge. The predicted hydrographs from both GEM formulations with and without recharge are shown in Figs. 6a and 6b. The flux GEM simulation results are comparable to those of the previous GEM using only 10% of the elements. That should not come as a surprise because by retaining the flux at all nodes numerical errors are considerably curtailed. In fact, as long as the minimum number of elements in the flux GEM to correctly interpolate the water table and fluxes has been achieved, excellent results can be expected with the method. That accounts for comparable results when 5 and 10 elements are used in the flux GEM simulation of this example.

Example 3
This example is one of the few transient nonlinear Boussinesq problems with an exact solution that was first developed by Sokolov and reported by Polubarinova-Kochina (1977). Transient flow takes in an unconfined aquifer with a horizontal bedrock in one spatial dimension x in which the water level in the stream changes with time at one end of the aquifer and a no-flux condition exists at the other end of the aquifer. There is no forcing term, and the flow dynamics in the aquifer arises from the interaction of the varying water in the stream and aquifer. In dimensionless form, the differential equation is
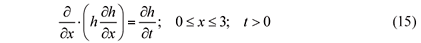
With the water level variation in the stream given by

there is a no-flux boundary at x = 3, while the water table distribution in the aquifer at initial time is

The exact solution is given by
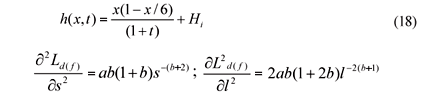
The example is simulated in 2 dimensions with the current formulation and the FEM by imposing no-flux boundaries at the upper and lower ends of the aquifer in the y direction. For both numerical methods, 6 uniform rectangular elements are used to discretise the domain so that the length of each element is 0.5, while the temporal dimension is uniformly discretised with a time step of 0.25. The fully implicit finite differencing with θ = 1 is used. The exact and the flux GEM solutions of the water table in the aquifer are presented in Fig. 7a at times t = 1, 3, 5, 7 and 10, while both solutions are presented in Fig. 7b for the hydrograph of discharge from the aquifer into the stream. Apart from the underestimation of the peak discharge by the flux GEM, due to the coarse time step adopted, the exact solution is corrected predicted by the numerical scheme. Comparison of the flux GEM and FEM is then carried out. Fig. 8a shows the temporal distribution of the relative errors in percentage averaged at all nodes where the water table is calculated in the aquifer, while Fig. 8b shows the relative errors in percentage of the discharge from the aquifer to the stream normalised by the peak discharge. Both results show that the flux GEM outperforms FEM in predicting the water table and discharge.
Example 4
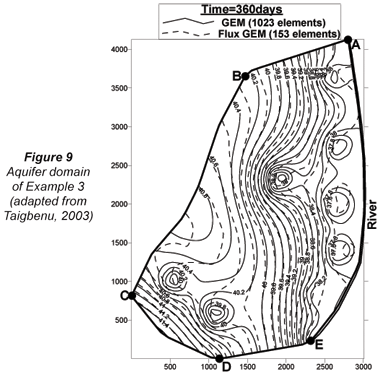
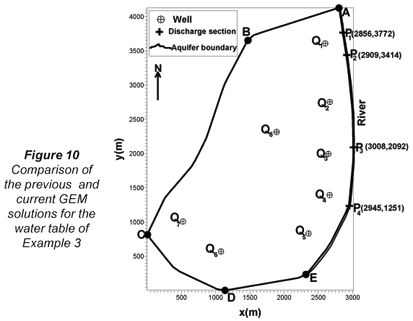
This example is a physically realistic stream-unconfined flow interaction in which regional flow occurs in an aquifer of 8.1 km2 located west of a river with adjoining length of about 4 km (see Fig. 9, adapted from Taigbenu, 2003). The locations and pumping rates of the 8 wells in operation in the aquifer are presented in Table 1, while uniform effective recharge occurs everywhere in the aquifer at a rate of 2.2 mm/d. The northern, southern and western boundaries of the aquifer, denoted in Fig. 9 as AB, DE and BC, are no-flux boundaries, while the south-western boundary CD allows in a discharge of 1.7 m3/d per metre length of boundary. There is hydraulic equilibrium initially between the aquifer and river with the occurrence of a uniform water elevation of 40 m above the aquifer bedrock. Thereafter, the water level in the stream falls exponentially with a depletion rate of 0.04/d, that is h = 38 + 2e–0.04t. The hydraulic conductivity and specific yield of the aquifer are 21.2 m/d and 0.2, respectively. A previous GEM simulation presented in Taigbenu (2003) had the aquifer discretised into 1 023 triangular elements. Here 153 linear triangular elements are used in the current flux GEM to discretise the aquifer. This represents 15% of the grid of the previous formulation. The temporal dimension is discretised uniformly, as previously, with a time step of 2 d. Comparison of the contours of water table levels at a time of 360 d from the previous GEM and the current GEM is made in Fig. 10, which indicates that both formulations predict similar regional flow regimes. Along the river, hydrographs are simulated at sections P1, P2, P3, and P4, whose coordinates are indicated in Fig. 9. There are discrepancies between the solutions from the 2 Green element models, although both solutions show a general trend of decrease in flow discharges at late times due to the effects of Wells Q1, Q2, Q3, Q4 and Q5 (Fig. 11). Further investigation into these discrepancies in the hydrographs prompted another simulation with the flux GEM using a finer grid of 285 triangular elements. The hydrographs are closer to those obtained with 153 elements, indicating that the current formulation which retains the fluxes everywhere is more accurate.


Conclusion
This revisit of thestream-aquifer flow problem has been prompted by the enhanced accuracy performance of a new formulation of the GEM that retains the fluxes at all grid points in the computational. Herein referred to as the flux GEM, its enhanced accuracy has been achieved with much coarser discretisation than its previous counterpart. The use of fewer elements to achieve high accuracy mitigates against the drawback of an increased number of unknowns that have to be solved by the current formulation. Of particular significance is the capability of the current formulation to accurately calculate the fluxes between the aquifer and the stream, which is the heart of the stream-aquifer problem. It is this capability that makes the current GEM formulation most attractive. This capability is demonstrated with 4 numerical examples where no more than 20% of the elements in contemporary numerical methods are required in the flux GEM to achieve comparable or higher accuracy.
Acknowledgements
Special thanks go to the National Research Foundation (NRF) which provided the financial support for this research work.
References
BEAR J (1979) Hydraulics of Groundwater. McGraw-Hill, NY. 120-123. [ Links ]
BOUSSINESQ J (1904) Recherches Theoretiques sur l'ecolement des Nappes d'eau infiltrees dans sol et sur le debit des sources. J. de Mathematiques pures et Appliquees 10 5-78, 363-394. [ Links ]
BUTTERWORTH JA, MACDONALD DMJ, BROMLEY J, SIMMONDS LP, LOVELL CJ and MUGABE F (1999) Hydrological processes and water resources management in a dryland environment III: Groundwater recharge and recession in a shallow weathered aquifer. Hydrol. Earth Syst. Sci. 3 (3) 345-352. [ Links ]
CHOW VT, MAIDMENT DR and MAYS LW (1988) Applied Hydrology. McGraw-Hill Book Co. Singapore. [ Links ]
DESAI CS (1973) Approximate solution for unconfined seepage. J. Irrig. Drain. Div. ASCE 99 71-87. [ Links ]
DILLON PJ and LIGGETT JA (1983) An ephemeral stream-aquifer interaction model. Water Resour. Res. 19 (3) 621-626. [ Links ]
FOX G (2003) Improving MODFLOW's river package for unsaturated stream/aquifer flow. Proc. 23rd AGU Hydrol. Days, 31 March 31 2 April, Colorado State University, Fort Collins, USA. 56-67. [ Links ]
GUO W (1997) Transient groundwater flow between reservoirs and water-table aquifers. J. Hydrol. 195 370-384. [ Links ]
HORNBERGER GM, EBERT J and REMSON I (1970) Numerical solution of the Boussinesq equation for aquifer-stream interaction. Water Resour. Res. 6 (2) 601-608. [ Links ]
HUGHES DA, HANNART P and WATKINS D (2003) Continuous baseflow separation from time series of daily and monthly streamflow data. Water SA 29 (1) 43-48. [ Links ]
HUNT B (2003) Unsteady stream depletion when pumping from semiconfined aquifer. J. Hydrol. Eng. 8 (1) 12-19. [ Links ]
HUYAKORN PS and PINDER GF (1983) Computational Methods in Subsurface Flow. Academic, San Diego, CA. [ Links ]
IBRAHIM HA and BRUTSAERT W (1965) Inflow hydrographs from large unconfined aquifers. J. Irrig. Drain. ASCE 94 21-38. [ Links ]
JENG DS, SEYMOUR BR, BARRY DA, LI L and PARLANGE JY (2005a) New approximation for free surface flow of groundwater: capillarity correction. Adv. Water Resour. 28 1032-1039. [ Links ]
JENG DS, SEYMOUR BR, BARRY DA, PARLANGE JY, LOCKINGTON DA and LI L (2005b) Steepness expansion for free surface flows in coastal aquifer. J. Hydrol. 309 85-92. [ Links ]
LIGGETT JA and LIU PL-F (1983) The Boundary Integral Equation Method for Porous Media Flow. George Allen & Unwin, London, UK. [ Links ]
LOCKINGTON P (1997) Response of unconfined aquifer to sudden change in boundary head. J. Irrig. Drain. ASCE 123 24-27. [ Links ]
McDONALD MG and HARBAUGH AW (1988) A Modular Three-Dimensional Finite Difference Groundwater Flow Model. US Geological Survey Techniques of Water Resources Investigations, Book 6. [ Links ]
POLUBARINOVA-KOCHINA PY (1977) Theory of groundwater movement. Nauka, Moscow. [ Links ]
PARLANGE JY and BRUTSAERT WA (1987) A capillarity correction for free surface flow of groundwater. Water Resour. Res. 23 (5) 805-808. [ Links ]
PRIEST S and CLARKE JS (2003) Stream-aquifer relations in the coastal area of Georgia and adjacent parts of Florida and South Carolina. In: Kathryn J (ed.) Proc. 2003 Georgia Water Resources Conference, 23-24 April 2004, University of Georgia, USA. [ Links ]
ROCHESTER EW and KRIZ GJ (1968) Model study of the boundary effects on ditch drainage. J. Irrig. Drain. ASCE 94 403-504. [ Links ]
RODRIGUEZ LB, CELLO PA and VIONNET CA (2006) Modeling stream-aquifer interactions in a shallow aquifer, Choele Choel Island, Patagonia, Argentina. Hydrogeol. J. 14 591-602. [ Links ]
SCHMITZ GH and EDENHOFER J (2000) Exact closed-form solution of the two-dimensional Laplace equation for steady groundwater flow with nonlinearized free-surface boundary condition. Water Resour. Res. 36 (7) 1975-1980. [ Links ]
SERRANO SE (1995) Analytical solutions to nonlinear groundwater flow equation in unconfined aquifers and effect of heterogeneity. Water Resour. Res. 11 2733-2742. [ Links ]
SERRANO SE (2003) Modeling groundwater flow under transient nonlinear free surface. J. Hydrol. Eng. 8 (3) 123-132 [ Links ]
SERRANO SE, WORKMAN SR, SRIVASTAVA K and CLEAVE BM (2007) Models of nonlinear stream aquifer transient. J. Hydrol. 336 199-205. [ Links ]
SINGH S and JAISWAL CS (2006) Numerical solution of 2D free surface to ditch drains in the presence of transient recharge and depth-dependent ET in sloping aquifer. Water Resour. Manage. 20 770-793. [ Links ]
SMAKHTIN VU (2001) Estimating continuous monthly baseflow time series and their possible applications in the context of the ecological Reserve. Water SA 27 (2) 213-217. [ Links ]
STRELTSOVA TD (1975) Unsteady unconfined flow into a surface reservoir. J. Hydrol. 27 95-110. [ Links ]
TAIGBENU AE (1995) The Green element method. Int. J. Num. Meth. Eng. 38 2241-2263. [ Links ]
TAIGBENU AE (1999) The Green Element Method. Kluwer Academic Publishers, Boston, US. 376 pp. [ Links ]
TAIGBENU AE (2003) A time-dependent Green's function-based model for stream-unconfined aquifer flows. Water SA 29 (3) 257-265. [ Links ]
TAIGBENU AE (2008) The flux-correct Green element formulation for linear, nonlinear heat transport in heterogeneous media. Eng. Anal. Boundary Elements 32 (1) 52-63. [ Links ]
TAIGBENU AE (2009) 2-D Internal flux compatibility equation of the flux Green element method for transient nonlinear potential problems. Numer. Method. Partial Differ. Equat. URL: http://www3.interscience.wiley.com/journal/122463186/abstract. >DOI: 10.1002/num.20491 [ Links ]
TAIGBENU AE and ONYEJEKWE OO (1999) Green's function-based integral approaches to nonlinear transient boundary-value problems (II). Appl. Math. Model. 23 241-253. [ Links ]
TELYAKOVSKIY AS and ALLEN MB (2006) Polynomial approximate solutions to the Boussinesq equation. Adv. Water Resour. 29 1767-1779. [ Links ]
TEO HT, JENG DS, SEYMOUR BR, BARRY DA and LI L (2003) A new analytical solution for water table fluctuations in coastal aquifers with sloping beaches. Adv. Water Resour. 26 (12) 1239-1247. [ Links ]
YPMA TJ (1995) Historical development of the Newton-Raphson method. SIAM Rev. 37 531-551. [ Links ]
Received 9 February 2009; accepted in revised form 10 March 2010.
* To whom all correspondence should be addressed.
+2711 717-7136; fax: +2711 717-7045;
e-mail: akpofure.taigbenu@wits.ac.za