Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Water SA
On-line version ISSN 1816-7950
Print version ISSN 0378-4738
Water SA vol.36 n.3 Pretoria Apr. 2010
A new approach to the step-drawdown test
Gianpietro Summa*
Monticchio Bagni, 85028 Rionero in Vulture (Potenza), Italy
ABSTRACT
In this paper a new approach to perform step-drawdown tests is presented. Step-drawdown tests known to date are performed strictly keeping the value of the pumping rates constant through all the steps of the test. Current technology allows one to let the submerged electric pumps work at a specific revolution per minute (r/min) and to suitably modify the rotation velocity at every step. The new approach presented in this paper is based on the idea of keeping the value of r/min fixed at every step of the test, instead of keeping constant the value of the discharge. This technique has been experimentally applied to a well and a description of the operations and results are presented in detail. This approach, in this unique case, made possible an understanding of how the discharge Q varies as a function of the drawdown sw. It also enables one monitor the approaching of the equilibrium between Q and sw, using both the variation of Q and sw with time. Moreover, it was observed that for the well in question the ratio Q/sw remains almost constant within each step.
Keywords: characteristic curve, pumping test, equipment/field techniques, hydraulic testing
Introduction
Step-drawdown tests are currently quite popular; they are the most frequently performed tests in the case of single wells (Kawecki, 1995). There are various reasons why they are performed: in the case of exploration wells, they enable determination of the proper discharge rate for the subsequent aquifer test; in the case of exploitation wells they can be used to develop an understanding of the behaviour of the well during pumping, in order to determine the optimum production capacity and to analyse the well's performance over time (Boonstra and Kselik, 2001).
Step-drawdown tests were introduced by Jacob (1947) in order to study how the discharge Q affects the drawdown sw of a well drilled in confined aquifers. He proposed the following equation:

where:
B is a numerical parameter which takes into account linear head losses of the aquifer
C is the analogous parameter for non-linear (quadratic) head losses, mainly imputable to the construction characteristics of the well (Driscoll, 1986)
Jacob (1947), deriving his equation, made the analogy between the drawdown sw of a well and the voltage drop ΔV through a resistor, and between the discharge Q and the electric current I. Under steady-state conditions, for confined aquifers, and following Dupuit's assumption, the coefficient B in Eq. (1) is constant with time and it can be directly derived from Dupuit's formula. Instead, under unsteady-state (transient) conditions, the coefficient B in Eq. (1) is time-dependent and, for confined aquifers, it may be represented through the Cooper-Jacob approximation of the Theis solution for an infinite uniform aquifer (Van Tonder et al., 2001).
As a matter of fact, comparing the Cooper-Jacob approximation of Theis solution with the Dupuit's formula, if the aquifer is infinite and not recharged, one finds that the radius R of influence of the well scales as 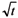 with time, and its time-derivative dR/dt scales as
with time, and its time-derivative dR/dt scales as  . If t is large, dR/dt is close to zero, i.e., R varies very slowly and it seems as if a steady-state has been achieved (De Marsily, 1986). The relations for confined aquifers are also applicable to unconfined aquifers as long as the drawdown is small in comparison with the aquifer thickness (Driscoll, 1986). The scientific literature on this topic is vast and variegated (see, for example, Kruseman and de Ridder (1994) and Driscoll (1986) and the references quoted therein).
. If t is large, dR/dt is close to zero, i.e., R varies very slowly and it seems as if a steady-state has been achieved (De Marsily, 1986). The relations for confined aquifers are also applicable to unconfined aquifers as long as the drawdown is small in comparison with the aquifer thickness (Driscoll, 1986). The scientific literature on this topic is vast and variegated (see, for example, Kruseman and de Ridder (1994) and Driscoll (1986) and the references quoted therein).
Usually, the step-drawdown test is the first step after a sequence of practical operations carried out for the construction of a new well. However, some authors have used the step-drawdown test to evaluate drawdowns in unconfined, heterogeneous and anisotropic aquifers with good results (Helweg, 1994).
Preliminary operations
After the well is drilled, preferably with the percussion method since in this case drilling fluids are not employed and the method increases the fractures in the rocks near the borehole walls, pumping tests are carried out: usually these are step-drawdown tests. Before one is able to perform the step-drawdown test described in this paper, some preparatory operations are needed in order to complete the construction and development of the well, along the lines suggested by Driscoll (1986): in particular, after the borehole has been made, it is necessary to know the maximum discharge obtainable in order to choose suitable dimensions of the filter, which are able to limit the water intake velocity to under 0.03 m/s (Driscoll, 1986).
In order to evaluate the maximum obtainable discharge use is made of an electric pump placed at the bottom of the well and which is able to completely empty it. If the borehole walls are stable, then it is possible to proceed with the pumping test without protection to the electric pump; on the contrary, if the borehole walls are unstable, then the pump can be shielded with a tube within which the pump is suitably placed. In the case in which the walls of the borehole are so weak as to be liable to collapse, it is necessary to install a temporary well screen (for example: a Johnson screen) with the largest slot openings available and with a rough gravel pack in the space between the well screen and the borehole. Sometimes it is also necessary to place some gravel coarseness at the bottom of the well screen.
At this point an electric pump capable of completely emptying the well has to be placed inside it. If no such electric pump is available, then an electric pump able to create the greatest possible drawdown should be used. It must be stressed that in the maximum discharge phase, even if of short duration, the aquifer near the borehole could be damaged, especially in porous media; but such risk is low in rocky formations. Obviously, in the case of a borehole with stable walls and no casing one can obtain the maximum discharge due exclusively to the aquifer (the best case), while in the other cases one can obtain a best approximation of such discharge. With such an approximation of the maximum discharge one should be able to choose the right dimension of the well screen to be installed in the well. Usually, such a choice is made taking into account the whole filtering surface, which typically extends over the entire saturated portion of the aquifer.
In order to perform good step-drawdown tests it is necessary to choose the dimensions of the well screen in such a way that the water intake velocity is less than 0.03 m/s (Driscoll, 1986), even under the greatest possible pumping rate (and thus under the greatest possible drawdown). For this reason, it is usually worthwhile to determine the dimensions of the well screen taking into account only a short portion (2 to 4 m, to be evaluated on a case-by-case basis) placed immediately above the pump intake. In this way, the risk of a turbulent flow inside the well due to well losses is minimised. It is also advisable to select the Johnson screen (Driscoll, 1986) because of its action against sand.
It is preferable to extend the tube below the well screen using a short piece of tube with a sealed end. In this way it is possible to install the electric pump with the water intake slightly below the well screen; moreover, sediments accumulated in the tube extension allow for evaluation of the amount of detritus transported by the water. In addition, installing a tube with a sealed end makes cleaning of the well easier.
Soon after the well screen has been installed, the construction of the well can be completed with the insertion of a suitable gravel pack between the tube and the borehole, along the whole length of the screen. The non-filtering portion of the interstice between the tube and the borehole must be suitably sealed. Often cement grout is placed in the interstice piece by piece in order to avoid crushing the tubes. It may be better to seal the interstice by alternating between cement grout and bentonite. In this phase, the electric pump can be placed near the bottom of the well and can be turned on to provide the maximum discharge for the development procedures. The development procedures are also useful in containing possible damages suffered by the aquifer during the short initial phase of maximum discharge determination.
It would be better to use an electric pump without a non-return valve. In this way, when the pump is stopped the naturally-generated inverse flux can destroy the sand bridges created during the maximum discharge phase (Driscoll, 1986). Only when the pumped water is clean should one then shut off the pump and wait the minimum period of time necessary for the well to restore its static level. Hence, the pump should be turned on and off many times until the pumped water is clean, in the beginning stages of pumping.
The electrically-driven pump used in this phase of the preliminary operations usually experiences some mechanical and thermal stresses which might severely damage it. For this reason, the succeeding step-drawdown tests should be carried out with a 2nd electro-pump.
Description of the operative method
In order to carry out the full step-drawdown test, it is necessary to prepare the well as shown in Fig. 1. Specifically, the following equipment must be set up:

• An electrically-driven submerged pump
• A frequency drive to control the pump
• An electromagnetic flow meter with an easy-to-read display for the measurement of the instantaneous discharge from the well
• An electric sounder and, if possible, a level probe placed at a fixed depth immediately above the electric pump to measure the drawdown
The electro-pump control by the frequency drive is an essential condition: the use of the frequency drive allows a smooth regulation of pump functioning, making it possible to keep the rotation velocity perfectly constant during a specific step and also to change the rotation velocity very smoothly between different steps.
Here the use of an electromagnetic flow meter is essential since it allows for instantaneous flow measurement, while the electric sounder, together with a level probe inside the well, provides us with safe, continuous measurement of the drawdown. Thus, it is possible to measure the instantaneous discharge and compare it with the relative instantaneous level measure. It then becomes possible to plan the execution of the step-drawdown test and to choose the more suitable number of steps, according to Kruseman and de Ridder (1994).
It is also important to check the maximum and minimum rotation velocity of the electric pump. For the minimum rotation velocity one can turn the pump on and gradually increase the rotation velocity till the pumped water does not reach the height of the surface. The velocity satisfying such condition is the minimum velocity. The maximum velocity is equal to the maximum rotation rate of the pump, in the case in which the electric pump is not able to empty the well. Otherwise, it can be determined by turning the electric pump on at its maximum velocity and then gradually reducing the rotation rate until the flow oscillations measured by the electromagnetic flow meter are dampened: i.e., the maximum rotation velocity will be the velocity corresponding to a stable and continuous discharge.
After the determination of the maximum and minimum velocities, it is important to wait a suitable interval of time that is needed for the well to restore its static level. Only after such time is it possible to start the step-drawdown test. Since the range of the rotation velocity is known, the number of steps and the relative velocities to proceed with the test can be chosen. Suppose, for example, that one has obtained a minimum rotation velocity of 1 800 r/min and a maximum rotation velocity of 2 800 r/min. Since one wants to perform a 3-step test, one could choose the following values: 1st step at 1 900 r/min; 2nd step at 2 100 r/min; 3rd step at 2 700 r/min. The more steps are used, the better the drawing of the characteristic curve will be.
With the above approach, it is possible to draw the 1st part of the characteristic curve with higher precision, since we are able to increase the discharge very gradually with the frequency drive. After the decision on the total number of the steps has been taken, the test is started from the 1st step, namely, that with the smallest rotation velocity. What is kept constant in this test is no longer the discharge, but the rotation velocity of the pump. It must be stressed here that the specific absolute value of the rotation velocity is not a parameter which could affect the execution and results of the test (it can obviously vary according to the type of electro-pump used for the test): the absolute rotation velocity and its variation are only a way to independently measure the variations of discharge Q and drawdown sw till the stabilisation within each step. Moreover, even if it is preferable to install the pump at the bottom of the borehole, a different installation depth does not invalidate the results of the test. The only 'interference' which could depend on the depth of pump installation is the length of the pipeline, but the additional friction head loss can be calculated and made negligible.
The main benefit of this new approach is that it is possible to reach the equilibrium (or the pseudo-equilibrium) at each step of the drawdown test, reducing to a minimum any perturbation to the system well-aquifer, which otherwise will be frequent, due to the repeated regulation manoeuvres needed to keep the discharge constant in the classical step-drawdown test (Castany, 1982). The measurement intervals for the discharge and the drawdown can be chosen, for example, as shown in Table 1.
Soon after the pump is turned on, the discharge begins a decreasing trend in time, while the drawdown starts to increase (Fig. 2). After a suitable interval of time, during which a pseudo steady-state or steady-state flow is approached, both the discharge and the drawdown reach a stabilisation point. After the stabilisation, it is important to check that the values of the discharge and those of the drawdown do not change over an interval of time that must be equal for every step of the whole test; this time merely defines the duration of the steps, and can be chosen to be, for example, 60 min from the beginning of the stabilisation. All this guarantees that the data gathered in every step are homogeneous and can be safely and significantly compared.
In this new approach the time duration of the whole test is not taken into account as a useful parameter for the subsequent analysis, since Q is constant only over a portion of the entire duration of a step: what is important is the time duration of each single step and the behaviour of Q and sw inside each single step. Moreover, the transition from a previous step to the following one requires an interval of a few seconds, for the increase in the rotation velocity of the pump (which cannot be made instantaneous) and such technical times are not counted. Therefore the time count is reset to zero at the beginning of every step, provided that, for the steps subsequent to 1st step, the values of Q and sw at the step time t=0 are those relative to the stabilisation point of the previous step (see Table 1).
After having collected the data from the 1st step, starting from the beginning until the stabilisation and for the following 60 min, the rotation velocity of the pump is suddenly increased to the value chosen for the execution of the 2nd step: the operations carried out for the 1st step are then repeated, and so on, for all of the steps planned for the step-drawdown test. Once the data acquisition is completed for all of the steps, one has on hand as many pairs of Q and sw as the performed steps and the characteristic curve of the well can be drawn. Moreover, using this approach once can draw the curves Q-t and sw -t for every step; since these trends are free from disturbance given by every possible regulation manoeuvre, they reveal themselves to be useful also in the study of the well-aquifer system.
Results from an actual experiment
The following section presents the results of an actual step-drawdown test carried out on a well that taps a confined and heterogeneous aquifer in southern Italy. The well, already described in Piscopo and Summa (2007), was drilled following the operative method described in the previous section, except for the length of the well screen which, for financial reasons, has been reduced to nearly a third of the aquifer thickness.
Four steps were performed. The results are listed in Table 1. For every step in discharge Q-t and sw-t curves were drawn, as shown in Fig. 2. As one can easily note from Fig. 2, for fixed rotation velocity the discharge decreases and the drawdown increases quite rapidly at the beginning of the test, while, starting from nearly 240 min after the beginning, these values stabilise and from this point on one can count the duration of the step in the step-drawdown test, previously fixed in 60 min. It is interesting to plot sw against Q; the result is shown in Fig. 3.
After 60 min, the Q and sw parameters of the 1st step were considered to be stabilised; they were recorded and we then proceeded with the test. We suddenly increased the rotation velocity to the value previously planned for the 2nd step. The measured values for Q and sw in this case are shown in Fig. 4a. As for the 1st step, we waited until the new stabilisation point was reached (after nearly 90 min) and then recorded the values of Q and sw for the following 60 min. In the same way, we proceeded with all the planned steps. The results for the 3rd and 4th steps are shown in Fig. 4b and Fig. 4c, respectively. In Table 2 the pairs of values for Q and sw recorded after the stabilisation for all the 4 steps are listed. Following this, the characteristic curve of the well could be drawn (Fig. 5).

The arc of the characteristic curve between Q=0 and the 1st step (Fig. 5) lacks experimental points: it was drawn as a mathematical extrapolation of the 'experimental' characteristic curve, and in Figs. 5 and 6 appears as a dashed line to distinguish it from the interpolated part.

Once the step-drawdown test is performed, it is possible to complete the construction of the well and to allow it to become operational. All of the information needed for proper use of the well, namely, the stratigraphy, the well design and the characteristic curve, are now available. If the preliminary pumping tests (see the Preliminary operations Section) were carried out in the same way as the final step-drawdown test, then it would be possible to significantly compare the results in order to evaluate the changes that have occurred to the well due to the installation of the well screen and due to the completion procedures. In this way the final step-drawdown test would become a sort of check on the correct execution of the completion operations of the well along the lines suggested by Driscoll (1986).
Discussion
The characteristic curve, derived as before, provides useful information on the hydraulic behaviour of the well and also gives information on its fair exploitation.
The step-drawdown test carried out in the previous section shows how for every step executed at fixed rotation rate it is not possible to have changes in the drawdown without having corresponding changes in the discharge. As a matter of fact, the characteristic curve is the graphical representation of such functional relation.
Remembering the analogy proposed by Jacob (1947) between Q and the electric current I, and between sw and the voltage drop ΔV, then the curve in the plane (Q, sw) is comparable to the characteristic curve of an elementary electrical device in the plane (ΔV, I ), and thus it can be seen as representing the well itself. Some comparisons between the classical test at constant discharge and this new approach follow in order. During a classical test at constant discharge Q it is possible to record only the drawdown sw and there is a very high probability that the results of the measurement of the constant discharge Q will be imprecise. Quite often, in fact, the measurement of the discharge Q is made with indirect methods such as the turbine water meter or the Woltmann water meter. All these measurement devices require a measurement time which is long relative to the time needed for the measurement of the drawdown sw. Thus, the measured discharge is actually a mean value over the measurement time.
The direct and instantaneous measurement provided by the electromagnetic flow meter in our approach, in addition to being more precise, allows a straight comparison with the corresponding instantaneous drawdown values. Moreover, the results of the step-drawdown tests carried out with our method keep the property of being readable, analysable and exploitable within the context of the classical approaches developed in the past years, starting from Jacob (1947). Our approach also provides additional information about the discharge variation with time for each step; such data can be used for further analyses.
For example, it is interesting to show, together with the characteristic curve on the plane (Q, sw), the trend of sw as a function of Q for each step before the stabilisation: in Fig. 6 the continuous line is the characteristic curve, while the dots of different colour and shape represent the dependence of sw on Q during the approach to the stabilisation (top-down) in each step; the stabilisation points are the intersections between the characteristic curve and the lines which interpolate each sequence of coloured dots.
We want to stress here that the most valuable information about the well is provided to the hydrogeologist by the characteristic curve or, even better, by the characteristic curves: they describe the hydraulic behaviour of the system well-aquifer under various circumstances, and also account for aquifer perturbations, both natural and artificial (human-induced). It would in fact be better to have at least 2 characteristic curves of the well, one obtained during the drought period of the aquifer, and the other obtained during the recharge period.
The characteristic curves are precious instruments to aid the judgement of the hydrogeologist, who has to carry out a fair exploitation of the well: for example, the curves enable the hydrogeologist to evaluate the suitable discharge or the suitable drawdown to be applied for a steady use of the well, or they enable determination of the maximum discharge safely extractable for a few hours during a given period of the year. Given a precise request about the discharge of the well by the customer, the characteristic curve allows one to choose the right pumping parameters to satisfy the demand. For example, if one requires a discharge of 5×10-3 m3/s from the well examined in this study, then we can find on the characteristic curve the drawdown corresponding to a discharge of 5×10-3 m3/s, and take such a value as a parameter for the steady use of the well, as explained in Piscopo and Summa (2007). If the characteristic curve is a curve obtained during a drought period of the aquifer, then the required discharge will with high probability always be available.
Conclusions
The new approach to the step-drawdown test presented in this paper, though based on a single field experiment, appears to:
• Greatly reduce the perturbations in the water flow which are usually generated during the classical tests at constant discharge
• Instantaneously record the values of the drawdown and those of the discharge with fine time resolution, from the beginning of the step to the stabilisation
• Perform actual tests of the same duration for each step, once the stabilisation is reached
• Rapidly draw a precise characteristic curve of the well, and thus give a hydraulic characterisation of the system well-aquifer
• Perform the usual analyses cited in the literature
• Carry out new analyses on the variation of the discharge Q with time t, in each step
Moreover, this approach poses new and interesting theoretical questions: for example, during the drilling operation of the borehole, when a discharge test is carried out at an open borehole with the aim of filter dimensioning, if the dimensioning procedure is performed correctly, what is the new meaning of the parameter C, introduced by Jacob (1947)? A comparison between the results of the final discharge test and the results of the test performed at an open borehole could also be seen as a direct test of the well itself. Finally, the characteristic curve, other than being a tool useful to decide a suitable and fair exploitation of the well, seems to show that it is not possible to have a drawdown without a corresponding variation of the discharge.
Acknowledgements
The author would like to thank Futurella Company, in the person of Mr. Nicola Del Negro, for the opportunity to conduct the field work. The author is grateful to the anonymous reviewers for their helpful and constructive comments. The author is grateful to Prof. Germano D'Abramo for his close friendship. The author is also grateful to Prof. Vincenzo Piscopo, Prof. Pantaleone de Vita and to Dr. Salvatore Grimaldi for a critical reading of the manuscript. A special thanks goes to Dr. Assunta Tataranni, support of my life.
References
BOONSTRA J and KSELIK RAL (2001) SATEM 2002: Software for Aquifer Test Evaluation. International Institute for Land Reclamation and Improvement. Publication 57. Wageningen, the Netherlands. 148 pp. [ Links ]
DE MARSILY G (1986) Quantitative Hydrogeology. Academic Press, Inc., Orlando, Florida. 440 pp. [ Links ]
CASTANY G (1982) Principles et méthodes de l'hydrogéologie. Dunod, Paris. 238 pp. [ Links ]
DRISCOLL FG (1986) Groundwater and Wells (2nd edn.). Johnson Filtration Systems, Inc., St. Paul, Minnesota. 1 089 pp. [ Links ]
HELWEG OJ (1994) A general solution to the step-drawdown test. Ground Water 32 (3) 363-366. [ Links ]
JACOB CE (1947) Drawdown test to determine effective radius of artesian well. Transaction, ASCE 112 (2312) 1047-1070. [ Links ]
KAWECKI MW (1995) Meaningful interpretation of step-drawdown tests. Ground Water 33 (1) 23-32. [ Links ]
KRUSEMAN GP and DE RIDDER NA (1994) Analysis and Evaluation of Pumping Test Data (2nd edn.). International Institute for Land Reclamation and Improvement Publication 47. Wageningen, the Netherlands. 377 pp. [ Links ]
PISCOPO V and SUMMA G (2007) Experiment of pumping at constant-head: an alternative possibility to the sustainable yield of a well. Hydrogeol. J. 15 (4) 679-687. [ Links ]
VAN TONDER GJ, BOTHA JF and VAN BOSCH J (2001) A generalised solution for step-drawdown tests including flow dimension and elasticity. Water SA 27 (3) 345-354. [ Links ]
Received 20 April 2009; accepted in revised form 23 February 2010.
*To whom all correspondence should be addressed.
+39 3471800719; fax: +39 0649934188;
e-mail: info@gianpietrosumma.it














