Serviços Personalizados
Artigo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em Google
Similares em Google
Compartilhar
Water SA
versão On-line ISSN 1816-7950
versão impressa ISSN 0378-4738
Water SA vol.36 no.3 Pretoria Abr. 2010
Biological sulphate reduction with primary sewage sludge in an upflow anaerobic sludge bed reactor – Part 6: Development of a kinetic model for BSR
J Poinapen; GA Ekama1
Water Research Group, Department of Civil Engineering, University of Cape Town, Rondebosch 7701, South Africa
ABSTRACT
A 2-phase (aqueous-gas) kinetic model for biological sulphate reduction (BSR) using primary sewage sludge (PSS) as carbon source is presented. The methanogenic anaerobic digestion (AD) model of Sötemann et al. (2005) is extended by adding the biological, chemical and physical processes associated with BSR, i.e. propionic acid degrading sulphate-reducing bacteria (SRB), acetoclastic SRB and hydrogenotrophic SRB, the aqueous weak acid/base chemistry processes of the sulphate and sulphide systems and an aqueous-gas sulphide exchange process. The model is validated with experimental data from 2 upflow anaerobic sludge bed (UASB) reactors fed various PSS COD/SO42- ratios under constant flow and load conditions at 35°C and 20°C. The kinetic model results, including the reactor pH (within 0.1 pH unit) compare well with the experimental results and with those calculated from a steady-state BSR model. The kinetic model confirms that: (1) at ambient temperature (20°C), the hydrolysis rate is significantly reduced compared with that at 35°C, which requires a longer sludge age (larger bed volume) in the UASB reactor; (2) the hydrolysis rate of the PSS biodegradable particulate organics (BPO) is the same under methanogenic and sulphidogenic conditions; (3) the PSS BPO are carbon deficient for BSR in that more electrons are donated than carbon supplied for the required alkalinity increase, with the result that the sulphide system supplies the alkalinity deficit; and (4) due to (3) there is zero CO2 gas generation and in effect the sulphide system establishes the reactor pH. This observation allows the carbon content of the utilised organics to be determined from the H2CO3* alkalinity increase in the reactor, which can be simply measured by titration methods.
Keywords: biological sulphate reduction, primary sewage sludge, upflow anaerobic sludge bed reactor, dynamic model, kinetics, stoichiometry, mixed weak acid/base chemistry
Nomenclature
| a | molar nitrogen composition of organics in CxHyOzNa |
| AB | acetogenic bacteria |
| AD | anaerobic digestion |
| Alk H2S | alkalinity with respect to the H2S reference species excluding the water species |
| bj | endogenous respiration rate, where j refers to the different SRB# |
| BPO | biodegradable particulate organics |
| BSR | biological sulphate reduction |
| C | carbon |
| COD | chemical oxygen demand |
| fPS'up | unbiodegradable fraction of PSS with respect to total COD (Sti) |
| FRBCOD | fermentable readily biodegradable (soluble) COD |
| FRBO | fermentable readily biodegradable (soluble) organics |
| FSA | free and saline ammonia |
| H2CO3* | alk alkalinity with respect to the H2CO3 reference species including the water species |
| HAc | acetic acid |
| HRT | hydraulic retention time |
| k | molar carbon composition of BSR biomass in CkHlOmNn |
| KH2S | Henry's law constant for sulphide |
| KI,j | sulphide inhibition kinetic constant for SRB species j# |
| KN,j | switching function sulphate concentration for SRB species j# |
| KS,j | Monod half saturation coefficient for SRB species j# |
| K'f, K'r | forward and reverse aqueous dissociation constants adjusted for ionic strength affects; additional subscripts HSO4, H2S refer to aqueous H2SO4 and H2S dissociations |
| K'f, K'r | forward and reverse gas exchange constants; additional subscript H2Sg refer to H2S gas exchange |
| l | molar hydrogen composition of BSR biomass in CkHlOmNn |
| m | molar oxygen composition of BSR biomass in CkHlOmNn |
| M | experimentally measured |
| MA | methanogenic archae |
| n | molar nitrogen composition of BSR biomass in CkHlOmNn |
| OLR | organic loading rate |
| P | theoretically predicted |
| PBR | packed bed reactor |
| pH2S | partial pressure of H2S gas |
| pK'S1, pK'S2 | 1st and 2nd dissociation constant for the sulphide weak acid base system corrected for ionic strength effects |
| PSS | primary sewage sludge |
| Qi | influent flow |
| Qw | waste flow |
| R1 | UASB Reactor 1 |
| R2 | UASB Reactor 2 |
| rj | endogenous mass loss rate for SRB species j# |
| Rh | hydraulic retention time |
| Rs | sludge age |
| Sim | simulation |
| Sj | substrate concentration for the SRB species j# |
| Sbp | biodegradable particulate COD concentration |
| Sbsa | acetic acid COD concentration |
| Sbsf | fermentable biodegradable soluble COD concentration |
| Sbsp | propionic acid COD concentration |
| SRB | sulphate reducing bacteria |
| SS | steady state |
| ST | total sulphide species concentration |
| Sup | unbiodegradable particulate COD concentration |
| T | temperature in ºC |
| TOC | total organic carbon |
| Total Alk | sum of weak acid/base subsystem alkalinities |
| UASB | upflow anaerobic sludge bed reactor |
| UCTADM1 | University of Cape Town Anaerobic Digester Model No. 1 |
| UCTADM1-BSR | University of Cape Town Anaerobic Digester Model No. 1 including biological sulphate reduction |
| UPO | unbiodegradable particulate organics |
| USO | unbiodegradable soluble organics |
| Vd | volume of digester (equivalent to bed volume, Vb) |
| VFA | volatile fatty acids |
| VSS | volatile suspended solids |
| x | molar carbon composition of organics in CxHyOzNa |
| y | molar hydrogen composition of organics in CxHyOzNa |
| Y# | specific yield coefficient (metabolic) |
| Y'# | specific yield coefficient (anabolic) |
| z | molar oxygen composition of organics in CxHyOzNa |
| Z# | biomass concentration mgCOD/ℓ |
| γB | electron-donating capacity of BSR biomass |
| γS | electron-donating capacity of biodegradable organics |
| µj | specific growth rate, where j refers to the different AD organisms# |
 | maximum specific growth rate Additional subscripts PS, AS and HS refer to propionate degrading, acetoclastic and hydrogenotrophic SRB respectively |
Introduction
The core unit process in the BioSURE® system is biological sulphate reduction (BSR) with primary sewage sludge (PSS). To assist in and optimise the design, operation of and research into this unit process, mathematical models are very useful process evaluation tools. Mathematical models provide quantitative descriptions of the treatment system of interest that allow prediction of the system response and performance.
The kinetic model of Sötemann et al. (2005) for methanogenic anaerobic digestion (AD) of PSS (UCTADM1) appeared most suitable to extend to include BSR and was therefore selected as a basis for the development of the kinetic model for BSR with PSS as substrate. To extend UCTADM1 to incorporate BSR, the kinetics and stoichiometry for the biological, chemical and physical processes of BSR in 2 phases (aqueous-gas) were developed. Integration of BSR into UCTADM1 was commenced by Van Wageningen et al. (2006) and Van Wageningen (2007) to model the flow through methanogenic and BSR digesters of Ristow et al. (2005). This paper reviews this kinetic model for BSR (called the UCTADM1-BSR) using PSS as energy source, and presents its application to the upflow anaerobic sludge bed (UASB) BSR reactors of Poinapen et al. (2009a; b). The kinetic model is revised and the necessary corrections and adjustments made – some of the changes involved:
• Replacing the unstable linear hydrogen sulphide inhibition function to a more stable one
• Including a temperature function to simulate the effect of temperature on PSS hydrolysis/acidification and BSR processes. After revision, the model is verified, calibrated and validated by modelling the 2 UASB BSR systems (R1 at 35°C and R2 at 20°>C) operated by Poinapen et al. (2009a; b) and the simulated results compared with those measured and calculated with the steady-state BSR model (Poinapen and Ekama, 2010).
Development of the kinetic model for BSR (UCTADM1-BSR)
The development of the kinetic model for BSR and its integration into UCTADM1 was conducted in 3 parts.
Part 1: The acidogenic process
In the AD of complex organics such as PSS, the hydrolysis/solubilisation process is usually the rate-limiting step. This bioprocess takes place first, followed by acidification, mediated by the acidogenic organism group. The products of these processes are volatile fatty acids (VFA), hydrogen (H2) and CO2, which then enter either the methanogenic or sulphidogenic (BSR) bioprocesses, which operate in competition (Fig. 1). Ristow et al. (2005) found that the hydrolysis/acidogenesis kinetics and rate are the same under methanogenic and sulphidogenic conditions. Therefore, only the BSR processes on the products of the hydrolysis/acidogenesis process need to be included in the model because the hydrolysis/acidogenesis process precedes both methanogenesis and sulphidogenesis. However, the sulphide end-product of BSR is inhibitory to the methanogens and sulphidogens, so this inhibition needs to be included in the dynamic model for BSR.
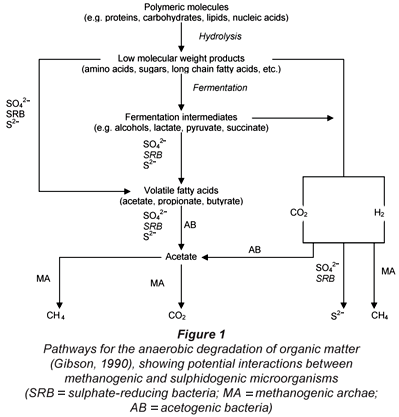
Part 2: Development of BSR biological processes
The approach of Kalyuzhnyi et al. (1998) formed the basis for the biological processes part of the kinetic model for BSR. These researchers identified 9 trophic groups of microorganisms that convert substrates into products in an anaerobic reaction sequence. These bacterial groups are:
1. Fermentative bacteria
(Sugars → Acetate)2. Butyrate-degrading acetogenic bacteria
(Butyrate → Acetate)3. Butyrate-degrading SRB
(Butyrate → Acetate & H2S)4. Propionate-degrading acetogenic bacteria
(Propionate → Acetate)5. Propionate-degrading SRB
(Propionate → Acetate & H2S)6. Acetoclastic methanogenic archae
(Acetate → Methane & CO2)7. Acetoclastic SRB
(Acetate → H2S & CO2)8. Hydrogenotrophic methanogenic archae
(H2 & CO2 → Methane)9. Hydrogenotrophic SRB
(H2 → H2S)
Of these 9 microorganism groups, only 3 SRB (5, 7 and 9) groups are of particular interest when integrating BSR with the methanogenic UCTADM1 model. This model already explicitly incorporates microorganism groups 1 (acidogens), 4 (acetogens), 6 (acetoclastic methanogens) and 8 (hydrogenotrophic methanogens). The butyrate-degrading acetogenic (2) and SRB (3) bacterial groups were not included in the model, as butyrate is not usually present in significant concentrations in sewage sludge digestion systems. However, if required these trophic groups and their respective processes can be incorporated. Thus, the process stoichiometry and kinetics for only the 3 SRB groups (5, 7 and 9) are considered for both the organism growth and endogenous decay.
Part 3: Development of aqueous chemistry and physical processes
The biological processes consume and produce significant acid/base species, e.g. VFA, sulphide and bicarbonate (dissolved CO2). The weak acid/base chemistry of these species (subsystems) needs to be incorporated in the model. The consumption and production of acid/base species influences the pH established in the digester, which in turn can influence the biologically-mediated processes. Hence, pH needs to be incorporated directly into the model as a model-predicted parameter, and its interaction with the biological processes modelled.
The weak acid/base systems already in UCTADM1 are water, acetate, propionate, carbonate, ammonium and phosphate. Weak acid/base systems associated with BSR are sulphide and sulphate and need to be added to the model.
Some of the AD (methanogenic and sulphidogenic) end-products are gases so their 2-phase (aqueous-gas) equilibrium processes need to be included (the third solid phase is not included at this stage). The carbon dioxide and ammonia gas exchange processes are already included in UCTADM1. Due to its low solubility, methane is produced directly to the gas phase. Hydrogen remains dissolved in the aqueous phase and is consumed by the hydrogenotrophic methanogens directly from the aqueous phase. So, the only gas to be added for BSR is sulphide. Sulphide is a highly soluble gas so usually very little (<1%) exits the digester in the gas phase. This was also observed experimentally (Poinapen et al., 2009a; b). In contrast, methane is very insoluble at low pressures (~atmospheric) so usually very little exits the digester in the dissolved phase.
In their steady-state BSR model, Poinapen and Ekama (2010) show that organics with COD/TOC ratio > 2.67, which includes PSS and VFA, are carbon deficient for BSR. These organics can donate more electrons than supply carbon for the alkalinity (HCO3-) required. This results in zero CO2 gas production, and the alkalinity deficit is supplied by the sulphide system. Accordingly, this affects the relative HS-/H2S concentrations, so in effect the sulphide system establishes the sulphidogenic digester pH, not the inorganic carbon system as in methanogenic digesters (Poinapen and Ekama, 2010).
The development of these 3 parts is described in more detail in the following sections. The end result essentially will be a 2-phase biological, chemical and physical process model for the AD of PSS, with competitive methanogenesis and sulphidogenesis.
Stoichiometry of the BSR growth and endogenous processes
BSR growth processes
The procedure of Sötemann et al. (2005) for UCTADM1 was followed where the stoichiometry for the growth bioprocesses was determined by adding the catabolic and anabolic stoichiometry, linked via the yield coefficient of each SRB group. The development of this growth process stoichiometry for each of the 3 SRB groups is described below. UCTADM1 has embedded in it a biomass composition of C5H7O2N1 and the development of the stoichiometry of both the growth and endogenous respiration processes of the organisms was based and programmed on this biomass composition. When calibrating their steady-state BSR model against the UASB system data, Poinapen and Ekama (2010) found the biomass composition to be approximately C5H7O2N0.55, which is the same as the UCTADM1 biomass composition, except for the N content. Because the BSR biomass production is very low (Table 6), small differences in biomass composition have a negligible influence on the predicted results. Therefore, it was not necessary to change the stoichiometric equations in the dynamic model to conform to a biomass composition of C5H7O2N0.55 and the dynamic model is expected to give results that are closely similar to those of the steady-state model.
The derivation of the stoichiometric equations for growth of BSR biomass of composition C5H7O2N1 is demonstrated below for the acetogens only. The stoichiometry of the other BSR organisms follows the same procedure.
Acetogenic sulphidogenesis (by propionate degrading SRB)
The reaction sequence for the substrate utilisation of propionate by the propionate degrading SRB (ZPS) is reported by Kalyuzhnyi et al. (1998) to be:

The anabolic growth process of ZPS was accepted to be identical to that of the methanogenic acetogenic biomass group in the UCTADM1 model because both species use propionate as substrate (Sötemann et al., 2005). This anabolic growth process producing biomass of composition C5H7O2N1 is:

Multiplying Eq. (2) by the anabolic organism yield (Y'PS), dividing it by 2 to form 1 mol of biomass, and adding the associated catabolism Eq. (1) gives:

Dividing Eq. (3) by Y'PS for 1 mol of acetogen biomass formation yields:
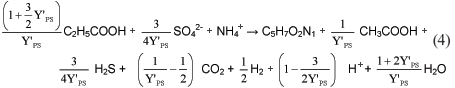
The stoichiometry, in terms of the anabolic organism yield Y'PS for the growth process of the propionate-degrading SRB, is taken directly from Eq. (4) and is listed in Table 1.
To represent the ratio of biomass formed per unit total substrate (in this case propionate) utilised, the anabolic yield (Y'PS) is changed to the metabolic (anabolic + catabolic) yield (YPS) which is the usual way of expressing yield. The metabolic yield (YPS) is obtained from Eq. (4).
From the stoichiometry (Table 1):
1 mol biomass (160 gCOD) is grown from  moles propionate. Expressing the metabolic (or true) yield YPS (mol/mol) in terms of Y'PS gives:
moles propionate. Expressing the metabolic (or true) yield YPS (mol/mol) in terms of Y'PS gives:

Changing Eq. (5) to make Y'PS its subject:

Rewriting the stoichiometric terms in Table 1 by substituting Eq. (6) for Y'PS and accepting that CO2 + H2O → H2CO3* gives the stoichiometry for propionate-utilising SRB in terms of the true (metabolic) organism yield as shown in Table 2.

Acetoclastic sulphidogenesis (by acetoclastic SRB) and hydrogenotrophic sulphidogenesis (by hydrogenotrophic SRB)
The same method described above for the propionate-degrading SRB was used for developing the stoichiometry for the growth of the acetoclastic SRB (ZAS) and the hydrogenotrophic SRB (ZHS), based on the reaction sequence for the catabolic and anabolic substrate utilisation taken from Kalyuzhnyi et al. (1998).
BSR Endogenous processes
The organism death/decay for the SRB groups was assumed to be the same as that for the methanogenic microorganism groups in the UCTADM1 model, and therefore the same approach was followed in the BSR model.
With endogenous mass loss, the biomass dies and releases its biodegradable organics (accepted to be all particulate) to the bulk liquid, adding to the biodegradable particulate organics (BPO) from the influent. Because the yield and endogenous mass loss rates of SRB biomass are very low, it was accepted that generation of unbiodegradable endogenous residue is negligible and so was neglected. Endogenous mass loss transforms the biomass BPO to the same composition as the influent BPO while conserving COD. An influent BPO composition of C3.35H7O1.45N0.45 was measured in this investigation (Poinapen and Ekama, 2010) which is slightly different to that measured by Sötemann et al. (2005), i.e. C3.5H7O2.0N0.196. Because this endogenous transformation may need to be done with different biomass and PSS BPO compositions, the transformation stoichiometry is developed in general for biomass of composition CkHlOmNn and an influent BPO composition of CxHyOzNa, i.e.

Re-writing the equation recognising that CO2 + H2O → H2CO3* gives:

where:
| A | = [k(3y-2z-9a)+l(z-3x)+m(2x+3a-y)+n(9x-3z)] / [4x+y-2z-3a] |
| = [k(3y-2z-9a)+l(z- 3x)+m(2x+3a-y)+n(9x-3z)]/γS | |
| B | = [4k + l -2m -3n] / [4x + y - 2z -3a] = γB/γS |
| C | = [k(y-2z-3a)+x(2m+3n-l)] / [4x+y-2z-3a] |
| = [k(y-2z-3a)+x(2m+3n-l)]/γS | |
| D | = [n(4x+y-2z)+a(2m-4k-l)] / [4x+y-2z-3a] |
| = [n(4x+y-2z)+a(2m-4k-l)]/γS |
The generalised stoichiometry equation for endogenous decay of all organism groups expressed in Eq. (8) is listed in Table 3.
From the compositions of the biomass (C5H7O2N1) and influent BPO organics (C3.35H7O1.45N0.45), the stoichiometry of the endogenous mass loss process simplifies to Eq. (9) which is summarised in Table 4.
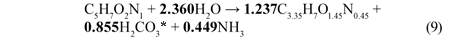
X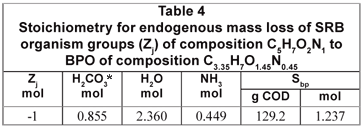
The biomass COD/VSS ratio is 1.412 mgCOD/mgVSS and 1 mol biomass has a COD of 160 gCOD. Therefore, 160 g biomass COD has a VSS of 113.1 gVSS which produces 160 gVSS or 1.237 mol BPO with a COD/VSS ratio of 1.682 mgCOD/mgVSS.
Kinetics of the BSR growth and endogenous processes
Growth kinetic rates
The approach adopted for the kinetic rate equations for the growth of SRB was taken from Kalyuzhnyi et al. (1998) as follows:
• The bacterial growth of each SRB group was modelled using the Monod kinetic equation in terms of the relevant substrates, with concomitant inhibition by undissociated H2S and pH.
• The undissociated H2S inhibition was formulated as first-order for all SRB bacterial groups.
Accordingly, the generalised specific growth rate (µj) equation for SRB wasdescribed by Kalyuzhnyi et al. (1998) as:

where
Si is the substrate concentration for SRB organism i, the middle term is the undissociated H2S inhibition equation with KI,j being the inhibition constant by undissociated H2S for the bacterial group j, and the last term is the sulphate switching function when [SO42-] is low.
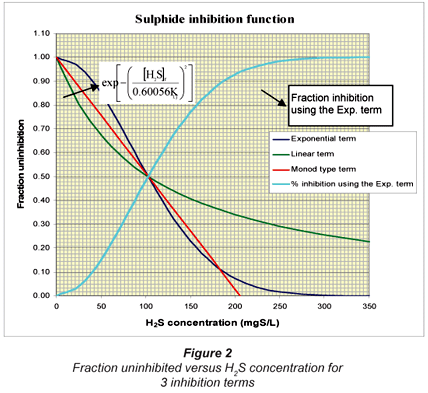
The H2S inhibition term  in Eq. (10) represents a 100% inhibition in SRB growth should [H2S]f = KI. However, this equation is found to be unstable and reversed when [H2S] is greater than the KI,j value. When [H2S] > KI,j, the inhibition term becomes negative and the model simulation results become unstable with a see-saw effect. This inhibition term therefore was replaced by a more stable one which approaches zero more gradually, i.e.
in Eq. (10) represents a 100% inhibition in SRB growth should [H2S]f = KI. However, this equation is found to be unstable and reversed when [H2S] is greater than the KI,j value. When [H2S] > KI,j, the inhibition term becomes negative and the model simulation results become unstable with a see-saw effect. This inhibition term therefore was replaced by a more stable one which approaches zero more gradually, i.e.

This term has an exponential behaviour and can never become negative. The factor 0.60056 was found by matching the linear (or first-order) inhibition term of Kalyuzhnyi et al. (1998) at the 50% inhibition point using the same value of KI. For example, if KI = 206 mgS/ℓ, and [H2S]f = 103 mgS/ℓ, then the  term and Eq. (11) must give the same 50% inhibition.
term and Eq. (11) must give the same 50% inhibition.
If instead of Eq. (11), a Monod type inhibition term is used, i.e.  the KIvalue will be 206/2 = 103 mgS/ℓ to give 50% inhibition at [H2S]f = 103 mgS/ℓ. Figure 2 illustrates the fraction uninhibited with [H2S] for the 3 inhibition terms. Also plotted is the fraction inhibition versus [H2S] concentration for the exponential inhibition term (Eq. (11)).
the KIvalue will be 206/2 = 103 mgS/ℓ to give 50% inhibition at [H2S]f = 103 mgS/ℓ. Figure 2 illustrates the fraction uninhibited with [H2S] for the 3 inhibition terms. Also plotted is the fraction inhibition versus [H2S] concentration for the exponential inhibition term (Eq. (11)).
Should pH inhibition be required, it can be added to the UCTADM1-BSR model. In integrating BSR with ADM1, Fedorovich et al. (2003) used the following pH inhibition function in ADM1:
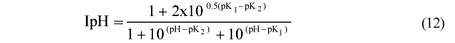
However, this pH inhibition was omitted from the UCTADM1-BSR model due to the uncertainty of its behaviour.
From the above, and omitting pH inhibition, the general form of the SRB growth rate equation is:

When incorporating BSR into the UCTADM1 model, the H2S inhibition term was also added to the existing kinetic rate equations for acidogenic, acetogenic and methanogenic bacterial groups. This was done by following the approach of Kalyuzhnyi et al. (1998) where:

In the literature, it is reported that the sensitivity of SRB to hydrogen sulphide toxicity depends on the bacterial species (Maillacheruvu and Parkin, 1996; O'Flaherty et al., 1998). Maillacheruvu and Parkin (1996) investigated the effect of H2S on propionate-oxidising, acetate-oxidising and hydrogenotrophic SRB and reported that acetotrophic SRB in particular were highly sensitive to H2S. Likewise, Yamaguchi et al. (1999) reported that acetate utilisers were more susceptible to H2S inhibition than hydrogen utilisers. In the UCTADM1-BSR model, the KI values of 185 mgS/ℓ and 550 mgS/ℓ for the propionate-degrading and the hydrogenotrophic SRB, respectively, were taken directly from Kalyuzhnyi et al. (1998) while that of acetotrophic SRB was refined during model calibration.
Endogenous mass loss kinetic rates
Kalyuzhnyi et al. (1998) and Sötemann et al. (2005) formulated the endogenous mass loss with first-order kinetics. Therefore, this approach is also used for the 3 SRB groups considered here. Accordingly, the general equation for the rate (i) of endogenous mass loss of SRB group at concentration Zj is:

where
bj = specific endogenous mass loss rate constant for the 3 SRB groups.
Matrix representation of the biological kinetic model for BSR
The complete bioprocesses stoichiometric and kinetic model for SRB represented in the Petersen matrix format is shown in Table 5. The matrix includes both the growth and endogenous decay processes for all 3 SRB groups, namely, the propionate-degrading SRB (ZPS, growth process S1 and endogenous mass loss process S2), acetotrophic SRB (ZAS, growth process S3 and endogenous mass loss process S4) and hydrogenotrophic SRB (ZHS, growth process S5 and endogenous mass loss process S6).
Values for the stoichiometric and kinetic constants
Van Wageningen (2007) used values for the stoichiometric and kinetic constants for the SRB from Kalyuzhnyi et al. (1998), who obtained these values from model fitting the data of Omil et al. (1996). These values are also employed here (Table 6).
The constants in Table 6 are expressed in terms of gram units. Since UCTADM1, and therefore also the kinetic model for BSR (Table 5), expresses concentrations as mole units, the constants were converted to the appropriate mole units. This was done by accepting a biomass composition of C5H7O2N1 and substrates (acetic acid, propionic acid and hydrogen) as per their known chemical composition (Table 7). In addition, because the kinetic rates are expressed in terms of total species concentrations in the literature sources, the half-saturation constants needed to be converted to express them in terms of the undissociated weak acid/base species, because this is the form in which they are utilised by the SRB. This was done in model application by multiplying the appropriate half-saturation constant by the undissociated species to total species concentration ratio (Van Wageningen, 2007), which in effect decreased the half-saturation concentrations by the undissociated species to total species concentration ratio. With this approach, the relative concentrations may change as the pH changes, which was considered more appropriate. In the neutral pH 6 to 8 range, the undissociated species concentrations are very low. Depending on the half-saturation concentrations, this results in very low growth rates for the SRB. In this model application, this did not lead to run-time problems because the precursor hydrolysis/acidogenesis process is very slow. In applications requiring high growth rates on VFA at neutral pH, utilising the undissociated species of the VFAs can lead to run-time problems (Van Zyl et al., 2008).
Inclusion of the aqueous chemical and physical processes
In the BSR processes described above, weak acid/base species are both produced and consumed. These species, together with their associated weak acid/base chemistry, need to be included in the kinetic model. In addition, the compound H2CO3*, which is both produced and consumed, and the compound H2S produced, have physical gas exchange processes with the gas phase which require inclusion in the model.
The aqueous chemistry processes were extracted from Musvoto et al. (1997), for the ammonia, carbonate, phosphate, acetate and water subsystems; from Sötemann et al. (2005) for the propionate subsystem; and from Tables 8 and 9 below for the sulphate and sulphide subsystems. In addition, the physical gas exchange processes for CO2 and NH3 were taken from Sötemann et al. (2005), whereas the H2S gas exchange processes were taken from Table 10. Following the approach of Sötemann et al. (2005), methane is included as a gas phase compound, that is, it is generated directly as a gas because it is very insoluble and is not utilised in any of the processes.



In the model, the gas compounds were accepted to remain part of the bulk liquid and exit the digester with the effluent flow. This is acceptable because at steady state the gas composition does not change. However, for dynamic simulations, the gas composition of the headspace may change with time and can influence the dissolved species bulk liquid concentrations through the gas exchange processes. In this case, a separate gas stream needs to be implemented following the processes set out in Batstone et al. (2002) and Sötemann et al. (2005).
Integrating the aqueous chemistry, physical and biological processes with UCTADM1
The biological processes (stoichiometric and kinetics), aqueous chemistry and physical processes relevant to BSR were integrated with the existing methanogenic UCTADM1 model in Aquasim (Reichert, 1998). This resulted in an integrated kinetic model for both BSR and methanogenesis in competition for the volatile fatty acids (VFA) and H2 substrates. Should BSR be required as the only biological process consuming the VFA and H2 substrates, the methanogenic processes can be switched off in the model application. This will result in a 'stand-alone' integrated 2-phase chemical, physical and biological process model for BSR with PSS as energy source. In a real BSR system, sulphidogenesis out-competes methanogenesis resulting in an exclusively BSR system, which was the case for the 2 UASB BSR systems (R1 at 35ºC and R2 at 20ºC) of Poinapen et al. (2009a; b), simulated with UCTADM1-BSR.
UCTADM1-BSR model application and validation
Systems simulated and influent characteristics
After calibration, the UCTADM1-BSR model was validated by applying it to simulate the 2 UASB BSR systems Poinapen et al. (2009a; b), viz:
• R1 at 1 500 mgSO42-/ℓ at 35ºC with PSS COD/SO42- ratio of 1.25 (Poinapen et al., 2009a – Part 1).
• R1 at 1 800 mgSO42-/ℓ at 35ºC with PSS COD/SO42- ratio of 1.44 and no NaHCO3 dosed to feed (Poinapen et al., 2009b).
• R2 at 1 500 mgSO42-/ℓ at 20ºC with PSS COD/SO42- ratio of 1.75 and no NaHCO3 dosed to feed (Poinapen et al., 2009b).
Table 11 lists the average measured (or calculated from measured results) influent characteristics of the 3 UASB BSR systems, and these values were used as inputs to the UCTADM1-BSR model. The COD units were converted to mole units with the relevant stoichiometric compositions of the organics, namely:
• Influent biodegradable particulate organics (BPO, Sbp) – stoichiometric composition of CxHyOzNa where x, y, z and a are determined from measured values (Poinapen and Ekama, 2010)
• Fermentable biodegradable soluble organics (FRBO, Sbsf) – represented by glucose (C6H1206)
• Biodegradable soluble acetic and propionic acids (Sbsa, Sbsp) – known stoichiometric compositions (C2H4O2 and C3H6O2 for associated and C2H3O2- and C3H5O2- for dissociated species respectively)
• Unbiodegradable soluble and particulate organics (USO, Susand UPO, Sup) – not converted since these are not degraded and utilised in the system and hence appear in the effluent (only Sus) and the waste (both Sus and Sup) flows respectively.

As mentioned earlier, the UASB reactor is simulated as a completely mixed digester because of the effect of the sludge recycle line which continuously mixed the top sludge with the bottom sludge.
Comparisons of the UCTADM1-BSR kinetic model predictions with experimentally measured and steady-state model data
The simulated results were compared with the experimental measured values and the steady-state model results. These comparisons are listed in Table 12.
It can be seen that there is a very good correlation between the experimental measured data and the simulated results from both the steady-state (SS) and the UCTADM1-BSR (kinetic) models.
The difference on one or two effluent concentrations may appear significant but the absolute difference is very small when compared with the removal concentrations (e.g. the effluent sulphate concentration as compared with the sulphate removal concentration). Moreover, some of the differences (though not significant) possibly come from imperfect mass balances – with the models all the mass balances (COD, S and N) are 100% while with the experimental data they are between 95 and 105%.
The gaseous CO2 production in the UCTADM1-BSR is zero as anticipated from the steady-state stoichiometry of BSR, where the PSS (C3.35H7O1.45N0.45) is carbon deficient (Poinapen and Ekama, 2010).
Another interesting outcome from the good UCTADM1-BSR model predictions is the successful integration and calibration of the sulphide inhibition term and the temperature dependency equation (in the case of R2 at 20ºC). The KI-as value for the acetoclastic SRB was found to be 206 mgS/ℓ for a 94% growth inhibition by the undissociated H2S using the exponential inhibition term exp[-([H2S]i/0.60056KI,j)2]. The θ value for the temperature dependency equation was 1.114 in the UCTADM1-BSR model, representing a 30% decrease in the PSS biodegradable organics hydrolysed when the temperature is decreased from 35ºC to 20ºC.
Conclusion
An integrated 2-phase (aqueous-gas) mixed weak acid/base chemistry and biological processes simulation model for competitive methanogenic and sulphidogenic anaerobic digestion with PSS as energy source for BSR (UCTADM1-BSR) was developed by Van Wageningen et al. (2006). This model was reviewed and modified to simulate the lab-scale UASB BSR systems. The kinetic model predictions (restricted to steady-state conditions) conform favourably to the experimental measurements and the SS model results and therefore provide support for the successful development, calibration and validation of the kinetic simulation model.
This model allows for 5 organic types (USO, UPO, BPO, FRBO, VFA) with different compositions in the influent feed. This characterisation structure conforms to the characterisation of municipal wastewater developed for activated sludge system models. Should a kinetic model with only BSR biological processes consuming the VFA and H2 substrates generated from PSS hydrolysis and acidification be required, the methanogenic processes can be switched off in the UCTADM1-BSR model. Moreover, although UCTADM1-BSR has been developed purposely for the situation where PSS serves as the feed substrate, it offers a much broader application. For instance, should the feed be a particulate substrate (e.g. a mixture of PSS and compost, compost alone or a mixture of PSS and waste activated sludge), only the feed substrate composition and kinetic constants for hydrolysis would require modification. For soluble organics (e.g. acetate or a mixture of VFA), they would be used directly as input to the model as they serve as intermediates in the processes already included in the model.
Acknowledgements
This research was financially supported by the Water Research Commission, the National Research Foundation and the University of Cape Town and is published with their permission.
References
BATSTONE DJ, KELLER J, ANGELIDAKI I, KALYUZHNYI SV, PAVLOSTATIS SG, ROZZI A, SANDERS WTM, SIEGRIST H and VAVILIN VA (2002) Anaerobic digestion model No 1, STR 13, IWA Publishing, London. 77 pp. [ Links ]
FEDOROVICH V, LENS P and KALYUZHNYI SV (2003) Extension of Anaerobic Digestion Model No.1 with Processes of Sulphate Reduction, Applied Biochemistry and Biotechnology Vol. 10. Department of Chemical Enzymology, Moscow State University, Moscow, 119992, Russia, and Sub-Department of Environmental Technology, Wageningen University, 6700 EV Wageningen, The Netherlands. [ Links ]
GIBSON GR (1990) Physiology and ecology of sulphate reducing bacteria. J. Appl. Bacteriol. 69 769-797. [ Links ]
KALYUZHNYI SV, FEDOROVICH V, LENS P, POL LH and LETTINGA G (1998) Mathematical modeling as a tool to study population dynamics between sulphate reducing and methanogenic bacteria. Biodegradation 9 (3-4) 187-199. [ Links ]
LOEWENTHAL RE, RISTOW NE, SÖTEMANN SW, WENTZEL MC and EKAMA GA (2005) Hydrolysis of primary sewage sludge under methanogenic, acidogenic and sulfate-reducing conditions. Final WRC Report 1216/1/05, Water Research Commission, Private Bag X03, Gezina, 0033, RSA. [ Links ]
MAILLACHERUVU KY and PARKIN GF (1996) Kinetics of growth, substrate utilisation and sulphide toxicity for propionate, acetate and hydrogen utilisers in anaerobic systems. Water Environ. Res. 68 1099-1106. [ Links ]
MUSVOTO EV, WENTZEL MC, LOEWENTHAL RE and EKAMA GA (1997) Kinetic-based model for mixed weak acid/base system, Water SA 23 (4) 311-322. [ Links ]
O'FLAHERTY V, MAHONY T, O'KENNEDY R and COLLERAN M (1998) Effect of pH on growth kinetics and sulphide toxicity thresholds of a range of methanogenic, syntrophic and sulphate-reducing bacteria. Process Biochem. 33 1-15. [ Links ]
OMIL F, LENS P, HULSHOFF POL LW and LETTINGA G (1996) Effect of upward velocity and sulphide concentration on volatile fatty acid degradation in a sulfidogenic granular sludge reactor. Process Biochem. 31 (7) 699-710. [ Links ]
POINAPEN J, EKAMA GA and WENTZEL MC (2009a) Biological sulphate reduction with primary sewage sludge in an upflow anaerobic sludge bed reactor –Part 1: Feasibility study. Water SA 35 (5) 525-534. [ Links ]
POINAPEN J, EKAMA GA and WENTZEL MC (2009b) Biological sulphate reduction with primary sewage sludge in an upflow anaerobic sludge bed reactor – Part 3: Performance at 20ºC and 35ºC. Water SA 35 (5) 543-552. [ Links ]
POINAPEN J and EKAMA GA (2010) Biological sulphate reduction (BSR) with primary sewage sludge in an upflow anaerobic sludge bed reactor – Part 5: Development of a steady-state model for BSR. Water SA 36 (3) 193-202. [ Links ]
REICHERT P (1998) Concepts Underlying a Computer Programme for the Identification and Simulation of Aquatic Systems (Aquasim 2.0), Swiss Federal Institute of Environmental Science and Technology (EAWAG), CH-8600, Switzerland. [ Links ]
SÖTEMANN SW, VAN RENSBURG P, RISTOW NE, WENTZEL MC, LOEWENTHAL RE and EKAMA GA (2005) Integrated chemical, physical and biological processes modelling Part 2 – Anaerobic digestion of sewage sludges. Water SA 31 (4) 545-568. [ Links ]
VAN WAGENINGEN HS, SÖTEMANN SW, RISTOW NE, WENTZEL MC and EKAMA GA (2006) Development of a kinetic model for biological sulphate reduction with sewage sludge as substrate. Water SA 32 (5) 619-626. [ Links ]
VAN WAGENINGEN S (2007) Development of a Kinetic Model for Biological Sulphate Reduction with Primary Sewage Sludge as Substrate. Masters dissertation, Department of Civil Engineering, University of Cape Town. [ Links ]
VAN ZYL PJ, EKAMA GA, WENTZEL MC and RIEDEL K-H (2008) Anaerobic Digestion of Fischer-Tropsch Reaction Water: Submerged Membrane Anaerobic Reactor Design, Operation and Modelling. Final Report to Sasol, Research Report No W131, Dept of Civil Engineering, Univ of Cape Town, Rondebosch, 7701, Cape, RSA. [ Links ]
YAMAGUCHI T, HARADA H, HISANO T, YAMAZAKI S and TSENG IC (1999) Process behaviour of UASB reactor treating a wastewater containing high strength sulphate. Water Res. 33 3182-3190. [ Links ]
Received 10 August 2009; accepted 15 February 2010.
1 To whom all correspondence should be addressed.
+2721 650 2585; fax: +2721 689 7471;
e-mail:George.Ekama@uct.ac.za














