Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Water SA
On-line version ISSN 1816-7950
Print version ISSN 0378-4738
Water SA vol.36 n.1 Pretoria Jan. 2010
Modelling the economic tradeoffs between allocating water for crop production or leaching for salinity management
N MatthewsI,*; B GrovéI; JH BarnardII; LD van RensburgII
IDepartment of Agricultural Economics, University of the Free State, PO Box 339, Bloemfontein 9300, South Africa
IIDepartment of Soil, Crop and Climate Science, University of the Free State, PO Box 339, Bloemfontein 9300, South Africa
ABSTRACT
Salinisation threatens the sustainability of irrigation agriculture and needs to be managed through leaching practices. Under conditions of water scarcity a tradeoff exists between allocating water for salinity management and production. Currently no model in South Africa is able to model explicitly the impact of salinity management through leaching on the economic efficiency of irrigation farming, taking the opportunity cost of water under limited water supply conditions into consideration. The main objective of this paper is to develop a robust non-linear optimisation model that is able to determine endogenously the impact of declining irrigation water quality on the economic efficiency of irrigation farming. A data envelopment framework was used to integrate recently developed soil water salinity crop-yield production functions and leaching functions to model the complex interactions involved in water allocation decisions. Results showed that it is profitable to reduce the area irrigated under limited water supply conditions in order to release water for leaching purposes. When more water, but still a limited amount of water, is allocated to the farmer, his willingness to pay for water will increase if irrigation water deteriorates. Thus, the conclusion is that leaching is profitable irrespective of the water supply conditions.
Keywords: salinity, leaching, economics, trade-off, non-linear optimisation, data envelopment analysis.
Introduction
Salinisation is a worldwide problem (Marcum, 2006), which also affects South African irrigation land. It has been estimated that between 5% and 12% of the total irrigation area of South Africa is moderately affected and between 1% and 12% is severely water-logged (WRC, 1996). Under water-logged conditions salt migrates to the rivers through natural pathways and artificial drainage systems (Smedema and Shiati, 2002). Because of the use and reuse of water for irrigation, water quality deteriorates temporally and spatially along river systems as farmers extract large amounts of water from the rivers for irrigation (Van Rensburg et al., 2008; Le Roux et al., 2007). Saline water affects crops indirectly through the osmotic component of the total soil water potential that reduces the plant-available water in the soil (West et al., 1986). Under severe salinity conditions, it will induce water stress and hence yield reductions as shown by Ehlers et al. (2007) and Dikgwatlhe et al. (2008). Soils are mainly affected through the impact of the salt on flocculation of soil particles or the dispersion of aggregates. Sodic water tends to disperse soil aggregates and hence restrict both the infiltrability and hydraulic conductivity of the soils, and by doing so increases the potential for greater runoff and water-logging (Nelson and Ham, 2000).
Irrigation management has become complex in the light of deteriorating water quality and demands research of an inter-disciplinary nature to support decision-making. Historically, decisions on when and how much to irrigate were mainly based on the biophysical conditions within the soil-plant-atmospheric continuum (Hillel, 2000). These include factors such as the evaporative demand of the crop, the storage capacity of the soil or plant available water and the sensitivity of specific growth stages, or the crop in general, to water stress (Stegman, 1983). Typically, the objective of irrigation scheduling was to maximise crop yield or to minimise crop water stress. English et al. (2002) argue that irrigation based on economic efficiency principles will be the new paradigm that will govern irrigation management in the light of limited water supplies that are threatened by deteriorating water quality. Economic efficiency requires the decision-maker to explicitly consider costs, revenues and the opportunity cost of water in his decisions.
Irrigators can mitigate the effect of salinity on profit margins through the introduction of more salt-tolerant crops or by managing the level of salt in the soil through leaching (Young, 2005). Under limited water supply conditions, the irrigator needs to decide between using the water to plant the maximum area, with reduced crop yield per hectare, or reducing the crop area thereby releasing some water for leaching purposes, which will increase the crop yield per hectare. Such a tradeoff is typically evaluated with an optimisation model. Critical to the analysis is the modelling of the non-linear relationship between the increasing leaching requirement, resulting from soil water salinity, and final crop yield as affected by soil water salinity. Within a South African context, Armour and Viljoen (2002; 2007) developed an optimisation model to evaluate on-farm options to mitigate salinisation. Due to a lack of data to quantify a continuous relationship that characterises the leaching requirement, expert opinion was employed to generate several activities, representing different combinations of soil and leaching fraction, in order to model the relationship. Potential problems exist with such a procedure with regard to robustness and the transferability of the generated database to other applications.
The main objective of this paper is to develop a robust non-linear optimisation model that is able to endogenously determine the impact of declining irrigation water quality on the economic efficiency of irrigation farming. The optimisation model integrates recently developed soil water salinity crop-yield production functions (Ehlers et al., 2007) and leaching functions (Barnard, 2006) within a data envelopment analysis framework in order to model the complex interactions involved in irrigation management with saline water. The model was applied to study the impact of deteriorating irrigation water quality on the economic efficiency of maize production under different irrigation water supply scenarios.
Data and procedures
Data
The data used in this study originated from field trials used to estimate the effect of deteriorating irrigation water quality on crops planted in soils with a shallow water table, as described in Ehlers et al. (2007). The trial was conducted in the lysimeter complex at Kenilworth Experimental Farm near Bloemfontein (University of the Free State) for 4 production seasons, including crops such as maize, beans, wheat and peas. The treatment comprised 5 water quality levels on 2 soil types classified according to the South African Classification System (Soil Classification Working Group, 1991), viz. a 1.8 m deep, yellow, fine sandy soil (Clovelly Setlagole) and a 1.8 m deep, red, fine sandy loam soil (Bainsvlei Amalia). The Bainsvlei soil has a higher mean silt and clay percentage over the profile than the Clovelly and therefore has better water retention properties than the Clovelly. The field trial data were used to estimate empirical models representing the effect of irrigation water quality on crop yield (Ehlers et al., 2007) and the amount of drainage water needed to leach excess salt from the soil (Barnard, 2006).
Relating soil water salinity to crop yield
Expected crop yield reductions due to increased soil salinity levels can be estimated with Maas and Hoffmann's (1977) threshold and gradient functions, confirmed by Ehlers et al. (2007) for South African conditions. When the soil-crop salinity threshold is exceeded, the crop cannot extract the required water from the soil and crop growth is suppressed due to the osmotic effect that occurs due to the lowering of the total water potential in the soil.
Following Maas and Hoffman (1977) the relationship between relative crop yield and soil salinity can be expressed as follows:

where:
Ya = actual crop yield realised (t·ha-1)
ym = maximum crop yield under non-saline conditions (t·ha-1))
b = rate of yield decrease per unit of excess salts above the threshold (percentage·mS-1m-1)
ECe = electrical conductivity from soil water-extract (mS·m-1)
a = salinity threshold of the crop (mS·m-1)
In the field trial study done by Ehlers et al. (2007), values for the salinity threshold and the percentage yield loss that resulted from deteriorating irrigation water quality were measured under controlled conditions. Important to note is that Ehlers et al. (2007) relate crop yield reduction to the electrical conductivity of the soil water (ECsw)and not ECe. The use of ECsw instead of ECe is justified because the crop was cultivated in a lysimeter where it is not a suitable practice to take destructive soil samples on a regular basis. Instead, soil water samples were obtained by extracting soil water under vacuum (-50 kPa) from the ceramic cups installed at 30 cm intervals in the profile of each lysimeter, on a weekly basis. Furthermore, Eq. 1 is only applicable under conditions of no water stress.
Converting irrigation water quality to soil water quality
Irrigation farmers generally know the quality of their irrigation water, which is typically expressed as total dissolved solids (mg·ℓ-1). The electrical conductivity of irrigation water (ECi) is directly related to the ionic composition of the water. According to the Department of Water Affairs and Forestry (1996) the conversion factor from total dissolved solids to EC for most South African waters is 6.5. Cognisance should be taken of the fact that Maas and Hoffman (1977) did not relate ECi to crop yield but ECe. The reason is that ECi is not the same as ECe because the concentration of salts in the soil is influenced by the soil colloids and hydrological processes in the soil. Therefore, some conversion is necessary to convert ECi to ECe before applying the salinity crop yield functions described in the previous section. As a rule of thumb, a conversion factor of 2 is used in the literature to convert ECi to ECe (Viljoen et al., 2006).
The field trial data from Ehlers et al. (2007) were used to test the conversion factor from ECi to ECsw. A conversion factor of 2.18 was obtained, which is close to the value of 2 used in the literature. However, it was found that a much better relationship between ECi and ECsw is obtained if the initial electrical conductivity of the soil water (ECin) before irrigation took place was taken into account. This was done for the field trial data of Ehlers et al. (2007) and the following coefficients where obtained in fitting the linear model:

where:
ECsw = soil water salinity after irrigation before leaching (mS·m-1)
ECi = irrigation water salinity (mS·m-1)
ECin = soil water salinity before irrigation (mS·m-1)
The R2 was 99% and both variables were statistically significant at a 1% test level. Most significant was the reduction in the mean absolute percentage error (MAPE) to 16% when ECi and ECin were included in the estimation.
Soil water salinity leaching function
Leaching of salts from the root zone of soils is the most effective means of removing excess salt. Barnard (2006) used the same lysimeter facility as Ehlers et al. (2007) to estimate the amount of drainage water required for leaching excess salts from sand to sandy loam soils.
According to Barnard (2006), the amount of drainage water required for reducing the ECsw of the root zone to a specific target soil water salinity level can be calculated as follows:

where:
D = drainage requirement for leaching excess salts (mm·ha)
lf = (ECa - ECi)/(ECsw - ECi) (leaching fraction)
ECa = target soil water salinity after leaching
ECsw = soil water salinity after irrigation before leaching (mS·m-1)
z = coefficient dependent on soil type
ds = depth of the soil (mm)
The value of the z-coefficient can be estimated from the mean coarse silt and clay percentage (S+C)% of the root zone (Barnard, 2006).

Equation (3) is used to relate the amount of irrigation water with a specific salinity level that is used for leaching to the resulting soil water salinity level (ECa) that will impact on crop yield.
Modelling crop yield as a function of leaching within a data envelopment analysis framework
The data envelopment analysis (DEA) technique of Banker et al. (1984) was used to simulate the non-parametric Maas and Hoffman (1977) salinity crop yield function for maize, taking the effect of leaching into account. DEA involves the use of linear programming methods in order to estimate a non-parametric piece-wise linear efficiency frontier form a set of data. Data points within the data set are then compared to the data points that form the efficiency frontier in order to calculate their relative efficiency to the frontier. The functioning of DEA within this paper is explained by means of Fig. 1.

Figure 1 shows that the Maas and Hoffman (1977) salinity crop yield function is characterised by a linear segment over which no reduction in maize yield takes place and a segment over which maize yield is reduced linearly when salinity exceeds the crop's salinity tolerance level. Within a DEA framework ECsw > 350 mS·m-1 is inefficient because higher crop yield is achievable with a better water quality. The function was therefore modelled in reverse or mirror image to ensure that the full extent of the Maas and Hoffman (1977) crop yield function is estimated with DEA procedures. In the reverse salinity crop-yield function, the threshold salinity level is achieved at an ECsw of 1370 mS·m-1. This was calculated as ECm – ECa (1720 – 350) mS·m-1 where ECm is the maximum soil water salinity level for which the graph is defined. The data points used to represent the efficiency frontier correspond to points A, B and C in Fig. 1. Within an output-orientated DEA model specification the objective is to determine with how much the output from an inefficient data point can be proportionally expanded to form part of the efficiency frontier without altering input quantities. The main purpose of the programming model is to determine the proportional weights attributed to the 2 data points that define the linear segment of the efficiency frontier for which the value of the ECsw needs to be interpolated.
To incorporate the impact of leaching salt on crop yield the soil water salinity level depicted in Fig. 1 corresponds to the soil water salinity level after leaching (ECa). The values of ECa are calculated by rearranging Eq. (3) and substituting Eq. (2) for ECsw resulting in the following function:
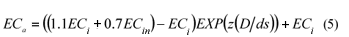
Through the use of ECa as the argument in a Maas and Hoffman (1977) salinity production function one is able to quantify the impact of irrigation water quality and leaching fractions on crop yield.
Optimisation model specification
The empirical model described in the previous section was used to develop an optimisation model to optimise the tradeoffs between allocating scarce water to irrigate larger areas or for salinity management through leaching. The convention is to use capital letters to represent variables that are endogenously determined by the optimisation model and small letters to represent the data parameters that are used in the calculations.
Objective function
The objective function of the model maximises gross income above specified costs. Specified costs include the costs of irrigation water applications to sustain crop production under conditions of no water stress and water applications for salinity management.
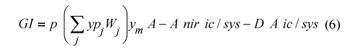
where:
GI = Gross income above specified costs to be maximised (R)
ym = Potential crop yield under non-saline conditions (t·ha-1)
ypj = Potential crop yield for point j on the reverse salinity crop yield efficiency frontier (t·ha-1)
A = Area planted (ha)
D = Drainage water required to leach excess salts (mm·ha)
Wj = Weights representing the contribution of the jth point on the efficiency frontier to yp (fraction)
p = Price of crop (R·t-1)
ic = Irrigation cost (water cost and cost to apply water) (R(mm·ha) -1)
sys = Irrigation system application efficiency (%)
nir = Net irrigation requirement of crop (mm·ha)
With maize as test crop, the 1st term in Eq. (6) calculates total gross income as the product of the area planted to maize (A), maize yield as affected by salinity ((∑ypjWj) ym) and the price of maize (p). Maize yield is a function of the soil water salinity level, which is a function of the irrigation water salinity level, initial soil water salinity and leaching management. The specific procedures used to model the impact of soil water salinity on crop yield are discussed in the following section. The last 2 terms respectively calculate the cost of applying water to ensure that the crop is irrigated to sustain crop yield under conditions of no water deficits and the cost of applying water for leaching purposes.
Crop yield estimation
Crop yield is estimated as a function of the average soil water salinity level, which is a function of the irrigation water quality, initial soil water salinity and the amount of leaching applied. The following equations are used to model the interactions between soil water salinity and crop yield within a DEA framework:

where:
ecswj= Soil water electrical conductivity of point j on the reverse salinity crop yield efficiency frontier (mS·m-1)
ecm = Maximum soil water electrical conductivity where yield potential is zero on the Maas and Hoffman (1977) function (mS·m-1)
Equation (9) corresponds with Eq. (5), and is used to calculate the soil water salinity level for which the crop yield needs to be interpolated within an output-orientated variable-returns to-scale (VRS) (Banker et al., 1984) DEA model. Equation (8) imposes the convexity condition in the VRS model specification to allow for the non-parametric function to exhibit piece-wise linear segments (Cooper et al., 2006). Equation (7) ensures that the interpolated input used for the reference units on the efficiency frontier does not exceed ecm – ECa when the output level is maximised for the reverse crop yield function.
Resource constraints
Total production is constrained by water and land availability with Eq. (10) and (11).
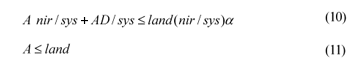
where:
land = Maximum amount of arable area available (ha)
α = Parameter used to parameterise water availability
Equation (10) is parameterised for 2 alternative irrigation water supply scenarios through the use of α. When α = 1 enough water is available to irrigate all the available irrigation land.
Results
The optimisation model is applied to determine whether it is economically viable to allocate water for leaching purposes in order to obtain higher crop yields in light of deteriorating water salinity levels. Results were generated given the following assumptions:
• A Bainsvlei Amalia soil with a combined silt and clay content of 8% was used for maize production
• An initial soil water salinity level of 350 mS·m-1
• Natural drainage is possible therefore the cost of artificial drainage was not considered
• The natural leaching effect of rainfall was not taken into consideration
• Irrigation refilled the soil water content to the drained upper limit
• A volumetric water levy was charged
• The irrigation water quality, eci, remains constant over the duration of the irrigation period
Furthermore, the assumption is made that 100 ha of land is available for the production of maize while 2 water supply scenarios are considered. Scenario 1 is characterised by a situation where enough water is available to irrigate 100 ha of maize without sustaining any crop yield loss due to salinity (α = 1). Thus, the farmer needs to reduce his area irrigated to release water for leaching purposes when irrigation water quality deteriorates further. With Scenario 2 water supply is assumed to be 10% more than that of Scenario 1 (α = 1.1). However, the area that can be irrigated remains at 100 ha.
Scenario 1
Figure 2 shows the tradeoff that exists between deteriorating irrigation water salinity and the on-farm margin above specified costs (a), the marginal value of irrigation water (b), soil water salinity (c), amount of water used to leach excess salt from the soil (d), the area under production (e) and crop yield (f).
The results in the graphs show that no tradeoff is modelled when the irrigation water salinity level (eci) is below 105 mS·m-1. As a result deteriorating irrigation water salinity does not alter the marginal value of water which is constant at a rate of ZAR21·m-3. Under conditions of relatively good irrigation water quality (eci < 105 mS·m-1), soil water salinity does not exceed the maize salinity threshold level of 350 mS·m-1. Since the maize salinity threshold is not exceeded, crop yield will not be affected and a maximum crop yield of 11.4 t·ha-1 is achieved. Since the maximum crop yield is achieved and leaching practices are not necessary, a maximum on-farm margin of R2.2 m. is achieved. Thus, the farmer will use all his available water to irrigate 100 ha without allocating any water for leaching purposes.
If irrigation water salinity (eci) deteriorates to levels above 105 mS·m-1, the salt build-up in the soil causes soil water salinity levels to exceed the crop's salinity threshold. The results show that it is profitable to reduce the area irrigated in order to release water to leach some salts from the soil to improve crop yields. Although leaching is practised, the level of leaching is not sufficient to improve soil water salinity to the crop's soil water salinity tolerance level. As a result, crop yield decreases, which also causes the productivity of water to decrease from a maximum of ZAR21·m-3 to ZAR12.67·m-3 if irrigation water salinity deteriorates to 600 mS·m-1. At first, it seems as though the productivity of water is in direct relation to the rate of yield decrease per unit of excess salt above the crop's salinity threshold level that is specified in the Maas and Hoffman (1977) salinity crop yield function. However, it is important to note that the actual water productivity modelled is higher due to leaching. Although crop yield losses are still occurring, the crop yield loss is less than it would have been if the farmer had not leached excess salts. Thus, the productivity of water is higher than would have been the case without leaching taking place. The results further showed that all the tradeoffs that were modelled are linear when irrigation water supply is limiting.
Scenario 2
The same variables were used in Fig. 3 to show the impact of deteriorating irrigation water salinity when 10% more water is available to the irrigator. The resulting tradeoffs show more complex relationships between the variables and differ significantly from the water-limiting scenario. As is the case for Scenario 1, crop yield is only affected if irrigation water salinity exceeds 105 mS·m-1 when no leaching takes place, and therefore no tradeoffs are modelled for eci values less than 105 mS·m-1. However, crop yield only starts to decrease when irrigation water salinity exceeds 195 mS·m-1 because enough irrigation water is available with Scenario 2 to leach salts from the soil to improve soil water salinity to the threshold salinity tolerance level of the crop. Thus, irrigation water availability does not limit the area irrigated or the level of leaching that is necessary to sustain maximum potential crop yield. As a result, no marginal values for irrigation water are calculated.
An interesting result is that the marginal value of water increases from ZAR12.35·m-3 at a constant rate of ZAR0.08·m-3·(mS·m-1)-1 to ZAR13.98·m-3 when irrigation water salinity increases to between 195 mS·m-1 and 525 mS·m-1. During this stage, the deterioration of water salinity increases the leaching requirement while water availability is inadequate to sustain the increase in leaching requirement. The available irrigation water is used to irrigate 100 ha and the remainder is used for leaching purposes. Thus, if more water had been available it would have been used to leach salt from the soil. The benefit attributed to the last cubic meter of water that is used for leaching is directly related to changes in the soil water salinity levels. Irrigation with more saline irrigation water results in increasing soil water salinity levels, which affect crop yields. However, the increase in soil water salinity level also causes the amount of salt that is leached by the last cubic meter of water used for leaching to increase. Because the reduction in crop yield due to higher soil water salinity levels is less than the crop yield increase derived from leaching, the overall result is positive and the marginal value of water increases under deteriorating irrigation water salinity.
If irrigation water quality deteriorates to levels of above 525 mS·m-1, crop yields would be affected to such an extent that it is profitable for the farmer to reduce his hectares under irrigation in order to release water for leaching. Although not clearly visible from the graphs, it is important to note that all the tradeoffs that are reported, except for area irrigated, are exactly the same as for Scenario 1 if irrigation water salinity exceeds 525 mS·m-1.
Conclusions
This study showed interesting relationships between the impact of increasing irrigation water salinity on economic efficiency and the maximum willingness to pay for irrigation water. These relationships are highly dependent on the interaction between water availability and the tradeoff that exists between using irrigation water to irrigate larger areas or using it to leach excess salt from the soil thereby increasing crop yield. Modelling results further showed that it is profitable to leach excess salt from the soil once the soil water salinity exceeds the crop's salinity threshold. The economic benefits of leaching are such that it is even profitable to reduce the area irrigated under limited water supply in order to release water to leach salt from the soil. When more water, though still a limited amount, is allocated to the farmer his willingness to pay for water will increase if irrigation water deteriorates. The last-mentioned may seem a paradox, but indicates that the added benefit from leaching outweighs the negative impact of deteriorating water quality on crop yield. Thus, the conclusion is that leaching is profitable irrespective of water supply conditions. However, water supply conditions have a significant impact on the willingness to pay for additional water. Although it is profitable to leach, costs associated with artificial drainage need to be taken into consideration, if natural drainage is not possible, to determine whether or not leaching is still financially feasible to cover the substantial long-term costs of artificial drainage and efficient disposal of leachate.
The modelling framework that was developed proved to be useful in analysing the interrelationships between allocating water for leaching management and using water for production. Cognisance should be taken of the assumptions that were made when modelling the interrelationships. The model uses seasonal production and leaching functions. Thus, the assumption is made that it is physically possible to leach the amounts that were estimated with the programming model. Decision-makers require more detailed information to facilitate leaching management. Future research should focus on the optimisation of water budget calculations through the season to test the feasibility of leaching. Such an approach will also allow for the inclusion of other factors such as timing of irrigations, irrigation system capacities and uniformity of applications in the analyses. Another aspect that was not covered in this research is the fact that leaching causes an externality that will impact negatively on the environment and other users. To internalise these costs to the farmer appropriately formulated policy is necessary.
Acknowledgements
Financial assistance provided by the Water Research Commission (WRC) is gratefully acknowledged. The views of the authors do not necessarily reflect those of the WRC.
References
ARMOUR RJ and VILJOEN MF (2002) The leaching paradox and return flow management options for sustainable irrigated agriculture. S. Afr. J. Econ. Manage. Sci.(Spec. Environ. Issue) 5 (2) 430-451. [ Links ]
ARMOUR RJ and VILJOEN MF (2007) An economic case for drainage for sustainable irrigation: Case studies in the Lower Vaal and Riet catchments. SAJEMS 10 (4) 470-481. [ Links ]
BANKER RD, CHARNES A and COOPER WW (1984) Some models for estimating technical and scale inefficiencies in data envelopment analysis. Manage. Sci. 30 (9) 1078-1092. [ Links ]
BARNARD JH (2006) Leaching of Excess Salts from the Root Zone of Apedal Soils. M.Sc. Agric. Dissertation, Department of Soil, Crop and Climate Sciences. University of the Free State, Bloemfontein. [ Links ]
COOPER WW, SEIFORD LM and TONE K (2006) Introduction to Data Envelopment Analysis and its Uses: With DEA-Solver Software and References. Springer Science, New York. [ Links ]
DIKGWATLHE SB, CERONIO GM and VAN RENSBURG LD (2008) Wheat (Triticum aestivum L.) growth and yield response to saline irrigation water under controlled conditions. S. Afr. J. Plant Soil 25 (3) 172-177. [ Links ]
EHLERS L, BARNARD JH, DIKGWATLHE SB, VAN RENSBURG LD, CERONIO GM, DU PREEZ CC and BENNIE ATP (2007) Effect of Irrigation Water and Water Table Salinity on the Growth and Water Use of Selected Crops. WRC Report No. 1359/1/07. Water Research Commission, Pretoria, South Africa. [ Links ]
ENGLISH MJ, SOLOMON KH and HOFFMAN GJ (2002) A paradigm shift in irrigation management. J. Irrig.. Drain. Eng. 128 (5) 267-277. [ Links ]
HILLEL D (2000) Salinity Management for Sustainable Irrigation. World Bank, Washington, DC. [ Links ]
LE ROUX PAL, DU PREEZ CC, STRYDOM MG, VAN RENSBURG LD and BENNIE ATP (2007) Effect of irrigation on soil salinity profiles along the Lower Vaal River, South Africa. Water SA 33 (4) 473-478. [ Links ]
MARCUM KB (2006) Use of saline and non-potable water in the turfgrass industry: Constraints and developments. Agric. Water Manage. 80 132-146. [ Links ]
MAAS EV and HOFFMAN GJ (1977) Crop salt tolerance – current assessment. J. Irrig. Drain. Div. Am. Soc. Civ. Eng. 103 115-134. [ Links ]
NELSON PN and HAM GJ (2000) Exploring the response of sugar cane to sodic and saline conditions through natural variation in the field. Field Crop Res. 66 245-255. [ Links ]
SMEDEMA LK and SHIATI K (2002) Irrigation and salinity: a perspective review of the salinity hazards of irrigation development in the arid zone. Irrig. Drain. Syst. 16 161-174. [ Links ]
SOIL CLASSIFICATION WORKING GROUP (1991) Soil Classification: A Taxonomic System for South Africa. Memoirs on the Agricultural Natural Resources of South Africa No. 15. Department of Agricultural Development, Pretoria, South Africa. [ Links ]
STEGMAN EC (1983) Irrigation scheduling: Applied timing criteria. Adv. Irrig. 2 1-30. [ Links ]
VAN RENSBURG LD, STRYDOM MG, DU PREEZ CC, BENNIE ATP and PRETORIUS JP (2008) Prediction of salt balances in irrigated soils along the lower Vaal River, South Africa. Water SA 34 (1) 11-17. [ Links ]
VILJOEN MF, ARMOUR RJ, OBERHOLZER JL, GROSSKOPF M, VAN DER MERWE B and PIENAAR G (2006) Multi-Dimensional Models for the Sustainable Management of Water Quantity and Quality in the Orange-Vaal-Riet Convergence System. WRC Report No. 1352/1/06. Water Research Commission, Pretoria, South Africa. [ Links ]
WRC (WATER RESEARCH COMMISSION) (1996) Policy proposal for irrigated agriculture in South Africa. Discussion document prepared by Backeberg GR, Bembridge TJ, Bennie ATP, Groenewald JA, Hammes PS, Pullen RA and Thompson H. WRC Report No. KV96/96. Water Research Commission, Pretoria, South Africa. [ Links ]
WEST DW, HOFFMANN GJ and FISHER MJ (1986) Photosynthesis, leaf conductance and water relations of cowpea under saline conditions. Irrig. Sci. J. 7 183-193. [ Links ]
YOUNG RA (2005) Determining the Economic Value of Water: Concepts and Methods. World Bank, Washington, DC. [ Links ]
Received 5 June 2009; accepted in revised form 12 November 2009.
* To whom all correspondence should be addressed.
+2751 401 2391; fax: +2751 401 3473;
e-mail: MatthewsN.sci@ufs.ac.za














