Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
Water SA
versión On-line ISSN 1816-7950
versión impresa ISSN 0378-4738
Water SA vol.36 no.1 Pretoria ene. 2010
Crop production management practices as a cause for low water productivity at Zanyokwe Irrigation Scheme
M FanadzoI; C ChiduzaI,*; PNS MnkeniI; I van der StoepII; J StevensIII
IDepartment of Agronomy, Faculty of Science and Agriculture, University of Fort Hare, Private Bag X1314, Alice 5700, South Africa
IIWSM Leshika Consulting, PO Box 39942, Moreleta Park, Pretoria 0044, South Africa
IIIDepartment of Agricultural Economics, Extension and Rural Development, University of Pretoria, Pretoria 0002, South Africa
ABSTRACT
Generally, smallholder irrigation schemes (SIS) in South Africa have performed poorly and have not delivered on their development objectives of increasing crop production and improving rural livelihoods. Limited knowledge of irrigated crop production among farmers has been identified as one of the constraints to improved crop productivity, but research that investigates the relationship between farmer practices and productivity is lacking. A monitoring study was therefore conducted at the Zanyokwe Irrigation Scheme (ZIS) in the Eastern Cape to identify cropping systems and management practices used by farmers and to determine how these were related to performance. Evidence from 2 case studies showed that water management limited crop productivity. Irrigation application and system efficiencies were below the norm and irrigation scheduling did not take crop type and growth stage into account. Monitoring of 20 farmers over a 3-yr period showed that cropping intensity averaged only 48% and that the yields of the 2 main summer crops, grain maize (Zea mays L.) and butternut (Cucurbita moschata) averaged only 2.4 and 6.0 t·ha-1, respectively. In addition to poor water management, other main constraints to crop productivity were inadequate weed and fertiliser management and low plant populations. The results indicated that a lack of basic technical skills pertaining to irrigated crop production among farmers was a possible cause of inadequate management. In this regard, it is expected that farmers could benefit from 'back to basics' training programmes in the areas of crop and irrigation water management. Research needs to focus on labour-saving production technologies, establishing farm-specific fertiliser recommendations, the identification and use of affordable sources of nutrients, as well as strategies to improve plant population in maize by preventing bird damage to newly-planted stands.
Keywords: smallholder irrigation schemes, cropping pattern, constraints to crop productivity, research agenda.
Introduction
Rural poverty is an important development challenge in South Africa (SA) (Laker, 2004) and irrigation has long been viewed as an option for improving rural livelihoods (FAO, 2001). However, most of the smallholder irrigation schemes (SIS) that were established in SA have performed poorly (Bembridge, 2000; Crosby et al., 2000; Oosthuizen, 2002; Perret et al., 2003; Denison and Manona, 2007), whilst in other countries irrigated agriculture has managed to address rural poverty and unemployment (Ferguson and Mulwafu, 2004). The poor performance of many SIS in SA has been attributed to socio-economic, political, climatic, edaphic and design factors (Bembridge, 2000), but Crosby et al. (2000) indicated that farmer practices may actually be constraining performance, identifying low yields as evidence of poor farmer performance.
Maize (Zea mays L.) is the most important summer grain crop in terms of both cultivated area and number of growers in SIS in SA. Maize grain yields of less than 3 t·ha-1 are common in many SIS (Van Averbeke et al., 1998; Bembridge, 2000; Machethe et al., 2004; Fanadzo, 2007), which supports the point raised by Crosby et al. (2000) above. Machethe et al. (2004) also identified limited knowledge and lack of skills in crop production among farmers as one of the constraints to improved productivity in SIS. In this regard, Denison and Manona (2007) recommended that crop production approaches including farmer training be considered alongside all other issues during revitalisation of SIS to improve on performance. However, little attention has been given to the study of cropping systems and management practices in SIS (Machethe et al., 2004), and to whether these factors could account for observed poor performance. Indeed, De Lange et al. (2000) noted that research and expenditure have tended to focus on infrastructure, and that often this has proved to be fruitless because the human capital was not developed to utilise and maintain the infrastructure effectively.
Monde et al. (2005) noted that, despite having access to an average of 4.2 ha of irrigated land per farmer, most farmers at Zanyokwe Irrigation Scheme (ZIS) were poor, with monthly incomes lower than the 2005 poverty datum line of ZAR626.98 per adult equivalent. They found that both cropping intensity and yields were low, with farmers attributing low crop performance indices to lack of adequate tillage services, fertiliser, seed, chemicals and irrigation equipment. This study, like many others carried out in SA, relied on farmer interviews, and due to the lack of farm records was limited in explaining and relating performance to factors cited by farmers.
The low levels of crop productivity noted in many SIS in SA imply low water use efficiencies (WUE), as available evidence indicates that water at the source is rarely limiting (Machethe et al., 2004; Stevens, 2007), and in some cases over-application has been noted (Machethe et al., 2004; Monde et al., 2005). Improving WUE in irrigation is a priority in SA. With the growing scarcity of water, significant increases in water productivity will have to come from improved agronomic practices rather than increasing the area under cultivation (Machethe et al., 2004).
Available evidence points to the need for driving crop productivity upwards in SIS in order to contribute to improved performance with regard to WUE, incomes and farmer livelihoods. In order to achieve yield increases of crops grown by farmers, there is a need to understand the cropping systems adopted, farmer management practices and how they relate to observed yields in SIS. The study of SIS cropping systems and their management could be used to identify and develop 'best management practices' as suggested by Laker (2004). The present study was therefore conducted to identify cropping systems and management practices used by farmers, using ZIS in the Eastern Cape as a case study to determine how these were related to performance.
Materials and methods
Study area description and background
Zanyokwe Irrigation Scheme (32°45′S; 27°03′E) is located in the central part of the Eastern Cape, between King William's Town and Fort Beaufort. The climate is semi-arid and relatively mild, with a mean annual rainfall of about 580 mm of which about 445 mm is received in summer. The estimated annual Class A evaporation is about 1 800 mm and frost may occur from mid-June to mid-August (Van Averbeke et al., 1998). Soils of the Oakleaf and Dundee form (Soil Classification Working Group, 1991) are dominant (Van Averbeke et al., 1998). The suitability of these soils for irrigation is moderate to moderately high (Loxton, 1983). ZIS uses sprinkler irrigation and the area irrigated is 471 ha. The low salinity/low sodium water (Hill et al., 1991) can be used for irrigation without any restrictions (Van Averbeke et al., 1998). The scheme is comprised of 6 villages with 61 farming households. The study was conducted from 2005/06 to 2007/08 at Burnshill and Lenye, which are the 2 biggest villages at ZIS. The 2 villages constituted 31 and 45% of farmers, and 25 and 35% of the cultivated area in the scheme, respectively.
Monitoring surveys
Monde et al. (2005) classified the farmers of ZIS into 3 wealth classes; non-poor (NP), poor (P) and ultra-poor (ULP), based on adult equivalent income (AEI) per month using the 2005 poverty datum line (PDL) of ZAR626.98 per adult equivalent. Households with AEI > PDL were considered NP; those with AEI < ½PDL were classified as ULP, while those falling between the 2 limits were classified as P. Among the 48 farmers in Burnshill and Lenye, 19 (40%) were ULP, 11 (22%) were P while 18 (38%) were NP. Stratified simple random sampling was used to select 8 NP, 5 P and 7 ULP farmers from the population of 48 farmers. The 20 farmers selected were monitored for 3 summer and winter seasons from 2005/06 to 2007/08.
During the growing season, records were kept on type of crops grown, crop areas, tillage practices, planting dates, cultivars, fertility management, weeding, irrigation management, labour and crop yields. Fortnightly visits were made to the scheme to collect data from the farmers through semi-structured interviews and field observations in farmers' fields. Monitoring of production practices was done on grain maize, green maize and butternut (Cucurbita moschata), which were the main summer crops. Crop cuts (FAO, 1982) were used to estimate maize grain yield in farmers' fields, while butternut yields were obtained from farmer records. For the crop cuts, stratified samples were taken from the up-slope, mid-slope and down-slope of each farmer's field in plots measuring 5 m × 5 m. Maize crop stand was estimated by counting the total number of plants in 5 × 90 cm rows, each measuring 20 m, to give an area of 90 m2 in each farmer's field. For the same area of 90 m2, the proportion of maize sold as green cobs was estimated by counting plants with harvested cobs and dividing this number by the plant population.
Case studies
The case study approach was used to monitor farmers, providing the opportunity to highlight successes and failures in production. Tools used for data collection included informal surveys, interviews, farmers' records and personal observations. Three farmers, one from each of the wealth classes, were monitored throughout the duration of the study. To monitor irrigation water management, 2 farmers were supplied with FullstopTM wetting front detectors (WFDs), devices used to observe how deep the wetting front has moved. The farmers kept records of the response of the WFDs in different crops. Irrigation distribution tests were done by setting up catch cans in a 3 m × 3 m grid between the sprinklers, replicated 3 times, and recording the amount of water collected in each can within a set period. The data collected were used to calculate a number of water-use efficiency performance indicators, including Christiansen uniformity coefficient, distribution uniformity, application efficiency and system efficiency.
Agronomic performance indicators
Production, measured as the biological output from the individual farms or yield per hectare, was used as the overall performance indicator (FAO, 1995). Additionally, cropping intensity (CI) was defined to evaluate land use intensity by the individual farmers. CI was expressed in terms of the number of crops that were cultivated on a particular surface area per year or the fraction of the total available land cropped in any given year (Noordwijk, 2002). These indicators define the farmers' management performance at field scale; however, the use of these indicators at the level of the irrigation scheme (average values) provides very useful information for determining improvements at scheme level, and also for carrying out comparisons among irrigation schemes (García-Vila et al., 2008).
Results
Socio-economic characteristics of farmers
The number of full-time farmers decreased from 19 (95%) in 2005/06 to 18 (90%) in 2006/07 and 2007/08, while part-time farmers, all NP, increased from 1 (5%) to 2 (10%). Only 3 (15%) NP farmers owned pick-up trucks. Nineteen (95%) farmers did not have access to family labour and relied on hired labour on either a temporary (80%) or permanent (20%) basis. Despite the hiring of labour, serious labour shortages were experienced during peak operations, and particularly during the festive season from mid-December to mid-January. Seven (35%) ULP and 4 (20%) P farmers were freeholders while 8 (40%) NP and 1 (5%) P farmers were leaseholders. The average size of arable land was 5.0 ha (range: 3.0-7.0 ha) and 4.5 ha (range: 2.0-11.0 ha) for freeholders and lessees, respectively. Seventeen (85%) farmers were men and the 3 (15%) women farmers were all widows. The average age of the farmers at the beginning of the study in 2005 was 52. Mean household size was 5 people with a range of 1 to 8. All P and ULP farmers had up to 8 years of formal education while all NP farmers had some tertiary education.
Cropping patterns
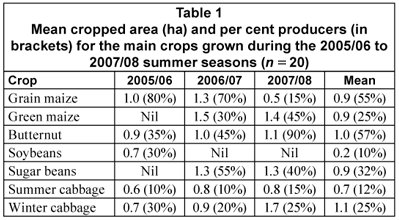
Green and grain maize, butternut and sugar beans (Phaseolus vulgaris) were the most popular summer crops while cabbage (Brassica oleracea var. capitata) was the main winter crop (Table 1). None of the ULP and P farmers produced green maize and none of the ULP farmers had any crop in winter in all 3 years.
The cropping patterns for the 3 years of monitoring are shown in Table 2.

Table 2 highlights that farmers produced a limited number of crops, with a mean 2.8 crops per farmer for the 3 years. The winter-cropped area averaged only 6.6% of the total area, translating to low CIs, averaging 48% for the 3 years. Chi-square test of independence showed a significant (p < 0.05) association between poverty status and CI; NP farmers had superior performance across the 3 years.
The main reason cited by ULP farmers for not producing in winter was lack of cash. For summer crop production, ULP farmers exclusively relied on contract farming and waited for outsiders who provided all basic production inputs. Sixty per cent of P farmers did not have a winter crop in all 3 years, while the other 40% had cabbage in winter. All NP farmers were lessees, had the largest pieces of land averaging 8.0 ha and had resources to initiate and manage their own crop production.
The predominant cropping patterns were a monoculture of maize, butternut-cabbage, maize-cabbage, and maize-butternut rotations. This is illustrated by a case study of 1 NP farmer who leased 11 ha of land in 2007/08 (Table 3) and achieved a CI of 85%. The cropping system resulted in maize-cabbage, maize-butternut and butternut-cabbage rotations on part of the field and a monoculture of maize on a hectare of land.
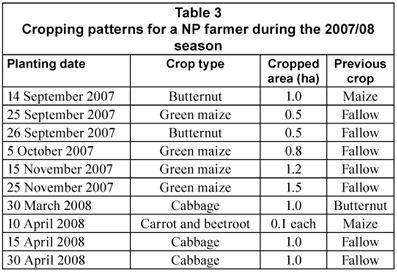
None of the ULP practiced crop rotation as illustrated by a case study of 1 farmer owning 5.8 ha of land on a freehold basis. The farmer only produced in summer, with 2 crops in each of the 3 years. In 2005/06, the farmer had grain maize (1.0 ha) and soybeans (0.5 ha) in summer, resulting in a CI of 26%. In 2006/07, the farmer had 1.5 ha of grain maize and 1 ha of sugar beans, giving a CI of 43%. In 2007/08, the farmer planted butternut (0.5 ha) and sugar beans (1.5 ha) to give a CI of 34%. The remainder of the land not used in summer was left fallow while all the land was left fallow in winter.
General production practices
Planting
For maize planting, all farmers relied on hiring 1 of the 2 tractor-drawn planters operating in the scheme. Planting time was not related to wealth class, but on access to a tractor, which was detemined on a 'first-come first-served' basis. Planting of grain maize commenced after mid-November and extended up to mid-March. Farmers used a combination of hybrid seed and open-pollinated varieties (OPVs). Whilst farmers used a combination of hybrids and OPVs for green maize production in 2006/07, all producers in 2007/08 used the hybrid cultivar SC701. However, one farmer used recycled seed of the hybrid cultivar. In 2007/08, 2 farmers established some of their green maize from seedlings purchased from a commercial nursery, to cope with bird damage to emerging seedlings and improve on crop stand.
Weed management
Weed-crop competition caused by inadequate weed control was among the major causes of poor yields observed in the scheme in all seasons. Major problem weeds were Cynodon dactylon and Cyperus esculentus in all crops. In addition to these, other important weeds in butternut were the broadleaves Ageratum conyzoides, Plantago major and Nicandra physaloides.
Grain maize: In 2006/07, 62% of grain maize producers only controlled weeds before planting; 15% never controlled weeds, 15% controlled weeds both pre- and post-emergence, and 8% controlled weeds only after emergence of the maize crop. Farmers who never controlled weeds or who did not exercise post-emergence weed control cited lack of knowledge on the type of herbicides that could be used in maize and other crops, while others cited lack of cash to purchase the herbicides. After failing to cope with the weeding requirements, 22% of maize grain producers abandoned their crop to weeds in 2006/07. Weed control in grain maize was mainly through tractor inter-row cultivation and use of herbicides, or a combination of the two. For pre-plant chemical control, glyphosate was applied to the previous season's weeds, resulting in the first flush of weeds for the current season emerging together with the crop after irrigation water was applied. The 3 grain maize producers in 2007/08 used cultivation to kill the first flush of weeds before planting, while for post-emergence weed control 2 sprayed atrazine at 5 ℓ·ha-1 and the third used tractor inter-row cultivation. Observations showed that tractor inter-row cultivation resulted in significant crop loss, as some plants were uprooted by the cultivator due to poor timing of cultivation and due to planting rows that were not straight.
Green maize: In 2006/07 and 2007/08, 25 and 22%, respectively, of producers applied a pre-plant herbicide, atrazine. For post-emergence weed control, 2 farmers used hand hoeing, while the other farmers relied on herbicides and inter-row cultivation in both seasons. Because of labour shortages, 1 farmer who used hand hoeing on 0.5 ha in 2006/07 only weeded along the crop rows once, at 3 weeks after emergence (WAE), whilst leaving the inter-row weedy. The main problem weeds in the farmer's field were C. esculentus and C. dactylon, which proved very difficult to control as they were observed to re-root after weeding. The ineffectiveness of weed control, compounded by failure to apply fertiliser, resulted in a crop that was so stunted that no marketable cobs could be obtained. Grain yield estimates done at the farmer's field indicated a yield of 255 kg·ha-1. The other farmer who relied on hand hoeing in 2007/08 completed the weeding operation when the maize was at the tasseling stage. He then applied top-dress fertiliser when the maize was at the silking stage and failed to harvest marketable cobs. The weeding labour requirement for the farmer was 365 hours·ha-1.
Butternut: The problem of weeds forced 29 and 22% of butternut producers, in 2006/07 and 2007/08, respectively, to abandon their crop plots and lose 100% of their crop after failing to cope with the weeding requirements. Due to the absence of registered herbicides for the post-emergence control of broadleaf weeds in butternut, post-emergence weed control in the crop was solely by hand hoeing. Only 2 farmers practised pre-plant weed control, using glyphosate to kill the first flush of weeds, while 78 and 89%, in 2006/07 and 2007/08, respectively, relied on post-plant weed control through hand hoeing. Poor crop stand in butternut was a common experience in all seasons, mainly because of late weed control. Weeding was usually started just before flowering at 3 WAE and extended for 1 to 2 weeks due to a shortage of labour. The mean labour requirement for weeding was 380 h·ha-1 with a range of 232 to 600 h·ha-1. Due to a shortage of labour, some farmers resorted to weeding around planting stations whilst the rest of the field remained weedy, a situation that aggravated weed infestation in the following crop.
Irrigation water management
Generally, infield water management at scheme level was weak. The in-field irrigation equipment used by farmers was in a state of dilapidation as many of the sprinkler systems used were very old and were not maintained well. Different standpipe lengths, sprinklers and nozzles were found in single laterals while many connections to the laterals often leaked due to worn-out threads.
Irrigation equipment: Of the 20 farmers monitored, 1 P and 4 ULP farmers owned between 12 and 18 sprinklers, while 1 ULP, 4 P and 5 NP, owned between 20 and 30 sprinklers. Three NP farmers owned between 40 and 60 sprinklers each, while 2 ULP farmers did not own any pipes or sprinklers and relied on borrowing from owners. On average, farmers owned 22 sprinklers with a range of nil to 60 sprinklers per farmer. All farmers cited inadequacy of pipes as a major constraint for effective irrigation of crops.
Scheduling: All farmers did not exercise objective scheduling methods, but used a combination of plant observation and the 'feel' method. They observed the condition of the soil and the crops as a basis for irrigation decisions. Irrigation schedules of 2 to 4 h stand time every 2 to 3 d were common. The irrigation schedule was generally constant regardless of crop type and growth stage, usually resulting in over-irrigation during the early crop growth stages and under-irrigation during the advanced growth stages. The 2 farmers who had to borrow pipes irrigated overnight.
A case study of a NP farmer showed that the farmer followed a fixed irrigation schedule of 2 to 3.5 h every 7 d, which translated to a gross application of 11.2 to 20.3 mm.h-1. Although the farmer applied almost the correct total amount of irrigation of 285 mm for winter cabbage, timing of irrigation applications was out of order. Analysis of the farmer's irrigation records showed that he over-irrigated by 19 and 85 mm in May and June, but under-irrigated by 8 and 45 mm in July and August, respectively. Irrigation records for butternut production indicated that though the farmer applied the correct amount of water in December and February; the amount applied in January (95 mm) was 53% of the crop water requirement of 180 mm. The total amount of water (320 mm) applied to the crop was 76% of the crop water requirement of 420 mm.
The ideal operating pressure for the Rain Bird 30 BH sprinklers used by farmers at ZIS is < 3 bars (300 kPa). However, a case study of 2 farmers indicated that the operating pressure at both farms exceeded 400 kPa. The gross and average application rates at the 2 farms were 10.14 and 5.81 mm.hr-1, and 6.05 and 2.87 mm.hr-1, respectively (Table 4). The application and system efficiencies at both farms were low (Table 4).

Fertility management
Farmers generally applied low amounts of fertilisers in all crops. Poor timing of application was another major cause of low productivity, particularly in butternut. Whilst all farmers relied on inorganic fertilisers, one (5%) NP farmer also used organic fertilisers in the form of cattle and chicken manure in all seasons. Two farmers, 1 each in 2006/07 and 2007/08, did not apply fertiliser to their maize. The reason given by 1 farmer for non-application at planting was to reduce the weed competition that comes with the first flush of weeds and to 'avoid feeding the weeds', whilst he could not top-dress because of lack of cash to buy the fertiliser. The other farmer also cited lack of cash to buy fertilisers as the reason for growing his maize without fertiliser. Fertility management in maize and butternut is shown in Table 5.
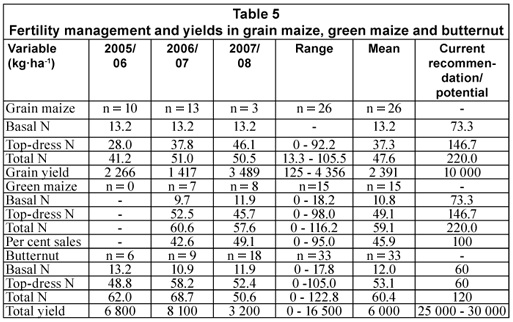
In all seasons and for all farmers, basal fertiliser in maize was applied using a tractor-drawn planter as 200 kg·ha-1 of compound fertiliser 2:3:4 (30) to give N, P and K levels of 13.3, 20.0 and 26.7 kg·ha-1, respectively. Top-dressing was done using lime ammonium nitrate (LAN 28%) and the quantities applied varied among farms. Similarly, fertiliser management in butternut varied across farms and seasons (Table 5). Observations indicated that in all seasons, all butternut producers applied about 20% of the entire N and all P and K at planting while the remaining 80% N was applied as top-dressing just before flowering at 3 WAE.
Plant population
Low plant populations were a common experience in all seasons, particularly in grain maize and butternut. Reduction of crop stand in maize was mainly caused by crows (Corvus corax) which fed on emerging seedlings. In butternut, low target populations and late weeding were the main cause of low crop stands. Plant populations in maize and butternut are presented in Table 6.
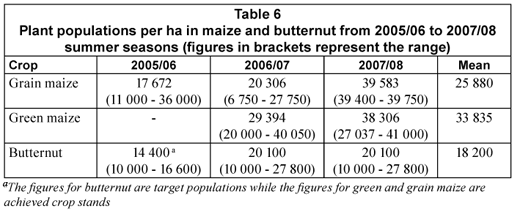
All maize was planted at a target population of 41 100 plants·ha-1. Crop establishment was poor in 2005/06 and 2006/07, partly due to poor seed coverage with conservation tillage and birds feeding on emerging seedlings. Achieved plant populations averaged 25 880 (63%) and 33 835 (82%) plants·ha-1 in grain and green maize, respectively (Table 6). The higher crop stand in green maize was partly attributed to superior crop establishment from transplants, which were not affected by bird damage, compared to direct seeded maize. The average plant population in butternut was 18 200 plants·ha-1 (Table 6).
Relationship between management practices and yields
Grain maize: In 2005/06, grain yield decreased significantly from 3.4 to 1.5 t·ha-1 when planting was delayed beyond the end of December (r = -0.68, p < 0.05). In 2006/07, there was a significant decrease in grain yield with poor weed management (r = -0.92, p < 0.01) and with decreased plant stand (r = -0.66, p < 0.05). Poor weed control resulted in an average yield decrease of 81% from 3.4 to 0.6 t·ha-1. In 2007/08 there was a significant decrease in grain yield with increase in cropped area (r = -1.00, p < 0.01). Grain yield decreased from 4.2 to 2.5 t·ha-1 when cropped area was increased from 0.3 to 1.2 ha. Stepwise regression showed that weed management (p < 0.01) followed by plant stand (p < 0.05) were the most important determinants of grain yield.
Green maize: In 2007/08 and 2006/07, 1 and 2 green maize producers, respectively, failed to obtain any marketable cobs. This was caused by inappropriate cultivar choice, poor or non-application of fertiliser and/or weed control. There were no significant correlations between management practices and yields in 2006/07. In 2007/08, per cent marketable cobs significantly decreased with delayed planting (r = -0.61, p < 0.05), increase in cropped area (r = -0.80, p < 0.01), reduced top-dress N (r = -0.84, p < 0.01) and low total N (r = -0.83, p < 001). Stepwise regression showed that top-dressing N followed by total N (p < 0.001) and basal N (p < 0.04) were the most important determinants of green maize productivity.
Butternut: Low average plant populations of 14 400 plants·ha-1 in 2005/06 resulted in fruits that were too big for the prescribed market. A case study of one NP farmer who had a contract to supply butternut to Pick 'n Pay supermarket in 2006/07 indicated that out of a total yield of 16.4 t·ha-1, only 8.5 t (52%) were of marketable size while 48% of the fruits were rejects. The non-marketable fruits were either too big or had blemishes and/or cracks, which reduced quality. The rejects could only be sold to local buyers and hawkers, but at lower prices. To improve on fruit size the farmer increased his target population from 14 000 to 25 000 plants·ha-1 with a resultant improvement in fruit size. Ninety percent of the fruits obtained by this farmer in 2007/08 were of marketable size and there was little investment required in grading.
In 2005/06, correlation coefficients indicated a significant decrease in yield with reduced N fertilisation (r = -0.93, p < 0.01) and with increase in cropped area (r = -0.80, p < 0.05). Failure to control weeds before planting (r = -0.92, p < 0.01) and decrease in plant population (r = -0.71, p < 0.05) resulted in a significant decrease in yield in 2006/07. In 2007/08 correlation coefficients indicated a significant decrease in yield with lack of pre-plant weed control (r = -0.64, p < 0.05). Results of stepwise regression showed that planting population and topdressing N followed by total N (p < 0.001) were the most important determinants of butternut yield.
Discussion
Results of this study indicate that farmer crop management practices compromised yields achieved in all major crops grown in ZIS. Yields achieved were a small fraction of the potential under irrigation. Main limiting factors were poor weed, fertiliser and water management, low plant populations, low cultivar selection and late planting. Similar factors were observed to be the main constraints to increased productivity of SIS elsewhere in SA (Van Averbeke et al., 1998; Bembridge, 2000; Perret et al., 2003; Machethe et al., 2004). The poor agronomic practices also suggest ineffective extension support to the ZIS farmers. Farmer assessment of the effectiveness of extension during the conduct of the study indicated a deterioration of services compared to baseline in 2005. However, farmers benefited from the continuous interaction with researchers and through feedback sessions and farmer information days in all of the 3 years of the study.
Productivity levels
Production, measured as the biological or economic output from the system either as yield or income generated, is the most obvious output and measure of the performance of a cropping system (FAO, 1995). It is a measure of the efficiency of the management of the cropping system and can be related to productivity (FAO, 1995). The study demonstrated that cropping systems at ZIS result in poor performance due to inefficient management. Yields obtained were generally low and below potential under irrigation (Table 5). The average grain yield of 2.4 t·ha-1 achieved by farmers at ZIS is only 20 to 30% of the potential of 9 to 12 t·ha-1 possible under irrigation in SA (Du Plessis and Bruwer, 2003; USDA, 2003). In butternut, the average yield of 6 t·ha-1 is 20 to 24% of the potential of 25 to 30 t·ha-1 (Department of Agriculture, 2005). These findings indicate that there are serious management problems leading to the low yields obtained by the farmers. Ongoing training on basic management practices such as cultivar selection, population management, fertiliser application and timing, and weed management options for different crops could help improve productivity.
Whilst CIs of 200% are possible under irrigation in the Eastern Cape (Van Averbeke et al., 1998), results of this study indicated low CIs averaging 48%. Similar low CI levels have been reported in SIS elsewhere in SA (Van Averbeke et al., 1998; Bembridge, 2000; Perret et al., 2003). Increased crop productivity with higher CIs is well documented (FAO, 2000; Hasnip et al., 2001; Tafesse, 2003). The low CIs affected total production and income achieved by farmers. Lack of motivation and resources were the 2 main factors responsible for the under-utilisation of land, particularly for the P and ULP farmers. Cropping intensity was also related to market availability; hence, the higher CIs in summer as maize and butternut had a ready market. The study indicated that there was very little cropping in winter and that the common crop was cabbage. The reason for this was the limited market for other vegetable crops such as spinach (Spinacea oleracea), beetroot (Beta vulgaris) and carrots (Daucus carota), and even the cabbage itself. Farmers relied on customers who came to buy the vegetables from the field. Thus, even at the low winter CIs, some of the cabbage was observed to rot in the field after farmers failed to secure customers on time. Partnership with agribusiness and diversification might be some of the ways to improve on CI.
Constraints to crop productivity
Weed management
Poor weed management was noted as the most important factor limiting productivity of maize and butternut, resulting in a 100% yield reduction in some cases. Poor weed control is known to decrease water and N use efficiency, the 2 most important inputs to achieving high yields under irrigation (Thomson et al., 2000). This becomes more critical in a case like ZIS where farmers apply low amounts of N to their crops. Cultural weed control methods, such as ploughing soon after harvesting and pre-plant weed control, may be some of the most effective methods to destroy the majority of weeds before they seed and replenish the soil seed bank (Fournier and Brown, 1999; Stall, 2007), as has been demonstrated by the farmers who are already practising these methods. The fact that some farmers were not knowledgeable about the different herbicides that could be used in various crop enterprises suggests that training in herbicide technology might improve adoption of this technology among farmers. In India and Nepal, the adoption of herbicide technology significantly improved after farmers attended training workshops on application techniques (Bellinder et al., 2002).
Leaving a greater proportion of fields fallow after harvesting the summer crop meant that weeds were able to grow and shed more seeds in the soil seed bank. Annual weed escapes are known to produce seed that will be in the soil and increase weed populations for the next several years, and perennial weeds may persist if not properly controlled (Stivers, 1999; Whitney, 1999). Rather than leaving fields idle after harvesting, fields should be ploughed and/or disked after harvest to prevent late summer and winter weed-seed production (Whitney, 1999). The challenge of weed management was most serious in butternut production due to lack of registered post-emergence herbicides for broadleaf weed control. Poor weed management was associated with increased pest damage on the butternut fruits. Weed control to kill the first flush of weeds prior to planting is one strategy that can be used by farmers to reduce weed pressure after emergence of the butternut crop. Weed management in butternut should focus on starting with a weed-free seedbed and then maximising weed suppression through augmentation of the competitive ability of the crop by using optimum plant populations (Canadian Organic Growers Field Crop Handbook, 1992).
Fertility management
Within the application rates used by farmers, results indicated a weak correlation between N application rate and maize grain yield, yet it is known that this relationship is strong (FSSA, 2007). This suggests that improper management of weeds, plant population and other factors could have masked this relationship. Not only did the farmers apply very low rates of fertilisers, but the timing of application, in many cases, was also wrong. For instance, while butternut growers applied 20% of the total N at planting, the recommendation is to apply 50 to 66% of the entire N at planting and the remainder as top-dressing (Boyhan et al., 1999; Department of Agriculture, 2005).
Use of inorganic fertilisers was one component of the green revolution that led to increased crop productivity. However, application of inorganic fertilisers has also faced important limitations due to high costs, highly variable nature of soils and inherent low nutrient conversion efficiency (AGRA, 2007). Average fertiliser use rates by smallholder farmers are considered too low and ineffective for sustaining crop and soil fertility (Gruhn et al., 2000). Application of low fertiliser levels means that the outflow of nutrients in most smallholder farms far exceeds inflows. Alternative sources of nutrients are therefore needed in situations where soil fertility needs to be rebuilt and high cost and supply quantities limit inorganic fertiliser application. While organic resources have been identified as reliable alternatives due to relatively easy access and easy procurement from the local environments (Omotayo and Chukwuka, 2009), farmer access to organic manure at ZIS was limited, presenting a challenge to the adoption of organic sources of nutrients.
The high mineralisation rates that characterise the semi-arid areas warrant a technology that adds high amounts of biomass into the soil (Omotayo and Chukwuka, 2009). Use of green manure cover crops has been suggested as one viable option because of their ability to regulate soil surface temperatures, increase soil organic matter, conserve soil moisture, and suppress weeds. The best crop for green manuring should have low production costs but still be able to fix enough N to meet the requirements for the following crop (Pauly, 2008). In Brazil, Lathwell (1990) reported total N accumulation in aboveground dry matter ranging from 58 to > 300 kg·ha-1 with the use of legume green manures under dryland conditions. Under irrigation, legume crops can fix more than 110 kgN·ha-1 (Pauly, 2008). Maize grain yields of up to 7.4 t·ha-1 were achieved when the legume green manure mucuna (Mucuna pruriens) was used as the only N source (Lathwell, 1990). Yields as high as those obtained with 200 kg·ha-1 of N fertiliser have been reported, an indication that green manure can be as effective as N fertiliser sources for maize (Lathwell, 1990). These results suggest use of green manures as a potential alternative to use of inorganic fertilisers in smallholder irrigation and warrants investigation.
One of the findings of this study was that farmers tended to apply low and blanket amounts of the inorganic fertilisers, especially at planting. The same was reported of farmers in the Limpopo Province (Machethe et al., 2004). According to Crosby et al. (2000), the interaction of moisture supply and nutrient supply is reciprocal such that if the farmer cannot irrigate, it is a waste to fertilise; and if a farmer cannot fertilise, it is a waste to irrigate. Thus, if smallholder irrigation farmers are to realise higher yields, there should be a balance between water application and fertiliser management. Therefore, for cropping systems to remain productive and sustainable, it is necessary to replenish the nutrients removed from the soil. In this respect, good weed management is of paramount importance to reduce weed-crop competition for supplied nutrients. In addition to crop rotation, farmers need to consider shifting from single cropping systems to multiple cropping systems, either sequential or intercropping.
Plant population
The higher yield potential made possible by a favourable water regime provided by irrigation can be achieved only with adjustments in plant population (Crosby et al., 2000). Maize is the agronomic species that is most sensitive to variations in plant density, such that for each production system there is a population that maximises grain yield (Sangoi, 2000). This study indicated that farmers planted all their maize at a target population of 41 100 plants·ha-1, yet under irrigation in SA the recommendation is to plant at 45 000 to 90 000 plants·ha-1, depending on yield potential and cultivar maturity class (Department of Agriculture, 2003). However, one could argue that farmers were right in opting for low target populations given that they could not afford higher or optimum fertiliser rates. Targeting the higher recommended populations when fertilisation is done at such low rates as are used at ZIS would result in even lower yields, due to intense intra-plant competition for limited nutrients. In spite of this, the low plant stands achieved by farmers resulted in more photosynthetically active radiation being transmitted to weeds under the crop canopy, thus exacerbating the problem of weed management noted in ZIS.
It was observed that damage to emerging maize seedlings by birds seriously reduced plant population. Transplanting is one strategy that is commonly used to establish crops when conditions are less favourable for direct seeding, such as when birds pose a threat to emerging seedlings. In South Africa, maize transplanting is used by some commercial farmers for production of green maize. The strategy, if adopted, is expected to improve plant population by eliminating the problem of bird damage to emerging seedlings. On-farm experiments conducted in ZIS during the 2006/07 and 2007/08 summer seasons indicated an increase in plant stand from 78 to 96% of the target with transplanting (Fanadzo et al., 2009).
Operational management of sprinkler systems
Sprinkler systems will only work well at the right operating pressure (Brouwer et al., 1988). Higher system pressure was the biggest contributing factor to poor system performances observed in the study. Operating sprinklers at pressure above the recommended, or use of different sprinklers and/or nozzles adjacent to each other in single laterals, resulted in poor distribution uniformity. Distribution uniformity is usually defined as a ratio of the smallest accumulated depths in the distribution to the average depths of the whole distribution (Ascough and Kiker, 2002). The distribution uniformity of a system has an effect on the system's application efficiency and on crop yield (Letey et al., 1984; Solomon, 1984; Solomon, 1990; Ascough and Kiker, 2002). Irrigation systems with poor distribution uniformity experience reduced yields due to water stress and/or water logging (Solomon, 1983, cited by Clemmens and Solomon, 1997).
Poor distribution uniformity can result in increased financial and environmental costs. Nutrients can be leached out of the soil due to excess water being applied to overcome poor irrigation uniformity (Ascough and Kiker, 2002). This would increase fertiliser and pumping costs, and may have environmental impacts if the excess runoff and deep percolation are contaminated with nutrients (Solomon, 1990). Pressure management can be applied simply by installing a pressure gauge at the beginning of the lateral and applying appropriate pressure to the system as indicated on the pressure gauge. What is therefore needed to improve system efficiency in ZIS is relatively inexpensive equipment. The importance of correct system operation and maintenance needs to be demonstrated to both farmers and extension officers.
Farmers were highly aware of the problem of poor irrigation management and blamed it on lack of training by the extension services. Farmers revealed that extension officers were not serving them effectively since they lacked the necessary technical knowledge, competency and commitment. The contact between extension officers and farmers was limited due to the unavailability of transport and the officers' diverse responsibilities for various other development projects. Farmers identified the lack of adequate number of laterals for effective irrigation of their crops as a major constraint for efficient crop production. These aspects would need to be addressed by the provincial Department of Agriculture as part of revitalising ZIS. The use of WFDs is one possible solution to irrigation management.
Impact of inadequate management as a factor in scheme productivity
Yield gap analysis is one technique that can be used to provide a quantitative estimate of the impact of inadequate management on overall scheme performance in ZIS. Pinnschmidt et al. (1997) define yield gap as the difference between an attainable yield level and the actual yield in farmers' fields. An analysis of grain maize and butternut yields at ZIS indicated that large gaps exist between yields achieved by farmers and those achieved with good management (Figs. 1 and 2). Only 2 (10%) NP farmers attained the 'maximum farmer yields', whilst the other 18 (90%) achieved lower yields. The average maize yield of 2.4 t·ha-1 is only 24% of maximum economic yield obtained in on-farm experiments in ZIS (Fanadzo et al., 2009). Also, the mean butternut yield of 6 t·ha-1 is only 22% of the maximum economic yield attained in on-farm trials in the scheme as part of this study.

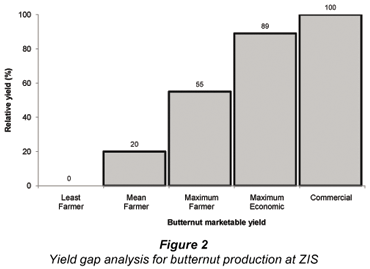
The fact that the yields from on-farm experiments were comparable to commercial yields suggests that it is not the current state of infrastructure that is most limiting to improved crop productivity at ZIS. Therefore, even with the current condition of infrastructure, investment in farmer capacity building could improve scheme performance. During the conduct of this study, farmers were exposed to demonstrations on cultivar selection, planting time, fertiliser, plant population and weed management, resulting in noticeable change in practice and yields achieved at farm level. A socio-economic impact assessment of the project under which this study was conducted indicated a 32.5% decrease in the number of ULP farmers and a 22.4% increase in NP farmers compared to the 2005 baseline, and this was ascribed to adoption of better management practices (Tshuma, 2009). These changes emphasise the need for investment in soft skills such as farmer training, adaptive trials and demonstrations for poverty alleviation through improved crop productivity at ZIS. The findings emphasise the potential that could be derived in strengthening the extension services at ZIS.
Conclusions
The study demonstrated that crop productivity in ZIS is limited by poor management of basic practices such as weed, fertiliser and water management as well as late planting, low plant populations and use of inappropriate varieties. This suggests lack of basic management skills for irrigated crop production as a possible cause of inadequate management. In this case, 'back to basics' training courses would be expected to benefit the farmers. This emphasises the need to take farmer production practices into consideration, as a basis to build up skills in the management of crop enterprises and the farm as a viable business, in any efforts to improve on the performance of SIS in SA. The study has improved our understanding of factors limiting crop productivity in ZIS and has provided a basis for a focused research agenda.
Future research need to focus on labour-saving production strategies, given the acute shortage of labour in ZIS. Consideration needs to be given to integrated weed management options with special emphasis on cultural weed management practices. In this respect, possible use of reduced herbicide dosages, conservation farming practices and use of draft animals warrants investigation. Sustainable agricultural technologies such as substitutes for inorganic fertilisers need to be investigated. There is a need to identify crops that are higher yielding, but less demanding as regards nutrient requirements.
Acknowledgements
This work was funded by the Water Research Commission through WRC Project No. K5/1477//4.
References
AGRA (2007) Alliance for a Green Revolution in Africa: AGRA at work. URL: www.agra-alliance.org/work/ (Accessed on 13 March 2008). [ Links ]
ASCOUGH GW and KIKER GA (2002) The effect of irrigation uniformity on irrigation water requirements. Water SA 28 (2) 235-242. [ Links ]
BEMBRIDGE TJ (2000) Guidelines for Rehabilitation of Small-Scale Farmer Irrigation Schemes in South Africa. WRC Report No. 891/1/00. Water Research Commission, Pretoria, South Africa. [ Links ]
BELLINDER RR, MILLER AJ, MALIK RK, RANJIT JD, HOBBS PR, BRAR LS, SINGH G, SINGH S and YADEV A (2002) Improving herbicide application accuracy in South Asia. Weed Technol. 16 (4) 845-850. [ Links ]
BOYHAN GE, GRANBERRY DM and KELLEY T (1999) Commercial squash production. Cooperative Extension Service, the University of Georgia College of Agricultural and Environmental Sciences. URL: http://pubs.caes.uga.edu/caespubs/PDF/C527.pdf (Accessed on 4 May 2007). [ Links ]
BROUWER C, PRINS C, KAY M and HEIBLOEM M (1988). Irrigation Water Management: Irrigation Methods. Training Manual No. 5. Food and Agricultural Organisation of the United Nations, Rome. [ Links ]
CANADIAN ORGANIC GROWERS FIELD CROP HANDBOOK (1992) Weed Management. URL: http://eap.mcgill.ca/MagRack/COG/COG Handbook/COGHandbook_1_7.htm (Accessed on 29 January 2009). [ Links ]
CLEMMENS AJ and SOLOMON KH (1997) Estimation of global irrigation distribution uniformity. J. Irrig. Drain. Eng. 123 (6) 454-461. [ Links ]
CROSBY CT, DE LANGE M, STIMIE CM and VAN DER STOEP I (2000) A Review of Planning and Design Procedures Applicable to Small-Scale Farmer Irrigation Projects. WRC Report No. 578/2/00. Water Research Commission, Pretoria, South Africa. [ Links ]
DE LANGE M, ADENDORFF J and CROSBY CT (2000) Developing Sustainable Small-Scale Farmer Irrigation in Poor Rural Communities: Guidelines and Checklists for Trainers and Development Facilitators. WRC Report No. 774/1/00. Water Research Commission, Pretoria, South Africa. [ Links ]
DENISON J and MANONA S (2007) Principles, Approaches and Guidelines for the Participatory Revitalisation of Smallholder Irrigation Scheme. Volume 1 – A Rough Guide for Irrigation Development Practitioners. WRC Report No. TT 308/07. Water Research Commission, Pretoria, South Africa. [ Links ]
DEPARTMENT OF AGRICULTURE (SOUTH AFRICA) (2003) Maize Production. National Department of Agriculture, Private Bag X144, Pretoria, South Africa. URL: http://www.nda.agric.za/docs/maizeproduction.pdf (Accessed on 12 September 2007). [ Links ]
DEPARTMENT OF AGRICULTURE (SOUTH AFRICA) (2005) Vegetable production in KwaZulu-Natal. National Department of Agriculture, Private Bag X144, Pretoria, South Africa.URL: http://agriculture.kzntl.gov.za/portal/Publications/ProductionGuidelines/VegetableProductioninKZN/tabid/264/Default.aspx (Accessed on 20/09/2008). [ Links ]
DU PLESSIS JG and DE V BRUWER D (2003) Short Growing Season Cultivars. ARC – Grain Crops Institute. Private Bag X1251. Potchefstroom 2520, South Africa. [ Links ]
FANADZO M (2007) Weed management by small-scale irrigation farmers – the story of Zanyokwe. SA Irrigation 29 (6) 20-24. [ Links ]
FANADZO M, CHIDUZA C and MNKENI PNS (2009) Comparative response of direct seeded and transplanted maize (Zea mays L.) to nitrogen fertilisation at Zanyokwe irrigation scheme, Eastern Cape, South Africa. Afr. J. Agric. Res. 4 (8) 689-694. [ Links ]
FAO (1982) Estimation of Crop Area and Yields in Agricultural Statistics. FAO Economic and Social Development Paper 22. Rome. [ Links ]
FAO (1995) Sustainable dryland cropping in relation to soil productivity. FAO Soils Bull. 72. Rome. [ Links ]
FAO (2000) South Africa: Affordable Irrigation Technologies for Smallholders: Opportunities for Technology Adaptation and Capacity Building. Programme Formulation Report No. 6 – December 2000. IPTRID Secretariat, Rome. [ Links ]
FAO (2001) Smallholder irrigation technology: prospects for sub-Saharan Africa. International Programme for Technology and Research in Irrigation and Drainage Knowledge Synthesis Report No. 3. IPTRID Secretariat, Food and Agriculture Organization of the United Nations, Rome. [ Links ]
FERGUSON AE and MULWAFU WO (2004) Irrigation Reform on Malawi's Domasi and Linkangala Smallholder Irrigation Schemes. URL: http://pdf.usaid.gov/pdf_docs/PNADE775.pdf (Accessed on 16 January 2009). [ Links ]
FSSA (2007) Fertilizer Handbook (6th revised edn.). The Fertilizer Society of South Africa. Lynnwood Ridge, Pretoria, South Africa. 298 pp. [ Links ]
FOURNIER AI and BROWN A (1999) (eds.) Crop Profile for Squash in Maryland. URL: http://www.ipmcenters.org/cropprofiles/docs/MDsquash.pdf (Accessed on 16 January 2009). [ Links ]
GARCÍA-VILA M, LORITE IJ, SORIANO MA and FERERES E (2008) Management trends and responses to water scarcity in an irrigation scheme of Southern Spain. Agric. Water Manage. 95 458-468. [ Links ]
GRUHN P, GOLLETI F and YUDELMAN M (2000) Integrated Nutrient Management, Soil Fertility and Sustainable Agriculture: Current Issues and Future Challenges. Food, Agriculture and Environment Discussion Paper 32. International Food Policy Research Institute, Washington D.C. [ Links ]
HASNIP N, MANDAL S, MORRISON J, PRADHAN P and SMITH L (2001) Contribution of Irrigation to Sustaining Rural Livelihoods. KAR Project R7879. Literature Review. Report OD/TN 109 [Online]. URL: http://www.hrwallingford.co.uk/downloads/publications/dlreports/odtn109.pdf (Accessed on 7 May 2006). [ Links ]
HILL, KAPLAN and SCOTT INC. (1991) Ciskei National Water Development Plan, Volume 1: Report. Hill, Kaplan & Scott Inc., Bellville, South Africa. [ Links ]
LAKER MC (2004) Development of a General Strategy for Optimising the Efficient Use of Primary Water Resources for Effective Alleviation of Rural Poverty. WRC Report No. KV149/04. Water Research Commission, Pretoria, South Africa. [ Links ]
LATHWELL DJ (1990) Legume Green Manures, Principles for Management Based on Recent Research. Cornell University. URL: http://www.fadr.msu.ru/rodale/agsieve/txt/vol3/3/a6.html (Accessed on 28 April 2009). [ Links ]
LETEY J, VAUX HJ and FEINERMAN E (1984) Optimum crop water applications as affected by uniformity of water infiltration. Agron. J. 76 435-441. [ Links ]
LOXTON RF (1983) A Master Preliminary Plan for Zanyokwe Irrigation Scheme. Loxton, Venn and Associates, Bramley, Johannesburg, South Africa. [ Links ]
Machethe CL, Mollel NM, Ayisi K, Mashatola MB, Anim FDK and Vanasche F (2004) Smallholder Irrigation and Agricultural Development in the Olifants River Basin of Limpopo Province: Management, Transfer, Productivity, Profitability and Food Security Issues. WRC Report No. 1050/1/04. Water Research Commission, Pretoria, South Africa. [ Links ]
MONDE N, MTSHALI S, MNKENI PNS, CHIDUZA C, MODI AT, BRUTSCH MO, DLADLA R and MTHEMBU BE (2005) A Situation Analysis Report on the Zanyokwe and Tugela Ferry Irrigation Schemes. University of Fort Hare, Alice, South Africa. [ Links ]
NOORDWIJK M (2002) Scaling trade-offs between crop productivity, carbon stocks and biodiversity in shifting cultivation landscape mosaics: the fallow model. Ecol. Model . 149 113-126. [ Links ]
OMOTAYO OE and CHUKWUKA KS (2009) Soil fertility restoration techniques in sub-Saharan Africa using organic resources. Afr. J. Agric. Res. 4 (3) 144-150. [ Links ]
OOSTHUIZEN LK (2002) Land and water resources management in South Africa. Paper presented at the working group on International Land and Water Resources Management (WG-ILWRM), 18th ICID Congress, Montreal, Canada, July 21-28, 2002. URL: http://afeid.montpellier.cemagref.fr/ILWRM/Sacase.pdf (Accessed on 24 April 2006). [ Links ]
PAULY D (2008) How much nitrogen can be fixed by a green manure crop? URL: http://www1.agric.gov.ab.ca/$department/deptdocs.nsf/all/faq7979 (Accessed on 28 April 2009). [ Links ]
PERRET S, LAVIGNE M, STIRER N, YOKWE S and DIKGALE S (2003) The Thabina irrigation scheme in a context of rehabilitation and management transfer: Prospective analysis and local empowerment. Final Report: Department of Water Affairs and Forestry, CIRAD-IWMI-UP, Pretoria, South Africa. [ Links ]
PINNSCHMIDT HO, CHAMARERK V, CABULISAN N, DELA PEÑA F, LONG ND, SAVARY S, KLEIN-GEBBINCK HW and TENG PS (1997) Yield gap analysis of rainfed lowland systems to guide rice crop and pest management. In: Kropff MJ, Teng PS, Aggarwal PK, Bouma J, Bouman BAM, Jones JW and Van Laar HH (eds.) Applications of Systems Approaches at the Field Level, Volume 2. Kluwer Academic Publishers, Dordrecht, the Netherlands. 321-338. [ Links ]
SANGOI L (2000) Understanding plant density effects on maize growth and development: an important issue to maximise grain yield. Ciência Rural 31 (1) 159-168. [ Links ]
SOIL CLASSIFICATION WORKING GROUP (1991) Soil classification: A taxonomic system for South Africa. Memoirs on the Agricultural Natural Resources of South Africa No. 15. Department of Agricultural Development, Pretoria, South Africa. [ Links ]
SOLOMON KH (1983) Irrigation Uniformity and Yield Theory. Ph.D. thesis, Utah State University, Utah State University, Logan, USA. [ Links ]
SOLOMON KH (1984) Yield related interpretations of irrigation uniformity and efficiency measures. Irrig. Sci. 5 161-172. [ Links ]
SOLOMON KH (1990) Sprinkler irrigation uniformity. Centre for Irrigation Technology, California State University, Fresno, USA. URL: http://www.wateright.org/site/publications/900803.html (Accessed on 20 April 2009). [ Links ]
STALL WM (2007) Weed Control in Cucurbit Crops (Muskmelon, Cucumber, Squash, and Watermelon). URL: http://edis.ifas.ufl.edu/WG029 (Accessed on 16 January 2009). [ Links ]
STEVENS JB (2007) Adoption of Irrigation Scheduling Methods in South Africa. Ph.D. Thesis. University of Pretoria, South Africa. 426 pp. [ Links ]
STIVERS L (1999) Crop Profile in New York. Cornell Cooperative Extension. URL: http://ipmwww.ncsu.edu/opmppiap/proidex.htm (Accessed on 10 October 2006). [ Links ]
TAFESSE M (2003) Small-scale irrigation for food security in sub-Saharan Africa. Report of a CTA Study Visit, Ethiopia. CTA Working Document No. 8031. URL: http://www.cta.int/pubs/wd8031.pdf (Accessed on 12 November 2005). [ Links ]
THOMSON TL, DOERGE TA and GODIN RE (2000) Nitrogen and water interactions in subsurface drip irrigated cauliflower: II. Agronomic, Economic and environmental outcomes. Soil Sci. Soc. Am. J. 64 412-418. [ Links ]
TSHUMA MC (2009). A socio-economic impact assessment (SEIA) of the Best Management Practices (BMP) project of the Zanyokwe irrigation scheme (ZIS) at farm level. M.Sc. Thesis, University of Fort Hare. 105 pp. [ Links ]
USDA (2003) Irrigated Corn Increases in South Africa. Production Estimates and Crop Assessment Division, Foreign Agricultural Service, May 27, 2003. URL: http://www.fas.usda.gov/pecad2/highlights/2003/05/south%5Fafrica/ (Accessed on 18 November 2006). [ Links ]
VAN AVERBEKE W, M'MARETE CK, IGODAN CO and BELETE A (1998) An Investigation into Food Plot Production at Irrigation Schemes in Central Eastern Cape. WRC Report No. 719/1/98. Water Research Commission, Pretoria, South Africa. [ Links ]
WHITNEY SP (1999) Crop Profile for Watermelon in Delaware. University of Delaware. URL: http://ipmwww.ncsu.edu/opmppiap/proindex.htm (Accessed on 10 October 2006). [ Links ]
Received 15 May 2009; accepted in revised form 17 November 2009.
* To whom all correspondence should be addressed.
+2740 602 2226; fax: +2786 628 2602;
e-mail: cchiduza@ufh.ac.za














