Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Water SA
On-line version ISSN 1816-7950
Print version ISSN 0378-4738
Water SA vol.35 n.5 Pretoria Oct. 2009
Evaluation of modifications to a physicochemical method for determination of readily biodegradable COD
A Escalas-CañellasI,II,*, MA Ortiz-BalderasII; MG Barajas-LópezI,II
ICentro de Investigación y Estudios de Posgrado, Facultad de Ingeniería, Universidad Autónoma de San Luis Potosí, Av. Dr. Manuel Nava 8, Edificio P, Zona Universitaria, C.P. 78290, San Luis Potosí, SLP, Mexico
IIPrograma Multidisciplinario de Posgrado en Ciencias Ambientales, Universidad Autónoma de San Luis Potosí, Av. Dr. Manuel Nava 201, 2do piso, Zona Universitaria, C.P. 78210, San Luis Potosí, SLP, Mexico
ABSTRACT
In the Mamais-Jenkins-Pitt method for determination of readily biodegradable COD (SS), 2 alternatives were proposed for the intermediate determination of soluble inert COD (SI). When a full-scale treatment plant exists, influent SI = effluent truly soluble COD. When there is no full-scale plant, then the truly soluble COD of the effluent of a 24 h fill-and-draw batch reactor treating the wastewater is taken as influent SI.
In this study, both SI methods were statistically compared on 24 wastewater samples from 2 municipal wastewater treatment plants (WWTPs). While average SI obtained for the 2 methods was the same, individual samples usually had very different SI values. In fact, virtually no correlation was found between the 2 methods. Also, the SS values obtained using both SI alternatives were statistically compared. A good correlation was observed, in spite of the poor SI correlation – low, dispersed SI values did not seriously affect the correlation between both SS determinations. A method was proposed for determination of the limit of detection and the limit of quantification (LOQ) for both SS methods. The LOQ resulted in 28.6 mg/l and 32.6 mg/l, respectively, for the full-scale and the laboratory-scale alternatives.
Some assumptions of the original laboratory-scale (LS) method could potentially be sources of error in SI determination. Two modifications to the laboratory-scale method were implemented in order to avoid these potential problems: Washing biomass with tap water, and correcting SI in the fill-and-draw reactor by the SI of the original biomass suspension.
These method modifications were tested on wastewater samples from the mentioned WWTPs. The fundamentals and results of both modifications are discussed in this paper, as well as the imprecision associated with estimating influent SI from effluent CODsol in all studied methods, and its impact on SS determination.
Keywords: readily biodegradable COD, physicochemical, wastewater
Nomenclature
| ASCE | American Society of Civil Engineers |
| ASM1 | Activated Sludge Model No. 1 |
| ASM2d | Activated Sludge Model No. 2d |
| ASM3 | Activated Sludge Model No. 3 |
| BNR | biological nutrient removal |
| BOD | biochemical oxygen demand |
| BTE | batch-test effluent |
| COD | chemical oxygen demand |
| CODsol | soluble COD (Mamais-Jenkins-Pitt method) |
| DO | dissolved oxygen |
| DOC | dissolved organic carbon |
| EFF | full-scale plant effluent |
| EPA US | Environmental Protection Agency |
| F/M | food to micro-organisms ratio |
| FS | full scale |
| HRT | hydraulic retention time |
| IWA | International Water Association |
| LOD | limit of detection |
| LOQ | limit of quantification |
| LS | laboratory scale |
| LSC | laboratory-scale method correcting effluent SI by biomass SI |
| LSC | laboratory-scale method correcting effluent SI by biomass SI |
| LSTW | laboratory-scale method using tap water for biomass washing |
| LSTW | laboratory-scale method using tap water for biomass washing |
| MCRT | mean cell retention time |
| PPT ' | Parque Tangamanga 1-B' WWTP |
| R2 | determination coefficient |
| RSD | relative standard deviation |
| SA | fermentation products |
| SBR | sequencing batch reactor |
| SF | fermentable matter |
| SI | soluble inert organic matter |
| SLP | State of San Luis Potosí, Mexico |
| SS | readily biodegradable organic substrate |
| TSS | total suspended solids |
| TTV | 'Tanque Tenorio-Villa de Reyes' WWTP |
| VML | volume of initial mixed liquor in a batch test |
| VSS | volatile suspended solids |
| VWW | volume of wastewater in a batch test |
| WEF | Water Environment Federation (USA) |
| WW | wastewater |
| WWTP | wastewater treatment plant |
| XI | particulate inert organic matter |
| XS | slowly biodegradable substrate |
Introduction
Increased usage of BNR has promoted COD fractionation as a tool for wastewater evaluation and process design and control (Spérandio and Paul, 2000). IWA models for BNR use several COD fractions as state variables, so COD fractions must be evaluated for model initialisation, calibration and validation. Both ASM1 and ASM3 models consider 4 wastewater COD components, namely: readily biodegradable organic substrate (SS), soluble inert organic matter (SI), slowly biodegradable substrate (XS) and particulate inert organic matter (XI) (Henze et al., 2000). Other wastewater COD fractions are biomass-related: biomass components, biomass decay particles and internal storage products. Though biomass can account for 10 to 20% of total organic matter in wastewater, not considering it in raw wastewater would not affect the modelling considerably (Henze, 1992). In this case, biomass would be included in the slowly hydrolysable organic fraction, according to the same author. In ASM2d, SS is split into fermentable matter (SF) and fermentation products (SA). However, SS is useful for ASM2d, since SF can be obtained as the difference between SS and SA. So, readily biodegradable COD is a basic and useful COD fraction, and several respirometric and physicochemical methods have been developed for SS determination.
In IWA models, SS and XS fractions are set in terms of their aerobic biodegradation rates, which can be determined by respirometry. Thus, several respirometric methods have been proposed or modified for estimation of readily biodegradable COD (Ekama et al., 1986; Spanjers and Vanrolleghem, 1995; Wentzel et al., 1999; Spérandio and Paul, 2000). At the same time SS is considered soluble, while XS is colloidal or particulate, which allows for physicochemical determination of SS. When compared to respirometric methods, physicochemical methods require simpler and cheaper apparatus, since they are usually based on filtration techniques. However, equivalence between both methods has been a subject of discussion. Filtration through 0.45 µm filters does not ensure the complete removal of colloidal matter, which is slowly biodegradable (Melcer, 2004). The 0.45 µm filtrate can include about 50% of XS, while the rest is SS and SI (Henze, 1992). The colloidal fraction has been successfully removed by either ultrafiltration (Dold et al, 1986) or flocculation and filtration (Mamais et al., 1993; Hu et al., 2002).
The method by Mamais et al. (1993) provides a simple physicochemical technique for determination of truly soluble COD (herein referred to as CODsol) and readily biodegradable COD. In this method wastewater CODsol is determined as the COD of the filtrate obtained after sample flocculation, and filtration through a 0.45 µm filter. Then, wastewater SI is determined as the CODsol of the effluent of an aerobic biological plant treating the studied wastewater. More precisely, 2 alternatives were given by Mamais et al. (1993) for SI:
- To determine SI as the effluent CODsol of a full-scale plant treating the wastewater (if a full-scale plant exists)
- In the absence of a full-scale plant, to determine CODsol as the effluent CODsol of a laboratory-scale fill-and-draw plant treating the wastewater of interest, and having a mean cell retention time (MCRT) of greater than 3 d and an HRT of 24 h.
Some assumptions of the Mamais et al. (1993) method could be potential sources of error in SI determination and, consequently, on SS, as discussed next.
In the full-scale (FS) alternative, it is assumed that effluent SS is null. According to a plant survey cited in WEF-ASCE (1998), 42 activated sludge treatment plants had an annual mean effluent BOD of 15.5 mg/l (EPA, 1981) with a wide range of plant averages, namely 11 mg/l to 39 mg/l. TSS averaged 18.5 mg/l, with a wide range too. Assuming effluent BOD and TSS being roughly equal, and assuming effluent SS having a BOD of approximately 50% of their weight (WEF-ASCE, 1998), soluble BOD would reasonably average 7.5 mg/l with a range of 5.5 to 19.5 mg/l in secondary effluents of activated sludge plants. In ASM1 and ASM3, soluble BOD, being soluble and biodegradable, can only be included in the SS fraction of COD. Though the 5.5 mg/l to 19.5 mg/l range is rather low, it can account for a considerable fraction of effluent soluble COD in municipal wastewaters, thus affecting SI determination by the FS alternative and, consequently, SS determination in the low SS range. The LS test conditions (24 h HRT, longer than FS activated sludge plants) could perhaps achieve lower effluent SS.
In this study, CODsol, SI and SS were determined by both the FS and LS alternatives of the Mamais et al. (1993) method, on wastewater samples of 2 municipal, activated sludge WWTPs, and the results of both alternatives were compared for SI and SS, in order to determine whether these methods were equivalent and, particularly, whether SI was lower, and SS higher, by the LS alternative.
Since influent SI can be assumed variable, effluent SI must be variable too, even considering equalisation effects throughout the plant. In a previous research, Escalas et al. (2003) studied dissolved organic carbon (DOC) evolution throughout a municipal, continuous-flow activated sludge plant. Though primary clarifiers provoked a clear peak reduction, and secondary treatment yielded a smooth effluent DOC curve, the effluent DOC range was still 13 mg/l to 34 mg/l over a period of one week. This is a considerable variability for soluble organic matter, which includes the inert soluble fraction. The SI subtracted from the CODsol in the method has an intrinsic variability that has not yet been evaluated and this issue is addressed in this paper.
In the LS alternative, a wastewater with a given SI is mixed with a biomass (mixed liquor) that has a different SI, since mixed liquor SI depends on the variable SI fed to the reactor in the previous batches. This could affect SI and SS determination.
In the present study, the issue of SI variability was addressed by analysing effluent CODsol variability in the effluent of the 2 WWTPs studied. In order to suppress or minimise the effect of mixed-liquor SI on LS effluent SI, two LS method modifications were essayed:
- To wash biomass with tap water before the LS test, in order to remove CODsol from biomass, thus suppressing the biomass interference on SI determination (LSTW alternative)
- To determine biomass SI, and correct effluent SI for this value (LSC alternative).
Experimental
General experimental design
Twenty-four wastewater samples and their corresponding full-scale secondary effluents were taken at 2 municipal wastewater treatment plants in the city of San Luis Potosí (SLP), central–north highlands of Mexico: Parque Tangamanga 1-B plant (PPT) and Tanque Tenorio-Villa de Reyes plant (TTV). In a first campaign, 16 wastewater samples were taken, corresponding to low and high influent concentration at the plants. A 22 factorial design (Montgomery and Runger, 2003) with 4 replicates was applied (4x22), with plant (TTV/PPT) and influent concentration (low/high) as design variables. Eight additional wastewater samples were taken at the PPT plant, 4 corresponding to high concentration and 4 to low concentration time bands, for a total of 24 samples between the 2 plants. A previous 24 h sampling (12 samples per plant) was performed in order to determine the time bands of low- and high-influent COD concentration. An overview of the general methodology is shown in Fig. 1.
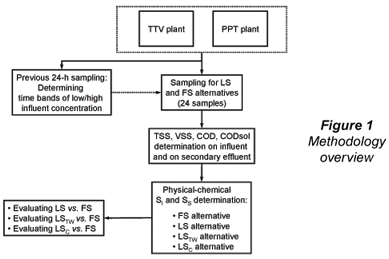
TSS, volatile suspended solids (VSS), COD and CODsol were determined on the samples, and the following alternatives were applied for SI and SS determination:
FS alternative: wastewater SI was determined as the CODsol of the secondary treatment effluent of the full-scale plant, in accordance with one of the Mamais et al. (1993) alternatives (Eq. (1) and (2)).

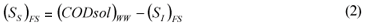
where:
(SI)FS is the un-biodegradable soluble COD according to the FS alternative
(CODsol)EFF is the truly soluble COD at the FS plant effluent, determined by the Mamais et al. (1993) method
(SS)FS is the readily biodegradable COD according to the FS alternative
(CODsol)WW is the truly soluble COD of wastewater
LS alternative: wastewater SI was determined as the effluent CODsol of a laboratory-scale 24 h fill-and-draw reactor, as in the other Mamais et al. (1993) alternative. Equations (3) and (4):

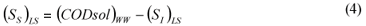
where:
(SI)LS is the wastewater un-biodegradable soluble COD according to the LS alternative (DQOsol) BTE is the truly soluble COD of the batch test effluent
LSTW alternative: As in the LS alternative, wastewater SI was determined from the effluent CODsol of a laboratory-scale 24 h fill-and-draw reactor. However, the biomass was first washed with tap water in order to remove the CODsol present in the mixed liquor, before mixing with wastewater for the batch test. This process results in a dilution of wastewater SI, so a correction must be applied to SI (Eq. (5)) before SS calculation (Eq. (6)).


where:
(SI)LSTW is the un-biodegradable soluble COD of wastewater according to this method alternative
VML and VWW are respectively the volumes of initial mixed liquor and wastewater used for the batch test
SS)LSTW is the readily biodegradable COD according to this method alternative
LSC alternative: As in the LS and LSTW alternative, wastewater SI was determined from the effluent CODsol of a laboratory-scale 24-h fill-and-draw reactor (Eq. (7)), but the SI of the initial mixed liquor was determined before addition of wastewater to the reactor (Eq. (8)), and a correction was applied to wastewater SI determination. An SI balance applied to the batch test can be written (Eq. (9)), which allows calculating the corrected wastewater SI (Eq. (10)). The usual calculation is applied for SS (Eq. (11)):


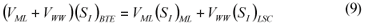
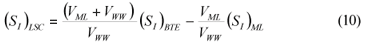
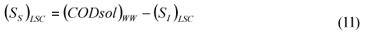
where:
(SI)BTE is the un-biodegradable soluble COD of the batch test effluent
(SI)ML is determined as the CODsol of the batch reactor mixed liquor before addition of wastewater
(SI)LSC is the un-biodegradable soluble COD of wastewater according to this procedure
FS and LS alternatives of the Mamais et al. (1993) method were compared in order to check for equivalence between both methods of SI determination. The resulting SS was also compared between both methods. Also, the LSTW and LSC alternatives were compared to the FS alternative, which was taken as reference.
Sampling and storage
Wastewater samples were taken at the 2 municipal wastewater treatment plants mentioned above (PPT and TTV). PPT is an 8 640 m3/d SBR plant with 2 alternating reactors, and TTV is a 60 500 m3/d continuous-flow activated sludge plant with enhanced primary treatment. Both flow rates are operational. At the PPT plant, grab influent samples were taken at the SBR feed-pipe discharge. At the TTV plant, characterisation was applied to grab samples of the secondary treatment influent, in order to avoid interference from the physicochemical primary treatment on the method essayed. Effluent grab samples were taken at the SBR discharge (PTT) or at the secondary settling effluent (TTV). Sampling after disinfection (PPT) or after full tertiary treatment (TTV) was avoided, in order to prevent chemical oxidation of effluent CODsol to interfere with the measured SI. Raw wastewater and mixed liquor samples were analysed and used in the batch tests upon arrival at the laboratory, while effluents and filtrates were stored at 4ºC for less than 12 h before analysis.
Standard analyses, CODsol, SI and SS
TSS, VSS, COD, pH and dissolved oxygen (DO) were determined according to Standard Methods (1998). COD was determined by the closed reflux, 5520 D spectrophotometric method (Standard Methods, 1998), using a DR/4000 spectrophotometer (Hach, Loveland, CO, USA). CODsol was determined by the Mamais et al. (1993) method of zinc sulphate flocculation, settling, and supernatant filtration through 0.45 µm filters (Whatman, cellulose nitrate membrane, Ø47 mm, 0.45 µm pore filters). SI was determined as detailed above (Eq. (1), (3) and (6)), depending on the method alternative. SS was always computed as the difference between CODsol and SI. Duplicate analyses were run for all samples. In the case of CODsol and SI, duplicate flocculation and filtration procedures were also run. Triplicate COD analyses were run on each sample replicate in the low-range COD method, duplicate analysis for the high-range method.
The high- and low-range variants of the Standard Methods (1998) spectrophotometric COD method were validated by analysing the potassium hydrogen phthalate calibration curves for linearity, limit of detection (LOD), limit of quantification (LOQ), repeatability and recovery. Linearity was evaluated through the determination coefficient (R2) (Miller and Miller, 2002). LOD was computed from the y-intercept absorbance in the calibration-line plus three times the standard deviation (3s) of the blank (from 10 blanks) (Miller and Miller, 2005). For the LOQ, a 5s criterion was applied (Eurachem, 1998). Repeatability was checked through the per cent relative standard deviation (RSD) of COD when computed from 3 calibration lines obtained on the same day (Eurachem, 1998).
Previous COD regime characterisation
Sample diversity was achieved by sampling 2 different plants at different times of the day, so they could present different concentration and COD composition. It was necessary to know the COD evolution of wastewater at the sampling points (COD regime) beforehand. So, samples were taken every 2 h at the sampling points of both plants, in a daylong sampling operation starting at 20:00. Plant influent (PPT), secondary treatment influent (TTV) and secondary effluent samples (both plants) were analysed for COD and CODsol. SI and SS were calculated in accordance with the FS alternative of the physicochemical method (Eq. (1) and (2)).
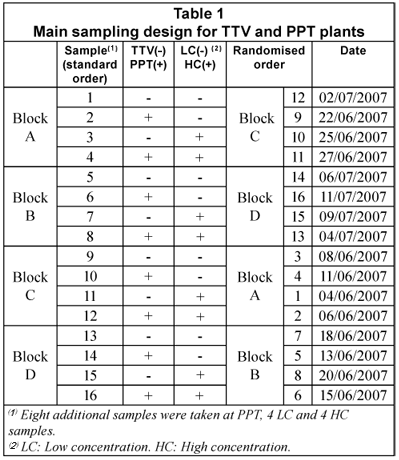
Main sampling design
Table 1 displays the main sample design, a 22 factorial with four replicates (4x22), based on the variables 'plant' (TTV/PPT) and 'COD concentration' (low/high). The replicates were set in four 22 blocks. Randomisation was applied inside each block, as a usual measure to ensure independent sampling. Due to higher COD and CODsol variability observed at that PPT, 8 additional samples were taken later at this plant for better characterisation, 4 samples corresponding to low concentration, and 4 to low concentration.
Laboratory-scale, 24-h batch tests
For the LS alternatives, mixed liquor from the biological reactors of each WWTP were mixed with wastewater and the mixture was kept aerated for 24 h. Mixed liquor samples were taken at the exit of the biological reactors (TTV) or at the end of the aerated 'react' phase of the SBR cycle (PPT). These biomasses were already acclimated to the wastewaters used in the batch tests, so they were directly used. Mixed liquor (0.5 ℓ) and appropriate wastewater volumes were mixed in order to maintain an F/M of 0.075 g COD/(g VSS.d). Duplicate batch tests were carried out for each sample and experimental condition, in 600 to 2000 ml beakers, aerated through ceramic diffusers. Dissolved oxygen was kept at above 2 mg/l throughout the tests.
Biomass washing
In the tests with previous tap water biomass washing, 0.5 l of mixed liquor from the full-scale plant were settled for 20 min in a 500 ml graduated cylinder. Thereafter the supernatant was decanted and tap water was added to complete the volume to 0.5 l. This process was repeated 2 more times to complete 3 settle-decant-refill operations, which allowed the removal of 99% of the original liquid phase.
Evaluation of method alternatives
The analytical precision of a given method alternative was evaluated through the standard deviation from a pair of sample replicates. First, sample standard deviations were calculated for each pair of replicates. Then, the squares of the maximum and the minimum sample standard deviations were compared in an F-test at 5% significance (Montgomery and Runger, 2003). If they resulted equal, all samples were assumed to have the same analytical variance which was then computed from individual sample standard deviations through the pooled estimator (sP2) (Eq. (12)):

This is a generalisation of the 2-sample pooled estimator in Montgomery and Runger (2003), where si is the analytical standard deviation of sample i, ni is the number of replicates for sample i, N is the number of samples (24 for all methods, except for LSTW, 16), sP is the pooled analytical standard deviation of the method.
If maximum and minimum individual variances were not equal in the above-mentioned F-test, it was concluded that there was not a common s for all samples, and the individual standard deviations lying outside the centred 95% percentile were discarded. Then a pooled s was calculated for the Nh samples sharing a common variance in the upper s range within the centred 95% percentile of standard deviations. These upper ranges included 75% to 100% of all samples. Finally, the analytical precision of a sample result (mean of two replicates) was calculated as Sp/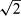 .
.
This analytical precision was applied to all (CODsol)WW and (CODsol)EFF determinations. However, when directly estimating influent SI from (CODsol)EFF in grab samples, precision is not only affected by analytical issues, but by the fuzzy relationship between (CODsol)EFF and influent SI, as discussed next. The following assumptions were applied to all influent SI values when directly estimated from (CODsol)EFF, as in Eq. (1), (3) and (7):
- Population means of influent and effluent SI are equal, as derived from ASM1 and Mamais et al. (1993) method assumptions
- However, it is not possible to precisely associate the CODsol of a given effluent grab sample to a particular influent sample, due to total or partial mixing and time-delays throughout the plant. Consequently, (CODsol)EFF of a grab sample, i.e. influent SI's estimate, should be considered a random variable having the same mean as influent SI, and a variance which can be estimated as the square standard deviation of all (CODsol)EFF values. Consequently, SI precision for grab effluent samples from a WWTP was estimated from the standard deviation of all effluent samples (herein called 'overall standard deviation').
Method comparison was carried out through 3 different approaches:
- Means of all samples by 2 methods were compared through t-tests at 5% significance, with previous investigation of equal/different variances using F-tests for variance comparison at 5% significance
- Means of 2 methods were also compared through paired t-tests (Montgomery and Runger, 2003)
- Regressions of method modifications against a reference method were performed. Equality of methods would be ideally proved through zero y-intercept, unit slope and unit R2 (Miller and Miller, 2005).
The FS alternative was taken as reference method for comparisons.
Variance estimation for linear combinations of variables
When estimated from a simple set of data, variance was estimated as the square standard deviation. When estimating the variance of a linear combination of variables (Eq. (13)), it was computed from the square standard deviations of the individual variables and their sample covariance, through a general equation assuming correlation (Montgomery and Runger, 2003) (Eq. (14)). This was the case in Eqs. (2), (4), (5), (6), (10) and (11), where SI and SS are linear combinations.

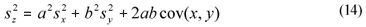
where
x, y and z are variables (e.g., CODsol, SI and SS),
a and b are the coefficients of the linear combination,
sx, sy and sz are the respective standard deviations, and
cov(xy) is the sample covariance of x and y.
Non-correlation was not assumed, so cov(xy) was always computed when using Eq. (14). When effluent SI was involved in these calculations, the overall SI standard deviation was used, while the analytical standard deviation was used for (CODsol)WW.
Limit of detection and limit of quantification for SS
The limit of detection is generally defined as the concentration which gives an instrument signal (y) significantly different from the blank signal. Typically, the sample signal should be greater than the mean blank signal plus three times the blank signal standard deviation, i.e., LOD = yB+3sB (Miller and Miller, 2002). Considering CODsol as the method 'signal', then effluent CODsol (i.e., SI) can be considered a blank for the method, since it nominally corresponds to zero SS, and its 'signal' is subtracted to the influent sample signal ((CODsol)WW) (see Eq. (2) and (4)). So, for an SS value to be detectable, wastewater CODsol should be significantly higher than effluent CODsol. Accordingly, the CODsol corresponding to the limit of detection was computed as the mean SI plus 3 times the standard deviation of SI (Eq. (15):

where:
(CODsol)LOD is the 'signal' corresponding to the limit of detection for SS
is the average SI and s(SI) is the overall standard deviation of SI
The limit of detection for SS was obtained from (CODsol)LOD by substituting this value into the regression equations of CODsol vs. SS (Fig. 6), and then isolating SS.
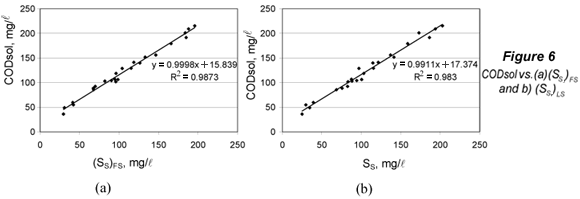
The limit of quantification was considered under a 5s criterion. The 'signal' corresponding to the LOQ was computed (Eq. (16)), and then the LOQ for SS was computed by substituting (CODsol)LOQ into the regression equations in Fig. 6, and then isolating SS.
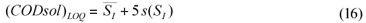
Results and discussion
COD method validation
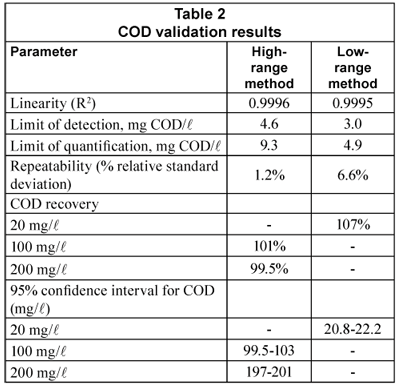
Table 2 displays the results of COD method validation. Linearity was excellent (0.9995 to 0.9996). LOD and LOQ for the low-range method were respectively 3.0 and 4.9 mg/l, below all COD or CODsol values obtained in this study, and well below most of them. LOD and LOQ for the high range method were nominally 4.6 and 7.7 mg/l, though the high range was 80-500 mg/l.
Previous COD regime characterisation
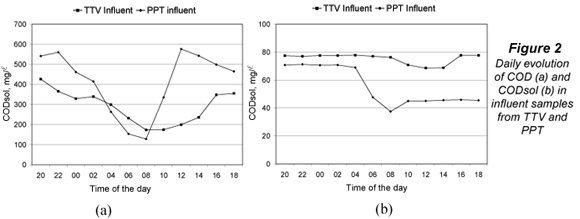
Figure 2 shows the evolution of COD (a) and CODsol (b) in influent samples from TTV and PPT. Both WWTPs presented typical COD daily oscillations, with a sharper COD profile at PTT, which does not have primary treatment and its peak-reduction effect mentioned above. The CODsol curve was also sharper for PPT, while the TTV curve was rather flat, making it difficult to define a high/low CODsol concentration regime. For this reason, time bands of high and low COD concentration were determined, and used to set up the experimental design for the main sampling.
The high concentration intervals were 16:00 to 04:00 (TTV) and 12:00 to 02:00 (PPT), while low-concentration intervals were, respectively, 06:00 to 14:00 and 04:00 to 10:00. Table 3 displays time bands and their COD and CODsol averages. The overall COD and CODsol ranges for all samples in both WWTPs were, respectively, 127 to 577 and 38 to 78 mg/l. The different wastewater origin and concentration ranges ensured considerable wastewater variability for the samples involved in the main sampling, as it was intended.
Results from the main sampling
Table 4 displays raw results from the main sampling at TTV and PPT plants, while Table 5 presents SI and SS obtained by the four method alternatives presented above (FS, LS, LSTW and LSC). These results are discussed below.
Influent CODsol
The influent CODsol had an overall average (both WWTPs) of 123 mg/l, with a range of 36 to 215 mg/l, much wider than in the main sampling. The analytical standard deviation of CODsol ranged 0 to 11.0 mg/l for the set of 24 samples (centred 95% percentile), with a pooled analytical standard deviation of 3.9 mg/l (3.2% RSD), 2.8 mg/l for the mean of 2 samples.
Precision of SI determination by the FS and LS alternatives
The analytical standard deviation of the pairs of replicates of (SI)FS ranged 0.1 to 2.9 mg/l (centred 95% percentile), with a pooled standard deviation of 1.2 mg/l to 0.9 mg/l for the mean of 2 samples – which is excellent. However, the overall standard deviation of SI by the FS method was computed for each WWTP, resulting in 6.7 mg/l at TTV plant (50% RSD), and 5.0 mg/l at PPT plant (29% RSD). These s values were found statistically equal in an F-test, and a pooled overall standard deviation of 5.7 mg/l was used for (SI)FS. These results indicate that a high relative imprecision (36% RSD) was found associated to SI determination as CODsol of the FS plant effluent.
Similar results were obtained for the LS alternative. The analytical precision – standard deviation of (SI)LS in individual samples – ranged 0.3 to 4.0 mg/l, with a pooled standard deviation of 1.6 mg/l to 1.1 mg/l for the mean's standard deviation. The overall standard deviation of estimating SI by the LS method was 6.7 mg/l (46% RSD) and 6.6 mg/l (38% RSD) for, respectively, TTV and PPT. Again, a high relative imprecision was associated to (SI)LS determination as the CODsol of the LS plant effluent. The pooled overall standard deviation for both plants was 6.6 mg/l (40% RSD).
As conclusion, the effluent CODsol of a single grab sample can be determined with a considerable precision (s = 1.2 mg/l). However, when attributing effluent CODsol to an (SI)EFF representing influent SI, the overall variability of effluent CODsol applies, which is much greater, ranging 5.0-6.7 mg/l (29 to 50% RSD) for the two plants and methods herein analysed.
Comparing FS and LS alternatives for SI determination
It would be reasonable that a 24 h HRT laboratory-scale reactor could yield lower effluent CODsol than the FS method, since the hypothesis of zero effluent SS seems more feasible for a 24 h HRT reactor. However, the overall means for the 2 series of 24 results (15.8 and 16.4 mg/l) were compared in a simple t-test for equal variances (verified through an F-test), resulting in statistically equal means. Also, a paired t-test was applied to the two series of SI values, resulting again in equality between the means. It can be conclude that the average (SI)FS and (SI)LS obtained from 24 samples were statistically equal for the set of samples obtained from the two WWTPs.
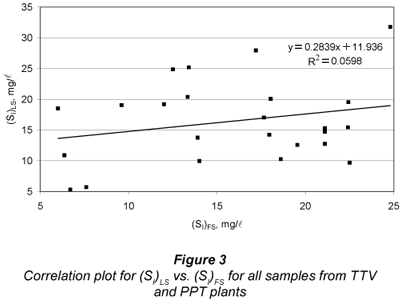
Finally, a correlation study between LS and FS alternatives was carried out for SI by running a linear regression of (SI)LS vs. (SI)FS. Figure 3 displays the correlation results. The determination coefficient was R2=0.0598, pointing to very low correlation between both methods. The y-intercept was quite imprecise and different from zero (11.9 mg/l± 8.4 mg/l), while the slope had large imprecision and was statistically null (0.284 ± 0.498). These results do not meet the conditions for equivalence between two analytical methods (Miller and Miller, 2005). Figure 3 shows great dispersion between (SI)LS and (SI)FS. The difference between both SI estimates distributes almost randomly over a wide range (-10.3 to +12.5 mg/l, 95% centred percentile) for a mean difference of 0.7 mg/l. In conclusion, while the SI averages of a number of samples by both methods were very close and statistically equal, a very poor correlation between (SI)FS and (SI)LS confirms that these methods proved to be non equivalent for individual sample determination. Regarding the hypothesis of (SI)LS being lower than (SI)FS, it was rejected in the t-tests.
SS by FS and LS alternatives
Table 5 displays the results from SS determination by these 2 method alternatives. Similar means (107 and 106 mg/l), ranges (29.6 to 197 and 25.1 to 203 mg/l) and overall standard deviations (50.6 and 50.9 mg/l) were obtained for, respectively, the FS and LS alternatives. Equivalence between both methods is discussed further in this section. First, LOD, LOQ and variance issues of these methods are addressed.
The limits of detection were computed for (SS)FS and (SS)LS. The LOD signal values ((CODsol)LOD) were respectively 33.0 and 36.4 mg/l. In order to calculate the corresponding LOD for SS, plots and regressions of CODsol vs. SS were performed (Fig. 6). The linearity was quite good (R2 of 0.987 and 0.983), so LOD(SS) a was computed from the regression equations in Fig. 6, resulting in 17.2 and 19.2 mg/l, respectively, for (SS)FS and (SS)LS. LOQ were analogously obtained and were 28.6 and 32.6 mg/l, respectively, for (SS)FS and (SS)LS. No sample fell below the limit of quantification for (SS)FS, while 2 samples (8.3%) did fall below that of (SS)LS. However, lower SS can be common in WWTP influents values. In fact, 15% of samples in Mamais et al. (1993) fell below this LOQ for (SS)FS, as well as 8% in Orhon et al. (1997), 17% in Spérandio and Paul (2000) and 57% in Ginestet et al (2002).
Standard deviation of (SS)FS replicates – computed through Eq. (14) – ranged between 5.7 and 17.0 mg/l. A pooled s existed for all (SS)FS (7.5 mg/l, 5.3 mg/l for the mean of 2 replicates). Since SS variance was computed through Eq. (14) the contributions of CODsol and SI variances were analysed, using s2 as variance estimates. (SI)FS accounted for 78% of (SS)FS variance, while CODsol variance represented 21% only. The rest was due to covariance. So, most of (SS)FS uncertainty was attributable to (SI)FS uncertainty. The latter derives from effluent CODsol variability and its fuzzy relationship with influent SI, as pointed above. Similar results were obtained for the LS alternative. Standard deviation of (SS)LS replicates – computed through Eq. (14) – ranged 6.6-15.5 mg/l. A pooled s could be computed (8.1 mg/l, 5.7 mg/l for the mean of two replicates). Since the (SS)LS range was 25.1 to 203 mg/l, RSD ranged, respectively, 22.9-2.8%.
Equivalence between FS and LS alternatives for SS is discussed next, based on the same tests applied to SI methods. An overall t-test for SS mean comparison (for variances found equal) was resulted in statistically equal averages at 5% significance; a paired t-test yielded the same result. So, the two means of 24 samples were statistically equal at 5% significance.
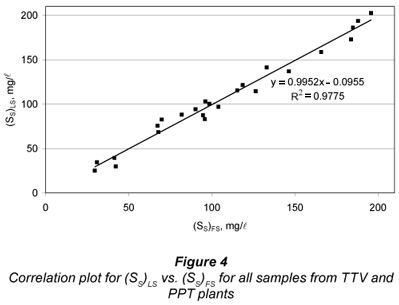
A correlation study between FS and LS alternatives for SS was carried out by running a linear regression of (SS)LS vs. (SS)FS (Fig. 4). A quite good linearity was obtained (R2=0.977), with statistically unit slope (0.995 ± 0.067) and statistically zero y-intercept (-0.01 ± 7.9 mg/l). These results indicate that FS and LS alternatives are equivalent. However, the standard error of estimate was 7.8 mg/l, showing some dispersion between both methods, particularly affecting the lower SS results. This can be mostly attributed to uncertainties in SI determination by both methods, as pointed above.
In conclusion, the main source of uncertainty for SS in FS and LS alternatives was the lack of precision in SI determination, which seriously affected SS determination in the low range. Also, SI imprecision greatly determined LOD and LOQ. In a regression analysis, FS and LS methods for SS proved to be equivalent though some dispersion between both methods was found, attributable to SI imprecision. Regarding the hypothesis of (SI)LS being lower than (SI)FS, it was rejected, since they were found statistically equal.
SI and SS by the LSTW alternative
The results of this section are shown in Tables 4 and 5. (DQOsol)BTE in LSTW alternative was somewhat lower than in the LS alternative. However, when the dilution correction was applied (Eq. (5)), higher (SI)LSTW values were obtained. The (SI)LSTW mean was 32.4 mg/l, vs. 15.8 mg/l the mean of the FS alternative. This difference was statistically significant (t-test at 5% significance). It has been shown that a common batch test (LS) estimated the same mean SI as the FS alternative. Obtaining systematically higher SI values in this modified LS test (LSTW) should be caused by the particular conditions of this method.
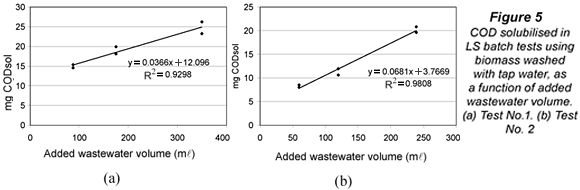
It was hypothesised that submitting biomass to tap water, with usually lower salinity and organic matter concentrations than mixed liquor or wastewater, could provoke some COD solubilisation either by desorption, osmotic processes or, even, biomass lysis. An experiment was used to confirm and eventually quantify solubilisation in the LSTW batch tests. A fixed amount of tap water washed biomass from PPT was mixed with three different volumes of the same influent sample from PPT. The volumes were calculated to keep three food to microorganism (F/M) ratios of 0.025, 0.05 and 0.1 g COD/(g VSS.d), corresponding to 25%, 50% and 100% of the full-scale plant F/M. The mixtures were aerated for 24 h in new LSTW tests, and replicates were run for each F/M ratio. The whole design was repeated on another day. Under no-solubilisation conditions, the final amount of CODsol (mg) in the batch test reactor should be proportional to the volume of wastewater added to the mixture, since CODsol had been removed from biomass by tap water washing. So, a plot of mg CODsol vs. wastewater volume should yield a line with positive slope, good linearity and zero y-intercept.
Figure 5 shows the plots of mg CODsol vs. added wastewater volume at the end of the LSTW batch tests. The lines presented quite good linearity (R2 of 0.930 and 0.981) and positive slope (0.037 and 0.068 mg CODsol/ml). The y-intercepts of the lines in Fig. 5 were statistically non-zero, as verified in t-tests at 5% significance (95% confidence intervals: 12.1 ± 3.2 and 3.8 ± 2.1 mg CODsol). These y-intercepts represent the extrapolation of residual CODsol if no wastewater volume had been added to the reactor. It means this CODsol was not supplied by wastewater, and could only be supplied by the biomass. Though these amounts can seem low or moderate, they are assigned to wastewater volumes between 60 and 350 ml, introducing an average concentration perturbation of +62 mg CODsol/l (ranging from +16 to +138 mg/l). The lower the wastewater volume, the higher the perturbation in CODsol concentration. The amounts of CODsol released per unit biomass were, respectively, 7.5 and 3.2 mg CODsol/g VSS. As a result of COD solubilisation, (SS)LSTW average and range in the main sampling were significantly lower than those of (SS)LS, in accordance with the higher SI obtained by the LSTW method.
In conclusion, the LSTW alternative led to COD solubilisation during the batch LS test, resulting in abnormally high SI values and lower SS estimates. Consequently, this alternative was discarded for SI and SS determination. Washing with a solution having a more controlled salinity and osmotic pressure could be explored as an alternative.
SI and SS by the LSC alternative
Table 5 displays the results for these variables, while Table 4 shows other variables required for calculations, namely means and standard deviations of CODsol, (CODsol)BTE and (CODsol)ML. The mean (SI)LSC was 12.9 mg/l, vs. 15.8 mg/l for the FS alternative. This difference was not significant in a t-test for different variances at 5% significance, neither in an analogous paired t test. However, (SI)LSC vs. (SI)FS presented very poor correlation (R2=0.0027) and a large standard error of estimate (38.8 mg/l), indicating that while the SI means of two sets of 24 samples were equal, individual samples presented large differences between the 2 method alternatives, which should not be considered equivalent.
In addition, 7 samples (29%) presented negative (SI)LSC values, which makes no sense. This can be attributed to a sharp variance amplification through (SI)LSC calculation, see Eq. (10), a linear combination of (SI)BTE and (SI)ML. For the samples studied, the a2 and b2 coefficients in Eq. (14) averaged 16.7 and 9.9, thus introducing a strong variance amplification in (SI)LSC calculation. While the independent variables in Eq. (10) ((SI)BTE and (SI)ML) had sample variances of 44.1 and 72.2 mg2/l2, the sample variance estimated through Eq. (14) for (SI)LSC was 1.465 mg2/l2, resulting in a standard deviation of 38.3 mg/l. This value is in accordance with that obtained from the 24 (SI)LSC values (38.0 mg/l). Since the mean difference between 1st and 2nd terms in the right side of Eq. (10) was just 12.9 mg/l, the probability of (SI)LSC being negative was 37%, assuming a normal distribution with µ=12.9 mg/l and σ=38.3 mg/l. Actually, 29% of samples presented negative (SI)LSC, as pointed out above.
(SS)LSC estimation resulted in high imprecision, with a pooled standard deviation of 38.6 mg/l (27.1 mg/l for the mean of 2 values) which would be unacceptable for at least the lower half of the (SS)LSC range, assuming a maximum acceptable RSD of 20%. Most of (SS)LSC variance (97%) was contributed by (SI)LSC. In conclusion, the LSC alternative did not allow a reliable SI estimation, mostly due to a sharp increase in SI variance, introduced via (SI)LSC calculation through Eq. (10). This resulted in excessively dispersed (SS)LSC values. Consequently, the proposed LSC alternative was discarded.
Importance of SI precision
It has been found that most of the methods' shortcomings derive from the lack of precision in SI determination by either the FS or the LS methods. Improving precision for SI would allow reliable physicochemical measurement of SS below the limits found in this study. This would require an improved calculation of influent SI from effluent CODsol, either by the FS or the LS alternative, taking into account influent and effluent CODsol regimes, as well as mixing conditions inside the WWTP.
Conclusions
A high relative imprecision is associated with determination of un-biodegradable soluble COD by the full-scale and the laboratory-scale variants of the Mamais et al. (1993) method. This is due to the variability of effluent CODsol both in full-scale and laboratory-scale plants, and to the fact that it is not possible to associate a grab effluent sample with a given influent sample, due to complete or partial mixing in the WWTP. FS and LS SI had relatively high standard deviations, and ranges somewhat greater than the mean SI values. When comparing the full-scale and the laboratory-scale variants, (SI)FS and (SI)LS averages were statistically equal at 5% significance. However, the differences between (SI)FS and (SI)LS in individual samples were very wide. In addition, a very poor correlation between (SI)LS and (SI)FS was found, indicating that these methods were not equivalent for the samples in this study.
The LOQ for (SS)FS and (SS)LS were respectively 28.6 mg/l and 32.6 mg/ℓ. Most samples (92%) were above these limits, because their SS were rather high. However, significant fractions of samples fell below this LOQ in some literature studies. Determination of SS by the FS and LS methods had standard deviations of, respectively 5.3 mg/l and 5.7 mg/l, mostly associated with SI determination uncertainty. This affected the precision of SS determination by both methods at low SS values.
On the other hand, good correlation was found between FS and LS alternatives (R2=0.978, zero y-intercept and unit slope), which means equality of the methods. However, a standard error of estimate of 7.6 g/l indicates a moderate dispersion between methods, relatively more important at low SS. The hypothesis of (SI)LS being lower than (SI)FS was rejected, since they were found statistically equal.
Washing biomass with tap water before the laboratory-scale test (LSTW alternative) resulted in significant COD solubilisation from biomass, which tended to overestimate SI and underestimate SS, especially at low F/M ratios. The solubilisation was quantified as a function of F/M, but the mechanism was not determined. Consequently, this method was discarded as a modification for suppressing influent mixed liquor SI interference. Washing with a solution having a more controlled salinity and osmotic pressure could be explored as an alternative.
The LSC alternative did not result in a statistically different average for SI when compared with the original LS method. However, a regression analysis could not conclude equality between both methods. In addition, Eq. (10) used to calculate (SI)LSC introduced a sharp increase in SI variance, resulting in much larger dispersion of results, including some negative, nonsense SI values. Under the conditions of this research, the probability of a sample to have a negative estimated (SI)LSC was 37%. This method was discarded as an alternative for improving SI and SS determination. However, increasing precision of SI determination in mixed liquor and batch test effluent could allow a re-evaluation of this method alternative.
Most of the methods' shortcomings derive from the lack of and precision in SI determination by either the FS or the LS methods. Improving precision for SI could allow more reliable physicochemical measurement of SI below the limit found in this study. It is possible that the assumption of SI conservation, implicit in the ASM1 model and in the Mamais et al. (1993) method, could be a source of uncontrolled error. However, SI generation in the biological reactors is difficult to quantify and would complicate this simple physicochemical method.
Acknowledgements
The authors thank the Comisión Estatal del Agua in San Luis Potosí for authorisations, Grupo Proaqua SA de CV and Degrémont de México SA de CV for plant information and sampling support. Ma. de los Angeles Ortiz Balderas received scholarships from CONACYT (No. 198456) and Santander-Universia. This research was funded through CONACYT Project No. C07-ACIPC-01-08.88, UASLP Projects C06-FAI-03-18.21, C07-FAI-11-33.69; Programa Integral de Fortalecimiento de la UASLP (PIFI 1.0 to 3.4) – Plan de Desarrollo del Cuerpo Académico Tecnología Ambiental 2006 – 2008 (P/CA-116 2006-24-36 and P/CA 116-2007-24-42).
References
DOLD PL, BAGG WK and MARAIS GvR (1986) Measurement of Readily Biodegradable COD Fraction in Municipal Waste Water by Ultrafiltration. UCT Report No. W57. Department of Civil Engineering, University of Cape Town, Rondebosch 7700, South Africa. [ Links ]
EKAMA GA, DOLD PL and MARAIS GvR (1986) Procedures for determining influent COD fractions and the maximum specific growth rate of heterotrophs in activate sludge systems. Water Sci. Technol. 18 (6) 91-114. [ Links ]
EPA (1981) Performance of Activated Sludge Processes: Reliability, Stability, Variability. EPA-6500/2 - 81-227, Washington, D.C. [ Links ]
ESCALAS A, DROGUET M, GUADAYOL JM and CAIXACH J (2003) Estimating DOC regime in a wastewater treatment plant by UV deconvolution. Water Res. 37 (11) 2627-2635. [ Links ]
EURACHEM (1998) Eurachem Guide – The fitness for purpose of analytical methods [on line]. Eurachem Group. URL: http://www.eurachem.org/guides/valid.pdf (Accessed on 8 November 2008). [ Links ]
GINESTET P, MAISONNIER A and SPÉRANDIO M (2002) Wastewater COD characterization: biodegradability of physico-chemical fractions. Water Sci. Technol. 45 (6) 89-97. [ Links ]
HENZE M (1992) Characterization of wastewater for modelling of activated sludge processes. Water Sci. Technol. 25 (6) 1-15. [ Links ]
HENZE M, GUJER W, MINO T and VAN LOOSDRECHT M (eds.) (2000) Activated Sludge Models ASM1, ASM2d and ASM3. Scientific and Technical Report No. 9. IWA Publishing, London. [ Links ]
HU Z, CHANDRAN K, SMETS BF and GRASSO D (2002) Evaluation of a rapid physical-chemical method for the determination of extant soluble COD. Water Res. 36 (3) 617-624. [ Links ]
MAMAIS D, JENKINS D and PITT P (1993) A rapid physical-chemical method for the determination of readily biodegradable soluble COD in municipal wastewater. Water Res. 27 (1) 195-197. [ Links ]
MELCER H (2004) Methods for Wastewater Characterization in Activated Sludge Modeling. WERF Report 99-WWF-3. IWA Publishing – Water Environment Research Federation. 7-9. [ Links ]
MILLER JN and MILLER JC (2005) Statistics and Chemometrics for Analytical Chemistry (5th edn.) Pearson Prentice-Hall, Harlow, UK. 268 pp. [ Links ]
MONTGOMERY DC and RUNGER GC (2003) Applied Statistics and Probability for Engineers (3rd edn.). John Wiley & Sons, New York. 720 pp. [ Links ]
ORHON D, ATES E, SÖZEN S and ÇOKGOR U (1997) Characterization and COD fractionation of domestic wastewaters. Environ. Pollut. 95 (2) 191-204. [ Links ]
SPANJERS H and VANROLLEGHEM P (1995) Respirometry as a tool for rapid characterization of wastewater and activated sludge. Water Sci. Technol. 31 (2) 105-114. [ Links ]
SPÉRANDIO M and PAUL E (2000) Estimation of wastewater biodegradable COD fractions by combining respirometric experiments in various So/Xo ratios. Water Res. 34 (4) 1233-1246. [ Links ]
STANDARD METHODS (1998) Standard Methods for the Examination of Water and Wastewater (20th edn.). American Public Health Association (APHA), American Water Works Association (AWWA), Water Environment Federation (WEF). Washington DC. [ Links ]
WEF-ASCE (1998) Design of municipal wastewater treatment plants. WEF Manual of Practice No. 8. ASCE Manuals and Reports on Engineering Practices No. 76 (Vol. II) Liquid Treatment Processes. WEF, Alexandria, VA, USA, and ASCE, Reston, VA, USA. [ Links ]
WENTZEL MC, MBEWE A, LAKAY MT and EKAMA GA (1999) Batch test for characterisation of the carbonaceous materials in municipal wastewaters. Water SA 25 (3) 327-335. [ Links ]
Received 10 February 2009;
accepted in revised form 14 July 2009.
* To whom all correspondence should be addressed.
+52 (444) 817-3381; fax: +52 (444) 817-3381;
e-mail: antoni.escalas@gmail.com














