Serviços Personalizados
Artigo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em Google
Similares em Google
Compartilhar
Water SA
versão On-line ISSN 1816-7950
versão impressa ISSN 0378-4738
Water SA vol.35 no.3 Pretoria Abr. 2009
Two new methods for the determination of hydraulic fracture apertures in fractured-rock aquifers
Richard Ayuk II Akoachere*; Gerrit van Tonder
Institute for Groundwater Studies, University of the Free State, Bloemfontein 9300, South Africa
ABSTRACT
Fracture apertures play a significant role in groundwater systems. For proper groundwater quantity and contamination management, fractures have to be properly characterised. However, due to their complexity, fracture characterisation is one of the main challenges for hydrogeologists all over the world. This is particularly important in South Africa, where aquifers are predominantly fractured. Two new methods have been developed to determine inclined and horizontal fracture apertures in fractured-rock aquifers. The first is a water-balance method, the slug-tracer (ST) test:
• The slug-tracer (ST) test
[b = (r2 / R2) Δ h]
and the second is a tracer-detection method, comprising the NAPL entry pressure (NEP) test and the NAPL injection pressure (NIP) test:
• The NAPL entry pressure (NEP) test
[b = 1/2Pe (r ρ g h)]
• The NAPL injection pressure (NIP) test
[b = 1/2Pe (ρ g V/ 2 π r)] and [b = 1/4Pe (M g) / m]
These mathematical formulations were developed from laboratory experimentation using transparent Perspex parallel plate physical models and 27 apertures of 0.008 mm to 6 mm, created by using aluminium foil and thickness gauges between 20 mm thick clamped Perspex plates. The ST test uses a slug to which is added NaCl as tracer (50 mg to 300 mg/ℓ). An EC meter is used to detect breakthrough in the observation boreholes.
The NEP test uses an NAPL (sunflower oil) hydraulic head and transducers to determine the entry pressure. Using these mathematical formulae, fracture apertures are then determined for horizontal and inclined apertures. The NIP test uses the entry pressure (by injection), recorded by transducers of an NAPL (sunflower oil) and its volume or mass to determine the fracture aperture for horizontal and inclined fractures. Results from smooth and rough (buffed to 10 x 20 µ) fracture surfaces gave accuracies of 96 to 98% for aperture determinations of 26 apertures from 0.04 to 6 mm.
Keywords: direct measurement of fracture aperture, fractured-rock aquifers
Introduction
All aquifers can be considered to fall on a continuum between porous media systems and conduit systems. In homogeneous porous media aquifers, groundwater flows through gaps between the sand grains (Cook et al., 1996). In heterogeneous porous media aquifers, systematic variation in the size of the sand grains leads to the existence of preferential flow zones. At the other extreme, in purely fractured media groundwater flows only in conduits, and the aquifer matrix between the conduits is impermeable and has no porosity. In fractured porous media water is also stored in the aquifer matrix between the conduits. In some cases the matrix permeability is negligible, although in other cases it can contribute significantly to flow. In reality, most fractured-rock aquifers are of the fractured porous media type. Models of groundwater flow, however, usually assume either homogeneous porous media or purely fractured media. Furthermore, models of groundwater flow in purely fractured systems usually assume that fractures are planar and parallel and many also assume that the fractures are identical. While these assumptions are unlikely to be true in reality, they provide a useful starting point for understanding groundwater behaviour in fractured rocks. Fractured-rock aquifers are comprised of a network of fractures that cut through a rock matrix. Characterisation of fractured-rock aquifers thus requires information on the nature of both the fractures and the rock matrix. Fractures can be characterised in terms of their dimensions (aperture, length, width), their location (orientation, spacing, etc.) and the nature of the fracture walls (e.g., surface roughness). The rock matrix is characterised by its pore size distribution, often expressed in terms of porosity and hydraulic conductivity. The fracture porosity (mf) is defined as the total volume of the aquifer occupied by open fractures. The matrix porosity (m) is the porosity of the rock matrix. In most cases, mf >> m. The total porosity (mt ) is given by: mt = mf + m.
Fractures (or joints) are planes along which stress has caused partial loss of cohesion in the rock. Conventionally, a fracture or joint is defined as a plane where there is hardly any visible movement parallel to the surface of the fracture; otherwise, it is classified as a fault. In practice, however, a precise distinction may be difficult, as at times within one set of fractures some planes may show some displacement whereas others may not exhibit any movement. Fractures can be classified in several ways based on their geometric relationship with bedding or foliation. Strike joints are those that strike parallel to the strike of the bedding or foliation of the rock. In dip joints, the strike direction of joints runs parallel to the dip direction of the rock. Oblique or diagonal joints strike at an angle to the strike of the rock. Bedding joints are parallel to the bedding plane. Further, depending upon the strike trend of fractures with respect to the regional fold axis, fractures are designated as longitudinal (parallel), transverse (perpendicular) or oblique (Singhal and Gupta, 1999).
The relationship between fractures and the stresses that form them are discussed in most structural geology texts. Sheeting joints are generally flat, or somewhat curved and nearly parallel to the topographic surface, and often develop due to release of overburden stress in granitoid rocks. They are closely developed near to the surface and their spacing increases with depth. Columnar joints are generated due to shrinkage in rocks; igneous rocks contract on cooling, whereas mud and silt shrink because of desiccation. As a result, polygonal and columnar joints develop. The columns are often 5- or 6-sided, generally range from a few centimetres to a metre in diameter, and are several metres high. In some cases, fractures become filled with minerals or clay deposits. Where they remain open, however, they can form channels for groundwater flow (Wang and Zhang, 2003). Because frictional forces operate along the fracture walls, the velocity of water moving through a fracture will be greatest toward the middle of the fracture. If the hydraulic gradient is constant, then the mean water velocity through a fracture (averaged over the fracture width) will increase as the distance between the walls increases. The mean velocity will also be greater if the fracture walls are flat and smooth, rather than irregular and rough.
While groundwater flow in fractured porous media occurs mainly through fractures, much of the water contained within these aquifers is stored within the matrix. This has important implications for the movement of contaminants or other dissolved substances. Even if the permeability of the matrix is very low, diffusion will cause mixing of solutes in water flowing through the fractures with those in the relatively immobile water in the rock matrix and pockets of no-flow-through fractures.
In practice, this means that dissolved substances usually appear to travel more slowly than water. Experimental studies have observed that very large particles (relative to water molecules and ions) like glass beads and bacteriophages may travel rapidly (because they move through the fractures and do not readily enter the small pores within the matrix), while smaller solutes (including most ions) move more slowly. For example, in fractured shale near Oak Ridge, Tennessee, velocities of small glass beads have been measured to be up to 200 m/d (McKay et al., 2000). In southern Ontario, Canada, bacteriophages have been observed to travel at 4 m/d, while dissolved bromide travels at only 4 cm/d (McKay et al. , 1993). This movement of solutes between the fractures and the matrix is referred to as matrix diffusion. It causes smaller molecules to appear to move more slowly than larger molecules, depending on their diffusion coefficients.
Early attempts to simulate flow in fractures described them as consisting of 2 parallel plates. The term 'mechanical aperture' is used to describe the aperture of a fracture measured directly using various length determining devices, while hydraulic aperture is the aperture derived from tests using fluid flow properties in fractures. Renshaw (1995) concluded that, for large apertures, hydraulic and mechanical apertures have similar values, but the relationship between the two is non-linear and breaks down for smaller fracture apertures, where fracture apertures approximate the scale of the fracture-surface roughness. Some other authors support the hypothesis that mechanical apertures and hydraulic apertures are not equal (National Research Council, 1996).
A number of authors have attempted to determine fracture apertures using 2 types of fracture aperture determinations:
• Laboratory methods
• Field methods.
Laboratory methods
These include but are not limited to:
• Nuclear magnetic resonance imaging
• Light transmission methods
• Silicon injection (SIN)
• Resin injection (RIN)
• Computer-aided tomography (CAT).
Injecting NAPLs and back-calculating the apertures from the entry pressure required to initiate flow Steele et al. (2006) calculated an aperture distribution for a rough-walled fracture by correlating capillary pressures observed during NAPL injection with local apertures in the fracture plane.
Field methods
There are 2 types of field methods:
• Direct measurements
• Indirect measurements.
Direct measurements
• Fracture spacing – this is the measurement of the distances between fractures using rulers, callipers, sonar devices, etc.
• Fracture orientation – this is the measurement of the characteristic orientation of the fracture plane(dip, strike, etc.).
Indirect measurements
• The mass balance aperture – this is derived from the mean residence time of a tracer, the flow rate, fracture geometry and the tracer test breakthrough (Tsang, 1992)
• Frictional loss aperture – this is determined by expressing the mean residence time of the tracer in terms of the transport velocity
• Hydraulic aperture – measurements of bulk permeability are converted to equivalent hydraulic aperture in slug tests (Hvorslev, 1951; Rutqvist, 1996). This requires assumptions regarding the number of fractures encountered. The mass balance aperture is greater than or equal to the hydraulic aperture, which in turn is greater than or equal to the frictional loss aperture (Tsang, 1992).
In our quest to completely characterise the University of the Free State, (Bloemfontein, South Africa) campus test site, 2 new methods for the direct determination of the fracture apertures in fracture rock aquifers were developed.
The new methods
At the time of writing this report, the 2 methods below were the only direct methods that could be used to determine the apertures of fractures in saturated fracture rock aquifers. The 2 new methods are:
• A water-balance method, i.e. the slug-tracer (ST) test
• A tracer-detection method, i.e. The NAPL entry pressure (NEP) test and the NAPL injection (NIP) test.
Mathematical formulations
The ST-test
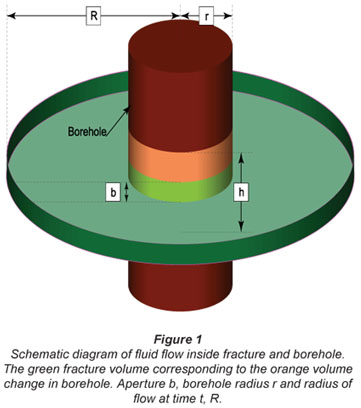
Consider a borehole in a fracture aquifer with a horizontal saturated aquifer. For a cylindrical tube in the borehole of radius r, the volume of fluid in the cylinder of column height h is V.

Consider a cylindrical section of the fracture of radius R, with an aperture b, in the borehole. If the volume of this cylindrical slice of the fracture in the cylindrical section of the fracture above is Vb:

If a slug of fluid is released from the cylinder in the borehole and the fluid flows into the fracture with aperture b, at a certain time t, the fluid will be displaced to the point R, and there will be a change of height Δh of volume Vh in the cylinder in the borehole. At that time t, fluid flowing from the cylinder through the fracture, will reach the point R and there will be a change of height Δh of volume Vh.

At this time t:

where:
b is the fracture aperture
r is the radius of the borehole
R is the distance from the centre of the borehole to the point of observation of flowing liquid from the borehole
Principles
This is based on the principles of:
• Conservation of mass
• Volume transfer.
A fixed cylindrical volume of fluid is transferred and conserved from the cylindrical tube in the borehole on the left to the cylindrical disk to the right in the fracture of thickness b (Fig. 1).
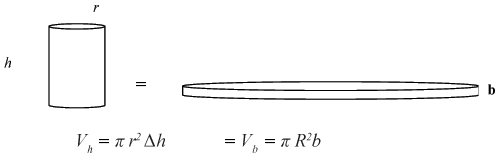
Assumptions
As with other measurements of the hydraulic properties of rock masses that assume radial symmetry, such as pump tests, the slug-tracer test results must be understood in terms of the model used. These tests are carried out with the following assumptions:
• The fracture behaves as a parallel plate
• Flow is radial and divergent
• There is only a single fracture within the test segment
• The fracture and rock mass are rigid and the matrix is impermeable
• The fracture aperture varies along the radius and is radically symmetrical about the borehole
• Advection, dispersion and diffusion are negligible due to the limited time and high velocities at play
• Bulk flow with laminar, turbulent, preferred and non-preferred flow paths as in natural fractures.
Apparatus
• Two packers
• A pump or compressor
• Two transducers
• EC meter
• A segment of perforated cylindrical piping
• An un-perforated cylindrical piping
• A stopper valve
• Water to which we add sodium chloride (slug-tracer). It is advisable to obtain water from the test borehole in order to avoid pollution.
• A borehole camera.
Procedures
Borehole parameters
Measure the observation and test borehole dimensions: diameter, height a.m.s.l., casing height, static water level, depth of the fracture whose aperture is to be measured, distance between test borehole and observation borehole, and the inclination of the fracture to the horizontal.
Slug parameters
Measure the parameters of the slug and apparatus: the amount of tracer (NaCl) in the slug water is determined by considering the background EC value, the dilution rate in the borehole and the detection limit of the EC meter to be used; the diameter of cylinder used to deliver the slug between the packers is D (= 2r); packer distance apart is (L); length of perforated pipe between the packers below static water level; length of un-perforated pipe above the upper packer.
Process
At the sealed lower end of the cylinder, attach the packers with the required spacing to contain the transducer and isolate the fracture between them. Attach the outer transducer above the upper packer. Couple the necessary number of pipes to make up the depth of the borehole. Attach the stopper valve at the section between the un-perforated and the perforated cylinder. Place the inner transducer in the perforated cylinder. Couple the perforated and un-perforated cylinders. Insert the assembly above into the borehole. Fix the assembly solidly to the borehole. Inflate the packers. Allow the packers to equilibrate with the hydrostatic pressure within the borehole, which can be seen from the data logger of the transducer. Using a large open-ended funnel, fill the un-perforated cylinder with the salted water (slug-tracer). Record the water level in the un-perforated cylinder. Note the time, date, place coordinates and test number. Open the flow valve. Record the rate of fall of head versus time of slug-tracer. Simultaneously, at the observation borehole, place the EC meter adjacent to the fracture (on same side as the test borehole) in the borehole. Record the arrival time of tracer, by recording the time at which the EC meter records a sudden surge in value.
The time at which the EC meter records the change corresponds to a time in the test borehole for a certain change in height of slug-tracer (Δh). Using the value of the distance between the test borehole and the observation borehole as R, the radius of the cylinder with the slug-tracer as r, together with Δh and Eq. (5) above, the hydraulic aperture of the fracture is calculated.
The NEP test
The pressure acting on a body is equal to the force over area:

Force is the mass M multiplied by the acceleration a

If the acceleration is due to gravity, then, a = g.
Thus, P = M a / A = M g / A.
The mass of a fluid is the volume of the fluid multiplied by the fluid density. Thus:

This gives:

However, if the volume of fluid in a borehole of radius r and height h is V
V = π r2 h

The area of entry of a fluid into the fracture of a borehole is the circular peel around the radius r of the borehole. If the said fracture has an aperture b, the area A over which the fluid pressure is exerted is that of the circular peel of length L, and width W. L will be equal to the circumference of the borehole around the fracture.
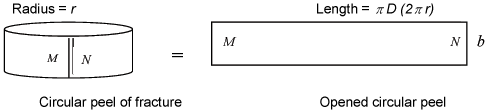
Thus:
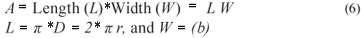

Therefore, P = π r2 h ρ g / 2 π r b
This gives:
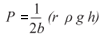
If the pressure P becomes equal to the entry pressure of the non-wetting fluid, then P becomes Pe.

This is the equation for the determination of the mechanical aperture of a fracture in a borehole using the entry pressure of a non-wetting fluid.

Pe is the entry pressure. Pnw is the pressure of the non-wetting fluid (NAPL), measured by transducer at entry into fracture. Pw is the pressure of the wetting fluid and water in the fracture, before the release of NAPL (Pankow and Cherry, 1996)
Apparatus
The apparatus are set up as in Fig. 1, with the exception of the fluid being a NAPL (sunflower oil).
Process
The double packer assembly is set up as in the ST-TEST above, but without filling the cylindrical tube with fluid. The lower valve is removed. Oil is poured into the cylinder by the use of a small tube. The oil level rises as more oil enters the cylinder. At a certain height h, the oil will enter the fracture and this will be recorded by the transducer in the cylinder and the oil level will start falling immediately, entering the fracture.
The value of the entry pressure is obtained from the recorded pressures in the transducer in the packer, and h is obtained from the transducer in the cylinder. Using Eqs. (8) and (9) above the aperture is calculated.
The NIP test
In particular settings, where the fracture is of shallow depth or very small, thus needing higher entry pressures than could be provided by the height of fluid in the cylinder as in the NAPL test above, it is preferable for the oil injection method to be used. Pressure is the force acting over an area.
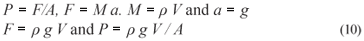
If A = 2 π r b as in (7) above, then P = ρ g V / 2 π r b. Since at entry P = Pe, therefore, Pe = ρ g V / 2 π r b.
From which:

And mass M, M = V ρ, thus:

This is the formula for the determination of the fracture aperture by injection of an NAPL.
Apparatus
The set-up is same as above with the exception that an injector pump is used to pump the oil from the surface into the space between the double packers (Fig. 2).
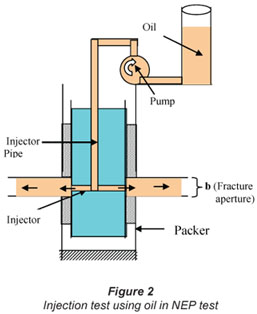
Process
The injector is placed outside the open-ended un-perforated cylinder between the packers. A variable-pressure oil-pump pumps the oil from a container of known volume at a constant rate. The pressure in the inter-packer region will build up until it reaches the breakthrough entry value. The transducer records the entry pressure value. The volume of fluid that has been pumped for the entry pressure is calculated based on the change in volume in the oil reservoir (Fig. 2), or by weighing the container, and the difference in mass of the fluid is converted into volume or used as values in Eq. (12), to determine the fracture aperture.
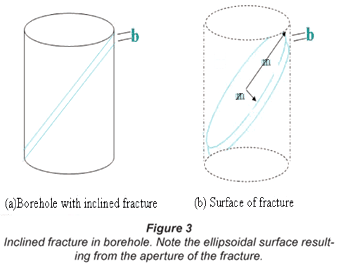
Inclined fractures
Horizontal fractures are common occurrences in fracture aquifers. Sometimes, fractures found in boreholes are inclined. The surface of the fracture in such boreholes is elliptical (Fig. 3). For the perimeter of an ellipse, there is no simple exact formula: There are simple formulas but they are not exact, and there are exact formulas but they are not simple (Jaleigh, 2000). However, there are 2 good approximations by Keppler and Ramajuan (Almkvist and Berndt, 1998) which give us accurate values within the domain in which we are applying the formula. For an ellipse with a minor axis n, and a major axis m, it has been found through laboratory experimentation that if the inclination to the horizontal is less than 45º, the value of the perimeter using Keppler's formula gives accurate values of aperture. While for inclinations of 45º to 89º, the Ramajuan formula gives accurate results.
P = 2 π
(Keppler)
P = 4m (Ramajuan)
Eq. (7) above becomes, A = 2 π 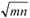 b, and Pe becomes:
b, and Pe becomes:
Pe = π r2 h. ρ g / 2 .b
thus:
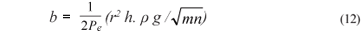
for fractures having inclinations of less than 45º to the horizontal.
or:
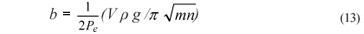
for fractures with inclinations of less than 45º to the horizontal by fluid injection.
While Eq. (7) becomes A = 4 m b and Pe becomes:
Pe = π r2 h. ρ g / 4 m b
thus:
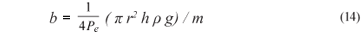
for fractures having inclinations of more than 45º to the horizontal (NEP TEST).
Since V = π r2 h

The mass of fluid during injection is M, M = V ρ, where V is volume and ρ is density of fluid. Eq. (14) becomes:

for fractures with inclinations of more than 45º to the horizontal by fluid injection (NIP test).
A fracture in a borehole with an inclination of 0º (less than 45º), a minor axis r and a major axis r will have a perimeter P. P = 2π 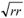 = 2 π r. This is the perimeter of a horizontal circular fracture. The circle is a special form of an ellipse with its major and minor axis equal.
= 2 π r. This is the perimeter of a horizontal circular fracture. The circle is a special form of an ellipse with its major and minor axis equal.
Laboratory experiments
Apparatus
Parallel plate physical models to replicate fractures in fractured-rock aquifers were built using 2 x 20 mm thick Perspex plates sandwiching gauge blades of known thicknesses (Fig. 5). Two such models were constructed: one made of 100 mm diameter circular Perspex plates; (Fig. 6) the other of 100 cm2 Perspex plates (Figs. 7 and 8).





A fracture of known aperture was created by clamping the Perspex plates together and sandwiching thickness gauge blades (Fig. 5). On one of the 2 Perspex plates, a 10 mm bore was drilled and a 10 mm diameter Perspex tube was glued to the Perspex plate to represent the borehole. The whole apparatus now represented a fractured-rock borehole. Using the above-listed method and procedure, the aperture determination experiments were carried out.
The distance between test and observation borehole was taken as the diameter of the circular Perspex plate or the edge of the square plate (R). The radius of the Perspex tube was taken as the radius of the borehole (r). The change in fluid level in the tube was Δh. The time taken for the water to move from the centre of the apparatus to the edge (t) was recorded.
Results
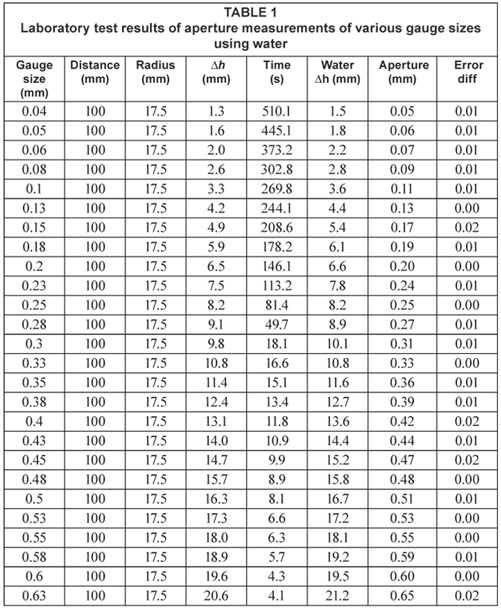
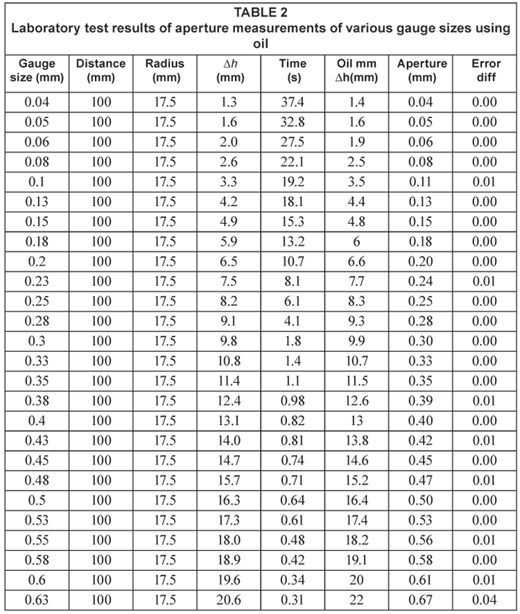
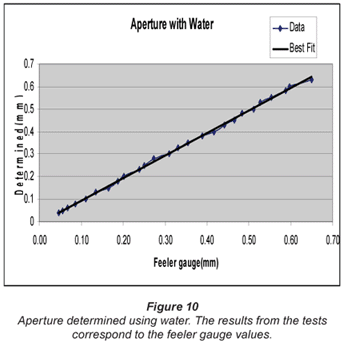
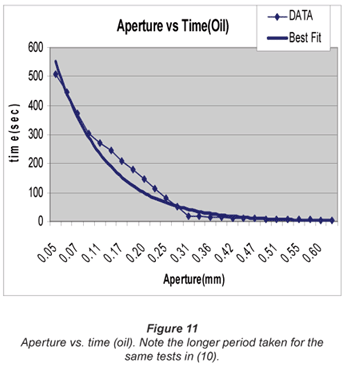
We used experiments carried out in the laboratory on boreholes made from Perspex (smooth- and rough-surfaced; buffed to 10 by 20 µ) to accurately determine 26 fracture apertures between 0.04 mm to 6 mm (Tables 1 and 2, Figs. 9 and 10). The calculated and the actual apertures were the same, with a maximum error difference of 0.02 mm using water and 0.04 mm using oil.

Discussion
Laboratory tests have given accuracy values of 60 to 75% for the determination of 26 apertures between 0.04 mm to 6 mm on parallel plate Perspex fractures for the ST tests (Figs. 8 and 9). Sunflower oil was also used to determine the apertures in the ST test (Figs. 10 and 11). The sunflower oil results were less accurate compared to those of water and it took 13 times more time for the oil to move across the same distance, under the same conditions although the oil is the non-wetting fluid. Temperature affects the use of oil. At temperatures below 8°C the time for the oil tests more than doubled due to the increased viscosity of the oil.
We can represent a fracture as a planar void with 2 flat parallel surfaces, as in our set-up above, to determine fracture flow parameters. The hydraulic conductivity of this fracture Kf is defined as:

where:
2b is the fracture aperture
ρ is the density of water
g is acceleration due to gravity and
µ is the viscosity of water.
The mean groundwater velocity through the fracture, vw, [author please confirm] can be calculated as the product of the fracture hydraulic conductivity and the hydraulic gradient:
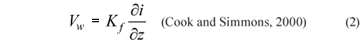
where:
δi / δz is the hydraulic gradient
The transmissivity of an individual fracture is then:
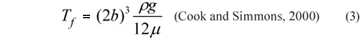
If the aquifer matrix is impermeable, then the transmissivity of any interval of the aquifer is calculated by summing the transmissivities of the fractures within that interval. Where an interval contains only a single fracture, the transmissivity of the interval is simply equal to the transmissivity of that fracture. If the aquifer matrix is impermeable but has significant porosity, then solute transport is affected by matrix diffusion. Suppose that water within a fracture initially has a solute concentration of zero, and we then release a conservative tracer into the fractures, at a concentration that we will denote by Co, and that this release continues over time t. The distance that the tracer will have moved after a given period of time, t, can be expressed:
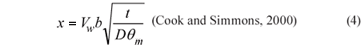
For freshwater at 20°C, β = 1.00 g/cm3, and µ = 1.00 Pa s, and so ρg / µ = 7.4 x 1011 m/d., where Vw is the water velocity within the fractures and D is the effective diffusion coefficient within the matrix. Thus for a water velocity in the fractures of 35 m/d, fracture aperture of 2b = 250 µ, matrix porosity m = 0.05 and diffusion coefficient D = 10-4 m2/yr, the solute will travel 1 386 m in 1 year. This is much less than the travel distance of the water, which is approximately 13 km (Vw m t). Whereas in porous media the distance travelled by a solute is directly proportional to the travel time, the distance travelled through a fracture is proportional to the square root of time. This means that if the solute travels 10 m in the first year, it will travel a further 4 m (and not 10 m) in the following year.
Consider a system of evenly spaced, identical, planar, parallel fractures in an impermeable rock matrix. The hydraulic conductivity of the medium in the direction parallel to the fractures can be expressed:
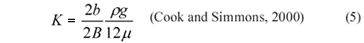
where:
K is fracture permeability in m2 /d
2B is the fracture spacing.
In any other direction the hydraulic conductivity is zero. This equation is sometimes referred to as the cubic law, because of the nature of the dependence of hydraulic conductivity on fracture aperture. A doubling of fracture aperture results in a factor-of-8 increase in hydraulic conductivity. For example, a fractured media with a fracture spacing of 2B = 1 m and fracture aperture of 2b = 250 µ, will have a hydraulic conductivity of approximately 10-5 m/s, similar to that of a coarse sand. It will also have the same hydraulic conductivity as a fractured media with a fracture spacing of 10 cm and fracture aperture of 115 µ. If the rock matrix is impermeable, then solute transport will be characterised by advection through the fractures, with diffusion into the immobile water in the matrix. An understanding of the relationship between water velocities and apparent solute velocities can be gained by considering 2 end-member scenarios. Firstly, suppose that there is no diffusion into the matrix. In this case, the apparent velocity of a tracer is equal to the water velocity through the fractures. On the other hand, suppose that diffusion is very rapid and that fractures are spaced very closely together, so that after a period of time diffusion of solute into the matrix may result in the solute concentration throughout the matrix being identical to the concentration within the fracture (fracture and matrix concentrations have equilibrated). Even though the water is moving only through the fracture, because of this equilibration it will appear as if the solute is moving evenly through the fracture and the matrix. In this case, the apparent tracer velocity is related to the velocity of the water in the fractures, Vw, by the ratio of the total porosity, m, to the fracture porosity, mf. The tracer velocity will be equal to the groundwater flow rate divided by the total porosity. This condition is sometimes referred to as equivalent porous media (EPM) for solute transport, and will occur when Dt/B2 is large (Van der Kamp, 1992; Cook et al., 1996). In between these 2 end-members, the apparent solute velocities will be less than the water velocity in the fractures, but greater than the EPM velocity. Such variation in hydraulic conductivity ranges is largely due to spatial variations in fracture aperture, fracture density, fracture length and fracture connectivity. There has been some discussion about how hydraulic conductivity in fractured-rock aquifers varies with the scale of investigation. Consider a system of evenly spaced, identical fractures. Clearly, at very small scales the hydraulic conductivity varies between that of the matrix, Km, and that of the fractures, Kf. However, when measurements are made at scales much larger than the fracture spacing the variability of hydraulic conductivity will be greatly reduced. At these scales, each measurement will return a value equal to the aquifer hydraulic conductivity. The scale beyond which the hydraulic conductivity approaches a constant value is referred to as the representative elementary volume (REV). However, when fractures are not evenly spaced and identical it is no longer clear that an REV exists. A number of people have argued that the hydraulic conductivity continues to increase as the scale of investigation increases because the probability of intersecting larger fractures increases. The basis of this proposition is that aquifers comprise a large number of very small fractures and a small number of large fractures. However, others have argued that above a certain scale of measurement, permeability begins to decrease with increasing scale, as fracture connectivity is reduced. This proposed decrease in conductivity at large scales is a consequence of fractures having finite lengths. The maximum hydraulic conductivity occurs at the scale that is just great enough for a single large cluster of fractures, that spans the entire network, to form (Renshaw, 1995).
As fracture networks become complex, it is no longer practical to characterise the system properties as the sum of individual fractures. Even for the simple parallel plate model, with identical planar fractures, characterisation of groundwater flow and solute transport requires estimates of fracture orientation, fracture spacing, fracture aperture, matrix porosity and matrix diffusion coefficient. Many of these parameters are difficult to measure accurately.
Because of this difficulty, approaches that aim to measure large-scale properties that integrate the small-scale variability are more likely to be successful than those that aim to characterise the small-scale variation (Cook, 2003). Furthermore, field approaches should focus on measurement of aquifer properties that are most closely related to the properties of interest. For example, if the investigator is interested in knowing the groundwater flow rate it is preferable to use methods that measure groundwater flow directly, rather than infer it from indirect methods (such as measurements of velocity or hydraulic conductivity) other than using estimates from modelling techniques (Cook, 2003). Similarly, if the investigator is interested in predicting the velocity of contaminants, it is preferable to perform tracer tests that measure solute velocities than to attempt to infer solute velocities from measurements of groundwater flow rate. In many cases, approximate direct methods may prove to be more useful than more accurate indirect methods (Cook and Simmons, 2000).
Fracture aperture is one of the most important parameters for the quantification of flow parameters in fractured-rock aquifers. Methods such as those developed above are becoming increasingly important for the characterisation of fractured-rock aquifers. Steele et al. (2006) carried out similar works for smaller fractures between 35 and 400 µ by carrying out traditional slug tests and using the slug test results in numerical simulations to estimate fracture aperture. Here, direct measurements using the new methods described above have been used to quantify the fracture apertures of fractures from 0.04 mm (40 µ) to 63 mm (63 000 µ).
References
ALMKVIST G and BERNDT B (1998) Gauss, Landen, Keppler, Ramajuan, the Arithmetic-Geometric mean, Ellipse, and the Ladies' Diary. The American Mathematical Monthly 95 (7) 585-608. [ Links ]
COOK PG (2003) A guide to regional groundwater flow in fractured rock aquifers. CSIRO, Land and Water, Glen, SA, Australia. 108 pp. [ Links ]
COOK PG and SIMMONS CT (2000) Using environmental tracers to constrain flow parameters in fractured rock aquifers, Clare Valley, South Australia. In: Faybishenko B, Witherspoon PA and Benson SM (eds.) Dynamics of Fluids in Fractured Rock. [ Links ] Geophys. Monogr. 122 337-347. [ Links ]
COOK PG, SOLOMON DK, SANFORD WE, BUSENBERG E, PLUMMER LN and POREDA RJ (1996) Inferring shallow groundwater flow in saprolite and fractured rock using environmental tracers. Water Resour. Res. 32 (6) 1501-1509. [ Links ]
HVORSLEV MJ (1951) Time lag and soil permeability in groundwater observations. Waterways Experiment Station Bulletin No. 36. US Army Corps of Engineers, Vicksburg, MI, USA. [ Links ]
JALEIGH B (2000) What is the formula for the perimeter of an ellipse? URL: http://home.att.net/~numericana/answer/ellipse.html#lu. [ Links ]
MCKAY LD, CHERRY JA, BALES RC, YAHYA MT and GERBA CP (1993) A field example of bacteriophage as tracers of fracture flow. Environ. Sci. Technol. 27 (6) 1075-1079. [ Links ]
MCKAY LD, SANFORD WE and STRONG JM (2000) Field-scale migration of colloidal tracers in a fractured shale saprolite. Ground Water 38 (1) 139-147. [ Links ]
NATIONAL RESEARCH COUNCIL (1996) Rock Fractures and Fluid Flow: Contemporary Understanding and Applications. National Academy Press, Washington, DC. [ Links ]
PANKOW JF and CHERRY JA (1996) Dense Chlorinated Solvents and other DNAPL's in Groundwater; history, behavior, and remediation. Potland, Oreg. Waterloo Press. 522 pp. [ Links ]
RENSHAW CE (1995) The relationship between mechanical and hydraulic apertures in rough-walled fractures. J. Geophys. Res. Solid Earth 100 (B12) 24629-24636. [ Links ]
RUTQVIST J (1996) Hydraulic pulse testing of single fractures in porous and deformable hard rocks. Q. J. Eng. Geol. 29 (2) 181-192. [ Links ]
SINGHAL BBS and GUPTA RP (1999) Applied Hydrogeology of Fractured Rocks. Kluwer, Dordrecht. 400 pp. [ Links ]
STEELE A, REYNOLDS DA, KUEPER BH and LERNER DN (2006) Field determination of mechanical apertures, entry pressure and relative permeability of fractures using NAPL injection. Geotech. 56 (1) 27-38. [ Links ]
TSANG YW (1992) Usage of equivalent apertures for rock fractures, as derived from hydraulic and tracer tests. Water Resour. Res. 28 (5) 1451-1455. [ Links ]
VAN DER KAMP G (1992) Evaluating the effects of fractures on solute transport through fractured clayey aquitards. Proc. 1992 Conf. Int. Assoc. of Hydrogeologists, Canadian National Chapter, Hamilton, Ontario. [ Links ]
WANG J and ZHANG J (2003) Laboratory determination of fracture aperture, permeability and stress relationships. China J. Coal 9 (2) 13-16. [ Links ]
Received 15 September 2008; accepted in revised form 30 March 2009.
Revised version. This paper was originally presented at the Groundwater Conference, 8-10 October 2007, Bloemfontein, South Africa.
* To whom all correspondence should be addressed.
+237 96246613; fax: +237 332 22 72 or +237 343 25 08;
e-mail: rakoachere_ayuk@yahoo.com














