Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
Water SA
versión On-line ISSN 1816-7950
versión impresa ISSN 0378-4738
Water SA vol.35 no.3 Pretoria abr. 2009
Hydrology, sediment transport dynamics and geomorphology of a variable flow river: the Mfolozi River, South Africa
SE GrenfellI, *; WN ElleryII
ISchool of Environmental Science, Memorial Tower Building, Howard College Campus, University of KwaZulu-Natal, Durban 4001, South Africa
IIDepartment of Environmental Science, Rhodes University, PO Box 94, Grahamstown 6140, South Africa
ABSTRACT
The co-efficient of variation for inter-annual streamflow of the Mfolozi River is extremely high at 79%. An analysis of flow frequency indicated that streamflow is skewed towards low-flow values, with a number of extremely large flood events occurring as outliers on the histogram. Streamflow variability in the Mfolozi River may be linked to multiple factors including a large catchment size, a seasonal climate of a dry winter and wet summer, evergreen vegetation in the catchment, variable precipitation and the occurrence of regionally pervasive climatic oscillations. This research aimed to address how streamflow variability impacted upon sediment transport and thus, geomorphology. It was found that sediment transport variability occurred at the intra- and inter-annual scale. Analysis of mean monthly sediment concentration and discharge showed a hysteresis effect, such that sediment concentration peaked prior to discharge in the early wet season. During the late wet season, peak discharges often had unexpectedly low sediment concentrations. Furthermore, data suggested the existence of long-term hysteresis that may be related to decadal-scale climatic oscillations that alter sediment availability and stream capacity, resulting in discharge peaking in 2000 and sediment concentration in 2005. However, more data are required to confirm this relationship. Variability in streamflow appears to share a causal relationship with sediment transport variability, as both are linked to variation in precipitation and the resultant impacts on vegetation growth and evapotranspiration rates. The variability of streamflow and sediment transport has implications for stream and floodplain geomorphology, and the hydrology of variable rivers should be considered when interpreting their geomorphology.
Keywords: flow variability, sediment transport, hysteresis, turbidity
Introduction and regional setting
Streamflow variability
The impact of variable river flows on fluvial geomorphological processes has only received adequate attention in dry-land environments (Tooth, 2000). However, many variable rivers do not fit into the category of dry-land rivers as defined by geomorphologists, even though they may experience similar hydrology in terms of variability. Rivers on the eastern seaboard of southern Africa, exhibiting similar variability to those of Australia, do not experience transmission losses and are not located in areas of low precipitation (e.g. Costelloe et al., 2003). Furthermore, flow is generally perennial. Despite modest precipitation on the eastern seaboard (±1 000 mm/a average), most of the region experiences a negative annual water budget due to the impact of evapotranspiration (Schulze, 1997). Tooth (2000) suggests that dry-land rivers are characterised by few large floods, with intervening low flows for the majority of the water year. This is similar to other authors' descriptions of variable rivers of Southern Africa, described as 'flashy' (Poff et al., 2006). The impact of variable flow hydrology on channel geomorphology has since been cause for much debate. In Tooth's (2000) description of dry-land rivers, large-magnitude floods are the major landscape driver, as low flows lack capacity to do extensive geomorphic work in intervening periods. Contrastingly, Heritage et al. (2001) found that the channel form of the Sabie River, South Africa, is not related to a single channel-forming discharge, but rather to low frequency, large flood events, as well as high frequency, comparatively low-flow events. In some cases, a combination of hydroclimatic trends and the occurrence of channel stabilising riparian vegetation may be important in determining channel shape (Dollar and Rowntree, 1995; Rowntree and Dollar, 1996; 1999).
Using measures of flow variability, this paper investigates how streamflow variability impacts upon sediment transport. Using the Mfolozi River as a case study, a river on the eastern seaboard of Southern Africa, it considers how flow variability may potentially affect floodplain geomorphology and processes.
Dettinger and Diaz (2000) showed that variation in annual precipitation was generally low worldwide, although variability in runoff has repeatedly been shown to be far greater in Southern Africa and Australia than in other continental areas, even when compared to areas of a similar climate (e.g. Puckridge et al., 1998; Dettinger and Diaz, 2000; Peel et al., 2001). Coefficients of variation (CV) for Southern Africa and Australia vary from 75 to 110%, as compared to global norms of between 20 and 45%. Poff et al. (2006), using principle component analysis, found that South African streams were characterised by flashy flows on an inter- and intra-annual scale, noting that streams in South Africa and Australia could be described as globally the most 'extreme'. As a result, Jenkins et al. (2005) refers to these areas as being characterised by 'boom and bust' hydrology and ecology. Variation does appear to follow some degree of cyclicity, such as the link between lower runoffs in the most variable regions during La Niña years and subsequent water years (McMahon and Finlayson, 2003; Puckridge et al., 2003; Dettinger and Diaz, 2000).
CVs of precipitation have been found to correlate only modestly with CVs of runoff (Dettinger and Diaz, 2000). Accordingly, Peel et al. (2001) found that only a small proportion of runoff variability could be accounted for by variability in precipitation. The increase in variability from precipitation to runoff indicates that variability is enhanced during the process of converting precipitation to runoff. The major contributor to flow variability has been attributed to the effects of evapotranspiration (e.g. Poff et al., 2006; Peel et al., 2001). Peel et al. (2001) showed that evapotranspiration was greatly increased in areas that were dominated by evergreen, as opposed to deciduous, trees. In addition, he found that climates with wet summers and dry winters were more conducive to increased runoff variability. Similarly, Dettinger and Diaz (2000) reported that summer precipitation generally contributed less to streamflow than did winter precipitation. A combination of these factors is likely to be the cause of heightened streamflow variability in Australia and Southern Africa. A correlation between catchment size and streamflow variability has also been noted by some authors (Peel et al., 2001; Dettinger and Diaz 2000; Puckridge et al., 1998). Overall, streams with large catchments, that receive most of their rainfall in summer, and that have greater proportions of evergreen trees as opposed to deciduous trees can be expected to experience the greatest amount of variability in streamflow.
The Mfolozi River, KwaZulu-Natal
The catchment of the Mfolozi River drains a 11 068 km2 portion of northern KwaZulu-Natal on the eastern seaboard of Southern Africa. The KwaZulu-Natal region was rejuvenated 20 million years ago (Ma) and 5 Ma when Southern Africa experienced 2 major uplift events that lifted the eastern seaboard by 250 m and 900 m respectively (Partridge and Maud, 1987). As a result, the region is currently in a long-term state of incision, with rivers considered to be relatively steep and fast flowing.
The Mfolozi River comprises two major tributaries, the Black Mfolozi, which arises in the north approximately 1 500 m a.m.s.l., and the more southerly White Mfolozi, which arises at an altitude of 1 620 m. The two rivers converge approximately 50 km west of the Mfolozi River's mouth to the sea. The majority of the catchment is under natural vegetation cover, largely because much of the catchment falls with the Mfolozi-Hhluhluwe Nature Reserve. Sixty percent of the remaining natural vegetation is grassland, with lesser areas of thicket and bush (21%) and natural forest and woodland (15%). Besides natural vegetation, just less than a quarter of the Mfolozi catchment falls under agriculture, the majority of which is small-scale subsistence and commercial forestry, and 13% of the catchment has been classified as degraded through overgrazing or excessive resource use. Less than 1% of the catchment is urban, with the major industrial centres of Mtubatuba, a timber and sugar-cane processing town, in the lower catchment and Vryheid, a coal-mining and quarrying district, in the upper catchment. The floodplain itself is predominantly used for the cultivation of sugar cane (65%), while the remainder falls within the iSimangeliso Park (previously St. Lucia Wetlands Park).
Precipitation is largely restricted to the summer months when approximately 80% of the rainfall occurs, peaking between November and April (Tyson, 1986). Mean annual precipitation in the catchment varies from 1 288 mm at the coastal town of St. Lucia, to 667 mm/a in the Umfolozi Game Reserve in the mid-upper catchment, to 914 mm/a at Nongoma in the upper catchment. Mean annual potential evapotranspiration is generally more than double that of precipitation, with atmospheric demands averaging 1 800 mm/a (Schulze, 1997).
Heavy rainfall is generally associated with easterly low-pressure cells that can remain in the region for up to 10 d (Tyson and Preston-Whyte, 2000). The occasional occurrence of tropical cyclones may lead to extremely high rainfall in the catchment, and therefore long recurrence interval flood events on the Mfolozi River. The most recent such event was that of Cyclone Domoina in 1987, which resulted in a peak discharge of approximately 16 000 m3·s-1, which constitutes approximately 3 times the 100-year return period flood. During the flood, current velocities of 2.6 m·s-1 were measured (Travers, 2006). The main mechanism for winter rainfall is the passage of cold fronts and coastal low-pressure systems. The Mfolozi catchment is thus at the interface of weather-producing systems derived from the south, in the form of mid-latitude cyclones, and weather systems originating towards the north in the tropical easterlies, such as easterly waves and lows, and occasionally tropical cyclones.
Methods
Catchment precipitation and streamflow of the Mfolozi River
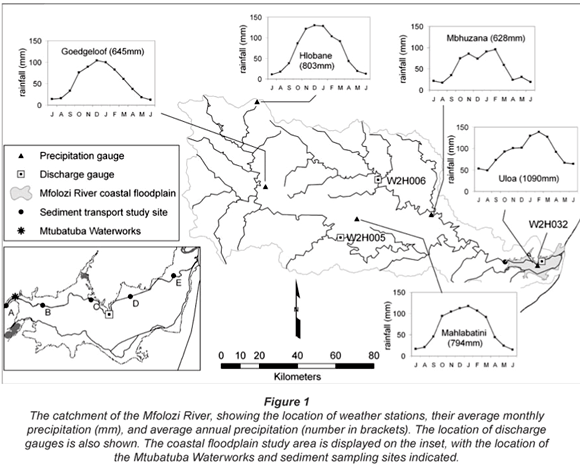
To assess seasonal aspects of rainfall in the catchment, precipitation records from 5 weather stations in the catchment were obtained from the South African Weather Bureau. Stations were located in the upper Black and White Mfolozi River catchments (Hlobane and Goedgeloof, n=89 and n=64 years respectively), in the mid-Black and White Mfolozi River catchments (Mbhuzana and Mahlabatini, n=24 and n=89 years respectively) and below the confluence on the coastal plain (Uloa Agricultural Office, n=75 years) (Fig. 1).
Three streamflow series were obtained from the South African Department of Water Affairs and Forestry for the Mfolozi River. Two of the data sets were of the major tributaries of the Mfolozi River, the Black and the White Mfolozi Rivers. The 3rd flow series was of the Mfolozi River below the confluence of its 2 major tributaries on the lower coastal floodplain (Fig. 1). The tributary flow records were much longer than those available for the Mfolozi gauge located on the lower floodplain, with only 10 years being available for analysis as compared to 40 years at the upper gauges.
The median annual discharge was calculated using all available records from each of the data sets. In addition, a mean annual discharge for each year was calculated in order to allow an inter-annual comparison. A percentage deviation from the long-term median was then calculated for each year in each data set in order to establish long-term variation. The amount of correlation between the gauging stations in terms of percentage deviation was also determined. A frequency analysis of percentage deviation values allowed an investigation into the comparative number and severity of wet and dry discharge years. Since the period of record for the Mfolozi River was short, the analysis was run using data for the Black and White Mfolozi Rivers.
In order to test relationships between rainfall and discharge in different areas of the catchment, correlations between rainfall (percentage deviation from the median of total annual precipitation) and discharge (percentage deviation from the median of annual mean precipitation) were also calculated. The co-efficient of variation (CV = standard deviation/mean x 100) for each of the discharge and rainfall gauge records were computed. In addition, the water budget for the quaternary catchment in which each rainfall gauge was located was calculated from Schulze's (1997) values of mean annual precipitation and potential evaporation.
Sediment transport
Sediment flux was assessed at 5 straight reaches on the lower Mfolozi floodplain between the 6th and 11th of March 2006 (A to E on the inset Fig. 1). Sites were selected such that they were equally spaced and represented areas of different floodplain slope. The same sampling method was used at Site A to E and took approximately 8 h.
Bed-load sediment
Bed load was measured using a Helley-Smith bed-load sampler constructed to the specifications of Emmett (1980) with a weight of approximately 30 kg and a sampling bag with a 0.25 mm mesh size. The weight of the Helley-Smith ensured there was no frictional drag as it was lowered into the water. At Sites A to E, 3 traverses were completed 10m apart to overcome the effect of channel bed-forms (Emmett, 1980; Carey, 1985). Each traverse was divided into 5 subsections and bed-load sampling was conducted at each one. Initially, 4 samples per subsection were collected, but this was subsequently reduced to 3 to ensure that the entire data set was collected within the day and error due to changing discharge could be reduced (e.g. Kleinhans and Ten Brinke, 2001). Unfortunately, this is likely to increase errors associated with flow and transport variability (e.g. Pitlick, 1988; Gaweesh and Van Rijn, 1994; Kleinhans and Ten Brinke, 2001), but was considered to be less important than error incurred through changing discharge. Overall, between 45 and 50 samples were collected at each sample site, exceeding Gomez and Troutman's (1997) recommendation of 40 samples to reduce random and systematic error. Sampling time per sample was between 3 and 4 min, and was measured to the nearest second.
Bed-load samples were dried and weighed. The dry weight of the combined samples at each subsection was used to calculate sediment flux and sediment discharge respectively. While the sampling period was limited to one week, the purpose of sampling bed-load sediment transport was not to calculate a long-term bed-load sediment transport value, but to determine the relative amount of bed-load sediment transported down the length of the river at the different sampling sites. The limited sampling period was considered to be suitable for this requirement. Dried samples were sieved in order to establish particle-size distribution.
Suspended sediment
Suspended load was sampled on the first of the three traverses at each sample site. Samples were taken at each of the 5 subsections at variable depths using an Eijelkamp Watertrap sampler, with a cylindrical volume of 1.22 ℓ. The aim was to sample at 0.5 m depth intervals, but it was sometimes necessary to sample more frequently when the channel was shallower than 1 m. The samples were transported in 2 ℓ plastic bottles for laboratory analysis. Particle-size of 10 of the suspended sediment samples was measured using a Malvern Mastersizer.
Turbidity was measured for each of the 38 samples using a calibrated turbidity meter. The sediment concentration of each sample was calculated by evaporating the sample, and then weighing the remaining sediment. It was assumed that the addition of dissolved solids to the suspended sediment through evaporation was negligible. The suspended sediment concentration was used to calculate overall suspended sediment discharge for each sample site in kg·s-1. These data were of limited use in terms of determining long-term suspended sediment trends as the data set had too few data points for the development of a sediment rating curve (e.g. Horowitz, 2002; Ferguson, 1987). However, sediment rating curves, representing the average relationship between discharge and sediment concentration, are not sensitive to seasonal variations in sediment transport, antecedent conditions and differences in sediment availability (Asselman, 2000), which were the effects under investigation. Furthermore, it seemed likely that strongly seasonal rainfall in the catchment would further increase scatter around the regression line, causing inaccuracy (Ferguson, 1986; Asselman, 2000).
To overcome the problem of developing a long-term understanding of sediment transport, an indirect measure of sediment concentration, the relationship between sediment concentration and turbidity was used (e.g. Walling, 1977). A 6-year record of turbidity, with records maintained every 1 to 2 h every day, was obtained from the Mtubatuba Waterworks located at the head of the floodplain. Sediment concentration for the turbidity record was calculated using the relationship between the known sediment concentration and turbidity of the 38 samples collected in this study. Lenzi et al. (2003) and Riley (1998) noted that using turbidity as a proxy for suspended sediment load could be erroneous if there was large variation in sediment mineralogy and particle size, or if the water contained high amounts of organic matter. However, Walling (1977) suggested using turbidity as a proxy was appropriate when sediment particles were clay- and silt-sized and catchments consisted of relatively homogeneous rock types. Since the R2 value for turbidity and sediment concentration was greater than that of Riley (1998), it was assumed that the error would remain constant, and therefore would not materially affect the study. Gippel (1995) suggested that this is a reasonable assumption, since sudden temporal changes from purely organic to purely mineral loads are rare in nature. Furthermore, Gippel (1995) also argued that the close correlation between sediment concentration and turbidity suggests that particle size variation in streams is either not usually great, or that particle size variations do correspond with changes in sediment concentration. As such, turbidity records were used to calculate mean annual and monthly sediment transport rates.
Depth profile, flow velocity and channel gradient
Along each transect, depth was measured using a weight attached to a measuring tape, while velocity was measured at frequent (every 0.5 m or less) depth intervals using a SEBA-current meter with a 125 mm diameter propeller. Both depth and velocity were measured at 4 to 6 m intervals across the channel such that an accurate cross-section and velocity profile could be drawn. Mean current velocity was calculated using an area-weighted average for each channel cross-section, which was then used to calculate discharge.
Channel gradient was calculated from the sample site's position on a longitudinal profile surveyed in April 2005 using a differential GPS with an on-site base station and roving GPS receiver. Results were accurate to within approximately 1 cm in x, y and z co-ordinates following processing and correction.
Results
Seasonal variation in streamflow
Precipitation in the catchment varies substantially in terms of timing and amount (Fig. 1). Rainfall at Hlobane Station, located in the north on the boundary of the Black and White Mfolozi catchments, and Goedgeloof Station, in the White Mfolozi River catchment, both peak in December. Mahlabatini Station contrastingly experiences a peak during January. Precipitation in the Mbhuzana and Uloa regions occurs as 2 distinct peaks; the 1st (lesser) peak occurs in November, while the 2nd (larger) peak occurs in February.
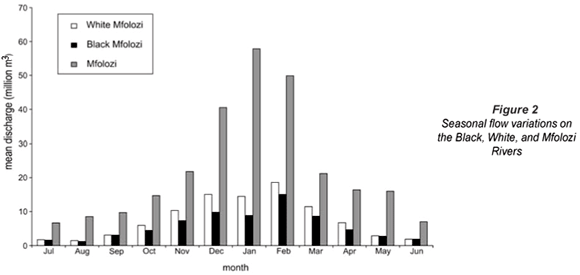
Seasonal discharge patterns of the Black and White Mfolozi Rivers are relatively similar (Fig. 2). Both rivers experience 2 peaks in discharge, one smaller peak in December, followed by a larger peak in February. The White Mfolozi River is larger in discharge than the Black Mfolozi River, and has a larger catchment (see Fig. 1). The Mfolozi River, as measured at the coastal gauge, shows only one distinct peak that occurs in January. There are substantial un-gauged tributary inputs below the two tributary gauges (see Fig. 1). As such, there is often a difference between the combined flows of the Black and White Mfolozi Rivers, and flow of the Mfolozi River. However, in 16% of the months on record, the combined discharges of the Black and White Mfolozi Rivers were found to exceed that measured on the Mfolozi River at the W2H032 gauge, suggesting that in these months discharge decreased downstream.
The relationships between rainfall stations and flow gauges were found to be positively correlated, generally with significance between p=0.01 and p=0.05. The positive correlation between rainfall variation at Mahlabatini and Goedgeloof rainfall stations, and the Mbhuzana and Hlobane Stations was significant at the 99% confidence level. Similarly, the correlation between discharge measured at the Black Mfolozi gauge and rainfall at Mahlabatini was also highly significant (p < 0.01). Discharge on the Mfolozi River and rainfall at the upper Goedgeloof gauge was significant at the 95% confidence level.
Contrastingly, the positive correlation between discharge on the White Mfolozi River and rainfall at Mbhuzana was not significant (p > 0.05). Discharge measured at the Mfolozi gauge was also correlated positively with precipitation at Hlobane, Mahlabatini, Mbhuzana, and Uloa, although this was not significant (p > 0.05).
Inter-annual variation in streamflow
The short duration of the Mfolozi River record made it unsuitable for long-term flow analysis. However, the strong correlation between the Black and Mfolozi Rivers, and the White and Mfolozi Rivers suggests that the long-term pattern is likely to be similar to that of its tributaries. As such, flow measured at the Black and White Mfolozi gauges is used as a proxy for variation of the combined flow. Variation from the median was plotted as a time series for the Black and White Mfolozi Rivers (Fig. 3). The moving average trend lines for each station display a similar pattern to each other. The most notable error in the data is the absence of a very high discharge in 1984 for the White Mfolozi River. However, in that year, a large deviation from the median is obvious on the Black Mfolozi River, the flood which it records damaged the gauge of the White Mfolozi and this result is therefore incorrect. Similarly, damage to both the gauges during a large flood in 1987 has resulted in the deviation from the median in 1987 being underrated.
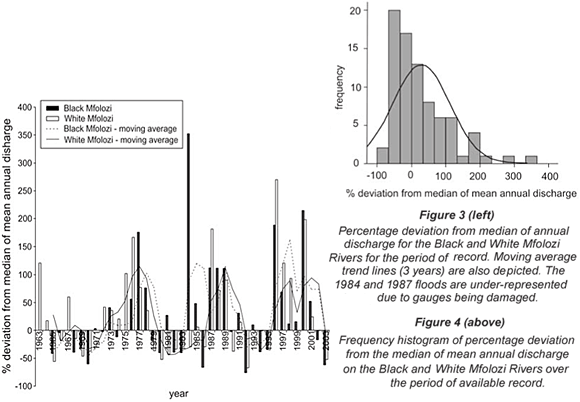
Nevertheless, there are several succeeding periods of dry and wet years represented in the data. Flow is below the median between 1965 and 1971, above the median from 1972 to 1978, and then below the median again between 1979 and 1983. A large flood marked 1984, and 1985 was also characterised by flows greater than the median flow, whereas in 1986 flow was less than the median flow. Two more generalised periods of greater than median flow occurred from 1987 to 1991 and between 1996 and 2001. The intervening period, 1992 to 1995 was a period of relatively low flow, as was 2002 and 2003.
A frequency histogram of percentage deviation from the median of mean annual flow on the Black and White Mfolozi Rivers is shown in Fig. 4. The frequency distribution differs quite strongly from a normal distribution, with a definite negative skewness. Despite the strong skew towards values lower than median, it is the set of positive deviations that have the greatest number of outliers (i.e. at + 250% and above). There are no similar outliers with a negative deviation.
The coefficients of variation for all of the discharge gauge records were high. The Black Mfolozi had the lowest CV at 61%, followed by the White Mfolozi at 69% and the Mfolozi River at 79%.
The Mbhuzana precipitation gauge showed the greatest amount of inter-annual variation, with a CV of 36.6%. This was followed by Mahlabatini (30.8%), Uloa (29.9%), Hlobane (26.6%), and Goedgeloof (22.6%). All the precipitation gauges are located in areas of a negative water budget, whereby atmospheric demand exceeds precipitation. The water budget, calculated for the quaternary catchment of each gauge from Schulze (1997), showed that Mbhuzana had the greatest atmospheric water demand in relation to precipitation, with an annual water deficit of –1 145 mm. This was followed by Goedgeloof (-1 132 mm/a), Mahlabatini (-1 077 mm/a), Hlobane (-1 019 mm/a), and Uloa (-621 mm/a).
Channel morphology and hydrology during low flows
Data collection during a week of March 2006 was found to correspond with the falling limb of a flood wave, as indicated by stage height measurements taken from the Uloa Bridge gauge (Fig. 5). Decreasing stage height corresponds with decreasing discharge measurements taken at various parts of the floodplain over the time period of the study.
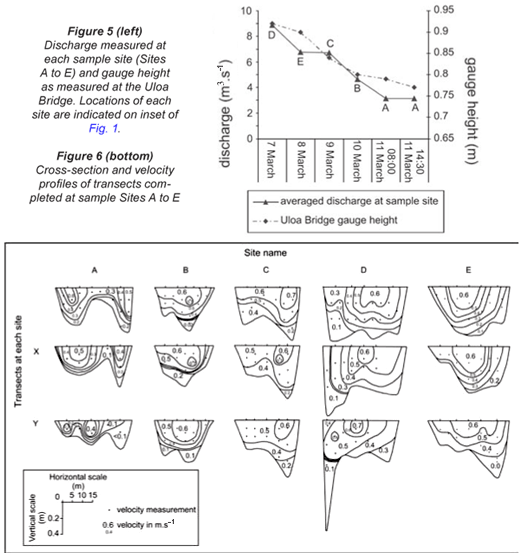
Channel width varied from 29 m at sample Site B to 41 m at Site D (Table 1). Transects B and C were found to have the fastest average flows, with a velocity of greater than 0.5 m2·s-1 at each (Fig. 6).
River gradients for each sample site were calculated from their location on an accurate floodplain longitudinal profile. These gradients therefore represent a regional stream gradient, rather than a localised stream gradient. Sample Site A had the highest stream gradient of 0.06% (Table 1). This was followed by sample Site C at 0.05% and Site B at 0.03%. Sample Sites D and E were located in an area of uniform stream gradient, with a slope of 0.02%.
Bed-load sediment transport
Bed-load discharge per unit width was found to correlate strongly with mean velocity (R2 = 0.9086), displaying a linear relationship when plotted logarithmically. Sediment transport was most closely related to velocity using a power function.
The particle size distribution of bed-load sediment during the period of study was relatively constant, with all transects having an average D50 particle size of medium grained sand, with the average D50 bed-load particle size being 0.35 mm in size. All particle size distributions were unimodal.
Comparisons of bed-load discharge between sample sites was complicated by the falling flood wave over the study period (Fig. 5). Nevertheless, bed-load sediment discharge was greatest at sample Sites B (1.02 kg·s-1) and C (1.08 kg·s-1), where velocities were greatest. Site A had the lowest bed-load sediment discharge, with 0.45 kg·s-1, while Sites D an E had bed-load discharges of 0.82 and 0.84 kg·s-1 respectively.
Suspended sediment transport
The lower Mfolozi River was dominated by suspended sediment loads, with ratios of suspended load to bed load varying from 2.7 and 10 to 1 during the sampling period. The D50 particle size of suspended sediment averaged 0.0052mm (very fine silt). Suspended sediment concentration was most closely related to discharge on a linear scale, with a regression co-efficient value of 0.6473. However, the small number of values on the regression line makes the development of a sediment rating curve invalid, as discussed previously.
Average suspended sediment concentration (kg·m-3) of the 38 samples was most closely related to turbidity (R2 = 0.9567) when a power equation was applied. The power equation, where T equals turbidity (ntu), is:
[suspended sediment] = 0.0093 T 0.674
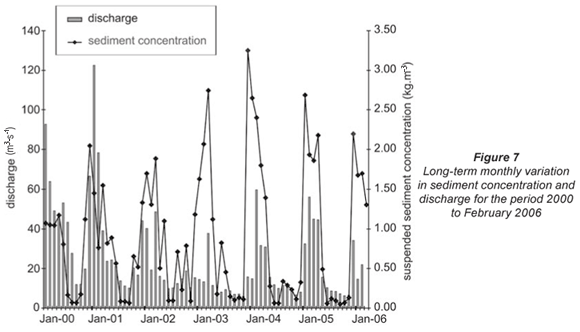
Thus, the turbidity record from the Mtubatuba Waterworks was used to construct a record of suspended sediment concentration. The suspended sediment discharge was then calculated by multiplying the suspended sediment concentration by the discharge. When the relationship between suspended sediment concentration and turbidity was applied to the years of record, it was found that sediment concentration was not significantly correlated to discharge (R2 = 0.2087). Figure 7, indicating variation in sediment concentration and discharge between 2000 and early 2006, further highlights the wide disparity between sediment concentration and discharge. Sediment concentrations were generally highest in 2004, followed by 2003 and 2005. High sediment concentrations were not always coincident with high discharges, as the highest discharges were recorded during 2001.
Discussion
Streamflow hydrology of the Mfolozi River catchment
The Mfolozi River catchment comprises 3 distinct regions characterised by differences in timing of maximum precipitation. In general, rainfall occurs later in the summer season as one moves towards the coast. In the interior, rainfall peaks in December. Towards the central catchment, peak rainfall occurs in January as represented by the Mahlabatini gauge. At the coast, and towards the mid-catchment in the north, peak rainfall occurs in February. The latter regions are also characterised by a lesser precipitation peak in November. There does not appear to be an obvious regional trend in terms of amount of precipitation experienced in the catchment, except that rainfall is highest near the coast.
The January discharge peak of the Mfolozi River is probably related to a combination of high rainfall in the mid-catchment in January and through-flow from December rains feeding into the drainage network. The reasons for the 2 peaks in discharge in the Black and White Mfolozi Rivers are not well understood, although it may be related to base flow from December and January rains in combination with February inputs. Similarly, the lack of correlation between discharge at the Mfolozi gauge, and catchment rainfall is likely an indication of the heterogeneity in rainfall over the catchment.
Discharge assessed on the monthly scale showed that the Mfolozi River was on occasion susceptible to transmission losses downstream, most frequently during summer. Of the transmission losses, 60% occurred during December and January. In 53% of the cases, transmission losses exceeded 30%, while in 26% of the cases, losses exceeded 50%. However, due to the short record of the Mfolozi River, combined with abstraction of water for irrigation on the Mfolozi River floodplain, it is difficult to characterise this as part of the river's hydrology. Nevertheless, the loss may reflect a combination of withdrawal for the cultivation of sugar cane on the floodplain and the effects of evapotranspiration.
Streamflow variability
Precipitation in the Mfolozi River catchment was found to be more variable than many other parts of the globe (e.g. in Dettinger and Diaz, 2000), with coefficients of variation for rainfall in the catchment varying from 36.6% at Mbhuzana to 22.6% at Goedgeloof. These translated to even higher CVs for streamflow, which seem to be related to catchment size, with the smallest catchment of the Black Mfolozi River experiencing the least variation in discharge (61%), and the larger Mfolozi River catchment, showing the greatest variation (79%), a relationship that has also been described by other authors (e.g. Puckridge et al., 1998). In global terms, the CV values can be considered extremely high and indicate highly variable streamflow (e.g. Dettinger and Diaz, 2000).
Peel et al. (2001) found that in addition to increasing basin size, catchments with summer rainfall and dry winters were most susceptible to variable streamflow. Peel et al. (2001) argue that continued evapotranspiration during the dry months results in continual depletion of water supplies. The Mfolozi River catchment is characterised by a range of factors that exacerbate streamflow variability, including high rainfall variability, a large proportion of evergreen vegetation in the catchment, a large catchment, as well as summer rainfall combined with a dry winter.
Dettinger and Diaz (2000) have suggested that variable rivers are characterised by relatively large inter-annual variation, with typically small base flow rates that persist throughout the year. A few, large but brief floods usually determine much of the total annual flow in a given year. This statement holds true for the Mfolozi River, with a high frequency of persistent low flows well below the median. Of particular interest is the occurrence of high positive deviations from the median, which represent sporadically occurring large flood events.
A visual analysis of percentage deviation from the median suggests a discharge cycle in the region of 6 to 7 years, with considerable variation around this figure. This is consistent with what other authors have found regarding variation associated with ENSO (e.g. Pasquini and Depetris, 2007; Zhang et al., 2007). However, more sophisticated analysis, such as that done by Amarasekera et al. (1997) for tropical rivers, is required to confirm whether ENSO could be responsible for some of the discharge variability. McMahon and Finlayson (2003) found that cyclical variability, in the form of quasi-cycles, often resulted in the characteristic persistent sequence of below median flow followed by above median flow in variable rivers.
Character of bed-load sediment transport on the lower floodplain
It was found that variation in bed-load transport could provide a means for the adjustment of stream channel morphology. Since bed-load transport is related to velocity, one might expect the variables of slope, hydraulic radius and roughness, as provided in Manning's equation, to have an indirect impact on the transport of bed-load sediment. In order to determine the influence of each variable in maintaining a particular stream channel shape for a specific discharge; width, average depth and average velocity were plotted against discharge for each of the transects (Fig. 8).
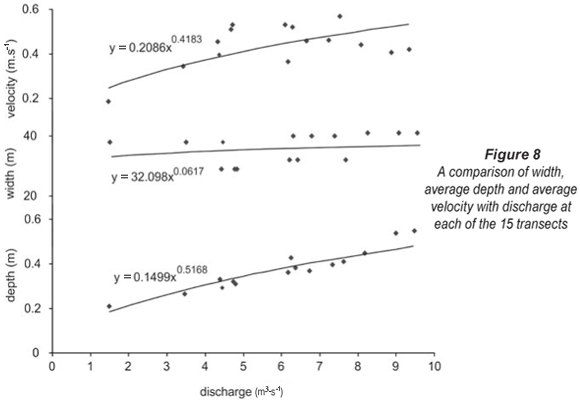
Leopold and Maddock (1953) describe the relationship between these variables and discharge as follows: W=dQª, U=eQb and D=fQc, where W = channel width, U = streamflow velocity, D = depth, Q = discharge, and a, b, c, d, e and f are empirical coefficients. The relative contribution of each variable to discharge is described by the values of a, b and c. The variable that is most capable of altering to accommodate discharge along the study reach was depth (c = 0.5168), followed narrowly by velocity (b = 0.4183) and then width (a = 0.0617). This suggests that differential aggradation and erosion along the streambed, through bed-load sediment transport, is an important mechanism for accommodating discharge. Since bed-load transport is a factor of stream velocity, velocity is the second most important factor in adjusting for discharge.
In contrast to Ellery et al. (2003), stream width is the least important variable in terms of discharge. In Ellery et al.'s (2003) study, constricting vegetation on the channel margin could alter channel width, causing concomitant changes to stream velocity and channel roughness. In this study, width is not easily altered, partly because of the low-flow regime of the Mfolozi River, which decreases the potential time available for erosion or aggradation of the stream banks. As a result, channel depth is the variable that may be altered most easily to accommodate discharge.
Over a long period of time, ongoing local erosion and deposition through differential bed-load transport will have an impact on the floodplain channel slope. The current regime of erosion and deposition along the study reach will, over the long term, lead to the river's longitudinal profile approaching grade (Fig. 9).
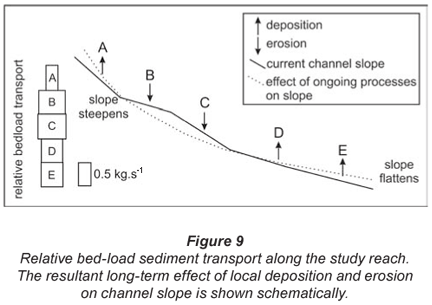
At Sites B and C, bed-load transport increases, indicating erosion of the channel bed. At Sites A, D and E, aggradation is occurring. However, the impact on slope at each site is varied. At Site A, ongoing deposition will cause channel steepening. While at Sites D and E, channel slope will decrease as deposition occurs. Similarly, erosion and enhanced bed-load transport at Site B will cause channel slope steepening, while the channel slope at C will lessen. Erosion at Sites B and C is a classic example of the longitudinal effects of erosion, whereby the lower region becomes flattened, while the upstream region becomes steeper. Locations of erosion and deposition are consistent with geomorphic zones described by Grenfell et al. (2009).
Sediment transport variability
The turbidity-sediment concentration relationship revealed a high degree of variability in sediment transport that was not related to discharge. Using discharge as a predictor of sediment transport would be completely invalid on the Mfolozi River due to high variability in sediment transport at the inter-annual and seasonal scales.
Sediment transport on the Mfolozi River is characterised by an annual hysteresis loop (Fig. 10). Sediment concentration usually peaked prior to peak discharges, with sediment concentrations generally highest in November and December. Thereafter, sediment concentrations generally decreased during the peak discharge months of January and February. Sediment concentrations between January and September were relatively low compared with discharge, with the lowest concentrations experienced during the lowest discharge month, August. Thus, hysteresis results in sediment concentration being greater than one would expect, in comparison to the linear trend line, during the months of October to December. In contrast, the months from January to September usually have lower than average sediment concentrations for their respective monthly discharges.
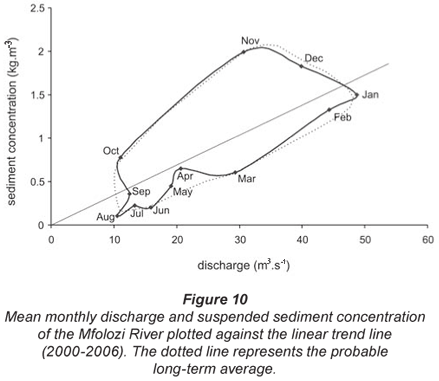
Using the annual hysteresis loop presented in Fig. 10, sediment supply is greatest in the early wet season (from October to December), and thereafter gradually decreases prior to peak discharge being reached in January. Variations in sediment transport can generally be interpreted in 2 ways. Either, the low seasonal discharge of the dry months leads to sediment accumulation in the catchment, or alternatively, decreased vegetation cover during the dry months leads to increased sediment availability. In the 1st scenario, it is exclusively the lack of transport capacity of overland runoff and the Mfolozi River in the dry months that leads to increases in sediment transport at the beginning of the wet season as capacity increases. In the 2nd scenario, it is not that the river gains capacity to transport sediment, but rather that the actual amount of sediment available for transport increases. There is a connection between the 2 scenarios in that sediment may become available during the dry months as vegetation dies back, but cannot be transported to river channels without overland flow from precipitation. Since some months show much higher sediment concentrations than other months with the same discharge, sediment transport capacity of the Mfolozi River cannot be a limiting factor in sediment transport. However, sediment transport capacity during the dry season into stream channels may be lacking. As a result, hysteresis on the Mfolozi River is likely to be caused by a combination of the 2 scenarios. During the dry season, sediment becomes available as vegetation cover decreases. However, movement of available sediment into river channels can only occur at the onset of the rainy season through overland flow. This results in the characteristically high sediment concentrations of the early season, which subsequently drops as the sediment available from the dry season is completely transported. As such, accumulation of available sediment during the dry months is considered in terms of a 'reservoir' by Picouet et al. (2001). Sediment concentrations drop as the 'reservoir' is depleted.
Mean annual suspended sediment concentration was plotted against annual discharge (Fig. 11). In 2000, 1 600 x 106 m3 of water transported 897 581 t of sediment down the course of the Mfolozi River, which approximates 561 t of sediment transported for every million m3 of water. In 2001, total discharge and sediment transport both dropped substantially. However, suspended sediment concentrations were higher and the sediment discharge to water discharge ratio increased from 561.2 in 2001, to 652.8 in 2002. Sediment transport was lowest in 2002, while discharge only reached the lowest value of all years in the following year. In 2003 and thereafter, annual sediment transport gradually increased, despite generally low but increasing discharges on the Mfolozi River. The sediment / discharge ratios in 2004 and 2005 were 1 068.4 and 1 423.1 respectively.
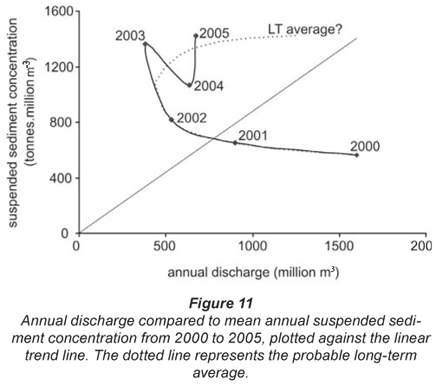
Thus, in addition to the existence of a mean annual hysteresis loop, there is substantial variation in sediment transport on the inter-annual scale. Indeed, it appears that there may be hysteresis effects in the long term (Fig. 11). Unfortunately, additional data would be required to confirm this relationship. Nevertheless, Fig. 11 shows that during 2000 and 2001, annual discharges were greatest, but sediment concentrations were comparatively low. Contrastingly, between 2002 and 2005, sediment concentrations were high relative to annual discharge.
Since it has already been shown that variations in sediment transport on the seasonal scale are related to sediment availability, it follows that inter-annual variation is also related to temporal changes in sediment variability, except on a longer time scale. Tucker and Slingerland (1997) suggest that increases in runoff and decreases in vegetation have a similar impact on drainage basins, with both resulting in sudden increases in sediment supply through expansion of the channel network. As such, many authors assume a relationship between precipitation and vegetative land cover (e.g. Coulthard and Macklin, 2001). In the Mfolozi River catchment, persistent increases and decreases in precipitation would result in changes in vegetation cover. Following a dry period, one would expect sediment concentrations to suddenly increase as sediment accumulated on slopes becomes available for transport by flowing rivers.
Long-term variability in sediment transport may be caused by factors similar to those that cause discharge variability. Firstly, variability in precipitation directly impacts on the amount of sediment that is likely to become available for transport in any year. And secondly, variability in catchment runoff (not streamflow) impacts upon how much sediment is likely to reach a stream channel for transport. Runoff variability is impacted by several factors such as antecedent conditions, vegetation cover, but perhaps most importantly, high evapotranspiration demands that give rise to variability in Southern Africa and Australia as is described by Peel et al. (2001). It therefore seems likely that rivers with variable discharges will be characterised by variability in sediment transport that exceeds variations in discharge.
Sediment yield
In the past, inter- and intra-annual sediment transport variability has not been acknowledged, with the result that suspended sediment loads have been overestimated. Previous estimates of suspended sediment loads were based on catchment size and runoff estimations, rather than direct measurement. Considering our current understanding of the relationship between sediment availability, runoff, discharge and resulting hysteresis, the use of catchment factors and runoff to estimate suspended load is awkward. Lindsay et al. (1996) estimated a suspended sediment transport of 1.24 x 106 t·a-1, which was based on measurements of suspended sediment on 1 d in January. Rooseboom (1975) estimated suspended sediment transport at 2.36 x 106 t·a-1. The current estimation, based on the relationship between turbidity and sediment concentration over a 6-year period is 6.8 x 105 t·a-1. This translates to an average suspended sediment yield of 61 t·km-2·a-1. Thus, Lindsay et al. (1996) and Rooseboom (1975) exceeded the current and most reliable estimate to date by 560 x103 and 1 680 x103 t·a-1 respectively.
In global and Southern African terms, sediment discharge from the Mfolozi River is extremely small, contributing an average 0.68 x 106 t annually. In comparison, the Orange and Zambezi Rivers contribute 17 and 20 x 106 t each year respectively (Milliman and Meade, 1983). However, a comparison of global sediment yields vs. discharge (from Milliman and Meade, 1983) and data for the Mfolozi River does suggest that the sediment yield is relatively high considering discharge. Overall though, it appears that the misconception that sediment transport is not variable over longer time periods, and that the Mfolozi River transports sediment in the same manner as regular rivers, has previously led to overestimations in sediment transport.
Flow and sediment transport variability: implications for fluvial geomorphology
The Mfolozi River, a variable river in terms of hydrology, may be considered variable in terms of sediment transport. As emphasised earlier, variability in sediment transport is unrelated to changes in discharge. Since the causes of sediment variability and streamflow variability are linked, it seems likely that most variable rivers are characterised by sediment transport variability. Sediment transport can be seen as an indication of a river's capacity to do geomorphic work, depending on the definition one adopts. It follows then that variable rivers may not only be characterised by variability in streamflow, but also by variability in terms of geomorphic change.
Flow on the Mfolozi River is usually low and is impounded by high levees on the coastal floodplain. While the actual proportion of the time that the Mfolozi River may have exceeded bank height is unknown due to management of the floodplain for sugar-cane cultivation, it is known that for most of each year, flow in the Mfolozi River is well below the long-term median. Streamflow is characterised by 'normal' low-flow years that are frequently below the long-term median. However, in addition to long periods of low flow, the frequency of discharge distribution also indicates a tail of high-flow outliers. It is these large flood outliers that are likely to mark periods of geomorphic change, for the same reason as in dry-land rivers. Years between large flood events lack the capacity to infill or erode flood-flow features.
The extreme flood event of 1984 on the Mfolozi River may be used to explore what is meant by flood event features. The 1984 floods followed the unusually far southward movement of tropical cyclone Domoina, resulting in discharges greater than 3 times the 100-year flood recurrence interval of the Mfolozi River (Travers, 2006). These flood discharges resulted in the river avulsing towards the south of the floodplain and depositing a lobe of bed-load-derived sediment 3 km wide and 10 km long, and averaging 5 m deep. The flood event has permanently altered the surficial geomorphology of the upper floodplain region, and without human intervention, would have resulted in the development of a new Mfolozi River course. Furthermore, since 1984, the effect of floodplain deposition on surface topography and floodplain dynamics has been minimal. It appears then, that on variable rivers, where sediment transport may also be variable, major geomorphic change occurs in spurts corresponding with 'outlier' flood events. However, the extent of the impact of large floods is not uniform, and is determined by the morphology and characteristics of a particular reach (Heritage et al., 2004; Parsons et al., 2006). Nevertheless, in some systems, geomorphic change in years intervening large flood events may be negligible.
Conclusion
The Mfolozi River may be described as a variable river hydrologically. In addition to this variability, the river is characterised by sediment transport variability on the intra- and inter-annual scale. More data are required to clarify how sediment transport changes in the long term and to confirm whether there is indeed long-term hysteresis on the Mfolozi River. However, as it stands, it can be readily seen that sediment transport variability is not related to changes in discharge. This variability highlights the importance of scepticism in studies that use the sediment rating-curve approach to determine sediment transport regimes on hydrologically variable rivers.
However, the main aim of this paper was to call for recognition of variable rivers as geomorphically distinct from more regular rivers, on the basis of variability in geomorphic work. It was found that suspended sediment transport was supply-limited in the Mfolozi River, and that differential sediment supply was probably related to rainfall seasonality, variability in precipitation and high rates of catchment evaporation. These same factors are responsible for variability in streamflow. More research on the geomorphology of variable rivers, with particular emphasis on process rates, is required.
Acknowledgements
Research costs were funded by the Norwegian Programme for Development, Research and Education. The National Research Foundation funded S Grenfell. The Mtubatuba Waterworks supplied turbidity records that made this study viable, and the Wiggins Waterworks provided access to their turbidimeter. The authors are particularly grateful to Warren Botes and Michael Grenfell for assistance in the field.
References
AMARASEKERA KN, LEE RF, WILLIAMS ER and ELTAHIR EAB (1997) ENSO and the natural variability in the flow of tropical rivers. J. Hydrol. 200 24-39. [ Links ]
ASSELMAN NEM (2000) Fitting and interpretation of sediment rating curves. J. Hydrol. 234 228-248. [ Links ]
CAREY WP (1985) Variability in measured bedload-transport rates. Water Resour. Bull. 21 (1) 39-48. [ Links ]
COSTELLOE JF, GRAYSON RB, ARGENT RM and McMAHON TA (2003) Modelling the flow regime of an arid zone floodplain river, Diamantina River, Australia. Environ. Modell. Software 18 693-703. [ Links ]
COULTHARD TJ and MACKLIN MG (2001) How sensitive are river systems to climate and land-use changes? A model-based evaluation. J. Quat. Sci. 16 (4) 347-351. [ Links ]
DETTINGER MD and DIAZ HF (2000) Global characteristics of stream flow seasonality and variability. J. Hydromet. 1 289-310. [ Links ]
DOLLAR ESJ and ROWNTREE KM (1995) Hydroclimatic trends, sediment sources and geomorphic response in the Bell River catchment, Eastern Cape Drakensberg, South Africa. S. Afr. Geogr. J. 77 (1) 21-32. [ Links ]
ELLERY WN, McCARTHY TS and SMITH ND (2003) Vegetation, hydrology, and sedimentation patterns on the major distributary system of the Okavango Fan, Botswana. Wetlands 23 (2) 357-375. [ Links ]
EMMETT WW (1980) A field calibration of the sediment trapping characteristics of the Helley-Smith Bedload sampler. USGS Professional Paper 1139, Washington. 44 pp. [ Links ]
FERGUSON RI (1986) River loads underestimated by rating curves. Water Resour. Res. 22 (1) 74-76. [ Links ]
FERGUSON RI (1987) Accuracy and precision of methods for estimating river loads. Earth Surf. Proc. Land. 12 95-104. [ Links ]
GAWEESH MTK and VAN RIJN LC (1994) Bedload sampling in sand-bed rivers. J. Hydraul. Eng. 120 (12) 1364-1384. [ Links ]
GIPPEL CJ (1995) Potential of turbidity monitoring for measuring the transport of suspended solids in streams. Hydrol. Proc. 9 (1) 83-97. [ Links ]
GRENFELL SE, ELLERY WN and GRENFELL MC (2009) Geomorphology and dynamics of the Mfolozi River floodplain, KwaZulu-Natal, South Africa. Geomorphol. doi:10.1016/j.geomorph.2008.12.011. [ Links ]
GOMEZ B and TROUTMAN BM (1997) Evaluation of process errors in bedload sampling using a dune model. Water Resour. Res. 33 (10) 2287-2398. [ Links ]
HERITAGE GL, BROADHURST LJ and BIRKHEAD AL (2001) The influence of contemporary flow regime on the geomorphology of the Sabie River, South Africa. Geomorphol. 38 197-211. [ Links ]
HERITAGE GL, LARGE ARG, MOON BP and JEWITT G (2004) Channel hydraulics and geomorphic effects of an extreme flood event on the Sabie River, South Africa. Catena 58 151-181. [ Links ]
HOROWITZ AJ (2002) The use of rating (transport) curves to predict suspended sediment concentration: a matter of temporal resolution. Turbidity and other Sediment Surrogates Workshop. April 30-May 2, Reno NV. [ Links ]
JENKINS KM, BOULTON AJ and RYDER DS (2005) A common parched future? Research and management of Australian arid-zone floodplain wetlands. Hydrobiol. 552 57-73. [ Links ]
KLEINHANS MG and TEN BRINKE WBM (2001) Accuracy of cross-channel sampled sediment transport in large sand-gravel bed rivers. J. Hydraul. Eng. 127 (4) 258-269. [ Links ]
LENZI MA, MAO L and COMITI F (2003) Interannual variation of suspended load and sediment yield in an alpine catchment. Hydrol. Sci. 48 (6) 899-915. [ Links ]
LEOPOLD LB and MADDOCK T (1953) The hydraulic geometry of stream channels and some physiographic implications. United States Geological Survey Professional Paper 252, Washington. 56 pp. [ Links ]
LINDSAY P, MASON TR, PILLAY S and WRIGHT CI (1996). Suspended particulate matter and dynamics of the Mfolozi estuary, Kwazulu-Natal: Implications for environmental management. Environ. Geol. 28 (1) 40-51. [ Links ]
McMAHON TA and FINLAYSON BL (2003) Droughts and anti-droughts: the low flow hydrology of Australian rivers. Freshwater Biol. 48 (7) 1147. [ Links ]
MILLIMAN JD and MEADE RH (1983) World-wide delivery of river sediment to the oceans. J. Geol. 91 (1) 1-21. [ Links ]
PARSONS M, McLOUGHLIN CA, ROUNTREE MW, ROGERS KH (2006) The biotic and abiotic legacy of a large infrequent flood disturbance in the Sabie River, South Africa. River Res. App. 22 187-201. [ Links ]
PARTRIDGE TC and MAUD RR (1987) Geomorphic evolution of Southern Africa since the Mesozoic. S. Afr. J. Geol. 90 179-208. [ Links ]
PASQUINI AI and DEPETRIS PJ (2007) Discharge trends and flow dynamics of South American rivers draining the southern Atlantic seaboard: An overview. J. Hydrol. 333 385-399. [ Links ]
PEEL MC, MCMAHON TA, FINLAYSON BL and WATSON FGR (2001) Identification and explanation of continental differences in the variability of annual runoff. J. Hydrol. 250 224-240. [ Links ]
PICOUET C, HINGRAY B and OLIVRY JC (2001) Empirical and conceptual modeling of the suspended sediment dynamics on a large tropical African river: the Upper Niger River basin. J. Hydrol. 250 19-39. [ Links ]
PITLICK J (1988) Variability of bed load measurement. Water Resour. Res. 24 173-177. [ Links ]
POFF NL, OLDEN JD, PEPIN DM and BLEDSOE BP (2006) Placing local stream flow variability in geographic and geomorphic contexts. River Res. App. 22 149-166. [ Links ]
PUCKRIDGE JT, SHELDON F, WALKER KF and BOULTON AJ (1998) Flow variability and the ecology of arid zone rivers. Mar. Freshwater Res. 49 55-72. [ Links ]
PUCKRIDGE JT, WALKER KF and COSTELLOE JF (2000) Hydrological persistence and the ecology of dryland rivers. Regul. Rivers: Res. Manage. 16 385-402. [ Links ]
RILEY SJ (1998) The sediment concentration-turbidity relation: its value in monitoring at Ranger Uranium Mine, Northern Territory, Australia. Catena 32 (1) 1-14. [ Links ]
ROOSEBOOM A (1975) Sedimentproduksiekaart vir Suid-Afrika. Technical Report No.61, Department of Water Affairs, Pretoria, South Africa. [ Links ]
ROWNTREE KM and DOLLAR ESJ (1996) Controls on channel form and channel change in the Bell River, Eastern Cape, South Africa. S. Afr. Geogr. J. 78 (1) 20-28. [ Links ]
ROWNTREE KM and DOLLAR ESJ. (1999). Vegetation controls on channel stability in the Bell River, Eastern Cape, South Africa. Earth Surf. Proc. Land. 24 127-134. [ Links ]
SCHULZE RE (1997) South African Atlas of Agrohydrology & Climatology. WRC Report No TT 82/96. Water Research Commission, Pretoria, South Africa. [ Links ]
TOOTH S (2000) Process, form and change in dryland rivers: a review of recent research. Earth-Sci. Reviews 51 67-107. [ Links ]
TRAVERS R (2006) The Mfolozi River rail bridge. Civ. Eng. SAICE 14 (3) 22-28. [ Links ]
TUCKER GE and SLINGERLAND R (1997) Drainage basin responses to climate change. Water Resour. Res. 33 (8) 2031-2047. [ Links ]
TYSON PD (1986) Climatic Change and Variability in Southern Africa. Oxford University Press, Cape Town. 220 pp. [ Links ]
TYSON PD and PRESTON-WHYTE RA (2000) The Weather and Climate of Southern Africa (2nd edn.) Oxford University Press, Cape Town. 395 pp. [ Links ]
WALLING DE (1977) Assessing the accuracy of suspended sediment rating curves for a small basin. Water Resour. Res. 13 (1) 531-538. [ Links ]
ZHANG Q, XU C, JIANG T and WU Y (2007) Possible influence of ENSO on annual maximum streamflow of the Yangtze River, China. J. Hydrol. 333 265-274. [ Links ]
Received 18 August 2008; accepted in revised form 21 January 2009.
* To whom all correspondence should be addressed.
Address at the time of submission: Geography Department, Rhodes
University, PO Box 94, Grahamstown 6140, South Africa.
e-mail: se.grenfell@gmail.com














